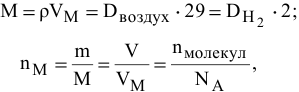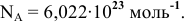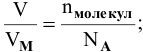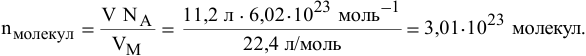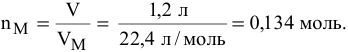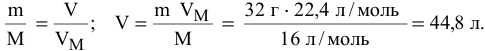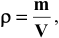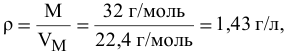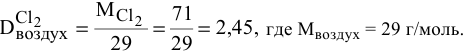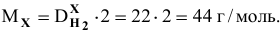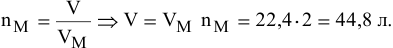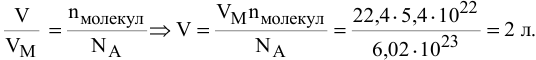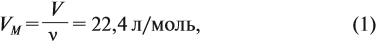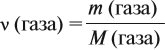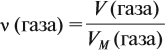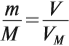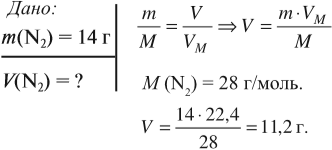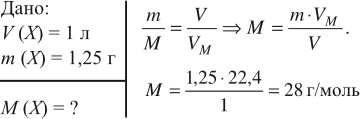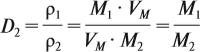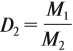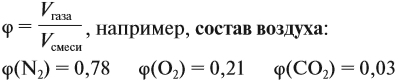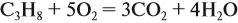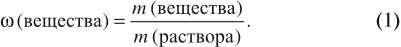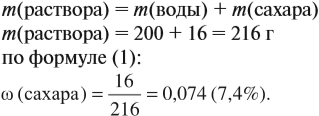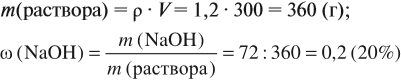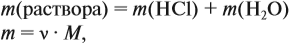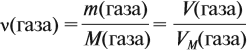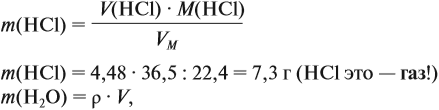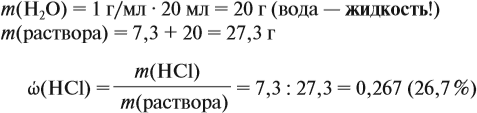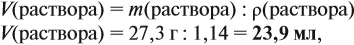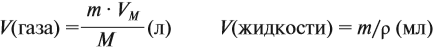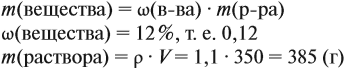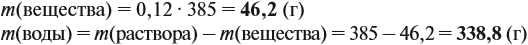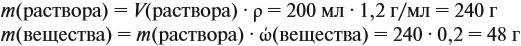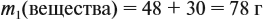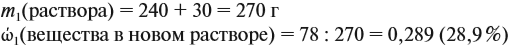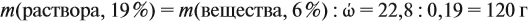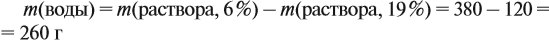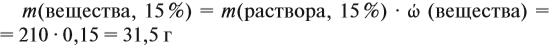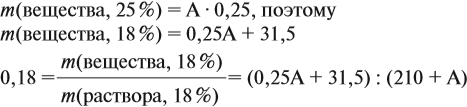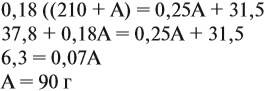Как найти относительную массу неизвестного газа

В этой статье мы коснемся нескольких краеугольных понятий в химии, без которых совершенно невозможно
решение задач. Старайтесь понять смысл физических величин, чтобы усвоить эту тему.

Я постараюсь приводить как можно больше примеров по ходу этой статьи, в ходе изучения вы увидите множество примеров
по данной теме.

Относительная атомная масса – A_r

Представляет собой массу атома, выраженную в атомных единицах массы. Относительные атомные массы указаны в периодической
таблице Д.И. Менделеева. Так, один атом водорода имеет атомную массу = 1, кислород = 16, кальций = 40.

Относительная молекулярная масса – M_r

Относительная молекулярная масса складывается из суммы относительных атомных масс всех атомов, входящих в состав вещества.
В качестве примера найдем относительные молекулярные массы кислорода, воды, перманганата калия и медного купороса:

M_r (O₂) = (2 × A_r(O)) = 2 × 16 = 32

M_r (H₂O) = (2 × A_r(H)) + A_r(O) = (2 × 1) + 16 = 18

M_r (KMnO₄) = A_r(K) + A_r(Mn) + (4 × A_r(O)) = 39 + 55 + (4 * 16) = 158

M_r (CuSO₄*5H₂O) = A_r(Cu) + A_r(S) + (4 × A_r(O)) + (5 × ((A_r(H) × 2) +
A_r(O))) = 64 + 32 + (4 × 16) + (5 × ((1 × 2) + 16)) = 160 + 5 * 18 = 250

Моль и число Авогадро

Моль – единица количества вещества (в системе единиц СИ), определяемая как количество вещества, содержащее столько же структурных единиц
этого вещества (молекул, атомов, ионов) сколько содержится в 12 г изотопа ¹²C, т.е. 6 × 10²³.

Число Авогадро (постоянная Авогадро, N_A) – число частиц (молекул, атомов, ионов) содержащихся в одном моле любого вещества.

Больше всего мне хотелось бы, чтобы вы поняли физический смысл изученных понятий. Моль – международная единица количества вещества, которая
показывает, сколько атомов, молекул или ионов содержится в определенной массе или конкретном объеме вещества. Один моль любого вещества
содержит 6.02 × 10²³ атомов/молекул/ионов – вот самое важное, что сейчас нужно понять.

Иногда в задачах бывает дано число Авогадро, и от вас требуется найти, какое вам дали количество вещества (моль). Количество вещества в химии
обозначается N, ν (по греч. читается “ню”).

Рассчитаем по формуле: ν = N/N_A количество вещества 3.01 × 10²³ молекул воды и 12.04 × 10²³ атомов углерода.

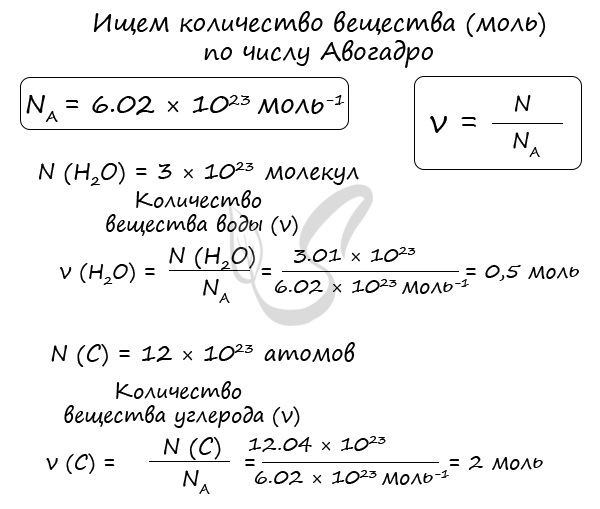
Мы нашли количества вещества (моль) воды и углерода. Сейчас это может показаться очень абстрактным, но, иногда не зная, как найти
количество вещества, используя число Авогадро, решение задачи по химии становится невозможным.

Молярная масса – M

Молярная масса – масса одного моля вещества, выражается в “г/моль” (грамм/моль). Численно совпадает с изученной нами ранее
относительной молекулярной массой.

Рассчитаем молярные массы CaCO₃, HCl и N₂

M (CaCO₃) = A_r(Ca) + A_r(C) + (3 × A_r(O)) = 40 + 12 + (3 × 16) = 100 г/моль

M (HCl) = A_r(H) + A_r(Cl) = 1 + 35.5 = 36.5 г/моль

M (N₂) = A_r(N) × 2 = 14 × 2 = 28 г/моль

Полученные знания не должны быть отрывочны, из них следует создать цельную систему. Обратите внимание: только что мы рассчитали
молярные массы – массы одного моля вещества. Вспомните про число Авогадро.

Получается, что, несмотря на одинаковое число молекул в 1 моле (1 моль любого вещества содержит 6.02 × 10²³ молекул),
молекулярные массы отличаются. Так, 6.02 × 10²³ молекул N₂ весят 28 грамм, а такое же количество молекул
HCl – 36.5 грамм.

Это связано с тем, что, хоть количество молекул одинаково – 6.02 × 10²³, в их состав входят разные атомы, поэтому и
массы получаются разные.

Часто в задачах бывает дана масса, а от вас требуется рассчитать количество вещества, чтобы перейти к другому веществу в реакции.
Сейчас мы определим количество вещества (моль) 70 грамм N₂, 50 грамм CaCO₃, 109.5 грамм HCl. Их молярные
массы были найдены нам уже чуть раньше, что ускорит ход решения.

ν (CaCO₃) = m(CaCO₃) : M(CaCO₃) = 50 г. : 100 г/моль = 0.5 моль

ν (HCl) = m(HCl) : M(HCl) = 109.5 г. : 36.5 г/моль = 3 моль

Иногда в задачах может быть дано число молекул, а вам требуется рассчитать массу, которую они занимают. Здесь нужно использовать
количество вещества (моль) как посредника, который поможет решить поставленную задачу.

Предположим нам дали 15.05 × 10²³ молекул азота, 3.01 × 10²³ молекул CaCO₃ и 18.06 × 10²³ молекул
HCl. Требуется найти массу, которую составляет указанное число молекул. Мы несколько изменим известную формулу, которая поможет нам связать
моль и число Авогадро.

Теперь вы всесторонне посвящены в тему. Надеюсь, что вы поняли, как связаны молярная масса, число Авогадро и количество вещества.
Практика – лучший учитель. Найдите самостоятельно подобные значения для оставшихся CaCO₃ и HCl.

Молярный объем

Молярный объем – объем, занимаемый одним молем вещества. Примерно одинаков для всех газов при стандартной температуре
и давлении составляет 22.4 л/моль. Он обозначается как – V_M.

Подключим к нашей системе еще одно понятие. Предлагаю найти количество вещества, количество молекул и массу газа объемом
33.6 литра. Поскольку показательно молярного объема при н.у. – константа (22.4 л/моль), то совершенно неважно, какой газ мы
возьмем: хлор, азот или сероводород.

Запомните, что 1 моль любого газа занимает объем 22.4 литра. Итак, приступим к решению задачи. Поскольку какой-то газ
все же надо выбрать, выберем хлор – Cl₂.

Моль (количество вещества) – самое гибкое из всех понятий в химии. Количество вещества позволяет вам перейти и к
числу Авогадро, и к массе, и к объему. Если вы усвоили это, то главная задача данной статьи – выполнена 🙂

Относительная плотность и газы – D

Относительной плотностью газа называют отношение молярных масс (плотностей) двух газов. Она показывает, во сколько раз одно вещество
легче/тяжелее другого. D = M (1 вещества) / M (2 вещества).

В задачах бывает дано неизвестное вещество, однако известна его плотность по водороду, азоту, кислороду или
воздуху. Для того чтобы найти молярную массу вещества, следует умножить значение плотности на молярную массу
газа, по которому дана плотность.

Запомните, что молярная масса воздуха = 29 г/моль. Лучше объяснить, что такое плотность и с чем ее едят на примере.
Нам нужно найти молярную массу неизвестного вещества, плотность которого по воздуху 2.5

Предлагаю самостоятельно решить следующую задачку (ниже вы найдете решение): “Плотность неизвестного вещества по
кислороду 3.5, найдите молярную массу неизвестного вещества”

Относительная плотность и водный раствор – ρ

Пишу об этом из-за исключительной важности в решении
сложных задач, высокого уровня, где особенно часто упоминается плотность. Обозначается греческой буквой ρ.

Плотность является отражением зависимости массы от вещества, равна отношению массы вещества к единице его объема. Единицы
измерения плотности: г/мл, г/см³, кг/м³ и т.д.

Для примера решим задачку. Объем серной кислоты составляет 200 мл, плотность 1.34 г/мл. Найдите массу раствора. Чтобы не
запутаться в единицах измерения поступайте с ними как с самыми обычными числами: сокращайте при делении и умножении – так
вы точно не запутаетесь.

Иногда перед вами может стоять обратная задача, когда известна масса раствора, плотность и вы должны найти объем. Опять-таки,
если вы будете следовать моему правилу и относится к обозначенным условным единицам “как к числам”, то не запутаетесь.

В ходе ваших действий “грамм” и “грамм” должны сократиться, а значит, в таком случае мы будем делить массу на плотность. В противном случае
вы бы получили граммы в квадрате 🙂

К примеру, даны масса раствора HCl – 150 грамм и плотность 1.76 г/мл. Нужно найти объем раствора.

Массовая доля – ω

Массовой долей называют отношение массы растворенного вещества к массе раствора. Важно заметить, что в понятие раствора входит
как растворитель, так и само растворенное вещество.

Массовая доля вычисляется по формуле ω (вещества) = m (вещества) / m (раствора). Полученное число будет показывать массовую долю
в долях от единицы, если хотите получить в процентах – его нужно умножить на 100%. Продемонстрирую это на примере.

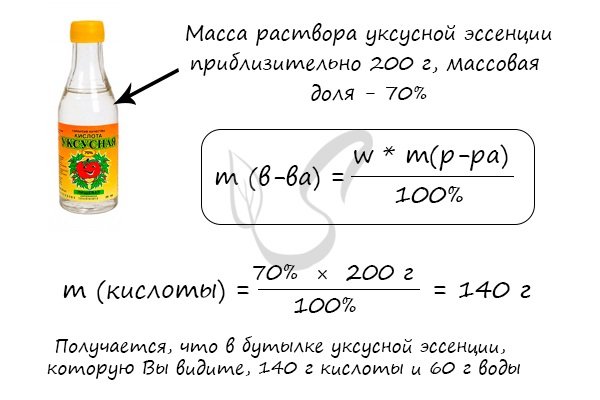
Решим несколько иную задачу и найдем массу чистой уксусной кислоты в широко известной уксусной эссенции.

Расчеты по газовым законам (нормальныеусловия)

Для осуществления любого расчета по газовым законам для нормальных условий используются следующие формулы:

где М — молярная масса, г/моль;

— плотность газа, г/л;

. ~ относительные плотности по воздуху и по водороду;

— число молей газа;

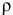
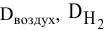
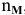
m — масса газа, г;

V — объем газа, л;

— молярный объем, = 22,414 л/моль;

— число молекул газа;

— число Авогадро,

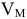
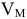
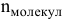
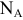
Используя эти две формулы, можно рассчитать, например:

• число молекул, содержащихся в определенном объеме газа;
• число молей, содержащихся в определенном объеме газа;
• объем, занимаемый определенной массой газа;
• массу определенного объема газа;
• плотность и относительную плотность газа по молярной массе газа;
• молярную массу неизвестного газа на основе плотности или относительной плотности.

Пример 16

Найти число молекул 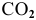, содержащихся в 11,2 л углекислого газа (н.у.).
Решение:

Пример 17

Определить число молей 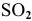, содержащихся в 3 л сернистого газа (и.у.).

Решение:

Пример 18

Найти объем, занимаемый 32 г 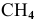(н.у.).

Решение:

Пример 19

Определить массу одного литра кислорода (н.у.).

Решение: 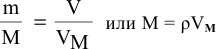, так как масса одного литра, по определению, — это плотность,

т.е. масса одного литра газа m = 1,43 г.

Пример 20

Найти относительную плотность хлора по воздуху.

Решение:

Пример 21

Найти молярную массу неизвестного газа, если относительная плотность его по водороду равна 22.

Решение:

Пример 22

Определить объем, занимаемый 2 моль углекислого газа (н.у.).

Решение:

Пример 23

Определить объем, занимаемый 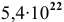молекулами кислорода (н.у.).

Решение:

Эти задачи взяты со страницы решения задач по неорганической химии:

Задачи с решением по неорганической химии

Возможно эти страницы вам будут полезны:

В ходе решения таких задач рекомендуется придерживаться алгоритма:

• внимательно прочитать условие задачи и выяснить, что у вас спрашивают;
• написать соответствующую формулу и проанализировать её;
• найти числовые значения требуемых величин, каждый раз записывая вначале формулу, а затем расчёт, учитывая размерность величин.

Задачи по теме «Газы»

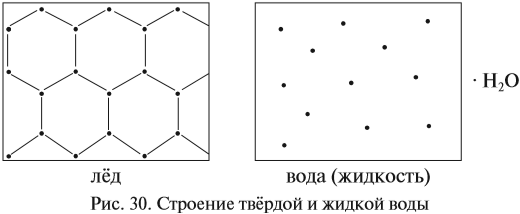
Известно, что вещества при нормальных условиях (н. у.) могут находиться в трёх агрегатных состояниях: твёрдом, жидком, газообразном. В твёрдом и жидком состояниях между молекулами (атомами) вещества имеются довольно сильные взаимодействия, в результате чего частицы находятся на небольших расстояниях друг от друга (рис. 30).

В газах расстояния между частицами очень велики, и силы взаимодействия ничтожны (рис. 31).

Поэтому равные объёмы любых газов содержат одинаковое число молекул. Это формулировка закона АВОГАДРО.

Следствием этого закона является:

1 моль любого газа при нормальных условиях (н. у.) занимает объём 22,4 литра.

Эта величина (22,4 л/моль) является молярным объёмом газа (V_М):

где V_M — молярный объём газа, моль/л; V — объём газа, л; ν — количество вещества газа, моль.

Таким образом, зная массу газа, можно определить:

Но для того же газа из формулы (1) имеем:

Отсюда для любого газа выполняется соотношение:

Задача 3. Какую массу имеет кислород объёмом 7 л?

Задача 4. Какой объём занимает азот массой 14 г?

Задача 5. Чему равна молярная масса газа, 1 л которого имеет массу 1,25 г?

Ответ. Молярная масса неизвестного газа 28 г/моль.

Пользуясь этими формулами, можно рассчитать объём, массу, молярную массу газа, например:

Известно, что

где ρ — плотность газа (г/л), поэтому:

ПОМНИТЕ! Эти формулы можно использовать лишь тогда, когда данные задачи (плотность газа, его объём) измерены при н. у.: 273 К, 1 атм.

Из формулы (3) вытекает понятие об относительной плотности газов (D_x). Эта величина, равная отношению плотностей двух газов:

где ρ₁ и М₁ — плотность и молярная масса одного газа, а ρ₂ и М₂ — плотность и молярная масса другого газа.

Относительная плотность газа показывает, во сколько раз данный газ тяжелее второго газа. Пользуясь этой формулой, можно легко определить молярную массу данного газа:

Выполняя такие расчёты, следует помнить, что:

• любая смесь газов, например воздух, именуется в задачах словом «газ»;
• средняя молярная масса воздуха, как показывают расчёты, равна 29 г/моль;
• по умолчанию, если не сказано иного, расчёты ведут для н. у.: 273 К, 1 атм.

Задача 6. Определить молярную массу газа, если:

а) плотность его равна 1,25 г/л;
б) плотность его по кислороду равна 0,75.

Решение.

Состав смеси газов, как правило, измеряют в объёмных процентах φ (фи).

Второе следствие, при помощи которого была экспериментально подтверждена гипотеза Авогадро (гипотеза стала законом уже после смерти автора!), заключается в следующем: объемы реагирующих газов относятся как их коэффициенты в соответствующем уравнении реакции.

Это следствие позволяет решать задачи «в уме», если известны объёмы реагирующих газов или количества вещества для них.

Задача 7. Какой объём кислорода потребуется для сжигания 6 л пропана?

Из уравнения реакции:

видно, что молярное соотношение пропана и кислорода составляет 1 : 5. Таким образом, объём кислорода в пять раз больше объёма пропана.

Ответ. Требуется 5 · 6 = 30 л кислорода.

Задачи для самостоятельного решения

3. Определить массы газов:

а) хлороводорода, объёмом 56 л;
б) озона О₃, объёмом 14 л.

4. Определить объёмы газов:

а) хлороводорода, массой 72 г;
б) аммиака NH₃, массой 3,4 г.

5. Определить молярные массы газов, если:

а) 2 л газа имеет массу 2,86 г;
б) 10 г газа занимает объём 7,47 л.

6. Определить молярную массу газа, если:

а) плотность его равна 1,52 г/л;
б) плотность по кислороду равна 1,81.

7. Какой объем занимает смесь, состоящая из 4 г метана и 22 г пропана?

8. Какой газ имеет большую массу: этан, объёмом 56 л или бутан, объёмом 44,8 л?

9. Существуют ли газообразные соединения серы легче воздуха?

10. Определите, не выполняя расчёт, какой из газов тяжелее воздуха: Не, Ar, CO₂, CH₄, N₂, O₂.

Задачи по теме «Способы выражения концентрации растворов»

Для того чтобы определить массовую долю растворенного вещества, нужно воспользоваться формулой:

Ответ может быть дан в долях (единицы): ω = 0,15; или в процентах: ω% = 15 %.

Задача 8. В 200 г воды растворили 16 г сахара. Определить ω(сахара) в полученном растворе.

Решение. В данном случае масса раствора неизвестна. Но:

Задача 9. В 300 мл раствора (ρ = 1,2 г/мл) содержится 72 г NаОН. Определить ω(NаОН) в этом растворе.

Решение. В этом случае масса раствора неизвестна, но известен объём. Найдём массу раствора:

Задача 10. В 20 мл воды растворили 4,48 л хлороводорода. Определить ω(НСl) в соляной кислоте. Плотность раствора равна 1,14 г/мл.

Решение. При растворении хлороводорода в воде получена соляная кислота, её масса равна:

где ν — количество вещества, моль; M — молярная масса вещества, причём для газов

откуда

где ρ — плотность воды (1 г/мл); V — объём воды, мл

Обратите внимание: в 20 мл воды растворили 4,48 л газа, но суммарный объём отнюдь не равен (4,48 + 0,02), т. е. 4,5 литра! Суммарный объём этого раствора равен:

т. е. при растворении более 4 литров газа объём жидкого раствора увеличился менее чем на 4 миллилитра!

Выводы.

1. Объёмы жидкостей и объёмы растворяемых газов суммировать нельзя.
2. При растворении в жидкости газы сжимаются более чем в 1000 раз.
3. Объёмы жидкостей и газов рассчитывают (исходя из значения массы) по-разному:

где m — масса, г; М — молярная масса, г/моль; V — объём (жидкости в мл, газа — в л); ρ — плотность жидкости, г/мл.

Пользуясь формулой (1) нетрудно рассчитать и массу раствора, и массу растворённого вещества. Но при этом следует учитывать, что обычно в задачах говорится (упоминается) о «5 %-ном растворе», «16 %-ном растворе» и т. д., т. е. массовая доля вещества выражена в процентах. В этом случае легко видеть, что:

• в 5 %-ном растворе ω(вещества) = 0,05;
• в 16 %-ном растворе ω(вещества)= 0,16 и т. д.

Зная массовую долю вещества в растворе, можно определить:

Задача 11. Сколько граммов соли и воды нужно взять для приготовления 350 мл (ρ = 1,1 г/мл) 12 %-ного раствора?

Решение. Из формулы (1) получаем формулу (2):

где ρ — плотность раствора (1,1 г/мл); V — объём раствора (350 мл), тогда

Задача 12. Сколько граммов 8 %-ного раствора можно приготовить, имея 64 г NaCl?

Решение. Из формулы (3):

Такие задачи можно решать, составляя пропорции. При этом следует знать, что массовая доля (в %) вещества показывает, сколько граммов вещества содержится (растворено) в 100 граммах раствора: 5 %-ный раствор ⇒ 5 г вещества в 100 граммах раствора.

Задача 13. Сколько мл 15 %-ного раствора (ρ = 1,1 г/мл) можно приготовить из 22,5 г вещества?

Обратите внимание: в пропорции в одном столбце должны совпадать и размерность, и наименование компонента, о котором идёт речь.

Задача 14. К 200 мл 20 %-ного раствора (ρ = 1,2 г/мл) добавили 30 г того же вещества. Определить массовую долю вещества в полученном растворе.

Решение. Определим в начале массу исходного раствора и растворённого вещества:

При добавлении новых порций растворяемого вещества, его масса увеличивается:

На ту же величину увеличивается масса раствора:

Задача 15. Сколько граммов 19 %-ного раствора и воды нужно взять для получения 380 г 6 %-ного раствора?

Решение. При добавлении воды масса растворённого вещества не меняется. Поэтому рассчитаем массу растворённого вещества в 6 %-ном растворе (столько же его будет и в 19 %-ном растворе):

Теперь можно рассчитать массу 19 %-ного раствора:

Теперь задумаемся: почему возросла масса исходного 19 %-ного раствора? Потому, что добавили воду. Значит, масса воды равна:

Ответ. Нужно добавить 260 г воды.

В случаях, когда изменяется и масса раствора, и масса вещества, нужно прибегнуть к приёму, когда неизвестная величина (о ней спрашивается в вопросе задачи), принимается за известную, и обозначается А.

Задача 16. Сколько граммов 25 %-ного раствора нужно добавить к 210 г 15 %-ного раствора, чтобы получить 18 %-ный раствор?

Решение. Пусть нужно добавить А граммов 25 %-ного раствора, тогда масса 18 %-ного раствора составит (210 + А) г. Определим массу вещества в 15 %-ном растворе:

аналогично:

Решим полученное уравнение:

Ответ. Нужно добавить 90 г 25 %-ного раствора.

Задачи для самостоятельного решения

11. В 300 г раствора содержится 45 г поваренной соли. Определить ω (NaСl) в этом растворе.

12. В 300 мл воды растворили 100 г сахара. Определить ω (сахара) в полученном растворе.

13. В 2 л раствора (пл. = 1,05 г/мл) содержится 105 г соли. Определить ω(соли) в этом растворе.

14. В 200 мл воды растворили 56 л аммиака NH₃. Определить ω (NH₃) в этом растворе.

15. Бромоводород объёмом 5,4 л затрачен на приготовление 8 %-ного раствора (пл. = 1,057 г/мл). Найти объём полученного раствора.

16. Сколько граммов воды и сахара нужно взять для приготовления 3 литров 30 %-ного сиропа? (Пл. = 1,13 г/мл.)

17. Какой объём 25 %-ного раствора можно приготовить из 150 г соли, если плотность раствора равна 1,2 г/мл?

18. К 500 мл 32 %-ной кислоты (ρ = 1,2 г/мл) добавили 1 л воды. Вычислить массовую долю кислоты в полученном растворе.

19. Смешали 25 г 16 %-ного раствора КОН с 30 мл 20 %-ного раствора КОН (плотность 1,2 г/мл). Вычислить массовую долю щёлочи в полученном растворе.

20. К 220 г 20 %-ного раствора поваренной соли добавили 44 мл воды и 36 г этой же соли. Вычислить массовую долю соли в полученном растворе.

21. Определить массу воды, которую нужно выпарить из 1 кг 3 %-ного раствора сульфата меди II для получения 5 %-ного раствора.

22. Сколько граммов воды нужно добавить к 50 г 70 %-ной уксусной кислоты, чтобы получить 5 %-ный уксус?

23. После добавления соды к 200 мл 16 %-ного раствора её (ρ = 1,17 г/мл) массовая доля вещества возросла до 20 %. Определить массу добавленной соды.

24. Какой объём 96 %-ной кислоты (ρ = 1,86 г/мл) необходимо добавить к 5 л 30 %-ной кислоты (ρ = 1,3 г/мл), для того чтобы получить 40 %-ный раствор?

Как вам известно, вещества могут находиться в твёрдом, жидком и газообразном состоянии. Молекулы жидкости и твёрдого вещества располагаются близко друг к другу. Это возможно благодаря тому, что молекулы притягиваются друг к другу. То есть существуют силы, которые удерживают молекулы жидкости или твёрдого вещества вместе. Из курса химии 8-го класса вы знаете, что эти силы называются силами межмолекулярного взаимодействия. Молекулы газов находятся на значительно большем расстоянии друг от друга, чем в случае жидкостей и твёрдых веществ. На таком расстоянии молекулы практически не взаимодействуют друг с другом. Поэтому, чтобы превратить жидкость или твёрдое вещество в газ, необходимо преодолеть силы межмолекулярного взаимодействия, отдалив молекулы друг от друга.

Переход в газообразное состояние осуществляется в результате нагревания веществ, находящихся в твёрдом или жидком состоянии (кипение жидкостей, возгонка твёрдых веществ).

Так как расстояние между молекулами газов значительно больше размеров самих молекул, то объём, который занимает газ, — это, по существу, объём свободного пространства между хаотически движущимися молекулами газа. Величина этого пространства определяется условиями, при которых находится газ, т. е. температурой и давлением. Эта величина примерно одинакова для всех газов. При этом объёмом, занимаемым самими молекулами, можно пренебречь. Отсюда следует закон Авогадро — в равных объёмах различных газов при одинаковых условиях содержится одинаковое число молекул.

Из закона Авогадро вытекают два основных следствия.

Первое следствие. Один моль любого газа при одинаковых условиях занимает одинаковый объём. Этот объём называется молярным объёмом газа (V_m), и измеряется в дм³/моль. Молярный объём газа равен отношению объёма газа к его количеству:

.

Величина V_m зависит от температуры и давления. Например, при нагревании газы расширяются. Значит, при нагревании увеличивается молярный объём газа. В связи с этим сравнение характеристик различных газовых смесей необходимо осуществлять при одинаковых условиях — температуре и давлении. В качестве эталона таких условий приняты нормальные условия (н. у.): температура таяния льда (0 °С или 273,15 K) и атмосферное давление (101,3 кПа). При нормальных условиях V_m = 22,4 дм³/моль.

Таким образом, из закона Авогадро следует, что 22,4 дм³ любого газа при нормальных условиях содержат 6,02 ∙ 10²³ молекул.

Второе следствие. Плотности газов относятся между собой как молярные массы газов.

Это видно из следующих соображений. Пусть имеется две порции различных газов. Рассчитаем их плотности:

газ 1: ;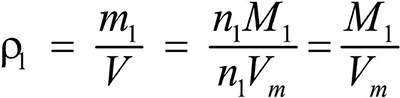

газ 2: .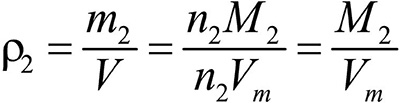

Разделив плотность первого газа на плотность второго, получим: .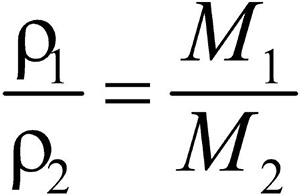

Отношение плотностей газов, равное отношению молярных масс, называется относительной плотностью одного газа по другому (D). D — величина безразмерная.

Зная D и молярную массу одного газа, легко найти молярную массу другого газа:

Пример 1. Относительная плотность газа по водороду равна 8. Определите молярную массу газа.

М(Х) = М(Н₂) ∙ D = 2 ∙ 8 = 16 г/моль.

Газ с такой молярной массой — метан СH₄.

Пример 2. Относительная плотность некоторого газообразного углеводорода по воздуху равна 2. Определите молярную массу углеводорода.

Средняя молярная масса воздуха равна 29 г/моль;

М(Х) = М(возд.) ∙ D = 29 ∙ 2 = 58 г/моль.

Углеводород с такой молярной массой — бутан С₄Н₁₀.

Следует отметить, что газы с молярной массой меньше 29 легче воздуха, больше 29 — тяжелее.

В расчётных задачах могут быть даны относительные плотности неизвестного газа по азоту, кислороду и другим газам. В этом случае для нахождения молярной массы неизвестного газа необходимо умножить относительную плотность на молярную массу соответственно азота (28 г/моль), кислорода (32 г/моль) и т. д.

Закон Авогадро широко применяется в химических расчётах. Поскольку для газов объёмы пропорциональны количествам (моль) веществ, то коэффициенты в уравнении реакции между газообразными веществами, отражающие количественное соотношение реагирующих веществ, пропорциональны объёмам взаимодействующих газов. Очевидно, что объёмы должны быть измерены при одинаковых условиях.

Пример 3. Какой объём кислорода потребуется для сжигания 2 дм³ пропана? Объёмы измерены при н. у.

Уравнение реакции горения пропана:

С₃Н₈ + 5О₂ 3СО₂ + 4Н₂О

Из закона Авогадро следует, что равные объёмы различных газов содержат одинаковое количество (моль) веществ. Пусть объём пропана равен 1 дм³. Тогда, согласно приведённому уравнению, для сжигания 1 дм³ пропана потребуется 5 дм³ кислорода. Следовательно, для сжигания 2 дм³ пропана потребуется:

1 дм³ С₃Н₈ — 5 дм³ O₂,

2 дм³ С₃Н₈ — 10 дм³ О₂

Ответ: V(О₂) = 10 дм³.

Смеси газов

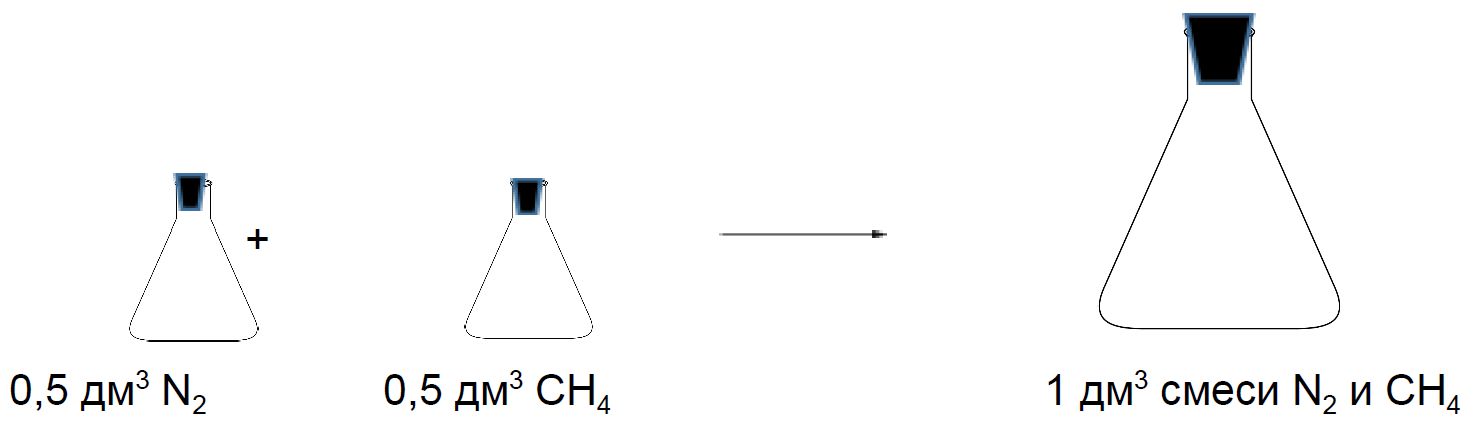
Рассмотрим две колбы объёмом 0,5 дм³. Одна колба заполнена азотом, а другая метаном. Давление и температура в колбах одинаковые. Если смешать содержимое этих колб, то полученная смесь займёт при таких же условиях объём 1 дм³.

Состав смеси газов часто выражают в объёмных долях. Объёмная доля газа обозначается греческой буквой φ (фи) и равна отношению объёма данного газа к объёму смеси. Рассчитаем объёмную долю азота в полученной выше смеси газов:

φ = = 0,5, или 50 %.

Пример 4. В результате пропускания 150 дм³ (н. у.) воздуха через избыток известковой воды выпало 0,201 г осадка. Найдите объёмную долю (%) углекислого газа в данном образце воздуха.

Уравнение реакции взаимодействия углекислого газа с известковой водой:

СО₂ + Са(ОН)₂ = СаСО₃ + Н₂О

Найдём количество (моль) карбоната кальция, выпавшего в осадок (M(CaCO₃) = 100 г/моль):

n(СаСО₃) = 0,201/100 = 0,00201 моль.

По уравнению реакции:

n(СаСО₃) = n(СО₂).

Рассчитаем объёмную долю углекислого газа в воздухе:

V(CO₂) = 0,00201 ∙ 22,4 = 0,045 дм³;

φ(СО₂) = 0,045/150 = 0,0003, или 0,03 %.

Ответ: φ(СО₂) = 0,03 %.

Пример 5. Объём смеси водорода с хлором составляет 50 см³. После взаимодействия газов осталось 10 см³ хлора. Найдите состав исходной смеси в объёмных долях. Все объёмы измерены при н. у.

Уравнение реакции взаимодействия водорода с хлором:

H₂ + Cl₂ 2HCl

Поскольку после взаимодействия осталось 10 см³ хлора, то 40 см³ исходной смеси прореагировало. Хлор и водород реагируют между собой в равных объёмных отношениях. Исходя из этих соображений, в реакцию вступили по 20 см³ хлора и водорода. Поскольку осталось 10 см³ хлора, то в первоначальной смеси было 20 см³ водорода и 30 см³ хлора.

Рассчитаем объёмные доли газов в исходной смеси:

φ(H₂) = 20/50 = 0,4, или 40 %;

φ(Cl₂) = 30/50 = 0,6, или 60 %.

Ответ: φ(H₂) = 40 %; φ(Cl₂) = 60 %.

Содержание:

1. Стехиометрические расчёты
2. Решение задач по уравнениям химических реакций
3. Закон авогадро и молярный объем газов
4. Доказательство закона Авогадро
5. Определение плотности газов
6. Нахождение объема, числа молекул, количества вещества по известной массе газа и обратные задачи
7. Относительная плотность газов
8. Нахождение относительной плотности
9. Расчет молярных масс газов по относительным плотностям газов
10. Расчет массы неизвестного газа по значению относительной плотности
11. Закон объемных отношений

Одним из важнейших химических понятий, на котором основываются стехио­метрические расчёты, является химическое количество вещества. Количество некоторого вещества X обозначается n(X). Единицей измерения количества вещества является моль.

Моль – это количество вещества, в котором содержится 6,02·10²³ молекул, атомов, ионов или других структурных единиц, из которых состоит вещество.

На странице -> решение задач по химии собраны решения задач и заданий с решёнными примерами по всем темам химии.

Стехиометрические расчёты

Стехиометрическими расчетами называют нахождение значений количества, масс и объемов веществ (реагентов и продуктов), участвующих в химических реакциях. Формульное количество вещества B (nB) и масса этого вещества (mB) связаны между собой соотношением.

Решение задач по уравнениям химических реакций

Вспомните! Уравнения химических реакций. Закон сохранения массы вещества. Составление и решение пропорции

По уравнениям химических реакций можно решать множество количественных задач. Мы остановимся на расчетных задачах по нахождению массы (m) и числа молей  продуктов реакции по известной массе участвующих в реакции веществ.

Решение задач осуществляется по следующему алгоритму:

Внимательно прочитать и коротко записать условие задачи. 

Составить уравнение соответствующей химической реакции.

В соответствии с коэффициентами вычислить количество , молярную массу (M), массу (m) веществ и записать эти данные под формулами этих веществ в уравнении.

Данные по условию задачи и искомые величины (х) записать над формулами этих веществ.

Составить пропорцию и найти неизвестную величину (х).

Записать ответ.

Задача 1. Сколько граммов хлорида натрия образуется при взаимодействии 92 г натрия с хлором?

Ответ: 234 г NаCl.

Задача 2. Сколько молей углекислого газа образуется при горении 36 г углерода?

Ответ:  3 моля 

Задача 3. Вычислите массу цинка (Zn), который должен взаимодействовать с соляной кислотой с выделением 10 г водорода.

Ответ: 325 г Zn.

Задача 4. Рассчитайте количество веществ оксида меди (CuO) и углекислого газа, полученных при разложении 5 г малахита а также их массу.

Расчет количества вещества:

Расчет по уравнению реакции:
а) 1 моль (м-т) : 2 моля (CuO) = 0,0225 моль (м-т) : х моль (CuO) 
х = 0,045 моль (CuO)

Ответ: 0,045 моль CuO, 3,6 г CuO.
       0,0225 моль  0,99 г 

Закон авогадро и молярный объем газов

 Какие газы вы знаете? Что такое плотность?

Многие  химические  вещества  существуют  в  газообразном  состоянии, например    и  др.  Встречаются  также  сложные  газообразные вещества: метан  углекислый газ  сернистый газ  хлороводород HCl, сероводород  и др. Газообразные вещества подчиняются физическим законам,  о  которых  вы  знаете  из  курса  физики.  Состояние  газообразных веществ характеризуется температурой, давлением и объемом.
Объем газов зависит от температуры и давления. При постоянном давлении и температуре расстояния между молекулами газообразных веществ примерно одинаковы. 
Из курса физики вам известно понятие «плотность» 

Отсюда: 

В таблице 8 приведены некоторые величины, характеризующие известные вам газы.

Рассчитаем объем 1 моля каждого газа (при н.у.):

Как видно из этих расчетов, объемы одного моля различных газов при нормальных условиях (н. у.), т. е. при температуре 0°С и давлении 1 атм (101,3 кПа), примерно одинаковы и составляют 22,4 л. При стандартных условиях (t = 25°С,  p = 101,3  кПа)  молярный  объем  составляет  24  л.  Эта величина называется молярным объемом и обозначается  (рис. 20). Молярным объемом газов  называют отношение объема газа (V) при н. у. к 
количеству вещества 

В 1 моль любых веществ, в том числе и газах, содержится одинаковое число молекул, которое называется числом Авогадро  моль

В равных объемах газов, взятых при одинаковых условиях, содержится одинаковое  число  молекул.  Этот  закон  был  сформулирован  итальянским ученым Авогадро в 1811 году. 

Плотностью газа при н. у. называется отношение молярной массы газа на молярный объем.

Плотность газа при нормальных условиях:

Доказательство закона Авогадро

Найдите число молекул и массы кислорода и углекислого газа объемом 50 л, взятых при нормальных условиях (н. у.).

Число молекул равных объемов (50 л)  газов, взятых при одинаковых условиях (н. у.), одинаково.

Расчет масс газов.

Массы газов разные.

Определение плотности газов

Найдите  плотности  кислорода  и  углекислого  газа  при  нормальных условиях.

Нахождение объема, числа молекул, количества вещества по известной массе газа и обратные задачи

а) Определите объем, число молекул, количество вещества 8,8 г углекислого газа при н. у.

б)  Рассчитайте  массу,  количество  вещества  и  число  молекул  67,2  л кислорода при н. у.

в) Рассчитать объем, массу, число молекул в 0,5 моль аммиака (н. у.).

г) Определите объем (н. у), массу и количество вещества сернистого газа числом молекул  

Нормальные и стандартные условия, молярный объем, число и закон Авогадро.

Относительная плотность газов

Кроме плотности веществ, в химии часто применяют понятие относительная плотность.

Относительной плотностью (D) одного газа по отношению к другому газу называется отношение масс газов, взятых в равных объемах при одинаковых условиях.

Часто  относительную  плотность  различных  газов  определяют  по отношению к водороду или воздуху.

По  формулам  относительных  плотностей  можно  рассчитать  значение молярной массы газов.

Нахождение относительной плотности

Рассчитайте относительные плотности кислорода и углекислого газа по водороду и воздуху

Расчет молярных масс газов по относительным плотностям газов

Рассчитать молярные массы газов, если известны относительные плотности:  

Расчет массы неизвестного газа по значению относительной плотности

Рассчитайте  массу  50  л  (н.  у.)  неизвестного  газа,  если  относительная плотность этого газа по воздуху равна 0,586. Какова относительная плотность по водороду?

 

Относительная плотность.

Закон объемных отношений

Напишем уравнение реакции между газообразными веществами, когда в результате реакции также образуется газ:

Отношение количеств реагирующих и образовавшихся веществ выглядит следующим образом: 2 : 1 : 2. Теперь возьмем отношение объемов этих газов при нормальных условиях:

Как  видим,  отношения  объемов  газов  соответствуют  отношениям коэффициентов перед формулами веществ в уравнении.

При одинаковых условиях объемы реагирующих газов и газообразных продуктов реакции относятся между собой как небольшие целые числа. Это закон объемных отношений Гей-Люссака.

Из рассмотренных примеров можно сделать вывод, что при решении задач удобно пользоваться коэффициентами, т.к. они в уравнениях химических реакций указывают объемные отношения веществ.

Определите объем кислорода, необходимого для окисления 60 л оксида серы (IV) до оксида серы (VI) по уравнению:

Закон объемных отношений.

Делаев выводы:

• 1.    Моль – мера количества вещества. В 1 моль любого вещества содержится число Авогадро структурных единиц (6,02-1023).
• 2.    Молярная масса вещества (М) численно равна относительной молекулярной массе (Мг).
• 3.    Расчеты по химическим уравнениям производятся на основе закона сохранения масс веществ.
• 4.    В равных объемах газов, взятых при одинаковых условиях, содержится одинаковое число молекул. (Закон Авогадро.)
• 5.    Относительной плотностью одного газа по отношению к другому газу (Dy(X)) называется отношение масс газов, взятых в равных объемах при одинаковых условиях.
• 6.    Объемы реагирующих газообразных веществ относятся между собой и к объемам образующихся газообразных продуктов, как небольшие целые числа, равные коэффициентам в уравнении химической реакции. (Закон объемных отношений Гей-Люссака.)
• 7.    При нормальных условиях (н. у.) любой газ занимает 22,4 л. Эта величина называется молярным объемом (У = 22,4 л/моль).

Услуги по химии:

1. Заказать химию
2. Заказать контрольную работу по химии
3. Помощь по химии

Лекции по химии:

1. Основные понятия и законы химии
2. Атомно-молекулярное учение
3. Периодический закон Д. И. Менделеева
4. Химическая связь
5. Скорость химических реакций
6. Растворы
7. Окислительно-восстановительные реакции
8. Дисперсные системы
9. Атомно-молекулярная теория
10. Строение атома в химии
11. Простые вещества
12. Химические соединения
13. Электролитическая диссоциация
14. Химия и электрический ток
15. Чистые вещества и смеси
16. Изменения состояния вещества
17. Атомы. Молекулы. Вещества
18. Воздух
19. Химические реакции
20. Закономерности химических реакций
21. Периодическая таблица химических элементов
22. Относительная атомная масса химических элементов
23. Химические формулы
24. Движение электронов в атомах
25. Формулы веществ и уравнения химических реакций
26. Химическая активность металлов 
27. Количество вещества
28. Энергия в химических реакциях
29. Вода 
30. Необратимые реакции
31. Кинетика
32. Химическое равновесие
33. Разработка новых веществ и материалов
34. Зеленая химия
35. Термохимия
36. Правило фаз Гиббса
37. Диаграммы растворимости
38. Законы Рауля
39. Растворы электролитов
40. Гидролиз солей и нейтрализация
41. Растворимость электролитов
42. Электрохимические процессы
43. Электрохимия
44. Кинетика химических реакций
45. Катализ
46. Строение вещества в химии
47. Строение твердого тела и жидкости
48. Протекание химических реакций
49. Комплексные соединения

Лекции по неорганической химии:

1. Важнейшие классы неорганических соединений
2. Водород и галогены
3. Подгруппа кислорода
4. Подгруппа азота
5. Подгруппа углерода
6. Общие свойства металлов
7. Металлы главных подгрупп
8. Металлы побочных подгрупп
9. Свойства элементов первых трёх периодов периодической системы
10. Классификация неорганических веществ
11. Углерод
12. Качественный анализ неорганических соединений
13. Металлы и сплавы
14. Металлы и неметаллы
15. Производство металлов
16. Переходные металлы
17. Элементы 1 (1А), 2 IIA и 13 IIIA групп и соединения
18. Элементы 17(VIIA), 16(VIA) 15(VA), 14(IVA) групп и их соединения
19. Важнейшие S -элементы и их соединения
20. Важнейшие d элементы и их соединения
21. Важнейшие р-элементы и их соединения
22. Производство неорганических соединений и сплавов
23. Главная подгруппа шестой группы
24. Главная подгруппа пятой группы
25. Главная подгруппа четвертой группы
26. Первая группа периодической системы
27. Вторая группа периодической системы
28. Третья группа периодической системы
29. Побочные подгруппы четвертой, пятой, шестой и седьмой групп
30. Восьмая группа периодической системы
31. Водород
32. Кислород
33. Озон
34. Водород
35. Галогены
36. Естественные семейства химических элементов и их свойства
37. Химические элементы и соединения в организме человека
38. Геологические химические соединения

Лекции по органической химии:

1. Органическая химия
2. Углеводороды
3. Кислородсодержащие органические соединения
4. Азотсодержащие органические соединения
5. Теория А. М. Бутлерова
6. Соединения ароматического ряда
7. Циклические соединения
8. Карбонильные соединения
9. Амины и аминокислоты
10. Химия живого вещества
11. Синтетические полимеры
12. Органический синтез
13. Элементы 14(IVA) группы
14. Азот и сера
15. Растворы кислот и оснований