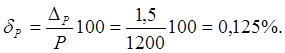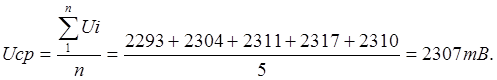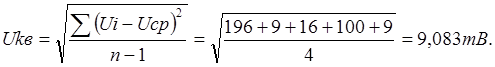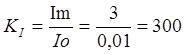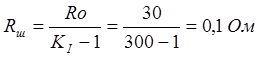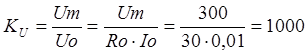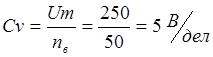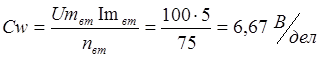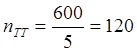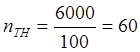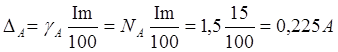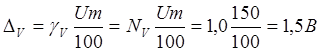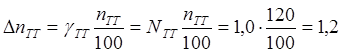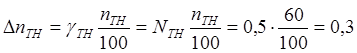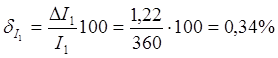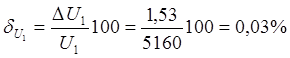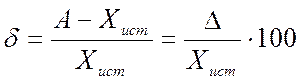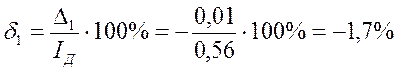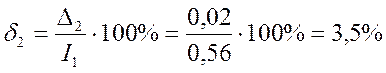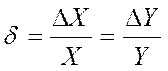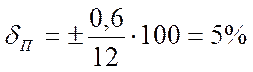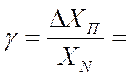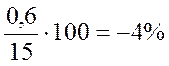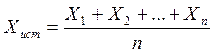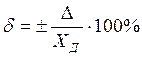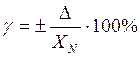Как найти инструментальную погрешность амперметра?
Мастер
(1220),
закрыт
6 лет назад
Сергей M.r
Высший разум
(516296)
6 лет назад
Инструментальная погрешность прибора определяется классом точности прибора .При классе точности прибора, например, 1.0 (1%) и пределе измерения 5 А максимально допустимая абсолютная погрешность измерения тока в любой точке шкалы будет равна 5*1/100=0.05 А . Таким образом, если Вы измеряете ток в 1 А, то относительная погрешность будет δ=(0.05/1)*100%=5%.
При измерении тока 4 А δ=(0.05/4)*100%=1.25%.
Это объясняет рекомендацию использовать при измерениях пределы близкие к возможному значению измеряемой величины.
Как-то так.
Удачи.
ThewiowdeУченик (155)
1 год назад
Здравствуйте. Не подскажите если у вольтметра по заданию не задан класс точности, цена деления его шкалы – 5 вольт, предельное значение – 30 вольт, то находится класс точности как отношение абсолютной погрешности к нормируемому значению (30 вольт, так как шкала начинается с нуля, на нём же и стрелка), выраженное в процентах, где абсолютная погрешность это инструментальная (цена деления на два, т. е. 5/2=2,5)? Тогда класс точности = 2,5/30 *100% = 8,33%? И, по-моему, ближайший к этому числу из стандартизированного ряда – 10?
Таня Андреева
Мыслитель
(5255)
6 лет назад
Для того, чтобы найти инструментальную погрешность прибора необходимо цену деления прибора поделить на 2! Это и будет погрешностью (Например: тебе необходимо найти погрешность обычной линейки. У неё цена деления равна 1 мм. Делишь на 2 и получаешь 0,5 мм!)
Ни один прибор в мире не является точным. Величина, которую он измеряет, всегда будет отличаться от истины на ту величину, которую еще называют его погрешностью. Данная погрешность и будет определять класс точности амперметра. Задачей всех производителей измерительной техники, заключается в том, чтобы эта погрешность была, как можно ниже и стремилась к нулю.
Погрешность амперметра устанавливается в результате поверки и сравнении показаний замеров одних и тех же величин с эталонным или образцовым прибором, имеющий более высокий класс точности. При этом значение, полученное на образцовом приборе, считаются действительными.
Что такое амперметр и какие величины он измеряет
Амперметр — измерительный прибор, который служит для измерения силы тока [І] в электроцепях. Единицей [І] по системе СИ является ампер [А]. Электрические цепи могут проводить ток разной силы, поэтому градуируют приборную шкалу амперметра с различной градацией от микроампера равного 1 мкА = 1×0-6 ампер до килоампера равного: 1 кА = 1 000 ампер.
Важно! В электроцепь амперметр включают последовательно, а для повышения границы измерений, используют специальные устройства: трансформаторы, шунты м магнитные усилители.
Поскольку ток в цепи напрямую зависит от величины сопротивления [R] элементов электроцепи, то собственное сопротивление прибора [Rа] должно быть предельно низким, стремится к нулю. Это приведет к уменьшению влияния устройства в процессе замеров тока в цепи, тем самым будет повышена точность измерения.
Разновидности амперметров
Они могут быть электромеханическими или аналоговыми, цифровыми или электронными. Базовый набор, как правило, состоит из детектора, передающего устройства и индикатора, самописца или запоминающего устройства.
Аналоговые устройства — самые старые из используемых инструментов. Хотя они надежны для статических и стабильных измерений, они не подходят для динамических и переходных условий. Кроме того, они довольно громоздкие и имеют ограничения из-за использования стрелочной индикации.
Электронные инструменты реагируют быстрее и способны мгновенно обнаруживать динамические изменения тока в сети. Примером является цифровой мультиметр, который способен измерить значения тока в динамическом или переходном режиме за секунды.
Виды погрешностей амперметра
Чтобы понять размер погрешности в измерениях, нужно сравнить полученные результаты с эталонными.
В метрологии используют для всех электротехнических измерителей, как для амперметров, так и для вольтметров, несколько видов погрешностей: абсолютную, относительную и приведенную.
Абсолютная погрешность амперметра — это разность Δ между результатом измерения, полученного на шкале прибора (Xи) и действительным значением силы тока в цепи (Xд). Абсолютная погрешность амперметра описывается простой формулой и выражается в единицах тока А.
Δх = Xд−Xи, А
где:
- Δх — дельта Х
- Xд — действительное показание силы тока, принимаемой по образцовому прибору;
- Xи — измеренное значение на шкале прибора.
Относительная погрешность (δ) — отношение абсолютной погрешности амперметра Δх к действительному показанию силы тока, принимаемому по образцовому прибору. Оно может быть указано как в процентах, тогда частное умножается на 100, либо выражаться в относительных единицах.
δ = (Δх : Xд)×100, %
Приведенная погрешность — это значение приведенное к диапазону измерения амперметра, приравненного к его шкале. Его получают в виде частного от абсолютной погрешности Δх и нормируемого значения (Xн), в значениях соответствующим абсолютной погрешности Δх умноженной на 100 %:
δпр = (Δх : Xн)×100, %
Класс точности
Это основная характеристика амперметра, которая согласно еще советскому действующему ГОСТ 1845-59, определяет границы возможных погрешностей.
Для всех электроизмерительных приборов, к которым он относится, класс точности (Кл) обозначается в числовом виде по значению, соответствующему предельной допустимой приведенной погрешности δпр, в %.
Все электрические амперметры подразделяются по точности на 8 классов, а затем по группам, которые является важным признаком их классификации:
- Образцовые: 0.05–0.1–0.2;
- лабораторные: 0.5–0.1;
- технические: 1.5–2.0–4.0.
Обратить внимание! Все приборы, у которых погрешность превышает 4%, являются внеклассными.
Образцовые применяют в электроизмерительных процессах для определения класса точности технических и лабораторных амперметров. Лабораторные применяются в научно-технических процессах при электротехнических исследованиях контроля ведения режимов, например на котельных, ГЭС, ТЭЦ и АЭС.
Важно! На панели амперметра класс точности указывается в кружках, квадратах и звездочках. Если он имеет неравномерную шкалу измерения, Кл обозначается ломаной линией.
Как определить класс точности
Согласно действующих государственных норм, производители амперметров обязаны гарантировать его относительную погрешность измерения, полученную по классу точности, указанной на измерительной панели и в паспорте на прибор. Кроме того, все измерительные приборы должны проходить периодическую поверку в метрологических центрах, на соответствие заводскому классу точности. Если такую аттестацию он не проходит, то не может использоваться в измерительных процессах.
Зная абсолютную погрешность и показание силы тока на шкале, можно просто получить реальную силу тока, действующую в цепи. При этом шкала для применения абсолютной погрешности считается равномерной.
Важно! При выборе шкалы стрелочного амперметра, нужно чтобы рабочее значение тока находилось, примерно, в 2/3 диапазона шкалы. Если стрелка будет находиться практически на 0 или на максимальном показатели шкалы, то относительная погрешность будет очень высокой, то есть доверять таким показаниям не рекомендуется.
Пример нахождения показания амперметра по приведенной погрешности
Для примера рассматривается аналоговый измеритель со шкалой до 25 А.
На шкале имеется обозначение класса точности 2.5, кружок или квадрат отсутствует, поэтому эта погрешность приведенная.
Y=Dх/Xп×100=+/- p
При Хп= 25А и значении p = 2.5 можно рассчитать абсолютную погрешность:
Δх =25/100×2.5=0.625 A
Если пользователь обнаружит на панели класс точности заключенный в квадрат, то погрешность нужно будет определять в процентном выражении от измеренного значения.
При показаниях по шкале Iи = 10 А, погрешность прибора не должна превышать
Δх =10×2.5/100=0.25
При показаниях по шкале Iи=2 А погрешность будет иной:
Δх =2×2.5/100=0.05
При показаниях по шкале Iи=25 А погрешность будет максимальной:
Δх =25×2.5/100=0.625
Вот почему важно, чтобы аналоговый прибор работал при измерениях в 2/3 рабочей шкалы.
Пример нахождения показания амперметра по относительной погрешности
Для того чтобы узнать погрешность для амперметра, имеющего класс точности 0.05/0.02, шкалу измерения 0…25 А. Δх определяют по измеряемому показанию на шкале 10А.
Поскольку класс точности задан как c/d, то расчет будет выполняться по формуле:
δ пр =+/-(с+d(xk/(x-1)))
Где:
- xk=25 А;
- х=10 А;
- с=0.05;
- d=0.02.
δ пр =100 Δх / xN
Нормирующее значение xN=xk=25 A,
δ пр =+/-(0.05+0.02(25/(10-1)))=0.105
Δх = δ пр×xN/100=0.105×25/100=0.026 A
Выбор амперметра по метрологическим характеристикам
Наиболее частым источником ошибки при измерении тока считается то, что амперметр имеет ненулевое входное сопротивление. Напряжение, возникающее на измерителе, приводит к снижению напряжения на тестируемом устройстве. Если уменьшение будет значительным, это приведет к значительно меньшему протеканию тока. Другими словами, измеритель не показывает ток, который фактически протекает в сети.
Для того чтобы максимально нивелировать эту погрешность, применяют два основных типа архитектуры измерения: шунтирующие амперметры и с обратной связью.
Погрешность, вызванная шунтирующим измерителем, определяемая в виде частного напряжения амперметра, деленная на выходное сопротивление.
Амперметры с обратной связью ближе к «идеальным». Он вырабатывает напряжение на пути обратной связи операционного усилителя с высоким коэффициентом усиления. Это напряжение также пропорционально измеряемому току, но не появляется на входе прибора. В результате чувствительные измерители с обратной связью, такие как электрометры и пикоамперметры, имеют нагрузку по напряжению, обычно ограниченную до 200 мкВ.
Для промышленных измерений наиболее часто применяются амперметры аналогового панельного типа. При их выборе следует учитывать такие моменты:
- Выбор типа. При измерении І постоянного, следует выбрать измеритель постоянного тока, то есть с магнитоэлектрическим измерительным механизмом. При измерении переменного тока нужно обратить внимание на форму волны и частоту. Если это синусоида, то измеряют только эффективное значение, с последующим преобразованием в максимальное или среднее значение.
- Класс точности. Чем более высокий класс точности измерителя, тем выше его цена, тем сложнее у него ремонт и метрологическая аттестация. Поэтому для выполнения большинства инженерных измерений достаточно класса точности 1.5, не стоит применять образцовые или лабораторные приборы.
- Выбор шкалы. Чтобы в полной мере использовать возможности амперметра по классу точности, измеряемый показатель должен быть в интервале 1/2 ~ 2/3 максимальной шкалы.
Важно! Внутреннее сопротивление — определяющая величина при выборе измерителя. Ее следует принимать в соответствии с величиной измеряемого импеданса, иначе это приведет к большим ошибкам измерения. Поскольку внутреннее сопротивление отражает энергопотребление самого измерителя, при измерении тока прибор с внутренним сопротивлением следует выбирать, как можно меньшим.
Видео по теме
Оценка погрешностей электрических измерений
Абсолютная
погрешность измерений, производимых
электроизмерительными приборами,
оценивается, исходя из класса точности
приборов. Обозначение класса точности
0,2; 0,5; 1,0 и т.д. не только характеризует
прибор в зависимости от системы,
конструкции, качества материалов,
точности градуировки и других факторов,
но и указывает, что погрешность показаний
прибора соответствующего класса в любом
месте шкалы не должна превышать 0,2%;
0,5%; 1%.
Если
обозначим через
максимально возможное показание прибора,
а через–
номер класса прибора, то получим
абсолютную погрешность прибора
.
Например,
вольтметр 0,2 класса (n
= 0,002),
шкала которого рассчитана на 50 В, имеет
абсолютную погрешность
,
а
амперметр класса 1,5, рассчитанный
на максимальное показание 5 А, имеет
абсолютную погрешность
.
Так
как абсолютная погрешность считается
одинаковой по всей шкале данного
электроизмерительного прибора, то
относительная погрешность
будет тем больше, чем меньше измеряемая
величина. Если, например, при помощи
указанного амперметра измерить ток
около 4А, то относительная погрешность
будет составлять 1,9%, а при измерении
силы тока около 1А – 7,5%.
При точных
измерениях следует пользоваться такими
приборами, чтобы предполагаемое значение
измеряемой величины составило 70-80% от
максимального (номинального) значения.
Поэтому применяют приборы, имеющие
несколько пределов измерений; при работе
с таким прибором его включают в цепь на
тот предел измерений, который достаточно
близок к предполагаемому значению
измеряемой величины.
Рассмотрим
вычисление погрешностей на следующем
примере.
Определить
погрешность измерения внутреннего
сопротивления элемента, электродвижущая
сила которого Е, напряжение на полюсах
U
и величина тока I.
Для измерения применены вольтметр
класса 0,5 ()
и
амперметр класса 1,0 ().Результаты
измерений следующие: Е = 2В, U
= 1,3 В,
I
= 1,2 А.
Абсолютные
погрешности измерений:
;
.
Вычисление
внутреннего сопротивления производим
по формуле
. (1)
Максимальная
относительная погрешность может быть
определена общеизвестным методом.
Логарифмируя выражение (1)
lnr
= ln(E-U)
– lnI,
находим относительную
погрешность
;
.
Эта
погрешность,
выраженная в процентах, составляет:
.
С
помощью формулы (1) находим внутренне
сопротивление r
и абсолютную погрешность
r:
Ом;
=
0,029 Ом =
0,03 Ом.
Следовательно,
внутреннее сопротивление
0,03)
Ом.
ЛАБОРАТОРНАЯ
РАБОТА № 1
Изучение электростатических полей методом электролитического моделирования
Цель
работы:
-
Ознакомиться
с одним из наиболее распространенных
способов изучения характеристик
электростатического поля с помощью
электролитической ванны. -
Практически
исследовать некоторые электростатические
поля.
Приборы и
принадлежности: электростатическая
ванна, набор электродов; индикатор нуля,
пантограф.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задача 1
Для
определения мощности в цепи постоянного тока были измерены напряжение сети U вольтметром класса точности NB
с пределом измерений Um, ток I амперметром класса точности Na
с пределом измерений Im. Определить
мощность, потребляемую приёмником, а также относительную и абсолютную
погрешности её определения.
Дано:
Найти:
Решение:
1) Найдем
мощность, потребляемую приемником
2) Класс
точности определяет приведенную погрешность
3) Найдем
абсолютную погрешность измерения тока и напряжения
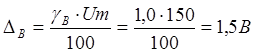
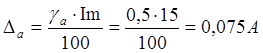
4) Найдем
абсолютную погрешность измерения мощности при косвенном измерении
5) Найдем
относительную погрешность измерения мощности
6) Доверительный
интервал результата измерения с вероятностью .
Задача 2
Проведено пять
независимых наблюдений одного и того же напряжения U.
Найти результат измерения и доверительную вероятность того, что абсолютная
погрешность измерения не превышает по модулю DU. Систематической погрешностью можно пренебречь.
Дано:
Найти:
Решение:
1) Определим
среднее арифметическое результатов измерения
2) Определяем
среднее квадратичное результатов измерения
3) Для
определения интервала и вероятности пользуются распределением Стьюдента, где
доверительный интервал равняется , где
– коэффициент Стьюдента,
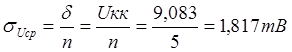
результата измерения.
4) Находим
доверительный интервал
5) Результат
измерения
Задача 3
Обмотка
магнитоэлектрического измерительного механизма имеет сопротивление RO и рассчитана на предельный длительный ток IO, при котором подвижная часть получает
наибольшее отклонение. Каким образом на базе указанного измерительного
механизма сделать амперметр с пределом измерений Im
и вольтметр с пределом измерений Um?
Дано:
Найти: ,
Решение:
1) Расчет
измерительной цепи амперметра
1.1
Определяем коэффициент расширения пределов измерения по току
1.2 Определяем сопротивление
шунта
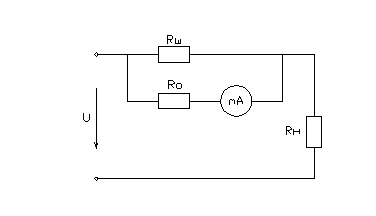
1.3
Схема измерительной цепи
2) Расчет
цепи вольтметра
2.1 Определяем коэффициент
расширения пределов измерения по напряжению
2.2 Определяем добавочное
сопротивление
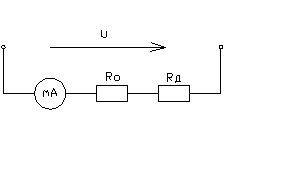
2.3
Схема включения
Задача 4
Определить
цену деления измерительных приборов:
1) амперметра, имеющего на шкале na делений и предел измерения Im;
2)вольтметра, имеющего nв делений шкалы и предел измерения Um;
3) ваттметра, имеющего nВТ делений шкалы и пределы измерений по току Im ВТ и напряжению Um
ВТ.
Дано:
Найти:
Решение:
1) Цена деления
амперметра
2) Цена деления
вольтметра
3) Цена
деления ваттметра
Задача 5
У вольтметра и
амперметра с пределами измерений Um и Im, включенных соответственно через измерительные
трансформаторы напряжения 6000/100 и тока 600/5, отчёт по шкале составил U2 и I2.
Определить напряжение и ток в сети, а также предел допускаемой абсолютной и
относительной погрешностей измерения, если известны класс точности приборов Na и Nв и
измерительных трансформаторов Nтн и Nтт. Привести схему измерения.
Дано:
Найти:
Решение:
1) Определим
коэффициенты трансформации трансформатора напряжения и тока
2) Определим
ток и напряжение в сети
3) Определим
абсолютные погрешности амперметра и вольтметра
4) Определяем
абсолютные погрешности коэффициентов трансформации трансформатора тока и
напряжения
5) Результирующие
абсолютные погрешности измерения тока и напряжения равны
6)
Относительные погрешности измерения тока и напряжения
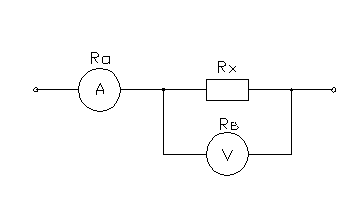
Задача 6
Определить
относительные погрешности измерения сопротивления Rx
в цепи постоянного тока с помощью амперметра и вольтметра при подключении их
двумя возможными способами. Сопротивление амперметра – Ra,
вольтметра – Rв. Сделать вывод о
целесообразности использования той или иной схемы.
Дано:
Найти: .
Решение:
Принципиальные
схемы
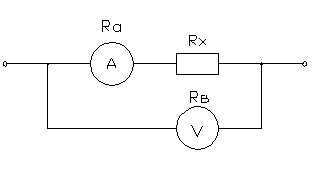
Схема
1 Схема 2
1) Для
схемы включения 1.
1.1.
Измеренное сопротивление.
1.2.
Определяем абсолютную погрешность.
1.3.
Определяем относительную погрешность.
ЛАБОРАТОРНАЯ РАБОТА № 3
по дисциплине «Управление, сертификация и инноватика
(Метрология, стандартизация и сертификация)»
ПОГРЕШНОСТИ ИЗМЕРЕНИЙ И ПОГРЕШНОСТИ СРЕДСТВ ИЗМЕРЕНИЯ
СОДЕРЖАНИЕ ЛАБОРАТОРНОЙ РАБОТЫ
1. Погрешности измерений
2. Погрешности средств измерений
- Контрольные вопросы Пример решения задачи Варианты задач
РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ
Законспектировать:
- Ответить на все контрольные вопросы, приведенные в конце лабораторной работы; Составить классификации погрешностей измерений и погрешностей средств измерений.
Знать:
- Основные виды погрешностей измерений; основные положения теории погрешностей; Погрешности средств измерений;
Решить:
· индивидуально каждый студент должен решить все варианты задач.
Оформление отчета:
· отчет выполняется индивидуально каждым студентом в отдельной тетрадке рукописным способом. Тетрадь начинается с титульного листа, где указаны ФИО студента и группа. Отчет по лабораторной работе начинается с названия и даты выполнения.
1. Погрешности измерений
Рассмотрим основные виды погрешностей измерения. В зависимости от формы выражения различают абсолютную и относительную погрешности.
Абсолютной называют погрешность измерений, выраженную в тех же единицах, что и измеряемая величина. Её определяют как:
D = А — Хист
или
D @ А – Хд
где А — результат измерения;
Хист — истинное значение измеряемой физической величины;
Хд — действительное значение измеряемой величины.
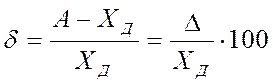
Относительная погрешность измерения (d) представляет собой отношение абсолютной погрешности измерений к истинному (действительному) значению измеряемой величины. Относительную погрешность в % определяют по формуле:
или
Пример. В результате измерения силы электрического тока в цепи I получен ряд значений: i1 = 0.55 A; i2 = 0.58 A; …in = 0.54 А. Вычислено среднее значение i = 0.56 А.
Погрешности D1 = i1 – i = 0,55-0,56 = -0,01 А; D2= i2 — i=0,58 -0,56=0,02 A;
Dn= in – i = 0,54-0,56 = -0,02 А являются абсолютными погрешностями измерений.
Приняв в качестве действительного значения среднее значение, т. е. iД = i, определим относительную погрешность отдельного измерения в ряду измерений:
В зависимости от условий и режимов измерения различают статические и динамические погрешности.
Статической называют погрешность, не зависящую от скорости изменения измеряемой величины во времени.
Динамической называют погрешность, зависящую от скорости изменения измеряемой величины во времени. Динамическая погрешность обусловлена инерционностью элементов измерительной цепи средства измерения.
В зависимости от характера проявления, возможностей устранения и причин возникновения различают систематические и случайные погрешности.
Систематической (Dc) называют составляющую погрешности измерения, остающуюся постоянной или закономерно изменяющейся при повторных измерениях одной и той же величины.
Причинами систематической погрешности могут быть:
— отклонение параметров реального средства измерения от расчетных значений, предусмотренных схемой;
— неуравновешенность деталей средства измерений относительно их оси вращения;
— погрешность градуировки или небольшой сдвиг шкалы и др.
Ряд постоянных систематических погрешностей в процессе измерения внешне себя не проявляют. Обнаружить их можно в процессе поверки путем сравнения результатов измерения рабочими средствами и образцовыми.
Случайной называют погрешность измерений, изменяющуюся случайным образом при повторных измерениях одной и той же величины.
Случайная погрешность возникает при одновременном воздействии многих источников, каждый из которых сам по себе оказывает незаметное влияние на результаты измерений, но суммарное воздействие всех источников может оказаться достаточно сильным.
Как правило, при выполнении измерений случайная и систематическая погрешности проявляются одновременно, поэтому погрешность измерения равна:
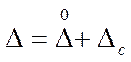
Заметим, что случайные погрешности представляют собой погрешности, в появлении каждой из которых не наблюдается какой-либо закономерности. Случайные погрешности неизбежны и неустранимы. Они всегда присутствуют в результате измерения. Они вызывают рассеяние результатов при многократном и достаточно точном измерении одной и той же величины при неизменных условиях, вызывая различие их в последних значащих цифрах.
В основе теории погрешностей лежат два положения, подтвержденные практикой:
· при большом числе измерений случайные погрешности одинакового значения, но разного знака встречаются одинаково часто;
· большие по абсолютному значению погрешности встречаются реже, чем малые.
Из первого положения следует важный для практики вывод, что при увеличении числа измерений случайная погрешность результата, полученного из ряда измерений, уменьшается вследствие того, что сумма погрешностей отдельных измерений данного ряда измерений стремится к нулю, т. е.
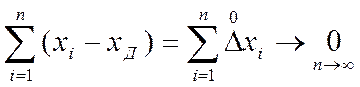
В ряду измерений выделяют также грубые погрешности и промахи, которые возникают из-за ошибок и неправильных действий оператора, а также при кратковременных, резких изменениях условий проведения измерений (появление вибрации, поступление холодного воздуха и т. д.).
При автоматических измерениях грубые погрешности и промахи автоматически исключаются в процессе обработки измерительной информации.
2. Погрешности средств измерений.
Отметим, что погрешности измерений определяются, главным образом, погрешностями средств измерений, но они не тождественны им.
В общем случае погрешность средства измерений (меры измерительного преобразователя, измерительного прибора) — это отклонение его реальной функции преобразования от номинальной.
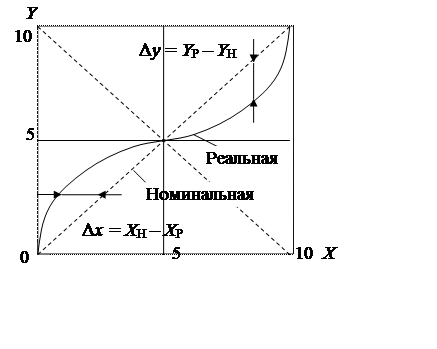
Отклонения реальной характеристики от номинальной, отсчитанные вдоль оси Х или оси У, т. е. разности вида Dy = Ур — Ун или Dx = Хр — Хн, есть абсолютные погрешности преобразования, выраженные в единицах величин Х или У (рис. 1).
Мерой точности абсолютная погрешность быть не может, т. к., например, DХ = 0.5 мм при измерении высоты пенного слоя пульпы, равной Х = 200 мм, достаточно мала, а при измерении толщины листа стали, при Х = 1 мм, эта погрешность очень велика.
Абсолютная погрешность измерительного прибора DXП — это разность между показанием прибора ХП и истинным (действительным) ХД значением измеряемой величины:
DXП = ХП – ХД.
Рис. 1. К пояснению понятия абсолютной погрешности
При этом за действительное значение физической величины при оценке погрешности рабочего средства измерений принимают показания образцового средства измерений, при оценке погрешности образцового средства — показания, полученные с помощью эталонного средства измерений.
Абсолютная погрешность измерительного преобразователя по входу — это разность между значением величины на входе преобразователя ХВ и истинным (действительным) значением этой величины на входе ХВД. При этом значение величины на входе ХВ определяется по истинному (действительному) значению величины на выходе преобразователя с помощью градуировочной характеристики, приписанной преобразователю. Таким образом,
DХВ =Х*ВД – ХВД,
где DХВ — погрешность измерительного преобразователя по входу;
Х*ВД — истинное (действительное) значение величины на выходе, найденное по градировочной характеристике преобразователя;
ХВД — истинное (действительное) значение преобразуемой величины на входе.
Абсолютная погрешность измерительного преобразователя по выходу — это разность между истинным (действительным) значением величины преобразователя на выходе DХВЫХ. Д и значением величины на выходе Х*ВЫХ. Д, определяемым по истинному (действительному) значению величины на входе с помощью градуировочной характеристики, приписанной преобразователю. Таким образом,
DХВЫХ. П = ХВЫХ. Д — Х*ВЫХ. Д,
где DХВЫХ. П — погрешность измерительного преобразователя по выходу;
ХВЫХ. Д — действительное значение преобразуемой величины на выходе преобразователя;
Х*ВЫХ. Д — действительное значение преобразуемой величины на выходе, определяемое по действительному значению ее на входе с помощью градуировочной характеристики.
Абсолютная погрешность — это разность между номинальным значением меры ХН и истинным (действительным) ХД воспроизводимой ею величины, т. е.
DХМ = ХН – ХД,
где DХМ — абсолютная погрешность мepы;
ХН — номинальное значение мepы;
ХД — действительное значение воспроизводимой мерой величины.
Пример. Погрешность меры длины (линейки) с номинальным значением 100 мм и действительным значением 100,0006 мм равна 0,6 мкм; погрешность меры сопротивления с номинальным значением 1 Ом и действительным значением 1,0001 Ом равна 0,0001 Ом.
Относительная погрешность меры или измерительного прибора (dП) — это отношение абсолютной погрешности меры или измерительного прибора к истинному (действительному) значению воспроизводимой или измеряемой величины.
Относительная погрешность меры или измерительного прибора, в процентах, может быть выражена как:
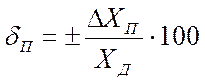
Относительная погрешность измерительного преобразователя по входу (выходу) — это отношение абсолютной погрешности измерительного преобразователя по входу (выходу) к истинному (действительному) значению величины на входе (выходе), определяемому по истинному значению величины на входе (выходе) с помощью номинальной характеристики, приписанной преобразователю.
Итак, относительная погрешность средства измерений, выражаемая в процентах или в относительных единицах, не остается постоянной вследствие изменения величин Х или Y по шкале измерительного устройства.
С учетом того, что относительная погрешность средства измерений не остается постоянной, то вводится понятие приведенной погрешности, в общем виде определяемой:
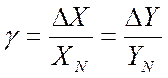
где g — приведенная погрешность средства измерений;
XN — нормирующее значение измеряемой величины.
Приведенная погрешность g измерительного прибора — это отношение абсолютной погрешности измерительного прибора DХП к нормирующему значению. Нормирующее значение XN — это условно принятое значение, равное или верхнему пределу измерений*, или диапазону измерений**, или длине шкалы***.
Приведенную погрешность обычно выражают в процентах:
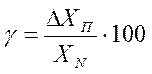
Приведенная погрешность позволяет сравнивать по точности приборы, имеющие разные пределы точности.
Пример. Определить абсолютную, относительную и приведенную погрешности амперметра с диапазоном измерения 0 -15 А при показании его ХП = 12 А и действительном значении измеряемой силы тока ХД = 12,6 А. За нормирующее значение примем верхний предел измерения Xv = 15 А.
Абсолютная погрешность амперметра
DХП = ХП – ХД = 12 — 12,6 = -0,6 А.
Относительная погрешность амперметра
Приведенная погрешность
При характеристике погрешностей средств измерений часто пользуются понятием предела допускаемой погрешности измерений.
Предел допускаемой погрешности средства измерений — это наибольшая, без учета знака, погрешность средства измерений, при котором оно может быть признано и допущено к применению. Определение применимо к основной и дополнительной погрешности средств измерений.
Пример. Одинаков ли предел допускаемой относительной погрешности измерения во всех точках шкалы автоматического потенциометра?
Для всех точек шкалы одинаков предел допускаемой абсолютной погрешности, определяемой классом точности средства измерений и диапазоном измерений, а предел допускаемой относительной погрешности измерения зависит от конкретной отметки шкалы, т. е. чем меньше показания прибора по шкале, тем больше относительная погрешность. Вследствие этого верхний предел показаний прибора нужно выбирать таким образом, чтобы значение измеряемой величины находилось в конце шкалы.
По происхождению различают инструментальные и методические погрешности средств измерений.
Инструментальные погрешности — это погрешности, вызываемые особенностями свойств средств измерений. Они возникают вследствие недостаточно высокого качества элементов средств измерений, К этим погрешностям можно отнести изготовление и сборку элементов средств измерений; погрешности из-за трения в механизме прибора, недостаточной жесткости его элементов и деталей и др. Подчеркнем, что инструментальная погрешность индивидуальна для каждого средства измерений
Методическая погрешность — это погрешность средства измерения, возникающая из-за несовершенства метода измерения, неточности соотношения, используемого для оценки измеряемой величины.
Основная и дополнительная погрешности. Деление это чисто условно. Погрешность средств измерений, определяемую для работающих в нормальных условиях, называют основной погрешностью. Нормальными условиями принято считать условия, когда температура окружающего воздуха t = (20 ± 5) 0C, относительная влажность W = 30 – 80 %, атмосферное давление Р = 630 — 795 мм рт. ст., напряжение питающей сети (U = (220 ± 4,4) В, частота питающей сети f = (50 ± 0,5) Гц. Такие условия выдерживаются в лабораторных условиях при градуировке средств измерений.
В реальных условиях производства эти параметры отличаются от лабораторных. Средства измерения помимо чувствительности к измеряемой величине обладают и некоторой чувствительностью к изменяющимся величинам окружающей среды, что приводит к искажению результатов измерения. Погрешность, появляющуюся у средств измерений, работающих в реальных производственных условиях, называют дополнительной погрешностью. Так же, как основная, дополнительная погрешность нормируется путем указания коэффициентов влияния изменения отдельных влияющих величин на изменение показаний в виде
α = 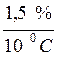
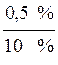
Систематические и прогрессирующие погрешности средств измерений вызываются: первые — погрешностью градуировки шкалы или ее небольшим сдвигом, вторые — старением элементов средства измерения. Систематическая погрешность остается постоянной или закономерно изменяющейся при многократных измерениях одной и той же величины. Особенность систематической погрешности состоит в том, что она может быть полностью устранена введением поправок. Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы только в данный момент времени. Они требуют непрерывной коррекции.
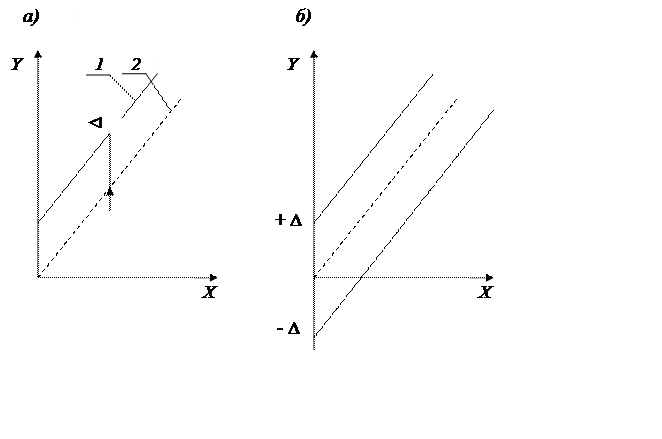
Аддитивные и мультипликативные погрешности. Аддитивная погрешность не зависит от чувствительности прибора и является постоянной для всех значений входной (измеряемой) величины в пределах диапазона измерений (рис.2).
Если реальная характеристика 1 средства измерения смещена относительно номинальной 2 (см. рис. 2) так, что при всех значениях преобразуемой величины Х выходная величина У оказывается больше (или меньше) на одну и ту же величину Δ, то такая погрешность называется аддитивной погрешностью нуля.
Рис. 2. К пояснению понятия аддитивной погрешности средства измерения
К аддитивным погрешностям средств измерений можно отнести погрешности, вызванные трением в опорах электроизмерительных приборов, погрешность дискретности (квантования) в цифровых приборах. Аддитивная погрешность может носить систематический характер. В этом случае она может быть скорректирована смещением шкалы или нулевого положения указателя.
В случае же, если аддитивная погрешность является случайной, то она не может быть скорректирована, и реальная характеристика средства измерения, смещаясь произвольным образом, но, оставаясь параллельной самой себе, образует полосу погрешностей, ширина которой остается постоянной для любых значений измеряемой величины Х (см. рис. 4.2, б).
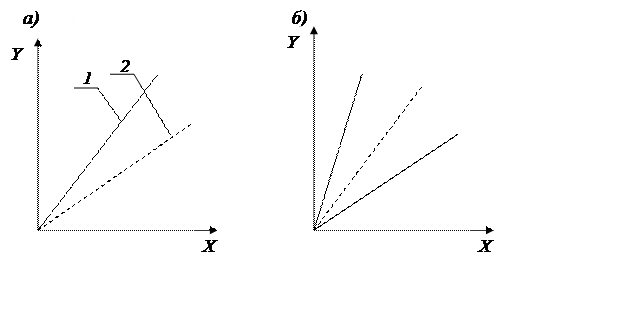
Мультипликативная погрешность – это погрешность чувствительности средства измерения. Она может иметь систематическую и случайную составляющие.
Сущность мультипликативной погрешности заключается в том, что если абсолютная погрешность возникает от некоторого независимого от Х изменения чувствительности преобразователя (изменение коэффициента деления делителя, добавочного сопротивления вольтметра и т. д.), то реальная характеристика 1 преобразователя отклоняется от номинальной 2 так, как это показано на рис. 4.3, а, или образует полосу погрешностей (рис. 4.3, б), если это отклонение является случайным.
Рис. 4.3. К пояснению понятия мультипликативной
погрешности измерений
КОНТРОЛЬНЫЕ ВОПРОСЫ К ЛАБОРАТОРНОЙ РАБОТЕ:
1. Что такое абсолютная погрешность измерений?
2. Что такое относительная погрешность измерений?
3. Что такое систематическая погрешность измерений?
4. Что такое случайная погрешность измерений?
5. Что такое промах?
6. В чем заключается отличие погрешности измерения от погрешности средства измерения?
7. Что такое абсолютная погрешность средства измерения?
8. Что такое относительная погрешность средства измерения?
9. Что такое приведенная погрешность? Для каких целей она рассчитывается?
10. Что такое относительная погрешность средства измерения по входу и по выходу?
11. Что такое инструментальная погрешность средства измерения?
12. Что такое методическая погрешность?
13. Что такое систематическая и прогрессирующая погрешности средств измерений?
14. Что такое аддитивная погрешность средства измерения?
15. Чем вызывается мультипликативная погрешность средства измерения?
ПРИМЕР РЕШЕНИЯ ЗАДАЧИ:
Амперметром с диапазоном измерения от 0 до 50 А произведен ряд измерений (табл. 1):
Таблица 1
|
Порядковый наблюдений |
Значение величины тока |
Порядковый наблюдений |
Значение величины тока |
|
1 |
20,5 |
9 |
20,5 |
|
2 |
20,1 |
10 |
20,7 |
|
3 |
20,5 |
11 |
20,5 |
|
4 |
20,5 |
12 |
20,3 |
|
5 |
20,2 |
13 |
20,9 |
|
6 |
20,6 |
14 |
20,1 |
|
7 |
20,3 |
15 |
20,6 |
|
8 |
20,7 |
· Произвести оценку результатов измерений (найти абсолютную, относительную и приведенные погрешности);
· За нормирующее значение принять верхний предел шкалы.
Решение:
|
№ |
Значение величины тока |
Истинное значение величины тока I , А |
Абсолютная погрешность(Δ) I , А |
Относительная погрешность(δ) % |
Приведенная погрешность (γ) % |
|
1 |
20,50 |
20,47 |
0,03 |
0,0015 |
0,0006 |
|
2 |
20,10 |
-0,37 |
-0,0184 |
-0,0074 |
|
|
3 |
20,50 |
0,03 |
0,0015 |
0,0006 |
|
|
4 |
20,50 |
0,03 |
0,0015 |
0,0006 |
|
|
5 |
20,20 |
-0,27 |
-0,0134 |
-0,0054 |
|
|
6 |
20,60 |
0,13 |
0,0063 |
0,0026 |
|
|
7 |
20,30 |
-0,17 |
-0,0084 |
-0,0034 |
|
|
8 |
20,70 |
0,23 |
0,0111 |
0,0046 |
|
|
9 |
20,50 |
0,03 |
0,0015 |
0,0006 |
|
|
10 |
20,70 |
0,23 |
0,0111 |
0,0046 |
|
|
11 |
20,50 |
0,03 |
0,0015 |
0,0006 |
|
|
12 |
20,30 |
-0,17 |
-0,0084 |
-0,0034 |
|
|
13 |
20,90 |
0,43 |
0,0206 |
0,0086 |
|
|
14 |
20,10 |
-0,37 |
-0,0184 |
-0,0074 |
|
|
15 |
20,60 |
0,13 |
0,0063 |
0,0026 |
Истинное значение:
Абсолютная погрешность: Δ = ХД – Хист
Относительная погрешность:
Приведенная погрешность:
ВАРИАНТЫ ЗАДАЧ:
Задача 1:
Вольтметром с диапазоном измерения от 0 до 250 В произведен ряд измерений (табл. 1):
Таблица 1
|
Порядковый наблюдений |
Значение величины напряжения |
Порядковый наблюдений |
Значение величины напряжения |
|
1 |
220 |
9 |
220 |
|
2 |
219 |
10 |
220 |
|
3 |
220 |
11 |
222 |
|
4 |
218 |
12 |
221 |
|
5 |
221 |
13 |
219 |
|
6 |
220 |
14 |
219 |
|
7 |
219 |
15 |
220 |
|
8 |
220 |
· Произвести оценку результатов измерений (найти абсолютную, относительную и приведенные погрешности);
· За нормирующее значение принять верхний предел шкалы.
Задача 2:
Омметром с диапазоном измерения от 0 до 300 МОм произведен ряд измерений (табл. 1):
Таблица 1
|
Порядковый наблюдений |
Значение величины сопротивления |
Порядковый наблюдений |
Значение величины сопротивления |
|
1 |
125 |
9 |
123 |
|
2 |
126 |
10 |
125 |
|
3 |
124 |
11 |
126 |
|
4 |
125 |
12 |
124 |
|
5 |
126 |
13 |
123 |
|
6 |
125 |
14 |
127 |
|
7 |
125 |
15 |
122 |
|
8 |
124 |
· Произвести оценку результатов измерений (найти абсолютную, относительную и приведенные погрешности);
· За нормирующее значение принять верхний предел шкалы.
* Верхний предел измерений. Значения величины, ограничивающие диапазон измерений снизу и сверху (слева и справа), называют соответственно «нижним пределом измерений» или «верхним пределом измерений».
* * Диапазон измерений — это область значений величины, в пределах которой нормированы допускаемые пределы погрешности средства измерений.
* * * Длина шкалы — это длина линии, проходящей через центры всех коротких отметок шкалы средства измерений и ограниченной начальной и конечной отметками. Она выражается в единицах длины, независимо от единиц, указанных на шкале.