Для треугольника:
![]() .
.
![]() , (37)
, (37)
т.е. квадрат
относительной погрешности вычисления
площади треугольника, прямоугольника,
параллелограмма равен сумме квадратов
относительных погрешностей измерений
основания и высоты фигуры.
Для трапеции:
![]() ,
,
относительная СКП
вычисления площади составит
![]() (38)
(38)
Если принять, что
относительные погрешности измерения
основания и высоты фигуры одинаковые
и равны
![]() ,
,
то из (45) найдем
![]() . (39)
. (39)
Пример: Основание
и высоту фигуры площадью P=100га,
измерили на местности с относительной
погрешностью
![]() ,
,
СКП площади составит![]() .
.
Для четырехугольника
по форме близкого к квадрату, в котором
измерены все стороны и два угла, т.е.
![]()
![]()
![]() и
и![]()
![]()
![]() ,
,
справедливо выражение
![]() (40)
(40)
Если для вычисления
площади четырехугольника, использовались
три известные стороны и два угла (40), то
![]() (41)
(41)
Пример: При
относительной погрешности измерений
![]() и СКП измерений угла
и СКП измерений угла![]() ,
,
относительная погрешность определения
площади составит![]() .
.
Из приведенных
примеров, очевидно, что относительная
погрешность вычисления площади
аналитическим способом несколько больше
относительной погрешности измеренных
линий и зависит не только от точности
измерений на местности, но и от применяемых
формул.
8.3. Вычисление площадей графическим способом
На плане контур,
площадь которого хотят определить
разбивают на геометрические фигуры, в
которых измеряют длины сторон и высоты.
Далее по формулам (38-44) находят площадь.
Существует ряд
условий при вычислении площадей
графическим способом, к которым относятся:
-
для вычисления
площадей участков, имеющих большое
количество углов, целесообразнее
вычислять площадь по графическим
координатам точек; -
при выборе
разбиваемой на плане фигуры, предпочтение
отдают треугольникам, причем наилучшим
вариантом являются равносторонние
треугольники
 ;
; -
если высоты или
основания представляют собой линии,
измеренные на местности (стороны
теодолитного хода), то для повышения
точности вычисления площадей, длины
этих линий не измеряют на плане, а берут
из результатов непосредственных
измерений; -
точность вычисления
площади неравностороннего треугольника
выше, если короткое основание (высота)
измерено на местности, а длинная высота
(основание) получена с плана -
для контроля и
повышения точности площадь определяют
дважды: по двум различным основаниям
и двум высотам. Затем сравнивают
расхождение полученных площадей и при
их допустимости
![]() ,
,
вычисляют среднее
значение.
8.4. Точность вычисления площадей графическим способом
Если в треугольнике
измерено по плану основание
![]() и
и
высота![]() ,
,
то погрешность вычисления площади можно
найти из выражения
![]() (42)
(42)
Погрешности
измерения основания и высоты по плану
можно считать одинаковыми
![]() ,
,
тогда с учетом![]() ,
,
получим погрешность вычисления площади
треугольника
![]() (43)
(43)
В случае если
![]() получим
получим![]() ,
,
но![]() ,
,
тогда
![]() (44)
(44)
Для трапеции,
прямоугольника и параллелограмма
обозначим
![]() и
и![]() ,
,
тогда погрешность вычисления площади
данных фигур составит
![]() (45)
(45)
В случае если
![]() получим
получим![]() ,
,
но![]() ,
,
тогда
![]() (46)
(46)
Из сравнения формул
очевидно, что погрешность вычисления
площади треугольника меньше погрешности
определения площадей других фигур.
Обозначив
![]() ,
,
гдеK
– коэффициент вытянутости фигуры, то
из (46) получим
![]() . (47)
. (47)
Так как площадь
треугольника
![]() и
и![]() ,
,
то
![]()
откуда.
Подставив выражение
![]() в (50) найдем
в (50) найдем
![]() (48)
(48)
Из анализа формул
(47) и (51) видно, что погрешность определения
площади вытянутого треугольника по
плану больше погрешности определения
площади треугольника при
![]() в
в![]() раз. Это заключение верно и для
раз. Это заключение верно и для
прямоугольника, трапеции и параллелограмма.
Пример. На плане
масштаба 1:500 измерены
![]() ,
,![]() .
.
Площадь треугольника![]() ,
,![]() ,
,
или в масштабе плана0,2м.,
![]() .
.
По формуле (51) найдем
![]() ,
,
или
![]() .
.
Если основание
![]() измерено на местности рулеткой с
измерено на местности рулеткой с
относительной погрешностью![]() ,
,
по формуле (44) получим

Следовательно,
погрешность измерения на плане короткого
основания
![]() снизило точность вычисления площади
снизило точность вычисления площади
треугольника в пять раз.
Если площадь
многоугольника разбита на
![]() треугольников с соотношением
треугольников с соотношением![]() ,
,
т.е.![]() ,
,
то погрешность определения его площади,
составит
![]() .
.
СКП площади каждого
треугольника определим по формуле
![]() ,
,
тогда
![]() .
.
Следовательно, на
точность определения площади контура
на плане не влияет на сколько треугольников
разбит этот контур. Нет необходимости
стремиться к тому, чтобы число треугольников
было наименьшим, а надо стараться, чтобы
выполнялось условие
![]() .
.
Погрешность
площади, вычисленной по графическим
координатам точек можно рассчитать по
формуле
![]() ,
,
в которой СКП
измерения координат на плане с помощью
измерителя принимают равной
![]() .
.
При измерении
площади контура с помощью квадратной
или параллельной палетками ее погрешность
характеризуется эмпирической формулой
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Измерение длины, площади, объема и времени
- Лабораторная работа №1. Измерение длины ребер, площади поверхности и объема прямоугольного параллелепипеда. Погрешность прямых и косвенных измерений
- Лабораторная работа №2. Измерение времени с помощью секундомера. Погрешность серии прямых измерений
п.1. Лабораторная работа №1. Измерение длины ребер, площади поверхности и объема прямоугольного параллелепипеда. Погрешность прямых и косвенных измерений
Цель работы
Научиться измерять длину с помощью линейки, определять площадь поверхности и объем прямоугольного параллелепипеда, находить абсолютные и относительные погрешности косвенных измерений.
Теоретические сведения
 |
Прямоугольный параллелепипед – это многогранник с шестью гранями, каждая из которых является прямоугольником. Прямоугольный параллелепипед имеет три измерения: длину, ширину и высоту. |
Пусть
длина (AD=BC=A_1 D_1=B_1 C_1=a)
ширина (AB=CD=A_1 B_1=C_1 D_1=b)
высота (AA_1=BB_1=CC_1=DD_1=c)
Площади верхней и нижней грани равны (S_1=ab), площади передней и задней граней равны (S_2=ac), площади левой и правой граней равны (S_3=bc).
Площадь поверхности прямоугольного параллелепипеда равна сумме площадей всех шести граней: $$ S_{пов}=2S_1+2S_2+2S_3=2(ab+ac+bc) $$ Объем прямоугольного параллелепипеда равен произведению всех трех измерений: $$ V=abc $$
Пусть измерения проводятся ученической линейкой с ценой деления (triangle=1 мм).
Тогда инструментальная погрешность измерений равна половине цены деления: $$ d=frac{triangle}{2}=0,5 мм $$ Абсолютная погрешность измерений при работе с линейкой равна инструментальной погрешности, поэтому для всех измерений: (triangle a=triangle b=triangle c=d=0,5 мм)
Относительные погрешности измерений (в долях, без процентов): $$ delta_a=frac{triangle a}{a}=frac da, delta_b=frac{triangle b}{b}=frac db, delta_c=frac{triangle c}{c}=frac dc $$ Выведем необходимые формулы.
Рассмотрим нижнюю грань. Её площадь (S_1=ab) является произведением двух длин.
Значит, относительная погрешность измерения площади равна сумме относительных погрешностей длин: $$ delta_{S1}=delta_a+delta_b $$ Аналогично для остальных граней: $$ delta_{S2}=delta_a+delta_c, delta_{S3}=delta_b+delta_c $$ Абсолютная погрешность измерения площади нижней грани: $$ triangle S_1=S_1cdotdelta_{S1}=abcdot(delta_a+delta_b)=abcdotleft(frac da+frac dbright)=abdcdotleft(frac ab+frac1bright)=abdcdotfrac{b+a}{ab}= d(a+b) $$ Аналогично для остальных граней: $$ triangle S_2=S_2cdotdelta_{S2}=d(a+c), triangle S_3=S_3cdotdelta_{S3}=d(b+c) $$ Абсолютная погрешность суммы измерений равна сумме абсолютных погрешностей. Получаем для площади поверхности: begin{gather*} triangle S_{пов}=2(triangle S_1+triangle S_2+triangle S_3)=2(d(a+b)+d(a+c)+d(b+c))=\ =2d(a+b+a+c+b+c)=4d(a+b+c) end{gather*}
Абсолютная погрешность определения площади поверхности прямоугольного параллелепипеда равна: $$ triangle S_{пов}=4d(a+b+c) $$ где (d) – инструментальная погрешность линейки, (a,b,c) – измеренные значения длины, ширины и высоты.
Найдем погрешность определения объема.
Объем равен произведению трех измерений, значит, относительная погрешность для объема равна сумме относительных погрешностей измерений: $$ delta_v=delta_a+delta_b+delta_c=frac da+frac db+frac dc=dleft(frac 1a+frac 1b+frac 1cright)=dcdotfrac{bc+ac+ab}{abc} $$ Абсолютная погрешность для объема: $$ triangle V=vcdotdelta_v=abccdot dcdotfrac{bc+ac+ab}{abc} = d(bc+ac+ab)=dcdotfrac{S_{пов}}{2} $$
Абсолютная погрешность определения объема прямоугольного параллелепипеда равна: $$ triangle V=dcdotfrac{S_{пов}}{2} $$ где (d) – инструментальная погрешность линейки, (S_{пов}) – площадь поверхности.
Приборы и материалы
Ученическая линейка, книга (или деревянный брусок).
Ход работы
1. Ознакомьтесь с теоретической частью работы, выпишите необходимые формулы.
2. Измерьте длину, ширину и высоту книги (бруска), (a,b,c).
3. Найдите площадь поверхности (S_{пов}) и объем (V).
4. Найдите абсолютные погрешности (triangle S_{пов}) и (triangle V).
5. Найдите относительные погрешности в процентах: $$ delta_{S_{пов}}=frac{triangle S_{пов}}{S_{пов}}cdot 100text{%}, delta_V=frac{triangle V}{V}cdot 100text{%} $$ 6. Дополнительное задание. Определите толщину одного листа книги, абсолютную и относительную погрешность этой величины.
7. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
Инструментальная погрешность линейки (d=frac{1 мм}{2}=0,5 мм)
Результаты измерений:
a=218 мм
b=147 мм
c=32 мм
Площадь поверхности: begin{gather*} S_{пов}=2(ab+ac+bc)=2(218cdot 147+218cdot 32+147cdot 32)=\ =2(32046+6976+4704)=87452 (мм^2) end{gather*} Объем: $$ V=abc=218cdot 147cdot 32=1025472 (мм^2) $$ Абсолютная погрешность определения площади поверхности (округляем до двух значащих цифр с избытком): $$ triangle S_{пов}=4d(a+b+c)=4cdot 0,5cdot (218+147+32)=2cdot 397=794 (мм^2)approx 800 (мм^2) $$ Полученную величину площади поверхности также округляем до сотен. Получаем: $$ S_{пов}=(87500pm 800) (мм^2) $$ Абсолютная погрешность определения объема: $$ triangle V=dcdotfrac{S_{пов}}{2}=0,5cdotfrac{87452}{2}=21863 (мм^3)approx 22000 (мм^3) $$ Полученную величину объема также округляем до тысяч. Получаем: $$ V=(1025000pm 22000) (мм^3) $$
Относительные погрешности (округляем до двух значащих цифр с избытком): begin{gather*} delta_{S_{пов}}=frac{triangle S_{пов}}{S_{пов}}cdot 100text{%}=frac{800}{87500}cdot 100text{%} approx 0,92text{%}\ delta_v=frac{triangle V}{V}cdot 100text{%}=frac{22000}{1025000}cdot 100text{%}approx 2,2text{%} end{gather*} Измеряем толщину книги между обложками: (h=23 мм)
Количество страниц в книге (N=688)
Количество листов в 2 раза меньше. Получаем толщину одного листа: $$ t=frac{h}{N/2}=frac{2h}{N}=frac{2cdot 23}{688}approx 0,0669 (мм)=66,9 (мк) $$ Количество листов – величина точная, без погрешностей.
Абсолютная погрешность для толщины листа зависит только от (triangle h): $$ triangle t=frac 2Ntriangle h=frac 2N d=frac{2}{688}cdot 0,5approx 0,0015 (мм)=1,5 (мк) $$ Толщина листа: $$ t=(66,9pm 1,5) мк $$ Относительная погрешность: $$ delta_t=frac{triangle t}{t}cdot 100text{%}=frac{1,5}{66,9}cdot 100text{%}approx 2,3text{%} $$
Выводы
На основании проделанной работы можно сделать следующие выводы.
Измерения проводились с помощью линейки с инструментальной погрешностью (d=0,5 мм).
Получена площадь поверхности книги $$ S_{пов}=(87500pm 800) мм^2, delta_{S_{пов}}approx 0,92text{%} $$ Объем книги: $$ V=(1025000pm 22000) мм^3, delta_Vapprox 2,2text{%} $$ Определяя толщину листа, мы использовали способ рядов и увеличили абсолютную точность измерений от 0,5 мм до 1,5 мк. Толщина листа: $$ t=(66,9pm 1,5) мк, delta_tapprox 2,3text{%} $$ С наибольшей точностью определена площадь поверхности, т.к. для нее относительная погрешность меньше всех.
С наименьшей относительной точностью определена толщина листа, зато абсолютная точность для этой величины очень высока – 1,5 микрона.
п.2. Лабораторная работа №2. Измерение времени с помощью секундомера. Погрешность серии прямых измерений
Цель работы
Научиться измерять время с помощью секундомера, определять абсолютную и относительную погрешность величины, полученной в серии прямых измерений.
Теоретические сведения
Математическим маятником называют груз небольших размеров, подвешенный на тонкой невесомой нерастяжимой нити.
Периодом колебаний математического маятника называют время, за которое он возвращается в исходную точку.
При отклонении математического маятника на малые углы (до 20°) период его колебаний (T) остается постоянной величиной. В действительности колебания постепенно затухают, но при достаточно длинной нити и тяжелом грузике, затухания происходят медленно.
Приборы и материалы
Секундомер, штатив, грузик на длинной нитке (не менее 50 см).
Ход работы
1. Закрепите нитку с грузиком в лапке штатива, как показано на рисунке.
2. Определите цену деления секундомера.
3. Отклоните грузик на небольшой угол, отпустите его и с помощью секундомера измерьте время, за которое маятник совершит 10 полных колебаний.
4. Повторите опыт 5 раз.
5. С помощью алгоритма определения истинного значения и абсолютной погрешности в серии измерений (см. §3 данного справочника) найдите точное значение и абсолютную погрешность времени 10 колебаний.
6. Найдите точное значение и абсолютную погрешность периода колебаний (T), рассчитайте относительную погрешность результата измерений.
7. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
Определение цены деления секундомера
 |
Два ближайших пронумерованных деления на основной шкале: begin{gather*} a=5 с\ b=10 с end{gather*} Между ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления.
Цена деления: begin{gather*} triangle=frac{b-a}{n+1}\ triangle=frac{10-5}{24+1}=frac15=0,2 c end{gather*} |
Инструментальная погрешность секундомера равна половине цены деления: (d=frac{triangle}{2}=0,1 c)
Измерения времени 10 колебаний
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t, c) | 15,3 | 14,9 | 15,2 | 15,5 | 15,1 | 76,0 |
| (triangle c) | 0,1 | 0,3 | 0 | 0,3 | 0,1 | 0,8 |
Найдем среднее время для 10 колебаний: begin{gather*} t_0=frac{15,3+14,9+15,2+15,5+15,1}{5}=frac{76,0}{5}=15,2 (c) end{gather*} Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от (t_0): $$ triangle_1=|15,3-15,2|=0,1; triangle_2=|14,9-15,2|=0,3 text{и т.д.} $$ Среднее абсолютное отклонение: $$ triangle_{cp}=frac{0,1+0,3+0+0,3+0,1}{5}=frac{0,8}{5}=0,16 (c) $$ Среднее абсолютное отклонение больше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,16right}=0,16 text{c} $$ Результат измерения времени 10 колебаний: begin{gather*} t=t_0pmtriangle t, t=(15,20pm 0,16) c end{gather*} Период колебаний в 10 раз меньше: $$ T=frac{1}{10}(t_0pmtriangle t), T=(1,520pm 0,016) c $$ Относительная погрешность измерений: $$ delta_T=frac{triangle T}{T_0}cdot 100text{%}=frac{0,016}{1,520}cdot 100text{%}approx 1,1text{%} $$
Выводы
На основании проделанной работы можно сделать следующие выводы.
Измерения проводились с помощью секундомера, для которого была определена цена деления (triangle=0,2 с) и соответствующая инструментальная погрешность (d=frac{triangle}{2}=0,1 с).
В данном случае абсолютная погрешность может быть заметно больше инструментальной, и поэтому для ее определения потребовалась серия экспериментов.
Полученный в серии из 5 экспериментов результат измерения времени 10 колебаний: $$ t=(15,20pm 0,16) c $$ Искомый период колебаний маятника: $$ T=(1,520pm 0,016) c, delta_T=1,1text{%} $$
При выполнении обмеров помещений с целью подготовки технического плана всегда возникают ошибки, связанные с погрешностями измерений. Непосредственно выполняются линейные измерения размеров помещений, а площадь помещений является расчетной величиной, которая имеет погрешность, зависимую от погрешностей прямых (линейных) измерений.
Допустимые ошибки измерений линий при технической инвентаризации установлены пунктом 11.10 Рекомендаций по технической инвентаризации и регистрации зданий гражданского назначения (Приняты Росжилкоммунсоюзом к введению в действие с 1 января 1991 года) и составляют:
для линий до 1 м +/- 1 см (1:100);
для линий до 6 м +/- 3 см (1:150);
для линий до 12 м +/- 5 см (1:200);
для линий до 24 м +/- 8 см (1:300);
для линий до 100 м +/- 30 см (1:400).
Применительно к квартирам почти все измеряемые линии находятся в пределах от 1 до 6 метров. Следовательно, возможно принять предельную ошибку измерения линии в среднем 3 см.
По правилам математической статистики для перехода от предельных ошибок (при принятии доверительного интервала равным 95%) к средним квадратическим погрешностям следует предельную ошибку разделить на 2. В этом случае средняя квадратическая погрешность измерения линии составит 1.5 см, или 0.015 м.
Погрешность измерения площади помещения целесообразно рассчитать по упрощенной методике. Для этого следует принять, что типичное помещение в квартире имеет прямоугольную форму и его площадь определяется произведением длины помещения на его ширину:
При этом погрешность измерения длины помещения – линии a (Da) обусловит погрешность площади в зависимости от длины помещения (DPa), а погрешность измерения ширины помещения – линии b (Db) обусловит погрешность площади в зависимости от ширины помещения (DPb). Графически эти погрешности будут выглядеть следующим образом:
Из рисунка очевидно, что
DPa= b * Da,
DPb= a * Db.
Величины DPa и DPb являются независимыми случайными величинами, поскольку они являются производными от независимых случайных величин (погрешностей измерения). В связи с этим общая погрешность определения площади согласно правилам сложения независимых случайных величин определяется путем их геометрического суммирования:
DP = √((DPa)2 + (DPb)2)
Выразив DPa и DPb через длину и ширину помещения и погрешности их измерения и приняв во внимание, что погрешность измерения ранее определена равной 0.015 м, получим:
DP = √(( b * Da)2 + (a * Db)2) = √(( b * 0.015)2 + (a * 0.015)2) = √(0.0152*( a2 + b2)) = 0.015 * √( a2 + b2)
В случае, если помещение представляет собой квадрат и a = b, P = a2, формула погрешности сводится к следующему:
DP = 0.015 * √( a2 + a2) =0.015 * √(2*a2) = 0.015 *√2 * √P
При подстановке в формулу различных значений соотношения a и b, можно найти зависимость между отношением a/b=K и погрешностью площади.
DP = 0.015 * √( b2 + (К*b)2) =0.015 * √(( 1+К2) *b2)
Принимая во внимание, что a = b*K, получим:
P=a*b = b2*K
или
b2 = P/K
Подставив последнее соотношение в формулу для погрешности определения площади, получим
DP = 0.015 * √(( 1+К2) *b2) = 0.015 * √(( 1+К2) *P/K) = 0.015 * √((( 1+К2)/K) *P)
Величина K = a/b, выражающая отношение длины помещения к его ширине, называется коэффициентом вытянутости геометрической фигуры. Для упрощения расчетов целесообразно не определять ее отдельно для каждого объекта, а определить ее среднее значение по представительной выборке и в дальнейшем пользоваться полученным результатом.
В качестве типичного объекта взята типовая секция дома проекта П44Т и выполнен расчет среднего весового значения этого коэффициента (за вес единичного определения коэффициента принята площадь данного помещения, вычисленная упрощенно, без учета сложной конфигурации). Полученный результат равен 1.67.
Для такого значения К получим
DP = 0.015 * √(( 1+К2)/K) *P) = 0.015 * √(( 1+1.672)/1.67) *P) = 0.015 * 1.506 * √P = 0.0226 * √P
Для перехода от средних квадратических значений погрешности к предельно допустимым применяется коэффициент 2 (при доверительном интервале 95%). В этом случае
DP предельн = 0.0451 * √P, кв. м.
Для упрощения расчетов возможно округлить коэффициент:
DP предельн = 0.05 * √P, кв. м.
Таким образом определяется предельная погрешность определения площади элементарного прямоугольника. Для перехода к предельной погрешности площади квартиры (как совокупности помещений) нужно провести геометрическое суммирование погрешностей по помещениям. Эта операция сводится к подстановке значения общей площади квартиры в последнюю формулу.
Возможно составить таблицу значений погрешности определения площади для квартир различной площади. Результаты приведены ниже.
Приведенная таблица погрешностей не учитывает возможные погрешности при возведении некапитальных стен, в результате чего измерения длины помещения по разным стенам могут дать различные результаты. Таблица применима только в отношении домов, построенных из типовых сборных ж/б элементов (как дома серии П44Т). Для монолитных домов, домов серии П111М (с легкобетонными перегородками) необходимо учитывать в расчетах указанную выше погрешность.
Для таких домов погрешность прямых измерений была определена по выборке натурных измерений помещений. В тестовом объекте (монолитный многоквартирный жилой дом) обмеры были выполнены по всему периметру всех помещений. Выла взята случайная выборка из 50 помещений прямоугольной формы. Погрешность измерений была определена по абсолютным отклонениям между измеренными длинами противолежащих сторон прямоугольника (всего 100 пар измерений, по 2 пары на помещение).
Значение средней квадратической погрешности по выборке составило 0.024 м. Это значение подставлено в формулу расчета погрешности площади вместо величины 0.015 м:
DP = 0.024 * 1.506 * √P = 0.036 * √P
предельная погрешность определения площади в этом случае составляет
DPпредельн = 2 * 0.036 * √P = 0.072 * √P
Для упрощения расчетов возможно округлить коэффициент:
DP предельн = 0.07 * √P, кв. м.
Таблица погрешностей определения площади для квартир различной площади для указанного случая приведена ниже.![[IMG]](https://img-fotki.yandex.ru/get/98971/13421369.2/0_bbfa5_ea7cf4e0_orig)
РЕКОМЕНДУЕМЫЕ ФОРМУЛЫ
РАСЧЕТА ПОГРЕШНОСТИ ОПРЕДЕЛЕНИЯ (ВЫЧИСЛЕНИЯ) ПЛОЩАДИ ЗДАНИЯ,
СООРУЖЕНИЯ, ПОМЕЩЕНИЯ, МАШИНО-МЕСТА
1. В случае если здание, сооружение, помещение, мащино-место имеет простейшую геометрическую фигуру в форме квадрата, прямоугольника, параллелограмма, среднюю квадратическую погрешность определения площади здания, сооружения, помещения, машино-места (mp) рекомендуется вычислять по формуле:
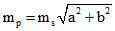 ,
,
где:
a и b – длина и ширина прямоугольника, у квадрата – длина сторон, у параллелограмма – длина основания и высота соответственно;
ms – средняя квадратическая погрешность определения линейных измерений.
2. В случае если здание, сооружение, помещение имеет простейшую геометрическую фигуру в форме треугольника, а площадь его определяется через произведение высоты на основание, то среднюю квадратическую погрешность определения площади здания, сооружения, помещения рекомендуется вычислять по формуле:
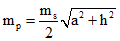 ,
,
где:
a – длина основания треугольника;
h – высота треугольника;
ms – средняя квадратическая погрешность определения линейных измерений.
3. При определении площади здания, сооружения, помещения путем разбивки такого объекта на простейшие геометрические фигуры и суммирования площадей таких фигур или площади помещения путем суммирования площадей всех частей такого помещения среднюю квадратическую погрешность определения площади здания, сооружения, помещения в пределах одного этажа, а также в случае одноэтажности объекта недвижимости рекомендуется вычислять по формуле:
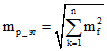 ,
,
где:
mf – средняя квадратическая погрешность определения площади простейшей фигуры или одной части помещения;
n – количество простейших геометрических фигур, на которые был разбит объект для определения площади, или количество частей, из которых состоит помещение.
4. В случае наличия нескольких этажей у здания, сооружения, расположения помещения на нескольких этажах и (или) наличия эксплуатируемой кровли среднюю квадратическую погрешность определения площади здания, сооружения, помещения рекомендуется вычислять по формуле:
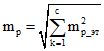 ,
,
где:
mp_эт – средняя квадратическая погрешность определения площади здания, сооружения, помещения в пределах одного этажа, а также эксплуатируемой кровли;
c – количество этажей у здания, сооружения, помещения, также при необходимости учитывается эксплуатируемая кровля.
5. Среднюю квадратическую погрешность определения площади застройки сооружения рекомендуется вычислять по формуле:
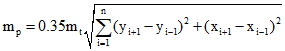 ,
,
где:
xi, yi – координаты характерных точек контура застройки сооружения;
mt – средняя квадратическая погрешность измерений положения точек контура застройки сооружения;
n – число характерных точек контура застройки сооружения.
Скачать документ целиком в формате PDF
Загрузить PDF
Загрузить PDF
Абсолютная погрешность – это фактическая ошибка, допущенная при измерении какой-либо величины. Относительная погрешность сравнивает абсолютную погрешность со значением измеряемой величины. Чтобы вычислить относительную погрешность, следует найти и абсолютную погрешность. Если вы измеряете предмет, длина которого равна 12 см, и вы допустили ошибку в 6 см, то относительная погрешность будет огромной. Но если длина измеряемого предмета равна 12 м, а ошибка – 6 см, то относительная погрешность будет значительно меньше, даже с учетом того, что абсолютная погрешность (6 см) не изменилась.[1]
-

1
Если вам дано ожидаемое значение, вычтите из него полученное вами значение, чтобы вычислить абсолютную погрешность. Как правило, ожидаемое значение находится в ходе тестовых или лабораторных испытаний. Ожидаемое значение является наиболее точным значением некоторой величины, которое используется при различных вычислениях. Чтобы получить абсолютную погрешность, сравните результаты ваших измерений с ожидаемым значением – так вы узнаете, насколько ваши результаты отличаются от ожидаемого значения. Для этого просто вычтите полученное вами значение из ожидаемого. Если разность отрицательная, превратите ее в положительную, проигнорировав знак «минус». Вы получите абсолютную погрешность.[2]
-
Например, вы хотите узнать точность измерения расстояния при помощи шагов. Вы идете от одного дерева к другому, считаете шаги и выясняете, что деревья расположены на расстоянии 5,4 м друг от друга. Это экспериментальное значение. Потом вы берете рулетку и измеряете точное расстояние между деревьями, которое равно 6 м. Это действительное значение. Абсолютная погрешность равна: 6 – 5,4 = 0,6 м = 60 см.[3]
-
Например, вы хотите узнать точность измерения расстояния при помощи шагов. Вы идете от одного дерева к другому, считаете шаги и выясняете, что деревья расположены на расстоянии 5,4 м друг от друга. Это экспериментальное значение. Потом вы берете рулетку и измеряете точное расстояние между деревьями, которое равно 6 м. Это действительное значение. Абсолютная погрешность равна: 6 – 5,4 = 0,6 м = 60 см.[3]
-

2
Теперь допустим, что абсолютная погрешность – это наименьшая единица измерения. Например, рулетка имеет миллиметровые деления, то есть ее наименьшей единицей является 1 мм. Таким образом, вы можете измерить расстояние с точностью до ± 1 мм; в этом случае абсолютная погрешность составляет 1 мм.
- Это верно для любых измерительных инструментов или систем. Например, на корпус многих научных инструментов, таких как прецизионные весы и измерительные приборы, наносят маркировку об абсолютной погрешности в виде «± ____».
-

3
Не забудьте приписать соответствующие единицы измерения. Предположим, что абсолютная погрешность равна 2 м. Такая информация позволит наглядно представить величину ошибки. Но если вы записываете, что погрешность равна 2, то эта цифра ничего не значит. Используйте те же единицы измерения, которыми вы пользовались в ваших измерениях.[4]
-

4
Попрактикуйтесь на нескольких примерах. Это наилучший способ научиться вычислять погрешность. Решите следующие задачи (ответы приведены в конце каждой задачи).
- На уроке химии в результате реакции ученик получил вещество массой 32 г. Известно, что действительное значение выхода этой реакции равно 34 г. Абсолютная погрешность равна ± 2 г.
- На уроке химии ученику необходимо 10 мл воды, чтобы вызвать реакцию; при этом погрешность капельницы составляет «± 0,5 мл». В этом случае абсолютная погрешность измерений равна ± 0,5 мл.
-

5
Уясните, что приводит к появлению погрешности и как ее устранить. Всякое научное исследование подразумевает наличие ошибок – даже в научных работах, за которые вручаются Нобелевские премии, сообщается о допущениях или погрешностях. Но если вы определите причину появления погрешности, вы, возможно, сможете устранить ее.[5]
- Человеческий фактор – наиболее распространенная причина появления ошибок. Сюда относятся неподобающие условия для проведения измерений и плохо продуманные эксперименты.
- Одной из причин появления ошибок может являться внезапное отключение энергии, недостаточное количество рабочего материала или изменение других условий, например, нехватка воды в результате ее испарения, внезапное изменение температуры окружающей среды и так далее.
- Еще одной причиной является несовершенство оборудования, используемого для измерений или исследований, например, прецизионных инструментов или горелок, которые обеспечивают неравномерное распределение тепла.[6]
Реклама
-

1
Разделите абсолютную погрешность на действительное значение исследуемой величины. Так вы вычислите относительную погрешность. Эта формула позволит вам выяснить, насколько полученное вами значение отличается от действительного значения изучаемой величины. Конечно, прекрасно, если относительная погрешность мала. Продолжим рассматривать пример с измерением расстояния между двумя деревьями.
- Абсолютная погрешность равна 0,6 м, а действительное значение равно 6 м.
- 0,6 м / 6 м
- Относительная погрешность равна 0,1 м.[7]
-

2
Полученный результат умножьте на 100, чтобы выразить относительную погрешность в процентах. Вы можете представить относительную погрешность в виде обыкновенной дроби, десятичной дроби или в процентах – в этом случае умножьте десятичную дробь на 100. Так вы узнаете, какой процент от полученного вами значения составляет погрешность. Если вы измеряете длину 60 м лодки, а погрешность составляет 0,6 м, то процент ошибки будет значительно меньше, чем при вычислении расстояния между деревьями (6 м) с погрешностью 0,6 м. Погрешность представляет собой небольшой процент от экспериментального значения. [8]
- 0,6 м / 6 м = 0,1 м
- 0,1 * 100 = 10% – относительная погрешность.
-

3
Вычислите относительную погрешность без нахождения абсолютной погрешности. Для этого выражение для вычисления абсолютной погрешности запишите в числителе выражения для нахождения относительной погрешности. Уяснив разницу между абсолютной и относительной погрешностями, нет необходимости отдельно вычислять абсолютную погрешность. Просто замените значение абсолютной погрешности на выражение для ее вычисления. Обратите внимание, что вертикальные черты обозначают абсолютную величину, то есть любое полученное значение нужно превратить в положительное.
- Относительная погрешность:
, где Е – экспериментальное значение, D – действительное значение.
- Умножьте это выражение на 100, чтобы выразить относительную погрешность в процентах.[9]
- Относительная погрешность:
-

4
Не забудьте приписать соответствующие единицы измерения. Предположим, что абсолютная погрешность равна 2 м. Такая информация позволит наглядно представить величину ошибки. Но если вы записываете, что погрешность равна 2, то эта цифра ничего не значит. Также не имеет смысла указывать погрешность в виде процентов от ошибки (10% от 0,6 м) – следует писать, например, так: относительная погрешность равна 10%.[10]
Реклама
Советы
- Удостоверьтесь, что экспериментальное значение и действительное значение измеряются в одних единицах измерения. Например, если экспериментальное значение измеряется в сантиметрах, а действительное значение – в миллиметрах, преобразуйте одну из этих единиц измерения в другую.
Реклама
Предупреждения
- Убедитесь, что вы правильно округляете числа.
Реклама
Похожие статьи
Об этой статье
Эту страницу просматривали 169 634 раза.
![[IMG]](https://img-fotki.yandex.ru/get/55905/13421369.2/0_bbf9f_194a810_orig)
![[IMG]](https://img-fotki.yandex.ru/get/28982/13421369.2/0_bbfa0_f0d5a6f3_orig)
![[IMG]](https://img-fotki.yandex.ru/get/98971/13421369.2/0_bbfa1_4538c891_orig)
![[IMG]](https://img-fotki.yandex.ru/get/58454/13421369.2/0_bbfa2_6c5c2a6a_orig)
![[IMG]](https://img-fotki.yandex.ru/get/93451/13421369.2/0_bbfa3_4956c37b_orig)
![[IMG]](https://img-fotki.yandex.ru/get/93451/13421369.2/0_bbfa4_3711ce17_orig)
