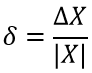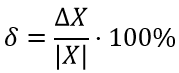Как найти относительную погрешность калькулятор

Как найти относительную погрешность калькулятор

Точное значение величины

Приближенное значение величины

Как вычислить относительную погрешность

Относительная погрешность приближенного числа – это отношение абсолютной погрешности к приближенному числу.

Для того чтобы вычислить относительную погрешность необходимо:
1. Вычислить абсолютную погрешность, то есть найти разность между приближенным числом и его точным значением.
2. Разделить абсолютную погрешность на точное значение величины.
3. Для получения округленного результата в процентах разделить абсолютную погрешность на приближенное значение величины и умножить получившееся частное на 100%.

Приведем пример, в помещении 23 человека, округлим это значение до 25. Тогда абсолютная погрешность = 25 – 23 = 2.

Относительная погрешность =

= 0.086956521739

Источник

Unit Converter

Enter the measured value and actual value into the calculator below to determine the relative error (%) and the absolute error. This calculator can determine any value given the other variables are known.

  • Percent Error Calculator
  • Percent Yield Calculator
  • Point Estimate Calculator
  • Sampling Error Calculator
  • Greatest Possible Error Calculator

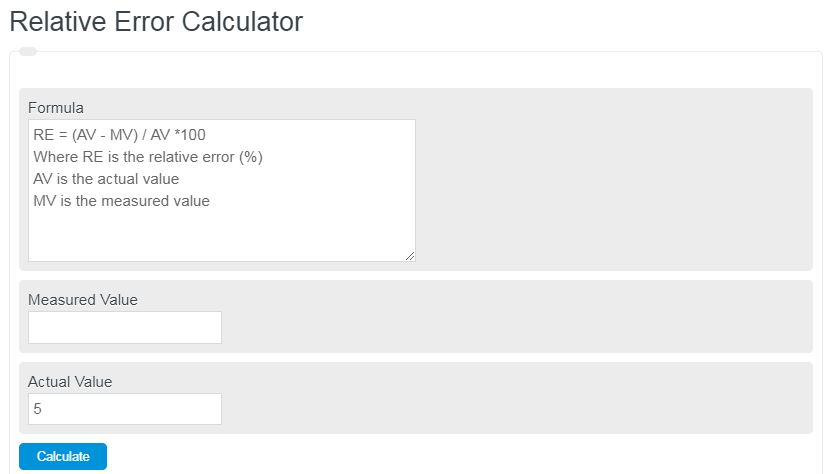
Relative Error Formula

  • Where RE is the relative error (%)
  • AV is the actual value
  • MV is the measured value

To calculate relative error, subtract the measured value from the actual value, divide that result by the actual value, then multiply by 100.

What is Relative Error?

As is the case with the standard error, the relative error is a measure of how close a measured value is to the true theoretical value.

In the case of chemistry, this could be the measured mass of the actual mass of a reaction.

How to calculate relative error?

The following is an example problem for calculating the relative error in an experiment or set of data.

First, determine the theoretical value the experiment should yield. For this example, we are going to assume that we are analyzing a chemical reaction that is supposed to yield a certain mass of a product.

In this case, the expected mass yield is 20 grams.

Next, perform the chemical process, and measure the actual mass that was yielded from the reaction.

For this problem, the actual mass is measured to be 19 grams.

Finally, calculate the relative error using the formula above.

RE = |AV – MV|/ AV *100

RE = |20 – 19 |/ 20 *100

RE = 5%

Relative vs Absolute Error

Relative and absolute errors are both measures of the variation in a set of data between an expected value and the actual outcome.

In the case of absolute error, this is simply a measure of the absolute difference between the expected value and the measured value.

In the case of relative error, that absolute difference is compared to the expected value in terms of a percentage of variation.

Relative Error Properties

There are several properties of relative error that are used to better understand the variation in data.

For one, the relative error is always positive. This is because the relative error uses the absolute value of the difference between the expected and true outcomes.

Absolute values, as we know, are always positive, and therefore, so is the relative error.

Another property of relative error is that it’s the absolute value of the percent error. In other words, the difference between percent error and relative error is that percent error can be negative while relative cannot.

Can relative error be greater than 100%?

In some instances, a relative error can be greater than 100%.

For example, if you have a theoretical value of 10 but the measured value comes out to be 25, the formula calculates the relative error as |10-25| / 10 *100 = 150%.

FAQ

What is a relative error?

The relative error is a measure the difference between an expected or theoretical outcome and the actual outcome that occurred.

Relative Error Calculator

Источник

Измеряя линей­ные размеры предметов измерительными инстру­ментами : линейкой, штангенциркулем, микрометром, проводя измерения времени секундомером или силы электрического тока или величины напряжения соответствующими электроизмерительными приборами Вы проводите прямые измерения.

Погрешность измерений

Любое измерение проводится с определенной точностью, при этом измеренное значение всегда отличается от истинного, так как инструменты измерения, методики и органы чувств человека несовершенны. Поэтому важную роль играет оценка погрешности измерений, результат измерений с учетом погрешности записывается в виде: X ± ΔX, где ΔX — абсолютная погрешность измерений.

Случайные и систематичес­кие погрешности

Погрешности подразделяются на случайные и систематичес­кие.
Систематические погрешности остаются постоянными или закономерно меняются в процессе измерения. Например неточность прибора, неправильная его регулировка ведет к систематической погрешности. Если причина систематической погрешности известна, то чаще всего такую погрешность можно исключить.
Случайные погрешности вызваны различными случайными факторами, влияющими на точность измерений. Например, при измерении секундомером отрезков времени, случайные погрешности связаны с различным (случайным) временем реакции экспериментатора на события запускающие и останавливающие секундомер. Чтобы уменьшить влияние случайной погрешности необходимо проводить многократное измерение физической величины.
Калькулятор ниже вычисляет случайную погрешность выборки прямых измерений для заданного доверительного интервала. Немного теории можно найти сразу за калькулятором.

PLANETCALC, Расчет погрешностей непосредственных измерений.

Расчет погрешностей непосредственных измерений.

Доверительная вероятность

Точность вычисления

Знаков после запятой: 3

Относительная погрешность в %

В большинстве случаев результат измерения подчиняется нормальному закону распределения, поэтому истинное значение измерения будет равно пределу:
x_0=lim_{n to infty} frac{1}{n}sum_{i=1}^{n} x_i
В случае ограниченного количества измерений, наиболее близким к истинному будет среднее арифметическое:
bar{x}=frac{1}{n}sum_{i=1}^{n} x_i

Согласно элементарной теории ошибок Гаусса случайную погрешность отдельного измерения характеризует так называемое среднеквадратическое отклонение:
S_n=left. sqrt{frac{sum_{i=1}^{n}{(x_i-bar{x})^2}}{n-1}} right, квадрат этой величины называется дисперсией. При увеличении этой величины возрастает разброс результатов измерений, т. е. увеличивается погрешность.

Для оценки погрешности всей серии измерений, вместо отдельного измерения надо найти среднюю квадратичную погрешность среднего арифметического, характеризующую отклонение bar{x} от истинного значения искомой величины x_0.
По закону сложения ошибок среднее арифметическое имеет меньшую ошибку, чем результат каждого отдельного измерения. Cред­няя квадратичная погрешность среднего арифметического равна:
S_{bar{x}}=frac{S_n}{sqrt{n}} = left. sqrt{frac{sum_{i=1}^{n}{(x_i-bar{x})^2}}{{n}({n-1})}} right
Стандартная случайная погрешность Δх равна:
Delta_{x}=t_{alpha,k}S_{bar{x}},, где t_{alpha,k} — коэффициент Стьюдента для заданной доверительной вероятности alpha и числа степеней свободы k = n-1.
Коэффициент Стьюдента можно получить по таблице или воспользоваться нашим калькулятором для вычисления квантилей распределения Стьюдента: Квантильная функция распределения Стьюдента. Следует иметь в виду, что квантильная функция выдает значения одностороннего критерия Стьюдента. Значение двустороннего квантиля для заданной доверительно вероятности alpha соответствует значению одностороннего квантиля для вероятности: 1-frac{1-alpha}{2}

Источник

Оценка погрешности прямых измерений

Следующий калькулятор может вычислить погрешность прямых измерений для заданной вами выборки и доверительного интервала.

Нас часто окружают прямые измерения: мы меряем линейкой, метром, микрометром, штангенциркулем, бывает измеряем силу электрического тока, напряжение и так далее.

Погрешность измерений

Все измерения делаются с определенной точностью, но часто значение, которое мы получаем при измерении, отличается от эталонного, мы полагаемся на свои чувства, а также на измерительные приборы, но ни те ни другие не совершенны. Именно по этому вычисление погрешности измерений несет особую роль в измерениях.

Результат измерений + учет погрешности можно записать как:

X ± ΔX,

где ΔX – абсолютная погрешность измерений.

Погрешности есть 2-х типов: случайные и постоянные (систематические).

К систематическим погрешностям можно отнести: неточность самого измерительного прибора.

К случайным погрешностям можно отнести: человеческий фактор при нажатии на секундомер например (можно нажать чуть раньше или позже). Чтобы уменьшить процент влияния такого рода фактора нужно испытание проводить много раз и считать среднее значение.

Следующий калькулятор может вычислить случайную погрешность выборки прямых измерений для заданного вами интервала.

Расчет погрешностей непосредственных измерений.

Доверительная вероятность:

 Относительная погрешность в %:

  • 15 декабря 2015
  • Статистика
Источник

Абсолютной погрешностью приближенной величины ∆X называется разность

∆X = |X — X0|

где
X — точное значение измеряемой величины (или истинное значение),
Х0 — приближенное значение (результат измерения)
Относительная погрешность — это отношение абсолютной погрешности этого числа к модулю соответствующего точного числа X
Абсолютная погрешность формула
или
Формула абсолютной погрешности

Замечание

Относительную погрешность количественно определяют в долях единицы или в процентах.

Погрешность отсчёта обычно принимают равной половине цены деления (или ценой наименьшего деления, если показание прибора происходит скачками, как например у секундомера).
Поправкой называется абсолютная погрешность, взятая с обратным знаком.

43185


Источник

Добавить комментарий