Ни один прибор в мире не является точным. Величина, которую он измеряет, всегда будет отличаться от истины на ту величину, которую еще называют его погрешностью. Данная погрешность и будет определять класс точности амперметра. Задачей всех производителей измерительной техники, заключается в том, чтобы эта погрешность была, как можно ниже и стремилась к нулю.

Погрешность амперметра устанавливается в результате поверки и сравнении показаний замеров одних и тех же величин с эталонным или образцовым прибором, имеющий более высокий класс точности. При этом значение, полученное на образцовом приборе, считаются действительными.
Что такое амперметр и какие величины он измеряет
Амперметр — измерительный прибор, который служит для измерения силы тока [І] в электроцепях. Единицей [І] по системе СИ является ампер [А]. Электрические цепи могут проводить ток разной силы, поэтому градуируют приборную шкалу амперметра с различной градацией от микроампера равного 1 мкА = 1×0-6 ампер до килоампера равного: 1 кА = 1 000 ампер.

Важно! В электроцепь амперметр включают последовательно, а для повышения границы измерений, используют специальные устройства: трансформаторы, шунты м магнитные усилители.
Поскольку ток в цепи напрямую зависит от величины сопротивления [R] элементов электроцепи, то собственное сопротивление прибора [Rа] должно быть предельно низким, стремится к нулю. Это приведет к уменьшению влияния устройства в процессе замеров тока в цепи, тем самым будет повышена точность измерения.
Разновидности амперметров
Они могут быть электромеханическими или аналоговыми, цифровыми или электронными. Базовый набор, как правило, состоит из детектора, передающего устройства и индикатора, самописца или запоминающего устройства.

Аналоговые устройства — самые старые из используемых инструментов. Хотя они надежны для статических и стабильных измерений, они не подходят для динамических и переходных условий. Кроме того, они довольно громоздкие и имеют ограничения из-за использования стрелочной индикации.
Электронные инструменты реагируют быстрее и способны мгновенно обнаруживать динамические изменения тока в сети. Примером является цифровой мультиметр, который способен измерить значения тока в динамическом или переходном режиме за секунды.
Виды погрешностей амперметра
Чтобы понять размер погрешности в измерениях, нужно сравнить полученные результаты с эталонными.

В метрологии используют для всех электротехнических измерителей, как для амперметров, так и для вольтметров, несколько видов погрешностей: абсолютную, относительную и приведенную.
Абсолютная погрешность амперметра — это разность Δ между результатом измерения, полученного на шкале прибора (Xи) и действительным значением силы тока в цепи (Xд). Абсолютная погрешность амперметра описывается простой формулой и выражается в единицах тока А.
Δх = Xд−Xи, А
где:
- Δх — дельта Х
- Xд — действительное показание силы тока, принимаемой по образцовому прибору;
- Xи — измеренное значение на шкале прибора.
Относительная погрешность (δ) — отношение абсолютной погрешности амперметра Δх к действительному показанию силы тока, принимаемому по образцовому прибору. Оно может быть указано как в процентах, тогда частное умножается на 100, либо выражаться в относительных единицах.
δ = (Δх : Xд)×100, %
Приведенная погрешность — это значение приведенное к диапазону измерения амперметра, приравненного к его шкале. Его получают в виде частного от абсолютной погрешности Δх и нормируемого значения (Xн), в значениях соответствующим абсолютной погрешности Δх умноженной на 100 %:
δпр = (Δх : Xн)×100, %
Класс точности
Это основная характеристика амперметра, которая согласно еще советскому действующему ГОСТ 1845-59, определяет границы возможных погрешностей.

Для всех электроизмерительных приборов, к которым он относится, класс точности (Кл) обозначается в числовом виде по значению, соответствующему предельной допустимой приведенной погрешности δпр, в %.
Все электрические амперметры подразделяются по точности на 8 классов, а затем по группам, которые является важным признаком их классификации:
- Образцовые: 0.05–0.1–0.2;
- лабораторные: 0.5–0.1;
- технические: 1.5–2.0–4.0.

Обратить внимание! Все приборы, у которых погрешность превышает 4%, являются внеклассными.
Образцовые применяют в электроизмерительных процессах для определения класса точности технических и лабораторных амперметров. Лабораторные применяются в научно-технических процессах при электротехнических исследованиях контроля ведения режимов, например на котельных, ГЭС, ТЭЦ и АЭС.
Важно! На панели амперметра класс точности указывается в кружках, квадратах и звездочках. Если он имеет неравномерную шкалу измерения, Кл обозначается ломаной линией.
Как определить класс точности
Согласно действующих государственных норм, производители амперметров обязаны гарантировать его относительную погрешность измерения, полученную по классу точности, указанной на измерительной панели и в паспорте на прибор. Кроме того, все измерительные приборы должны проходить периодическую поверку в метрологических центрах, на соответствие заводскому классу точности. Если такую аттестацию он не проходит, то не может использоваться в измерительных процессах.

Зная абсолютную погрешность и показание силы тока на шкале, можно просто получить реальную силу тока, действующую в цепи. При этом шкала для применения абсолютной погрешности считается равномерной.

Важно! При выборе шкалы стрелочного амперметра, нужно чтобы рабочее значение тока находилось, примерно, в 2/3 диапазона шкалы. Если стрелка будет находиться практически на 0 или на максимальном показатели шкалы, то относительная погрешность будет очень высокой, то есть доверять таким показаниям не рекомендуется.
Пример нахождения показания амперметра по приведенной погрешности
Для примера рассматривается аналоговый измеритель со шкалой до 25 А.

На шкале имеется обозначение класса точности 2.5, кружок или квадрат отсутствует, поэтому эта погрешность приведенная.
Y=Dх/Xп×100=+/- p
При Хп= 25А и значении p = 2.5 можно рассчитать абсолютную погрешность:
Δх =25/100×2.5=0.625 A
Если пользователь обнаружит на панели класс точности заключенный в квадрат, то погрешность нужно будет определять в процентном выражении от измеренного значения.
При показаниях по шкале Iи = 10 А, погрешность прибора не должна превышать
Δх =10×2.5/100=0.25
При показаниях по шкале Iи=2 А погрешность будет иной:
Δх =2×2.5/100=0.05
При показаниях по шкале Iи=25 А погрешность будет максимальной:
Δх =25×2.5/100=0.625
Вот почему важно, чтобы аналоговый прибор работал при измерениях в 2/3 рабочей шкалы.
Пример нахождения показания амперметра по относительной погрешности
Для того чтобы узнать погрешность для амперметра, имеющего класс точности 0.05/0.02, шкалу измерения 0…25 А. Δх определяют по измеряемому показанию на шкале 10А.
Поскольку класс точности задан как c/d, то расчет будет выполняться по формуле:
δ пр =+/-(с+d(xk/(x-1)))
Где:
- xk=25 А;
- х=10 А;
- с=0.05;
- d=0.02.
δ пр =100 Δх / xN
Нормирующее значение xN=xk=25 A,
δ пр =+/-(0.05+0.02(25/(10-1)))=0.105
Δх = δ пр×xN/100=0.105×25/100=0.026 A
Выбор амперметра по метрологическим характеристикам
Наиболее частым источником ошибки при измерении тока считается то, что амперметр имеет ненулевое входное сопротивление. Напряжение, возникающее на измерителе, приводит к снижению напряжения на тестируемом устройстве. Если уменьшение будет значительным, это приведет к значительно меньшему протеканию тока. Другими словами, измеритель не показывает ток, который фактически протекает в сети.
Для того чтобы максимально нивелировать эту погрешность, применяют два основных типа архитектуры измерения: шунтирующие амперметры и с обратной связью.

Погрешность, вызванная шунтирующим измерителем, определяемая в виде частного напряжения амперметра, деленная на выходное сопротивление.
Амперметры с обратной связью ближе к «идеальным». Он вырабатывает напряжение на пути обратной связи операционного усилителя с высоким коэффициентом усиления. Это напряжение также пропорционально измеряемому току, но не появляется на входе прибора. В результате чувствительные измерители с обратной связью, такие как электрометры и пикоамперметры, имеют нагрузку по напряжению, обычно ограниченную до 200 мкВ.
Для промышленных измерений наиболее часто применяются амперметры аналогового панельного типа. При их выборе следует учитывать такие моменты:
- Выбор типа. При измерении І постоянного, следует выбрать измеритель постоянного тока, то есть с магнитоэлектрическим измерительным механизмом. При измерении переменного тока нужно обратить внимание на форму волны и частоту. Если это синусоида, то измеряют только эффективное значение, с последующим преобразованием в максимальное или среднее значение.
- Класс точности. Чем более высокий класс точности измерителя, тем выше его цена, тем сложнее у него ремонт и метрологическая аттестация. Поэтому для выполнения большинства инженерных измерений достаточно класса точности 1.5, не стоит применять образцовые или лабораторные приборы.
- Выбор шкалы. Чтобы в полной мере использовать возможности амперметра по классу точности, измеряемый показатель должен быть в интервале 1/2 ~ 2/3 максимальной шкалы.
Важно! Внутреннее сопротивление — определяющая величина при выборе измерителя. Ее следует принимать в соответствии с величиной измеряемого импеданса, иначе это приведет к большим ошибкам измерения. Поскольку внутреннее сопротивление отражает энергопотребление самого измерителя, при измерении тока прибор с внутренним сопротивлением следует выбирать, как можно меньшим.
Видео по теме
Как найти инструментальную погрешность амперметра?
Мастер
(1220),
закрыт
6 лет назад
Сергей M.r
Высший разум
(516430)
6 лет назад
Инструментальная погрешность прибора определяется классом точности прибора .При классе точности прибора, например, 1.0 (1%) и пределе измерения 5 А максимально допустимая абсолютная погрешность измерения тока в любой точке шкалы будет равна 5*1/100=0.05 А . Таким образом, если Вы измеряете ток в 1 А, то относительная погрешность будет δ=(0.05/1)*100%=5%.
При измерении тока 4 А δ=(0.05/4)*100%=1.25%.
Это объясняет рекомендацию использовать при измерениях пределы близкие к возможному значению измеряемой величины.
Как-то так.
Удачи.
ThewiowdeУченик (155)
1 год назад
Здравствуйте. Не подскажите если у вольтметра по заданию не задан класс точности, цена деления его шкалы – 5 вольт, предельное значение – 30 вольт, то находится класс точности как отношение абсолютной погрешности к нормируемому значению (30 вольт, так как шкала начинается с нуля, на нём же и стрелка), выраженное в процентах, где абсолютная погрешность это инструментальная (цена деления на два, т. е. 5/2=2,5)? Тогда класс точности = 2,5/30 *100% = 8,33%? И, по-моему, ближайший к этому числу из стандартизированного ряда – 10?
Таня Андреева
Мыслитель
(5255)
6 лет назад
Для того, чтобы найти инструментальную погрешность прибора необходимо цену деления прибора поделить на 2! Это и будет погрешностью (Например: тебе необходимо найти погрешность обычной линейки. У неё цена деления равна 1 мм. Делишь на 2 и получаешь 0,5 мм!)
Оценка погрешностей электрических измерений
Абсолютная
погрешность измерений, производимых
электроизмерительными приборами,
оценивается, исходя из класса точности
приборов. Обозначение класса точности
0,2; 0,5; 1,0 и т.д. не только характеризует
прибор в зависимости от системы,
конструкции, качества материалов,
точности градуировки и других факторов,
но и указывает, что погрешность показаний
прибора соответствующего класса в любом
месте шкалы не должна превышать 0,2%;
0,5%; 1%.
Если
обозначим через
![]() максимально возможное показание прибора,
максимально возможное показание прибора,
а через![]() –
–
номер класса прибора, то получим
абсолютную погрешность прибора
![]() .
.
Например,
вольтметр 0,2 класса (n
= 0,002),
шкала которого рассчитана на 50 В, имеет
абсолютную погрешность
![]() ,
,
а
амперметр класса 1,5, рассчитанный
на максимальное показание 5 А, имеет
абсолютную погрешность
![]() .
.
Так
как абсолютная погрешность считается
одинаковой по всей шкале данного
электроизмерительного прибора, то
относительная погрешность
![]() будет тем больше, чем меньше измеряемая
будет тем больше, чем меньше измеряемая
величина. Если, например, при помощи
указанного амперметра измерить ток
около 4А, то относительная погрешность
будет составлять 1,9%, а при измерении
силы тока около 1А – 7,5%.
При точных
измерениях следует пользоваться такими
приборами, чтобы предполагаемое значение
измеряемой величины составило 70-80% от
максимального (номинального) значения.
Поэтому применяют приборы, имеющие
несколько пределов измерений; при работе
с таким прибором его включают в цепь на
тот предел измерений, который достаточно
близок к предполагаемому значению
измеряемой величины.
Рассмотрим
вычисление погрешностей на следующем
примере.
Определить
погрешность измерения внутреннего
сопротивления элемента, электродвижущая
сила которого Е, напряжение на полюсах
U
и величина тока I.
Для измерения применены вольтметр
класса 0,5 (![]() )
)
и
амперметр класса 1,0 (![]() ).Результаты
).Результаты
измерений следующие: Е = 2В, U
= 1,3 В,
I
= 1,2 А.
Абсолютные
погрешности измерений:
![]() ;
;
![]() .
.
Вычисление
внутреннего сопротивления производим
по формуле
![]() . (1)
. (1)
Максимальная
относительная погрешность может быть
определена общеизвестным методом.
Логарифмируя выражение (1)
lnr
= ln(E-U)
– lnI,
находим относительную
погрешность
![]() ;
;
![]() .
.
Эта
погрешность,
выраженная в процентах, составляет:
![]() .
.
С
помощью формулы (1) находим внутренне
сопротивление r
и абсолютную погрешность
![]() r:
r:
![]() Ом;
Ом;
![]()
![]() =
=
![]() 0,029 Ом =
0,029 Ом =![]() 0,03 Ом.
0,03 Ом.
Следовательно,
внутреннее сопротивление
![]()
![]() 0,03)
0,03)
Ом.
![]() ЛАБОРАТОРНАЯ
ЛАБОРАТОРНАЯ
РАБОТА № 1
Изучение электростатических полей методом электролитического моделирования
Цель
работы:
-
Ознакомиться
с одним из наиболее распространенных
способов изучения характеристик
электростатического поля с помощью
электролитической ванны. -
Практически
исследовать некоторые электростатические
поля.
Приборы и
принадлежности: электростатическая
ванна, набор электродов; индикатор нуля,
пантограф.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задача 1
Для
определения мощности в цепи постоянного тока были измерены напряжение сети U вольтметром класса точности NB
с пределом измерений Um, ток I амперметром класса точности Na
с пределом измерений Im. Определить
мощность, потребляемую приёмником, а также относительную и абсолютную
погрешности её определения.
Дано: ![]()
Найти: ![]()
Решение:
1) Найдем
мощность, потребляемую приемником
![]()
2) Класс
точности определяет приведенную погрешность
![]()
3) Найдем
абсолютную погрешность измерения тока и напряжения
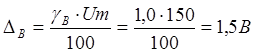 ,
,
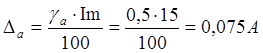 .
.
4) Найдем
абсолютную погрешность измерения мощности при косвенном измерении
![]()
5) Найдем
относительную погрешность измерения мощности
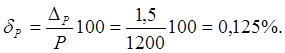
6) Доверительный
интервал результата измерения с вероятностью ![]() .
.
![]()
Задача 2
Проведено пять
независимых наблюдений одного и того же напряжения U.
Найти результат измерения и доверительную вероятность того, что абсолютная
погрешность измерения не превышает по модулю DU. Систематической погрешностью можно пренебречь.
Дано: ![]()
Найти: ![]()
Решение:
1) Определим
среднее арифметическое результатов измерения
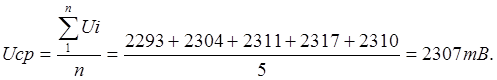
2) Определяем
среднее квадратичное результатов измерения
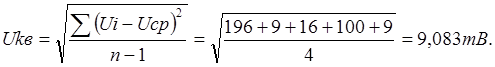
3) Для
определения интервала и вероятности пользуются распределением Стьюдента, где
доверительный интервал равняется ![]() , где
, где
![]() – коэффициент Стьюдента,
– коэффициент Стьюдента,
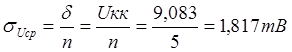 – среднее квадратичное отклонение
– среднее квадратичное отклонение
результата измерения.
4) Находим
доверительный интервал
![]()
5) Результат
измерения
![]()
![]()
Задача 3
Обмотка
магнитоэлектрического измерительного механизма имеет сопротивление RO и рассчитана на предельный длительный ток IO, при котором подвижная часть получает
наибольшее отклонение. Каким образом на базе указанного измерительного
механизма сделать амперметр с пределом измерений Im
и вольтметр с пределом измерений Um?
Дано: ![]()
Найти: ![]() ,
, ![]()
Решение:
1) Расчет
измерительной цепи амперметра
1.1
Определяем коэффициент расширения пределов измерения по току
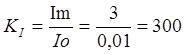
1.2 Определяем сопротивление
шунта
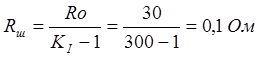
1.3
Схема измерительной цепи
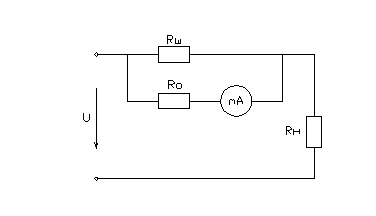
2) Расчет
цепи вольтметра
2.1 Определяем коэффициент
расширения пределов измерения по напряжению
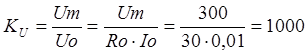
2.2 Определяем добавочное
сопротивление
![]()
2.3
Схема включения
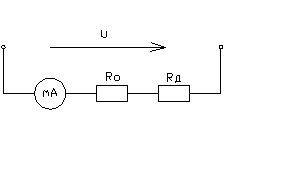
Задача 4
Определить
цену деления измерительных приборов:
1) амперметра, имеющего на шкале na делений и предел измерения Im;
2)вольтметра, имеющего nв делений шкалы и предел измерения Um;
3) ваттметра, имеющего nВТ делений шкалы и пределы измерений по току Im ВТ и напряжению Um
ВТ.
Дано: ![]()
Найти: ![]()
Решение:
1) Цена деления
амперметра

2) Цена деления
вольтметра
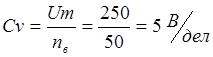
3) Цена
деления ваттметра
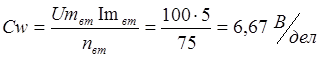
Задача 5
У вольтметра и
амперметра с пределами измерений Um и Im, включенных соответственно через измерительные
трансформаторы напряжения 6000/100 и тока 600/5, отчёт по шкале составил U2 и I2.
Определить напряжение и ток в сети, а также предел допускаемой абсолютной и
относительной погрешностей измерения, если известны класс точности приборов Na и Nв и
измерительных трансформаторов Nтн и Nтт. Привести схему измерения.
Дано: ![]()
Найти: ![]()
Решение:
1) Определим
коэффициенты трансформации трансформатора напряжения и тока
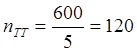
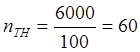
2) Определим
ток и напряжение в сети
![]()
![]()
3) Определим
абсолютные погрешности амперметра и вольтметра
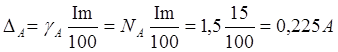
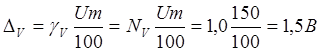
4) Определяем
абсолютные погрешности коэффициентов трансформации трансформатора тока и
напряжения
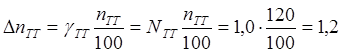
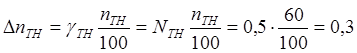
5) Результирующие
абсолютные погрешности измерения тока и напряжения равны
![]()
![]()
6)
Относительные погрешности измерения тока и напряжения
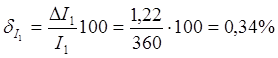
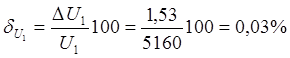
Задача 6
Определить
относительные погрешности измерения сопротивления Rx
в цепи постоянного тока с помощью амперметра и вольтметра при подключении их
двумя возможными способами. Сопротивление амперметра – Ra,
вольтметра – Rв. Сделать вывод о
целесообразности использования той или иной схемы.
Дано: ![]()
Найти: ![]() .
.
Решение:
Принципиальные
схемы
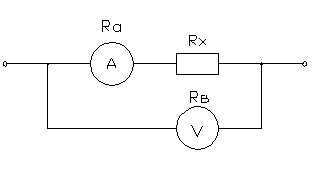
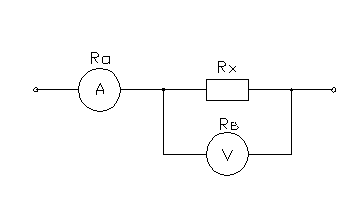
Схема
1 Схема 2
1) Для
схемы включения 1.
1.1.
Измеренное сопротивление.
![]()
1.2.
Определяем абсолютную погрешность.
![]()
1.3.
Определяем относительную погрешность.
Ни один прибор в мире не является точным. Величина, которую он измеряет, всегда будет отличаться от истины на ту величину, которую еще называют его погрешностью. Данная погрешность и будет определять класс точности амперметра. Задачей всех производителей измерительной техники, заключается в том, чтобы эта погрешность была, как можно ниже и стремилась к нулю.

Погрешность амперметра устанавливается в результате поверки и сравнении показаний замеров одних и тех же величин с эталонным или образцовым прибором, имеющий более высокий класс точности. При этом значение, полученное на образцовом приборе, считаются действительными.
V. Точность измерительных приборов.
Точность измерительного прибора – это его свойство, характеризующее степень приближения показаний данного измерительного прибора к действительным значениям измеряемой величины и определяется той наименьшей величиной, которую с помощью этого прибора можно определить надёжно.
Точность прибора зависит от цены наименьшего деления его шкалы и указывается или на самом приборе, или в заводской инструкции (паспорте). Заметим, что точность измерений
обратно пропорциональна относительной погрешности измерений Е: = .
Погрешность электроизмерительных приборов определяется классом точности (или приведенной погрешностью Епр), который указывается на лицевой стороне прибора соответствующей цифрой в кружке. Классом точности прибора К называют выраженное в процентах отношение абсолютной погрешности
к предельному (номинальному) значению хпр измеряемой величины, т. е. к наибольшему её значению, которое может быть измерено по шкале прибора (предел измерения):.
Зная класс точности и предел измерения прибора, можно рассчитать его абсолютную погрешность:
.
Эта погрешность одинакова для любого измерения сделанного с помощью данного прибора. Классов точности семь: 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. Приборы первых трех классов точности (0,1; 0,2; 0,5) называются прецизионными
и используются при точных научных измерениях, приборы остальных классов точности называются
техническими
. Приборы без указания класса точности считаются внеклассными.
Пример. Сила тока измеряется в цепи амперметром, класс точности которого К=0,5, а шкала имеет предел измерения Iпр=10 А. Находим абсолютную погрешность амперметра:
Отсюда следует, что амперметр позволяет измерять силу тока с точностью не более 0,05 А, и поэтому нецелесообразно делать отсчёт по шкале прибора с большей точностью.
Допустим, что с помощью данного амперметра были измерены три значения силы тока: I1=2 А; I2=5 А; I3=8 А. Находим для каждого случая относительную погрешность:
; .
Из этого примера следует, что в третьем случае относительная погрешность самая маленькая, то есть чем больше величина отсчёта по прибору, тем меньше относительная погрешность измерения. Вот почему для оптимального использования приборов рекомендуется их подбирать так, чтобы значение измеряемой величины находилось в конце шкалы прибора. В этом случае относительная погрешность приближается к классу точности прибора. Если точность прибора неизвестна, то абсолютная погрешность принимается равной половине цены наименьшего деления (линейка, термометр, секундомер). Для штангенциркуля и микрометра – точность их нониусов (0,1 мм, 0,01 мм).
Примечания: 1) При отсчетах следует следить за тем, чтобы луч зрения был перпендикулярен шкале. Для устранения так называемой ошибки параллакса на многих приборах устанавливается зеркало («зеркальные приборы»). Глаз экспериментатора расположен правильно, если стрелка прибора закрывает свое изображение в зеркале.
2) При косвенных измерениях (например, определение объема цилиндра по его диаметру и высоте) следует определять все измеряемые вершины с приблизительно одинаковой относительной точностью.
3) При обработке результатов измерений следует помнить, что точность вычислений должна быть согласована с точностью самих измерений. Вычисления, произведенные с большим, чем это необходимо, числом десятичных знаков, приводят к большому объему ненужной работы. Например, если хотя бы одна из величин в каком-либо выражении определена с точностью до двух значащих цифр, то нет смысла вычислять результат с точностью, большей двух значащих цифр. В тоже время в промежуточных расчетах рекомендуется сохранять одну лишнюю цифру, которая в дальнейшем – при записи окончательного результата – будет отброшена. В теории погрешностей из существующих правил округления имеется следующее исключение: при округлении погрешностей последняя сохраняемая цифра увеличивается на единицу, если старшая отбрасываемая цифра 3 или больше 3.
4) Примеры окончательной записи результатов измерений:
ТОЧНОСТЬ ИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
Качество измерительного прибора характеризуется его точностью, которая оценивается погрешностью измерения.
Из рассмотрения вышеизложенного вытекает, что безукоризненно точное измерение электрических величин технически невозможно, т.е. истинное значение измеряемой величины не может быть установлено с помощью измерительного прибора. Поэтому за истинное значение принимают действительное значение измеряемой величины.
Разность между значением величины, измеренной с помощью рабочего прибора а
,, и истинным ее значением
а
называегся абсолютной погрешностью измерения:
Чем меньше абсолютная погрешность в сравнении с измеряемой величиной, тем выше качество измерения. Для характеристики качества измерения вводится относительная погрешность измерения:
Так как величины аи ах
мало отличаются друг от друга, то часто вместо
а
подставляют величину
а„
полученную непосредственно из опыта. На значение абсолютной погрешности измерения влияют главным образом погрешность отсчета показаний, несовершенство методов измерения и погрешность самих приборов.
Погрешности электроизмерительных приборов подразделяются на основные и дополнительные. Основные погрешности характеризуют качество самого прибора, дополнительные погрешности обусловлены отклонением условий эксплуатации от нормальных. Отношение наибольшего значения основной абсолютной погрешности к верхнему пределу измерения прибора определяет качество самого прибора. Это отношение называется приведенной погрешностью. Приведенную погрешность обычно выражают в процентах, и по значению приведенной погрешности все приборы подразделяются на 8 классов точности: 0.05; 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4,0. Приборы, имеющие приведенную погрешность более 4%, считаются внеклассными (это щитовые и учебные приборы). Однако класс точности прибора не определяет точность самого измерения. Для доказательства этого положения в случае, когда абсолютная погрешность не зависит от а
, умножим и разделим выражение относительной погрешности на верхний предел измерения ам:
УО посчитали различия в классах точности ИПУ и ОДПУ причиной роста объёмов КР на СОИ
С требованиями устанавливать в МКД приборы учёта с разными классами точности, то есть в погрешности измерений, не согласилась группа управляющих организаций. Они подали административный иск в Верховный суд РФ с требованием признать недействующим п. 138 ПП РФ № 442.
Управляющие организации указали, что данный пункт противоречит ч. 1 ст. 1 ГК РФ и ч. 1 ст. 1 ЖК РФ. Также он ставит участников отношений по приобретению и оплате фактически потреблённой электроэнергии в неравное положение. Поэтому нормы п. 138 ПП РФ № 442 нарушают принципы равенства участников гражданских правоотношений и равенства участников регулируемых жилищным законодательством отношений по владению, пользованию и распоряжению жилыми помещениями.
Различный механизм работы ИПУ и ОДПУ приводит к увеличению разницы между показаниями общедомового счётчика и показаниями индивидуальных приборов учёта. Объём ресурсов, потреблённых домом с целью содержания общего имущества, значительно превышает норматив и расходы по его оплате ложатся на плечи УО.
Из-за разной погрешности приборов учёта, показания которых учитываются при расчёте платы за электроэнергию для граждан и для лиц, оплачивающих КР на СОИ, возникает ситуация, когда за одинаковый объём ресурса плательщикам выставляются к оплате различные суммы. Все погрешности приборов учёта трактуются в пользу жителей дома, что нарушает принципы справедливости, добросовестности и равенства.
Из-за этого, как указали в иске управляющие организации, они вынуждены оплачивать завышенные суммы за электроэнергию, потреблённую на содержание общего имущества собственников в многоквартирных домах, что приводит к ухудшению их финансового положения и увеличению размера задолженности перед РСО.
Плюсы и минусы установки в многоквартирном доме «умных» счётчиков
213115
Определение класса точности.
Для того, чтобы пользоваться качественным оборудованием для измерений различных величин необходимо знать погрешность, с какой проводит измерения именно это устройство. Технические характеристики любого измерительного прибора включают в себя следующие показатели, которые обычно указывают на шкале:
- единицу измерения величины, которую определяет устройство;
- система принципа действия (магнитоэлектрическая, электромагнитная, индукционная и другие)
- класс точности прибора;
- положение шкалы устройства (горизонтальное, вертикальное или наклонное);
- напряжение, при котором проводилось испытание изоляции корпуса;
- заводской номер и год выпуска.
- род тока, при котором необходимо проводить измерения ( постоянный, переменный).
Одной из характеристик технического измерительного средства является класс точности – величина, определяемая несколькими погрешностями, а именно их пределами. Формула для определения этой характеристики устройства выглядит следующим образом:
γ = ΔXнаиб / Xпр⋅× 100%, где
ΔXнаиб – максимальная абсолютная погрешность измерений;
Xпр – наибольшее значение на шкале прибора.
Класс точности прибора называют еще приведенной погрешностью. По этому показателю все измерительные аппараты делят на восемь классов:
Приборы, имеющие такие группы погрешностей, называют прецизионными, от английского слова «precision», означающего в переводе на русский – точность. Это самые точные устройства и их применяют при проведении лабораторных исследований.
Следующие четыре класса точности:
используют в технической промышленности, и они так и называются – технические.
Производители измерительных технических устройств проставляют его класс точности на шкале, если пометки нет – аппарат считается внеклассным, а его погрешность в измерениях больше 4%.
Класс точности приборов является характеристикой точности в отношении самих устройств, однако этот показатель не определяет точность проведенных измерений. К примеру, класс точности амперметров характеризуется границами абсолютной погрешности и не гарантирует , что в эти показания не внесут коррективы такие показатели как действие магнитного поля, частота переменного тока и перепады температур, а также другие внешние раздражители.
Классы точности приборов могут быть проставлены как латинской буквой, так и арабской или римской цифрами. Числовые арабские значения означают, что основным показателем точности является приведенная погрешность и должны учитываться наибольшее и наименьшее значения ряда измерений. Римская цифра при обозначении класса точности говорит о том, что точность прибора определялась по значению относительной погрешности.
Если при маркировке класса точности прибора на шкале указано дробное число ( к примеру –« 0,01/0,02»), то это означает, что приведенная погрешность при максимальной шкале равна ±0,01%, а в начале ±0,01%. Это применимо в высокочастотных электроизмерительных приборах.
Виды погрешностей амперметра
Чтобы понять размер погрешности в измерениях, нужно сравнить полученные результаты с эталонными.

В метрологии используют для всех электротехнических измерителей, как для амперметров, так и для вольтметров, несколько видов погрешностей: абсолютную, относительную и приведенную.
Абсолютная погрешность амперметра — это разность Δ между результатом измерения, полученного на шкале прибора (Xи) и действительным значением силы тока в цепи (Xд). Абсолютная погрешность амперметра описывается простой формулой и выражается в единицах тока А.
Δх = Xд−Xи, А
где:
- Δх — дельта Х
- Xд — действительное показание силы тока, принимаемой по образцовому прибору;
- Xи — измеренное значение на шкале прибора.
Относительная погрешность (δ) — отношение абсолютной погрешности амперметра Δх к действительному показанию силы тока, принимаемому по образцовому прибору. Оно может быть указано как в процентах, тогда частное умножается на 100, либо выражаться в относительных единицах.
δ = (Δх : Xд)×100, %
Приведенная погрешность — это значение приведенное к диапазону измерения амперметра, приравненного к его шкале. Его получают в виде частного от абсолютной погрешности Δх и нормируемого значения (Xн), в значениях соответствующим абсолютной погрешности Δх умноженной на 100 %:
δпр = (Δх : Xн)×100, %
Класс точности
Во время лабораторных измерений требуется знать точность измерительных средств, которые в свою очередь обладают определенными характеристиками и различаются по устройству. Каждое из средств измерения (СИ) имеют определенные неточности, которые делится на основные и дополнительные. Зачастую возникают ситуации, когда нет возможности или просто не требуется производить подробный расчет. Каждому средству измерения присвоен определенный класс точности, зная который, можно выяснить его диапазон отклонений.
Вовремя выяснить ошибки измерительного средства помогут нормированные величины погрешностей. Под этим определением стоит понимать предельные, для измерительного средства показатели. Они могут быть разными по величине и зависеть от разных условий, но пренебрегать ими не стоит ни в коем случае, ведь это может привести к серьезной ошибке в дальнейшем. Нормированные значения должны быть меньше чем покажет прибор. Границы допустимых величин ошибок и необходимые коэффициенты вносятся в паспорт каждого замеряющего размеры устройства. Узнать подробные значения нормирования для любого прибора можно воспользовавшись соответствующим ГОСТом.

Класс точности измерительного прибора
Обобщающая характеристика, которая определяется пределами погрешностей (как основных, так и дополнительных), а также другими влияющими на точные замеры свойствами и показатели которых стандартизированы, называется класс точности измерительного аппарата. Класс точности средств измерений дает информацию о возможной ошибке, но одновременно с этим не является показателем точности данного СИ.
Средство измерения – это такое устройство, которое имеет нормированные метрологические характеристики и позволяет делать замеры определенных величин. По своему назначению они бывают примерные и рабочие. Первые используются для контроля вторых или примерных, имеющих меньший ранг квалификации. Рабочие используются в различных отраслях. К ним относятся измерительные:
- приборы;
- преобразователи;
- установки;
- системы;
- принадлежности;
- меры.
На каждом средстве для измерений имеется шкала, на которой указываются классы точности этих средств измерений. Они указываются в виде чисел и обозначают процент погрешности. Для тех, кто не знает, как определить класс точности, следует знать, что они давно стандартизованы и есть определенный ряд значений. Например, на устройстве может быть одна из следующих цифр: 6; 4; 2,5; 1,5; 1,0; 0,5; 0,2; 0,1; 0,05; 0,02; 0,01; 0,005; 0,002; 0,001. Если это число находится в круге, то это погрешность чувствительности. Обычно ее указывают для масштабных преобразователей, таких как:
- делители напряжения;
- трансформаторы тока и напряжения;
- шунты.

Обозначение класса точности
Обязательно указывается граница диапазона работы этого прибора, в пределах которой значение класса точности будет верно.
Те измерительные устройства, которые имеют рядом со шкалой цифры: 0,05; 0,1; 0,2; 0,5, именуются как прецизионные. Сфера их применения – это точные и особо точные замеры в лабораторных условиях. Приборы с маркировкой 1,0; 1,5; 2,5 или 4,0 называются технические и исходя из названия применяются в технических устройствах, станках, установках.
Возможен вариант, что на шкале такого аппарата не будет маркировки. В такой ситуации погрешность приведенную принято считать более 4%.
Если значение класса точности устройства не подчеркнуто снизу прямой линией, то это говорит о том, что такой прибор нормируется приведенной погрешностью нуля.

Грузопоршневой манометр, класс точности 0,05
Если шкала отображает положительные и отрицательные величины и отметка нуля находится посередине такой шкалы, то не стоит думать, что погрешность во всем диапазоне будет неизменной. Она будет меняться в зависимости от величины, которую измеряет устройство.
Если замеряющий агрегат имеет шкалу, на которой деления отображены неравномерно, то класс точности для такого устройства указывают в долях от длины шкалы.
Возможны варианты измерительных аппаратов со значениями шкалы в виде дробей. Числитель такой дроби укажет величину в конце шкалы, а число в знаменателе при нуле.
Описание
Приборы представляют собой щитовые приборы магнитоэлектрической системы с креплением подвижной части на кернах, с равномерной шкалой, с нулевой отметкой на краю или внутри диапазона измерений.
Принцип действия приборов основан на взаимодействии магнитного поля постоянного магнита с электрическим током, проходящим по обмотке рамки.
Конструктивно приборы выполнены в малогабаритных пластмассовых корпусах, защищающих измерительный механизм от загрязнений, повреждений, попадания пыли и брызг.
Приборы изготавливаются для эксплуатации в условиях умеренного, тропического климата, а так же для эксплуатации на морских судах. Приборы М42300.8, М42301.8, М4272.8, М4276.8 изготавливаются только для эксплуатации в условиях умеренного климата.
По согласованию с потребителем приборы М42300, М42301 могут быть изготовлены в специальном исполнении и предназначены для работы в условиях с повышенными механическими характеристиками эксплуатации.
Приборы М4272, М4276 могут изготавливаться со сменными шкалами с обозначением (с).
Приборы М42301 могут изготавливаться в исполнении с возможностью подсветки шкалы с обозначением (п) и чистой шкалой.
Приборы относятся к невосстанавливаемым, одноканальным, однофункциональным изделиям.
Фотография общего вида приборов представлена на рисунке 1.
Схема пломбировки от несанкционированного доступа, обозначение места нанесения знака поверки представлены на рисунке 2.
а) общий вид прибора с нулевой отметкой шкалы внутри диапазона измерений
б) общий вид прибора с нулевой отметкой шкалы на краю диапазона измерений
Обозначение на рисунке приборов:
1 — клеймо ОТК (место клеймения заполняется мастикой),
2 — поверительное клеймо (место клеймения заполняется мастикой).
3 — дата выпуска (краска штемпельная).
а) Схема пломбировки и клеймения микроамперметров, миллиамперметров, амперметров и вольтметров М42300, М42301
Обозначение на рисунке приборов:
1 — клеймо ОТК (место клеймения заполняется мастикой),
2 — поверительное клеймо (место клеймения заполняется мастикой),
3 — дата выпуска (краска штемпельная).
б) Схема пломбировки и клеймения микроамперметров, амперметров и вольтметров М42303
Обозначение на рисунке приборов:
1 — клеймо ОТК (место клеймения заполняется мастикой),
2 — поверительное клеймо (место клеймения заполняется мастикой).
3 — дата выпуска (краска штемпельная).
в) Схема пломбировки и клеймения миллиамперметров, амперметров и вольтметров М4264М
Обозначение на рисунке приборов:
1 — клеймо ОТК (место клеймения заполняется мастикой),
2 — поверительное клеймо (место клеймения заполняется мастикой),
3 — дата выпуска (краска штемпельная).
г) Схема пломбировки и клеймения миллиамперметров, амперметров и вольтметров М4272, М4276
Обозначение на рисунке приборов:
1 — клеймо ОТК (место клеймения заполняется мастикой),
2 поверительное клеймо (место клеймения заполняется мастикой),
3 — дата выпуска (краска штемпельная).
д) Схема пломбировки и клеймения миллиамперметров, амперметров и вольтметров М4278
Обозначение на рисунке приборов:
1 — клеймо ОТК (место клеймения заполняется мастикой),
2 — поверительное клеймо (место клеймения заполняется мастикой),
3 — дата выпуска (краска штемпельная).
е) Схема пломбировки и клеймения миллиамперметров, амперметров и вольтметров М42607, М42608
п.З
| ( | |
| Y «Г- г’
/\ L. |
iv __1J А |
п.1 У V п.2
Обозначение на рисунке приборов:
1 — клеймо ОТК (место клейметтия заполняется мастикой),
2 — поверительное клеймо (место клеймения заполняется мастикой),
3 — дата выпуска (краска штемпельная).
ж) Схема пломбировки и клеймения миллиамперметров, амперметров и вольтметров М42609
Рисунок 2 — Схема пломбировки от несанкционированного доступа, обозначение места
нанесения знака поверки.
Нормирование
Классы точности средств измерений сообщают нам информацию о точности таких средств, но одновременно с этим он не показывает точность измерения, выполненного с помощью этого измерительного устройства. Для того, чтобы выявить заблаговременно ошибку показаний прибора, которую он укажет при измерении люди нормируют погрешности. Для этого пользуются уже известными нормированными значениями.й
Нормирование осуществляется по:

Формулы расчета абсолютной погрешности по ГОСТ 8.401
Каждый прибор из конкретной группы приспособлений для замера размеров имеет определенное значение неточностей. Оно может незначительно отличаться от установленного нормированного показателя, но не превышать общие показатели. Каждый такой агрегат имеет паспорт, в который записываются минимальные и максимальные величины ошибок, а также коэффициенты, оказывающие влияние в определенных ситуациях.
Виды маркирования
Классы точности абсолютно всех измерительных приборов подлежат маркировке на шкале этих самых приборов в виде числа. Используются арабские цифры, которые обозначают процент нормированной погрешности. Обозначение класса точности в круге, например число 1,0, говорит о том, что ошибочность показаний стрелки аппарата будет равна 1%.
Если в обозначении используется кроме цифры еще и галочка, то это значит, что длина шкалы применяется в роли нормирующего значения.
Латинские буквы для обозначения применяются если он определяется пределами абсолютной погрешности.
Существуют аппараты, на шкалах которых нет информации о классе точности. В таких случаях абсолютную следует приравнивать к одной второй наименьшего деления.
Пример нахождения показания амперметра по приведенной погрешности
Для примера рассматривается аналоговый измеритель со шкалой до 25 А.

На шкале имеется обозначение класса точности 2.5, кружок или квадрат отсутствует, поэтому эта погрешность приведенная.
Y=Dх/Xп×100=+/- p
При Хп= 25А и значении p = 2.5 можно рассчитать абсолютную погрешность:
Δх =25/100×2.5=0.625 A
Если пользователь обнаружит на панели класс точности заключенный в квадрат, то погрешность нужно будет определять в процентном выражении от измеренного значения.
При показаниях по шкале Iи = 10 А, погрешность прибора не должна превышать
Δх =10×2.5/100=0.25
При показаниях по шкале Iи=2 А погрешность будет иной:
Δх =2×2.5/100=0.05
При показаниях по шкале Iи=25 А погрешность будет максимальной:
Δх =25×2.5/100=0.625
Вот почему важно, чтобы аналоговый прибор работал при измерениях в 2/3 рабочей шкалы.
Пределы
Как уже говорилось раньше, измерительный прибор, благодаря нормированию уже содержит случайную и систематические ошибки. Но стоит помнить, что они зависят от метода измерения, условий и других факторов. Чтобы значение величины, подлежащей замеру, было на 99% точным, средство измерения должно иметь минимальную неточность. Относительная должна быть примерно на треть или четверть меньше погрешности измерений.

Базовый способ определения погрешности
При установке класса точности в первую очередь нормированию подлежат пределы допустимой основной погрешности, а пределы допускаемой дополнительной погрешности имеют кратное значение от основной. Их пределы выражают в форме абсолютной, относительной и приведенной.
Приведенная погрешность средства измерения – это относительная, выраженная отношением предельно-допустимой абсолютной погрешности к нормирующему показателю. Абсолютная может быть выражена в виде числа или двучлена.
Если класс точности СИ будет определяться через абсолютную, то его обозначают римскими цифрами или буквами латиницы. Чем ближе буква будет к началу алфавита, тем меньше допускаемая абсолютная погрешность такого аппарата.

Класс точности 2,5
Благодаря относительной погрешности можно назначить класс точности двумя способами. В первом случае на шкале будет изображена арабская цифра в кружке, во втором случае дробью, числитель и знаменатель которой сообщают диапазон неточностей.
Основная погрешность может быть только в идеальных лабораторных условиях. В жизни приходится умножать данные на ряд специальных коэффициентов.
Дополнительная случается в результате изменений величин, которые каким-либо образом влияют на измерения (например температура или влажность). Выход за установленные пределы можно выявить, если сложить все дополнительные погрешности.
Случайные ошибки имеют непредсказуемые значения в результате того, что факторы, оказывающие на них влияние постоянно меняются во времени. Для их учета пользуются теорией вероятности из высшей математики и ведут записи происходивших раньше случаев.

Пример расчета погрешности
Статистическая измерительного средства учитывается при измерении какой-либо константы или же редко подверженной изменениям величины.
Динамическая учитывается при замерах величин, которые часто меняют свои значения за небольшой отрезок времени.
