Как найти относительную погрешность температуры

Версия для печати

В соответствии с уравнением (1) погрешность результата измерения объёма газа, приведенного к стандартным условиям, обусловлена следующими составляющими:

• погрешностью измерения объёма газа счётчиком в рабочих условиях;
• погрешностью измерения и регистрации абсолютной температуры газа;
• погрешностью измерения и регистрации абсолютного давления газа;
• методической погрешностью реализации алгоритма измерительной задачи вычислителем (далее – методическая погрешность вычислителя);
• методической погрешностью определения коэффициента сжимаемости;
• погрешностью определения объёма газа при стандартных условиях, которая связана с введением условно-постоянных значений величин (МИ 3235-2009).

Рассмотрим каждую из вышеперечисленных составляющих погрешности измерения объёма газа.

Погрешность измерения объёма газа в рабочих условиях определяется относительной погрешностью δp применяемого счётчика (турбинного, ротационного, вихревого) в соответствии с его паспортными метрологическими характеристиками.

Способы вычислений относительных погрешностей измерений и регистраций по каналам вычислителя (с учётом дополнительных погрешностей) абсолютной температуры δT и абсолютного давления δp подробно рассмотрены в ПР 50.2.019-2006 и МИ 3235-2009. Кроме того, в рекомендации МИ 3235-2009 анализируется случай измерения абсолютного давления газа посредством датчика избыточного давления и барометра. Кратко приведём основные шаги вычислений относительных погрешностей измерений и регистрации (по каналам вычислителя) абсолютного давления и абсолютной температуры. Для получения числовых данных примем, что узел учёта газа оснащён первичными измерительными преобразователями (датчиками):

• температуры с пределами измерений от -50°С до +50°С и абсолютной погрешностью ± (0,25 + 0,0035|t|) °C; абсолютная погрешность показаний и регистрации температуры по каналу вычислителя не выходит за пределы допускаемых значений ±0,1 °С;
• абсолютного давления с верхним пределом измерений 0,63 МПа и приведенной погрешностью ±0,25%; дополнительная погрешность преобразователя давления от изменения температуры окружающей среды на каждые 20°С составляет (0,025(P_В/P) + 0,125)%; нормальные условия поверки преобразователя абсолютного давления t_nom = (20 ± 5) °C;
• или избыточного давления и барометром; датчик избыточного давления промышленной группы “МИДА” имеет верхний предел измерений 0,4 МПа и пределы основной приведенной погрешности ±0,25%; дополнительная погрешность этого измерительного преобразователя, связанная с изменением температуры окружающей среды, составляет 0,25% на каждые 10 °С; условия поверки датчика избыточного давления нормальные (20±5) °С;
• приведенная погрешность показаний и регистрации давления по каналу вычислителя (при использовании любого из вышеперечисленных датчиков) не выходит за пределы допускаемых значений ±0,05%.

Примем, что счётчик измеряет объём газа с параметрами состояния: t = 15°C, P(abc) = 0,15 МПа. Температура в помещении, где расположен датчик давления, равна 26°С. Допустим, что атмосферное давление при измерении объёма газа не меняется и составляет 0,0997 МПа (приблизительно 747 мм рт.ст.). Относительная погрешность широко применяемых барометров, как правило, равна ±1%.

Учитывая представленные первичные данные, рассмотрим примеры вычисления относительных погрешностей измерений и регистраций абсолютной температуры и абсолютного давления, которые далее используются в качестве начальных данных при расчёте погрешности измерения объёма газа, приведенного к стандартным условиям.

Вычисление относительной погрешности измерения и регистрации абсолютной температуры выполняется следующим образом:

• находим относительную погрешность измерения абсолютной температуры первичным преобразователем:

  

  t = 15°C – температура газа;

• относительная погрешность регистрации температуры по каналу вычислителя:

  

Следовательно, относительная погрешность измерения и регистрации температуры по каналу “первичный измерительный преобразователь – вычислитель” определяется выражением:

Проведём расчёт относительной погрешности измерения и регистрации абсолютного давления газа, при этом рассмотрим два случая измерения этой величины: посредством датчика абсолютного или избыточного давления:

относительная погрешность измерения абсолютного давления первичным измерительным преобразователем абсолютного давления газа вычисляется по формуле:

где γ_p – приведенная погрешность первичного измерительного преобразователя абсолютного давления;

p_max – верхний предел измерений датчика абсолютного давления;

p = 0,63 МПа – абсолютное давление газа;

дополнительная погрешность датчика абсолютного давления, вызванная изменением температуры окружающей среды, описывается выражением:

t_p = 26°C- температура воздуха в помещении, где размещен датчик давления;

t_nom = 20°C – температура, при которой проведена поверка первичного измерительного преобразователя абсолютного давления;

относительная погрешность показаний и регистрации абсолютного давления по каналу вычислителя равна:

γ_pcl = 0,05% – приведенная погрешность показаний и регистрации абсолютного давления по каналу вычислителя.

Относительная погрешность измерения и регистрации абсолютного давления по каналу “первичный измерительный преобразователь абсолютного давления – вычислитель” рассчитывается по формуле:

В случае применения датчика избыточного давления абсолютное давление газа представлено суммой p = p_b + p_вх, где p_b – атмосферное давление, измеряемое барометром; p_вх – избыточное давление газа.

Относительная погрешность измерения избыточного давления первичным измерительным преобразователем избыточного давления газа вычисляется по формуле, аналогичной формуле (5):

γp = 0,25% – основная приведенная погрешность первичного измерительного преобразователя избыточного давления;

p_max = 0,4 МПа – избыточное давление газа;

дополнительная погрешность датчика избыточного давления, вызванная изменением температуры окружающей среды, рассчитывается в соответствии с выражением:

t_p = 26°C- температура воздуха в помещении, где размещен датчик избыточного давления;

t_nom = 20°C – температура, при которой проведена поверка первичного измерительного преобразователя избыточного давления;

относительная погрешность показаний и регистрации избыточного давления по каналу вычислителя равна:

γpcl = 0,05% – приведенная погрешность показаний и регистрации избыточного давления по каналу вычислителя.

Принимая во внимание равенство (9), несложно получить выражение для относительной погрешности измерения и регистрации избыточного давления по каналу “первичный измерительный преобразователь избыточного давления – вычислитель”:

где δ_p1, δ_p2, δ_p3 – составляющие относительной погрешности измерения и регистрации избыточного давления по каналу вычислителя рассчитываются по формулам (10-12);

δ_pb – относительная погрешность измерения атмосферного давления (по условию ±1%).

Полученный по формуле (13) результат находится на уровне результата формулы (8), хотя “теоретически” измерение абсолютного давления газа посредством датчика абсолютного давления точнее. Близость относительных погрешностей результатов измерений абсолютного давления объясняется удачным выбором датчика избыточного давления, у которого верхний предел измерений расположен достаточно близко от значения измеряемой величины.

Примечание. Вычисления в числовых примерах вопреки правилам округления погрешностей выполнены до трёх значащих цифр после запятой с тем, чтобы дать “почувствовать” изменение составляющих погрешностей.

После подробных числовых примеров расчёта относительных погрешностей измерения и регистрации по каналам вычислителя абсолютного давления и абсолютной температуры вернёмся к обсуждению оставшихся составляющих погрешности измерения объёма газа при стандартных условиях, которые перечислены в начале п.5.

Методическая относительная погрешность вычислителя δ_ВЧ устанавливается на стадии проведения испытаний с целью утверждения типа средства измерений и также содержится в его паспортных данных. Наиболее часто встречающиеся методические погрешности вычислителей находятся в диапазоне ±(0,02-0,05)%.

Методическая относительная погрешность определения коэффициента сжимаемости приведена в ГОСТ 30319.2-96, также обобщённые оценки этой погрешности даны в ГОСТ Р 8.662-2009 (ISO 20765-1). В соответствии с рекомендациями ГОСТ 30319.2-96 в наиболее благоприятных областях определения методов NX 19 мод. и GERG 91 мод. примем |δ_K| = 0,11%

Алгоритм оценивания относительной методической погрешности измерения объёма газа, возникающей вследствие приближения условно-постоянных значений величин, подробно изложен в МИ 3235-2009. В рамках рассматриваемой измерительной задачи за условно-постоянные величины вследствие рассмотренной выше оснащённости типового узла учёта принимают величины, характеризующие состав газа. Выбор условно-постоянных величин зависит от метода определения коэффициента сжимаемости: в случае применения методов NX 19 мод. или GERG 91 мод. за условно-постоянные величины принимают молярные доли углекислого газа и азота x_CO2, x_N2 и плотность газа p_c при стандартных условиях; если используется уравнение состояния AGA8, то условно-постоянными являются молярные доли x_i, i = 1,…,21, всех компонентов природного газа.

Зная погрешности результатов измерений абсолютного давления, абсолютной температуры и молярных долей компонентов природного газа, необходимо оценить их влияние на результат измерения объёма газа при стандартных условиях, т.е. требуется вычислить частные составляющие погрешности измерения объёма газа при стандартных условиях, обусловленные погрешностями измерений величин, входящих в уравнение измерений (1). В настоящей рекомендации частные составляющие погрешности измерений объёма газа при стандартных условиях определяются путём численного расчёта, в основу которого положено классическое практическое определение абсолютной погрешности Δ результата измерения абстрактной физической величины A.

Δ = A – A_Д, (14)
где A_Д – действительное значение физической величины.

При определении частной составляющей погрешности измерения объёма газа по формуле (14) за действительное значение объёма принимают результат вычислений по формуле (1) для действительных значений входящих в неё величин. За результат измерения объёма принимают его значение, найденное по той же формуле (1), при изменённом значении (относительно действительного) входящей в неё какой-либо одной физической величины. Для корректного определения частной составляющей погрешности по формулам (1) и (14) изменение значения рассматриваемой физической величины в формуле (1) должно быть обусловлено погрешностью её измерения. Тогда, в соответствии с выражением (14) частная составляющая абсолютной погрешности измерения объёма газа при стандартных условиях, обусловленная погрешностью измерения, например абсолютного давления, запишется в виде:

где:

V_с,p – задаётся выражением (1);

Δp_i = δ_p • p_i – изменение значения давления в рабочих условиях, связанное с погрешностью его измерения.

Коэффициент сжимаемости природного газа в общем случае является функцией абсолютного давления, абсолютной температуры и состава газа. В формуле (16) для краткости введён вектор x = {x_j}, j = 1,…,n молярных долей компонентов газовой смеси.

Выполнив несложные преобразования разности (15) с учётом выражений (1) и (16), получим формулу для относительной частной составляющей погрешности измерения объёма газа при стандартных условиях δV_с,p, обусловленную погрешностью измерения давления:

где:

Рассуждая как в предыдущем случае, запишем выражение для абсолютной частной составляющей погрешности измерения объёма газа при стандартных условиях, которая связана с погрешностью измерения абсолютной температуры:

где:

V_с,T – как и прежде, определяется выражением (1).

После подстановки в равенство (18) выражений (1) и (19) и последующих несложных преобразований, получим формулу для относительной частной составляющей погрешности измерения объёма газа при стандартных условиях, связанную с погрешностью измерения абсолютной температуры:

где:

Аналогично оценивается составляющая погрешности измерения объёма, приведенного к стандартным условиям, обусловленная погрешностями определения компонентного состава, т.е. погрешностями измерения молярных долей компонентов при использовании для определения коэффициента сжимаемости уравнения состояния AGA8 или погрешностями определения молярных долей углекислого газа и азота, а также погрешностью измерения плотности газа при стандартных условиях, если коэффициент сжимаемости газа рассчитывают по методу NX 19 мод. или GERG 91 мод.

Для определённости рассмотрим случай измерения молярных долей всех компонентов природного газа (уравнение состояния AGA8).

Примем, что изменению подверглось найденное экспериментально значение одной молярной доли из компонентного состава. Тогда, по определению, легко записывается оценка абсолютной частной составляющей погрешности измерения объёма газа при стандартных условиях, которая обусловлена таким изменением результата измерения молярной доли компонента (j = 1,…,21):

где:

V_{с, x} – по-прежнему, определяется выражением (1);

Δx – изменение вектора состава, которое, по условию, имеет проекции на оси координат (0,…,Δx_j,…,0), j = 1,…,21.

После простых преобразований равенства (21) с учётом (1) и (22) несложно установить формулу для относительной частной составляющей погрешности измерения объёма газа при стандартных условиях, которая связана с изменением значения одной молярной доли (какого-то компонента) вследствие погрешности её измерения:

где ΔK_xj = K ( p, T, x₁,…,x_j + Δx_j,…,x₂₁) – K ( p, T, x₁,…,x_j,…,x₂₁)
j = 1,…,21

Относительную методическую составляющую погрешности измерения объёма газа при стандартных условиях, которая имеет место вследствие введения условно-постоянных значений величин, оценим согласно МИ 3235-2009. Для числовой оценки этой составляющей погрешности достаточно применения формулы:

где K = K(p,T,x; K* = K(p_b, p_вх,T,x_h) – коэффициенты сжимаемости природного газа в рабочей и “смещенной” точках. Смещение реальных рабочих условий вызвано введением условно-постоянных величин: p_b– атмосферного давления; x_h – компонентного состава газа, который задаётся либо молярными долями всех компонентов, либо молярными долями углекислого газа и азота в сочетании с плотностью газа для стандартных условий; P_ex – избыточное давление газа.

На практике методическую составляющую погрешности измерения объёма газа, заданную формулой (24), достаточно надёжно можно оценить только численно, непосредственно вычисляя коэффициент сжимаемости газа в рабочей и смещённой (из-за сделанного приближения условно-постоянных значений величин) точках. Если узел учёта оснащён датчиком абсолютного давления, то условно-постоянными являются только значения величин, характеризующих состав газа.

После того как определены все составляющие, можно вывести формулу для относительной погрешности результата измерения объёма газа при стандартных условиях, полученного с помощью турбинных, ротационных и вихревых счётчиков газа. При построении формулы используем следующую модель: считаем, что все составляющие (включая методические) погрешности измерения объёма газа при стандартных условиях рассматриваются как случайные величины, характеризующиеся равномерной плотностью вероятности. Для справедливости такого представления необходимо принять, что все выявленные в соответствии с природой причин их порождающих систематические погрешности учтены в виде поправок к результатам измерения физических величин, участвующих в определении объёма, а оставшиеся не исключённые систематические погрешности согласно РМГ 29-99 также рассматриваются как квазислучайные величины.

При сложении случайных величин складываются их дисперсии, являющиеся мерой их среднеквадратичных отклонений (СКО). Распределение плотности вероятности суммы случайных величин с произвольными плотностями вероятностей согласно центральной предельной теореме близко к нормальному распределению, если число слагаемых более трёх. В соответствии с изложенной моделью найдём СКО относительной погрешности измерения объёма газа при стандартных условиях, используя “геометрический” закон сложения СКО составляющих погрешности. Границы погрешности измерения объёма газа при стандартных условиях устанавливаются для доверительной вероятности p = 0,95 посредством коэффициента t = 1,132. Учитывая изложенные модельные представления, в ранее принятых обозначениях несложно записать формулу для расчёта относительной погрешности измерения объёма газа при стандартных условиях с помощью турбинного, ротационного или вихревого счётчика:

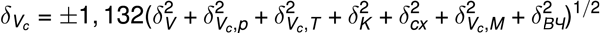
В формуле (25):

δ_V – относительная погрешность измерения объёма газа в рабочих условиях – заданная величина на основании описания типа средства измерения – счётчика газа;

δ_Vс,P – относительная погрешность измерения объёма газа, приведенного к стандартным условиям, – обусловлена погрешностью измерения и регистрации абсолютного давления, определяется выражением (17);

δ_Vс,T – относительная погрешность измерения объёма газа, приведенного к стандартным условиям, – имеет место из-за погрешности измерения и регистрации абсолютной температуры, определяется формулой (20);

δ_K – относительная погрешность определения коэффициента сжимаемости газа – заданная величина по ГОСТ 30319.2-96 или ГОСТ Р 8.662-2009 (δ_K ≈ 0,11%);

верхний радикал в выражении (26) используется в сочетании с уравнением состояния AGA8,

δ_Vс,xj – определяются формулой (23), j=1,…,21;

нижний радикал в выражении (26) применяется в случае определения коэффициента сжимаемости по методам NX 19 мод. или GERG 91 мод.; относительные составляющие погрешности измерения объёма при
стандартных условиях δ_Vс,CO₂, δ_Vс,N₂,
δ_Vс,P_c также определяются выражением (23), если считать, что вектор
компонентного состава x при использовании методов NX 19 мод. или
GERG 91 мод. имеет проекции x₁ = x_N2, x₂ =
x_CO2, x₃ = p_с

δ_Vс,M – относительная методическая погрешность измерения объёма газа при стандартных условиях, вызванная введением условно-постоянных значений величин, – определяется соотношением (24);

δ_ВЧ – относительная методическая погрешность вычислителя – заданная величина в соответствии с описанием типа средства измерения (примем на основании анализа описаний типа аналогичных средств измерений, что эта погрешность равна ±0,05%).

Выведенная формула (25) в сочетании с одним из упомянутых уравнений состояния природного газа позволяет выполнить расчёт относительной погрешности измерения объёма газа при стандартных условиях на узле учёта, оснащённом турбинным, ротационным или вихревым счётчиком газа. Далее будут приведены результаты численных расчётов, демонстрирующие применимость разработанного метода (алгоритма) для решения конкретных задач, связанных с проектированием и эксплуатацией узлов учёта газа.

< назад / К содержанию / вперед >

4.1
Вычислить коэффициент линейного
расширения по формуле (1.2):

,
(1.2)

где
t
– изменение
температуры,

t
= t
– t_о
, ^оС
или
К

Внимание!
Значение разности
температур t
не зависит от выбора единиц измерения
(в кельвинах К
или в
градусах ^оС
)!

t_о
– начальная температура, ^оС;

t
– конечная температура, ^оС;

ℓ –
абсолютное изменение длины тела при
изменении

температуры
на t

ℓ =
ℓ – ℓ_о,
мм

где
ℓ_о
– начальная длина при температуре t_о,
мм,

ℓ – конечная
длина при температуре t,
мм.

4.2
Результаты вычислений записать в таблицу
3.1.

5 Вычисление относительной и абсолютной погрешности

Общие
замечания. Погрешность определения
значения коэффициента теплового
расширения 
определяется суммой погрешностей
измерений приборов: индикатора, линейки,
термометра.

5.1
Вычислить относительную погрешность
определения коэффициента линейного
расширения 
по формуле:

,
(5.1)

где

– относительная
погрешность определения ,
безразмерная величина;

в
числителях дробей в формуле (5.1):

(ℓ),
ℓ_о
,(t)
– погрешности
измерений приборов:

(ℓ)=
0,01 мм
– индикатора;

ℓ_о
= 1 мм
– линейки;

(t)=
1К
– термометра;

в
знаменателях дробей в формуле (5.1):

ℓ,
ℓ_о
,t
– полученные
экспериментальные значения (таблица
3.1):

ℓ – изменение
длины по индикатору, мм;

ℓ_о
– начальная длина, мм;

t
– разность температур, К.

5.3
Выразить 
в процентах
и записать в таблицу 3.1.

5.4
Вычислить абсолютную погрешность
определения коэффициента линейного
теплового расширения для данного
вещества 
по формуле
(5.2).

Поскольку
смысл относительной погрешности:

,

тогда

,
(5.2)

где

– абсолютная
погрешность определения ,
К^-1;

 –
относительная погрешность, вычисленная
по формуле (5.1) (без
%);

 –
полученное
в данной работе значение коэффициента
линейного теплового расширения (таблица
3.1), К^-1.

5.3
Записать значения погрешностей в
таблицу 3.1.

6 Запись полученных результатов

Полученные
результаты – значение коэффициента
линейного теплового расширения для
данного вещества с абсолютной погрешностью,
единицами измерения и относительной
погрешностью, а также табличное значение
записать следующим образом:

где

_{(вещество)}
= _эксп
±

_эксп
– полученное в данном эксперименте
значение коэффициента линейного
теплового расширения;

_таблич
– «табличное» значение коэффициента
линейного теплового расширения для
данного вещества, взятое из таблиц
Приложении А (или любого справочника).

Пояснения
к форме записи результатов:

Примечания.

• В
  окончательной записи результатов
  значения a
  и его абсолютной погрешности ∆
  a
  округлить до целых значений (или до
  десятых долей).

• Количество
  знаков после запятой в значениях a
  и ∆a
  – должно
  быть одинаковым.

• Значение
  относительной
  погрешности
  выразить в
  процентах
  и округлить до десятых долей процента).

• Не
  забудьте записать единицы измерений
  a
  , ∆a
  , a
  _табл !

Подборка по базе: МОРДА НА РЕШЕНИЕ КомГВ.docx, Математика. Решение производных и теория вероятностей..docx, Практичсекая работа Собеседование решение задач.docx, Эконометрика решение.docx, Политолог решение.docx, задача 1. решение docx.docx, Практическая Решение экспериментальных хадач Немет (1).docx, ТК – 10. Решение.docx, 9 класс математический маятник решение задач.docx, бланк на решение.docx

На платформу весов поставили эталонную гирю весом 1 кг. Весы показали значение 1,005 кг. Определить абсолютную и относительную погрешности измерения. Найти приведенную погрешность весов, если верхний предел измерения (нормирующее значение) равен 5 кг.

Решение

Абсолютную погрешность находим по формуле:

Δ = x_изм – x_д

где x_изм и x_д – измеренное и действительное значения величины.

Δ = 1,005–1=0,005кг

Относительную погрешность определим по формуле:

Определим приведенную погрешность:

-верхний предел измерений средства измерений

Задача 2.

При поверке методом сличения последовательно включили поверяемый и эталонный амперметр. Эталонный амперметр показал 2,4 А, поверяемый амперметр показал 2,45 А. Предел измерений поверяемого амперметра 3 А. Для поверяемого амперметра определить абсолютную, относительную и приведенную погрешности.

Δ = x_изм – x_д

где x_изм и x_д – измеренное и действительное значения величины. За действительное значение применяем показания эталонного амперметра.

Δ =2,45–2,4=0,05А

Определим относительную погрешность:

Определим приведенную погрешность:

Задача 3.

Поверяемый термометр в тающем льду показал 0,5ºС, а в кипящей воде 101ºС. Предел измерений термометра 150ºС. Определить абсолютные погрешности термометра при этих температурах и максимальную приведенную погрешность термометра.

Действительно значение температуры кипения – Т_к=100ºС

Действительное значение температуры таяния льда Т_т=0ºС

Определим абсолютные погрешности термометров:

-при измерении температуры таящего льда:

Δ = x_изм – x_д=0,5-0=0,5 ºС

-при измерении температуры кипения воды:

Δ =101-100=1 ºС

Определим максимальную приведенную погрешность прибора:

Задача 4.

Приведенная погрешность манометра равна 0,5 %, диапазон измерения 0…10 МПа. Определить относительные погрешности измерения давлений 1 МПа и 9 МПа.
Относительная погрешность результата измерения определяется выражением:

где – абсолютная погрешность

Абсолютная погрешность будет определяться выражением:

– приведенная погрешность.

-абсолютная погрешность при измерении давлений:

МПа

-относительная погрешность при измерения давления 1МПа

-относительная погрешность при измерения давления 9МПа

Задача 5

Определить допустимую приведенную погрешность акселерометра для измерения виброускорения 60 м/с² с погрешностью ± 2 м/с². Диапазон измерения акселерометра 0…100 м/с².

Максимальное измеренное значение виброускорения:

Х_max=60+2=62 м/с²

Минимальное измеренное значение виброускорителя:

Х_min=60-2=58 м/с²

Допуск:

IT=62-58=4м/с²

Определим основную допустимую абсолютную погрешность акселерометра:

Δ= 0,33∙IТ=0,33∙4=1,32м/с²

Определим допустимую приведенную погрешность прибора:

%

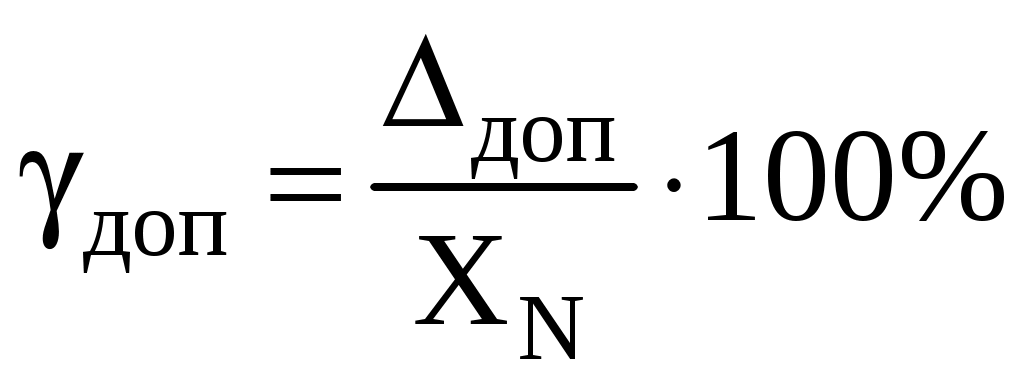
Задача 6.

Напряжение на выводах солнечной батареи должно превышать 1,20 В. При приемочных испытаниях батареи было получено значение 1,21 В. Можно ли обосновано утверждать, что солнечная батарея годна к эксплуатации, если измерение произведено с относительной погрешностью 0,25 %?
Определим абсолютную погрешность измерения

Δ = x_изм – x_д=1,21-1,2=0,01 В

Определим относительную погрешность измерения

Так как относительная погрешность измерения превышает относительную погрешность прибора, можно утверждать, что батарея не годна к эксплуатации

Задача 7

На бензоколонке заливают бензин с абсолютной систематической погрешностью Δ = – 0,1 л. Вычислите относительные погрешности, возникающие при покупке 16 л и 40 л бензина.

Относительную погрешность определим по формуле:

Относительная погрешность при заливке 16л

Относительная погрешность при заливке 40л

Задача 8.

Оценить абсолютную погрешность измерения температуры человеческого тела, если после начала измерения прошло время t =3 мин. Показания термометра изменяются по экспоненциальному закону:

Где температура тела Θт = 36,6ºС, температура окружающего воздуха Θокр = 23ºС. постоянная времени Т = 1 мин. Инструментальной погрешностью термометра пренебречь.

Изменение температуры за 1 минуту

=8,37

=8,37^ºС

Т.е. через 1 минуту термометр нагреется до температуры: 23+8,37= 31,37ºС

Изменение температуры за вторую минуту:

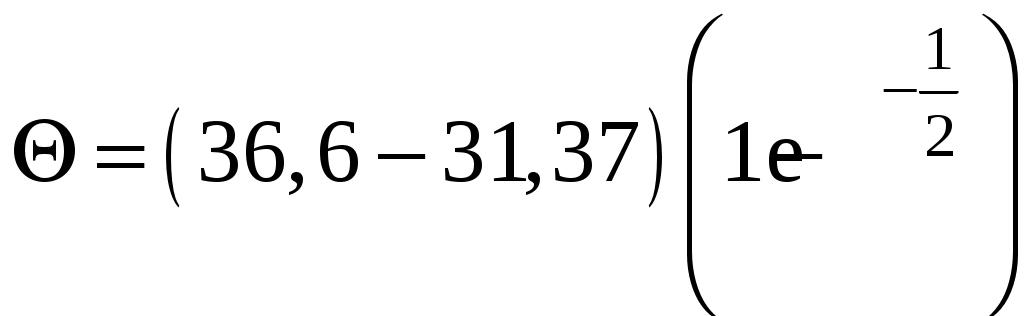=2,04

=2,04^ºС

Т.е. через 2 минуты термометр нагреется до температуры: 31,37+2,04= 33,41 ºС

Изменение температуры за третью минуту:

=0,9

=0,9^ºС

Т.е.ч ерез 3 минуты термометр нагреется до температуры: 33,41+0,9= 34,31 ºС

Тогда абсолютная погрешность измерения составит:

Δ=36,6-34,31=2,29 ^ºС

Задача 9.

Используя условия задачи 8, оцените минимально необходимое время измерения температуры человеческого тела, чтобы относительная погрешность не превышала 0,2 %.
Для того чтобы относительная погрешность не превышала 0,2% относительная погрешность измерения должна быть не больше:

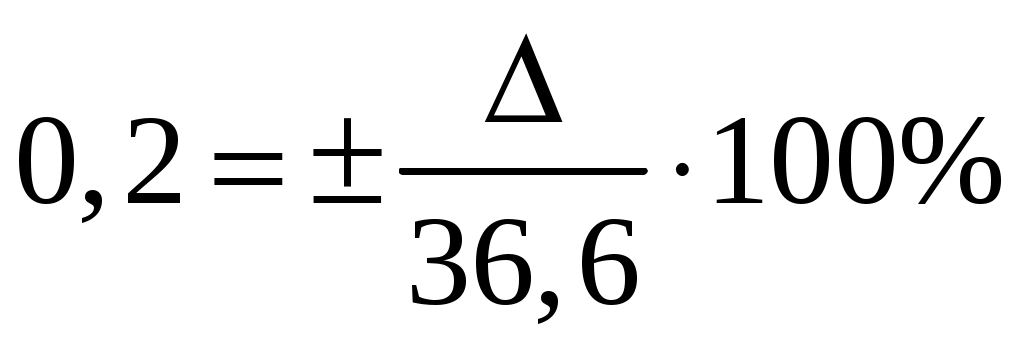, Δ=0,07ºС

Измеренная температура должна соответствовать:

36,6-0,07=36,53ºС

Проводя расчеты по формуле:

Получаем t=6,5мин.

Задача 10

Основная относительная погрешность измерителя сопротивления равна 0,1 %. Определить относительную погрешность измерителя при температуре 45 ºС, если его дополнительная относительная погрешность от изменения температуры равна 0,005(Θ – Θ_н), где Θ –температура окружающей среды; Θ_н – нормальная температура, равная 20 °С.
Дополнительная погрешность:

0,005(Θ – Θн)=0,005(45-20)=0,125%

Относительная погрешность измерителя находится по формуле:

Ответ: 0,16%