В практике измерения массы применяется разнообразные приборы и устройства, которые отличаются назначением, областью применением, принципом работы. В данное время на рынке весового оборудования число конструктивных модификаций весов исчисляется тысячами.
В 21 веке используются в основном электронные весы, но также на практике еще изредка применяются механические, а именно рычажные и даже пружинные весы.
Электронные весы подразделяются по принципу взвешивания на:
- Весы для статического взвешивания – весы платформенные, весы автомобильные, вагонные весы, товарные весы и лабораторные аналитические и прецизионные.
- Весы для взвешивания в движении – весы автомобильные подкладные, вагонные весы статико-динамические, весы вагонные динамические.
- Весы автоматические беспрерывного действия для суммарного учета – конвейерные весы и чеквейеры.
- Весы дискретного действия для суммарного учета автоматические – бункерные весы, автоматические весы-дозаторы и другие.
Погрешность весов при взвешивании
Для того, чтобы разобраться, что же такое погрешность весов при взвешивании, немного нужно окунуться в метрологическую терминологию. Погрешность измерения — это отклонение результата измерения от истинного значения измеряемой физической величины, обозначение ∆.
∆ = х – х ист
Результат измерения – найденное значения физической величины опытным путем с использованием специальных технических средств, обозначение х. Истинное значение физической величины – значение физической величины, которое идеальным образом в количественном и качественном отношении отражало бы соответствующее свойство объекта измерения, обозначение х ист. Физическая величина – свойство, в качественном отношении характерна для многих объектов, явлений или процессов, но в количественном отношении индивидуальное для каждого из них. В зависимости от выбранной классификационной характеристики существуют различные классификации погрешностей измерения, среди которых можно выделить наиболее распространенные:
- по форме выражения;
- по источникам возникновения;
- по закономерностям возникновения и проявления
По форме выражения погрешности делятся на абсолютные и относительные.
Абсолютная погрешность
Абсолютная погрешность весов – разность между результатом измерения массы груза на весах и истинным значением массы данного груза. Абсолютная погрешность по значению равна погрешности измерения и равна
∆ = х – х ист .
Относительная погрешность другие виды погрешностей
Относительная погрешность весов– это отношение абсолютной погрешности весов к условно истинному значению измеряемой величины, то есть к условно истинному значению массы груза, взвешиваемого на весах. Относительная погрешность равна: 
где δ – относительная погрешность; Δ – абсолютная погрешность; 
– истинное значение физической величины – истинное значение массы взвешиваемого груза. Основная погрешность (абсолютная, относительная) весов – это погрешность весов, определенная при нормальных условиях. Нормальные условия(i) – совокупность нормированных рабочих условий, которые устанавливаются для обеспечения достоверности взаимного сравнения результатов измерений. Нормированные рабочие(i) условия – условия эксплуатации, устанавливающие диапазон значений влияющих величин, при которых метрологические характеристики весов находятся в пределах нормированных максимально допустимых погрешностей. Нормированные рабочие условия имеют такие показатели: – диапазон температур от минус 10 ºС до плюс 40 ºС; – относительная влажность – 98 % при температуре 25 ºС.
Дополнительные погрешности весов
Дополнительная погрешность –погрешность весов, которая дополнительно возникает при эксплуатации весов в условиях отклонения хотя бы одной из влияющих величин от нормированного значения.
По источникам возникновения погрешности измерения бывают инструментальные, методические и личные (погрешности оператора).
Инструментальная погрешность весов – составляющая погрешности измерения, обусловленная свойствами средства измерительной техники, в данном случае весов. Методическая погрешность – составляющая погрешности измерения, обусловленная несовершенством метода измерения или несоответствием объекта измерения его модели, принятой для измерения. Погрешность оператора – составляющая погрешности измерения, обусловленная индивидуальными свойствами оператора/весовщика.
По закономерностям возникновения и проявления различают систематические, случайные и чрезмерные погрешности.
Систематическая погрешность весов – составляющая общей погрешности измерения, остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины. Случайная погрешность весов – составляющая общей погрешности измерения, меняется случайным образом (как по знаку, так и по величине) при повторных измерениях одной и той же величины. Чрезмерная погрешность – погрешность измерения, которая существенно превышает ожидаемую при данных условиях погрешность. Погрешность весов имеет свои пределы допустимых значений, которые регламентируются нормативным документом – стандартом. Результат значения измеряемой массы груза на весах в пределах допустимых погрешностей весов является приемлемым. Также есть термин «предел допустимой погрешности»(i), вот его значение: предел допустимой погрешности – это самая большая разница, положительная или отрицательная, установленная нормативным документом – стандартом между показанием весов и соответствующим действительным значением рабочих эталонов мер массы (гирь) при условии, что весы находятся в исходном положении и до нагрузки грузом имели нулевые показания.
Дискретность весов – цена действительного деления весов
Дискретность весов – это значение, выраженное в единицах массы, равное: – разнице между значениями двух последовательных отметок шкалы – для аналогового отображения измеряемого значения массы; или – разнице между значениями двух последовательно отраженных показаний – для цифрового отображения измеряемого значения массы. Дискретность весов обозначается, как d.
Цена поверочного деления весов
Цена поверочного деления – значение, выраженное в единицах массы, используемой для классификации, оценки соответствия, поверки весов(ссылка). Цена поверочного деления весов обозначается, как e.
Классы точности весов
Класс точности – обобщенная метрологическая характеристика, определяется границами основной и дополнительной погрешностей весов, а также другими метрологическими характеристиками весов. Классы точности устанавливают в процессе проектирования весов с учетом проведенных испытаний в ходе проведения оценки соответствия требованиям Технического регламента, под действие которого попадают весы. Если в нормативном документе, Техническом регламенте, стандарте, или технических условиях, регламентирующего технические требования к весам конкретного типа, установлено несколько классов точности, то класс точности конкретных весов допускается присваивать при выпуске из производства и проведению испытаний на соответствие метрологическим характеристикам. А также понижать класс точности возможно по результатам периодической поверки (или другого вида поверки) в порядке, предусмотренном действующей методикой поверки данного типа весов.
Класс точности весов для статического взвешивания
Неавтоматические взвешивающие устройства, а именно весы для статического взвешивания: платформенные весы, железнодорожные весы, автомобильные весы, которые используются в законодательно регулируемой метрологии, попадают под действие Технічного регламенту щодо неавтоматичних зважувальних приладів и должны отвечать требованиям стандарта ДСТУ EN 45501 «Метрологічні аспекти неавтоматичних зважувальних приладів». Весы квалифицируют в соответствии с: – ценой поверочного деления e шкалы весов, которая отражает абсолютную точность; – количеством поверочных делений n шкалы, которая отражает относительную точность. Максимально допустимые погрешности выражают через значение цены поверочного деления e. Более подробно о количестве поверочных делений n. Количество поверочных делений n – это отношение значения максимальной нагрузки Max весов до значения цены поверочного деления. Зная максимальную нагрузку Max весов и цену поверочного деления e шкалы весов можно высчитать количество поверочных делений n : n = Max / e Согласно ДСТУ EN 45501 весы для статического взвешивания подразделяются на такие классы точности: – специальный класс точности I – высокий класс точности II – средний класс точности III – обычный класс точности IIII Цена поверочного деления e, количество поверочных делений шкалы n и минимальную нагрузку Min в соответствии с классом точности весов для статического взвешивания приведены в таблице 1. Таблица 1.
| Класс точности весов для статического взвешивания | Цена поверочного деления шкалы, e | Количество поверочных делений, n = Мах / е | Минимальную нагрузка, Min (нижняя граница | |
| минимальное | максимальное | |||
| Специальний (І) | 0,001 г ≤ е a) | 50 000 | – | 100 е |
| Высокий (ІІ) | 0,001 г ≤ е ≤ 0,05 г | 100 | 100 000 | 20 е |
| 0,1 г ≤ е | 5 000 | 100 000 | 50 е | |
| Средний (ІІІ) | 0,1 г ≤ е ≤ 2 г | 100 | 10 000 | 20 е |
| 5 г ≤ е | 500 | 10 000 | 20 е | |
| Обычный (ІІІІ) | 5 г ≤ е | 100 | 1 000 | 10 е |
| a) Обычно невозможно выполнить испытания или поверку весов с е <1 мг из-за неопределенности испытательных нагрузок |
Класс точности весов для динамического взвешивания
Для динамического взвешивания есть также разнообразные типы весов. Класс точности весов для динамического взвешивания обозначается цифрами: 0,2; 0,5; 1; 2. Например, класс точности 0,5 подразумевает, что: 
Рассмотрим для наглядности весы вагонные для динамического взвешивания, которые используются в законодательно регулируемой метрологии, попадают под действие Технічного регламенту засобів вимірювальної техніки и отвечают требованиям стандарта ДСТУ OIML R 106-1 «Ваги залізничні платформні автоматичні. Частина 1 . Загальні технічні вимоги. Методи випробування». Согласно ДСТУ OIML R 106-1 вагонные весы для динамического взвешивания подразделяются на 4 класса точности, более подробно в Таблице 2.
Таблица 2
| Класс точности | Процент от значения массы одного вагона или всего поезда | |
| при проведении оценки соответствия, периодической поверке | во время эксплуатации | |
| 0,2 | ± 0,10 % | ± 0,2 % |
| 0,5 | ± 0,25 % | ± 0,5 % |
| 1 | ± 0,50 % | ± 1,0 % |
| 2 | ± 1,00 % | ± 2,0 % |
При взвешивании вагона
Предел допускаемой погрешности во время взвешивания в движении сцепленных или расцепленных вагонов должен соответствовать наибольшему из следующих значений: а) значению, вычисленному по таблице 2 и округленном до ближайшего значения, кратного цене деления шкалы е b) значению, вычисленному по таблице 2 для массы отдельного вагона, которая составляет до 35% от наибольшего значения массы вагона, и округленном до ближайшего значения, кратного цене деления шкалы или c) 1 d.
Пример взвешивания вагона для весов вагонных динамического взвешивания 2-го класса точности:
Масса контрольного вагона = 100 т Наибольшая масса вагона Max = 100 т Цена деления шкалы е = 0,2 т Предел допустимой погрешности в соответствии с пунктом: Таблица 2 пункт a) 1% · 100 т = 1 т; Таблица 2 пункт b) 35% от Max · 100 т = 35 т, следующим образом: 1% = 0,35 т или 0,4 т (округленное значение) для 90% (54 из 60) контрольных вагонов; 2% = 0,7 т для 10% (6 из 60) контрольных вагонов; Таблица 2 пункт c) 1 d = 0,2 т;
При взвешивании поезда
Предел допускаемой погрешности во время взвешивания в движении поезда должен соответствовать наибольшему из следующих значений: а) значению, вычисленному по таблице 2 и округленном до ближайшего значения, кратного цене деления шкалы е b) значению, вычисленному по таблице 2 для массы отдельного вагона, которая составляет до 35% от наибольшего значения массы вагона, умноженного на количество контрольных вагонов этого поезда (не более 10 вагонов) и округленном до ближайшего значения, кратного цене деления шкалы е или c) 1 d для каждого вагона данного поезда, но не более 10 d.
Пример взвешивания поезда для весов вагонных для динамического взвешивания класса точности 1:
Количество вагонов в поезде = 50 Количество контрольных вагонов в поезде = 15 Масса контрольного вагона = 100 т Наибольшая масса вагона Max = 100 т Цена деления шкалы е = 0,2 т Предел допускаемой погрешности соответствии с пунктом: Таблица 2 пункт a) 0,5% · 100 т · 15 контрольных вагонов = 7,5 т; Таблица 2 пункт b) 35% Max · 10 контрольных вагонов = 350 т 0,5% · 350 т = 1,75 т, значение округляется до ближайшей погрешности шкалы Таблица 2 пункт c) 1 d · 10 контрольных вагонов = 2 т.
Вывод
Рассмотрев такие метрологические характеристики весов, как погрешность, дискретность – действительная цена деления, цена поверочного деления и класс точности, видно, что эти характеристики взаимозависимы друг от друга и при изменении одной из характеристик, меняется тип весов. Со значением «тип весов» можно ознакомится в следующей статье.
Лабораторные весы применяются в научной сфере и в производственных отраслях, например, в фармацевтике и ювелирном деле. Мы расскажем, как определить точность лабораторных весов, и рассмотрим критерии выбора на конкретных примерах.
Проблемы при определении точности весов
Главным критерием для выбора аналитических весов является высокая точность измерений. Для оценки точности используются следующие параметры:
- погрешность при взвешивании;
- стандартная и расширенная неопределенность;
- возможный диапазон измерений.
Но в методических рекомендациях часто содержатся требования к классу точности прибора, а не к фактической точности взвешивания. При этом составители методики приводят ссылку на ГОСТ, действующий во время составления рекомендаций. Однако стандарты, разработанные в СССР, не подходят для нашего времени.
В СССР все произведенные весы соответствовали единому стандарту. Для выбора нужно было знать класс точности. В наши дни производители применяют стандарты в добровольном порядке. На рынке присутствует множество устройств, характеристики которых не соответствуют ГОСТу. Подобные устройства проходят утверждение в Росстандарте после серии испытаний.
Существуют и лабораторные весы, которые не соответствуют ГОСТу и не проходили утверждение в Росстандарте. Использовать такие приборы можно только для измерений, которые не подлежат государственному регулированию.
Для чего нужна калибровка оборудования
Фактическая точность весов не зависит от соответствия ГОСТу или утверждения в Росстандарте. В международной практике большинство исследований проводятся на калиброванных приборах, класс которых не соответствует общепринятым стандартам.
Именно калибровка, а не наличие сертификатов, гарантирует точный результат взвешивания. При калибровке не имеет значения погрешность, указанная в документах. Целью калибровки является определение реальных показателей. В процессе калибровки устанавливается неопределенность измерений и поправки на систематические погрешности.
ГОСТ Р ИСО/МЭК 17025-2006 разрешает лабораториям использовать не только весы, прошедшие поверку, но и калиброванные приборы. На калиброванных приборах возможно измерение массы маленьких навесок.
Например, когда относительная погрешность не превышает 1%, масса навески не должна быть менее 100 мг. Когда относительная погрешность не более 0,1%, допустимая масса груза должна быть не менее 1 г.
Выбор лабораторных весов по рекомендациям
Рассмотрим типичные формулировки из нормативно-методических документов, которые содержат требования к точности прибора или точности измерений. Для оценки корректности формулировок мы будем разбирать конкретные примеры.
Пример №1
Формулировка: «Лабораторные весы, соответствующие ГОСТ Р 53228-2008».
В этой формулировке нет конкретных требований к точности прибора или точности взвешивания. Упоминание любого из стандартов в методической документации значительно уменьшает число вариантов. Из списка исключаются устройства, не прошедшие сертификацию и поверку.
Приведенный ГОСТ содержит перечень требований к весовому оборудованию, составленный с учетом всех возможных погрешностей. В этот перечень входят:
- Требования к конструкции прибора.
- Возможные погрешности в допусках.
- Описание допустимых методов работы.
- Допустимые условия эксплуатации.
- Требования к квалификации персонала.
Стандарт включает методы оценки выполнения всех перечисленных требований. Текст стандарта занимает 140 листов. Основой для написания стандарта стал перевод рекомендации Р76 (1)-2006 от Международной организации законодательной метрологии.
Ссылка на упомянутый стандарт бесполезна: он содержит требования к идеальным устройствам. ГОСТ написан для узкого круга специалистов, которые занимаются разработкой, изготовлением, тестированием весов. Описанные в нем стандарты пока не достижимы на практике, но возможно максимально к ним приблизится.
Согласно упомянутому ГОСТу, класс точности весов зависит от основной величины «е». Величина «е» показывает предел допускаемой погрешности, который при эксплуатации в 2 раза выше, чем при поверке.Как величина «е» связана с классом точности приборов, показано в таблицах.
Таблица №1 — «Определение класса точности весового оборудования».
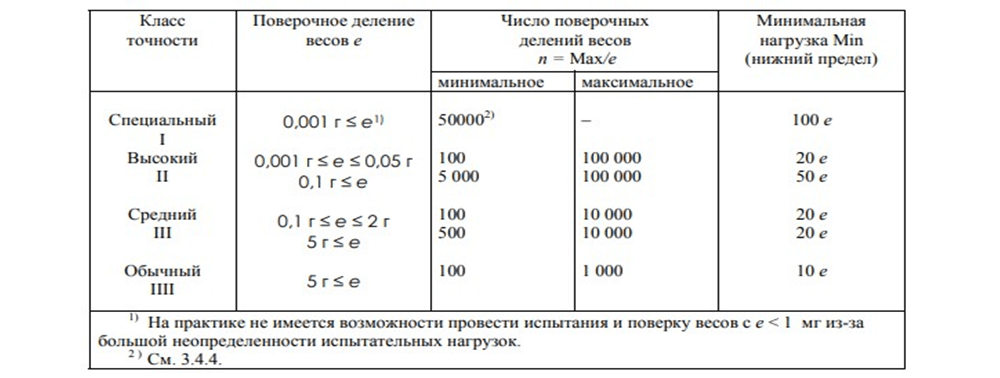
Таблица №2 — «Зависимость погрешности от уменьшения или увеличения нагрузки».
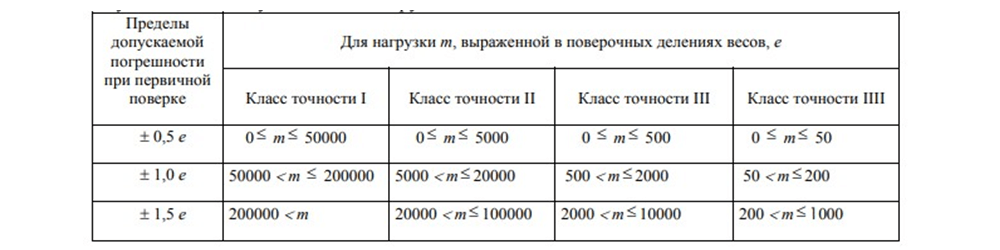
Пример №2
Формулировка: «Весы, соответствующие II классу точности согласно ГОСТ Р 53228-2008».
Таблица №1 показывает, что к II классу точности относятся весы с «е» не менее 1 мг. Лаборатория может закупить приборы с е = 1 мг или е = 10 мг. Требование будет выполняться в обоих случаях. Но погрешность устройств будет отличаться в 10 раз. Для ограничения выбора следует указывать не только класс точности, но и допустимое значение величины «е».
Пример №3
Формулировка: «Весы, соответствующие ГОСТ Р 53228-2008, точность которых равна 0,0001 г.»
По РМГ 29-99, точность весов — характеристика, которая указывает близость погрешности к нулю. Чем меньше значение погрешности, тем выше точность устройства. Согласно этому определению, термин «точность» не может использоваться в связке с каким-либо числом.
Возможно, под термином «точность» составители рекомендаций имели в виду предел допустимой погрешности 0,0001 г. = 0,1 мг. Но в таком случае выполнить условие невозможно. В приведенном ГОСТ минимальный предел допустимой погрешности составляет 1 мг. (см. таблицу №1).
Предположение о том, что в формулировке подразумевается цена деления, является еще менее вероятным. Цена деления не является характеристикой, которая указывает на точность прибора.
Пример №4
Формулировка: «Лабораторные весы II класса точности по ГОСТ 24104-88Е».
Упомянутый ГОСТ действовал до 1 июля 2002 года. Этот стандарт связывает предел допускаемой погрешности с двумя характеристиками:
- класс точности прибора;
- наибольший предел взвешивания.
Таблица №3 — «Зависимость погрешности от НПВ прибора».
Допустим, что в одной лаборатории грузы массой 1 г. взвешивают на весах с НПВ = 1 г. В другой лаборатории для этого используют прибор с НПВ = 200 г. При взвешивании грузов с одинаковой массой погрешность будет отличаться в 30 раз. Но формально измерения соответствуют единому стандарту.
Кроме того, в редакциях ГОСТ 24104 от 1980, 1988 и 2001 гг. содержались некорректные значения пределов допускаемой погрешности (для устройств I класса точности). Некорректность с точки зрения метрологии заключалась в отсутствии стандартных гирь, которые смогли бы обеспечивать заявленные погрешности. А также в том, что обозначенные пределы учитывали только случайную составляющую.
Пределы погрешностей в устаревших редакциях были равны среднеквадратическому отклонению показаний, умноженному на 3. Но эта формула верна только в одном случае: если проводить все измерения с образцовой гирей, как при поверке или калибровке. Формула не учитывает реальную погрешность гирь, которые участвуют в работе, и погрешность неравноплечести.
Пример №5
Формулировка: «Весы типа ВЛР-200 или другой модели, не уступающей им по метрологическим характеристикам».
Требование выглядит простым: в нем указана конкретное оборудование, которое можно закупить для лаборатории. Кажется, что нужно значение погрешности можно посмотреть в характеристиках прибора.
Но на самом деле ВЛР-200 — не электронные, а механические весы. Указанная модель относится к равноплечим приборам. Для взвешивания грузов требуется использовать комплект гирь и брать поправку на погрешность.
Как работать с прибором ВЛР-200:
- На одну чашу ставится груз, а на другую — гири, которые могут его уравновесить. При этом возникает погрешность неравноплечести.
- Для исключения погрешности неравноплечести выполняется повторное взвешивание того же груза.
- Точность измерений определяется по методу Борда, Гаусса или Менделеева. Для расчетов можно использовать номинальную или действительную массу гирь с учетом поправок.
Чтобы рассчитать длину носителя, нужно сложить длину стикера с длиной промежутка и умножить результат на число стикеров. Расчет для приведенного примера выглядит так: (40+2) х 600 = 25200 мм или 25,2 м.
Возможная длина риббона: 74, 300 и 450 м. Чтобы рассчитать соотношение, следует разделить длину риббона на рассчитанную длину носителя. Например, одного риббона длиной 300 м хватит для печати на 300 / 25,2 = 11,9 рулонов. Следовательно, при закупке расходных материалов для принтера нужно соблюдать пропорцию 1 к 12.
Таблица №4 — «Определение погрешности неравноплечести».
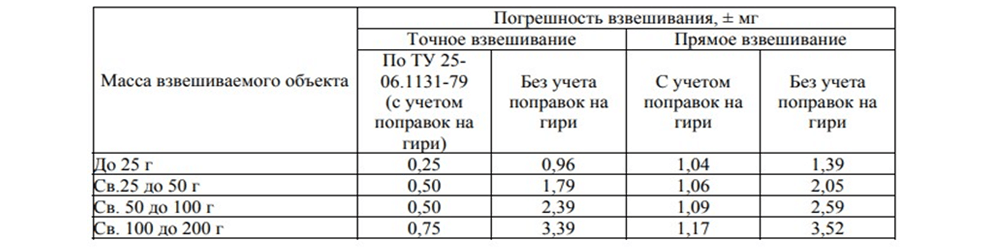
Таблица показывает, что погрешность при взвешивании грузов массой до 25 г. может различаться в 6 раз.
Пример №6
Формулировка: «Весы с относительной погрешностью не более 0,1% и наличием государственной поверки».
Допустим, возможная масса груза от 1 г. до 100 г., а масса посуды не превышает 40 г. В таком случае при взвешивании грузов массой 1 г. допускается абсолютная погрешность в 1 мг. Цена одного деления должна быть в 5-10 раз меньше, чем абсолютная погрешность: 0,1 мг. или 0,2 мг. На практике весы с ценой одного деления 0,2 мг. встречаются крайне редко.
Максимальный предел взвешивания не должен быть менее 140 грамм (для грузов массой 100 г. и лабораторной посуды массой 40 г.) Кроме перечисленных характеристик, при покупке весов нужно обратить внимание на наличие сертификата о государственной поверке.
Пример №7
Формулировка: «Предел относительной неопределенности составляет 0,1% для 3-кратного среднеквадратического отклонения из 10 результатов, при этом доверительная вероятность равна 99,73%».
Выбрать подходящие весы можно по характеристикам, указанным производителем. Для подбора оборудования подходит таблица №5.
Таблица №5 — «Определение минимальной массы навески».
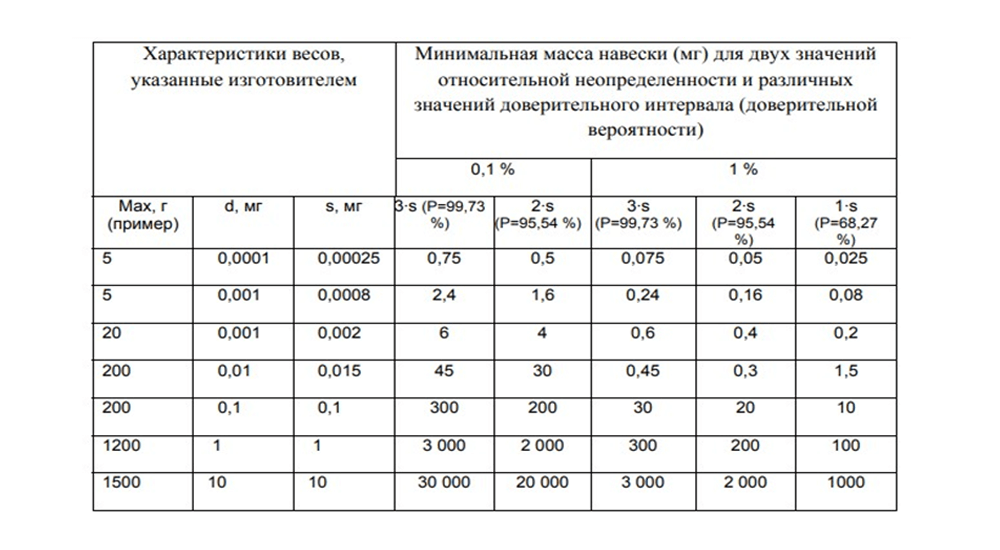
Для оценки неопределенности измерений следует провести калибровку весов в лаборатории. На отклонение показаний влияют:
- Условия внешней среды: температура, влажность.
- Наличие сквозняка: для повышения точности нужно установить ветрозащитный экран.
- Выбранный критерии стабильности результатов в меню.
- Квалификация оператора: степень его аккуратности при работе.
- Используемая посуда: чем меньше вес посуды, тем меньше будет отклонение.
При относительной неопределенности 0,1% и доверительной вероятности 99,73% минимальная навеска равна 300 мг. Если значение доверительной вероятности равно 95,54%, то минимальная навеска составляет 200 мг. Если в лаборатории придется взвешивать грузы с массой 1 мг, нужно будет использовать ультрамикровесы с ценой одного деления 0,0001 мг.
Выводы
При выборе лабораторных весов главным критерием служит погрешность или неопределенность измерений. Оба критерия могут быть абсолютными или относительными. Если сфера проведения измерений подлежит государственному регулированию, для выбора используются установленные требования по погрешности. Если измерения не регулируются государством, то для выбора весов можно использовать стандартную или расширенную неопределенность.
Приемлемой для указания в нормативно-методических документах является формулировка:
Электронные весы, обеспечивающие в диапазоне от … до … г. относительную погрешность (или относительную неопределенность) измерений не более … %.
Как определить точность весов, как прочитать точность по обозначениям
Как определить точность весов, как прочитать точность по обозначениям
Весы являются измерительным инструментом и предназначены для измерения веса. Единицей измерения веса является килограмм, а также его производные грамм, тонна, миллиграмм и т.д.
Поскольку абсолютно точно вес измерить невозможно, то показания весов могут считаются достоверными с определенной погрешностью измерения. С другой стороны, показания результатов взвешивания на индикаторе электронных весов отображаются с некоторой дискретностью, обозначаемой величиной d.
Например, если дисплей торговых весов AP-15М показывает вес 1 кг, то при добавлении груза весом 3 г показания будут равны 1,005 кг, т.е. будут меняться с дискретностью d = 5 г. Многие ошибочно полагают, что эта величина d и является погрешностью измерения веса. Однако это не так.
Предельно допустимая погрешность измерений определяется специальной метрологической величиной е – ценой поверочного деления.
Обычно производитель весов гарантирует следующее соотношение: d = e. Как правило, об этом сообщено на дисплее конкретных весов, а также на “шильдике” – алюминиевой пластинке с заводским номером, прикрепленной к корпусу. Данное равенство позволяет установить связь между дискретностью показаний и погрешностью измерения.
Связь предельно допускаемой погрешности измерений с e для весов каждого класса точности приведена в соответствующих ГОСТах. Можно также посмотреть эти данные в описаниях типа средства измерения, являющихся неотъемлемым дополнением к метрологическому сертификату.
В частности, при эксплуатации весов для статического взвешивания ГОСТом допускается следующая трехступенчатая характеристика погрешности: в начале диапазона взвешивания вплоть до 500 е погрешность составляет е, до 2000е составляет ±2е, в конце диапазона равна ±3е. Таким образом, весы AP-15М в диапазоне до 2,5 кг имеют погрешность показаний 5 г, в диапазоне от 2,5 кг до 10 кг погрешность равна 10 г , свыше составляет 15 г.
Обратите внимание, что если на весах не указано d = e, то последний разряд в отсчете не гарантируется, и его можно использовать только как справочный (не для торговых операций, в частности).
Другими важными метрологическими характеристиками являются наибольший (НПВ) и наименьший (НмПВ) пределы взвешивания. Вне этих пределов показания весов считаются недостоверными. Например, если Вы выбрали весы AP-15М для Вашего магазина, то Вы должны знать, что они имеют НПВ=15 кг и НмПВ=100г.
Внимание! Знать наименьший предел взвешивания принципиально важно, т.к. весы индицируют вес на дисплее даже в случае, если измеряемый вес меньше НмПВ, однако достоверными эти показания считать нельзя.
Не требуйте от весов высокой точности измерения одновременно с большим значением НПВ. Решите сначала, что Вам важнее. Для точного взвешивания лучше выбрать весы с меньшим значением e и небольшим НПВ соответственно.
В некоторых типах весов CAS для увеличения точности используется так называемый многодиапазонный режим измерений, при котором весь интервал от наименьшего до наибольшего пределов взвешивания разбивается на два или три участка со своими значениями d и e. Это увеличивает динамический диапазон измерений и позволяет ввести для каждого диапазона свою дискретность показаний индикатора. В случае с AP-15M дискретность показаний будет последовательно меняться как 1 г, 2 г и 5 г соответственно.
На выбор модели влияет ряд функциональных особенностей: набор реализованных в весах функций, конструктив (размеры платформы, выносной или встроенный индикатор, защита от перегрузки и т.д.), тип питания, наличие интерфейса, условия эксплуатации – некоторые модели выпускаются в повышенном пыле- и влагозащитном исполнении или с тензодатчиком и платформой из нержавеющей стали. При выборе убедитесь, относятся ли требующиеся Вам функции к стандартной комплектации или опциям. В последнем случае нашей компании может потребоваться.
Как пример пренебрежения метрологией весовых измерений можно привести буквальное использование потребителем так называемой счетной функции весов. Эта функция реализована в счетных весах САS моделей CS, AC и заключается в двухступенчатом процессе измерения сначала среднего веса одинаковых изделий (путем взвешивания пробы из их определенного количества), а затем – неизвестного их количества в рабочей порции по ее весу. В рекламных проспектах иногда приводят результат счета с точностью до штуки, не указывая никак, какова реальная погрешность счета в штуках. Такая точность – формальный результат, который получен микропроцессором весов при выполнении арифметической операции деления. Часто иллюстрируют эту задачу счетом метизов, которые хотя бы из-за неоднородности по весу могут иметь неопределенность до 10%. Совершенно очевидно, что в этом случае указывать результаты счета с точностью до штуки абсурдно.
Всё довольно просто: требования к статическим весам изложены в ГОСТ Р 53228-2008 часть 1.
Весы изготавливаются 4-х классов точности: специальный, высокий, средний, обычный. В зависимости от класса определено значение поверочного деления “е”, количество поверочных делений n = Max/e, минимальная нагрузка и пр.
Погрешность весов на разных интервалах взвешивания разная – см. п. 3.5.1, п. 3.5.2 ГОСТ.
Если у вас Max=6000 кг и “е” (для примера) 0,5 кг, то n= 12000. Это соответствует весам высокого (II)класса. В зависимости от интервала взвешивания погрешность весов должна составлять:
– при поверке:
– от Min до 5000е вкл. (2500 кг): +/-0,5е (+/-0,25 кг);
– от 5000е (2500 кг) до 20000 е вкл. (6000 кг и более): +/- 1е (+/-0,5 кг);
– от 20000е до 100000е вкл.: +/- 1,5е;
– в эксплуатации погрешности удваиваются:
– от Min до 2500 кг вкл.: +/-0,5 кг;
– от 2500 кг до 6000 кг: +/- 1 кг.
-….
Выходит, что если хотите получить погрешность весов в эксплуатации не более +/- 0,5 кг во всём диапазоне измерения, вам нужны весы высокого класса точности (II) с “е”= 0,1 кг и с n =60000, потому что с “е”= 0,2 кг погрешность весов будет +/-0,6 кг.
Хотя весы можно сделать и не по ГОСТу, у вас, наверное, так и будет.
Требования к точности весов очень высокие. Интересно, собираетесь ли вы испытывать их в целях утверждения типа СИ.
Как известно, ни одну физическую величину, в том числе и массу тела, невозможно определить с абсолютной точностью. Всегда есть погрешность измерений.
Результат взвешивания есть в общем случайная величина, определяемая совокупностью ряда различных факторов:
- чувствительностью;
- постоянством показаний весов;
- правильностью установки весов;
- температурными условиями, при которых проводили взвешивание;
- опытом работника, выполнявшего взвешивание;
- рядом других факторов.
Поэтому массу груза всегда определяют с какой-то погрешностью.
Погрешность измерений
Погрешность измерений – алгебраическая разность между полученным при измерении и действительным значениями измеряемой величины.
Причинами, вызывающими погрешности, могут быть:
- неправильный отсчет показаний стрелки;
- неправильная оценка цены деления шкалы;
- неверная запись результата;
- преждевременный или запоздалый отсчет;
- сдвиг или сотрясение весов, не замеченные наблюдателем, и т. д.
Погрешность результата измерения может быть представлена по-разному. Если ее выражают в тех же единицах, что и измеряемую величину, погрешность называют абсолютной.
Однако по величине абсолютной погрешности трудно судить о точности выполненного измерения. Этого недостатка лишен второй способ выражения погрешности результата измерения — в ее долях (или процентах).
Погрешность, выраженную таким способом, называют относительной. Все погрешности измерений можно разделить на систематические и случайные.
Они в большей или меньшей степени сказываются на результатах взвешивания. Чтобы знать, с какой точностью выполнено измерение, уметь исключать некоторые погрешности из результатов измерений, а влияние других снизить до минимума, необходимо разбираться в погрешностях, сопутствующих взвешиванию, и причинах, их вызвавших.
Систематическая погрешность измерений
Это постоянная по величине и знаку или переменная, изменяющаяся по определенному закону при повторных измерениях одной и той же величины, погрешность.
Систематическая погрешность входит в любой результат, несмотря на число повторных взвешиваний данного груза.
По виду причины, вызвавшей ту или иную систематическую погрешность при взвешивании, выделяют погрешность:
- обусловленную неправильной установкой и сборкой весов;
- возникшую из-за неравенства плеч коромысла, рычагов и т. д.;
- связанную с недостаточно точной подгонкой массы гирь;
- вызванную непостоянством температуры, при которой выполняли взвешивание;
- обусловленную действием аэростатической силы, если взвешивание выполняли в воздушной среде, и т. д.
Все перечисленные причины можно предвидеть и тем самым свести их влияние до минимума или полностью исключить из результата взвешивания.
Однако даже полностью исключив систематическую погрешность, нельзя добиться точного совпадения результатов многократного взвешивания одного и того же груза, так как любому измерению сопутствуют случайные погрешности.
Случайная погрешность
Она изменяется случайным образом при повторных измерениях одной и той же величины. Случайная погрешность не может быть полностью исключена из результатов взвешивания.
Однако сказанное не относится ко всей совокупности случайных погрешностей, возникающих при том или ином измерении. Выполняя ряд повторных взвешиваний, при помощи теории вероятностей и математической статистики можно несколько уточнить результат измерения, т. е. найти значение измеряемой величины, более близкое к истинному по сравнению с результатом одного измерения.
Промахи и грубые погрешности
Причинами, вызывающими промахи, могут быть:
- неправильный отсчет показаний стрелки;
- неправильная оценка цены деления шкалы;
- неверная запись результата;
- преждевременный или запоздалый отсчет;
- сдвиг или сотрясение весов, не замеченные наблюдателем, и т. д.
Однако, не все результаты взвешивания, которые значительно отличаются от других, можно характеризовать как промахи. Поэтому значительный интерес представляют способы выявления промахов.
