Как найти относительную шероховатость трубы

Шероховатость стенок трубопровода: типы и влияние

Твердые стенки, ограничивающие поток жидкости, всегда в той или иной степени обладают известной шероховатостью. Шероховатость стенок характеризуется величиной и формой различных, порой самых незначительных по размерам, выступов и неровностей, имеющихся на стенках, и зависит от материала стенок и их обработки.

Шероховатость — это совокупность неровностей поверхности с относительно малыми шагами на базовой длине. Измеряется в микрометрах (мкм).

Обычно с течением времени шероховатость изменяется от появления ржавчины, коррозии, отложения осадков и т.д.

Абсолютная шероховатость

В качестве основной характеристики шероховатости служит так называемая абсолютная шероховатость – κ, представляющая собой среднюю величину указанных выступов и неровностей, измеренную в линейных единицах.

Некоторые значения шероховатости стенок трубопровода приведены в таблице ниже

Трубы	κ, мм
Чистые цельнотянутые из латуни, меди и свинца	0,01
Новые цельнотянутые стальные	0,05-0,15
Стальные с незначительной коррозией	0,2-0,3
Новые чугунные	0,3
Асбоцементные	0,03-0,8
Старые стальные	0,5-2,0

В случае когда величина выступов шероховатости стенки трубы меньше, чем толщина вязкого (ламинарного) подслоя неровности стенки полностью погружены в этот слой.

При этом турбулентная часть потока не будет входить в непосредственное соприкосновение со стенками и движение жидкости, а следовательно, и потери энергии не будут зависеть от шероховатости стенок, а будут зависеть только от свойств самой жидкости.

Если величина выступов такова, что они превышают толщину вязкого подслоя, то неровности стенок будут выступать в турбулентную область, увеличивая беспорядочность движения и существенным образом влиять на величину потерь энергии.

В этом случае каждый отдельный выступ можно сравнить с плохо обтекаемой поверхностью, находящейся в окружающем её потоке жидкости и являющейся источников образования вихрей.

В соответствии с написанным выше поверхности условно разделяют на гидравлически гладкие (первый случай) и шероховатые (второй вариант).

На самом деле, толщина вязкого подслоя непостоянна и уменьшается с увеличением числа Рейнольдса. У гидравлически гладких стенок с возрастанием числа Рейнольдса тоже начинает проявляться шероховатость, так как вязкий подслой становиться тоньше и выступы шероховатости, которые первоначально полностью располагались в этом слое, начинают выходить из него, выступая в турбулентную зону.

Следовательно, одна и та же стенка в зависимости от величины числа Рейнольдса может вести себя по разному:

  в одном случае – как гладкая
  в другом – как шероховатая.

Поэтому абсолютная шероховатость стенок трубопровода не может полностью характеризовать влияние стенок на движение жидкости. Естественно, что стенки с одной и той же абсолютной шероховатостью в потоках небольших поперечных размеров должны будут вносить большие возмущения в поток жидкости и оказывать большее сопротивление движению, чем в потоках большого сечения.

Относительная шероховатость и относительная гладкость.

Для характеристики влияния шероховатости на величину гидравлических сопротивлений, а так же исходя из условий соблюдения подобия, в гидравлике вводится понятие относительная шероховатость – ε.

Под термином относительная шероховатость понимают безразмерное отношение абсолютной шероховатости к некоторому линейному размеру, характеризующему сечение потока(например, к радиусу трубы r, к глубине жидкости в открытом потоке h и т.п.).

Таким образом

ε = κ / r

В некоторых случаях вводят понятие относительной гладкости ε^/ как величины обратной относительной шероховатости

ε^/ = r / κ

В действительно, как показали исследования, на величину гидравлических сопротивлений влияет не только абсолютное значение шероховатости (высота выступов), но также в значительной степени их форма и густота. Учесть влияние этих факторов непосредственными измерениями шероховатости практически невозможно.

Видео о шероховатости

В настоящее время для того, чтобы охарактеризовать шероховатость стенки трубы при гидравлических расчетах обычно пользуются понятием – эквивалентной шероховатости. Этот эквивалент представляет собой такую величину выступов однородной абсолютной шероховатости, которая дает при подсчетах одинаковую с действительной шероховатостью величину потерь напора.

Вместе со статьей “Шероховатость стенок трубопровода: типы и влияние” читают:

С
точки зрения инженерных приложений
главными являются следующие задачи: а)
как определить потери напора (энергии);
б)
как распределены скорости по сечению
трубы.

10.1. Абсолютная и относительная шероховатость

На
потери напора по длине при турбулентном
режиме может оказывать влияние
шероховатость стенок. Под шероховатостью
будем понимать присутствие у любой
поверхности неровностей (выступы и
впадины).
При
заводском изготовлении труб шероховатость
их внутренних стенок носит нерегулярный
характер, как по высоте, так и по
расположению, и поэтому одним параметром
охарактеризована быть не может. Несмотря
на это, в технических расчетах выбирают
единственный параметр, а именно среднюю
высоту выступов шероховатости; ее
обозначают k
(или Δ).

Абсолютной
шероховатостью k
называют среднюю высоту выступов
шероховатости.

Опыты
показали, что при одной и той же величине
абсолютной шероховатости влияние ее
на величину гидравлического сопротивления
различно в зависимости от диаметра
трубы. Поэтому вводится величина
относительной шероховатости
.

Относительной
шероховатостью называется отношение
абсолютной шероховатости к диаметру
трубы, т.е.
.

10.2. Закономерности изменения коэффициента гидравлического трения

Потери
напора по длине трубопровода обычно
находят по формуле (9.14). При этом основной
задачей является определение коэффициента

гидравлического
трения
.
В общем случае коэффициент гидравлического
трения может зависеть от двух безразмерных
параметров – числа

Re
=

и k/d,
т.е.
.

На
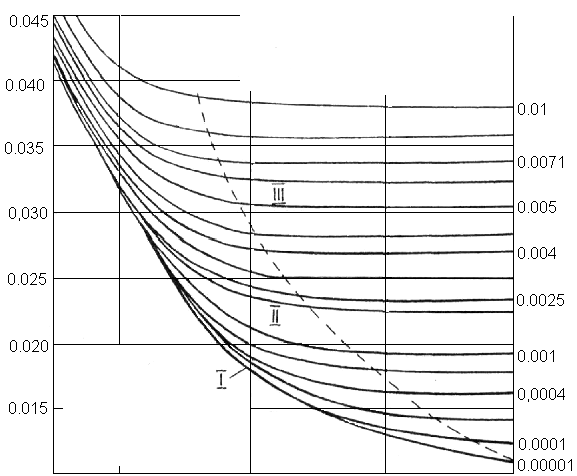
рис. 10.1 представлен экспериментальный
график зависимости коэффициента
от числа Рейнольдса, на нем изменение
коэффициентапредставлено рядом кривых, каждая из
которых соответствует определённой
относительной шероховатости, т.е.
отношениюk/d.

На
графике можно выделить три области: I
– область гидравлически гладких труб,
соответствующую сравнительно малым
числам Рейнольдса, II
– область доквадратичного сопротивления,
III
– область квадратичного сопротивления.
В области гидравлически гладких труб
коэффициент
зависит от числа Рейнольдса, в
доквадратичной области коэффициентзависит от числаRe
и от относительной шероховатости, а в
области квадратичного сопротивления
– только от относительной шероховатости.

10<<500

500<

Re_d<2300

Рис.
10.1. График Мурина – Шевелёва

10.3. Зависимости для коэффициента гидравлического сопротивления и области их применения

Для определения
потерь по длине применяется формула
Дарси-Вейсбаха

h₁
= λ.

Чтобы
выбрать соответствующую зависимость
для λ,
предлагается простой алгоритм. Обычно
заданы: расход Q,
диаметр трубы d,
кинематический коэффициент вязкости
ν
и величина эквивалентной шероховатости
k_э
(из таблиц) для данного материала. В
табл. 10.1 приведены значения k_э
для труб из разных материалов.

Таблица
10.1

Трубы, их материалы и состояние стенок	k, мм
Стальные цельнотянутые новые	0,02 – 0,07
Стальные цельнотянутые, находившиеся в эксплуатации	0,2 – 0,5
Стальные цельнотянутые после продолжительной эксплуатации, сильно заржавленные	До 1,0
Железные оцинкованные	0,15 – 0,18
Чугунные асфальтированные новые	0,13
Чугунные новые	0,25
Чугунные, находившиеся в эксплуатации	1,4

Определяют:

а)
среднюю скорость V==;

б)
число Рейнольдса Rе
=
;

в)
относительную шероховатость
.

1.
Если Rе
< 2300,
то имеет место ламинарный режим и

λ
=
.
(10.1)

2.
Если Rе
> 4000,
то определяют величину параметра

Rе.

3.
Если Rе<10,
то имеет место гладкостенная зона
сопротивления и λ
определяется по формуле Блазиуса

λ
=
.
(10.2)

4.
Если 10 <
Rе<500,
то имеет место доквадратичная зона
сопротивления и λ
определяется по формуле Альтшуля

λ
= 0,11

(10.3)

5.
Если Rе>500,
то имеет место квадратичная зона
сопротивления и λ
определяется по формуле Шифринсона

λ
= 0,11

.
(10.4)

Задача
10.1.
Определить, какой степени средней
скорости пропорциональны потери по
длине в каждой из зон сопротивления.

Решение.
Используется формула Дарси-Вейсбаха
(9.14) и зависимость для
в соответствующей зоне сопротивления.

1.
Для ламинарного режима
64/Rе
и потери h_l
выразятся так

или,
сокращая числитель и знаменатель на V,

.

В
правой части последней формулы первый
сомножитель не зависит от скорости и
величина h_l
имеет вид h_l
=

,
т.е.
потери в ламинарной зоне сопротивления
пропорциональны первой степени скорости.

2. В
зоне квадратичного сопротивления λ
определяется по формуле λ=0,11,
а
потери выразятся так h_l=0,11.

Так
как первый сомножитель в правой части
не зависит от скорости, то потери h_l
пропорциональны
скорости в квадрате, откуда и название
зоны – квадратичная зона сопротивления.

Задача
10.2.
Поток в трубе находится в квадратичной
зоне сопротивления. Как изменятся потери
по длине в этой трубе, если расход в ней
увеличить в два раза?

Решение.
Учитывая решение задачи 10.1, заключаем,
что если расход увеличить в два раза,
то и средняя скорость увеличится в два
раза и поэтому (поскольку зона квадратичная)
потери возрастут в 2²,
т.е. в 4 раза.

Задача
10.3.
Отрезок трубы внутренним диаметром
d₁=100
мм был заменен отрезком трубы такой же
длины, но внутренним диаметром d₂,
в 2 раза меньшим: d₂=50
мм.

Определить,
как изменились потери на этом участке
при такой замене. Расход воды остался
таким же; считаем для упрощения решения,
что в обоих случаях квадратичный режим,
изменение λ
не учитываем.

Решение.
Для решения задачи достаточно определить
отношение потерь h₁
в трубе с d₁=100
мм к h₂
в трубе с d₂=50
мм. Выражения для h₁
и h₂
по формуле Дарси-Вейсбаха (9.14)

и
.
Их отношение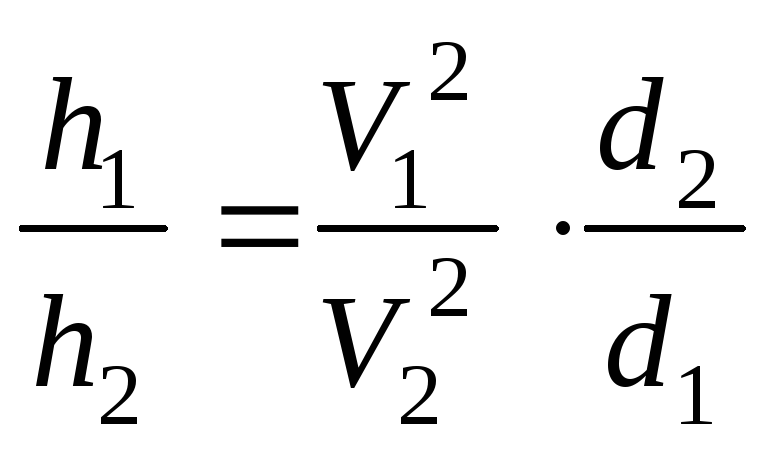.(10.5)

Согласно уравнению
неразрывности

или

.

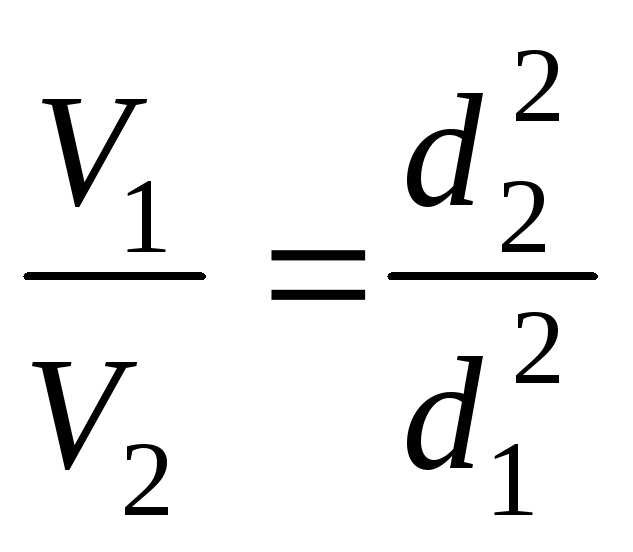
Если возведем обе
части последнего равенства в квадрат,
получим

.
(10.6)

Подставляя
(10.6) в (10.5), имеем окончательно
.

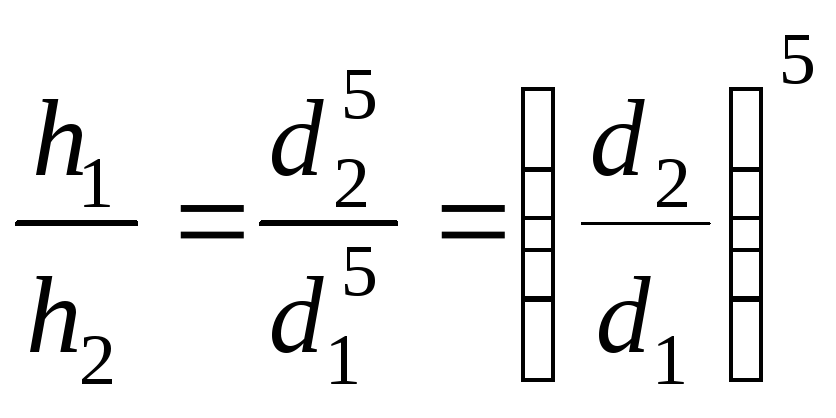
Если
,
то

.

Таким
образом, потери увеличились в 32 раза!
Если учесть, что
также зависит от диаметра, то получим
несколько меньшее число.

Этот
же результат возможно получить, оценивая
порядок величин, а именно, потери
выражаются зависимостью

или

.(10.7)

Средняя скорость
выражается так

V=Q/S
или V~1/d
²,

т.е.
при
обратно пропорциональна квадрату
диаметра, а средняя скорость в квадрате,
соответственно, обратно пропорциональна
четвертой степени диаметра, т.е.

V²
~1/d
⁴
.
(10.8)

Имея
в виду (10.7) и (10.8), получаем в данном случае

h₁~1/d
⁵,

т.е.
потери обратно пропорциональны диаметру
в пятой степени. Этот результат имеет
большое значение при гидравлических
расчетах водопроводных сетей.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

10-я лекция.

11. ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ

11.0. Число Рейнольдса. Характеристика режимов течения вязкой жидкости

11.1  Основные сведения. Эпюры скоростей. Относительная шероховатость

11.2. Коэффициент сопротивления трения по длине трубопровода при турбулентном потоке.

11.3 Гидравлически гладкая труба.

11.4. Относительная шероховатость. Турбулентное течение в шероховатых  трубах

11.5  Опыты Никурадзе

11.6. Реальные шероховатые трубы. Опыты Мурина и теплотехнического института.

Рекомендуемые материалы

11.7.  Турбулентное течение в некруглых трубах

11.1. Число Рейнольдса. Характеристика режимов течения вязкой жидкости.

Исследования, проведенные Осборном Рейнольсом в лабораторных условиях,  позволили установить критерий, характеризующий режим движения вязкой жидкости в трубах и руслах.

Под  руслами понимаются  трубопроводы и каналы в гидрораспределителях, гидромашинах и других гидравлических устройствах,  и каналы с открытой свободной поверхностью жидкости. 

Другими исследователями были установлены  зависимости, связанные с сопротивлением трения   потоку рабочей жидкости.

Использование подобия позволило определить  расчетные коэффициенты сопротивлению трения в реальных условиях.

Проблема механического подобия ставится следующим образом.

“Возможно ли прежде, чем создать какое-либо устройство, установить закономерности его действия, произведя опыты на геометрически подобной ему модели меньших размеров?”.

При изучении режимов движения жидкости использовалось подобие между явлениями на моделях русел и трубопроводов, проводившимися в лабораторных условиях и явлениями, имевшими место в натуре, то есть в реальных руслах и трубопроводах.

Для адекватности выводов, сделанных на модели в лабораторных условиях, было установлено, что должны соблюдаться следующие условия подобия.

Имеются две подобные системы одинаковой физической природы. Одна система, предназначенная для исследований в лабораторных условиях, будет иметь индекс – м, означающий “модель”.

Вторая система, для которой выполняются исследования, реальная конструкция или машина будет иметь индекс – н, означающий “натура”.

Однородные части обеих систем должны удовлетворять условиям подобия так, чтобы коэффициенты подобия имели одно и тоже значение при изучении комплекса или отдельных частей машины. Для этого должны соблюдаться следующие условия.

а) Основные коэффициенты подобия.

1.Геометрическо подобие – подобие размеров будет соблюдаться при пропорциональности диаметров,  длин трубопроводов, радиусов их закруглений в натуре и на модели:

2. Материальное подобие  – подобие  масс геометрически соответственных объемных элементов в модели и в натуре: 

3. Подобие времени эксперимента в лаборатории и в натуре

Механическое состояние любой системы определяется тремя независимыми физическими величинами: длина , масса и время. Из основных коэффициентов подобия можно образовать  производные коэффициенты подобия.

4. Кинематическое подобие – подобие скоростей V₁ и V₂   и ускорений а₁ и а₂   :

коэффициент для скоростей                 

коэффициент для ускорений                 

За характерные скорости берутся  средние скорости на оси. 

4. Механическое или силовое подобие соблюдается, если в сравниваемых точках потока отношения сил одинаковы. Используя выражение для второго закона Ньютона, получим, что  подобие сил на натуре и моде соблюдается при соотношениях:

коэффициент для сил

4.1 Связь между влиянием сил трения (явление вязкости в жидкости) и действием внешних сил, может быть оценена при использовании закона Ньютона о трении в жидкости

 

Используя ранее полученное коэффициент для внешних сил по второму закону Ньютона, так как действие силы трения также изменяет ускорение массы жидкости, приравняем, коэффициент для внешних сил коэффициенту, полученному для сил трения

  чтобы это равенство соблюдалось,

отношение коэффициентов кинематических вязкостей  должно быть равно

  

Внеся в это равенство дополнительно, вместо λ^-1 = λ² λ^-3 и сгруппировав,  имеем

.   

 (11.1)

Связь  сил инерции и сил вязкости при изучении подобных течений на модели и в натуре выражается числом Рейнольдса.

Число Рейнольдса есть отношение сил инерции к силам вязкости в потоках реальной жидкости.

Если число Рейнольдса мало, то в потоке преобладают силы вязкости, если велико – силы инерции.

11.2. Основные сведения о турбулентном режиме течения жидкости. Эпюры скоростей. Относительная шероховатость.

11.2.1. Фиксация скоростей и давлений при турбулентном движении.

Для турбулентного течения в отличии  от ламинарного  характерны пульсации скоростей и давлений, перемешивание  жидкости.

В фиксированной точке потока величина скорости может быть измерена и зафиксирована во времени с помощью трубки полного напора или “трубки Пито” (рис.11.2).

Трубка, повернутая под углом 90°(рис.11.2), устанавливается отверстием навстречу потоку, рядом с ней устанавливается пьезометр. Скорость V  частиц  жидкости, попадающих в отверстие трубки,  тормозится и  уменьшается до нуля, а давление увеличивается на величину скоростного напора. Столб  жидкости в трубке Пито поднимается над уровнем в пьезометре на высоту равную скоростному напору.

. Измерив,  разность высот жидкости в трубке Пито и пьезометре, можно определить скорость жидкости в данной точке.

Запишем уравнение Бернулли для струйки, которая попадает в трубку вдоль  ее оси. Для сечений 0-0 имеем Р₀ и V₀,   и 1-1 P₁,V₁ =0:

Вокруг трубки давление также близко к  Р=Ро, , следовательно,  из предыдущего имеем

Скорость во время записи колеблется около среднего значения. Траектории частиц, проходящих через данную неподвижную точку пространства в разные моменты времени, представляют собой кривые линии различной формы, (рис.11.1).

11.2.2. Характеристики турбулентного течения.

Турбулентное течение неустановившееся, так как значения скоростей и давлений, а также траектории частиц, изменяются по времени.

Для расчетов, усредняют скорости и давления.  Если средние значения скоростей и давлений потока мало изменяются во времени, то по средним значениям принято считать турбулентное течение установившимся.

Средние скорости при турбулентном течении распределены более равномерно по сечению трубопровода в сравнении с  ламинарным течением.

Коэффициент (рис.11.3) Кориолиса , учитывающий неравномерность распределения скоростей в уравнении Бернулли, при турбулентном течении меньше, чем при ламинарном течении.   При ламинарном течении коэффициент Кориолиса  не зависит от Re и равен приблизительно двум, при турбулентном течении  близок к единице.

Поскольку при турбулентном течении отсутствует слоистость потока и происходит перемешивание  жидкости, касательное напряжение  τ  на стенке трубы в турбулентном потоке больше, чем при ламинарном при тех же числах Re, благодаря перемешиванию и  переносу жидкости  в поперечном направлении,  

При турбулентном режиме при Re >Re_кр  потери  энергии на трение по длине значительно больше, чем при ламинарном при тех же размерах трубы, расходе и вязкости жидкости.

При ламинарном режиме потери напора на трение возрастают пропорционально скорости в первой степени, а при переходе к турбулентному течению заметен скачок сопротивления и изменение сопротивления  по кривой  близкой к параболе (рис.11.4).

Ввиду сложности турбулентного течения и трудностей его аналитического исследования до настоящего времени для него не имеется достаточно строгой и точной его теории.

11.2. Коэффициент сопротивления трения по длине

трубопровода при турбулентном потоке.

Основной расчетной формулой для потерь напора при турбулентном течении в круглых трубах является эмпирическая формула Вейсбаха— Дарси

‚

где λ_т – коэффициент потерь на трение при турбулентном течении, или коэффициент Дарси.

При турбулентном течении потеря напора на трение пропорциональна скорости во второй степени, а  коэффициент потерь на трение в формуле для данной трубы можно считать величиной постоянной.

11.3 Турбулентное течение в области гидравлически гладких труб.

Для практических расчетов потерь, связанных с турбулентным течением жидкостей в трубах были проведены экспериментальные исследования, и  установлено, что коэффициент λ_т зависит от   сочетания двух  факторов: неровностей в трубе и числа Рейнольдса.

На графике функциональных зависимостей, связывающих коэффициент λ, неровности в трубе и число Re выделены две области: область гидравлически гладких труб и область гидравлически шероховатых труб.

Труба  называется гидравлически гладкой, когда ее шероховатость не влияет на коэффициент λ_т  и соответственно на сопротивление потоку.

К гидравлически гладким трубам можно отнести цельнотянутые трубы из цветных металлов, включая и алюминиевые сплавы, а также высококачественные бесшовные стальные трубы. Такие трубы применяются в топливопроводах и гидросистемах. Водопроводные стальные и чугунные трубы гидравлически гладкими не считают.

В области гидравлически гладких труб при турбулентном течении в эмпирические зависимости для коэффициента λ_т , как и для ламинарного движения входит только число Рейнольдса:

λ_т = f(Re).

Основную роль в образовании потерь энергии при турбулентном течении играет перемешивание  и рассеивание кинетической энергии завихренных частиц.

Исследования турбулентного течения жидкости при небольших скоростях в области гидравлически гладких труб показали, что на стенке трубы образуется ламинарный подслой (рис.11.5). Это тонкий слой жидкости, движение в котором является слоистым и происходит без перемешивания. В его пределах скорость растет от нуля на стенке до некоторой величины V_л  на границе слоя. Толщина δл ламинарного слоя невелика, причем оказывается, что число Re, подсчитанное по толщине δ_л, скорости V_л и кинематической вязкости ν, есть величина постоянная,  как постоянно Re_кр для течения в трубах.

Re = V_л δ_л/ν= const

При увеличении скорости потока толщина δ_л ламинарного слоя уменьшается.

11.4. Турбулентное течение в области в шероховатых  труб.

Относительная шероховатость.

Труба  называется гидравлически шероховатой, когда на ее внутренней поверхности ламинарный подслой мал или отсутствует.

Относительной шероховатостью называется отношение ∆/d, где ∆ – средняя высота бугорков неровностей (шероховатостей) внутри трубы, d — диаметр трубы.

Одинаковая абсолютная шероховатость может совершенно не оказывать влияния на сопротивление трубы большого диаметра, но значительно влияет на сопротивление трубы малого диаметра.

Если все бугорки шероховатости имеют один и тот же размер ∆ и одинаковую форму, такая шероховатость называется  равномерно распределенной зернистой шероховатостью.

Область “гидравлически шероховатых труб” состоит из двух частей.

В первой части   λ_т зависит от числа Re и от шероховатости внутренней поверхности трубы, выраженной в виде относительной величины

λ_т =f(Re, ∆/d)

Во второй части λ_Т  зависит только от шероховатости внутренней поверхности трубы

λ_т = f(∆/d),

11.5  Опыты Никурадзе

 Сотрудник Прандтля в Геттингене Никурадзе выполнил опыты  по определению  сопротивления труб с искусственно созданной равномерно распределенной зернистой шероховатостью на внутренней поверхности.

Шероховатость была получена путем приклейки песчинок определенного размера, полученного просеиванием песка через специальные сита. Сначала внутренние стенки труб покрывались лаком, затем труба заполнялась песком определенной зернистости, с диаметром  равным средней неровности ∆, песчинки приклеивались к стенкам однородным слоем, потом опять покрывалась лаком и высушивалась.

Испытания были проведены в диапазоне относительных шероховатостей ∆/r₀ от 1/500  до   1/15) при числах Рейнольдса Re=500 – 10⁶.

На рис.11.6 представлены результаты этих испытаний и построены зависимости lg(1000λ) от lg Re для значений ∆/r₀. ∆ – высота бугорков, r₀ – радиус трубы.

1.Область ламинарного режима. Уравнение прямой А, определяющей область ламинарного режима течения,  получено из формулы для λл= 64/Re умножением на 1000 и логарифмированием

lg(1000λл) = lg 64000 – lgRe.

От  прямой А до осей координат находится область ламинарного режима, в которой  коэффициент  сопротивления λл зависит только от Re, определяется по формуле для ламинарного режима течения

λ= 64/Re.

2.Область гидравлически гладких труб при турбулентном режиме. Уравнение прямой В, определяющей эту область получено из формулы для Блазиуса  λ_тр = 0,316/ умножением на 1000 и логарифмированием

lg(1000λт) = lg 316 – (¼) lgRe.

2.1. Под прямой В до оси абсцисс находится область “гидравлически гладких труб”, коэффициент  сопротивления λл зависит только от Re  и определяется по формуле Блазиуса  или Конакова для ламинарного режима течения.

При  Re< 10⁵ (сто тысяч) применяется формула Блазиуса

λ_тр = 0,316/ .                (11.2)

При Re> 10⁵ применяется формула Конакова

λ_тр = 1/(1,8*lgRe-1,5)²          (11.3)

Штриховыми линиями показаны зависимости λ_тр для труб с различной относительной шероховатостью ∆/r₀.

2.2. Переходная область.  Особенность турбулентного режима течения в этой области в том, что при увеличении числа Re (скорости) толщина  ламинарного слоя δ_л уменьшается. Для турбулентного потока при малых числах Re толщина ламинарного слоя больше высоты бугорков шероховатости, бугорки находятся внутри ламинарного слоя, обтекаются плавно (безотрывно) и на сопротивление не влияют. При увеличении Re толщина δ_л уменьшается, бугорки шероховатости начинают выступать за пределы слоя и влияют на сопротивление.

Над  областью гидравлически гладких труб  начинается переход к режиму шероховатых труб, для труб  с шероховатостью ∆/r₀ = 1/15, 1/30 и  λт  yже зависит не только от Re, но и от шероховатости и его значения  отклоняются от прямой В сверху.  

По числу  Рейнольдса  нижняя граница переходной области  Re_гл ≥ 20d/Δ, верхняя  граница – Re_кв < 500 d/Δ.

В переходной области значения λ определяются по графику    или по ф-ле Альтшуля

              ( 11.4)

Следует отметить, что средние значения эквивалентной шероховатости для

– новых цельнотянутых труб Δ =0,1мм,

– для бывших в употреблении  Δ = 0,2 мм

3. Область гидравлически шероховатых труб.

Для определения коэффициента λт используются графики или формула Никурадзе

     ( 11.5 )

или формула  Шифринсона

   (11.6).

Для старых водопроводных труб (стальных и чугунных) ∆ = 1 мм, применима формула

Область шероховатых труб, где λ зависит только от отношения  ∆/r₀  называется квадратичной или автомодельной зоной.

При больших Re коэффициент λ_т перестает зависеть от Re и становится постоянным для данной относительной шероховатости. Участки этих штриховых линий параллельны оси абсцисс.

При больших числах  Re толщина ламинарного слоя уменьшается, бугорки шероховатости обтекаются турбулентным потоком с вихревыми образованиями, этим  объясняется квадратичный закон сопротивления, характерный для данной области.

11.6. Реальные шероховатые трубы. Опыты Мурина

и теплотехнического института.

Опыты Никурадзе проводились на трубах, снабженных искусственной, равномерно распределенной зернистой шероховатостью. Для натуральных шероховатых труб закон изменения λ_т от Re получается иным. На рис.11.7   в полулогарифмических координатах даны результаты опытов, проведенных во Всесоюзном теплотехническом институте Г.А. Муриным. 

Коэффициент λ_т для натуральных шероховатых труб на графике указан в зависимости от Re для разных значений d/∆_э.

Отношение названо d/∆_э “относительной гладкостью труб”  в отличии от “относительной шероховатости” ∆/d в работе Никурадзе, где ∆_э — абсолютная шероховатость, эквивалентная по сопротивлению зернистой шероховатости в опытах  Никурадзе. 

Различие в характере кривых, представленных на рис.11.7 и рис.11.6 объясняется тем, что в натурной трубе (см.рис.11.7) бугорки шероховатости имеют различную высоту и при увеличении числа Re начинают выступать за пределы ламинарного слоя при разных  Re.

Поэтому переход от линии, соответствующей сопротивлению гладких труб, к горизонтальным прямым соответствующим квадратичному закону, происходит для натурных труб более плавно без провала кривых, характерного для графика  Никурадзе.

На этом графике можно выделить также три области.

1.Область гидравлически гладких труб.

При Re < 20 d/∆_э используют  формулу  Блазиуса для гладких труб

1.2.Переходная зона.

При 20 d/∆_э < Re < 500 d/∆_э используют универсальную формулу А. Д. Альтшуля

                     (11.7)

1.2. Зона шероховатых труб.

При Re > 500 d/∆_э для режима квадратичного сопротивления (автомодельности):

,        (11.8)

где ∆_э –  эквивалентная абсолютная шероховатость; d –  диаметр трубы.

Таким образом, путем сравнения численного значения отношения  d/∆_э с числом Re можно установить границы указанных выше областей (режимов) турбулентного течения в шероховатых трубах.

11.7.  Турбулентное течение в некруглых трубах

На практике часто приходится иметь дело с турбулентным течением в некруглых трубах, применяемых, например, в охлаждающих устройствах (радиаторах, теплообменниках, охлаждающих трактах двигателей и др.).

Рассмотрим расчет потерь на трение при турбулентном течении в трубе с поперечным сечением произвольной формы. Суммарная сила трения, действующая на внешнюю поверхность потока длиной l,

Т = П*l*τ₀,

где П — периметр сечения; τ₀  –  касательное напряжение на стенке, зависящее в основном от динамического давления, т.е. от средней скорости течения и плотности жидкости .

Расход жидкости и  заданная площадь сечения S  определяют среднюю  скорость.  Сила трения пропорциональна периметру сечения.

При некруглом сечении для оценки влияния формы на потерю напора при турбулентном и при ламинарном течении  вводят гидравлический радиус Rг, равный  отношению площади сечения S некруглой трубы к периметру П его сечения и гидравлический диаметр Dг.

Rг = S/П.

1) Тогда для прямоугольника со сторонами a b получим S=ab, П = 2(a+2b),

Rг = S/П = (ab)/(2(a+b)).

2) Для квадрата Rг = S/П = (a²)/(4a) = a/4.

3) Для зазора а, при а<<b: Rг = S/П = .

16. Сплошные системы разработки – лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

Для круглого сечения : Rг = S/П =. Откуда Dг = 4Rг.

Тогда для прямоугольника Dг = 4Rг = 4*(аb)/2(a+b) = 2*(аb)/(a+b), для квадрата Dг = 4*(а/4) = а, для зазора  Dг = 4Rг = 4*(а/2)=2а.

Для определения потерь при турбулентном и  при ламинарном режиме можно пользоваться формулой Вейсбаха—Дарси. Таким образом, для любой формы сечения

                          (11.9)

При этом коэффициент λ_т  подсчитывают по тем же формулам, а число Рейнольдса выражают через гидравлический диаметр D_г :

Re = (VD_г)/ν.

Содержание

• Происхождение шероховатости
• Значения шероховатости для некоторых коммерческих материалов
• Определение абсолютной шероховатости
• Ламинарный поток и турбулентный поток
• Коэффициент трения
• Старение труб
• Ссылки

Относительная шероховатость и абсолютная шероховатость – это два термина, которые используются для описания набора существующих неровностей внутри промышленных труб, по которым транспортируются жидкости. Абсолютная шероховатость – это среднее или среднее значение этих неровностей, переведенное в среднее изменение внутреннего радиуса трубы.

Абсолютная шероховатость считается свойством используемого материала и обычно измеряется в метрах, дюймах или футах. Со своей стороны, относительная шероховатость – это отношение абсолютной шероховатости к диаметру трубы, поэтому она является безразмерной величиной.

Относительная шероховатость важна, поскольку такая же абсолютная шероховатость более заметно влияет на тонкие трубы, чем на большие.

Очевидно, что шероховатость труб взаимодействует с трением, которое, в свою очередь, снижает скорость, с которой жидкость движется внутри них. В очень длинных трубах жидкость может даже перестать двигаться.

Поэтому очень важно оценить трение при анализе потока, поскольку для поддержания движения необходимо прикладывать давление с помощью насосов. Компенсация потерь требует увеличения мощности насосов, что сказывается на расходах.

Другими источниками потери давления являются вязкость жидкости, диаметр трубы, ее длина, возможные сужения и наличие клапанов, кранов и колен.

Происхождение шероховатости

Внутренняя часть трубы никогда не бывает полностью гладкой и гладкой на микроскопическом уровне. Стены имеют неровности поверхности, которые сильно зависят от материала, из которого они сделаны.

Кроме того, после эксплуатации шероховатость увеличивается из-за накипи и коррозии, вызванной химическими реакциями между материалом трубы и жидкостью. Это увеличение может составлять от 5 до 10 раз больше заводской шероховатости.

Для коммерческих труб значение шероховатости указывается в метрах или футах, хотя, очевидно, они будут действительны для новых и чистых труб, потому что со временем шероховатость изменит свое заводское значение.

Значения шероховатости для некоторых коммерческих материалов

Ниже приведены общепринятые значения абсолютной шероховатости промышленных труб:

– Медь, латунь и свинец: 1,5 х 10 ^-6 м (5 х 10 ^-6 футов).

– Чугун без покрытия: 2,4 x 10 ^-4 м (8 х 10 ^-4 футов).

– Кованое железо: 4,6 х 10 ^-5 м (1,5 х 10 ^-4 футов).

– Клепанная сталь: 1,8 х 10 ^-3 м (6 х 10 ^-3 футов).

– Коммерческая сталь или сварная сталь: 4,6 x 10 ^-5 м (1,5 х 10 ^-4 футов).

– Чугун с асфальтовым покрытием: 1,2 x 10 ^-4 м (4 х 10 ^-4 футов).

– Пластик и стекло: 0,0 м (0,0 фута).

Относительную шероховатость можно оценить, зная диаметр трубы, изготовленной из рассматриваемого материала. Если обозначить абсолютную шероховатость как а также а диаметр как D, относительная шероховатость выражается как:

а также_р = e / D

В приведенном выше уравнении используется цилиндрическая труба, но в противном случае величина, называемая гидравлический радиус, в котором диаметр заменен на четырехкратное значение.

Определение абсолютной шероховатости

Для определения шероховатости труб были предложены различные эмпирические модели, учитывающие геометрические факторы, такие как форма неровностей в стенах и их распределение.

Примерно в 1933 году немецкий инженер Й. Никурадсе, ученик Людвига Прандтля, покрыл трубы песчинками разного размера, известные диаметры которых и являются абсолютной шероховатостью. а также. Никурадзе работал с трубками, для которых значения e / D варьировались от 0,000985 до 0,0333,

В этих хорошо контролируемых экспериментах шероховатости были распределены равномерно, что на практике не происходит. Однако эти значения а также они по-прежнему являются хорошим приближением для оценки влияния шероховатости на потери на трение.

Шероховатость, указанная производителем трубы, фактически эквивалентна шероховатости, созданной искусственно, как это сделали Никурадсе и другие экспериментаторы. По этой причине его иногда называют эквивалентный песок (эквивалент песка).

Ламинарный поток и турбулентный поток

Шероховатость трубы – очень важный фактор, который следует учитывать в зависимости от режима движения жидкости. Жидкости, для которых важна вязкость, могут двигаться в ламинарном режиме или в турбулентном режиме.

В ламинарном потоке, при котором жидкость движется упорядоченно слоями, неровности на поверхности трубы имеют меньший вес и поэтому обычно не принимаются во внимание. В этом случае именно вязкость жидкости создает напряжения сдвига между слоями, вызывая потери энергии.

Примерами ламинарного потока являются струя воды, выходящая из крана с низкой скоростью, дым, начинающий хлынуть из зажженной ароматической палочки, или начало струи чернил, впрыскиваемой в струю воды, как определено Осборном Рейнольдсом. в 1883 г.

Вместо этого турбулентный поток менее упорядочен и более хаотичен. Это поток, в котором движение нерегулярно и не очень предсказуемо. Примером может служить дым от ароматической палочки, когда он перестает плавно двигаться и начинает образовывать серию нерегулярных струй, называемых турбулентностью.

Безразмерный числовой параметр, называемый числом Рейнольдса N_р указывает, есть ли у жидкости тот или иной режим, по следующим критериям:

Без_р <2000 поток ламинарный; Без_р > 4000 поток турбулентный. Для промежуточных значений режим считается переходным, а движение неустойчивым.

Коэффициент трения

Этот коэффициент позволяет найти потерю энергии из-за трения и зависит только от числа Рейнольдса для ламинарного потока, но в турбулентном потоке присутствует относительная шероховатость.

да F – коэффициент трения, для его определения существует эмпирическое уравнение, называемое уравнением Коулбрука. Это зависит от относительной шероховатости и числа Рейнольдса, но разрешить его непросто, поскольку F не указано явно:

Вот почему были созданы такие кривые, как диаграмма Муди, которые позволяют легко найти значение коэффициента трения для данного числа Рейнольдса и относительной шероховатости. Опытным путем были получены уравнения, которые действительно имеют F явно, что довольно близко к уравнению Колебрука.

Старение труб

Существует эмпирическая формула для оценки увеличения абсолютной шероховатости в результате использования, зная значение заводской абсолютной шероховатости. а также_или:

е = е_или + αт

куда а также это грубость после т прошедших лет, а α – коэффициент с единицей измерения м / год, дюйм / год или фут / год, называемый скорость ежегодного увеличения шероховатости.

Первоначально вычитается для чугунных труб, но хорошо работает с другими типами труб из металла без покрытия. В них pH жидкости важен с точки зрения ее долговечности, поскольку щелочные воды значительно уменьшают поток.

С другой стороны, трубы с покрытием или пластик, цемент и гладкий бетон не испытывают заметного увеличения шероховатости со временем.

Ссылки

1. Беляди, Хосс. Выбор и проектирование химикатов ГРП. Получено с: sciencedirect.com.
2. Цимбала, C. 2006. Механика жидкости, основы и приложения. Mc. Гроу Хилл. 335- 342.
3. Францини, Дж. 1999. Механика жидкости с применением в машиностроении. Mc. Гроу Хилл. 176–177.
4. Мотт, Р. 2006. Механика жидкости. 4-й. Издание. Pearson Education. 240-242.
5. Ратнаяка, Д. Гидравлика. Получено с: sciencedirect.com.