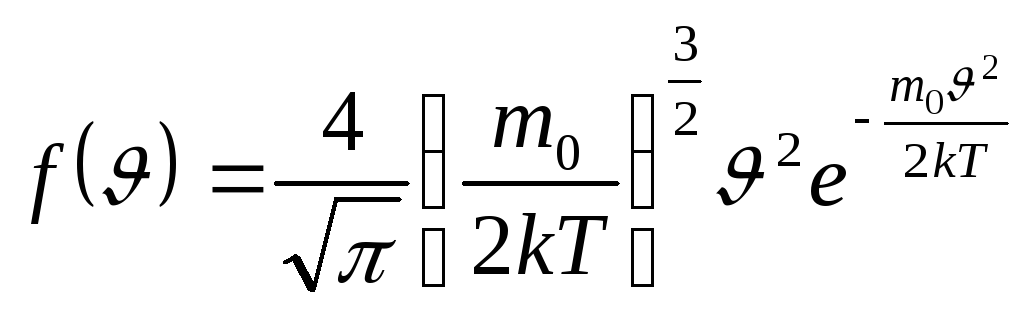Иногда нас может интересовать относительная скорость двух молекул 
Величина этой скорости в реальном газе будет определять частоту и характер столкновений молекул. В зависимости от кинетическои энергии относительного движения 
произойдет упругое или неупругое столкновение молекул, Поэтому вычисление
среднего квадрата и среднего модуля относительной скорости молекул в газе представляет определенный интерес.
Пусть одна из молекул движется со скоростью 
, а другая — со скоростью 
Тогда относительная скорость будет 
а ее модуль
Величина 
зависит от скоростей 
молекул, движение которых можно считать независимым, а скорости 
распределенными по Максвеллу. Тогда функция распределения случайной величины 
будет определяться произведением двух максвелловских функций 
можно выразить с помощью обычных формул:
и
Сначала вычислим 
используя соотношение
где 
угол между векторами 
и
Средний квадрат относительной скорости можно переписать в виде:
откуда, считая функции нормированными, получим:
В последнем выражении угол 
зависит от направления скоростей 
что затрудняет интегрирование. Однако значение последнего интеграла в нашем случае можно найти. Для этого угол 
следует отсчитывать от направления вектора 
вектор 
рассматривать соответственно в сферических координатах. Тогда, учитывая изотропность движения 
молекулы, последний интеграл в (3.40) можно приравнять нулю:
так как
Поэтому окончательно получим:
Если массы 
молекул одинаковы, то средний квадрат относительной скорости 
будет в 2 раза больше среднего квадрата скорости отдельных молекул газа:
Вычислить среднюю скорость относительного движения оказывается несколько труднее. Для этого перепишем выражение (3.38) в следующем виде:
где
Для вычисления этого выражения необходимо от рассмотрения движения 
молекул в пространстве перейти к рассмотрению их относительного движения 
и движения от центра масс 
Скорость центра масс 
определим из закона сохранения количества движения:
Считая массы молекул одинаковыми 
получим:
при этом относительная скорость
Два последних равенства позволяют выразить скорости 
через скорости 
Преобразуем соответственно и элемент объема фазового пространства скоростей по формуле (2.31):
где якобиан преобразования 
равен
Подставляя 
в виде 
и (3.44) в выражение (3.41), получим:
Пределы интегрирования по 
сохраняются и для интегрирования по 
как видно из формул (3.37) и (3.42).
В силу изотропности движения молекул в газе будем рассматривать лишь модули скоростей 
Тогда элемент пространства скоростей 
можно представить как
Теперь искомое выражение будет иметь следующий вид:
Интегрируя 
(можно воспользоваться интегралами из Приложения), получим:
Таким образом, абсолютное значение средней относительной скорости 
для одинаковых молекул оказывается в -2 раз больше средней абсолютной скорости молекул 
Средняя скорость молекул
В физике выделяют 2 скорости, характеризующие движение молекул: средняя скорость движения молекул и средняя квадратичная скорость.
Средняя скорость движения молекул
Средняя скорость движения молекул называется также скоростью теплового движения молекул.
Формула средней относительной скорости молекул в физике представлена следующим выражением:
υotn=28kTπm0=2υ.
Средняя квадратичная скорость
Средняя квадратичная скорость движения молекул газа это следующая величина:
υkυ=1N∑i=1Nυi2
Формулу средней квадратичной скорости можно переписать так:
υkυ2=∫0∞υ2Fυdυ.
Проводя интегрирование, аналогичное интегрированию при получении связи средней скорости с температурой газа, получаем:
υkυ=3kTm0=3RTμ
Именно средняя квадратичная скорость поступательного движения молекул газа входит в состав основного уравнения молекулярно-кинетической теории:
p=13nm0υkυ,
где n=NV – это концентрация частиц вещества, N – это количество частиц вещества, V – это объем.
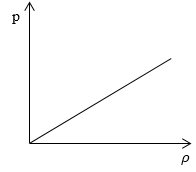
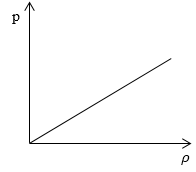
Необходимо определить, как изменяется средняя скорость движения молекул идеального газа с увеличением давления в процессе, изображенном на графике (рисунок 1).
Рисунок 1
Решение
Запишем выражение для средней скорости движения молекул газа следующим образом:
υ=8kTπm0
Из графика видно, что p~ρ или p=Cρ, где C – это некоторая константа.
m0=ρn, p=nkT=Cρ→kT=Cρn
Подставив m0=ρn, p=nkT=Cρ→kT=Cρn в υ=8kTπm0, получаем:
υ=8kTπm0=8Cρπnnρ=8Cπ
Ответ: В процессе, представленном на графике, с увеличением давления средняя скорость движения молекул не меняется.
Можно ли найти среднюю квадратичную скорость молекулы идеального газа, если известно: давление газа (p), молярная масса газа (μ), а также концентрация молекул газа (n)?
Решение
Применим выражение для υkυ:
υkυ=3RTμ
Помимо этого, из уравнения Менделеева-Клайперона и зная, что mμ=NNA:
pV=mμRT=NNART.
Поделим правую и левую части pV=mμRT=NNART на V, и зная NV=n, получаем:
p=nNART→RT=pNAn
Подставляем p=nNART→RT=pNAn в выражение для среднеквадратичной скорости υkυ=3RTμ, получаем:
υkυ=3pNAμn
Ответ: По заданным в условии задачи параметрам среднеквадратичная скорость движения молекул газа вычисляется при помощи формулы υkυ=3pNAμn.
Для характеристики движения молекул в физике используют две скорости: среднюю и среднюю квадратичную скорость молекул.
Важно. Следует обязательно понимать, что в реальных условиях мы не можем точно знать ни конкретное число молекул в системе, ни тем более скорость каждой из них в конкретный момент времени. Это обусловлено неимоверно гигантским числом частиц в реальных и даже сколько-нибудь приближенных к ним системах. Например, в 1 см3 при давлении 200 мм. рт. ст. содержится 4,18*1018 молекул водорода. Говоря более понятными категориями, это более чем 4 миллиарда миллиардов. Заметим, что указанное давление меньше атмосферного почти в 4 раза. Последнее в среднем равняется 760 мм. рт. ст. Разрежённый водород по своим свойствам наиболее близок к идеальному газу. В данном случае физика вынуждена иметь дело с распределениями скоростей и энергий частиц.
Что такое средняя скорость движения молекул
Среднюю скорость движения молекул часто именуют скоростью их теплового движения.
Определение 1
Вид формулы средней относительной скорости молекул в физике можно представить выражением:
[text { Vотн }=sqrt{2} sqrt{frac{8 R T}{pi m_{0}}}]
Выражение под корнем – средняя скорость молекул идеального газа.
Как определить среднюю квадратичную скорость движения молекул
Определение 2
Средней квадратичной скоростью молекул идеального газа называют величину равную квадратному корню из среднего арифметического величины квадратов скоростей каждой из молекул.
Средняя скорость молекул равна:
[leftlanglemathrm{V}_{mathrm{KB}}rightrangle=sqrt{frac{1}{N} sum_{i=1}^{N} v_{i}^{2}}]
Если обе её части возвести в квадрат и проинтегрировать, то получим выражение:
[langlemathrm{VKB}rangle^{2}=int_{0}^{infty} v^{2} F(v) d v]
Ещё одно выражение для среднеквадратичной скорости:
[leftlangle V_{K B}rightrangle=sqrt{frac{3 k T}{m_{0}}}=sqrt{frac{3 R T}{mu}}]
Именно она присутствует в уравнении, именуемом основным уравнением молекулярно-кинетической теории
P = (1/3)nm*<Vкв>
Где n – концентрация молекул, которая вычисляется делением их общего числа на объём.
Пример. 1.
Рассмотрим простейший случай, чтобы использование интегрирования не затруднило понимание сути явления и помогло лучше понять материал. Вычислим как меняется средняя скорость движения молекул в идеальном газе при линейном увеличении его давления. График следующий:
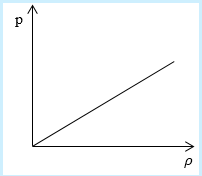
Напомним, что средняя скорость частиц:
[mathrm{Vcp}=sqrt{frac{8 R T}{pi m_{0}}}]
Если присмотреться к представленному графику, то можно заметить, что P приблизительно равно ρ. Эти две величины можно связать соотношением
P=C*ρ
Где С – некоторая постоянная величина, константа.
Далее считаем m0= ρ/n, p = n*k*T = C* ρ. Отсюда следует, что k*T = (C*ρ)/n.
Нужно лишь подставить эти значения в формулу для средней скорости:
[V c p=sqrt{8 mathrm{kT} / pi mathrm{m}}=sqrt{(8 mathrm{C} rho / pi mathrm{n})(mathrm{n} / rho)}=sqrt{8 mathrm{C} / pi}]
В полученном выражении нет ни одной переменной величины, т. е. при увеличении давления, вопреки ожиданиям, скорость оказалась неизменной.
Ответ: В процессе, который был дан нам на графике, при увеличении давления средняя скорость молекул никак не меняется.
Нет времени решать самому?
Наши эксперты помогут!
Пример. 2.
Определим среднюю квадратичную скорость молекул газа при условии, что нам известны его давление (P), молярная масса (M) и концентрация частиц (n).
Воспользуемся формулой:
[leftlanglemathrm{V}_{kappa в}rightrangle=sqrt{frac{3 k T}{m_{0}}}=sqrt{frac{3 R T}{mu}}]
Также нам потребуется уравнение Менделеева-Клайперона
Здесь мы воспользовались тем, что:
m/μ = N/Na
PV = (m/μ)*RT = (N/Na)*RT
Если обе части этого уравнения поделить на V и принять во внимание, что
(N/V) = n, то можно получить
P = (n/Na)*RT. Отсюда находим, что RT = (p*N)/n
Если мы это подставим в выражение для среднеквадратичной скорости [leftlangle V_{K B}rightrangle=sqrt{3 mathrm{kT} / mathrm{m}_{0}}=sqrt{3 mathrm{RT} / mu}], получим, что средняя квадратичная скорость движения молекул газа: [leftlangle V_{K B}rightrangle=sqrt{left(3 rho N_{a}right) /(mu mathrm{n})}]
Ответ: Формула средней квадратичной скорости молекул исходя из данный нам условий следующая:
[leftlangle V_{K B}rightrangle=sqrt{left(3 rho N_{a}right) /(mu mathrm{n})}]
3.5 Распределение
Максвелла
Существуют и
другие распределения, используемые в
физике, кроме рассмотренных выше.
Распределение большого числа молекул
идеального газа (не квантовых частиц),
находящегося в состоянии термодинамического
равновесия, по модулям скоростей
подчиняется закону распределения
Максвелла.
Для получения дифференциального
распределения Максвелла (см.[1,2]) будем
искать число частиц, скорости которых
лежат в очень малом интервале d
вблизи
некоторой скорости
Пусть
dn
– число частиц в единице объёма, скорости
которых лежат в интервале от
до
d
Это
число пропорционально интервалу
скоростей d
,
а также пропорционально числу частиц
в единице объёма. Можно записать так:
,
(3.18)
где
–
плотность вероятности скорости, которая
означает долю частиц в единице объёма,
скорости которых лежат в единичном
интервале скоростей вблизи скорости
Тогда доля частиц, скорости которых
лежат в интервале от
до
d
может
быть найдена как
(3.19)
Поскольку число
частиц, даже в малых объёмах вещества,
очень велико, то
имеет смысл вероятности того, что любая
частица идеального газа в единице объёма
имеет скорость, лежащую в интервале
скоростей от
до
d
Распределение
Максвелла в дифференциальной форме,
как показано в [1-3], имеет вид:
(3.20)
Вид дифференциального
распределения Максвелла при разных
значениях температуры представлен на
рисунке 3.10. Площадь заштрихованной
криволинейной трапеции на рис.3.10 численно
равна доле частиц, скорости которых
лежат в интервале от
до
d
Скорость
,
соответствующая максимуму плотности
вероятности
,
называется наиболее
вероятной скоростью.
При
выполняется равенство
.
Отсюда получаем, что наиболее вероятная
скорость равна:
или
(3.21)
В отличие от
распределения Гаусса, распределение
Максвелла не симметрично относительно
абсциссы максимума функции распределения.
Это обусловлено наличием в формуле
(3.20) квадрата модуля скорости, кроме
экспоненты. При малых скоростях
преобладает вклад
,
поэтому при этих скоростях вид кривой
дифференциального распределения
(рис.3.10) близок к параболе, при
основной
вклад вносит экспонента, которая убывает
гораздо быстрее, чем растёт парабола.
Площадь фигуры под кривой (
)
на рис.3.10 равна единице (условие
нормировки) и выражает факт существования
молекулы. При возрастании температуры
увеличивается наиболее вероятная
скорость, а плотность вероятности,
соответствующая этой скорости,
уменьшается, но площадь фигуры под
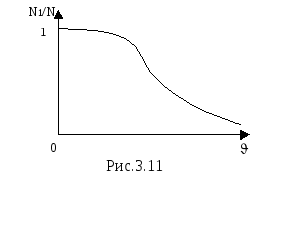
кривой остаётся неизменной. Интегральное
распределение Максвелла показано на
рисунке 3.11. Здесь N1/N
– доля частиц, скорости которых превышают
скорость
.
Таким образом,
распределение Максвелла – это равновесное
распределение идеального газа. Оно
устанавливается благодаря столкновениям
молекул, которые приводят систему к
тепловому равновесию.
3.6.
Распределение Максвелла для относительных
(приведённых) скоростей
Для решения задач
удобно использовать формулу Максвелла
в форме, где скорости молекул выражены
в относительных единицах, приняв за
единицу скорости наивероятнейшую
скорость молекул. Обозначим относительную
(или приведённую) скорость через
.
Распределение Максвелла в дифференциальной
форме будет иметь вид:
,
или
,
здесь
,
а
.
Графическое изображение f(U)
приведено
на рисунке 3.12. Для быстрого определения
f(U)
можно использовать таблицы, приведённые,
например, в [1] .
П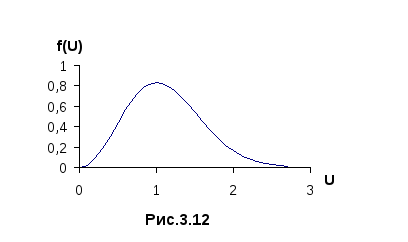
ри
решении задач на распределение Максвелла
необходимо сначала определить интервал
скоростей
и сравнить его со скоростями U1
и U2
– границами интервала. Если интервал
скоростей мал по сравнению со скоростями,
можно использовать дифференциальное
распределение Максвелла. Если интервал
скоростей велик, то нужно использовать
интегральное
распределение Максвелла.
Предположим, что нужно найти долю
молекул, относительные скорости которых
лежат в большом интервале от U1
до
U2.
В этом случае, чтобы избежать излишних
математических трудностей, нужно найти
сначала долю частиц, скорости которых
превышают скорость U1
:
.
Затем нужно найти
долю частиц, скорости которых превышают
скорость U2
:
.
После этого можно
найти долю частиц, скорости которых
лежат в большом интервале от U1
до
U2:
.
Для определения
доли частиц, скорости которых не
превышают, например, скорость U1,
необходимо учесть условие нормировки,
выражающее факт существования частицы:
.
Тогда долю частиц, скорости которых не
превышают скорость
U1
, находим
как:
.
3.7 Средние
скорости молекул
Распределение
Максвелла позволяет определить несколько
средних скоростей: наиболее вероятную
скорость, среднюю арифметическую
скорость и среднюю квадратичную скорость.
Скорость
,
соответствующая максимуму плотности
вероятности
,
называют наиболее
вероятной скоростью.
Для идеального газа, находящегося в
состоянии термодинамического равновесия
при температуре Т, она определяется из
условия
и
равна
или
.
Средняя
квадратичная скорость
определяется как квадратный корень из
среднего квадрата скорости
и
связана со средней кинетической энергией
поступательного движения молекул. Чтобы
найти её с помощью распределения
Максвелла, нужно определить отношение
суммы квадратов скоростей молекул,
содержащихся в единице объёма, к числу
молекул в этом объёме:
.
Для идеального
газа, находящегося в состоянии
термодинамического равновесия при
температуре Т, она равна
или
(3.22)
Среднюю
арифметическую скорость
определяют как отношение суммы всех
скоростей всех молекул в единице объёма
к числу молекул в единице объёма:
.
Для
идеального газа, находящегося в состоянии
термодинамического равновесия при
температуре Т , она равна :
.
. (3.23)
Эти
скорости мало отличаются друг от друга
по своим численным значениям :
.
Экспериментально
равновесное распределение частиц по
скоростям было обнаружено Штерном,
Истерманом и Симпсоном в 1947 году. Описание
экспериментов см. в [1-3].
Екатерина Владимировна Мосина
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Различают следующие скорости, характеризующие движение молекул.
Средняя скорость движения молекул
средняя скорость движения молекул $leftlangle vrightrangle $, которая определяется как:
где N — число молекул. Или, среднюю скорость можно найти как:
где $Fleft(vright)=4pi {left(frac{m_0}{2pi kT}right)}^{frac{3}{2}}expleft(-frac{m_0v^2}{2kT}right)v^2$ — функция распределения молекул по модулю скорости, указывающая долю молекул со скоростями, находящимися в единичном интервале $dv$ около величины скорости $v$, $m_0$- масса молекулы, $k$- постоянная Болцмана, T — термодинамическая температура. Для того, чтобы определить, как средняя скорость молекулы связана с макропараметрами газа, как системы частиц, найдем значение интеграла (2).
Произведем замену:
Следовательно:
Подставим (4) и (5) в (3), получим:
Проведем интегрирование по частям, получим:
где R — универсальная газовая постоянная, $mu $- молярная масса газа.
Среднюю скорость движения молекул называют также скоростью теплового движения молекул.
Средняя относительная скорость молекул:
[leftlangle v_{otn}rightrangle =sqrt{2}sqrt{frac{8kT}{pi m_0}}=sqrt{2}leftlangle vrightrangle left(7right).]
Средняя квадратичная скорость
Средней квадратичной скоростью движения молекул газа называют величину:
[leftlangle v_{kv}rightrangle =sqrt{frac{1}{N}sumlimits^N_{i=1}{{v_i}^2}}left(8right).]
Или
[{leftlangle v_{kv}rightrangle }^2=intnolimits^{infty }_0{v^2Fleft(vright)dv left(9right).}]
Проводя интегрирование, которое аналогично интегрированию при получении связи средней скорости с температурой газа, получим:
[leftlangle v_{kv}rightrangle =sqrt{frac{3kT}{m_0}}=sqrt{frac{3RT}{mu }}left(10right).]
Именно средняя квадратичная скорость поступательного движения молекул газа входит в основное уравнение молекулярно-кинетической теории:
[p=frac{1}{3}nm_0{leftlangle v_{kv}rightrangle }^2left(11right),]
где $n=frac{N}{V}$ — концентрация частиц вещества, $N$- число частиц вещества, V- объем.
«Средняя скорость молекул» 👇
Пример 1
Задание: Определите, как изменяется средняя скорость движения молекул идеального газа при увеличении давления в процессе, представленном на графике (рис.1).
Рис. 1
Решение:
Запишем выражение для средней скорости движения молекул газа в виде:
[leftlangle vrightrangle =sqrt{frac{8kT}{pi m_0}} left(1.1right)]
По графику видим, что $psim rho или p=Crho , $ где C- некоторая константа.
[m_0=frac{rho }{n}, p=nkT=Crho to kT=frac{Crho }{n} left(1.2right).]
Подставим (1.2) в (1.1), получим:
[leftlangle vrightrangle =sqrt{frac{8kT}{pi m_0}}=sqrt{frac{8Crho }{pi n}frac{n}{rho }}=sqrt{frac{8C}{pi }}left(1.3right)]
Ответ: В процессе, изображенном на графике, с ростом давления средняя скорость движения молекул не изменяется.
Пример 2
Задание: Можно ли вычислить среднюю квадратичную скорость молекулы идеального газа, если известны: давление газа (p), молярная масса газа ($mu $) и концентрация молекул газа (n)?
Решение:
Используем выражение для $leftlangle v_{kv}rightrangle :$
[leftlangle v_{kv}rightrangle =sqrt{frac{3RT}{mu }}left(2.1right).]
Кроме того, из уравнения Менделеева — Клайперона и зная, что $frac{m}{mu }=frac{N}{N_A}$:
[pV=frac{m}{mu }RT=frac{N}{N_A}RTleft(2.2right).]
Разделим правую и левую части (2.2) на V, зная, что $frac{N}{V}=n$ получим:
[p=frac{n}{N_A}RTto RT=frac{pN_A}{n} left(2.3right).]
Подставим (2.3) в выражение для среднеквадратичной скорости (2.1), имеем:
[leftlangle v_{kv}rightrangle =sqrt{frac{3pN_A}{mu n}} left(2.4right).]
Ответ: По заданным в условии задачи параметрам среднеквадратичную скорость движения молекул газа вычислить можно с помощью формулы $leftlangle v_{kv}rightrangle =sqrt{frac{3pN_A}{mu n}}.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
