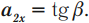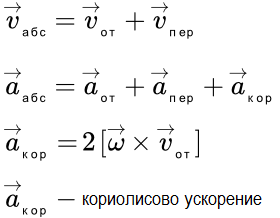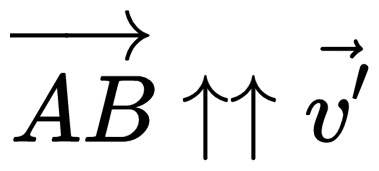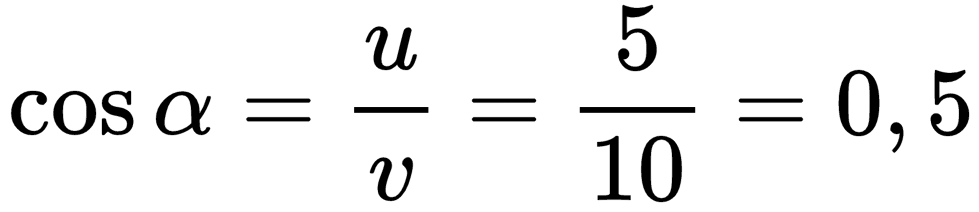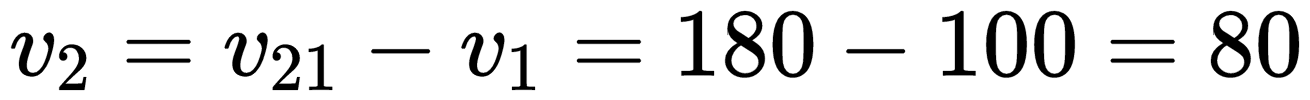Как найти относительную скорость по графику

2.2.1 Как перевести из км/ч в м/с и т. д?

В задачах часто необходимо переводить из одних единиц измерения в другие:

1 км/ч = (1000 м)/(3600 с) = 5/18 м/с,

1 м/с = 18/5 км/ч,

1 км/с = 1000 м/с,

1 см/с = 0,01 м/с,

1 м/мин = 1/60 м/с.

Например, если то для того, чтобы перевести в м/с, нужно умножить на 5/18:

2.2.2 Как найти скорость тела, если известен закон движения?

Закон равномерного движения имеет вид:

Видим, что в этой формуле скорость стоит коэффициентом перед временем. Поэтому, если в условии задачи дан закон движения, необходимо посмотреть на коэффициент перед t — это и есть скорость.

Например, пусть закон движения имеет вид: В данном случае коэффициент перед t равен 5, следовательно,

2.2.3 Как определить скорость по графику координаты от времени?

Закон равномерного движения имеет вид:

Графиком этого закона является прямая линия. Так как  — коэффициент перед t, то является угловым коэффициентом прямой.

Для графика 1:

То, что график 1 «поднимается вверх», означает — тело едет в положительном направлении оси Ox.

Для графика 2:

То, что график 2 «опускается вниз», означает — тело едет в отрицательном направлении оси Ox.

Для определения и выбираем такие точки на графике, в которых можно точно определить значения, как правило, это точки, находящиеся в вершинах клеток.

2.2.4 Как найти закон движения, если известны координаты тела в моменты времени и ?

Пусть в момент времени тело находилось в точке с координатой а в момент времени тело находилось в точке с координатой

Для времени имеем:

Для времени имеем:

Решая систему уравнений (2.19) и (2.20), получим

2.2.5 Как найти графически момент и координату встречи двух тел?

Пусть даны законы движения двух тел: и Согласно пункту 2.5 графиками обоих законов являются прямые линии. Необходимо на одном графике построить оба закона.

Графики пересекаются в одной точке. Координаты этой точки и являются временем и местом встречи.

2.2.6 Как аналитически найти координату и время встречи двух тел?

Пусть даны законы движения двух тел: и В момент встречи тела оказываются в одной координате, то есть и необходимо решить уравнение:

Решение уравнения имеет вид:

Для нахождения координаты достаточно подставить вместо t найденное значение в любой из законов движения:

или

2.2.7 Как найти среднюю скорость, если тело половину пути проехало со скоростью а вторую половину пути

По определению (2.8):

В нашем случае, так как на каждой половине пути тело едет с постоянной скоростью, то

Получаем

В общем случае, если весь путь разбить на n равных участков, на каждом из которых тело едет с постоянной скоростью, то

Формула справедлива только если весь путь разбит на равные участки. Если же разбиение будет иное, то, естественно, формула для нахождения средней скорости, будет иной.

2.2.8 Как найти среднюю скорость, если тело половину времени проехало со скоростью а вторую половину времени

По определению (2.8):

В нашем случае, так как каждую половину времени тело едет с постоянной скоростью, то

Получаем

В общем случае, если все время разбито на n равных промежутков, на каждом из которых тело едет с постоянной скоростью, то

Формула справедлива только если все время разбито на равные промежутки. Если же разбиение будет иное, то, естественно, формула для нахождения средней скорости, будет иной.

2.2.9 Как найти скорость, с которой движется моторная лодка по течению реки?

Согласно формуле скорость тела относительно неподвижной системы отсчета (в нашем случае земли), равна векторной сумме скорости подвижной системы отсчета u (в нашем случае — скорость реки) и скорости в подвижной системе отсчета (в нашем случае — собственная скорость лодки).

При движении по течению вектора и направлены в одну сторону, следовательно, получаем сложение двух векторов, направленных в одну сторону — используем формулу (1.15):

Таким образом, при движении любого тела по течению его скорость определяется формулой

2.2.10 Как найти скорость, с которой движется моторная лодка против течения реки?

Согласно формуле скорость тела относительно неподвижной системы отсчета (в нашем случае земли) равна векторной сумме скорости подвижной системы отсчета u (в нашем случае — скорость реки) и скорости в подвижной системе отсчета (в нашем случае — собственная скорость лодки).

Перепишем формулу в виде:

Вектора и направлены в одну сторону, следовательно, получаем вычитание двух векторов, направленных в одну сторону — используем формулу :

2.2.11 Как найти скорость, с которой движется моторная лодка, если ее скорость направлена перпендикулярно течению реки?

Согласно формуле скорость тела относительно неподвижной системы отсчета (в нашем случае земли), равна векторной сумме скорости подвижной системы отсчета u (в нашем случае — скорость реки) и скорости в подвижной системе отсчета (в нашем случае — собственная скорость лодки).

В данном случае вектора и направлены перпендикулярно, следовательно, получаем задачу о сложении взаимно перпендикулярных векторов — используем формулу :

2.2.12 Как найти расстояние, на которое снесет лодку, если ее скорость направлена перпендикулярно скорости реки?

В результате сложения скоростей по формуле скорость тела относительно земли равна и направлена по прямой OD. В результате, когда тело окажется на противоположном берегу, оно попадет в точке D, и его снесет на длину

Треугольник OAB подобен треугольнику OCD:

2.2.13 Как найти скорость, с которой движется моторная лодка, если ее скорость направлена под углом φ к скорости течения реки?

Согласно формуле скорость тела относительно неподвижной системы отсчета (в нашем случае земли), равна векторной сумме скорости подвижной системы отсчета u (в нашем случае — скорость реки) и скорости в подвижной системе отсчета (в нашем случае — собственная скорость лодки).

В результате сложения скоростей по формуле скорость тела относительно земли равна и направлена по прямой OB. Как видим, получили треугольник, в котором известен один из углов — Тогда по теореме косинусов:

2.2.14 Как найти расстояние, на которое снесет лодку, если ее скорость направлена под углом к скорости течения реки?

В результате сложения скоростей по формуле скорость тела относительно земли равна и направлена по прямой OB. В результате, когда тело окажется на противоположном берегу, оно попадет в точке В, и его снесет на длину

В задачах, когда движение происходит в плоскости, то есть и вдоль оси Ox, и вдоль оси Oy, необходимо введение системы координат для того, чтобы упростить рассмотрение задачи.

Проекция

Проекция

Формулы и не просто результат математической операции нахождения проекции, и имеют физический смысл: со скоростью тело плывет вдоль оси Ox, то есть по течению; со скоростью тело переплывает реку. Например, время, за которое тело переплывет реку, можно найти просто поделив ширину реки на

Тогда

2.2.15 Под каким углом α нужно направить собственную скорость лодки, чтобы за минимальное время переплыть реку?

Согласно формуле скорость, с которой лодка переплывает реку, равна:

Очевидно, что время будет минимальным, если будет максимальным, то есть

2.2.16 С какой скоростью машина обгоняет вторую машину, если они движутся в одну сторону?

Пусть 1-ая машина движется вправо со скоростью а 2-ая машина также движется вправо со скоростью Скорость обгона — это скорость, с которой 1-ая машина движется относительно 2-ой, то есть — это относительная скорость, и она определяется формулой :

Так как и направлены в одну сторону, то получили задачу о вычитании векторов, направленных в одну сторону — формула :

Заметим, что при обгоне, естественно поэтому  

2.2.17 За какое время проедут мимо друг друга два поезда, двигающиеся в одном направлении?

Пусть длина 1-го поезда а скорость 2-го поезда Скорость обгона определяется формулой Тогда

2.2.18 С какой скоростью машина едет навстречу вторую машину, если они движутся в противоположных направлениях?

Пусть 1-ая машина движется вправо со скоростью а 2-ая машина движется влево со скоростью Скорость движения навстречу — это скорость, с которой 1-ая машина движется относительно 2-ой, то есть — это относительная скорость, и она определяется формулой :

Перепишем эту формулу в виде:

Так как и направлены в одну сторону, то получили задачу о вычитании векторов, направленных в одну сторону — формула :

2.2.19 За какое время проедут мимо друг друга два поезда, двигающиеся в противоположных направлениях?

Пусть длина 1-го поезда а скорость 2-го поезда Скорость обгона определяется формулой Тогда

2.2.20 Как найти относительную скорость, если тела движутся по взаимно перпендикулярным направлениям?

Пусть 1-ая машина движется вправо со скоростью а 2-ая машина движется перпендикулярно первой со скоростью Относительная скорость определяется формулой :

Так как вектора и перпендикулярны, то воспользуемся формулой :

Кинематика

Механика — это раздел физики, изучающий механическое движение тел.

Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.

Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если

• расстояние, которое проходит тело, много больше его размера;
• расстояние от данного тела до другого тела много больше его размера;
• тело движется поступательно.

Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.

Важно! 
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.

Основная задача механики — определить положение тела в пространстве в любой момент времени.

Механическое движение и его виды

Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение может быть:
1. по характеру движения

• поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
• вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
• колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;

2. по виду траектории

• прямолинейным — это движение, траектория которого прямая линия;
• криволинейным — это движение, траектория которого кривая линия;

3. по скорости

• равномерным — движение, при котором скорость тела с течением времени не изменяется;
• неравномерным — это движение, при котором скорость тела с течением времени изменяется;

4. по ускорению

• равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
• равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.

Относительность механического движения

Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.

Правило сложения перемещений

Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:

где ​( S )​ — перемещение тела относительно неподвижной системы отсчета;
​( S_1 )​ — перемещение тела относительно подвижной системы отсчета;
​( S_2 )​ — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.

Правило сложения скоростей

Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:

где ​( v )​ — скорость тела относительно неподвижной системы отсчета;
​( v_1 )​ — скорость тела относительно подвижной системы отсчета;
​( v_2 )​ — скорость подвижной системы отсчета относительно неподвижной системы отсчета.

Относительная скорость

Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.

Пусть ( v_1 ) — скорость первого тела, а ( v_2 ) — скорость второго тела.
Определим скорость первого тела относительно второго ( v_{12} ):

Определим скорость второго тела относительно первого ( v_{21} ):

Следует помнить, что траектория движения тела и пройденный путь тоже относительны.

Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:

Если скорости направлены под углом ​( alpha )​ друг к другу, то относительная скорость рассчитывается по теореме косинусов:

Скорость

Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.

Обозначение — ​( v )​, единицы измерения — ​м/с (км/ч)​.

Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:

Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:

Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.

Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.

Ускорение

Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.

Обозначение — ​( a )​, единица измерения — м/с².
В векторном виде:

где ​( v )​ – конечная скорость; ​( v_0 )​ – начальная скорость;
​( t )​ – промежуток времени, за который произошло изменение скорости.

В проекциях на ось ОХ:

где ​( a_n )​ – нормальное ускорение, ​( a_{tau} )​ – тангенциальное ускорение.

Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:

Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:

Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.

Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если ( a_{tau} ) ≠ 0, ( a_n ) = 0, то тело движется по прямой;
если ( a_{tau} ) = 0, ( a_n ) = 0, ​( v )​ ≠ 0, то тело движется равномерно по прямой;
если ( a_{tau} ) = 0, ( a_n ) ≠ 0, тело движется равномерно по кривой;
если ( a_{tau} ) = 0, ( a_n ) = const, то тело движется равномерно по окружности;
если ( a_{tau} ) ≠ 0, ( a_n ) ≠ 0, то тело движется неравномерно по окружности.

Равномерное движение

Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.

Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:

Проекция вектора скорости на ось ОХ:

Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:

График скорости (проекции скорости)

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ​( t )​, тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ​( t )​, тело движется против оси ОХ.

Перемещение при равномерном движении – это величина, равная произведению скорости на время:

Проекция вектора перемещения на ось ОХ:

График перемещения (проекции перемещения)

График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:

График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью ( t ), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.

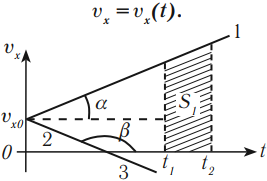
По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время ( t ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Координата тела при равномерном движении рассчитывается по формуле:

График координаты представляет собой зависимость координаты от времени: ​( x=x(t) )​.

График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:

График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:

Прямолинейное равноускоренное движение

Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:

При движении с ускорением скорость может как увеличиваться, так и уменьшаться.

Скорость тела при равноускоренном движении рассчитывается по формуле:

При разгоне (в проекциях на ось ОХ):

При торможении (в проекциях на ось ОХ):

График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:

График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ​( a_x )​ > 0.
График 2 лежит под осью t, тело тормозит, ( a_x ) < 0.

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равноускоренном движении – прямая.
График 1 направлен вверх, тело движется равноускоренно в положительном направлении оси ОХ, ​( v_{0x} )​ > 0, ​( a_x )​ > 0.

График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, ( v_{0x} ) > 0, ( a_x ) < 0,

График 3 направлен вниз, тело движется равноускоренно против оси ОХ, ( v_{0x} ) < 0, ( a_x ) < 0. По графику зависимости скорости от времени можно определить перемещение, пройденное телом за промежуток времени ​( t_2-t_1 )​. Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Перемещение при равноускоренном движении рассчитывается по формулам:

Перемещение в ​( n )​-ую секунду при равноускоренном движении рассчитывается по формуле:

Координата тела при равноускоренном движении рассчитывается по формуле:

Свободное падение (ускорение свободного падения)

Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.

Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).

Обозначение – ​( g )​, единицы измерения – м/с².

Важно! ( g ) = 9,8 м/с², но при решении задач считается, что ( g ) = 10 м/с².

Движение тела по вертикали

Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:

Если тело падает вниз без начальной скорости, то ​( v_0 )​ = 0.
Время падения рассчитывается по формуле:

Тело брошено вверх:

Если брошенное вверх тело достигло максимальной высоты, то ​( v )​ = 0.
Время подъема рассчитывается по формуле:

Движение тела, брошенного горизонтально

Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали со скоростью ​( v_0=v_{0x} )​;
2. равноускоренного движения по вертикали с ускорением свободного падения ​( g )​ и без начальной скорости ​( v_{0y}=0 )​.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Дальность полета:

Угол между вектором скорости и осью ОХ:

Движение тела, брошенного под углом к горизонту (баллистическое движение)

Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали;
2. равноускоренного движения по вертикали с ускорением свободного падения.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Время подъема на максимальную высоту:

Максимальная высота подъема:

Время полета:

Максимальная дальность полета:

Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ​( v_0 )​, с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ​( alpha )​, под которым тело брошено, будет равен углу, под которым оно упадет.

При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:

Это облегчает решение задач:

Движение по окружности с постоянной по модулю скоростью

Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.

Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.

Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ​( a_{цс} )​, единицы измерения – ​м/с^2​.

Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ​( T )​, единицы измерения – с.

где ​( N )​ – количество оборотов, ​( t )​ – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ​( nu )​, единицы измерения – с^–1 (Гц).

Период и частота – взаимно обратные величины:

Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ​( v )​, единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:

Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ​( omega )​, единицы измерения – рад/с .

Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:

Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:

Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:

Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ​( v_1 )​, и все точки обода колеса движутся относительно его центра с такой же линейной скоростью ( v_1 ), то относительно дороги мгновенная скорость разных точек колеса различна.

Мгновенная скорость нижней точки ​( (m) )​ равна нулю, мгновенная скорость в верхней точке ​( (n) )​ равна удвоенной скорости ​( v_1 )​, мгновенная скорость точки ​( (p) )​, лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ​( (c) )​ – по теореме косинусов.

Основные формулы по теме «Кинематика»

Для школьников.

Повторяем кинематику (относительность движения тел).

Имеет смысл говорить о скорости тела (материальной точки) относительно некоторого другого тела (системы отсчёта, связанной с этим другим телом).

Понятия материальной точки и системы отсчёта даны в Занятии 1.

Наиболее простым понятным примером является случай, когда лодка переплывает реку под прямым углом к берегу.

Скорость лодки в системе отсчёта, связанной с Землёй (неподвижной системе отсчёта), называют абсолютной скоростью.

Скорость лодки в системе отсчёта движущейся относительно Земли (движущейся системе отсчёта) называют относительной скоростью.

Вводится ещё понятие переносной скорости. Переносная скорость – это скорость движущейся системы отсчёта относительно неподвижной системы отсчёта (при поступательном движении). В рассматриваемом случае переносная скорость – это скорость течения реки относительно берега.

Тогда скорость лодки относительно берега (абсолютная скорость) выразится как векторная сумма относительной и переносной скоростей:

Второе и третье уравнения позволяют найти относительную скорость материальной точки (они вытекают из первого уравнения).

Примеры и решённые задачи на эти уравнения даны в Занятии 12 и в задачах 4 – 7, 8 – 9, 10 – 11, в задаче для студентов.

Сейчас же рассмотрим решение следующей задачи.

ЗАДАЧА.

Тело (материальная точка М) перемещается вдоль радиуса диска (относительно диска) со скоростью 30 см/с. Диск вращается с угловой скоростью 4 рад/с. Найти абсолютную скорость точки М в момент времени, когда она находится на расстоянии 10 см от центра диска (когда расстояние ОМ равно 10 см).

Решение.

Так как диск вращается (его движение не поступательное), то переносная скорость есть скорость того “места” в движущейся системе, где в данный момент времени находится материальная точка М.

Известная нам скорость 30 см/с является относительной скоростью.

Переносная скорость точки М в рассматриваемый момент времени найдётся через произведение угловой скорости вращения диска на радиус ОМ. Она равна 40 см/с.

Абсолютную скорость точки М найдём по теореме Пифагора:

Ответ: абсолютная скорость точки М в момент её нахождения на расстоянии ОМ, равном 10 см, равна 50 см/с.

Теперь посмотрим, как находится скорость одного движущегося тела относительно другого движущегося тела на примере следующей задачи.

К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.

Ссылки на занятия по механике даны в конце Занятия 1.

Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .

Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.

Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70

Сложное движение точки. Теорема Кориолиса

Здесь мы покажем, что при сложном движении, абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.
Абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова (поворотного) ускорений:
,
где – кориолисово ускорение.

Пример применения изложенной ниже теории приводится на странице “Сложное движение точки. Пример решения задачи”.

Сложное (составное) движение точки

Часто встречаются случаи, когда точка совершает известное движение относительно некоторого твердого тела. А это тело, в свою очередь, движется относительно неподвижной системы координат. Причем движение точки относительно тела и закон движения тела относительно неподвижной системы координат известны или заданы. Требуется найти кинематические величины (скорость и ускорение) точки относительно неподвижной системы координат.

Такое движение точки называется сложным или составным.

Сложное или составное движение точки – это движение в подвижной системе координат. То есть движение точки описывается в системе координат, которая сама совершает движение относительно неподвижной системы координат.

Далее, для ясности изложения, будем считать, что подвижная система координат жестко связана с некоторым твердым телом. Мы будем рассматривать движение точки относительно тела (относительное движение) и движение тела относительно неподвижной системы координат (переносное движение).

Относительное движение точки при сложном движении – это движение точки относительно тела (подвижной системы координат) считая, что тело покоится.

Переносное движение точки при сложном движении – это движение точки, жестко связанной телом, вызванное движением тела.

Абсолютное движение точки при сложном движении – это движение точки относительно неподвижной системы координат, вызванное движением тела и движением точки относительно тела.

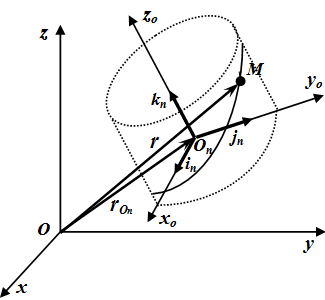
Пусть Oxyz – неподвижная система координат, O_n x_o y_o z_o – подвижная система координат, жестко связанная с телом. Пусть – единичные векторы (орты), направленные вдоль осей x_o , y_o , z_o подвижной системы координат. Тогда радиус-вектор точки M в неподвижной системе определяется по формуле:
(1) ,
где – радиус-вектор точки O_n – начала подвижной системы координат, связанной с телом.

Относительная скорость и ускорение

При относительном движении изменяются координаты x_o , y_o , z_o точки относительно тела. А векторы являются постоянными, не зависящими от времени. Дифференцируя (1) по времени, считая постоянными, получаем формулы для относительной скорости и ускорения:
(2) ;
(3) .

Относительная скорость точки при сложном движении – это скорость точки при неподвижном положении тела (подвижной системы координат), вызванная движением точки относительно тела.

Относительное ускорение точки при сложном движении – это ускорение точки при неподвижном положении тела, вызванное движением точки относительно тела.

Переносная скорость и ускорение

При переносном движении изменяются векторы , определяющие положение тела. Относительные координаты точки x_o , y_o , z_o являются постоянными. Дифференцируя (1) по времени, считая x_o , y_o , z_o постоянными, получаем формулы для переносной скорости и ускорения:
(4) ;
(5) .

Переносная скорость точки при сложном движении – это скорость точки, жестко связанной с телом, вызванная движением тела.

Переносное ускорение точки при сложном движении – это ускорение точки, жестко связанной с телом, вызванное движением тела.

Производные по времени от – это скорость и ускорение начала подвижной системы координат O_n : ; .

Найдем формулы для производных по времени от векторов . Для этого возьмем две произвольные точки твердого тела A и B . Их скорости связаны соотношением:

(см. страницу “Скорость и ускорение точек твердого тела”). Рассмотрим вектор , проведенный из точки A в точку B . Тогда
.
Дифференцируем по времени и применяем предыдущую формулу:
.
Итак, мы нашли формулу для производной по времени от вектора, соединяющего две точки тела:
.
Поскольку векторы жестко связаны с телом, то их производные по времени определяются по этой формуле:
(6) , , .

Подставляем в (4):

.
Таким образом, выражение (4) приводит к формуле для скорости точек твердого тела.

Выполняя подобные преобразования над формулой (5), получим формулу для ускорения точек твердого тела:
,
где – угловое ускорение тела.

Абсолютная скорость и ускорение

При абсолютном движении изменяются как векторы , определяющие положение тела, так и относительные координаты точки x_o , y_o , z_o .

Абсолютная скорость точки при сложном движении – это скорость точки в неподвижной системе координат.

Абсолютное ускорение точки при сложном движении – это ускорение точки в неподвижной системе координат.

Теорема о сложении скоростей

При составном движении абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.

Доказательство

Дифференцируем (1) по времени, применяя правила дифференцирования суммы и произведения. Затем подставляем (2) и (4).
(1) ;
(7)
.

Теорема Кориолиса о сложении ускорений

При составном движении абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова (поворотного) ускорений:
,
где
– кориолисово ускорение.

Доказательство

Дифференцируем (7) по времени, применяя правила дифференцирования суммы и произведения. Затем подставляем (3) и (5).
(7) .

.

В последнем члене применим (6) и (2).

.
Тогда
.

Автор: Олег Одинцов . Опубликовано: 23-10-2015

Основные понятия кинематики. Скорость. Средняя скорость. Относительная скорость. Сложение перемещений и скоростей

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Этот урок посвящён разделу физики, который называется кинематика. Мы узнаем, что изучает кинематика, основные понятия этого раздела. Также на этом уроке будут подробно показаны решения трёх типовых задач различной сложности, которые взяты из сборника задач для подготовки к единому государственному экзамену. Задачи на нахождение средней и относительной скорости.

Относительность механического движения

теория по физике 🧲 кинематика

Под относительностью понимают зависимость чего-либо от выбора системы отсчета. Так, покой и движение тела, его положение в пространстве всегда относительны. Человек, сидящий внутри движущегося автомобиля, покоится относительно этого автомобиля. Но относительно предметов снаружи он движется с некоторой скоростью.

Относительность перемещения

Пусть движение материальной точки (МТ) описывается относительно двух систем отсчета: подвижной (ПСО) и неподвижной (НСО). Зная, как эта точка движется относительно ПСО, и, как ПСО движется относительно НСО, можно вычислить перемещение точки относительно НСО. В этом заключается правило сложения перемещений:

s′ — перемещение МТ относительно НСО, s ₁— перемещение МТ относительно ПСО, s ₂ — перемещение ПСО относительно НСО.

Чтобы применять правило сложения перемещений, нужно уметь складывать вектора.

Полезные факты

• Если тело движется в направлении движения ПСО, то модуль его перемещения относительно НСО равен сумме модулей перемещения этого тела относительно ПСО и перемещения ПСО относительно НСО:

• Если тело движется противоположно движению ПСО, то модуль его перемещения относительно НСО равен разности модулей перемещения этого тела относительно ПСО и перемещения ПСО относительно НСО:

• Если тело движется под прямым углом по отношению к направлению движения ПСО, то модуль его перемещения относительно НСО равен корню из суммы квадратов перемещений этого тела относительно ПСО и перемещения ПСО относительно НСО:

• Если относительно ПСО тело покоится, то его перемещение относительно НСО равно перемещению ПСО относительно НСО: при s₁=0,перемещение s′ = s₂
• Если тело движется относительно двух НСО, то его перемещение относительно НСО₁ равно перемещению движения относительно НСО₂. В этом случае одну из систем можно принять за ПСО с нулевой скоростью. Тогда ее перемещение относительно НСО будет равно 0. При s₂=0,перемещение s′ = s₁

Пример №1. Человек прошел в автобусе 2 метра в направлении заднего выхода. За это же время автобус успел переместиться относительно остановки на 10 м. Найти перемещение человека относительно автобусной остановки.

Так как человек двигался в сторону конца автобуса, он двигался противоположно его движению. В этом случае его перемещение будет равно модулю разности перемещений, совершенных человеком относительно автобуса и автобусом относительно остановки:

Относительность скорости в ПСО и НСО

Тела и системы отсчета могут двигаться с различной скоростью. Но, зная скорость движения МТ относительно ПСО и скорость движения ПСО относительно НСО, можно вычислить скорость движения МТ относительно НСО. В этом заключается правило сложения скоростей:

v′ — скорость МТ относительно НСО, v — скорость МТ относительно ПСО, u — скорость движения ПСО относительно НСО.

Складывая векторы скоростей, нужно пользоваться правилами сложения векторов.

Полезные факты

• Если тело движется в направлении движения ПСО, то модуль его скорости относительно НСО равен сумме модулей скорости этого тела относительно ПСО и скорости ПСО относительно НСО:

• Если тело движется противоположно движению ПСО, то модуль его скорости относительно НСО равен разности модуля скорости этого тела относительно ПСО и скорости ПСО относительно НСО:

• Если тело движется под прямым углом по отношению к направлению движения ПСО, то модуль его скорости относительно НСО равен корню из суммы квадратов скорости этого тела относительно ПСО и скорости ПСО относительно НСО:

• Если относительно ПСО тело покоится, то его скорость относительно НСО равна скорости ПСО относительно НСО: при v=0,скорость v′ = u
• Если тело движется относительно двух НСО, то его скорость относительно НСО1 равна скорости движения относительно НСО2. В этом случае одну из неподвижных систем можно принять за ПСО с нулевой скоростью. При u=0,скорость v′ = u

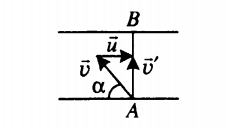
Пример №2. Моторная лодка должна пересечь реку, скорость течения которой равна 5 км/ч, по кратчайшему пути. Собственная скорость лодки равна 10 км/ч. Определить, под каким углом к берегу должна быть направлена лодка, чтобы она не отклонялась от кратчайшего пути.

Кратчайшим путем между двумя параллельными линиями является отрезок, заключенный между этими линиями при условии, что он лежит на прямой, пересекающей эти линии под прямым углом. На рисунке этот путь отметим отрезком АВ.

Лодка движется прямолинейно. Поэтому направление ее скорости относительно берега совпадает с направлением перемещения:

Векторы скоростей образуют прямоугольный треугольник, и собственная скорость лодки направлена к берегу под некоторым углом α. Косинус этого угла равен отношению прилегающего катета (скорости лодки относительно реки) к гипотенузе (скорости течения реки):

Косинусу 0,5 соответствует угол, равный 60 градусам.

Относительная скорость двух тел

Понятие относительной скорости вводится, когда рассматривается движение двух тел относительно друг друга внутри одной и той же системы отсчета (СО). Примером служат два движущихся автомобиля, в то время как их движение рассматривается относительно неподвижного объекта.

Относительная скорость равна векторной разности скоростей первого и второго тела относительно СО:

v _отн — относительная скорость, или скорость первого тела относительно второго, v ₁ и v ₂ — скорость первого и второго тела относительно СО.

Варианты обозначения относительной скорости и их проекций:

• v ₁₂ — скорость первого тела относительно второго. Ее проекция равна:

• v ₂₁ — скорость второго тела относительно первого. Ее проекция равна v_21x = v_2x — v_1x

Для вычисления относительной скорости движения тела важно уметь применять правила вычитания векторов.

Полезные факты

• Если тела движутся в одном направлении, то относительная скорость равна модулю разности скоростей первого и второго тела:

• Если тела движутся в противоположных направлениях, то относительная скорость равна сумме скоростей первого и второго тела:

• Если тела движутся взаимно перпендикулярно, то относительная скорость равна корню из суммы квадратов скоростей первого и второго тела:

Пример №3. Два автомобиля движутся противоположно друг другу. Скорость первого автомобиля относительно дороги равна 100 км/ч. Скорость второго автомобиля относительно первого равна 180 км/ч. Найти модуль скорости второго автомобиля относительно дороги.

Так как автомобили движутся в противоположном направлении, относительная скорость равна сумме скоростей первого и второго автомобиля. Поэтому скорость второго равна разности относительной скорости и скорости движения второго тела, которым в данном случае является первый автомобиль:

Скорость второго автомобиля относительно дороги равна 80 км/час.

Правила сложения векторов

Эта таблица иллюстрирует правила сложения векторов на примере векторов a и b . Результатом их сложения является вектор c .

Сложение двух сонаправленных векторов
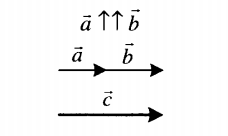	Суммой двух сонаправленных векторов является вектор, направленный в ту же сторону. Его длина равна сумме длин слагаемых векторов: c = a + b.
Сложение двух противоположно направленных векторов
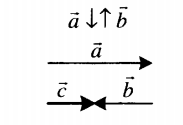	Суммой двух противоположно направленных векторов является вектор, направленный в сторону большего по модулю вектора. Его длина равна модулю разности длин слагаемых векторов: c = |a – b|.
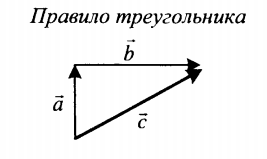
Сложение двух векторов, расположенных друг к другу под углом
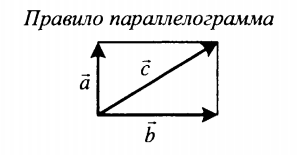
Суммой двух векторов, расположенных друг к другу под углом является вектор, направление которого определяется графически методом треугольника или параллелограмма. Его длина зависит от величины угла, под которым расположены два слагаемых векторов.
	Если слагаемые векторы перпендикулярны, для вычисления длины вектора их суммы используется теорема Пифагора: .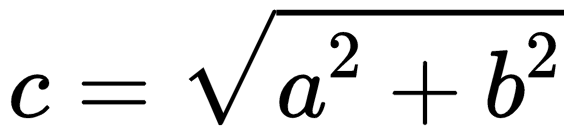
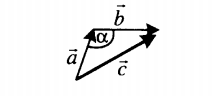	Если слагаемые векторы расположены под тупым углом α, для вычисления длины вектора их суммы используется теорема косинусов: .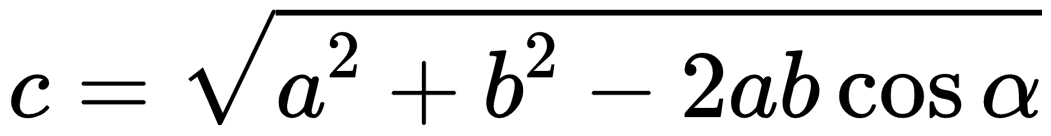
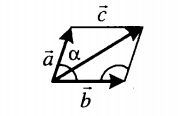	Если слагаемые векторы расположены под острым углом α, для вычисления длины вектора их суммы используется теорема косинусов: .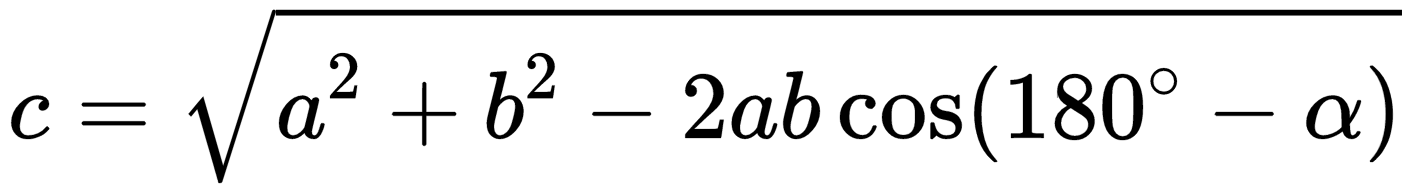

Правила вычитания векторов

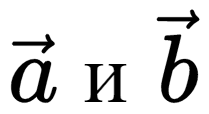
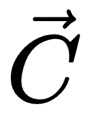
Эта таблица иллюстрирует правила вычитания векторов на примере векторов Результатом их вычитания является вектор .

Вычитание двух сонаправленных векторов
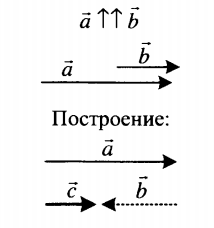	Разностью двух сонаправленных векторов является вектор, направленный в сторону большего по модулю вектора. Его длина равна модулю разности длин вычитаемых векторов: c = |a – b|.
Вычитание двух противоположно направленных векторов
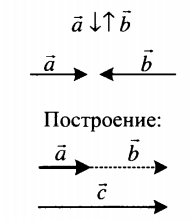	Разность двух противоположно направленных векторов есть вектор, направленный в сторону уменьшаемого вектора. Его длина равна сумме длин вычитаемых векторов: c = a + b.
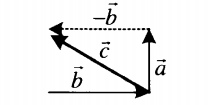
Вычитание двух векторов, расположенных друг к другу под углом
Разностью двух векторов, расположенных друг к другу под углом является вектор, являющийся обратным вектору, образующемуся при сложении этих векторов. Его направление определяется графически. Его длина зависит от величины угла, под которым расположены два слагаемых векторов.
	Если вычитаемые векторы перпендикулярны, для вычисления длины вектора их разности используется теорема Пифагора: .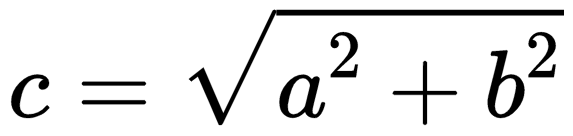
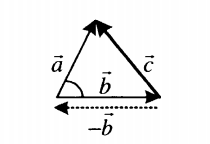	Если вычитаемые векторы расположены под углом α, для вычисления длины вектора их разности используется теорема косинусов: .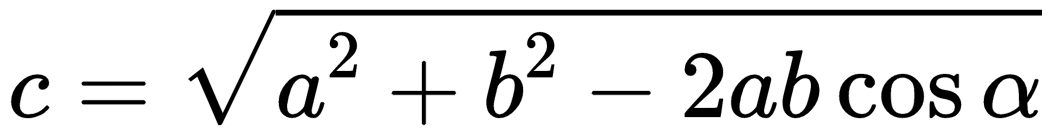

Два автомобиля движутся по прямому шоссе, первый — со скоростью v , второй — со скоростью –4 v . Найти скорость второго автомобиля относительно первого.

Алгоритм решения

1. Записать данные в определенной системе отсчета.
2. Изобразить графическую модель ситуации задачи.
3. Записать классический закон сложения скоростей в векторном виде.
4. Записать классический закон сложения скоростей в векторном виде применительно к условиям задачи.
5. Найти искомую величину.

Решение

Записываем данные относительно Земли:

• Скорость первого автомобиля относительно оси ОХ: v ₁ = v .
• Скорость второго автомобиля относительно оси ОХ: v ₂ = –4 v .

Изображаем графическую модель ситуации. Так как у второго автомобиля перед вектором скорости стоит знак «–», первый и второй автомобили движутся во взаимно противоположных направлениях.

Записываем закон сложения скоростей в векторном виде:

v ′ — скорость второго автомобиля относительно оси ОХ ( v ₂), v — скорость второго автомобиля относительно системы отсчета, связанной с первым автомобилем, u — скорость движения первого автомобиля относительно оси ОХ ( v ₁).

Закон сложения скоростей в векторном виде применительно к условиям задачи будет выглядеть так:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Записываем закон сложения скоростей в векторном виде:

v ′ — скорость автомобиля относительно земли ( v ₁), v — скорость второго автомобиля относительно системы отсчета, связанной со вторым автомобилем, u — скорость движения второго автомобиля относительно земли ( v ₂). По условию задачи в качестве системы отсчета нужно выбрать второй автомобиль. Так как система отсчета, связанная со вторым автомобилем, и первый автомобиль движутся в одном направлении, классический закон сложения скоростей в скалярном виде будет выглядеть так:

Отсюда скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем:

По условию задачи ответом должен быть модуль этой скорости. Модуль числа 50 есть 50.Ответ: 50

pазбирался: Алиса Никитина | обсудить разбор | оценить

[spoiler title=”источники:”]

http://interneturok.ru/lesson/physics/11-klass/podgotovka-k-ege/osnovnye-ponyatiya-kinematiki-skorost-srednyaya-skorost-otnositelnaya-skorost-slozhenie-peremescheniy-i-skorostey

[/spoiler]