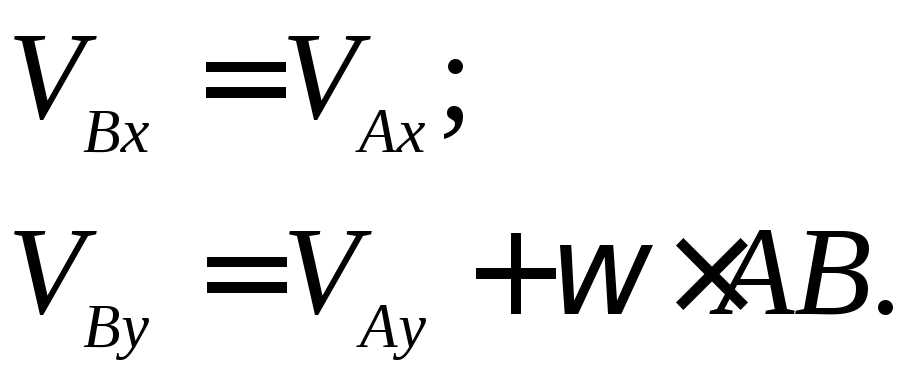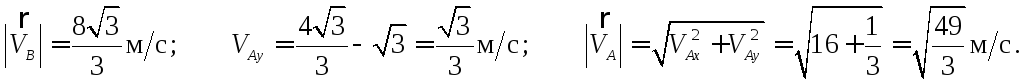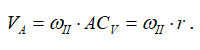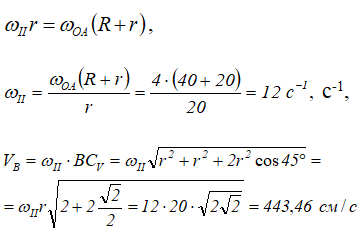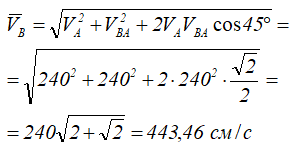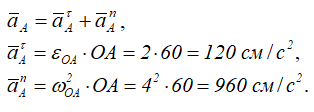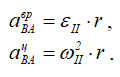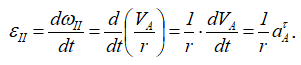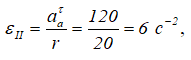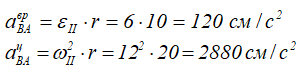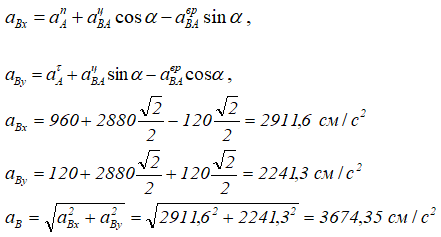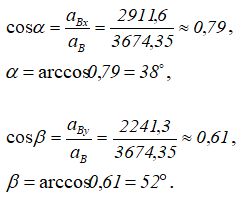Как найти относительную скорость точки колеса

где V1.2- скорость первого тела относительно второго (относительная скорость), V1 – скорость первого тела (абсолютная скорость, V2 – скорость второго тела (абсолютная скорость). Для удобства нужно
ввести понятие (условное) абсолютной и относительной скоростей. Абсолютной скоростью назовем скорость тела относительно неподвижной системы и обозначать будем с одиночным индексом. Относительной –
относительно подвижной системы и обозначать будем с двойным индексом. Тогда векторное правило (1) легко применять используя «порядок индекса». Таким же образом можно поступать и в случае перемещений
и ускорений!

Рассмотрим это на некоторых примерах:

Решение:

В любой момент времени скорости
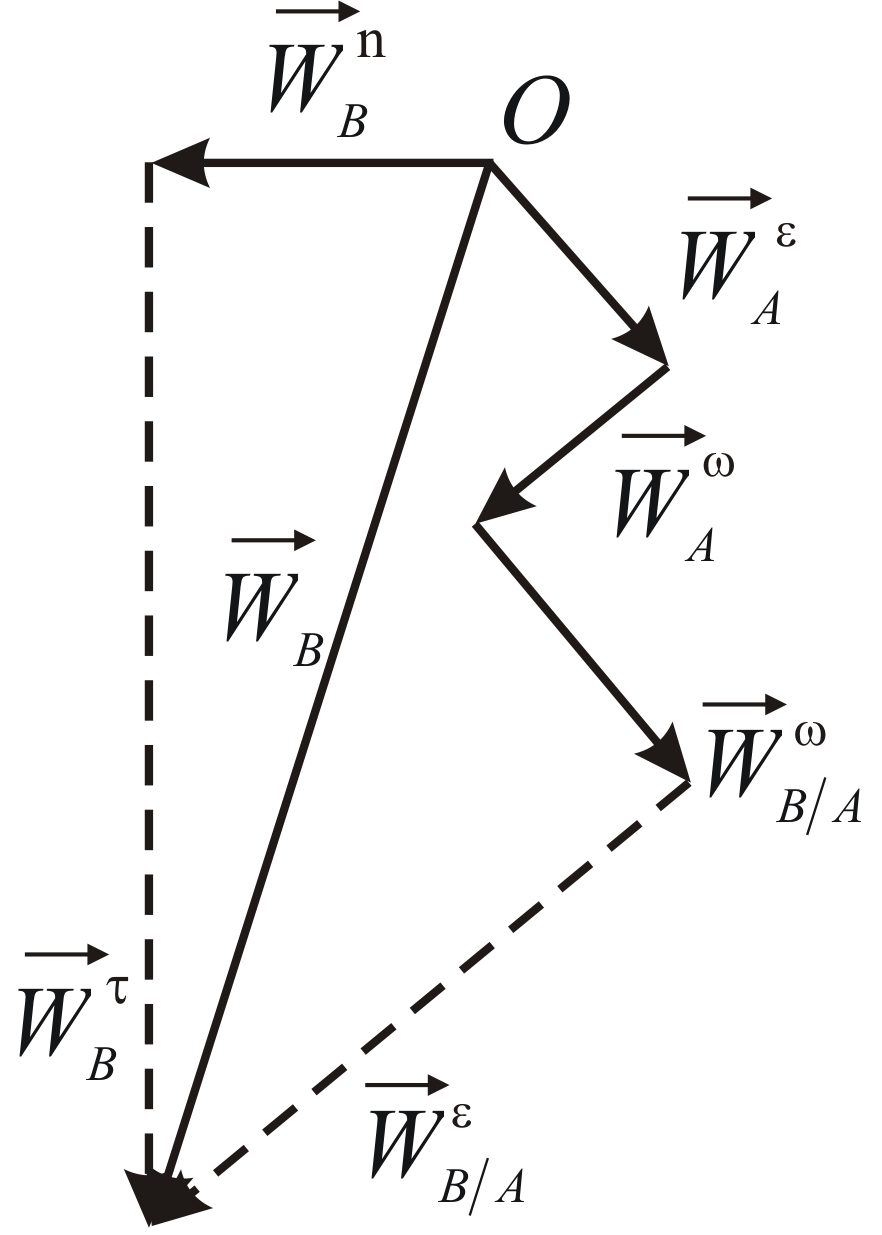
любых двух точек плоской фигуры
исвязаны равенством

Рис. 2.3

(a)

Вектор
представляет собой скорость, полученную
точкойпри вращении плоской фигуры вокруг оси,
проходящей через полюсперпендикулярно плоской фигуре. Этот
вектор направлен перпендикулярно
отрезку(по касательной к окружности, которую
описывает точкапри вращении тела вокруг оси),
причем в сторону вращения тела (Рис.
2.3). В соответствии с формулой Эйлера

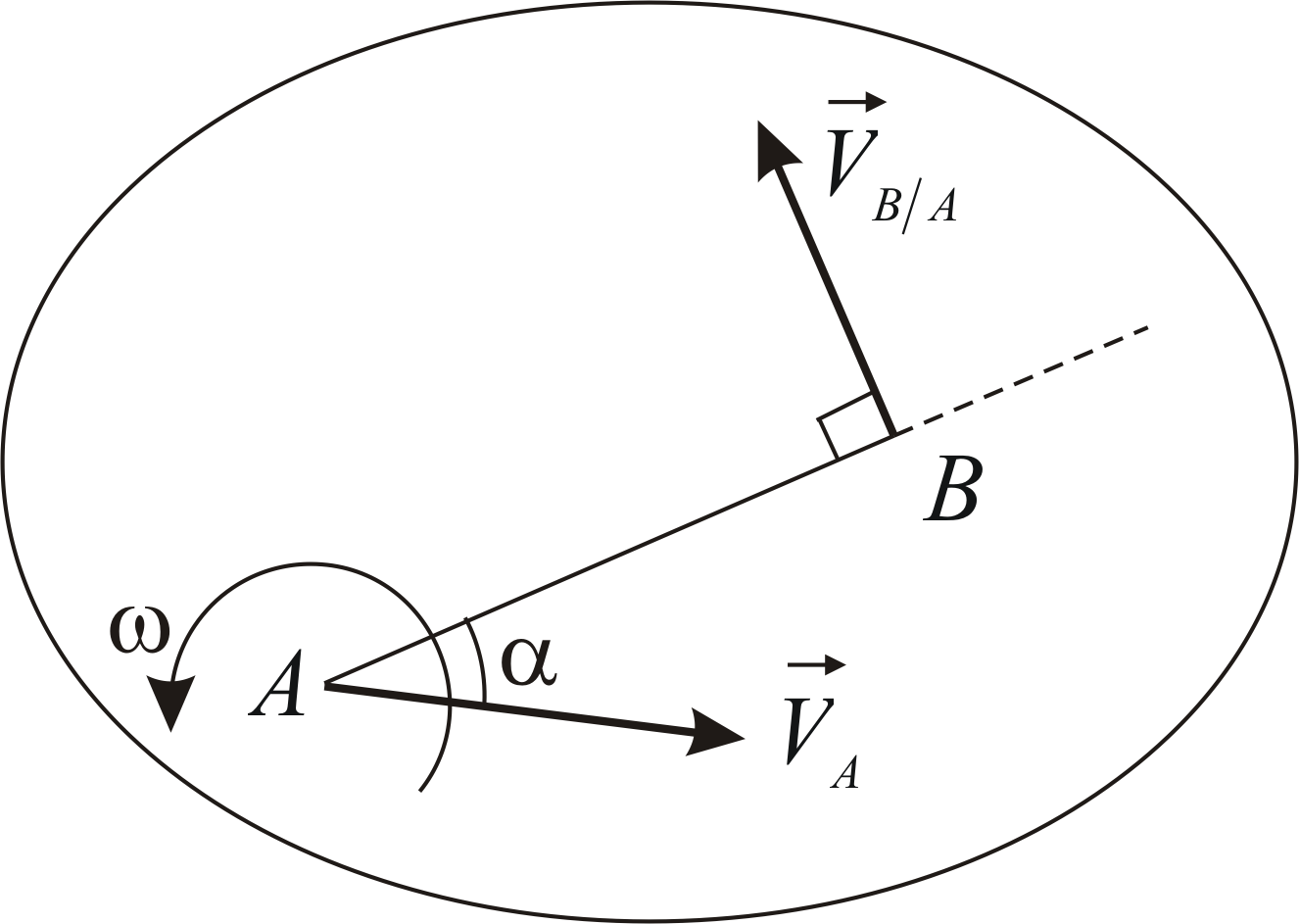
Пример 2.4

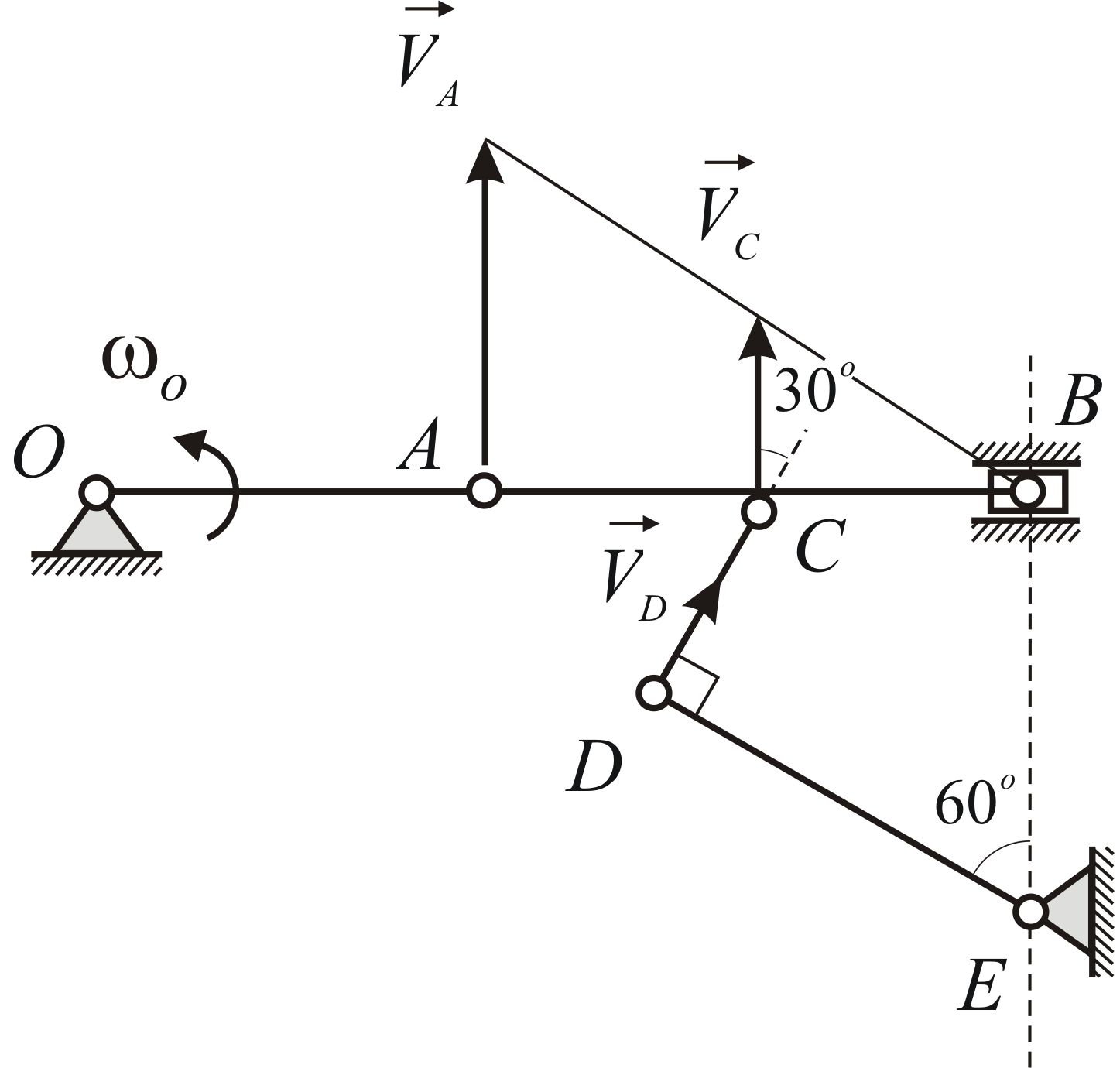
Пластина совершает плоскопараллельное
движение. В данный момент времени угловая
скорость пластины равна
,
проекция на осьскорости точкипластины равна.
Скорость точкиобразует с осьюугол(Рис. 2.4). Определить модули скоростей
точеки,
если.

Рис. 2.4

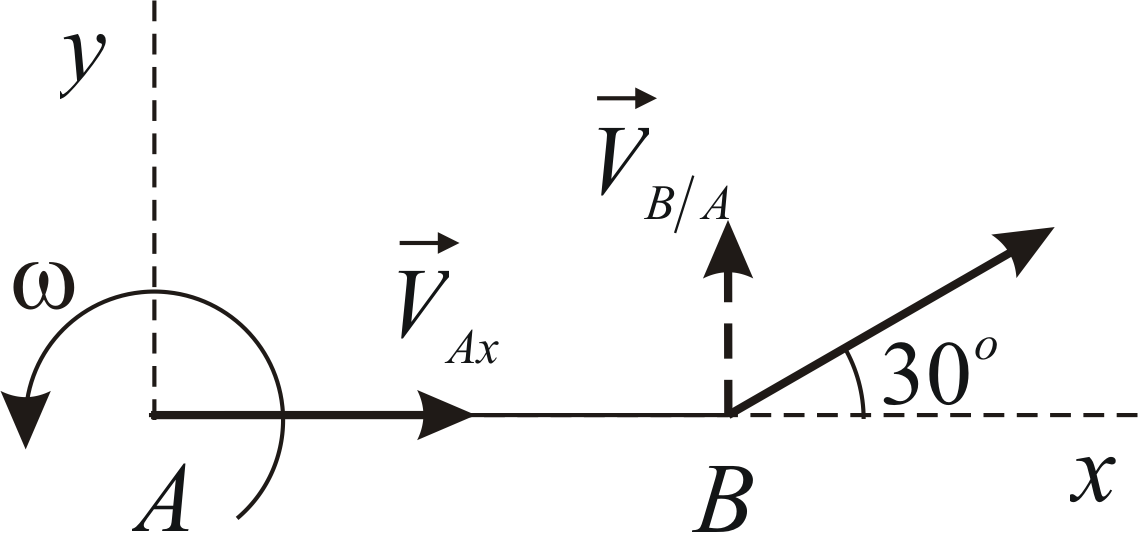
Запишем уравнение (a)
в проекциях на координатные оси:

или

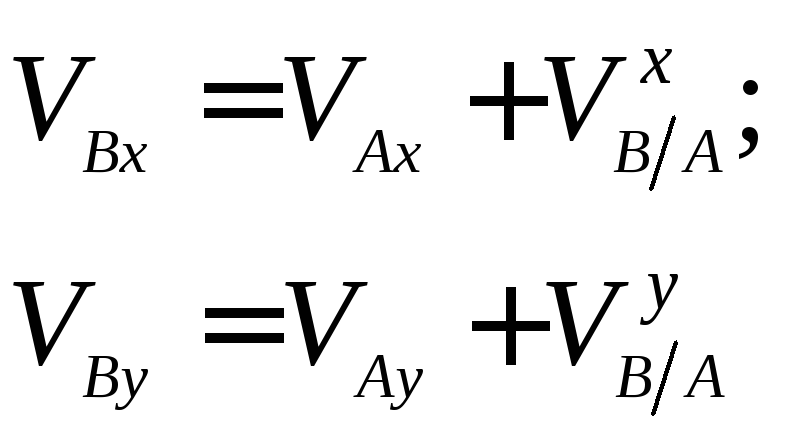
Учитывая данные задачи, получаем:

или

Отсюда:

Следует заметить, что прямое
использование формулы (a)
целесообразно в довольно небольшом
числе случаев. В некоторых задачах имеет
смысл использовать так называемую
теорему о проекциях. Поскольку векторперпендикулярен отрезку,
из формулы (a) получаем
утверждение:

проекции скоростей концов отрезка,
соединяющего две точки абсолютно
твердого тела, на направление этого
отрезка равны.

Пример 2.5

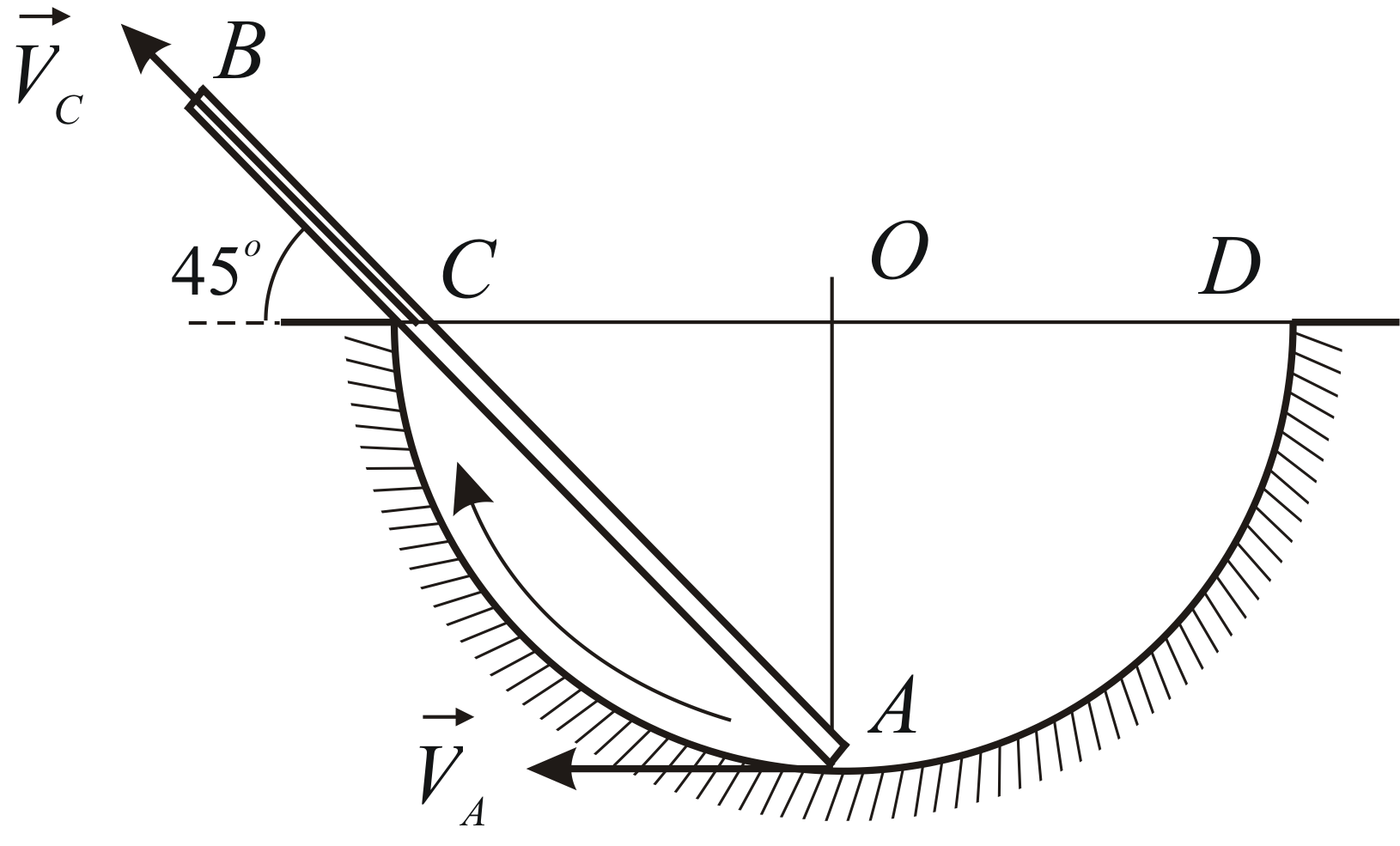
Стержень
движется в плоскости рисунка, причём
его конецвсё время находится на полуокружности,
а сам стержень всё время касается
неподвижного выступа,
расположенного на диаметре(Рис. 2.5). Определить скоростьточки стержня, касающейся выступа, в
тот момент времени, когда радиусперпендикулярен,
если известно, что скорость точкив этот момент.

Рис. 2.5

Заметим, что направления скоростей
точекив данный момент времени известны.
Скорость точкинаправлена по касательной к траектории,
т.е. по касательной к окружности в нижней
точке. Скорость точкинаправлена вдоль стержня, т.к. по условию
задачи стержень не отрывается от выступа.
Таким образом, для заданного положения
стержня известны углы, которые образуют
векторы скоростей точекис отрезком.
В таком случае целесообразно использовать
теорему о проекциях скоростей:

Решение задач с помощью мгновенного
центра скоростей. Основной способ
определения поля скоростей при
плоскопараллельном движении твёрдого
тела основан на использовании мгновенного
центра скоростей.

Как уже говорилось, за полюс можно
принять любую точку плоской фигуры. В
данный момент времени различные точки
тела имеют разные скорости. За полюс
имеет смысл принимать точку, скорость
которой в данный момент времени равна
нулю.

Точка, принадлежащая плоской фигуре
или неизменно с ней связанная, скорость
которой в данный момент времени равна
нулю, называется мгновенным центром
скоростей.

Рис. 2.6

Скорость любой точкиплоской фигуры определяется так же, как
если бы тело вращалось вокруг оси,
проходящей через мгновенный центр
скоростей перпендикулярно плоскости
движения плоской фигуры (Рис. 2.6):

Пример 2.6

Кривошипн0-шатунный механизм связан
шарнирно в середине
шатуна со стержнем,
а последний – со стержнем,
который может вращаться вокруг оси.
Определить угловую скорость стержняв указанном на Рис. 2.7 положении механизма,
если точкиирасположены на одной вертикали; угловая
скоростькривошипаравна 8 рад/с,

Рис. 2.7

Стерженьвращается вокруг неподвижной оси.
Скорость точкиопределяем по формуле Эйлера:

Движение стержня
плоскопараллельное. Мгновенный центр
скоростей находится в точке.
Учитывая, что скорости точек тела
пропорциональны расстояниям до
мгновенного центра скоростей, получаем:

Отсюда:

Движение стержня
плоскопараллельное. Скорость точкинаправлена по касательной к окружности
радиуса,
которая является траекторией точки.
При заданном положении механизма
направление скорости точкисовпадает с направлением стержня.
Для определения скорости точкиимеет смысл использовать теорему о
проекциях скоростей:

Остаётся определить угловую скорость
стержня
.
Поскольку движение этого стержня
вращательное, используем формулу Эйлера:

Пример 2.7

Колесо радиуса
катится без скольжения по неподвижной
поверхности (Рис. 2.8). Скорость центра
колеса.
Определить скорости точеки

Рис. 2.8

Мгновенный центр скоростейнаходится в точке касания колеса и
дороги. Зная скорость центра, находим
угловую скорость колеса:

Скорости точек колеса определяем по
формуле Эйлера:

Качение колеса представляет интерес
еще и в том отношении, что позволяет
проиллюстрировать смысл формулы (a).
Пусть колесо, движение которого мы
рассматриваем, – ведущее колесо, т.е.
оно принудительно вращается некоторым
приводом. Рассмотрим возможные
режимы движения.

Может случиться так, что колесо
вращается, но автомобиль не перемещается
– буксует. В этом случае движение колеса
представляет собой вращение вокруг
неподвижной оси
.
Все точки колеса будут описывать
окружности с центром в точке,
радиусы которых равны расстояниям от
этих точек до оси колеса. Скорость любой
точки направлена по касательной к этой
окружности и определяется по формуле
Эйлера.

Другое возможное движение колеса
представляет собой качение с
проскальзыванием. Автомобиль при этом
перемещается, но колеса вращаются
несоразмерно быстро. Скорость оси колеса
отлична от нуля и вступает в свои права
формула (a). Скорость,
например, точки,
которая в первом случае была ее полной
скоростью, становится скоростью,
полученной точкойпри вращении колеса вокруг оси.
Полная же скорость точкитеперь геометрически складывается из
скорости точкии скорости, полученной точкойпри вращении колеса вокруг оси

Заметим, что в этом случае движение
оси (т.е. автомобиля) и вращение колеса
происходят независимо друг от друга и
каждое из них должно быть задано.

Последний режим движения колеса –
качение без скольжения. Именно этот
случай рассмотрен в примере 2.7. Движение
оси и вращение колеса оказываются
взаимосвязанными. В каждое мгновение
очевидно положение точки, скорость
которой равна нулю. В такой ситуации
при определении скоростей точек колеса
удобнее за полюс брать не точку
,
а мгновенный центр скоростей.

ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В
АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:

Из сборника задач И.В.Мещерского: 16.3;
16.10; 16.15; 16.16; 16.19; 16.24; 16.28; 16.29; 16.31;
16.32; 16.33; 16.34; 16.35; 16.36; 16.38; 16.39.

Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА –
теория и практика»: комплект СР-20.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 6

Пример 2.8

Определить скорость и ускорение ползуна
кривошипного механизма, а также угловую
скорость и угловое ускорение шатунав положении, изображенном на Рис. 2.9.
Кривошипвращается замедленно, имея в данный
момент времени угловую скоростьи угловое ускорение.
Ползун движется по криволинейной
направляющей, имеющей в данном положении
механизма радиус кривизны.
Дано:.

Зная направления скоростей точек
и,
построим мгновенный центр скоростейстержня,
после чего определим угловую скорость
стержня

и скорость точки

Попытка определить угловое ускорение
стержня
,
используя определение

закончится неудачей, поскольку зависимость
неизвестна.

Для определения ускорения точки
принимаем за полюс точку.
Поскольку известны траектории всех
точек во всех их движениях, представим
ускорения точек их составляющими:

Вычислим векторы, входящие в уравнение
.

Рис. 2.9

Точка
принадлежит вращающемуся телу.
Определяем модули составляющих ускорения
этой точки:

направления векторов показаны на
Рис. 2.9.

Точка
движется по криволинейной направляющей.
Касательное и нормальное ускорения
точкиопределяются по формулам:

направления составляющих ускорения
показаны на Рис. 2.9. По приведенной
формуле не удается вычислить касательное
ускорение точки
,
поскольку неизвестны зависимости
расстоянийиот времени.

Находим составляющие ускорения,
полученного точкой
при вращении шатунавокруг оси.
Заметим, что вращательное ускорение
остается неизвестным по модулю, поскольку
неизвестно угловое ускорение шатуна:

Таким образом, из шести векторов,
входящих в равенство
,
только два неизвестны по модулю. Определим
эти неизвестные из уравнения.
Это уравнение можно решить аналитически
или геометрически. Рассмотрим оба
способа решения.

Имеет смысл выбрать координатные
оси так, чтобы в каждое уравнение в
проекциях входила только одна неизвестная.
Направим ось
вдоль(перпендикулярно),
а осьпо направлению(перпендикулярно).
Записывая уравнениев проекциях на ось,
получаем:

Отсюда

Отрицательный знак говорит о том,
что предполагаемое направление вектора
было выбрано ошибочно; в действительности
этот вектор направлен в противоположную
сторону.

Записывая уравнение
в проекциях на ось,
получаем:

Отсюда

Рис. 2.10

Вычислив,
можем определить угловое ускорение
стержня:

Рассмотрим геометрический способ
решения уравнения
.
Построим в масштабе сумму векторов,
стоящих в правой части уравнения.
От некоторой точкиотложим,
от его конца отложим,
а затем(Рис. 2.10). Остается построить,
модуль которого неизвестен. Проведем
через конецпунктирную прямую, параллельную.
Конец суммы векторов, стоящих в правой
части уравнения,
лежит на этой прямой.

Обратимся к левой части уравнения
.
Отложим от точкиизвестный вектор.
Через его конец проведем пунктирную
прямую, параллельную вектору.
Точка пересечения построенных прямых
определяет положение конца вектора
ускорения точки.

Пример 2.9

Колесо радиуса
катится без скольжения по прямолинейному
пути (Рис. 2.11). Ось колеса движется
ускоренно, имея в данный момент времени
скоростьи ускорение.
Определить проекции ускорение любой
точкиобода колеса на оси координат.

Принимая за полюс точку
,
получаем:

причем

где
– угловая скорость колеса;– его угловое ускорение.

Рис. 2.11

Зная положение мгновенного
центра скоростей колеса – точка касания
колеса и дороги, определяем угловую
скорость колеса:

В рассматриваемой задаче расстояние
от точки
,
скорость которой известна, до мгновенного
центра скоростейсо временем не изменяется. Это
обстоятельство позволяет найти угловое
ускорение колеса в данный момент времени
по определению углового ускорения:

,

так как

представляет собой проекцию вектора
ускорения точкина направление её вектора скорости,
которая в рассматриваемом случае равна.

Записывая уравнение
в проекциях на координатные оси, получаем
проекции вектора ускорения точки:

Пример 2.10

Колесо радиуса
катится без скольжения по криволинейной
поверхности (Рис.2.12). Ось колеса движется
ускоренно, имея в данный момент времени
скоростьи касательное ускорение.
Определить проекции ускорения любой
точкиобода колеса на заданные координатные
оси, если радиус кривизны в точкеравен.

Рис. 2.12

Задача решается так же, как в
примере 2.9, но в отличие от предыдущей
задачи, траектория точки– кривая линия. У точкипоявляется вторая составляющая ускорения
– нормальная:

В результате получаем:

Пример 2.11

Колесо радиуса
катится без проскальзывания по
прямолинейному пути. Ось колеса движется
равномерно со скоростью(Рис. 2.13). Определить ускорение любой
точкиколеса.

Рис. 2.13

Ось колеса движется равномерно
и прямолинейно. Следовательно, точка– мгновенный центр ускорений. Для любой
точкиколеса получаем:

Но угловая скорость колеса
постоянна и, следовательно, угловое
ускорение колеса равно нулю.

Тогда

Таким образом, ускорение любой точки
совпадает с осестремительным ускорением,
полученным этой точкой при вращении
колеса вокруг оси, проходящей через
центр колеса
перпендикулярно плоскости движения.

ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В
АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:

Из сборника задач И.В.Мещерского: 18.11;
18.13; 18.16; 18.18; 18.22; 18.23; 18.25; 18.26;
18.28; 18.37; 18.38; 18.39; 18.40.

Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА –
теория и практика»: комплекты СР-21;

СР-22.

ПРАКТИЧЕСКИЕ
ЗАНЯТИЯ № 7-8

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #

  03.03.2015560.03 Кб15PSY – recommendation.pdf
• #
• #

Рассмотрим задачи, когда тело вращаясь вокруг оси, движется вдоль прямой.

Задача 1.

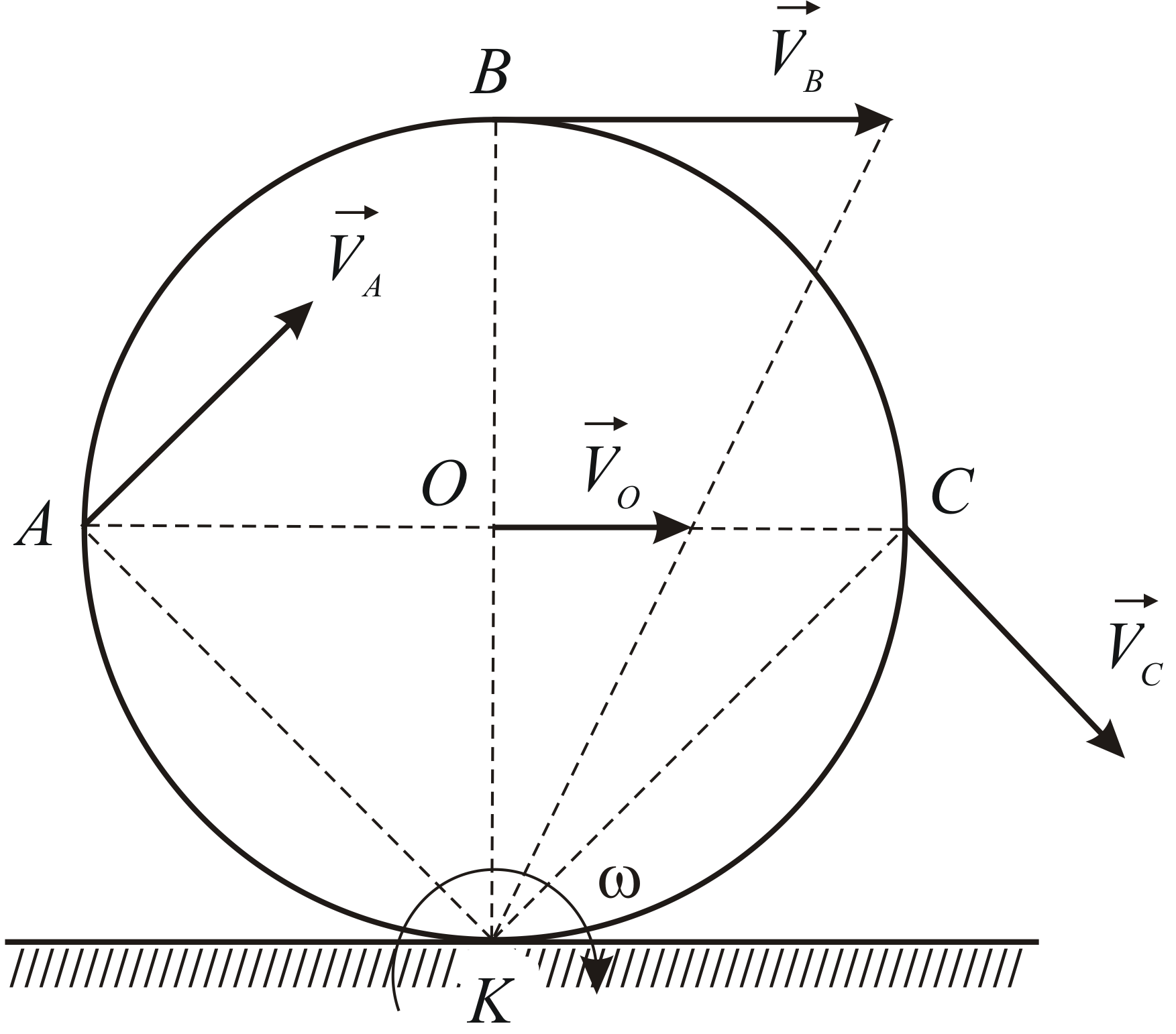
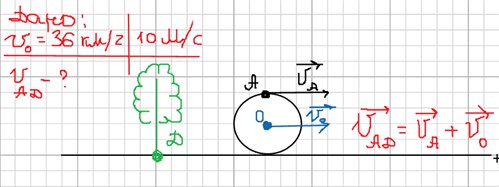
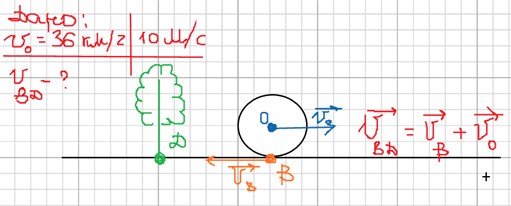
Машина движется со скоростью 36 км/ч. С какой скоростью относительно поверхности Земли движутся точки на верхней части колеса (в точке А)?

Решение.

Чтобы решать подобного рода задачи, договоримся поверхность Земли называть неподвижной системой отсчёта и свяжем её с точкой Д, а также , что скорость движения машины и скорость движения оси колеса равны.

И вспомним:

1. Если при движении колеса нет проскальзывания (пробуксовки), то линейная скорость точек обода колеса (ϑ_а, ϑ_в, ϑ_с) и скорость движения оси колеса ϑ_о по модулю равны.
2. Линейная скорость – скорость, с которой точки колеса движутся вокруг оси. Линейная скорость всегда направлена по касательной к траектории движения, проведённой в данной точке наблюдения.
3. Закон сложения скоростей. Скорость тела (в нашей задаче скорость точки обода колеса) относительно неподвижной системы отсчёта (относительно точки Д)  численно равна векторной сумме  линейной скорости тела (ϑ_а, ϑ_в, ϑс) относительно подвижной системы отсчёта (точки О – оси колеса) и скорости подвижной системы отсчёта относительно неподвижной  (ϑ_о).

Итак, приступим к решению, сделав чертёж к этой задаче и записав закон сложения скоростей  для данного случая.

Т.к. / ϑ_а/ = / ϑ_о/ и векторы  ϑ_а и ϑ_о сонаправлены,  то ϑ_ад = 2ϑ_а ,  ϑ_ад = 2 · 10 м/c = 20 м/c.

Ответ: ϑ_ад = 20 м/c.

Задача 2.

Для машины из 1 задачи рассчитать с какой скорость относительно поверхности Земли движутся точки на нижней части колеса (в точке В)?

Решение.

Сделаем чертёж к этому условию.

Т.к. /ϑ_в/ = /ϑ_о/ и векторы  ϑв и ϑ_о противоположно направлены, 

то ϑ_вд = 0 м/c.

Ответ: ϑ_вд = 0 м/c.

И разберём ещё один случай.

Задача 3.  

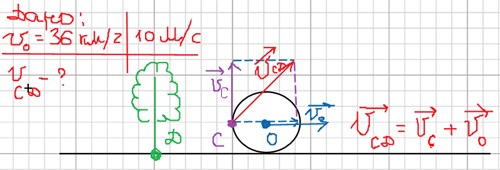
Для машины из 1 задачи рассчитать с какой скорость относительно поверхности Земли движутся точки на части колеса (в точке С)?

Решение.

Сделаем  внимательно чертёж к этому условию.

Здесь уже векторы  ϑс и ϑ_о  направлены в разные стороны относительно  друг друга и вектор ϑ_сд  необходимо сначала построить, используя или правило треугольника, или правило параллелограмма. В данном случае результирующий вектор ϑ_сд  будет гипотенузой прямоугольного треугольника, где катетами являются векторы ϑ_с и ϑ_о.

Т.к. /ϑ_с/ = /ϑ_о/. То ϑ_сд ² = ϑ_с² + ϑ_о² = 2ϑ_о²

ϑ_сд = √(2ϑ_о²) = √2ϑ_о,  округлим √2 до 1,4

ϑ_сд = 1,4 · 10 м/c = 14м/c

Ответ: ϑ_сд = 14м/c

Если внимательно читать эту статью, то можно увидеть схожий алгоритм решения всех задач. Трудность может заключаться в посторении результирующего вектора. Но если в этом разобраться, то на контрольной решить подобную задачу можно за считанные минуты. Удачи!

Остались вопросы? Не знаете, как решать задачи по физике?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Парадокс колеса

На приведённом рисунке хорошо видно, что все точки расположенные на радиусе колеса при совершении им одного оборота занимают те же самые места, на которых они были до начала вращения. Иными словами все точки радиуса колеса за один оборот перемещаются на одно и то же расстояние.

В то же время из школьного курса математики известно, что длина окружности равна:

Если прокатить колесо по поверхности и затем замерить пройденный им путь, то он будет точно соответствовать длине его окружности. Таким образом, две точки колеса: центр вращения и точка на внешней окружности проходят путь точно соответствующий приведённому расчёту. Но вот в отношении меньших радиусов мы приходим к выводу, что траектория их движения противоречит каноническому утверждению.

Так путь пройденный точкой, расположенной на половине радиуса колеса (r = R/2) должен быть равен:

C(r) = пиR, т.е. в половину меньше траектории точки расположенной на внешней окружности.

Но на самом деле она проходит фактически путь вдвое больший.

Соотношение фактически пройденной траектории и фактической дины окружности описываемый соответствующим радиусом растёт с уменьшением радиуса, фактически до бесконечности. Но в точке вращения он вновь возвращается к единице.

Самое удивительное в том, что если вырезать любую внутреннюю часть колеса и измерить его окружность, то она точно будет соответствовать вычисленной по канонической формуле.

Рассмотренный парадокс усиливается в случае, если колесо прокатывается с внешней стороны другой окружности. В этом случае траектория внутренних радиусов становится больше траектории точки на внешнем радиусе. И, наоборот, при прокатывании с внутренней стороны их траектория становится меньше.

Таким образом, можно сделать вывод о том, что траектория точек расположенных на внутренних радиусах колеса зависти не от величины собственного радиуса, а от радиуса внешней окружности. Что при этом происходит с материальными точками колеса расположенных на этих радиусах в пространстве остаётся загадкой.

Единственно разумное объяснение этого феномена предложил Галилей. Он считал, что поскольку фактическая траектория движения внутренних точек значительно больше фактической длины окружности, то точки внутренних радиусов проходят наблюдаемую траекторию с большей скоростью, чем это предписано им физикой [1]:

V = w*R, где w — угловая скорость вращения колеса.

Фактически линейная скорость внутренних точек колеса должна описываться уравнением:

V = n*w*r, где n = R/r
R – внешний радиус колеса;
r – внутренний радиус.

Иными словами линейная скорость точек внутренних радиусов является величиной постоянной и зависит только от внешнего радиуса колеса.

Вывод прямо скажем обескураживающий, но иного разумного объяснения пока ни кто не предложил.

Математически парадокс колеса в интерпретации Галилея описывается следующим уравнением:

dV = w*(R-r), где
dV – изменение скорости движения внутренних точек колеса;
R – внешний радиус колеса;
r – внутренний радиус колеса.
При r = R dV = 0
При r = 0 dV = w*R

Иными словами, изменение скорости точек расположенных на внутренних радиусах колеса меняется пропорционально от 0 на внешнем радиусе до V=w*R в центре вращения колеса. Поэтому ось колеса перемещается в пространстве с той же скоростью, которая соответствует линейной скорости вращающегося движения внешней окружности колеса при его прямолинейном движении. Соответственно такую же скорость имеют и все внутренние точки колеса.

С физической точки зрения полученный результат интерпретируется как движение жёсткого стержня, расположенного перпендикулярно направлению линейного движения оси вращения. Если рассмотреть движение такого стержня без привязки его к вращательному движению, то не трудно заметить, что все материальные точки стержня имеют одну и ту же скорость.

Преобразование вращательного движения в линейно-поступательное в данном случае решается методом рычага в рамках курса теоретической механики, которой к сожалению во времена Галилея ещё не существовало.

[1] Очевидно, именно по этому, этот парадокс практически не обсуждается в научной литературе.

Поскольку один из комментаторов так возбудился после прочтения этой статьи, что внёс меня в свои чёрные списки, и у меня нет возможности ему ответить иным путём, поэтому использую материал статьи не по назначению.

Сазонов Сергей 3 сентября 2019 года в 12:54

Писать рецензию на Вашу бредятину «Парадокс колеса» считаю излишним (много чести) — найдите в детском журнале «Квант» за 1975 год статью «ЦИКЛОИДА» . Там — примерно этот круг вопросов. Парадокса нет.
(конец цитаты)

К сожалению, найти указанный журнал в Интернете не смог, поэтому не смог лично ознакомиться со статьёй. Но уже само её название «ЦИКЛОИДА» говорит о том, Сергей Сазонов не видит разницы между прямой и циклоидой. В парадоксе колеса траектория меньшего радиуса разворачивается не в виде циклоиды, а в виде прямой линии. В этом то, как раз, и заключается парадокс. С другой стороны, то, что этим парадоксом интересовались Аристотель, Галилей, и возможно другие, не менее, замечательные умы человечества, говорит о том, что парадокс действительно существовал.
Уничижительное отношение к оппонентам явный признак ограниченной умственной деятельности. Конечно, можно было и не обращать внимание на подобные выпады, но, к сожалению, подобный уровень комментаторов встречается не так уж редко, поэтому считаю необходимым противостоять банальному хамству.

Задача 1.1 (3)

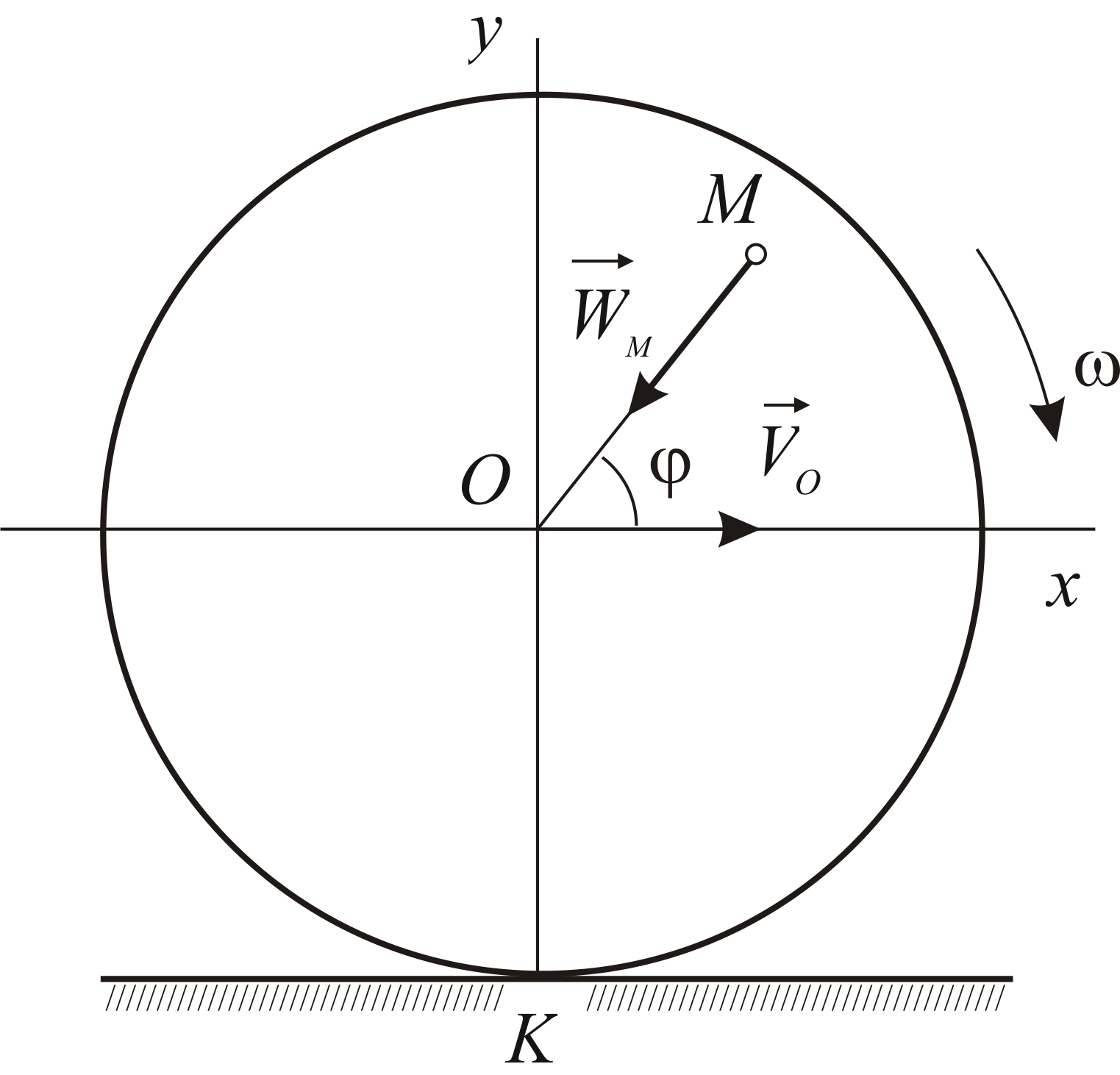
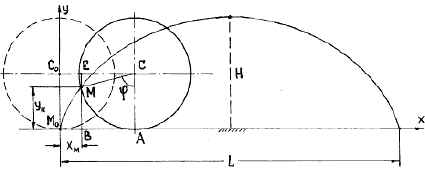
Найти уравнения движения точки М обода колеса радиуса R вагона, который движется по прямолинейному участку пути со скоростью V. Колесо катится без скольжения. Точка М в начальный момент движения соприкасалась с рельсом, т.е. занимала положение М₀ (рис. 1.1).

Изобразим на расчетной схеме (рис. 1.1) оси координат х и у, начало координат поместим в начальное положение точки М₀.

Рассмотрим два положения колеса: в начальный момент t = 0 и в текущий момент времени t.

Отметим положение точки М на ободе колеса и положение центра С колеса в момент t, координаты точки: x_м = М₀В, у_м = МВ.

Расстояние от центра колеса до рельса остается постоянным и равным R; это значит, что центр C колеса движется по прямой, параллельной оси х. За время t центр колеса переместится на расстояние C₀C = Vt (закон равномерного движения точки C), одновременно колесо повернется на угол j .

Чтобы получить уравнения движения точки М, надо координаты этой точки представить как функции времени.

Из расчетной схемы (рис. 1.1) видно, что

Из треугольника МЕС имеем;

МЕ = Rsin (90° – j ) = Rcosj ,

ЕC = Rcos (90° – j ) = Rsinj ,

Тогда х_м = Vt – Rsinj , (a)

Найдем зависимость угла j от времени t: так как колесо катится без скольжения, то длина дуги АМ окружности обода колеса (рис.1.1) равна длине отрезка М₀А.

но длина дуги АМ равна также произведению радиуса R на центральный угол j ; поэтому Vt = Rj , отсюда .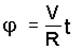

Теперь уравнения (а) будут иметь вид

; .

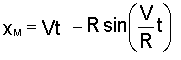
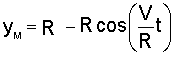
Полученные уравнения представляют собой уравнения движения точки М. В аналитической геометрии показано, что это параметрические уравнения циклоиды (параметром в данном случае является время t). Таким образом, траектория точки обода колеса, движущегося по прямолинейному участку пути без проскальзывания, является циклоидой. Длина одной ветви циклоиды L (рис. 1.1) равна 2p R, высота – H = 2R.

Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях – решение задачи

Основные законы и формулы, применяемые при решении задач

Вращательное движение вокруг неподвижной оси

Рассмотри твердое тело, вращающееся вокруг неподвижной оси z . Сделаем рисунок. Ось вращения направим перпендикулярно плоскости рисунка, на нас. Пусть φ – угол поворота тела вокруг оси, отсчитываемый от некоторого начального положения. За положительное направление выберем направление против часовой стрелки. Угловая скорость ω равна производной угла поворота по времени t :
.
При , тело вращается против часовой стрелки; при – по часовой. Вектор угловой скорости направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

Угловое ускорение ε равно производной угловой скорости по времени:
.
Вектор углового ускорения также направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

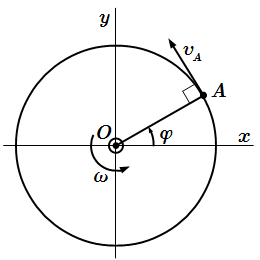
Скорость точки при вращательном движении тела вокруг неподвижной оси

Рассмотрим точку A , принадлежащую твердому телу. Опустим из нее перпендикуляр OA на ось вращения. Пусть – расстояние от точки до оси. Траекторией движения точки A является окружность (или дуга) с центром в точке O радиуса .

Абсолютное значение скорости точки A определяется по формуле:
.
Вектор скорости направлен по касательной к траектории (окружности), перпендикулярно отрезку OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор угловой скорости .

Касательное (или тангенциальное) ускорение точки A определяется аналогично скорости:
.
Оно направлено по касательной к окружности, перпендикулярно OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор углового ускорения .

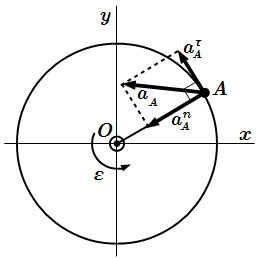
Ускорение точки при вращательном движении тела вокруг неподвижной оси

Нормальное ускорение всегда направлено к центру окружности и имеет абсолютную величину
.

Полное ускорение точки A , или просто ускорение, равно векторной сумме касательного и нормального ускорений:
.
Поскольку векторы и перпендикулярны, то абсолютная величина ускорения точки A определяется по формуле:
.

Поступательное прямолинейное движение

Теперь рассмотрим прямолинейное поступательное движение тела. Направим ось x вдоль его линии движения. Пусть s есть перемещение тела вдоль этой оси относительно некоторого начального положения. Тогда скорость движения всех точек тела равна производной перемещения по времени:
.
При , вектор скорости направлен вдоль оси x . При – противоположно этой оси.

Ускорение точек тела равно производной скорости по времени, или второй производной перемещения по времени:
.
При , вектор ускорения направлен вдоль оси x . При – противоположно.

Соприкосновение тел без проскальзывания

Рассмотрим два тела, находящиеся в зацеплении без проскальзывания. Пусть точка A принадлежит первому телу, а точка B – второму. И пусть, в рассматриваемый момент времени, положения этих точек совпадают. Тогда, если между телами нет проскальзывания, то скорости этих точек равны:
.
Если каждое из тел вращается вокруг неподвижной оси, то равны соответствующие касательные ускорения:
.
Если одно из тел движется поступательно (пусть это второе тело), то ускорение его точек равно касательному ускорению точки соприкосновения первого тела:
.

Пример решения задачи

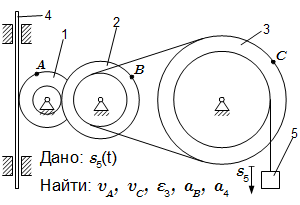
Механизм состоит из ступенчатых колес 1, 2, 3, находящихся в зацеплении и связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес. Радиусы ступеней колес равны соответственно: у колеса 1 – r₁ = 2 см, R₁ = 4 см, у колеса 2 – r₂ = 6 см, R₂ = 8 см, у колеса 3 – r₃ = 12 см, R₃ = 16 см. На ободьях колес расположены точки A, B и C. Задан закон движения груза: s₅ = t 3 – 6t (см). Положительное направление для s₅ – вниз.

Определить в момент времени t = 2 скорости точек A, C; угловое ускорение колеса 3; ускорение точки B и ускорение рейки 4.

Указания. Эта задача – на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что проскальзывание в ременной передаче и в точках сцепления колес отсутствует. То есть скорости точек колес, находящихся в зацеплении равны, а скорости точек ремня равны скорости точек, лежащих на ободе колес, связанных ременной передачей.

Дано:
t = 2 с; r₁ = 2 см, R₁ = 4 см; r₂ = 6 см, R₂ = 8 см; r₃ = 12 см, R₃ = 16 см; s₅ = t 3 – 6t (см).

Определение скорости и ускорения груза 5

Груз 5 совершает поступательное движение. Поэтому скорости (и ускорения) всех его точек равны. В условии задачи задано смещение s груза относительно некоторого начального положения. Дифференцируя по времени t , находим зависимость скорости точек груза от времени:
.
Дифференцируя скорость груза по времени, находим зависимость ускорения груза от времени:
.

Находим скорость и ускорение груза в заданный момент времени :
см/с;
см/с 2 .

Определение угловых скоростей и ускорений колес

Груз 5 связан нитью с внутренним ободом колеса 3. Поэтому скорости точек внутреннего обода колеса 3 равны скорости груза:
.
Отсюда находим угловую скорость колеса 3 для произвольного момента времени:
.
Здесь подразумевается, что и являются функциями от времени t . Дифференцируя по t , находим угловое ускорение колеса 3:
.
Находим значения угловой скорости и углового ускорения в момент времени с. Для этого подставляем найденные значения и при с:
с –1 ;
с –2 .

Рассмотрим колесо 2. Его внутренний обод связан нитью с внешним ободом колеса 3. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 2 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .

Рассмотрим колесо 1. Его внутренний обод находится в зацеплении с внешним ободом колеса 2. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 1 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .

Итак, мы нашли:
ω ₁ = 5.3333 с –1 , ω ₂ = 1.3333 с –1 , ω ₃ = 0.5 с –1 , ε ₁ = 10.6667 с –2 , ε ₂ = 2.6667 с –2 , ε ₃ = 1 с –2 .

Определение скоростей точек A и C

Точка A лежит на окружности радиуса R₁ с центром в точке O₁, расположенной на оси вращения. Поэтому скорость этой точки направлена по касательной к окружности и по абсолютной величине равна
см/с.

Точка C лежит на окружности радиуса R₃ с центром O₃ на оси вращения. Скорость этой точки:
см/с.

Определение ускорения точки B

Точка B лежит на окружности радиуса R₂ с центром O₂, расположенном на оси вращения. Касательное (или тангенциальное) ускорение этой точки направлено по касательной к окружности в сторону, на которую указывает угловое ускорение (по часовой стрелке). По абсолютной величине оно равно
см/с 2 .

Нормальное ускорение всегда направлено к центру окружности. По абсолютной величине оно равно
см/с 2 .

Полное ускорение равно векторной сумме касательного и нормального ускорений:
.
Поскольку касательное ускорение перпендикулярно нормальному, то для абсолютной величины полного ускорения имеем:
см/с 2 .

Определение ускорения рейки 4

Рейка 4 движется поступательно по направляющим. Она находится в зацеплении с внешним ободом колеса 1. Поэтому ее скорость равна скорости точек внешнего обода колеса 1:
.
Дифференцирую по времени, получаем ускорение рейки в произвольный момент времени:
.
Подставляем численные значения для момента времени t = 2 с :
см/с 2 .

см/с; см/с; с –2 ; см/с 2 ; см/с 2 .

Автор: Олег Одинцов . Опубликовано: 25-10-2019

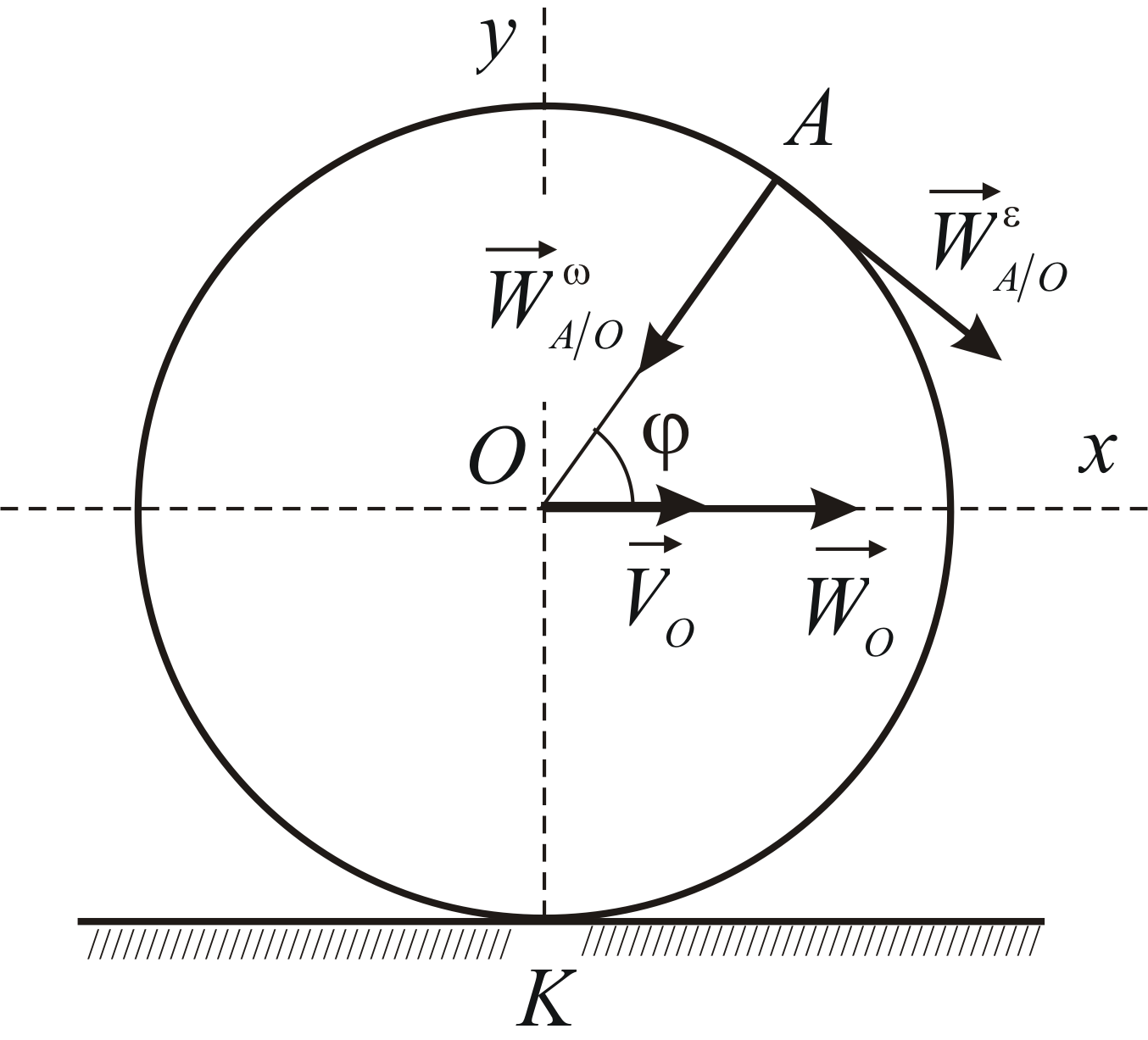
Пример решения задачи по определению величины и направления скорости и полного ускорения точки колеса, для момента времени, когда угол будет равен заданному значению.

Задача

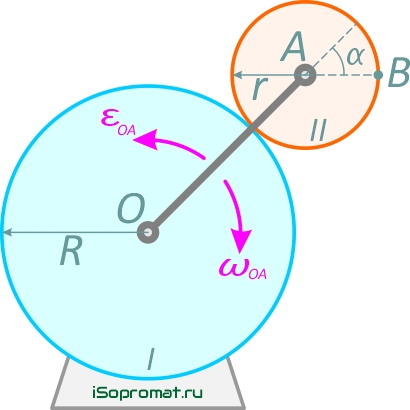
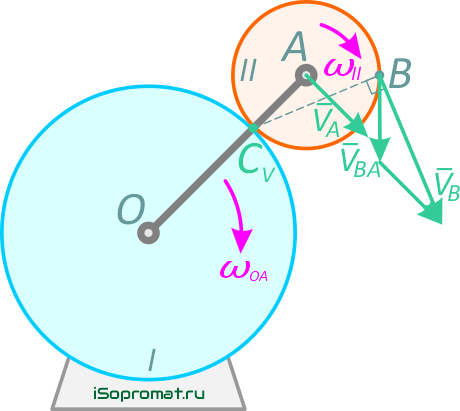
Кривошип ОА, вращаясь вокруг оси, перпендикулярной плоскости чертежа и проходящей через точку О, приводит в движение колесо II, которое катится без скольжения по неподвижному колесу I.

Рис. 2

Найти скорость и ускорение точки В колеса II, для момента времени, когда угол α=45°,
если R=40 см, r=20 см, ω_OA=4 с^-1, ε_OA=2 с^-2 (рис. 2).

Другие примеры решений >
Помощь с решением задач >

Решение

Теория по теме

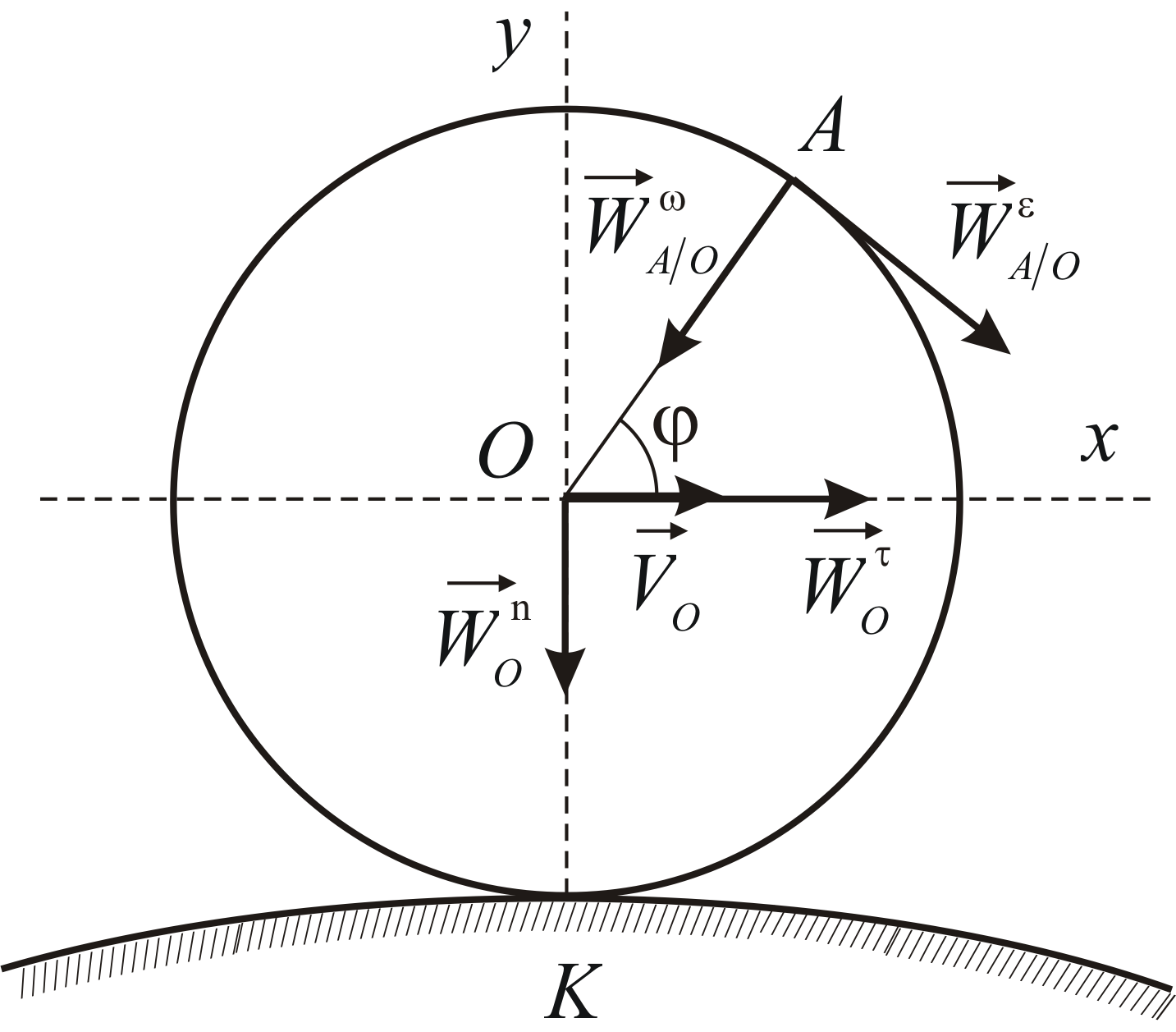
Колесо II движется в плоскости чертежа, т.е. совершает плоскопараллельное движение.

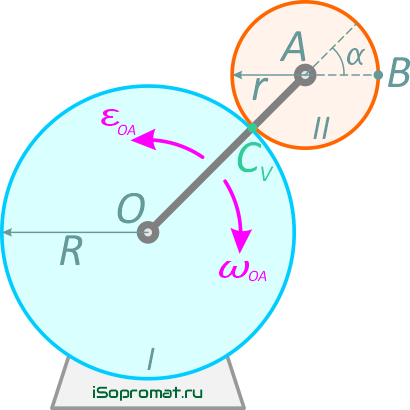
По условию, колесо I неподвижно, значит, точка соприкосновения колес является МЦС для колеса II.

Рис. 2.10

Обозначим ее как C_V (эта точка не принадлежит кривошипу ОА). Скорость точки В определяется выражением

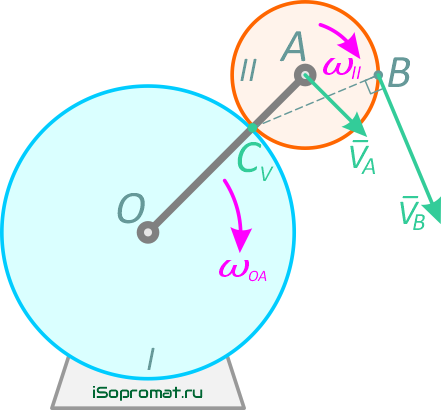
и направлена перпендикулярно отрезку ВС_V, в сторону вращения колеса II (рис. 2.11)

Рис. 2.11

Для определения угловой скорости ω_II запишем выражение для скорости точки А.

С другой стороны, точка А принадлежит кривошипу ОА. Скорость точки А, принадлежащей кривошипу, определяется выражением

и направлена ⊥ОА в сторону вращения кривошипа ОА. Из этих рассуждений следует:

Найдем скорость точки В, используя теорему о скоростях точек плоской фигуры. Для этого примем точку А за полюс.

Тогда

Величина и направление скорости точки А определяются из условий движения кривошипа ОА.
V_A=ω_OA×OA
и вектор V_A⊥ОА и направлен в сторону вращения кривошипа (рис. 2.12).

Рис. 2.12

Скорость V_BA — это скорость точки В во вращательном движении вокруг полюса А.

Величина скорости
V_BA=ω_II×r=12×20=240 см/с
и этот вектор направлен ⊥ отрезку АВ в сторону вращения колеса II.

Чтобы сложить V_A и V_BA, перенесем вектор V_A в конец вектора V_BA. Соединяя начало вектора V_BA с концом вектора V_A, получим вектор V_B. Из построения:

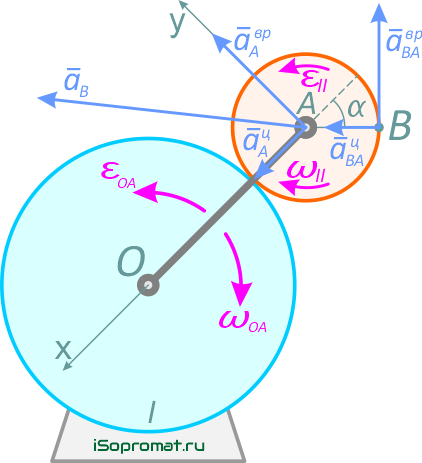
Определим ускорение точки В.

Согласно теореме об ускорении точки плоской фигуры, ускорение точки В можно определить из выражения

где a_A — ускорение точки А, принятой за полюс;

a_BA — ускорение точки В во вращательном движении, вокруг полюса А.

Рис. 2.13

Точка А – принадлежит колесу II и кривошипу ОА, движение которого известно, тогда

Ускорение a_BA (ускорение во вращательном движении) состоит из двух слагаемых:

где

Найдем ε_II по определению:

Подставляя числовые значения, получим

тогда

Ускорение точки В найдем, спроецировав все векторы уравнения

на выбранные оси координат ОХ и OY.

Углы, которые составляют вектор ускорения a_B с осями ОХ и OY, определим через направляющие косинусы.

Скорость и ускорение точки В колеса II, для момента времени, когда угол α=45° найдены.

Другие примеры решения задач >