Содержание
- Учебный вопрос №3 «Определение по карте абсолютных высот и взаимного превышения точек, определение крутизны скатов».
- Определение формы и крутизны скатов
- Высоты точек местности (абсолютные и относительные), превышения.
- Основные формы рельефа местности и их изображение на планах и картах.
- 2.2 Абсолютные и относительные высоты точек земной поверхности
- 3.1 Ориентирование линий
- 3.2 Ориентирование линий по истинному и магнитному меридианам
Учебный вопрос №3 «Определение по карте абсолютных высот и взаимного превышения точек, определение крутизны скатов».
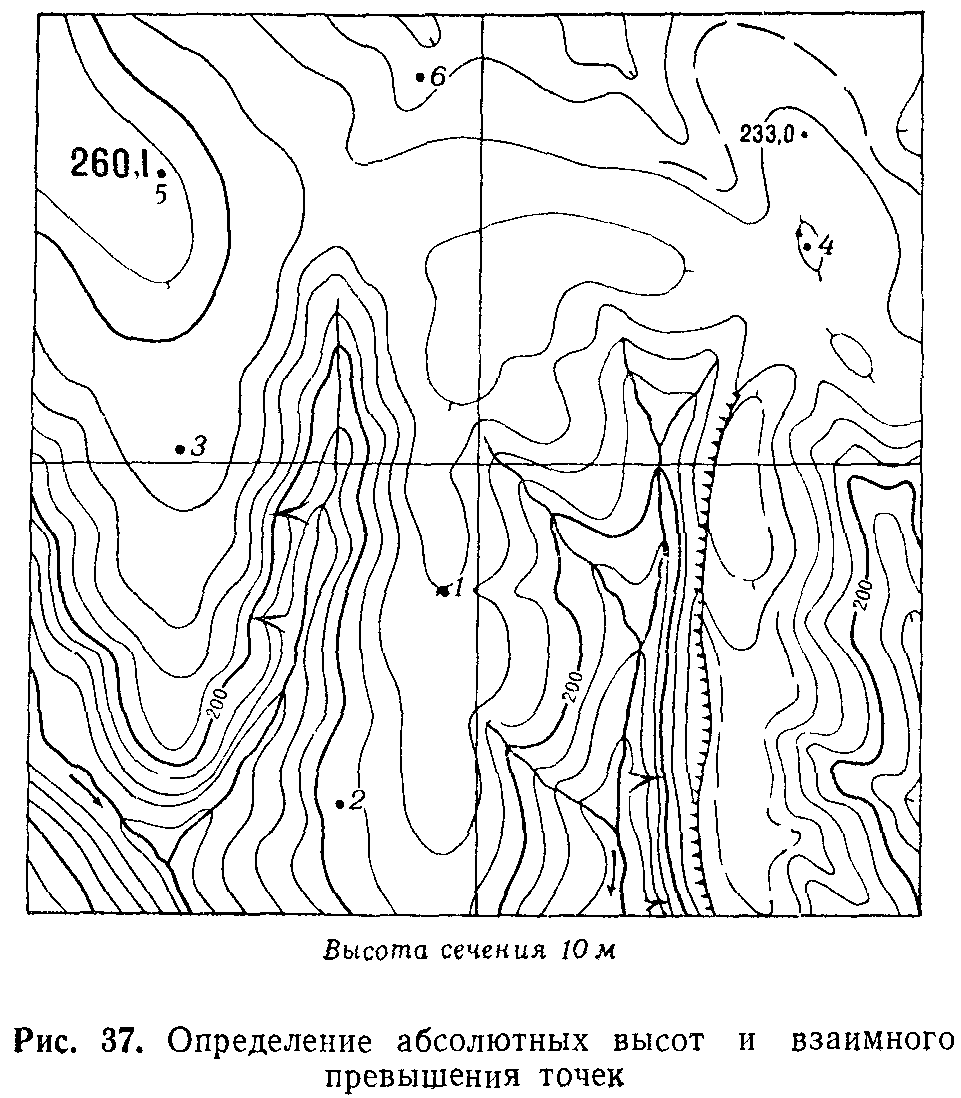
Высоты точек местности по карте определяют по горизонталям, используя имеющиеся на ней высотные отметки.
Если определяемая точка расположена на горизонтали, то ее абсолютная высота, очевидно, равна высоте этой горизонтали. Если же точка находится между горизонталями, то надо определить отметку ближайшей к ней нижней горизонтали и прибавить к этой отметке превышение данной точки над горизонталью. Это превышение определяется на глаз. Например, (рис. 37), абсолютная высота точки 1 будет 230 м, так как горизонталь, на которой она расположена, лежит на три высоты сечения выше горизонтали с отметкой 200 м. Высота точки 2 равна 205 м: она расположена посредине между горизонталями, одна из которых имеет высоту 200 м (утолщенная горизонталь), а другая 210 м. Точки 3 и 4 имеют примерно одну и ту же высоту – 242 м.
Превышение одной точки над другой определяется как разность их абсолютных высот. Если же точки расположены на одном и том же скате, то задача решается просто путем подсчета числа промежутков между горизонталями этих точек: превышение между ними равно произведению высоты сечения на полученное число промежутков между горизонталями. Например, точка 5 на рис. 37 расположена выше точки 6 на 45 м (4,5 промежутка между горизонталями) и выше точки 2 на 55 м.
Точность определения высот точек, отметки которых не подписаны на карте, равна: для характерных точек рельефа, расположенных на вершинах, гребнях, водосливах, бровках и пологих скатах неровностей, – примерно 0,3 – 0,5 высоты сечения, а для точек, расположенных на крутых скатах, где невозможно проведение полугоризонталей, она примерно в 3-4 раза меньше.
Определение формы и крутизны скатов
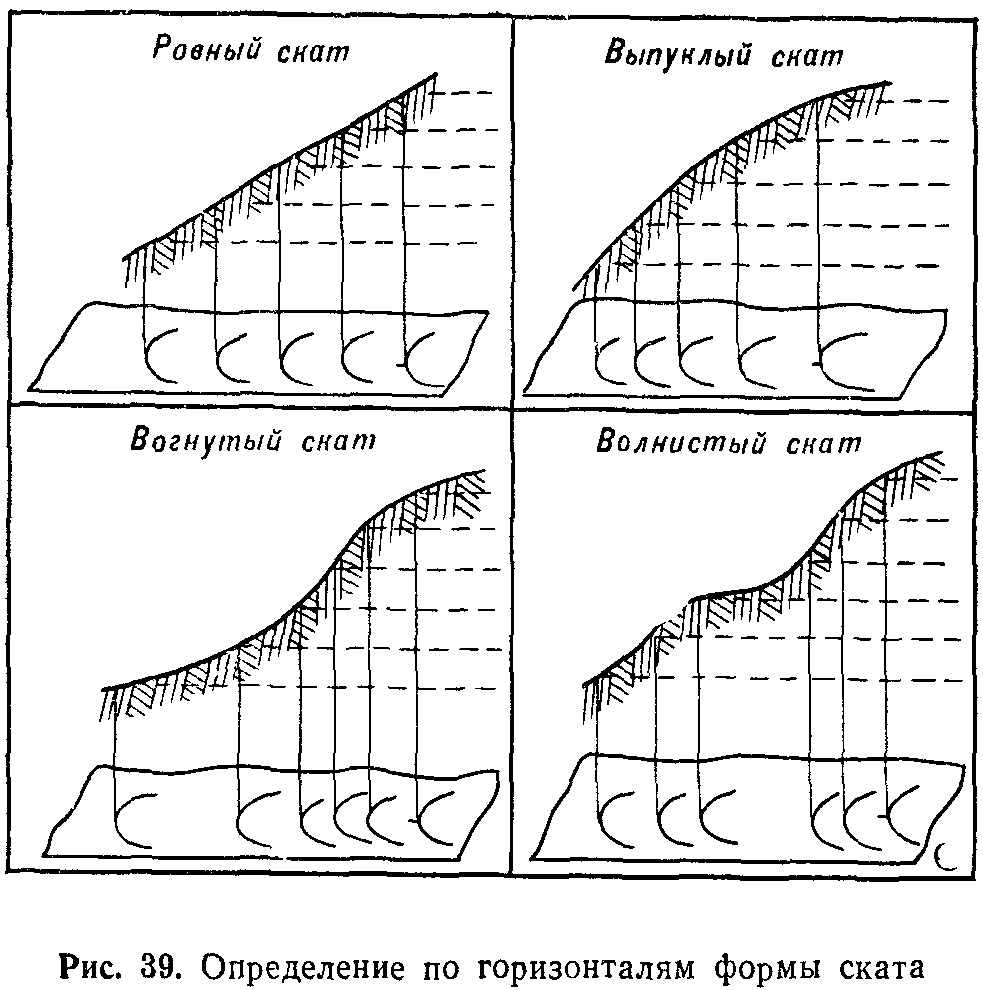
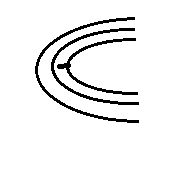
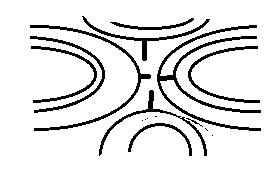
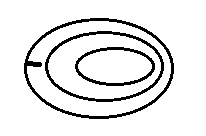
Форма ската определяется по взаимному расположению горизонталей на скате (рис. 39). Если скат ровный, то его горизонтали на карте располагаются на равных расстояниях одна от другой; при вогнутом скате они учащаются к вершине, а при выпуклом, наоборот, – к подошве. При волнистом скате горизонтали учащаются и разреживаются в нескольких местах в зависимости от количества перегибов ската.
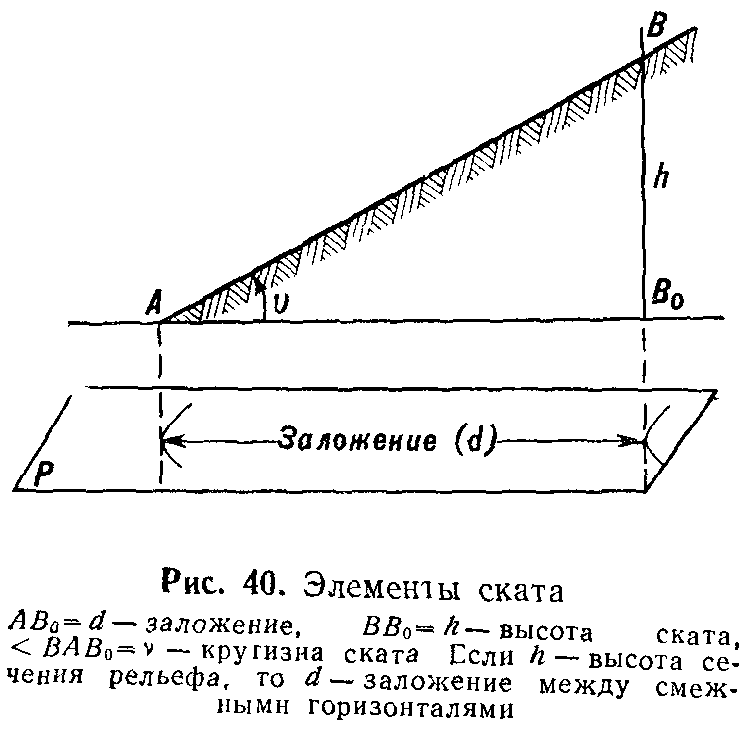
Крутизна ската, т. е. угол его наклона v (рис. 40), вычисляется по формуле
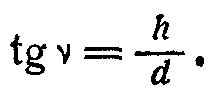 (1)
(1)
Приближенно угол v, если он не больше 25°, может быть подсчитан по формуле
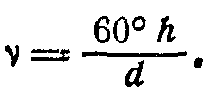 (2)
(2)
Эти зависимости и лежат в основе всех способов определения крутизны скатов. Наиболее употребительны из них следующие.
А Определение крутизны скатов по шкале заложений (рис 41) шкалой заложений называется график, который печатается на всех листах топографических карт масштаба 1 : 100 000 и круп нее – рядом с линейным масштабом. Вдоль основания графика подписана крутизна скатов в градусах. На перпендикулярах к основанию отложены в масштабе карты соответствующие им заложения: в левой части шкалы – заложения при основной высоте сечения, а в правой – при пятикратной, т. е. заложения между двумя смежными утолщенными горизонталями.
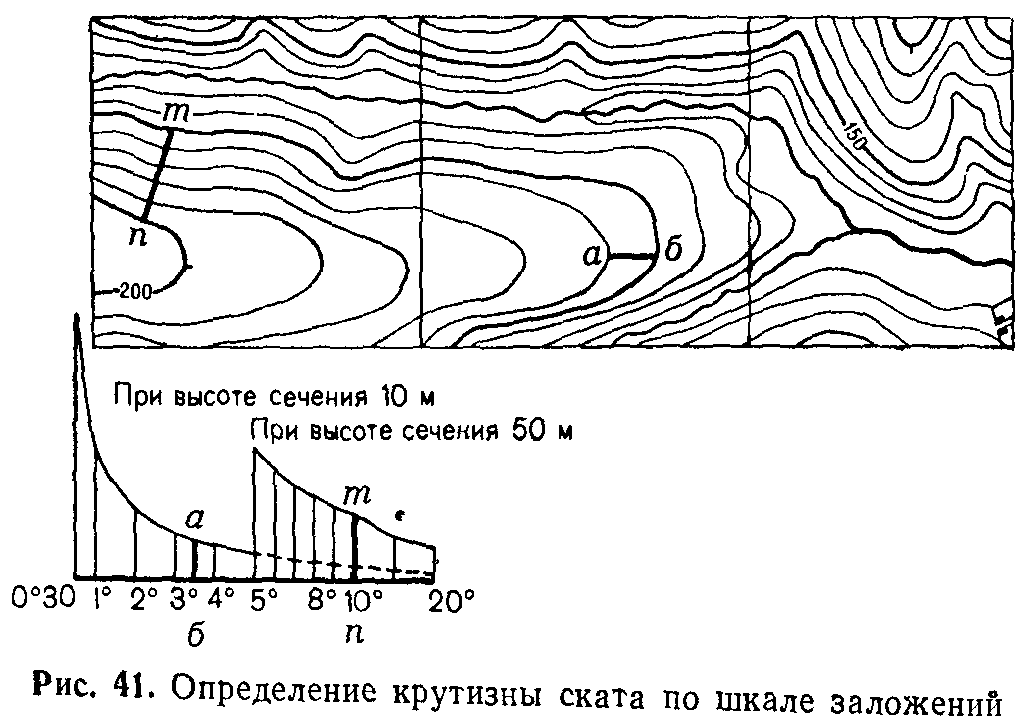
Для определения крутизны ската надо взять циркулем или с помощью полоски бумаги расстояние между двумя смежными горизонталями на интересующем нас скате и затем, приложив этот отрезок к шкале, как показано на рис. 41, прочитать внизу число градусов крутизны. В нашем примере крутизна ската вдоль отрезка ab равна 3°,5.
Если горизонтали на скате расположены очень близко одна к другой и взять циркулем расстояние между ними затруднительно, тогда удобнее пользоваться правой частью шкалы, беря при этом по карте заложения между соседними утолщенными горизонталями. В нашем примере крутизна ската по отрезку mn равна 10°.
Точность определения крутизны скатов по шкале заложений равна примерно 0,3-0,4 цены деления этой шкалы в том ее интервале, в котором определяется крутизна данного ската.
Б. Оценка крутизны скатов на глаз. Расчеты по формуле (2) показывают, что на всех топографических картах с нормальной высотой основного сечения (т. е. при Л = 0,02 величины масштаба карты) заложению в 1 см соответствует крутизна ската в 1°,2 или округленно в 1°, а заложению в 1 мм соответствует крутизна ската в 10°. Поэтому на указанных картах применимо следующее общее правило для приближенного определения крутизны ската на глаз: определяемая крутизна ската во столько раз больше (меньше) 1°, во сколько раз его заложение между смежными сплошными горизонталями меньше (больше) 1 см.
Например, на карте масштаба 500 м в 1 см с высотой сечения 10 м крутизна ската будет примерно равна: при заложении ската 0,5 см – 2°, при заложении 0,1 см– 10°, при заложении 2 см – 0°,5.
Это правило применимо и на картах, на которых высота сечения отличается от нормальной. При этом, однако, надо полученное по указанному правилу число градусов увеличить (уменьшить) во столько же раз, во сколько высота основного сечения на карте больше (меньше) нормальной. Если она больше нормальной, то для уточнения надо в полученный при этом результат ввести поправку, прибавив по 1° на каждые 4°.
Например, на карте масштаба 1:25 000 с высотой основного сечения 10 м (нормальная высота сечения 5 м) заложению в 0,5 см соответствует 5° (4+1), а заложению в 1 мм – 25° (20 + 5).
Источник
Высоты точек местности (абсолютные и относительные), превышения.
При использовании изображения земной поверхности на плоскости для составления проекта требуется иметь не только очертания предметов в горизонтальной проекции, но и представления о неровностях земной поверхности, крутых и пологих местах, превышения точек.
Неровности земной поверхности характеризуются высотами точек. Высотой точки называют отрезок отвесной линии от этой точки до уровенной поверхности, принятой за начало отсчета высот(балтийская система). Обычно высоту точки определяют относительно уровенной поверхности океана(абсолютная высота). Если высоту определяют относительно какой-либо уровенной поверхности, проходящей через произвольную точку, то высоту называют условной. Разность высот точек называют превышением между точками. Превышение всегда сопровождается знаком + или — . для небольших рассояний уровенную поверхность можно принять за горизонтальную(разница 300м-5мм). Высоты точек земной поверхности преимущественно являются положительными и лишь для точек, расположенных ниже уровенной поверхности океана, например на Прикаспийской низменности(-28м) – отрицательными. В России началом отсчета служит нуль Кронштадского футштока, где отмечен средний уровень воды в Финском заливе. 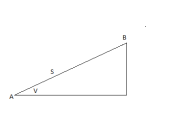
Основные формы рельефа местности и их изображение на планах и картах.
Земная поверхность не является плоскостью. Даже участка равнинной местности небольшой площади нельзя считать плоскими. Различные возвышения и углубления учитывают при строительстве различных объектов. Рельеф – совокупность неровностей земной поверхности. Рельеф местности постоянно изменяется под влиянием сил, действующих внутри Земли, колебаний температуры, действия воды, ветра, растений с течением времени.
Из разнообразных неровностей земной поверхности можно выделить основные формы рельефа: горы, котловины, хребты, лощины, седловины.
Горой называют возвышенность конической формы. Гору высотой менее 200м над окружающей поверхностью называют холмом. Самую высокую точку горы называют вершиной, от которой во все стороны местность понижается. Боковые поверхности горы называют скатами, которые в нижней части заканчиваются подошвой. Остроконечную верхнюю часть горы называют пиком, а плоскую — плато.
Котловиной называют углубление конической или чашеобразной формы. Самую низкую точку котловины называют дном, от нее во все стороны местность повышается. Боковые поверхности называются скатами, которые в верхней части заканчиваются бровкой. Небольшие котловины с крутыми скатами называют воронками.
Хребет – возвышение удлиненной формы, складка земной поверхности. Линию вдоль хребта, проходящую по самым высоким точкам, называют водоразделом, а боклвые части скатами.
Лощина – углубление удлиненной формы. Линию вдоль лощины, проходящую по самым низким точкам, называют водотоком, а бока – скатами, которые заканчиваются бровками.
Широкие лощины с пологими скатами называются долинами, а с крутыми и каменистыми – ущельями. Лощины в виде глубоких промоин, образующиеся под действием текучих вод, называют оврагами. С течением времени обрывы оврага осыпаются, зарастают травой и образуют балки.
Седловина – имеет форму седла, представляет сочетание двух хребтов со сходящимися водоразделами в характерной точке А и двух лощин с расходящимися от этой точки водотоками.
Для изображения рельефа местности в характерных точках (на вершинах, дне, водоразделах, водотоках и тд.) определяют высоты и подписывают их на планах и картах.
Для изображения рельефа местности на планах и картах применяют условные обозначения, которые дают представление о формах рельефа земной поверхности, крутизне скатов, высотах точек и превышениях. Существует несколько способов изображения и обозначения рельефа.
Рельеф местности на плане можно представить с помощью надписей высот характерных точек. При большом числе этих надписей можно судить о формах рельефа и крутизне скатов, но их обилие делает план трудночитаемым и не дает наглядного представления о рельефе.
Наиболее распространен способ изображения рельефа на планах и картах горизонталями.
Горизонталь – след, получающийся от сечения земной поверхности уровенной поверхностью, т.е. это воображаемая линия на земной поверхности, проходящая через точки с одинаковыми высотами. При изображении рельефа горизонталями уровенные поверхности, секущие земную поверхность, отстоят одна от другой на одинаковом расстоянии, называемом высотой сечения рельефа. Горизонтали проецируются на горизонтальную плоскость М для изображения их на плане.
Высоты горизонталей подписывают либо в разрыве горизонталей, либо у их концов так, чтобы нижняя часть цифр располагалась ниже по скату. Высоты горизонталей всегда кратны высоте сечения рельефа.

При выборе высоты сечения рельефа учитывают:
Масштаб плана или карты
Характер рельефа местности
Если отдельные детали рельефа, находясь между горизонталями, не отображаются при выбранной высоте сечения, то в этих местах проводят полугоризонтали, т.е. линии, проходящие через точки с одинаковыми высотами, кратные половине и четверти высоты сечения рельефа.
Источник
2.2 Абсолютные и относительные высоты точек земной поверхности
Абсолютной высотой точки земной поверхности называется расстояние от этой точки по отвесной линии до уровенной поверхности, принятой за начало счета. Числовое значение высоты называется отметкой.
В странах СНГ счет абсолютных высот ведется от среднего уровня Балтийского моря, от нуля Кронштадтского футштока. Если расстояние от точки земной поверхности берется не до уровенной поверхности моря, а до какой-нибудь другой условной поверхности, то и отметка называется условной. Величины Аа=НА и ВЬ = НВ (рисунок 6) есть абсолютные высоты точек А и В земной поверхности. Расстояние от точки земной поверхности по отвесной линии до уровенной поверхности, проведенной через другую точку, называется относительной высотой или превышением одной точки над другой. Величина h есть превышение точки В над точкой А. Превышение может иметь знак плюс или минус в зависимости от положения определяемой точки. Если определяемая точка находится выше по отношению к другой, то превышение положительное, а если ниже, то отрицательное.

Рисунок 6 — Высоты точек А и В земной поверхности
3.1 Ориентирование линий
Ориентировать линию местности — это значит найти ее направление относительно какого-либо другого направления, принимаемого за исходное.
В качествеисходныхв геодезии принимают направленияистинного (географического) меридиана,магнитного меридиана либо осевого меридиана зоны (осьОХ или линия, ей параллельная).В зависимости от выбранного исходного направления ориентирным углом можетбыть истинный азимут, магнитный азимут, дирекционный уголилирумб.
3.2 Ориентирование линий по истинному и магнитному меридианам
Горизонтальный угол (от 0 до 360°), отсчитываемый по ходу часовой стрелки от северного направления истинного меридиана до данного направления, называется истинным азимутом А (рисунок.7, а). Направление истинного меридиана на местности может быть получено из астрономических наблюдений
Горизонтальный угол (от 0 до 360°), отсчитываемый по ходу часовой стрелки от северного направления магнитного меридиана до данного направления, называется магнитным азимутом Аm (рисунок 7, а) Направление магнитного меридиана определяется при помощи приборов с магнитной стрелкой (компаса или буссоли).
Магнитный меридиан, как правило, не совпадает с истинным в данной точке земной поверхности, образуя с ним некоторый угол δ, называемый склонением магнитной стрелки.
Угол δ отсчитывается от истинного меридиана до магнитного и может быть восточным (со знаком плюс) и западным (со знаком минус).
Зная склонение магнитной стрелки в данной точке, можно осуществить переход от магнитного азимута направления к истинному по формуле А=Ам+(± δ)

Рисунок 7 — Истинный и магнитный азимуты
В различных точках земного шара склонение магнитной стрелки имеет разные значения. Так, на территории СНГ его величина изменяется от +10,2 до —14,5°. Склонение магнитной стрелки в одной и той же точке существенно изменяется со временем. Различают вековые (на 22,5° за 500 лет), годовые (до ±8′) и суточные (порядка ±15″ и более) изменения склонения магнитной стрелки.
Вследствие указанных причин положение магнитного меридиана может быть установлено лишь приближенно, и ориентирование линий с помощью магнитных азимутов допускается только при составлении планов небольших участков местности.
В геодезии принято различать прямое и обратное направления линий местности. Если направление линии MN с точки М на точку N (рисунок 7, б) считать прямым, то NM будет обратным направлением той же линии. В соответствии с этим угол Аi является прямым азимутом MN в точке М, а А2 — обратным азимутом той же линии в точке N.
Вследствие сферичности Земли меридианыв различных точках, расположенных на одной линии,не параллельнымежду собой. Поэтомуазимутлинии в каждой ее точке имеетразличное значение. Угол между направлениями меридианов в данных двух точках линии называется сближением меридиановγ.Зависимость между прямым и обратными азимутами линииMN определится выражением
где Δλ — разность долгот меридианов, проходящих через точки М и N; φ— средняя широта ориентируемой линии (для территории СНГ величина сближения меридианов достигает более минуты на 1 км дуги параллели).
Источник
Практическая работа «Определение относительной высоты точек и форм рельефа на топографической карте».
Цели практической работы:
– формирование у обучающихся способностей к рефлексии на основе фиксирования изученного материала по изображению земной поверхности на плоскости;
– решение задач по определению абсолютной и относительной высоты, распознавать высоты на физической и топографической картах;
Необходимые принадлежности: топографическая карта 1:25000, масштабная линейка, треугольник, карандаш средней твердости, ластик.
1. Этап мотивации. Проверка готовности к выполнению практической работы и рабочего места.
Все ли пользуются навигаторами, ГИС, интерактивными картами?
2. Этап актуализации.
Определение абсолютной и относительной высоты, горизонталей. Простейшие задачи по определению относительной высоты.
3. Этап локализации затруднений.
Вызвали ли у вас эти задания затруднения. Вычисления? Если нет, то мы с вами вполне готовы к сегодняшней работе.
4. Этап целеполагания.
Как чувствует себя человек, создающий топографическую карту?
5. Этап выполнения практической работы.
Изображение рельефа на топографических картах дает полное и достаточно подробное представление о неровностях земной поверхности, их форме и взаимном расположении, превышениях и абсолютных высотах точек местности, преобладающей крутизне и протяженности скатов. На современных топографических картах рельеф изображается горизонталями в сочетании с условными знаками обрывов, скал, оврагов, промоин, осыпей, оползней и т. д. Изображение рельефа дополняется подписями абсолютных высот характерных точек местности, горизонталей, размеров отдельных форм рельефа и указателями направления скатов.
Сущность изображения рельефа горизонталями. Горизонталь – это замкнутая линия, изображающая на карте горизонтальный контур неровностей, все точки которого на местности расположены на одной высоте над уровнем моря. Горизонтали можно представить как линии, полученные в результате сечения местности уровенными поверхностями, то есть поверхностями, параллельными уровню воды в океанах.

Рис.1 Изображение рельефа горизонталями.
Рассмотрим сущность изображения рельефа горизонталями. На рис.1 изображен остров с вершинами А и Б и береговой линией D, Е, F. Замкнутая кривая d e f представляет собой изображение береговой линии в плане. Поскольку береговая линия является сечением острова уроненной поверхностью океана, изображение этой линии на карте представляет собой нулевую горизонталь, все точки которой имеют высоту, равную нулю.
Допустим, что уровень океана поднялся на высоту h, тогда образуется новое сечение острова воображаемой секущей плоскостью h – h. Проектируя это сечение с помощью отвесных линий, получим на карте изображение первой горизонтали, все точки которой имеют высоту h. Точно так же можно получить на карте изображение и других сечений, выполненных на высотах 2h, Зh, 4h и т. д. В результате на карте будет иметь место изображение рельефа острова горизонталями. При этом рельеф острова изображается тремя горизонталями, – охватывающими остров целиком, и двумя горизонталями, охватывающими отдельно каждую из вершин.
Вершина А несколько выше 4h, а вершина В несколько выше Зh относительно уровня океана. Скаты возвышенности А круче, чем скаты возвышенности В, поэтому в первом случае горизонтали на карте расположены ближе друг к другу, чем во втором. Из рисунка видно, что способ изображения рельефа горизонталями позволяет правильно не только отображать формы рельефа, но и определять высоты отдельных точек земной поверхности по высоте сечения рельефа и крутизне скатов.
Высота сечения рельефа – это разность высот двух смежных секущих поверхностей. На карте она выражается разностью высот двух смежных горизонталей. В пределах листа карты высота сечения рельефа, как правило, является постоянной. На рис.2 показан вертикальный разрез (профиль) ската.

Рис.2 Профиль ската.
Через точки М, N, О проведены уровенные поверхности на расстоянии друг от друга, равном высоте сечения Л. Пересекая поверхность ската, они образуют кривые линии, ортогональные проекции которых в виде трех горизонталей показаны нижней части рисунка. Расстояния mn и no между горизонталями являются проекциями отрезков MN и NO ската. Эти проекции называются заложениями горизонталей.
Определение высот точек. Абсолютную высоту какой-либо точки местности, отметка которой на карте не подписана, определяют по отметке ближайшей к ней горизонтали. Поэтому необходимо уметь определять отметки горизонталей, используя отметки других горизонталей и характерных точек местности, подписанных на карте.
Например, отметку горизонтали а (рис.3) можно определить по отметке высоты 197,4 и высоте сечения рельефа 10 м.

Рис.3 Определение отметки горизонтали по отметке точки.
Отметка горизонтали а равна 190 м. Зная отметку горизонтали а, можно легко определить отметки всех других горизонталей. Так, горизонталь b будет иметь отметку 160 м, так как она расположена ниже горизонтали а на величину, равную трем высотам сечения рельефа (30 м). В случае когда точка расположена между горизонталями, находят высоту ближайшей к ней горизонтали и к полученной высоте прибавляют превышение данной точки над горизонталью, определенное на глаз. Например, мельница, обозначение которой находится между горизонталями (рис.3), имеет абсолютную высоту 162 м.
Определение взаимного превышения точек заключается в установлении величины, указывающей, насколько одна точка выше или ниже другой. При расположении точек на одной горизонтали их взаимное рис превышение равно нулю, так как их высоты одинаковы. Если определяемые точки совпадают с точками, высоты которых подписаны на карте, их взаимное превышение равно разности этих высот.
В случае когда точки расположены на одном скате или на разных скатах близко друг к другу, подсчитывают число промежутков между горизонталями и. к целому числу добавляют их доли, которые оценивают на глаз. Полученное число умножают на высоту сечения рельефа и таким образом получают взаимное превышение указанных точек.
Когда точки расположены на значительном расстоянии друг от друга, определяют их абсолютные высоты. Разность этих высот и будет взаимным превышением точек.
Задание 1. На карте (рисунок 4) найти точки А, В, С. Определить по горизонталям абсолютные высоты Точек А, В, С.
Сначала находим высоту сечения рельефа. На топографических картах ее подписывают под графиком линейного масштаба. Затем для получения Набс точки определяют высоту горизонтали, лежащей от точки вниз по склону. На понижение склона указывают специальные знаки – бергштрихи, а также положение русел рек. После этого на глаз оценивают расстояние между верхней и нижней горизонталями, а также положение точки между ними.
На рис. 1 горизонтали проведены через 10 м. Чтобы найти Набс точки пересечения полевых дорог, по утолщенной горизонтали с отметкой высоты 200 м определяют высоту горизонталей, находящихся выше по склону: 210, 220 и 230 м. Точка расположена между горизонталями 220 и 230 м, примерно на 1/3 ниже горизонтали 230 м. При высоте сечения 10 м это ≈ 3 м, значит, искомая высота точки Набс. = 227 м.
Относительную высоту между двумя точками, или превышение, определяют как разность двух абсолютных высот этих точек.
Превышение точки с отметкой 177,8 над точкой с высотой 236,3 (геодезический пункт) отрицательное: h = 177,8 – 236,3 = =-58,5 м. Ответ: h =-58,5 м. Относительные высоты склонов удобно определять по числу промежутков между горизонталями на них. Высота склона равна произведению числа основных горизонталей на высоту сечения.
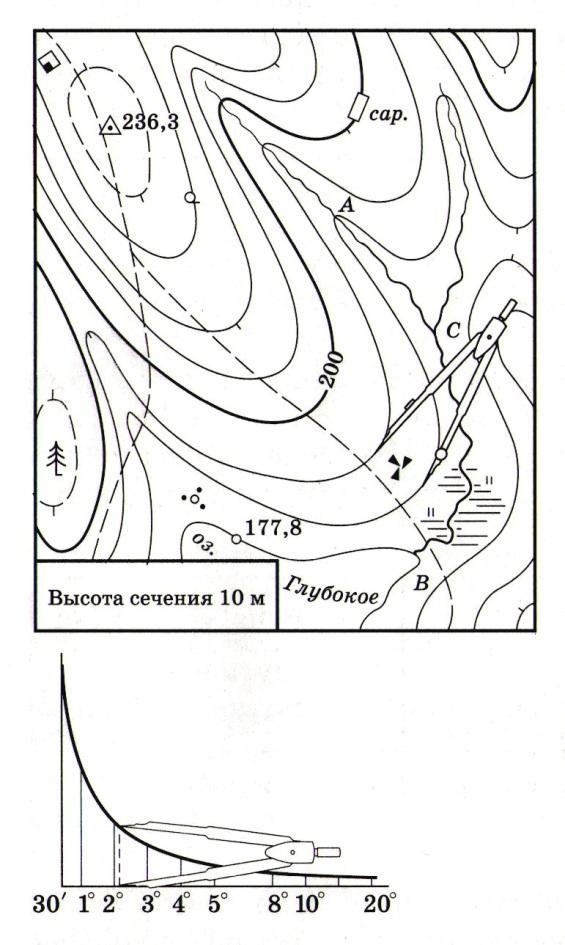
Рис.4 Фрагмент рельефа и график заложений
/ ru
▶ Видеоинструкция
Эта карта показывает оцененную компьютерным алгоритмом по данным рельефа красоту вида, открывающегося с каждой обработанной точки. Более тёплым цветам соответствуют более красивые места.
На настоящий момент построены карты горного Алтая, Хакасии, Тывы и Кузбасса, Грузии и Крыма, а также части Казахстана, окрестностей Байкала, Дальнего Востока, Монголии, Гималаев и Альп.
Клавиша Tab переключает карту подложки
с рельефа на спутник и обратно,
пробел переключает слои
видов и уклонов.
Прозрачность дополнительных слоёв можно менять
, повторно нажимая на их кнопки слева вверху или вращая колёсико мышки с нажатым Ctrl (а если навести на кнопку слоя, то можно и без Ctrl).
2.1. Определение на карте абсолютных высот и относительных превышений точек местности
(Статья: 2.1. Определение на карте абсолютных высот и относительных превышений точек местности)

Абсолютная высота
— высота точки земной поверхности над уровнем моря; определяется по отметкам высот и горизонталей (на рис. 9 это высоты с отметками 33,1 и 49,8).
Высота сечения рельефа
— расстояние по высоте между двумя смежными секущими плоскостями.
Относительная высота
(взаимное превышение точек)
— высота точки местности над другой, она определяется как разность абсолютных высот этих точек (на рис. 9 относительная высота равна 16,7 (49,8-33,1)).
Расчеты по карте
С помощью карты можно решить очень много практических задач, не выходя на местность. По карте можно определить: масштаб данной карты, расстояние между любыми местными предметами, размеры любой площади, крутизну скатов, высоты любых точек местности, взаимное превышение точек, видимость точек, количество деревьев в лесу, количество воды в реке и многое другое.
Как определить Масштаб.
Приведем некоторые примеры.
Обычно на каждой карте дается линейный, численный и текстовой масштаб. Но как быть, если по той или другой причине его не оказалось? Опытный специалист по внешнему виду карты может сразу назвать ее масштаб. Если же вы этого сделать не можете, то следует прибегнуть к следующим способам.
По километровой сетке. Ее сторона соответствует определенному количеству сантиметров. Если это расстояние равно 2 см, то масштаб карты в 1 см — 500 м, то есть 1 :50 000; если 4 см, то масштаб карты соответственно будет 1: 25 000.
По номенклатуре листа определение масштаба карты было показано выше.
По длине дуги меридиана. Для того чтобы пользоваться этим способом, нужно твердо помнить, что одна географическая минута по меридиану равна примерно 2 км (точнее 1,85). Подписи градусов и минут имеются на карте, и, кроме того, каждая минута выделена шашечкой. Так, например, на рисунке 42 длина одной минуты равна примерно 4 см. Это значит, что масштаб данной карты будет 1: 50 ООО.
Как измерить расстояние.
Чтобы определить расстояние между двумя точками,
вначале измеряют это расстояние на карте, а затем, пользуясь численным или линейным масштабом карты, определяют действительное значение этого расстояния на местности. Если требуется определить расстояние не по прямой, а по извилистой дороге, пользуются специальным прибором—курвиметром (рис. 43). Это прибор для измерения длины кривых линий. Основанием курвиметра служит колесико, длина окружности которого известна. Вращение колесика передается на стрелку, поворачивающуюся по круговой шкале. Зная число оборотов колесика, катящегося- по измеряемой линии, легко определить и ее длину.
Как измерить площадь.
Геометрическим способом. Измеряемая площадь разбивается на сеть треугольников, квадратов, трапеции, площади которых вычисляются по известным формулам. Сумма площадей известных фигур даст общую площадь, заключенную в контуре.
С помощью сетки квадратов. Очень удобно определять площадь при помощи миллиметровой сетки, которую наносят на прозрачную бумагу или пленку. Такую сетку прикладывают на контур карты и подсчитывают число квадратных миллиметров. Зная, чему равен 1мм2 карты на местности (для масштаба 1:100000 — 1 мм2 равен гектару, то есть 100 X 100 м), легко определить площадь на карте.
Как определить крутизну ската.
Расстояние между горизонталями, так называемое заложение, показывает крутизну ската.
Основные способы определения крутизны скатов следующие.
По шкале заложений определение крутизны скатов было рассмотрено выше.
Вычислением. Измерив по карте заложение d и зная высоту сечения ft, крутизну ската а можно определить по формуле: а = ,
где а—крутизна ската в градусах;
d — расстояние
между двумя смежными горизонталями в миллиметрах.
С помощью линейки или на глаз. На советских топографических картах стандартная высота сечения для каждого масштаба установлена такой, что заложению в 1 см соответствует крутизна около 1°. Из вышеприведенной формулы видно, что во сколько раз заложение меньше одного сантиметра, во столько раз крутизна ската больше одного градуса. Отсюда следует, что заложению в 1 мм соответствует крутизна 10°, заложению в 2 мм — 5°, заложению в 5 мм — 2° и т. д.
Как определить высоту точек местности по карте.
Определение по карте высот точек над уровнем моря (абсолютных высот) производится с помощью отметок на горизонталях. Если точка расположена на горизонтали, то задача сводится к определению отметки этой горизонтали. Если такой отметки на ней нет, то ее определяют по отметкам ближайших горизонталей илц точек, высота которых обозначена на карте. Если точка находится между горизонталями, то для определения ее отметки надо установить направление ската, определить высоту ближайшей к ней нижней горизонтали, а затем прибавить к ней превышение данной точки. Оно определяется на глаз. Определение превышения одной точки над другой (относительное) определяется также с помощью отметок горизонталей.
Как определить взаимную видимость точек местности. . Это надо знать при выборе наблюдательных пунктов, скрытых подступов, а также в случаях, когда необходимо установить, как просматривается местность с вероятных наблюдательных пунктов противника. Определение по карте взаимной видимости сводится к тому, чтобы, не будучи на местности, установить, нет ли на направлении на-
блюдения какой-либо возвышенности или местного предмета, который будет перекрывать вашу линию видимости.
Определение видимости точек может быть выяснено наиболее просто и точно построением треугольника. Для этой цели соединяют на карте точки НП (наблюдательного пункта) и Ц (цели) прямой линией (рис. 44) и отмечают на этой линии точку возможного укрытия цели У. В конкретном примере это может быть высота с горизонталью 180. Определив, какая из этих трех точек (НП, Ц, У) самая низкая, ставят около нее нуль, а у остальных точек подписывают их превышение по отношению к этой нулевой точке. В нашем примере цель является нулевой точкой, укрытие выше ее на 15 м, а наблюдатель на 25 м. Из точек, имеющих превышение над нулевой точкой, восстанавливают перпендикуляры к линии НП — Ц и откладывают на них (в произвольном, но в одинаковом масштабе) значение превышений (15 и 25). Затем прикладывают линейку к полученным точкам на перпендикулярах и проводят прямую линию (луч зрения). Если эта прямая пройдет выше нулевой точки, то последняя видна не будет. В нашем примере цель не видна.
Для того чтобы она была видна наблюдателю, надо подняться примерно на 5—6 м (см. пунктирную линию на треугольнике).
Как определить количество дров, которые можно заготовить в лесу, изображенном на карте?
Исходя из характеристики леса, допустим q~3*5, известно, что высота деревьев — 20 м, толщина стволов деревьев — 0,3 м, а расстояние между ними — 5 м. Полагая, что ствол каждого дерева имеет форму конуса, основа-
А чтобы узнать, сколько кубометров леса растет на одном гектаре, нужно определить общее количество деревьев на этой площади. Для нашего примера деревья отстоят друг от друга на 5 м, значит, на расстоянии 100 м будет расположено 20 деревьев, а на площади 100 X 100 м — 400. Объем древесины из такого леса на одном гектаре будет равен 0,47 X 400 = 188 м
Сколько воды в реке? Чтобы ответить на этот вопрос, надо знать среднюю скорость течения и поперечную площадь реки. Скорость течения реки указывается на карте, а поперечная площадь отсутствует. Но если воспользоваться шириной реки и ее глубиной и считать поперечную площадь ее — площадью треугольника или, более близкой к действительности, трапеции (нижнее основание ее равно половине ширины реки), то сравнительно просто можно подсчитать и секундный расход воды в реке.
Таковы те простейшие расчеты, которые можно выполнить по карте, не выходя на местность
. Но главная задача карты все же сводится к изучению местности, изображенной на ней, и возможности ориентироваться на ней с помощью карты и компаса.
Как выбрать карту в зависимости от поставленных задач?

Топографические карты – разновидность географических. Они несут подробную информацию о плане местности, указывая расположение различных технических и природных объектов друг относительно друга.
Работа с топографической картой не сложна, главное знать, с чего начать и на что необходимо обратить внимание. Это помогает решить любые задачи, связанные с получением необходимой информации о местности.
Топографические карты различаются по масштабам выполнения. Все они несут менее или более детальную информацию о местности, поэтому в зависимости от поставленных задач нужно выбирать и нужную карту.
Масштаб карты обозначается сбоку или снизу карты. Он показывает соотношение размеров: обозначенного на карте к натуральному. Таким образом, чем знаменатель больше, тем материал менее подробный. Допустим, карта 1:10000 будет иметь в 1 сантиметре 100 метров. Чтобы узнать расстояние в метрах между объектами, с помощью линейки измеряется отрезок между двумя пунктами и умножается на второй показатель.
- Самым детальным является топографический план, его масштаб 1:5000 включительно. Он не считается картой, и является не таким точным, так как не берёт во внимание положения о том, что Земля круглая. Это несколько искажает его информативность, тем не менее, план является незаменимым при изображении культурно-бытовых и хозяйственных объектов. Кроме того, план может показывать и микрообъекты, которые сложно найти на карте (допустим, растительность и грунты, контуры которых слишком малы для изображения в других материалах).
- Топографические карты масштабом 1:10000 и 1:25000 считаются среди карт максимально подробными. Их используют для хозяйственных нужд. Они изображают населённые пункты, промышленные объекты и объекты сельского хозяйства, дороги, гидрографическую сеть, болота, ограждения, границы и т. д. Такие карты наиболее часто используются для получения информации о местности, которая не имеет значительного лесистого покрова. Наиболее достоверно в них изображены объекты хозяйствования.
- Карты с масштабом 1: 50000 и 1:100000 менее подробны. Они схематично изображают контуры лесов и иных крупных объектов, изображение которых не требует большой детализации. Такие карты удобно использовать для аэронавигации, составляя маршруты дорог и так далее.
- Менее подробные карты используются в военных целях для выполнения поставленных задач по планированию различных операций.
- Карты с масштабом до 1:1000000 позволяют правильно оценить общую картину местности.
Определившись с поставленной задачей, выбор материала представляется абсолютно несложной задачей. В зависимости от того, насколько нужна детальная информация о местности, выбирается и нужный масштаб карты.
Измерение расстояний на картах и планах. Для измерения расстояния на карте его берут на циркуль-измеритель и переносят на помещённый под южной рамкой карты линейный масштаб.
Более точно расстояние измеряют линейкой с миллиметровыми делениями. Отсчёт по линейке, выраженный в сантиметрах, умножают на число метров, указанное в именованном масштабе карты.
|
|
Рис. 4.5. Поперечный
масштаб |
Ещё точнее измерения выполняются с применением поперечного масштаба (рис. 4.5.). На металлической линеечке через m интервалов выгравированы параллельные линии – горизонтали (обычно m = 10). К ним восставлены перпендикуляры – вертикали, расстояние между которыми называют основанием масштаба d (обычно d = 2 см). Крайнее левое основание разделено на n частей и через полученные точки проведено n наклонных линий – трансверсалей (обычно n =10 или 5). Длины отрезков, параллельных основанию, на поперечном масштабе равны: между соседними вертикалями – d, между соседними трансверсалями – d/n. Длины отрезков между вертикалью и исходящей из той же точки трансверсалью изменяются в пределах от 0 до d/n. Наименьшее деление поперечного масштаба, определяющее его точность, равно d/(mn).
Для удобства пользования поперечным масштабом деления основания и горизонтали оцифровывают в соответствии с масштабом плана. Оцифровка на рисунке соответствует масштабу 1:500.
Для измерения расстояния берут его в раствор циркуля-измерителя. Правую его ножку ставят на одну из вертикалей поперечного масштаба, а левую – на одну из трансверсалей, но так, чтобы обе ножки оказались на одной и той же горизонтали. Измеренное расстояние равно сумме расстояний, соответствующих числу охваченных раствором циркуля целых оснований, десятых долей основания и сотых, оцениваемых по положению ножки циркуля на трансверсали. На рисунке отрезок ab имеет длину 20+3+0,7=23,7 м. Длина отрезка cd равна 30+5+0,45=35,45 м. Из второго примера видно, что длину отрезка удаётся измерить с точностью половины наименьшего деления (в данном случае 0,05 м).
Для измерения длин извилистых линий служит специальный прибор — курвиметр, снабжённый колёсиком, которое прокатывают вдоль измеряемой линии. Вращение передаётся на стрелку циферблата, по которому прочитывают измеренное расстояние.
Определение координат точек. Для определения географических координат служит минутная рамка карты. Через круглые значения минут широты на западной и восточной рамках южнее определяемой точки прочерчивают линию. На рис. 4.6, а показан отрезок такой линии с широтой 57°20¢. Взяв на циркуль-измеритель расстояние а от определяемой точки M до прочерченной линии, откладывают его на рамке карты и, по десятисекундным делениям соображают число секунд. На рисунке широта точки M равна 57°20¢32″.
Для определения долготы через одинаковые значения минут на северной и южной рамках прочерчивают вертикальную линию. Расстояние от точки до линии переносят измерителем на северную или южную рамку и соображают число секунд.
Прямоугольные координаты определяют, пользуясь километровой сеткой, линии которой параллельны координатным осям x и y. Координаты точки P (рис. 4.6, б) определяются по формуле
xP= xю+ Dx, yP= yз+ Dy,
где xю и yз — значения координат на линиях сетки, проходящих южнее и западнее точки Р. Они подписаны (в километрах) на выходах линий за рамку. Отрезки Dx и Dy измеряют.

Рис. 4.6. Определение координат точек: а — географических; б – прямоугольных.
Повысить точность определения координат точки Р можно, измерив расстояния a и b до ближайших южной и северной линий сетки, а также расстояния c и d до ближайших западной и восточной линий сетки. Отрезки Dx и Dy, выраженные в метрах, вычисляют по формулам
, , (4.1)
где множитель 1000 — длина стороны квадрата километровой сетки в метрах.
Дополнительный эффект измерения отрезков a, b, c, d и использования формул (4.1) состоит в ослаблении погрешностей, вызванных деформацией бумаги. Такой же прием может быть применен и при определении географических координат.
Определение углов ориентирования. Дирекционный угол направления отрезка на карте измеряют транспортиром как угол, отсчитываемый по направлению часовой стрелки от северного направления линии километровой сетки до направления отрезка. При необходимости перед измерением отрезок удлиняют до пересечения с линией сетки.
Для определения азимута А направления сначала измеряют его дирекционный угол a. Затем вычисляют азимут: А=a+g, где g — сближение меридианов, значение которого подписано под южной рамкой карты и показано на помещённой там же схеме.
Можно азимут измерить и непосредственно. Через одноименные значения минут долготы проводят вертикальную линию — меридиан. Угол между северным направлением меридиана и направлением отрезка и есть азимут.
Под южной рамкой карты и на схеме указано также склонение магнитной стрелки d, позволяющее вычислить магнитный азимут направления по формуле Ам= А-d.
Определение высот точек. Высота точки, лежащей на горизонтали, равна высоте горизонтали. Высоты отдельных горизонталей подписаны в их разрыве. Высоты других горизонталей легко сообразить, зная высоту сечения рельефа, а также высоты подписанных горизонталей и высоты тех характерных точек рельефа, у которых подписаны их отметки. При этом учитывают, что высоты горизонталей кратны высоте сечения рельефа.
Высота точки M, расположенной между двумя горизонталями (рис. 4.7) определяется по формуле
,
где Hг — высота меньшей горизонтали, h – высота сечения рельефа, а отрезки a и b – заложение ската и расстояние от точки до горизонтали, измеряемые по карте линеечкой.
Построение профиля. Для построения профиля по линии, проведенной на карте, определяют высоты точек в местах её пересечения с горизонталями, водораздельными и водосливными линиями. Измеряют горизонтальные расстояния до них от начальной точки линии. При построении профиля по горизонтальной оси откладывают расстояния, а по вертикальной — высоты. Для наглядности вертикальный масштаб принимают крупнее горизонтального (в 10, а то и в 50 раз).
Определение уклонов и углов наклона. Отрезки линий на земной поверхности обычно имеют наклон, отчего начало и конец отрезка находятся на разных высотах. Разность их высот – превышение, а проекция отрезка на горизонтальную плоскость – его горизонтальное проложение.
Уклоном i линии называется отношение превышения h к горизонтальному проложению d:
i = h / d. (4.2)
Для определения по карте уклона линии на участке KL между двумя горизонталями (рис. 4.7) измеряют его горизонтальное проложение – заложение d. Поскольку концы отрезка лежат на смежных горизонталях, превышение h между ними равно высоте сечения рельефа, подписанному под южной рамкой карты. Воспользовавшись формулой (4.2), вычисляют уклон, который принято выражать в тысячных. Если, например, h=1 м, d=48 м , то уклон равен i =1 м / 48 м = 0,021=21‰.
Рис. 4.7. Определение высоты точки M и уклона на отрезке KL
С другой стороны, отношение превышения h к горизонтальному проложению d равно тангенсу угла n наклона линии. Поэтому
i = tg n,
что позволяет, вычислив уклон определить по нему угол наклона.
При пользовании картой углы наклона не вычисляют, а определяют с помощью графика заложений (рис. 4.8), расположенного под южной рамкой карты. По горизонтальной оси графика отложены углы наклона, а по вертикальной — соответствующие этим углам заложения d, выраженные в масштабе карты и рассчитанные по формуле
d = h ¤ (M tg n),
где h — высота сечения рельефа, а M – знаменатель масштаба карты.
Рис. 4.8. График заложений
Для определения угла наклона отрезка KL (рис. 4.7), расположенного между горизонталями, берут его в раствор циркуля и на графике заложений (рис. 4.8) находят такой угол, над которым ордината равна раствору циркуля d. Это и есть искомый угол наклона.
При необходимости многократного определения уклонов пользуются графиком уклонов, построенным аналогично графику заложений, но с отложением по горизонтальной оси не углов наклона, а уклонов.
Проведение линии с уклоном, не превышающим заданного предельного. Необходимость решения такой задачи возникает, например, при выборе трассы для будущей дороги. Вычисляют соответствующее заданному предельному уклону iпр заложение, выраженное в масштабе карты, (здесь M – знаменатель масштаба). .
| Рис. 4.9. Построение линии с заданным уклоном | Рис. 4.10. Водосборная площадь |
Чтобы уклон линии не превосходилiпр, ни одно заложение на ней не должно быть меньше, чем рассчитанноеd. Если расстояние между горизонталями больше рассчитанного, направление линии можно выбирать произвольно. В противном случае в раствор циркуля берут отрезок, равный d, и строят ломаную линию, умещая между горизонталями рассчитанное предельное заложение (рис. 4.9).
Определение границ водосборной площади (бассейна). Водосборной называют площадь, с которой дождевые и талые воды поступают в данное русло. Определение водосборной площади необходимо, например, при проектировании дороги для расчёта отверстия моста или трубы.
Для определения границ водосборной площади на карте проводят водораздельные линии, а затем от проектируемого сооружения к водораздельным линиям проводят линии наибольшего ската, перпендикулярные горизонталям.
Например, водосборная площадь, для точки Р, где предстоит строительство трубы, (рис. 4.10), ограничена штриховой линией, образованной водораздельной и двумя линиями наибольшего ската.
Специальные условные знаки используются для изображения рельефа местности на картах и планах местности.
Перед тем как изобразить горы и равнины, холмы и впадины, необходимо определить абсолютную и относительную высоту нужных точек.
Абсолютная высота — высота точки над уровнем океана (моря).

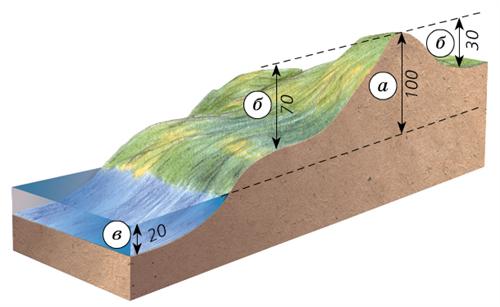
Абсолютная высота (а), относительная высота (б), абсолютная глубина (в) в метрах
Уровень моря принимают за (0) метров, так как все моря и океаны сообщаются между собой и находятся примерно на одном уровне.
Абсолютная высота отдельных вершин на суше обозначается точкой и числом. Число показывает высоту над уровнем моря. Глубина показывается только числом и так же отсчитывается от уровня Мирового океана:


В России точкой отсчёта является средний уровень Балтийского моря, определённого на основе многолетних наблюдений в городе Кронштадте (нуль Кронштадтского футштока).

Нуль Кронштадтского футштока
Москва в среднем находится на (156) м выше уровня моря, Санкт-Петербург — на (3) м выше уровня моря.
Абсолютные высоты наиболее важных объектов на планах и картах подписаны цифрой и обозначены точкой — отметкой высоты.
На суше есть впадины, которые лежат ниже уровня моря. В этом случае перед значением высоты ставят знак «(-)», например (-)(27).
Глубину морей и океанов также отсчитывают от уровня моря.

Наибольшие высоты материков и глубины океанов в метрах
Относительная высота — превышение одной точки поверхности над другой.

Если абсолютная высота холма равна (200) м над уровнем моря, а абсолютная высота равнины — (50) м, то относительная высота холма равна (150) м ((200 – 50 = 150)).
В статье речь пойдет о том, что такое высота – абсолютная и относительная. Высота – это термин, используемый в географии. На примере будут показаны различия между двумя этими понятиями. После прочтения статьи у вас сложится устойчивое понятие о двух видах высот в географии, и будет легче ориентироваться на местности и решать практические задачи.
Что такое высота и зачем ее используют в географии?
Любой географический объект, расположенный на поверхности Земли, обладает определенным набором координат (широта и долгота), а также высотными характеристиками. Рельеф нашей планеты неоднороден, где-то доминируют высокие горы, где-то глубоко вниз уходят бездонные впадины и ущелья. Понятие высоты было придумано людьми, чтобы максимально точно описать те или иные особенности рельефа земной поверхности.
Кроме того, понятие высоты используется на топографических и высотных картах. Подписанная высота позволяет отобразить на плоской поверхности карты объемный рельеф. Как правило, все высоты измеряются в метрах – стандартизированной единице из международной системы. Высоты могут принимать как положительные, так и отрицательные значения. На земной поверхности диапазон высот колеблется от -400 метров (впадина Мертвого моря) до 8848 метров (высочайшая вершина мира – гора Эверест). Для того чтобы лучше понять, чем отличаются высоты, необходимо ввести понятие абсолютная и относительная высота.
Абсолютная высота
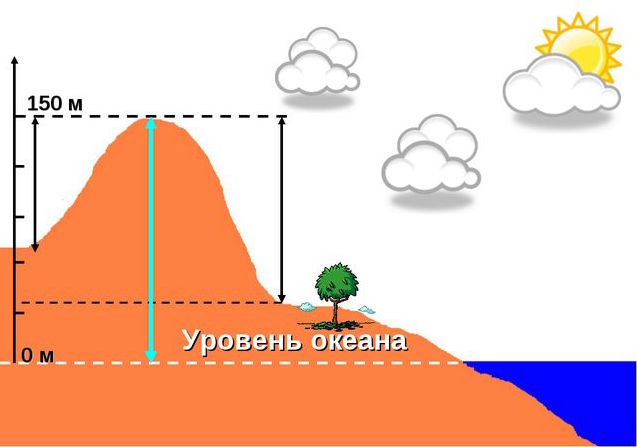
Понятие абсолютной высоты тождественно понятию высоты над уровнем моря, или высоты н.у.м. Так, абсолютная высота той или иной точки земной поверхности представляет собой превышение этой точки над среднегодовым уровнем моря в той или иной системе морских высот. В России все абсолютные высоты измеряются относительно нулевой отметки в Кронштадте, которая расположена у самой кромки воды в этом северо-западном городе.
В других странах существуют иные нулевые уровни, однако суть понятия абсолютной высоты от этого не меняется. Абсолютная высота измеряется в метрах над уровнем моря. Она может принимать как положительные, так и отрицательные значения. На рисунке выше абсолютная высота холма показана голубой стрелочкой. Нет строгого соотношения понятий и значений абсолютной и относительной высоты. Абсолютная высота может быть больше, меньше или равна относительной.
Относительная высота
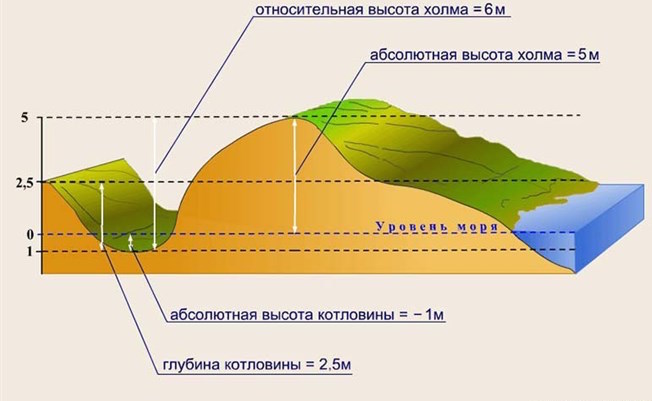
Относительная высота по определению представляет собой превышение двух любых точек земной поверхности относительно друг друга. Сразу следует отметить, что в отличие от абсолютной высоты, относительная всегда принимает строго положительные значения, поскольку численно равняется разности точек с большей и меньшей абсолютными высотами.
Если обратиться, к примеру, к рисунку выше, можно заметить, что абсолютная высота холма составляет 5 метров, при этом относительная высота того же самого холма равняется уже 6 метрам. Как так вышло? Все довольно просто и следует из понятия относительной высоты. Так, авторы данного рисунка решили измерить относительное превышение холма (положительной формы рельефа с положительной величиной высоты) над котловиной (отрицательной формой рельефа с отрицательными значениями абсолютной высоты). Для этого они вычли из абсолютной высоты самой высокой точки (холма, 5 м) абсолютную высоту самой низкой точки, над которой искали превышение холма (-1 м). По правилу сложения и вычитания, 5 – (-1) = 6. Именно 6 метров составляет превышение холма над котловиной, и этому значению равняется абсолютная высота.
Строго говоря, у холма может быть бесконечно большое количество относительных высот, все зависит от того, относительно чего мы будем ее измерять. Для примера найдем относительную высоту самого высокого холма (на рисунке справа) от холма пониже, он показан в левой части. Из разницы абсолютных высот этих положительных форм рельефа (5 метров для высокого и 2,5 метра для низкого холмов) получаем, что относительная высота самого большого холма от низкого холма составляет 5-2,5=2,5 метра. По аналогии с данным примером можно найти относительные высоты чего угодно. Теперь можно ответить на вопрос, как определить абсолютную и относительную высоты.
Как измеряют относительные высоты?
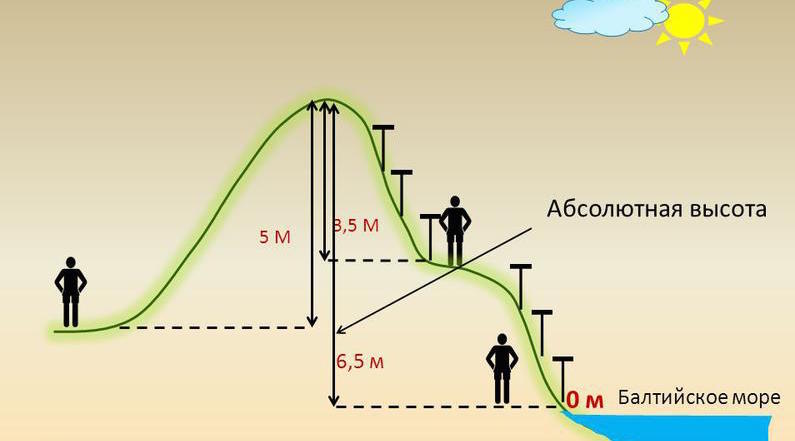
Теперь вы поняли, чем абсолютная высота отличается от относительной в географии. Для определения относительных высот удобно пользоваться специальным прибором – рейкой. Для этого в начальной точке, относительно которой ищется превышение, ставится рейка. Условно эта точка принимается за высоту с отметкой 0. Далее, как показано на рисунке выше, необходимо двигаться вверх по холму или горе до тех пор, пока вы не достигнете высоты рейки, и самая высокая ее точка не окажется ниже уровня ваших ног.
Тогда необходимо зафиксировать точку на холме, которая соответствует положению самой высокой точки рейки, стоящей на нулевом уровне, и сместить рейку в данную точку. Таким образом, на второй точке относительная высота будет равна 1 высоте рейки. Операцию нужно проделать до тех пор, пока вы не достигнете самой высокой точки холма. В этом случае относительная высота будет равняться сумме всех высот переставляемой рейки.
Вместо рейки можно использовать любой предмет, высота которого известна заранее. Если под рукой нет совсем ничего, относительную высоту можно измерить по своему собственному росту, проделав описанные выше манипуляции. Кроме того, относительную высоту легко можно измерить как разность абсолютных высот, если они заранее известны.
Как измеряют абсолютные высоты?
Абсолютную высоту измерить таким способом в полевых условиях не получится. Конечно, можно было бы, однако для этого потребовалось бы наличие в непосредственной близости поверхности моря. Чтобы найти абсолютную высоту, необходимо воспользоваться картой местности или приборами спутникового позиционирования, в которых есть возможность автоматического определения высоты.
Теперь у вас есть устойчивое представление о том, чем отличаются абсолютная высота и относительная высота. Успехов в решении практических географических задач и в повседневном ориентировании в условиях окружающей среды!

