Загрузить PDF
Загрузить PDF
Относительный риск — это статистический термин, которым обозначают риск возникновения определенного события в одной группе по отношению к другой. Он часто используется в эпидемиологии и в доказательной медицине, где этот показатель позволяет рассчитать риск развития заболевания после воздействия определенного фактора (например, медикамента, способа лечения или фактора окружающей среды) по сравнению с отсутствием данного фактора. Эта статья научит вас рассчитывать относительный риск.
Шаги
-
1
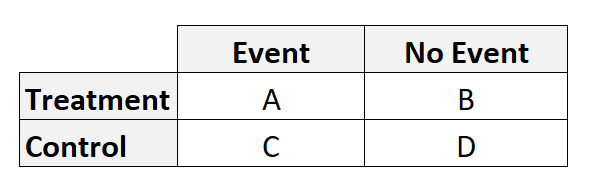
Нарисуйте таблицу 2×2. Такие таблицы лежат в основе многих эпидемиологических расчетов.
- Перед тем как приступать к созданию своей таблицы 2×2, вы должны разобраться в переменных:
- A = Количество человек, подвергшихся воздействию фактора и заболевших
- B = Количество человек, подвергшихся воздействию фактора, но не заболевших
- C = Количество человек, не подвергавшихся воздействию фактора, но заболевших
- D = Количество человек, не подвергавшихся воздействию фактора и не заболевших
- Составим таблицу 2×2 для примера.
- На примере 100 курильщиков и 100 некурящих проводится исследование развития рака легких.
- Мы можем сразу заполнить часть таблицы. Заболевание — рак легких, фактор — курение, численность каждой группы — 100 человек, общая численность участвующих в исследовании — 200 человек.
- По итогам исследования рак легких был выявлен у 30 курильщиков и 10 некурящих. Теперь можно заполнить оставшуюся часть таблицы.
- Так как A — это количество человек, подвергшихся воздействию фактора и заболевших (то есть курильщиков, больных раком легких), мы знаем, что это число равно 30. Мы можем вычислить B путем вычитания A из общей численности курильщиков: 100 – 30 = 70. Аналогично, C — это количество некурящих, больных раком легких, равное 10, тогда D равно 100 – 10 = 90.
- Перед тем как приступать к созданию своей таблицы 2×2, вы должны разобраться в переменных:
-
2
Рассчитайте относительный риск, используя таблицу 2×2.
-
3
Интерпретируйте результаты расчета относительного риска.
- Если относительный риск равен 1, то разницы в риске между двумя группами нет.
- Если относительный риск меньше 1, то риск в группе, подвергшейся воздействию фактора, ниже, чем в не подвергавшейся.
- Если относительный риск больше 1 (как в нашем примере), то риск в группе, подвергшейся воздействию фактора, выше, чем в не подвергавшейся.
Реклама
Об этой статье
Эту страницу просматривали 14 057 раз.
Была ли эта статья полезной?
Download Article
Download Article
Relative risk is a statistical term used to describe the chances of a certain event occurring among one group versus another. It is commonly used in epidemiology and evidence-based medicine, where relative risk helps identify the probability of developing a disease after an exposure (e.g., a drug treatment or an environmental event) versus the chance of developing the disease in the absence of that exposure.[1]
This article will demonstrate how to calculate relative risk.
-
1
Draw a 2×2 table. A 2×2 table is the basis for many epidemiological calculations.[2]
- Before you can draw a 2×2 table yourself, you must understand the variables:
- A = The number of people who both had the exposure and developed the disease
- B = The number of people who had the exposure but did not develop the disease
- C = The number of people who did not have the exposure but did develop the disease
- D = The number of people who neither had the exposure nor developed the disease
- Let’s do an example 2×2 table.
- A study looks at 100 smokers and 100 non-smokers, and follows them for development of lung cancer.
- Right away, we can fill in part of the table. The disease is lung cancer, the exposure is smoking, the total numbers of each group is 100, and the total of all the people in the study is 200.
- At the end of the study, they found that 30 of the smokers and 10 of the non-smokers developed lung cancer. Now we can fill in the rest of the table.
- Since A = the number of people exposed who got the disease (i.e. smokers who got lung cancer), we know this is 30. We can calculate B simply by subtracting A from the total: 100 – 30 = 70. Similarly, C is the number of non-smokers who got lung cancer, which we know is 10, and D = 100 – 10 = 90.[3]
- Before you can draw a 2×2 table yourself, you must understand the variables:
-
2
Calculate the relative risk using the 2×2 table.
Advertisement
-
3
Interpret the results of relative risk.
- If the relative risk = 1, then there is no difference in risk between the two groups.
- If the relative risk is less than 1, then there is less risk in the exposed group relative to the unexposed group.[5]
- If the relative risk is greater than 1 (as in the example), then there is greater risk in the exposed group relative to the unexposed group.[6]
Advertisement
Add New Question
-
Question
Can relative risk calculation be use for other study designs than a case study?
Yes, it certainly can. It can be use in Cohort and Case-Control Studies where the objective is based on the incidence of developing a medical condition in the exposed and unexposed groups.
-
Question
How can I calculate relative risk for a number with more than 5 digits?
The process remains the same no matter how large the numbers are.
-
Question
What is an exposed and unexposed group?
The exposed group includes people who have been exposed to a certain disease. The unexposed group includes people who have not been exposed to the disease.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Study designs such as cohort studies and clinical trials allow the researcher to calculate incidence, whereas case-control studies do not. Thus, relative risk can be calculated for cohort studies and clinical trials, but not for case-control studies. Odds ratios can be used to estimate relative risk for a case-control study.
Thanks for submitting a tip for review!
Advertisement
About This Article
Thanks to all authors for creating a page that has been read 359,699 times.
Did this article help you?
В статистике относительный риск относится к вероятности события, происходящего в экспериментальной группе, по сравнению с вероятностью события, происходящего в контрольной группе.
Он рассчитывается как:
Относительный риск = (вероятность события в экспериментальной группе) / (вероятность события в контрольной группе)
Как правило, вот как интерпретировать значения относительного риска:
- Относительный риск < 1 : событие менее вероятно в группе лечения.
- Относительный риск = 1 : вероятность возникновения события в каждой группе одинакова.
- Относительный риск > 1 : событие с большей вероятностью может произойти в группе лечения.
Следующие примеры показывают, как интерпретировать значения относительного риска на практике.
Пример 1: относительный риск < 1
Предположим, мы хотим знать, влияют ли упражнения на риск развития какого-либо заболевания.
Мы собираем данные и обнаруживаем, что у 28% людей, которые регулярно занимаются спортом, развивается это заболевание, в то время как у 50% людей, которые не занимаются регулярно, это заболевание развивается.
В этом сценарии мы рассчитали бы относительный риск как:
- Относительный риск = P (событие в группе лечения) / P (событие в контрольной группе)
- Относительный риск = P(заболевание при физической нагрузке) / P(заболевание без физической нагрузки)
- Относительный риск = 0,28/0,50
- Относительный риск = 0,56
Поскольку относительный риск меньше 1, это говорит нам о том, что это заболевание с меньшей вероятностью развивается у людей, которые занимаются спортом.
В частности, можно сказать, что вероятность развития этого заболевания у человека на 44% ниже (1 – 0,56 = 0,44), если он регулярно занимается спортом.
Пример 2: относительный риск = 1
Предположим, мы хотим знать, влияет ли какая-то новая учебная программа на способность студентов сдать тот или иной экзамен.
Мы собираем данные и обнаруживаем, что 40% студентов, которые используют новую программу обучения, сдают экзамен, а 40% студентов, которые не используют программу обучения, также сдают экзамен.
В этом сценарии мы рассчитали бы относительный риск как:
- Относительный риск = P (событие в группе лечения) / P (событие в контрольной группе)
- Относительный риск = P(пройти с новой программой) / P(пройти без новой программы)
- Относительный риск = 0,40 / 0,40
- Относительный риск = 1
Поскольку относительный риск равен 1, это говорит нам о том, что человек с одинаковой вероятностью сдаст экзамен независимо от того, использует он новую программу обучения или нет.
Пример 3: относительный риск > 1
Предположим, мы хотим знать, влияет ли курение на риск развития рака легких.
Мы собираем данные и обнаруживаем, что у 70% курящих людей развивается рак легких, а у 5% некурящих людей развивается рак легких.
В этом сценарии мы рассчитали бы относительный риск как:
- Относительный риск = P (событие в группе лечения) / P (событие в контрольной группе)
- Относительный риск = P(рак легких при курении) / P(рак легких без курения)
- Относительный риск = 0,70/0,05
- Относительный риск = 14
Поскольку относительный риск больше 1, это говорит нам о том, что у человека больше шансов заболеть раком легких, если он курит.
В частности, можно сказать, что у человека в 14 раз больше шансов заболеть раком легких, если он курит.
Интерпретация относительного риска в таблице непредвиденных обстоятельств
Часто вам может потребоваться рассчитать и интерпретировать относительный риск, используя таблицу 2×2, которая имеет следующий формат:
Мы можем использовать следующую формулу для расчета относительного риска в таблице 2×2:
Относительный риск = [A/(A+B)] / [C/(C+D)]
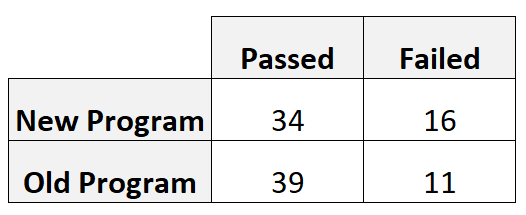
Например, предположим, что 50 баскетболистов используют новую тренировочную программу, а 50 игроков используют старую тренировочную программу. В конце программы мы проверяем каждого игрока, чтобы увидеть, проходят ли они определенный тест навыков.
В следующей таблице 2×2 показаны результаты:
Мы бы рассчитали относительный риск как:
- Относительный риск = [A/(A+B)] / [C/(C+D)]
- Относительный риск = [34/(34+16)] / [39/(39+11)]
- Относительный риск = 0,68/0,78
- Относительный риск = 0,872
Поскольку относительный риск меньше 1, это указывает на то, что вероятность прохождения ниже по новой программе по сравнению со старой программой.
В частности, мы могли бы сказать, что у человека на 12,8% меньше шансов (1 – 0,872 = 0,128) пройти тест навыков, если он использует новую программу.
Дополнительные ресурсы
Следующие руководства предлагают дополнительную информацию об отношениях шансов и относительном риске:
Как интерпретировать коэффициенты шансов
Как рассчитать отношение шансов и относительный риск в Excel
Медстатистика, медицинская статистика 👁 Прочитано 13 228 раз
А. Радостный, NewsForLife.info
- Доверительный интервал
- Отношение шансов
- Шанс
- Отношение шансов
- Пример
- Относительный риск (ОР)
- Достоверность, статистическая значимость (P – уровень)
- Критика
- Графическое представление результатов мета-анализа (блобограмма)
- Литература
Доверительный интервал
Доверительный интервал ДИ (confidence interval, CI ) — это диапазон значений, который с заданной степенью вероятности включает полученные данные.
Пример. Исследуемая величина — количество заболеваний на тысячу человек. Выяснилось, что в среднем было 60 заболеваний, а ДИ 95% (52, 73). Это означает, что, с вероятностью 95% заболеет не менее 52 и не более 73 человека.
Клиническая значимость эффекта велика, когда доверительный интервал узок.
Отношение шансов
Сначала давайте обсудим понятие «шанс», а потом перейдём к отношению шансов.
Шанс
Существует несколько дефиниций, однако в целях вычисления отношения шансов используется понятие «шансы в пользу». Вы часто слышали выражение типа: «пять к одному, что он выиграет». Это как раз шансы в пользу.
Итак, в рассматриваемом контексте:
шанс — это отношение вероятности того, что событие произойдёт, к вероятности того, что событие не произойдёт: да/нет, выиграет/проиграет, упадёт/вырастет и т.п.
Увеличь свои шансы!
ТОП-10 реально выполнимых методов продления ТВОЕЙ жизни
Хотя в русском языке слова «шанс» и «вероятность» часто используются как синонимы, но здесь шанс не равен вероятности.
Например, вероятность того, случайная карта, извлечённая из колоды, в которой 36 карт, окажется красной масти составит 0,5 = 50% = (16 карт красных мастей / 32 карты в колоде). А шанс того, что такая карта будет красной масти составит: 1:1 = (16 карт красных мастей / 32 карты в колоде) : (16 не красных / 32 карты).
ВАЖНО! Врачи склонны рассматривать риск с точки зрения группы пациентов, тогда как пациенты интерпретируют риск применительно к себе-любимому.
Например, психиатр сообщал пациентам, что при приеме флуоксетина была «30–50% вероятность развития сексуальной проблемы». При этом оказалось, что, по мнению пациентов, это означало трудности во время половины их сексуальных контактов. Между тем доктор желал проинформировать, что из каждых десяти человек, принимающих флуоксетин, три-пять будут испытывать затруднения [1].
Отношение шансов
Отношение шансов ОШ (OR — odds ratio) – это величина, которая количественно определяет силу связи между двумя событиями (признаками) A и B в пределах одной и той-же выборки (пример см. далее).
OШ=(A+/А-) : (В+/В-).
|
есть |
нет |
|
|
Событие А |
A+ |
А- |
|
Событие В |
B+ |
B- |
Два события независимы тогда и только тогда, когда OШ=1. Чем ближе значение OШ к 1, тем меньше различий в эффективности сравниваемых вмешательств.
Если OШ>1, то появление B повышает шансы наличия A (по отношению к отсутствию B).
Если OШ<1, то наличие одного события (признака) уменьшает шансы другого события (признака).
Пример
Допустим, что 100 добровольцам задают два вопроса:
-
Каково Ваше артериальное давление?
-
Сколько алкоголя Вы употребляете?
Далее, для каждого участника можно определить обладает ли он свойством
А — часто употребляет алкоголь
и свойством
B — высоким артериальным давлением.
В результате опроса всей сотни участников можно построить показатель, который количественно характеризует связь между признаками A и B в изучаемой группе.
|
В: высокое давление |
норма |
Всего |
|
|
А: часто употребляет алкоголь |
12 |
20 |
32 |
|
не часто употребляет алкоголь |
4 |
64 |
68 |
Отношение шансов (ОШ):
OШ=(A+/А-) : (В+/В-).
-
A+/А- = 12/20=0,6.
-
В+/В-=4/64= 0,0625
-
Разделим шансы, полученные в п. 1, на шансы, полученные в п.2, — это и будет отношение шансов (ОШ). ОШ = 0,6/0,0625 = 9,6.
Если ОШ превышает 1, наличие признака А ассоциируется с признаком B в том смысле, что наличие B повышает (по отношению к отсутствию В) шансы наличия A. В нашем умозрительном примере это означает, что частое употребление алкоголя почти десятикратно повышает шансы появления гипертонии.
Опасность для клинической интерпретации ОШ возникает когда вероятность случая высока, при этом преувеличиваются имеющиеся различия, если предположение о редком заболевании не выполняется.
Важно знать, что отношение шансов является симметричным относительно обоих событий, а потому и не отражает причинно-следственных связей. Оно не доказывает, что B вызывает A, или A вызывает B.
Для расчёта отношения шансов с 95% доверительным интервалом см. онлайн калькулятор.
В медицинской литературе отношение шансов нередко путают с относительным риском.
РАССЫЛКА «ЗДОРОВЬЕ И АНТИСТАРЕНИЕ»
Относительный риск (ОР)
Риск события (или заболевания) — это просто количество случаев, когда оно произошло, делённое на общее число случаев, когда оно может произойти. В нашем примере для тех, кто часто употребляет алкоголь риск высокого давления 12/32 = 0,375=37,5%. А для малопьющих он будет 4/(68)= 0,059=5,9%.
Относительный риск ОР (RR — relative risk) — отношение рисков появления определённого события в группах сравнения.
Для нашего примера
ОР = 0,375/0,059 = 6,4.
Если ОР > 1, то частота развития изучаемого исхода выше в основной группе, чем в контрольной.
При ОР < 1 — частота развития изучаемого исхода ниже в основной группе, чем в контрольной.
Т.е. в рассматриваемом случае риск развития гипертонии выше в 6,4 раз при употреблении алкоголя.
Для расчёта относительного риска с 95% доверительным интервалом — см. онлайн калькулятор.
Достоверность, статистическая значимость (P – уровень)
P-значение (англ. P-value), p-уровень значимости, p-критерий — это мера уверенности в «истинности» результата.
Чем меньше p-критерий, тем выше уверенность в правильности результатов, полученных при анализе выборки.
Во многих медицинских исследованиях p- уровень, равный 0,05 (5%) считается приемлемым.
Критика
Применение p-значений для проверки нулевых гипотез в работах по медицине и естественным наукам подвергается критике со стороны многих специалистов. Отмечается, что их использование нередко приводят к ситуации, когда отвергается правильная нулевая гипотеза, иными словами, исследователи находят связь там, где её нет вовсе.
Нулевая гипотеза — принимаемое по умолчанию предположение о том, что не существует связи между двумя наблюдаемыми событиями.
В частности, журнал Basic and Applied Social Psychology (BASP) в 2015 году вовсе запретил публикацию статей, в которых используются p-значения. Редакторы журнала мотивировали это тем, что сделать исследование, в котором получено p < 0,05 не очень сложно, и такие низкие значения p слишком часто становятся оправданием для низкопробных исследований.
Графическое представление результатов мета-анализа (блобограмма)
Не буду специально изощряться и придумывать картинки и объяснения. Возьму готовые материалы [2], которые многократно можно встретить в интернете, например, здесь. Далее идёт большая цитата из указанного источника.
На рисунке даётся пример результатов мета-анализа, рассматривающего побочные эффекты со стороны печени при интенсивной терапии статинами по сравнению со стандартной схемой назначения у пациентов, перенёсших острый коронарный синдром и пациентов со стабильной стенокардией. В качестве регистрируемого события было принято трёхкратное (и более) повышение активности печёночных трансаминаз.
Результаты, полученные в каждом из исследований показаны на блобограмме в виде квадратов. От каждого квадрата отходит горизонтальная линия, показывающая доверительный интервал (в данном случае он равен 95%) для зафиксированного в этом исследовании исхода.
Вертикальная линия по центру рисунка — линия «отсутствия различий», которая в данном случае соответствует отношению шансов 1,0.
Если горизонтальная линия (доверительный интервал) результатов исследования не пересекает линию «отсутствия различий», то существует 95% вероятность того, что различия между сравниваемыми группами действительно существуют. Если же доверительный интервал результата пересекает вертикальную линию, это означает что:
1) либо нет достоверных различий между изучаемыми вмешательствами;
2) либо размер выборки недостаточен для определения истинного результата;
3) ромб отображает обобщённый результат всех анализируемых исследований. Ширина ромба отображает доверительный интервал для обобщённого результата;
4) поскольку ромб не пересекает линию «отсутствие различий», результат можно считать статистически значимым, т.е. назначение высоких доз статинов достоверно сопровождается повышенным риском развития побочных эффектов со стороны печени по сравнению с умеренными дозами.
Сегодня пользователи сайта особенно интересуются этим:
- >>> Свежие новости
- >>> Таурин. Когда, сколько, какой, кому, побочки. Как…
- >>> Глутатион. Когда, сколько глутатиона, какой, кому,…
- >>> Кремний. Когда, сколько, какой, кому, побочки. Как…
- >>> Цинк. Когда, сколько, какой, кому, побочки. Дефицит. Избыток
ПОДЕЛИСЬ ЭТОЙ ИНФОРМАЦИЕЙ С ДРУГОМ!
Литература
- A’Court C, Stevens R, Heneghan C. Against all odds? Improving the understanding of risk reporting. Br J Gen Pract. 2012;62(596):e220‐e223. doi:10.3399/bjgp12X630223.
- Клиническая фармакология и фармакотерапия в реальной врачебной практике : мастер-класс : учебник / В. И. Петров. — М. : ГЭОТАР-Медиа, 2014.
медицинская статистика, медстатистика
Статистический анализ данных когортного исследования.
Статистический
анализ данных когортного исследования
основан на способах
выявления различий показателей
абсолютного риска в группах сравнения
(опытной и контрольной группе). Результат
абсолютного
сравнения
(разницы показателей) дает величину,
которую называют по-разному, что осложняют
чтение публикаций:
-
атрибутивный
(добавочный, избыточный) риском
(attributable risk-AR); -
разница
рисков
(risk difference-RD); -
в
последнее время в публикациях используют
термин снижение
абсолютного риска (САР) экспериментальных
исследованиях (испытаниях).
Все
эти названия обозначают одно и то же –
на сколько
заболеваемость в группе экспонированных
лиц больше, чем в группе неэкспонированных.
Напомним,
что используемый иногда термин абсолютный
риск в качестве синонима атрибутивного
риска не является корректным.
Результат
относительного сравнения
(отношения показателей) также называется
по-разному:
-
относительный
риск (ОР) –
(relative risk – RR): -
реже
отношение
рисков
(показателей)-
(risk ratio).
Независимо
от названия полученная величина
показывает во
сколько раз зболеваемость в опытной
группе отличается от заболеваемости в
контрольной группе.
Относительный
риск не несет информации, ни о величинах
сравниваемых показателей заболеваемости,
(величинах абсолютного риска), ни,
соответственно, о величине атрибутивного
риска. Даже при высоких значениях
относительного риска, если заболевание
редкое, значения сравниваемых абсолютных
рисков может быть совсем небольшим,
Относительный риск используется для
ориентировочной и наглядной оценки
силы связи между воздействием и
заболеванием.
Для
более полной оценки различий показателей
используют дополнительную величину,
называемую по разному: этиологическая
доля (etiological
fraction
– EF),
атрибутивная
фракция
(доля, пропорция)-(attributable proportion), реже
приписываемая
пропорция. Все термины отражают
удельный
вес (долю)
тех случаев болезни, которые могли бы
быть предотвращены при отсутствии
влияния фактора риска. Другими словами,
это доля тех случаев в группе риска (но
не во всем населении), которые связывают
(приписывают) с непосредственным влиянием
фактора риска. Формулу расчета смотри
далее в описании расчетов по данным
таблицы
«два на два»
Величину EF
в
экспериментальных исследованиях в
русскоязычной литературе
нередко называют снижением
относительного риска (СОР).
Использование
таблицы «два на два»
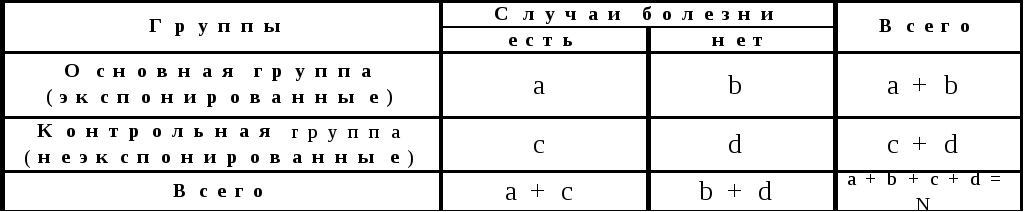
Таблица 3
.Принципиальная форма таблицы «два на
два» для когортных аналитических
исследований.
Такая
таблица заполняется только
абсолютными
величинами, что
позволяет рассчитать следующие
показатели:
1.
а) абсолютный
риск для основной (RF+)
группы:
б)
абсолютный
риск для контрольной (RF–)
группы:
(в этих и
других формулах: 10n – размерность
показателя)
2. Атрибутивный (добавочный) риск (ar), снижение абсолютного риска (сар):
,
или AR
(САР) = RF+
– RF
3.
относительный
риск (RR):
,
или
Значение
относительного
риска
(RR): используется для ориентировочной
оценки причинно-следственной
связи
между фактором риска и возникновением
болезни. При этом:
-
значение
RR равное 1 рассматривается как отсутствие
связи между фактором и болезнью; -
если
величина RR больше 1 считается, что чем
больше RR, тем выше риск заболеть тех
лиц, которые подвергались воздействию
фактора, т.е. изучаемый фактор является
фактором риска; -
если
величина RR меньше 1, значит, риск заболеть
экспонированных лиц ниже, чем у тех на
кого изучаемый фактор не воздействовал
и, следовательно, данный фактор, вероятно,
оказывает благоприятное воздействие
на здоровье.
4.
этиологическую долю (EF)
или снижение относительного риска (СОР)
можно
рассчитать по любой из представленных
формул:
1)
2)
3)
где:
-
абсолютный
риск в %, -
группа
F+ – группа
населения, подверженная влиянию фактора
риска – основная группа; -
группа
F
– группа населения неподверженная
влиянию фактора риска – контрольная
группа; -
EF
(СОР) чаще
всего выражается в процентах .
5.
2
(хи-квадрат),
(критерий Пирсона, критерий согласия,
соответствия), необходимый для
статистической оценки гипотезы
причинно-следственной связи.
Критерий
2
(хи-квадрат), так же как и другие
статистические методы оценки различия
переменных позволяет принять, или
отвергнуть нулевую гипотезу, которая
в данном случае утверждает, что выявленные
различия в частоте заболеваний в
сравниваемых группах определяются
исключительно случайной ошибкой.
Величина критерия 2
позволяет:
-
оценить
достоверность различий заболеваемости
в опытной и контрольной группе; -
высказать гипотезу
о наличие связи между заболеваемостью
и изучаемым фактором.
Формула расчета
2:
,
Эта формула
применяется, если N
больше 40. Однако при этом если одно из
значений (a, b, c или d ) в таблице «два на
два» будет меньше 5, но больше 0, следует
использовать другую формулу (с поправкой
Йетса):
В других случаях
вместо критерия 2
рекомендуется
использовать точный критерий Фишера
Уровень ошибки и,
соответственно, уровень достоверности
различий заболеваемости в сравниваемых
группах, а, следовательно, и уровень
достоверности суждения о наличии
связи между
фактором и заболеваемостью зависит от
значения 2
и определяется
по таблице 2-распределения
(она есть в
любом статистическом справочнике).
Для таблицы
«два на два»:
2
= 3,841 соответствует уровню ошибки –
р=0,05
2
= 6,635 соответствует уровню ошибки – р=0,01
Таким образом,
значение 2
, позволяющее
отвергнуть нулевую гипотезу, должно
быть (для
таблицы «два на два»)
не менее
3,841.