Услышит ли эхо человек, стоящий в комнате на расстоянии (3) м от стены?
- Звук распространяется со скоростью (340~frac{м}{с}).
- Его путь составит (3+3=6~м) до стены и обратно относительно говорящего.
- Рассчитаем, через какое время звук вернётся по формуле равномерного движения волнового фронта:
t=Sυ; вычислим: t=6340≈0,02 с. - (0,02~с<0,06~с), поэтому условия для восприятия эха не будут выполняться.
А еще образованию эхо будут мешать любые находящиеся в комнате предметы, ведь они могут поглощать звук, а также отражать звуковые волны. В помещении с рыхлыми поверхностями – тканью, коврами, шторами, обоями – звук в основном поглощается. Из-за этого речь людей в помещении звучит разборчиво и чётко, так как не возникает эха.
Другое дело – большие пустые помещения, в них стены, пол и потолок находятся далеко друг от друга. В таких помещениях звуковых волны накладываются друг на друга в результате отражения от поверхностей помещения, и образуется гул. Избавиться от нежелательного явления можно, используя специальные материалы, поглощающие звук. Этими материалами облицовывают стены таких помещений.
Что такое эхо
Это – результат восприятие наблюдателем отраженной от препятствий волны.
Когда мы говорим про эхо, то чаще всего подразумеваем акустическое явление. Звуковое эхо – это отражение звука. Мы часто слышим эхо в горах, в лесу, среди зданий – везде, где есть препятствия, от которых звук может отразиться.
Интересный факт – ухо человека не может отличить первоначальный звук от отраженного, если задержка составляет менее одной пятнадцатой доли секунды.
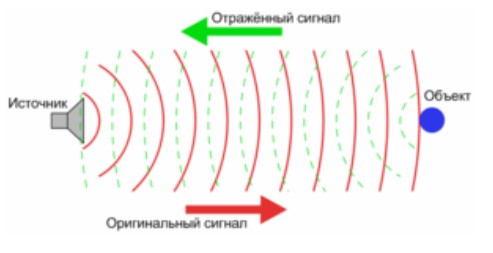
В наиболее общем смысле определения, под волной подразумевается не только акустическая, но также электромагнитная и другие волны.
Существуют разные виды эха:
- однократное эхо – волна отражается один раз и возвращается к наблюдателю;
- многократное эхо – возникает несколько звуковых откликов;
- реверберация – многочисленное эхо в небольшом помещении, сливающееся в сплошной звук.
- мировое эхо – явление в диапазоне радиоволн. Заключается в возвращении радиоволн через время от 1 до 40 и более секунд после начала радиопередачи. Интересно, что точного объяснения явлению мирового эха пока нет.
Применение явления эха
Некоторые животные используют особый вид связи – эхолокацию – для общения между собой и ориентирования на местности.
На принципе отражения волн построена работа многих приборов – сонаров, эхолотов, радаров, громкоговорителей и др.
Первый гидролокатор был изобретен в конце первой мировой войны, но принцип действия таких приборов остается неизменным и в настоящее время.
Рассмотрим работу эхолота. Этот прибор представляет собой гидролокатор и используется для исследования рельефа дна водоемов. Вместо звукового сигнала в эхолоте применяется ультразвук, а для обработки данных применяется ЭВМ.
Эхо также может быть нежелательным явлением. Так, при записи вокала и речи в помещениях устанавливаются специальные звукопоглощающие материалы.
Гидролокатор корабля посылает ультразвуковой сигнал вертикально вниз. Сигнал возвращается через 3 секунды. Какая глубина моря под кораблем?
Решение.
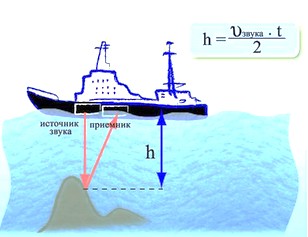
Скорость звука (и ультразвука) в воде составляет 1500 метров в секунду. За три секунды сигнал проходит расстояние до дна и обратно:
S=v·t
Разделим это значение на два и получим глубину:
h=S2=v·t2=1500·32=2250 м
Ответ: 2250 метра
Отражение волн на границе двух сред при нормальном падении
Предположим, что имеются две среды I и II (рис. ), между которыми существует плоская граница раздела, нормальная к оси х и проходящая через начало координат. Удельное акустическое сопротивление первой среды пусть будет R1 = р1с1

а второй — R2 = р2с2. Если из первой среды нормально к границе раздела падает на эту границу плоская волна, то часть энергии проходит во вторую среду также в виде плоской волны, а часть отражается от границы раздела и идет обратно в первую среду. Введем обозначения:
для первой среды:

Эти амплитуды могут быть комплексными, т. е. иметь различные фазы.
Можно написать следующие выражения для скорости частиц и звукового давления.

На границе двух сред (х = 0) значения скорости и давления должны непрерывно переходить из одной среды в другую, т. е. ни скорость, ни давление в любой момент времени не должны испытывать скачка на границе.
Возникновение скачка скорости означало бы также и появление скачка смещения, т. е. разрыв сплошности на границе сред, что следует считать невозможным. Наличие постоянно сохраняющегося скачка давления также физически невозможно, так как давление в двух бесконечно близких слоях двух сред должно мгновенно выравниваться. Скачок давления мог бы существовать, если бы на границе был расположен слой источников звука, а скачок скоростей — если бы на границе был слой диполей. Поскольку предполагать наличие на границе подобных источников нет никаких оснований, мы вправе считать, что давление и скорость частиц меняются при переходе границы непрерывно.
Таким образом, на границе будем иметь:

Между давлением и скоростью частиц существует известное соотношение ![]() причем знак плюс соответствует прямой волне, а знак минус — обратной. Для первой среды впадающей волне
причем знак плюс соответствует прямой волне, а знак минус — обратной. Для первой среды впадающей волне ![]() а в отраженной волне
а в отраженной волне ![]() для второй среды
для второй среды ![]()
Подставляя эти выражения в граничное условие для скоростей и давлений, получим два уравнения:

Из этих уравнений можно определить отношения скоростей:

Для отношения давлений получим:

Если R2 > R1 т.е. если вторая среда акустически более „жесткая», чем первая, то числитель первого соотношения (3, 3) будет отрицательным. Это значит, что скорость частиц при отражении претерпевает изменение фазы на π или отраженная волна имеет обратную фазу по сравнению с падающей волной. Разности фаз между скоростями частиц в падающей и проходящей волне нет независимо от того, будет ли R2 больше или меньше R1 Очевидно также, что в то время как скорость частиц при отражении от более жесткой среды меняет фазу на тс, фаза давления остается неизменной.
Если R2 < R1 т. е. вторая среда акустически более „мягкая», то фаза скорости частиц при отражении остается без изменения, в то время как давление меняет свою фазу на тс. Наконец, при R2 = R1 отраженной волны не появляется, и распространение во вторую среду происходит беспрепятственно. В этом случае, очевидно,
![]()
где отношение с1 / с2 — есть показатель преломления. В случае падения под косым углом при переходе из одной среды в другую, при соблюдении условия R2 = R1 (но р2 ≠ р1 ) будет происходить частичное отражение.
Коэффициентом проникновения энергии из одной среды в другую следует назвать отношение интенсивности проходящей волны к интенсивности падающей волны:

Так как формула (3, 5) симметрична относительно R1 и R2, то коэффициент проникновения энергии будет одинаков независимо от того, идет ли волна из первой среды во вторую или из второй в первую. Например, при переходе из воды в воздух (или наоборот) т = 0,0011, т. е. 0,9989 всей падающей энергии отражается обратно от границы. Для воды и стали т = 0,013. Для воды и некоторых сортов дерева т ≈ 1, т. е. почти весь звук проникает из воды в дерево.
При отражении на границе двух слоев воздуха с разностью температур ∆θ легко найти, что ![]() . Если
. Если ![]() — происходит почти полное проникновение и отражается лишь
— происходит почти полное проникновение и отражается лишь ![]() звуковой энергии. Легко также найти отражение на границе сухого и насыщенного паром воздуха (при той же температуре), для которого плотность примерно на 1/220 меньше, а скорость звука на 1/440 больше. Отраженная звуковая энергия составит
звуковой энергии. Легко также найти отражение на границе сухого и насыщенного паром воздуха (при той же температуре), для которого плотность примерно на 1/220 меньше, а скорость звука на 1/440 больше. Отраженная звуковая энергия составит ![]() от падающей.
от падающей.
Обратим внимание, что даже при очень малом т, например, при переходе из воздуха в воду, звуковое давление в воде на основании уравнения (3,4) будет практически в два раза больше, чем в падающей из воздуха волне. Полное давление в воздухе и в воде на границе почти точно равно удвоенному давлению в падающей волне. Если в воздухе и в воде применяется один и тот же приемник давления (например, гидрофон), то в воде звук, приходящий из воздуха, будет воспринят как столь же сильный, несмотря на то что в воду проникает ничтожная часть звуковой энергии. При использовании приемника скорости, согласно соотношению (3,3), получим во второй среде очень малые величины.
Пусть отражение происходит от абсолютно твердой поверхности R2 = ∞. В отраженной волне фаза скорости противоположна фазе скорости для падающей волны, а амплитуда ее равна амплитуде падающей волны, поэтому сумма скоростей на границе равна нулю:
![]()
Так как фаза давления не меняется, то на границе давление удваивается:
![]()
Таким образом, на твердой стенке при отражении будет узел стоячей волны и удвоенная амплитуда звукового давления. Этот случай имеет место практически только в том случае, если реализованы условия образования плоской отраженной волны, а именно, когда размеры плоской отражающей поверхности значительно больше длины волны, и дифракционные явления на краях не меняют существенно общую картину отражения. Если, наоборот, длина волны сильно превышает размеры отражающей поверхности, то благодаря дифракции звук огибает ее, плоская отраженная волна не возникает и связанного с ней увеличения давления на границе не происходит. По этой причине микрофон с жесткой диафрагмой (конденсаторный) при очень высоких частотах, когда диаметр диафрагмы микрофона гораздо больше длины волны, показывает в два раза большее давление, чем в бегущей волне; наоборот, при достаточно низких частотах он покажет истинное звуковое давление. Такого рода поправки необходимо делать при акустических измерениях.
Отражение от абсолютно твердой плоской поверхности при наклонном падении звука.
Пусть волна, падающая слева (рис) на абсолютно твердую поверхность под углом θ, за некоторый промежуток времени распространяется на отрезок АО = S.

Длину отрезка можно выразить через координаты х,у точки А:
![]()
Величина S играет теперь в уравнении волны роль фазового пути, которую раньше, например в формуле (3,1), играла координата х, причем за положительное направление S принято направление распространения волны. Для падающей волны потенциал скоростей будет:
![]()
Аналогично для отраженной волны отрезок ОА’ по ходу волны равен S’ = — х соs θ’ —у sin θ’, где θ’ — угол отражения, и потенциал скорости будет равен:
![]()
Сумма Ф1 и Ф’1 двух решений (3,7) и (3,8) должна удовлетворять линейному дифференциальному уравнению волны, что следует из принципа суперпозиции. На границе (при х = 0) должно быть соблюдено при любых у равенство нулю нормальной компоненты скорости:
![]()
Этому условию мы удовлетворим, приняв
![]()
Следовательно, амплитуда отраженной волны равна амплитуде падающей и угол отражения равен углу падения. Итак, для потенциала скоростей получим:

В этом выражении множитель ![]() характеризует волну, бегущую вдоль оси у в отрицательном направлении (т. е. вниз — на рис). Скорость этого следа волны найдем из соотношения с’= w / (k sinθ), так как волновое число в данном случае равно k sinθ. Следовательно,
характеризует волну, бегущую вдоль оси у в отрицательном направлении (т. е. вниз — на рис). Скорость этого следа волны найдем из соотношения с’= w / (k sinθ), так как волновое число в данном случае равно k sinθ. Следовательно,
![]()
Из формулы ясно, что фазовая скорость следа волны больше, чем скорость звука с. Множитель соs (kxсоsθ) в уравнении (3,9), зависящий только от х, показывает, что амплитуда волны испытывает периодические изменения по направлению оси х. Таким образом, волна, бегущая вдоль оси у, «модулирована» в пространстве по закону соs (kx соsθ). В плоскостях, перпендикулярных оси х, амплитуда имеет везде одинаковое значение. Плоскость максимальных амплитуд мы получим, полагая кxсоsθ = nπ. Расстояние между плоскостями максимальной амплитуды будет больше полуволны. Таким образом, параллельно отражающей поверхности образуются интерференционные полосы
будет больше полуволны. Таким образом, параллельно отражающей поверхности образуются интерференционные полосы
с расстояниями между пучностями и узлами, равными  (рис.). Эти волны можно назвать „псевдостоячими». Параллельно отражающей поверхности, как уже сказано, бежит волна со скоростью
(рис.). Эти волны можно назвать „псевдостоячими». Параллельно отражающей поверхности, как уже сказано, бежит волна со скоростью
равной формуле 3.10, модулированная по фронту. Поток энергии в этой волне направлен параллельно оси у, т. е. вдоль границы. Если θ = 0 (нормальное падение), то из уравнения (3.9) получим:
![]()
В этом случае волна вдоль поверхности исчезает, и мы имеем процесс обычных стоячих волн с узловыми плоскостями, отстоящими на λ / 2 друг от друга. Стоячая волна характеризуется выражением, в котором переменные х и t входят раздельно в двух множителях. Важно отметить, что при θ = 0 скорость следа волны (3,10) равна бесконечности, поток же энергии вдоль стенки равен при этом нулю.

Совершенно такой же процесс, как при отражении под углом, мы получим при наложении двух плоских волн одинаковой амплитуды, идущих под углом друг к другу. Пусть волны идут в направлениях АА’ и ВВ’ лежащих под углом 180° — 2θ (првый рис. ). Перпендикулярно оси у везде скорость частиц будет равна нулю, так как ввиду симметрии ^-компоненты скорости в двух составляющих волнах будут равны и противоположны друг другу. Аналогичная картина волн, соответствующая отражению от стенки с другой стороны, будет иметь место и в правом полупространстве х’ > 0. Картина отражения плоской волны АО от абсолютно твердой поверхности может быть, таким образом, формально представлена как наложение на прямую волну АА’ ее „зеркального» отражения в плоскости Y = 0, т. е. волны ВВ’.
Пусть границей раздела двух сред является плоскость Х = 0 (на ниж. рис.) и на эту границу раздела падает под углом θ1 плоская волна.

В первой среде возникает плоская, отраженная под углом θ1 волна; во второй среде возникает преломленная под углом θ2 волна. Удельное акустическое сопротивление первой среды обозначим через R1=p1c1, второй — R2=p2c2. Напишем отдельно волновые уравнения для каждой среды:

Давления и нормальные компоненты скорости на границе раздела с обеих сторон должны быть одинаковы. Поэтому граничные условия могут быть записаны так:

Потенциалы скоростей в I и II средах можно представить в виде:

Легко показать, что b1 = b2 = b. Действительно, скорости движения следа волны вдоль оси у в I и II средах, равные соответственно w / b1 и w / b2, должны быть равны. В самом деле,
если вдоль границы с левой стороны движется максимум или минимум давления, то в силу непрерывности давления с правой стороны, параллельно ему, также должен двигаться максимум или минимум давления, равный по величине и с той же скоростью. Таким образом,

Мы получили закон Снеллиуса, который соблюдается не только для звука, но и для любых волновых процессов. Подставляя в граничные условия (3, 13) выражения (3, 14), получим:

Из этой системы уравнений можно определить отношения амплитуд:

Из этих формул при одинаковых плотностях двух сред (р1 = р2) после некоторых преобразований найдем:

Формулы (3,18) и (3,19) совпадают с формулами Френеля для коэффициента отражения света, поляризованного соответственно параллельно или перпендикулярно плоскости падения .
Подставляя а1 и а2 в уравнение (3,17) и используя закон преломления, получим:

Коэффициент отражения и коэффициент проникновения волны давления найдем, учитывая, что р = jwpФ:

Принимая во внимание, что на основании (3,14) амплитуды потенциалов скоростей связаны с соответствующими амплитудами Q скорости частиц соотношениями ![]() определим коэффициент отражения rq и коэффициент проникновения tq волны скорости частиц:
определим коэффициент отражения rq и коэффициент проникновения tq волны скорости частиц:
![]()
Из формулы (3,17) следует, что отраженной волны не будет при условии:
![]()
Учитывая закон преломления, получим:

Если ![]() то ctg θ1 будет положителен и может быть найден некоторый угол θ1 в пределах от 0 до 90°, при котором отсутствует отражение звука на границе двух сред. Например, для этилового спирта р1 = 0,79; и
то ctg θ1 будет положителен и может быть найден некоторый угол θ1 в пределах от 0 до 90°, при котором отсутствует отражение звука на границе двух сред. Например, для этилового спирта р1 = 0,79; и ![]() и для хлороформа р2 = 1,49 и
и для хлороформа р2 = 1,49 и ![]() Для этих сред из уравнения (3,21) следует, что
Для этих сред из уравнения (3,21) следует, что
![]()
Если скорость звука во второй среде гораздо меньше, чем в первой (с1 < с2) то sinθ2 ≈ 0 и θ2 ≈ 0. Таким образом, вторая среда может пропускать волны только в направлении нормали к границе раздела. Таким свойством обладает, например, модель, состоящая из тонких капилляров, перпендикулярных к границе раздела (модель Рэлея). При этих условиях
![]()
Вообще говоря, в этих случаях удельное сопротивление второй среды может быть комплексным и характеризоваться некоторым нормальным импедансом Z2 (таким свойством обладают, например, многие пористые звукопоглощающие материалы применяемые в архитектурной акустике). Если среду, на которую падает звук, можно характеризовать нормальным импедансом Z2 то коэффициент отражения

Полное внутреннее отражение звука на плоской границе двух сред.
Из закона преломления (3,16) следует, что sinθ2 = ( c2 / c1 ) sinθ2 если с1 > с2 и sinθ1 > ( c1 / c2 ), то sinθ2 > 1 и ![]() будет мнимым. Величина а2 = k2 cosθ2 будет также мнимой и ее можно представить в виде:
будет мнимым. Величина а2 = k2 cosθ2 будет также мнимой и ее можно представить в виде:
![]()
Нетрудно показать, что угол преломления в данном случае является чисто мнимой величиной jθ’2, определяемой из соотношения ![]() Относительная амплитуда отраженной волны получается на уравнения (3,17):
Относительная амплитуда отраженной волны получается на уравнения (3,17):

Так как числитель и знаменатель — сопряженные комплекс-
ные величины, то модуль А’1 / А1 равен единице, т. е. амплитуда
отраженной волны равна амплитуде падающей (|rp| = 1) и происходит полное внутреннее отражение волны. Множитель ![]() указывает, что отраженная волна сдвинута по фазе на угол 2ε по отношению к падающей.
указывает, что отраженная волна сдвинута по фазе на угол 2ε по отношению к падающей.
Во второй среде

Суммарная волна в первой среде, согласно уравнению (3,14), имеет вид:
![]()
Для волны во второй среде

Мы должны взять только отрицательный знак показателей при ах, так как при положительном знаке мы имели бы во второй среде безграничное нарастание амплитуды, что не имеет физического смысла.
Уравнение (3.23) представляет волну, бегущую вдоль отрицательной оси у, т. е. вдоль границы раздела, причем амплитуда ее убывает вдоль волновых фронтов по мере удаления от границы по закону ![]() . Такие волны можно назвать волнами, модулированными вдоль фронта.
. Такие волны можно назвать волнами, модулированными вдоль фронта.
Скорость убывания амплитуды волны определяется величиной а, которую мы найдем, учитывая связь между а1 и а2 вытекающую из волновых уравнений (3,11) и (3,12). Подставляя в них величины Ф1 и Ф2 из равенств (3,14), получим:
![]()
Так как b1 = b2 = b, то из этих соотношений следует, что
![]()
Подставляя значения а1 и b из соотношения (3,15), найдем:

Отсюда видно, что при sin θ > (c1 / c2) получим для а2 мнимое значение, модуль которого

При критическом угле, т. е. при sin θ = (c1 / c2), а=0. Следовательно, амплитуда вдоль фронта волны (во второй среде) затухать не будет, а возникает плоская волна, бегущая параллельно границе. Если же sin θ > (c1 / c2) т. е. θ1 больше критического угла полного внутреннего отражения, то a > 0 и амплитуда вдоль фронта волны будет быстро уменьшаться.
При θ1 = π/2 получается наибольшее значение а:
![]()
Когда аrcsin ( c1/c2 ) < θ1 < π/2, то величины а будут лежать в пределах от 0 до аmax.
Для случая падения звука из воздуха в воду

На длине λ / 2π волна во II среде ослабнет уже в е раз. На рис. представлен снимок ультразвуковых волн на границе раздела

вазелинового масла (сверху) и насыщенного раствора NаСl (снизу). Граница раздела точно соответствует нижнему краю темной горизонтальной полосы (полоса мениска). Во второй среде, поскольку θ1 > 55° (критический угол), ясно видны фронты волн, идущих параллельно границе раздела и постепенно ослабевающих по мере углубления во вторую среду.
Из уравнения (3,23) получим для звукового давления
![]()
и для компонент скоростей частиц по осям х и у

Таким образом, скорости частиц по осям х и у не совпадают по фазе: одна из них опережает другую на 90°. Это значит, что суммарное движение частиц во II среде происходит по эллипсам, лежащим в плоскости падения звукового луча (плоскость ху).
Прохождение звука через плоский слой
При косом падении звука (под углом θ1 из среды I (рис.) с постоянными р1 и c1 на слой жидкости или газа с постоянными р2 и с2 (среда II) и толщиной d, за которым лежит снова бесконечная среда I, отраженные волны возникают как на первой, так и на второй границе; проходящая волна будет только одна — прямая.

В соответствии с этим намечается следующая схема решения задачи. Потенциал скоростей в первой среде (слева от слоя) выразится суммой двух членов (см. первое уравнение (3,14)), а во второй среде — аналогичной формулой, в которую вместо a1 и b1, войдут величины а2 = k2 соs θ2 и b2 = k2 соs θ2. На первой границе (х = 0) и на второй (х =d) должны выполняться условия непрерывности звукового давления и скорости частиц, которые дают 4 уравнения для определения относительных потенциалов скоростей отраженной волны A’ / A, проходящей через слой A2 / A1, и двух (прямой и отраженной) волн во второй среде. Решая эти уравнения, можно найти коэффициент отражения (rp) и проникновения (tp) волны давления (через слой):

При δ=1, что соответствует условию (3,20), мы получим при некотором угле падения полное проникновение волн через слой без всякого отражения. Кроме того, полное проникновение будет наблюдаться при соблюдении условия сtga2d=∞, из которого следует:

Для очень тонкого слоя (или для длинных волн) при а2d <1 и не слишком больших или малых величинах δ получим:
![]()
Таким образом, при заданном угле падения, а следовательно, при заданных θ2 и b отражение от тонкого слоя прямо пропорционально частоте. Анализ выражения (3,24) показывает, что при углах падения θ1 больших критического (а2 мнимое), уже не происходит полное внутреннее отражение на слое, как это имеет место на границе полупространства. Волны во второй среде, бегущие параллельно передней границе слоя, на задней границе будут иметь известную амплитуду, величина которой при достаточно малых толщинах слоя d или при углах падения, близких к критическому, может быть достаточно велика. Таким образом, вдоль второй (задней) границы будут двигаться волны сжатия и разрежения, что неизбежно вызовет возмущения в среде за слоем и приведет к возникновению проходящей волны во второй среде. Нетрудно показать, что в очень тонком слое почти вся энергия будет проходить через него даже при углах, больших критического. При углах падения, близких к 90°, волны во второй среде очень сильно ослабевают уже при проникновении на глубину одной волны. Отсюда ясно, что при скользящем падении на слой, толщина которого больше λ, получится очень малое проникновение звука через слой, т. е. почти полное отражение.
При падении под углом 0° формулы (3,24) и (3,25) примут вид:

При очень тонком слое или при очень низких частотах (к2d<1) и большом акустическом сопротивлении второй среды (R2 > R1)

где М2 = р2d —масса слоя на 1 см². Отношение энергии падающей волны к энергии волны прошедшей (коэффициент звукоизоляции слоя) будет приближенно равно:
![]()
Можно представить себе следующую электроакустическую аналогию для данного случая. Напряжение А1 включается в цепь, содержащую последовательное соединение индуктивного сопротивления wM2 и активного сопротивления 2R1 . Сила тока (скорость) в цепи будет равна ![]() а падение напряжения на сопротивлении 2R1 будет
а падение напряжения на сопротивлении 2R1 будет ![]() Отношение полной мощности цепи к мощности, расходуемой на сопротивлении 2R1 (коэффициент звукоизоляции), равно (A1 / A2)² , что приводит к формуле (3,27).
Отношение полной мощности цепи к мощности, расходуемой на сопротивлении 2R1 (коэффициент звукоизоляции), равно (A1 / A2)² , что приводит к формуле (3,27).
При нормальном падении мы вправе применить формулы (3, 26) и (3,27) к твердой стенке, например к некоторой монолитной перегородке. При прохождении звука через перегородки, находящиеся в воздухе, всегда ![]() и потому
и потому

Для воздуха р1c1 = 41 и η≈1/170 M2²f². Звукоизоляция перегородки в децибелах будет равна:
![]()
Эта формула подобна известному в архитектурной акустике „весовому закону» звукоизоляции. Для тонкой кирпичной стены (d=10см) с весом 200 кг/м² (или 20 г/см²) при 1024 гц получится звукоизоляция 64 дб. Полученная из опыта звукоизоляция равна 58 дб, т. е. -меньше в 4 раза. Следует учесть, что указанный опыт соответствует условиям не нормального, а диффузного (по всем возможным направлениям) падения. Расхождение объясняется еще и тем, что перегородка, закрепленная по некоторому контуру, ведет себя как диафрагма, способная изгибаться. Такая диафрагма передает звук также посредством изгибных колебаний, помимо волн сжатий и разрежений, которые учитываются формулами (3, 26) и (3, 27). Особенно сильно это сказывается на низких частотах.
Интересен случай прохождения звука из жидкости через слой твердого тела снова в жидкость. Рассмотрим нормальное падение звука из воды на железную пластину толщиной d= 1 cм и переход его снова в воду. В этом случае

Для частот, меньших 2000 гц, первый член будет значительно меньше единицы η ≈ 1, т. е. звукоизоляция практически отсутствует; вся энергия проходит через железную пластину. При частоте
f ≈ 6000 гц, η ≈ 2, а при частоте f ≈ 125 000 гц (k2d= π /2) звукоизоляция достигает максимального значения, равного η ≈179 (22,5 дб). При f ≈ 250000 гц (k2d = π, d = λ2 / 2) звукоизоляция снова равна единице. Вообще максимумы η будут получаться при f ≈ 125000 • (2n + 1 ) гц, а минимумы, равные единице, при f ≈ 125000 • (2n)гц (рис.).
Для слоя с акустическим сопротивлением R2, значительно меньшим, чем R1, например воздуха или губчатой резины (R2 ≈ 40), между двумя слоями жидкости или твердого тела, из формулы (3, 26) получим коэффициент звукоизоляции:

Для воздушной прослойки в воде R1 / 2R2 = 1,83 * 10³. При очень
низких частотах или очень тонких слоях, когда k2d < (2R2 / R1) , первый член будет мал по сравнению со вторым, близким к единице и η≈1. С увеличением частоты η резко возрастает и при условии k2d = π / 2 , достигнет величины (1,83-10³)² (около 65 дб), затем начнет уменьшаться и при k2d = π , (d = λ2 / 2) будет равен единице. Ход изменения η аналогичен изображенному на рис. . При низких частотах, когда k2d < 1 коэффициент звукоизоляции можно представить в виде:

Электроакустическая аналогия в этом случае формально выразится параллельным соединением упругого сопротивления ![]() v=sd — объем слоя, соответствующий площади S)
v=sd — объем слоя, соответствующий площади S)

и активного сопротивления ![]() где R1— акустическое сопротивление среды за промежуточным слоем). Отношение токов (скоростей) в этих ветвяхбудет равно
где R1— акустическое сопротивление среды за промежуточным слоем). Отношение токов (скоростей) в этих ветвяхбудет равно ![]() Абсолютная вели-чина отношения полного тока |q1|, протекающего через параллельное соединение R2 / 2 и zv к току будет равна
Абсолютная вели-чина отношения полного тока |q1|, протекающего через параллельное соединение R2 / 2 и zv к току будет равна

Величина скорости |qv + q2| определяется давлением на входе, которое пропорционально амплитуде потенциала скоростей (А1) в падающей волне, а величина |q2| пропорциональна амплитуде (A2) волны, проходящей за слой. Коэффициент звукоизоляции, равный (A1 / A2)² , определится тогда из выражения (3,28).
При Zv < (Rs / 2) движение замыкается почти целиком на упругую
прослойку и η становится велико; при Zv > (Rs / 2) (что может быть при очень тонкой прослойке или при соблюдении условия k2d = πn) сопротивление Rs / 2 „шунтируется» большим сопротивлением и скорость q2 становится почти равной скорости q1 что приводит к отсутствию звукоизоляции слоя η ≈ 1).
Отметим, что в данном случае электрическая аналогия выражается „параллельным» соединением сопротивлений слоя и среды, хотя геометрически они стоят последовательно друг с другом; для слоя, имеющего R2 > R1 мы имели аналогию в форме последовательного соединения.
Прохождение звука через слой (среда II) между двумя различными средами (I и III)
Вывод формул для этого случая проводится по ранее изложенному методу. Для нормального падения звука (θ1 = 0) коэффициент звукоизоляции

где R1 = р1c1, R2 = p2c2 и R3 = p3c3 — акустические сопротивления сред I, II и III. Эта формула может быть применена и для твердых тел. Когда k2d<1 и λ2 > d, а также k2d≈πn, т. е. sin k2d≈0, получим:

Это соотношение совпадает с равенством (3,5) для случая прохождения через границу двух сред. Таким образом, для очень тонких слоев или очень низких частот, а также при условии ![]() звукоизоляция не зависит от свойств промежуточного слоя. Если sin k2d≠0, то присутствие промежуточного слоя увеличивает звукоизоляцию, когда R2 лежит по величине между R1 и R3, если этого нет, то наличие слоя уменьшает звукоизоляцию. Если sink2d = 1, т.е.
звукоизоляция не зависит от свойств промежуточного слоя. Если sin k2d≠0, то присутствие промежуточного слоя увеличивает звукоизоляцию, когда R2 лежит по величине между R1 и R3, если этого нет, то наличие слоя уменьшает звукоизоляцию. Если sink2d = 1, т.е.

Из формулы (3,29) видно, что если R2 лежит между R1 и R3, то соотношение (3,30) выражает минимум звукоизоляции; если ![]() то η= 1, т. е. звукоизоляции нет.
то η= 1, т. е. звукоизоляции нет.
Условие d=(n + 0.5)(λ/2) для минимума звукоизоляции, т. е. для наибольшей звукопрозрачности, аналогично условию, применяемому в оптике для расчета „просветляющих» слоев. Для иллюстрации применения „просветляющиха слоев в акустике рассмотрим случай прохождения звука из воды в воздух, при котором просветляющий слой должен иметь![]() Вещества, обладающие таким акустическим сопротивлением, найти невозможно. Однако можно искусственно создать такой материал, используя резину с воздушными пузырьками. Нетрудно видеть, что если из общего объема (V1 + V2) часть V2 заполнена воздухом, а часть V1 относится к резине, то модуль объемной упругости такого сложного материала
Вещества, обладающие таким акустическим сопротивлением, найти невозможно. Однако можно искусственно создать такой материал, используя резину с воздушными пузырьками. Нетрудно видеть, что если из общего объема (V1 + V2) часть V2 заполнена воздухом, а часть V1 относится к резине, то модуль объемной упругости такого сложного материала

где х’ и х»— модули объемной упругости ..соответственно резины и воздуха (для резины модуль примерно такой же, как и для воды, т. е. ![]() для воздуха при звуковых колебаниях
для воздуха при звуковых колебаниях ![]() ).
).
Плотность сложного материала будет достаточно точно равна ![]() где р’ ≈ 1,1—плотность резины. Для квадрата акустического сопротивления слоя получим:
где р’ ≈ 1,1—плотность резины. Для квадрата акустического сопротивления слоя получим:

Приравнивая эту величину значению ![]() получим V1 / V2 ≈ 1 / 2.55 что соответствует 27% содержания пузырьков воздуха в общем объеме.
получим V1 / V2 ≈ 1 / 2.55 что соответствует 27% содержания пузырьков воздуха в общем объеме.
На прошлом уроке мы с вами затрагивали вопрос о распространении звуковых волн. Давайте вспомним, что звуковые волны — это упругие продольные волны, которые, воздействуя на слуховой аппарат человека, вызывают слуховые ощущения. Для распространения звуковых волн необходимо наличие среды. То есть в вакууме звуковые волны распространяться не могут.
— А что произойдёт, если на пути звуковой волны появится препятствие?
Чтобы ответить на этот вопрос, давайте рассмотрим ситуацию, когда на пути звуковой волны встаёт плоская твёрдая поверхность, например, стена. Так как звуковая волна является продольной волной сжатия и разрежения, то, передаваясь от одного слоя молекул воздуха к другому, сгущение дойдёт до воздушного слоя, прилегающего к поверхности стены. Получив толчок, частицы этого слоя ударятся о стену, оттолкнутся от неё и образуют новую волну сгущения, бегущую в обратном направлении. Этот процесс называют отражением звука.

В большинстве случаев плоские твёрдые поверхности отражают около девяносто пяти процентов звука. Однако какой бы жёсткой ни была стена, стоящая на пути звуковой волны, всё равно часть звука проникает внутрь. Чем массивнее стена, тем меньше она пропускает звук. И наоборот, чем стена тоньше, легче и мягче, тем слабее отражается от неё звук.

Ослабление звуковой волны называют поглощением звука.
Чтобы показать, что звук действительно отражается от преград, проведём такой опыт. Возьмём в качестве источника звука громкоговоритель. Приёмником звука нам будет служить микрофон, соединённый с осциллографом — прибором, позволяющим регистрировать звук. Поставим громкоговоритель и микрофон на расстоянии метра под некоторым углом друг к другу. Включим источник звука — прибор звук не регистрирует.
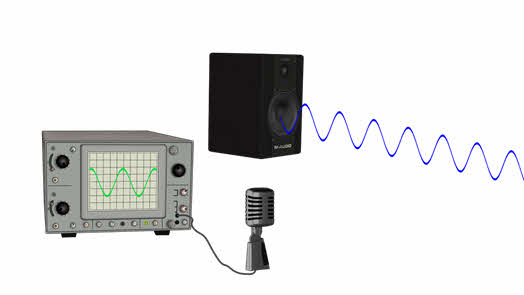
А теперь на пути звуковой волны поставим экран. При некотором его положении прибор покажет, что звук попадает в микрофон.
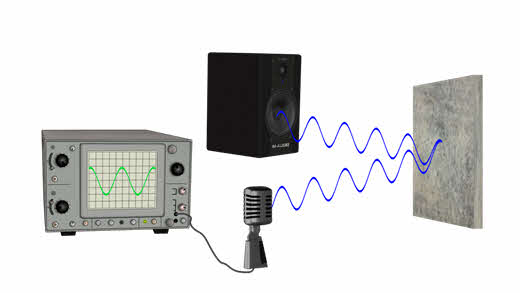
Если провести линии, указывающие направление распространения звука от источника к экрану и от экрана к приёмнику, а также восставить перпендикуляр в точку падения звуковой волны, то не трудно заметить, что угол падения равен углу отражения.
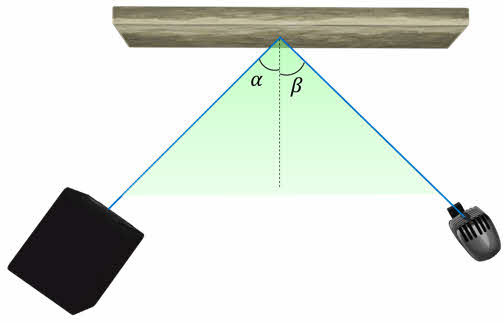
Поскольку при взаимодействии звуковой волны со стеной волна отражается, то возникает закономерный вопрос: можем ли мы услышать эту отражённую звуковую волну?
Оказывается, можем, но только в том случае, когда между первоначальным и отражённым звуками проходит не менее 1/15 секунды. Это звуковое явление хорошо знакомо всем, и его называют эхом.
Эхо можно услышать в горах, в больших пустых помещениях и так далее. Однако в обычных жилых помещениях мы эхо не слышим. Давайте посмотрим почему. Итак, предположим, что мы находимся в обычной комнате на расстоянии 3 метров от стены. Звук нашего голоса должен пройти расстояние от нас до стены и обратно, то есть шесть метров. Если принять, что скорость звука равна 340 м/с, то время, которое затратит звуковая волна на преодоление этого расстояния, составит порядка 0,2 секунды. Как видим, интервал между двумя воспринимаемыми звуками значительно меньше того, который необходим, чтобы услышать эхо.

Но то, что мы не слышим эха в обычной комнате, не означает, что мы не слышим отражение звука от её стен. Дело в том, что в закрытых помещениях, кроме звука, создаваемого источником, мы слышим и его многократные отражения. Однако из-за очень малого значения интервала времени между этими отражениями мы не можем их различить как отдельные звуки, а воспринимаем это как увеличение длительности первоначального звука.
Эффект увеличения длительности звука из-за его отражения от различных препятствий называют реверберацией.
Например, в одном из лучших в акустическом плане зале — Колонном зале Дома Союзов в Москве — время реверберации составляет около 1,75 секунды, когда он наполнен публикой, и около 4 секунд в пустом.
Если отражающих поверхностей много, и они находятся на разных расстояниях, то отражённые звуковые волны дойдут до ушей в разное время. В этом случае эхо будет многократным.
Именно многократным эхом и объясняются раскаты грома во время грозы.
На свойствах звука отражаться от гладких поверхностей основано действие рупора, изобретённого в 1670 году Сэмюелем Морландом. Рупор представляет собой расширяющуюся трубу, чаще круглого или прямоугольного сечения. При его использовании, звук распространяется не по всем направлениям, а образует узконаправленный пучок. За счёт этого его мощность усиливается, и он способен преодолеть большее расстояние.

Некоторые представители животного мира способны ориентироваться в пространстве издавая направленные ультразвуковые колебаний и воспринимать их после отражения от препятствий. Это, например, летучие мыши, дельфины, птицы гуахаро, гнездящиеся в глубоких пещерах Венесуэлы, и стрижи-саланганы, живущие в пещерах Юго-Восточной Азии.
Мы уже упоминали, что способ определения местоположения тел по отражённым от них ультразвуковым сигналам называется эхолокацией. Она широко используется в мореплавании для определения косяков рыбы, глубины дна водоёма и его рельефа. Для этих целей на днище судна помещается излучатель и приёмник звука. Излучатель посылает короткие ультразвуковые сигналы. А компьютер, анализируя время задержки и направление отражённых сигналов, распознаёт размер объекта и определяет его положение.
Теперь поговорим ещё об одном интересном звуковом явлении — об акустическом резонансе. Вы уже знаете, что резонанс возникает тогда, когда частота вынуждающей силы совпадает с собственной частотой колебательной системы. В этом случае происходит увеличение до наибольшего значения амплитуды установившихся вынужденных колебаний.
Например, если рукой дёргать шнур в такт его собственным колебаниям, то со временем можно заметить увеличение амплитуды колебаний.
Резонанс может быть вызван и звуковыми колебаниями. Например, если влажный палец двигать по краю бокала, то бокал будет издавать звенящие звуки. Хотя это и незаметно, палец движется прерывисто и передаёт стеклу энергию короткими порциями, заставляя бокал вибрировать.
Стенки бокала также начинают вибрировать, если на него направить звуковую волну с частотой, равной его собственной. Если амплитуда станет очень большой, то бокал может даже разбиться.

Проведём ещё один опыт. Возьмём два камертона с одинаковой собственной частотой колебаний и поставим их так, чтобы отверстия ящиков, на которых они укреплены, смотрели друг на друга. Ударим молоточком по одному из камертонов. Он зазвучит. Затем приглушим его, прикоснувшись к нему рукой. Мы услышим звучание другого камертона. Это происходит из-за того, что второй камертон начинает совершать колебания под действием звука, созданного колебаниями первого камертона. Так как частоты собственных колебаний камертонов одинаковы, то возникает резонанс: амплитуда колебаний второго камертона становится достаточно большой, чтобы звучание было слышно.
Если изменить собственную частоту колебаний второго камертона, например, надев на него резиновое колечко, то он не будет отзываться на колебания звучащего камертона, и явления резонанса не произойдёт.
А теперь давайте посмотрим, какую роль играют ящики, на которых устанавливают камертоны. Для этого проделаем такой опыт. Укрепим в лапке штатива камертон, а под ним поставим сосуд с водой.
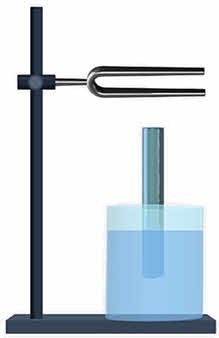
Поместим в воду широкую стеклянную трубку и заставим вибрировать над её отверстием камертон. Вынимая постепенно трубку из воды, мы будем увеличивать столбик воздуха в ней. При определённой длине столба воздуха мы отчётливо услышим звук. Если же продолжать вынимать трубку, то звук станет ослабевать, пока совсем не перестанет быть слышимым. В этом случае на колебания камертона отзывается воздушный столб в сосуде. Очевидно, что наиболее громкое звучание воздушного столба наступает, когда собственная частота его колебаний совпадает с частотой колебаний камертона. Это и есть условие резонанса. Такой закрытый с одного конца сосуд называют резонатором.
Для камертона резонатором служит деревянный ящик, открытый с одного конца. В музыкальных инструментах — это деки, которые усиливают издаваемые струнами звуки и придают звучанию инструмента характерный тембр.

У человека также имеются резонаторы — это гортань и полость рта, усиливающие издаваемые им звуки. Существует выражение: «От громкого голоса дрожали стёкла». Здесь имеется ввиду возникновение акустического резонанса. Известен исторический факт, когда по причине резонанса при пении Фёдора Ивановича Шаляпина дрожали (то есть резонировали) даже хрустальные подвески люстр.
На расстоянии 400 мот наблюдателя рабочие вбивают сваи с помощью копра. Каково время между видимым ударом молота о сваю и звуком удара, услышанным наблюдателем? Скорость звука в воздухе 340 м/с.
Ультразвуковой эхолот улавливает отраженный от дна моря сигнал через время t после его испускания. Если скорость ультразвука в воде равна v, то глубина моря равна
Звуковой сигнал, отразившись от препятствия, вернулся обратно к источнику через 5 с после его испускания. Каково расстояние от источника до препятствия, если скорость звука в воздухе 340 м/с?
1700 м
850 м
425 м
3400 м
Сигнал гидролокатора подводной лодки, отразившись от цели, отстоящей от нее на 3 км, зарегистрирован через 4 с после его отдачи. Частота колебаний в волне от гидролокатора 10 кГц. Определите длину звуковой волны в воде.
15 см
3,75 см
7,5 см
30 см
На каком расстоянии от корабля находится айсберг, если посланный гидролокатором ультразвуковой сигнал был принят обратно через 3 с? Скорость ультразвука в воде принять равной 1500 м/с.
2250 м
1000 с
4500 м
500 м
Отражение и преломление звука на границе двух сред.
Звуковые
волны имеют длины волн порядка от
нескольких сантиметров до десятков
метров. Волна с частотой 20 гц
имеет в воздухе
длину примерно 16 ж, с частотой 10 000 гц
— 3,3 см,
поэтому отражение по
законам, полученным нами для отражения
волн ранее, возможно лишь при достаточно
больших размерах предметов, на которые
падают звуковые волны. В противном
случае происходит так называемое явление
дифракции, волны
огибают препятствия и заходят в область
геометрической тени.
Отражение
от больших препятствий (для частот
порядка 5—10 кг от
предметов с площадью поверхности 0,5—1
![]() )
)
происходит с соблюдением
равенства углов падения и отражения.
При
падении на границу раздела двух сред,
скорости распространения звука в
которых различаются, часть звуковой
энергии отражается, а часть проходит
во вторую среду (рис.3), при этом лучи
падающий, преломленный и отраженный
лежат в одной плоскости и синус угла
падения так относится к синусу угла
преломления, как скорость звука в первой
среде относится к скорости во второй
среде:
![]() .
.
(8)
Величина
п называется
показателемпреломления.
Если
интенсивность звука в первой среде
![]() ,
,
а во второй![]() ,
,
то
![]() (9)
(9)
где
![]() –коэффициент
–коэффициент
проникновения. Какпоказал один из создателей
теоретической физики Релей,
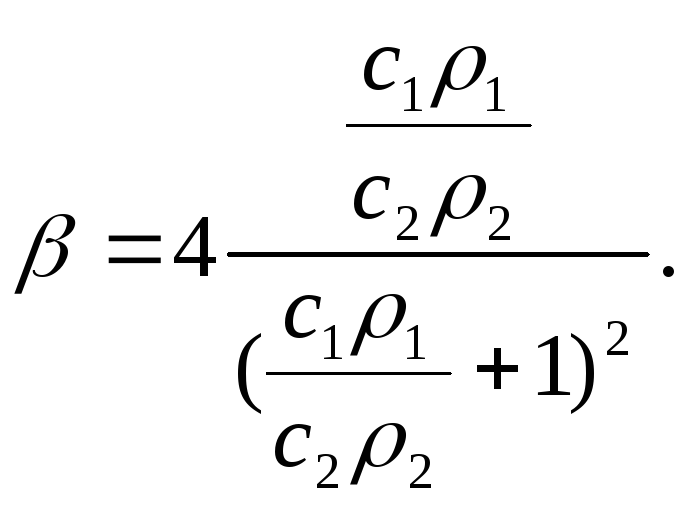 (10)
(10)
Коэффициент
проникновения зависит от отношения
акустических сопротивлений сред.
Если
![]() то
то![]() (11)
(11)
Если
![]() то
то![]() (12)
(12)
Коэффициент
отражения, очевидно, равен R=1-![]() .
.
Следовательно,
интенсивность преломленного звука:
![]() (13)
(13)
а интенсивность
отраженного:
![]() (14)
(14)
Распространение звука.
Расчеты
поглощения звука в воздухе показывают,
что волна с частотой 1000 гц
при 20 °С ослабевает
в е раз
на расстоянии примерно 115 км.
Учет влияния
теплопроводности снижает эту личину
до 81 км. Однако
в действительности звук в атмосфере
затухает много быстрее. Причина этого
в том, что на его распространение влияют
ветер, температура и влажность воздуха,
наличие слоев различной плотности.
Рисунок 3 поясняет влияние ветра.
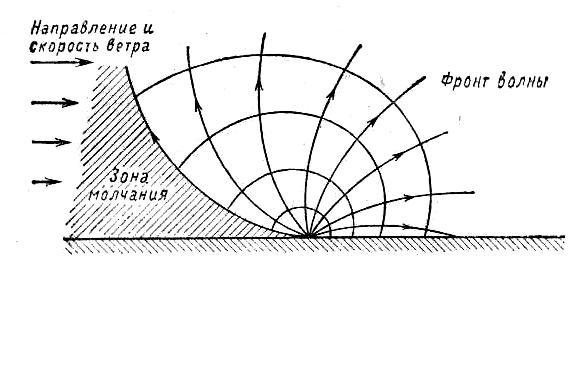
Рис. 3
Сферическая волна
от точечного источника в однородной
атмосфере должна распространяться с
одинаковой скоростью во всех направлениях.
Но если имеет место ветер, скорость его
и скорость волны складываются
геометрически. Так как скорость ветра
у земли меньше (вследствие трения о ее
поверхность), а с высотой растает, то
отдельные части фронта волны движутся
относительно земли с разной скоростью.
Если волна
распространяется под некоторым углом
навстречу г.пру, то лучи, как можно
усмотреть из построения на чертеже,
вгибаются вверх, а с противоположной
стороны от источника прижимаются к
земле. Поэтому звук слышен на большем
расстоянии от источника с подветренной
стороны, чем с наветренной.
На рисунке 4
изображено распространение звуковой
волны, когда температура воздуха убывает
с высотой.

Рис. 4
В теплом воздухе
звук распространяется (при прочих равных
условиях) быстрее, чем в холодном (см.
равенство 4). В звуковой волне лучи
загибаются вверх. Если температура
слоев воздуха, прилегающих к земле,
ниже, чем на некоторой высоте (что бывает
в ясные ночи, когда земля и прилегающие
к ней слои воздуха быстро остывают
вследствие излучения), лучи прижимаются
к земле. Поэтому в жаркий день, когда
земля и нижние слои воздуха сильно
нагреты, расстояние, на котором слышен
звук, заметно меньше, чем в ясную ночь.
Если в слое, лежащем на какой-то высоте
над землей, температура воздуха
меняется скачком (а следовательно,
вместе с изменением скорости звука
меняется и акустическое сопротивление
2реды), то звук, дойдя до него, отражается
к земле; отразившись от ее поверхности,
он испытывает вновь отражение от слоя
температурного скачка и т. д. При этом
дальность распространения звука может
сильно возрасти, так как энергия звуковой
волны концентрируется в границах
некоторого сравнительно ограниченного
слоя.
Движение
воздуха в атмосфере всегда турбулентно.
Поэтому скорость и температура в каждой
точке воздушного потока пульсируют по
величине, а скорость, кроме того, и
по направлению. Это приводит к возникновению
мелких неоднородностей в атмосфере и
к рассеянию на них звуковой энергии,
а следовательно, к значительному
увеличению затухания звука. Многие
источники звука излучают волны низких
частот: инфразвуковые и близкие к ним.
Источниками таких звуковых колебаний
являются, например, взрыв, шум двигателя,
ветер и т. п. Благодаря своей низкой
частоте эти звуки могут распространяться
на сравнительно большие расстояния.
На высоте 50—70км в
атмосфере имеется слей озона, сильно
поглощающий тепловые лучи,
благодаря чему
температура этого слоя резко повышена
(50—70°С). Звук сильного взрыва, доходя
до этого слоя, отражается и возвращается
к поверхности земли. Звук, идущий вдоль
поверхности земли, сильно затухает
в силу рассеяния на неровностях
поверхности, на турбулентных
неоднородностях в прилегающих к земле
слоях воздуха. Поэтому вокруг источника
взрыва на поверхности земли образуется
чередование зон, в которых звук слышен,
с зонами, в которых он не слышен.
На
распространение звука в воде, так же
как и в воздухе, влияет наличие
течений, температурных градиентов,
турбулентных неоднородностей. Но влияние
их сказывается значительно сильнее,
чем в воздухе. Кроме того, благодаря
различному содержанию солей плотность
морской воды может сильно меняться от
слоя к слою, что так же, как и изменение
температуры, вызывает изгибание
(рефракцию) лучей.
Скачкообразное изменение температуры
или солености воды обусловливает
многократные отражения звука, образование
звуковых каналов. На распространение
звука в воде
сказывается наличие
в ней мельчайших пузырьков воздуха,
мелких животных и водорослей. Все это
чрезвычайно усложняет картину
распространения звука в естественных
водоемах.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
