Как найти отрезки на которые делится диагональ

Как найти отрезки на которые делится диагональ

Как найти отрезки на которые разделилась диагональ при пересечении диагоналей трапеции, зная основания и эту диагональ?

araz salmanli



Профи

(632),
на голосовании



7 лет назад

Основания трапеции ABCD,AD=20 см, BC=15 см, длина диагонали AC равна 35 см. В каком отношении делится диагональ AC точка пересечения диагоналей?

Голосование за лучший ответ

Владимир Шмелев.

Просветленный

(44346)


7 лет назад

Через подобные тр. и отношение сходственных сторон можно найти в каком отношении делится диагональ AC точкой пересечения диагоналей (а то, что AC равна 35 см нужно только чтобы найти длины эти отрезков)

araz salmanliПрофи (632)

7 лет назад

А подобных тр. нету, условие только это. Через коэффициент подобности не получится.

Владимир Шмелев.
Просветленный
(44346)

Источник

Как решать задачи, в которых диагональ трапеции делит ее среднюю линию на отрезки?

Как правило, такие задачи сводятся к рассмотрению двух треугольников.

Задача 1.

Диагональ трапеции делит ее среднюю линию на отрезки длиной c и d. Найти основания трапеции.

diagonal-trapecii-delit-srednyuyu-liniyu-na-otrezkiДано: ABCD — трапеция,

AD ∥ BC, MN — средняя линия,

MN∩AC=K, MK=c, KN=d.

Найти: AD, BC.

Решение:

diagonal-trapecii-delit-srednyuyu-liniyu1) Рассмотрим треугольник ACD.

СN=DN и KN ∥ AD (так как по условию MN — средняя линия трапеции).

Следовательно, по теореме Фалеса, AK=KC.

Значит, KN — средняя линия треугольника ACD.

По свойству средней линии треугольника,

    [KN = frac{1}{2}AD, Rightarrow AD = 2KN = 2d.]

2) Рассмотрим треугольник ABC.

AM=MB (так как MN- средняя линия трапеции), AK=KC (по доказанному). Следовательно, MK — средняя линия треугольника ABC,

    [MK = frac{1}{2}BC, Rightarrow BC = 2MK = 2c.]

Ответ: 2c, 2d.

Вывод:

Диагональ трапеции делит ее среднюю линию на отрезки, равные половинам оснований.

Задача 2.

Основание AD трапеции ABCD на 6 см больше основания BC, а средняя линия равна 7 см. Найти длины отрезков, на которые диагональ AC делит среднюю линию.

Решение:

Рисунок — как и в задаче 1.

Пусть BC=x см, тогда AD=x+6 см.

По доказанному выше,

    [MK = frac{1}{2}x(cm),KN = frac{1}{2}(x + 6)(cm).]

    [MN = MK + KN,]

    [frac{1}{2}x + frac{1}{2}(x + 6) = 7]

    [frac{1}{2}x + frac{1}{2}x + 3 = 7]

    [x + 3 = 7]

    [underline {x = 4} ]

    [MK = frac{1}{2} cdot 4 = 2(cm),KN = frac{1}{2}(4 + 6) = 5(cm).]

Ответ: 2 см, 5 см.

Источник

Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.

Ира Люблю длинные вопросы и ответы на БВ.

Смотрим скрин. Я достроила отрезок АН – параллельный и равный BD. Также достроила отрезок HD- параллельный и равный АВ. Получился параллелограмм ABDH в котором средняя линия равна основанию АВ = 10, а искомый отрезок ЕG = IE = АВ/2 = 10/2 = 5 ед. (условные единицы), потому что треугольники AHD и DBA равны по всем параметрам, и диагональ в параллелограмме делит его среднюю линию пополам.

Мой ответ: Больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей равен 5-ти условным единицам.

автор вопроса выбрал этот ответ лучшим

Знаете ответ?

Источник

Рассмотрим базовые задачи на подобные треугольники в трапеции.

I. Точка пересечения диагоналей трапеции  — вершина подобных треугольников.

диагонали трапеции пересекаются и образуют треугольники

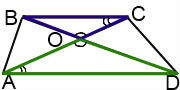
Рассмотрим треугольники AOD и COB.

подобные треугольники в трапеции при пересечении диагоналей

Визуализация облегчает  решение задач на подобие. Поэтому подобные треугольники в трапеции выделим разными цветами.

1) ∠AOD=∠COB (как вертикальные);

2)∠DAO=∠BCO (как внутренние накрест лежащие при AD ∥ BC и секущей AC).

Следовательно, треугольники AOD и COB подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

    [frac{{AD}}{{BC}} = frac{{DO}}{{BO}} = frac{{AO}}{{CO}}.]

Задача.

Одна из диагоналей трапеции равна 28 см и делит другую диагональ на отрезки длиной 5 см и 9 см. Найти отрезки, на которые точка пересечения диагоналей делит первую диагональ.

Решение:

AO=9 см, CO=5 см, BD=28 см. BO =?, DO- ?

Доказываем подобие треугольников AOD и COB. Отсюда

    [frac{{AD}}{{BC}} = frac{{DO}}{{BO}} = frac{{AO}}{{CO}}.]

Выбираем нужные отношения:

    [frac{{DO}}{{BO}} = frac{{AO}}{{CO}}.]

Пусть BO=x см, тогда DO=28-x см. Следовательно,

    [frac{{28 - x}}{x} = frac{9}{5}]

    [9x = 5(28 - x)]

    [9x + 5x = 140]

    [x = 10]

BO=10 см, DO=28-10=18 см.

Ответ: 10 см, 18 см.

 Задача

Известно, что О — точка пересечения диагоналей трапеции ABCD (AD ∥  BC). Найти длину отрезка BO, если AO:OC=7:6 и BD=39 см.

Решение:

Аналогичн0, доказываем подобие треугольников AOD и COB и

    [frac{{DO}}{{BO}} = frac{{AO}}{{CO}}.]

Пусть BO=x см, тогда DO=39-x см. Таким образом,

    [frac{{39 - x}}{x} = frac{7}{6}]

    [7x = 6(39 - x)]

    [x = 18]

Ответ: 18 см.

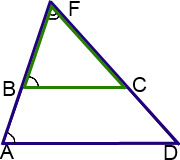
II. Продолжения боковых сторон трапеции пересекаются в точке.

продолжения боковых сторон трапеции пересекаются в точке

Аналогично задаче I, рассмотрим треугольники AFD и BFC:

1) ∠F — общий;

2)∠ DAF=∠CBF (как соответственные углы при BC ∥ AD и секущей AF).

Следовательно, треугольники AFD и BFC подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

    [frac{{AD}}{{BC}} = frac{{AF}}{{BF}} = frac{{DF}}{{CF}}.]

Задача

Продолжения боковых сторон AB и CD  трапеции ABCD пересекаются в точке F. Меньшее основание BC равно 4 см, BF=5 см, AB=15 см. Найти большее основание трапеции.

Решение:

Доказываем, треугольники AFD и BFC — подобны.

Следовательно,

    [frac{{AD}}{{BC}} = frac{{AF}}{{BF}},]

    [AF = AB + BF = 15 + 5 = 20cm,]

    [frac{{AD}}{4} = frac{{20}}{5}]

    [5AD = 80]

    [AD = 16]

Ответ: 16 см.

В следующий раз рассмотрим задачи на отношение площадей подобных треугольников.

Источник

Основания трапеции относятся как 3:11 , длина диагонали равна 42см. Найдите отрезки, на которые делит эту диагональ другая диагональ трапеции.

Светило науки – 30838 ответов – 105369 раз оказано помощи

Обозначим точку пересечения диагоналей АС и ВД через О. Треугольники ВОС и АОД подобны по двум углам (<ВОС=<АОД как вертикальные и <ВСО=<САД как накрест лежащие)Запишем отношение ВС/АД=ВО/ОД=СО/АО. По условию ВС/АД=3/11.

Тогда СО/АО=3/11 ⇒СО=3х, АО=11х, АС=СО+АО=14х=42, х=3 – это коэффициент пропорциональности. ВО/ОД=3х/11х, ВО=3*3=9, ОД=11*3=33

Светило науки – 2564 ответа – 23475 раз оказано помощи

всего 3+11 = 14 частей

42: 14=3

11*3=33

3*3=9

Ответ: 9 и 33

Остались вопросы?

Новые вопросы по предмету Математика

Источник

Добавить комментарий