Отношением двух отрезков называется отношение их длин.
Рассмотрим два отрезка (AB) и (VN), где отрезок (AB) в (2) раза больше второго отрезка.

Отношение отрезков (AB) и (VN) равно (2 : 1):
Можно также сказать, что отношение отрезков (VN) и (AB) равно (1 : 2):
В этом примере отрезок (AR) равен трём единицам, а (VZ) равен двум единицам.

Отношение отрезков (AR) и (VZ) равно (3 : 2):
ARVZ=32
или
Если отношение отрезков (a) и (b) равно отношению отрезков (c) и (d), т. е.
ab=cd
,
то эти отрезки называются пропорциональными.
Сравниваем данные ранее отрезки, они не пропорциональны, т. к.
ABVN≠ARVZ
.
Рассмотрим данные рисунки:


Сравним отношения отрезков
ABVNиAHVT
.
ABVN=21иAHVT=4221=21
.
Значит,
ABVN=AHVT
— эти пары отрезков пропорциональны.
Чтобы записать отношение отрезков, необходимы два отрезка. Чтобы найти пропорциональные отрезки, необходимы две пары отрезков.
Пропорциональные отрезки


4.5
Средняя оценка: 4.5
Всего получено оценок: 497.
4.5
Средняя оценка: 4.5
Всего получено оценок: 497.
Пропорциональные отрезки очень важны для определения подобия фигур. К тому же, правильно нареченные пропорционально рисунки помогают в правильном решении математических задач. Именно поэтому так важно разбираться в данной тематике.

Опыт работы учителем математики – более 33 лет.
Определение
Пропорциональными отрезками называются отрезки, у которых имеется постоянный коэффициент пропорциональности. Под коэффициентом пропорциональности понимается отношение длин отрезков.

Согласно определению пропорциональных отрезков, два отрезка всегда пропорциональны между собой, поскольку их длины не меняются со временем. Значит, не меняется и коэффициент пропорциональности.
Несмотря на это, чаще всего под пропорциональными отрезками понимают отрезки с коэффициентом кратным 0,5. Например, отрезки с коэффициентом 2,5, 1,5, 2 и тому подобные.
Пропорциональными будут являться и отрезки, составляющие подобные фигуры. Это действует в обе стороны. Если фигуры подобны, то их стороны пропорциональны, если все стороны пропорциональны, то фигуры подобны.
Подобные фигуры
Нужно понимать, что подобными фигурами могут быть не только треугольники, но вообще любые фигуры в геометрии, если все углы этих фигур равны, а длины сторон пропорциональны.

Но при этом признаки подобия существуют только для треугольников. Их всего 3:
- Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Пропорциональными могут быть только отрезки, как объекты имеющие длину. Прямая или луч бесконечны, а потому не могут быть подобными.
Пример
Решим небольшую задачу на пропорциональность отрезков. Имеется 3 пропорциональных отрезка. Каждый из которых больше предыдущего. Первый отрезок равен 5, третий 20. Необходимо найти длину второго отрезка.
Отрезки пропорциональны, значит отношение больших к меньшим будет постоянным. Обозначим неизвестны отрезок за х и решим уравнение.
$${хover{5}}={20over{x}}$$
Перенесем выражение из правой части в левую. Приведем получившееся выражение под один знаменатель и решим дробно-рациональное уравнение.
$${хover{5}}-{20over{x}}=0$$
$${{х^2-100}over{5x}}=0$$
$$х^2-100=0$$
$х^2=100$ – х может являться положительным или отрицательным числом , но отрезок не может иметь отрицательную длину, значит х=10.
Задача решена

Что мы узнали?
Мы узнали, что такое пропорциональные отрезки. Выделили области, где могут быть применены навыки обращения с пропорциональными длинами и привели пример на заданную тему.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Эдуард Ройтбурд
5/5
Оценка статьи
4.5
Средняя оценка: 4.5
Всего получено оценок: 497.
А какая ваша оценка?
Пропорциональные отрезки — отрезки, для длин которых выполняется пропорция.
Отношением отрезков AB и CD называется отношение их длин, то есть 
Говорят, что отрезки AB и СD пропорциональны отрезкам 

.
Например, отрезки AB и СD, длины которых равны 2 и 1 см, пропорциональны отрезкам 


Понятие пропорциональности аналогичным образом вводится и для большего числа отрезков:
Понятие пропорциональных отрезков используется в теореме Фалеса, а также в аффинной геометрии.
См. также[править | править код]
- Отношение направленных отрезков
- Двойное отношение
Пропорциональность отрезков
Прежде всего следует указать самый простой пример получения двух пар отрезков, отношения которых равны. Возьмем какое-нибудь рациональное число, например, 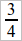 , и построим 2 пары различных отрезков, отношения которых равны этому числу; тогда получим
, и построим 2 пары различных отрезков, отношения которых равны этому числу; тогда получим 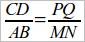 (чер. 79) равенство двух отношений. Здесь вводятся термины: «пропорция», «пропорциональные отрезки», «крайние члены» и т. д.
(чер. 79) равенство двух отношений. Здесь вводятся термины: «пропорция», «пропорциональные отрезки», «крайние члены» и т. д.
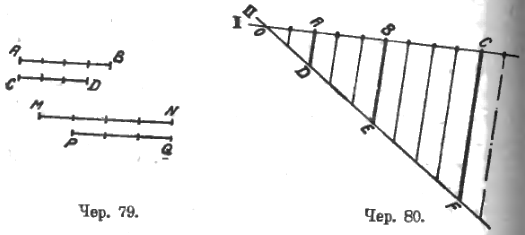
Далее переходим к более сложному построению (чер. 80): строим две прямых I и II, пересекающихся в точке O. На I-ой прямой откладываем равные отрезки от точки O (их на чертеже отложено 10) и строим через их концы ряд параллельных; тогда на II-ой прямой получим также ряд равных отрезков (это знание является побочным результатом при рассмотрении задачи о делении отрезка на сколько-угодно равных частей). Тогда мы можем, выбрав лишь некоторые точки деления, например, A, B и C, получить на I-ой прямой пары соизмеримых отрезков, отношение которых легко выражается числом. Например:
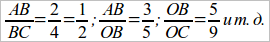
После построения параллельных на II-ой прямой получим также соизмеримые отрезки, соответствующие отрезкам на I-ой прямой (точке A соотв. точка D, точке B – точка E и т. д.). Для этих отрезков получим:
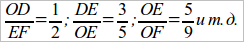
Является возможность написать ряд пропорций, например:
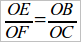
Итак, мы здесь имеем такой способ построения пропорциональных отрезков: на I-ой прямой строим ряд равных отрезков, через их концы строим ряд параллельных, выбираем на I-ой прямой ряд точек, вроде A, B и C, и на II-ой берем соответствующие (т. е. лежащие на тех же параллельных) точки.
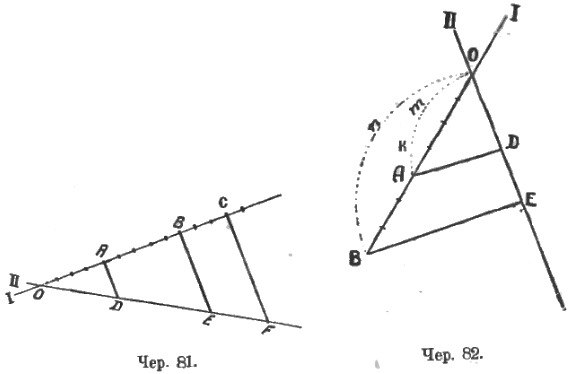
Само собою напрашивается упрощение этого построения: нет нужды строить все параллельные, а достаточно лишь построить параллельные через избранные точки. Приходим к построению, данному на чер. 81, где уже точки A, B и C выбраны несколько иначе. И здесь, не смотря на то, что промежуточные параллельные не построены, мы с уверенностью пишем пропорции:
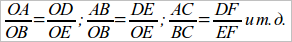
Возникает мысль о возможности дальнейшего упрощения, нельзя ли не откладывать на I-ой прямой равные отрезки, а сразу, взять где-либо точки A, B и C и через них построить параллельные? Необходимо, конечно, этот вопрос расследовать. Ограничимся лишь двумя точками (чер. 82). На I-ой строим где угодно точки A и B и затем строим: AD || BE – получаем на II-ой прямой соотв. точки D и E. Здесь мы имеем на I-ой прямой 3 отрезка OA, AB и OB и соотв. им отрезки на II-ой прямой. Выберем какую-либо пару отрезков на I-ой прямой, например, OA и OB. Мы можем написать символ 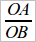 и знаем, что он выражает число, но не знаем какое, – быть может рациональное, быть может иррациональное. Наш вопрос, выше намеченный, сводится к следующему: равны ли или нет отношения (или числа)
и знаем, что он выражает число, но не знаем какое, – быть может рациональное, быть может иррациональное. Наш вопрос, выше намеченный, сводится к следующему: равны ли или нет отношения (или числа) 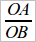 и
и 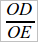 ? Разобрать этот вопрос теперь возможно лишь при помощи признака, установленного в конце предыдущей главы.
? Разобрать этот вопрос теперь возможно лишь при помощи признака, установленного в конце предыдущей главы.
Схема выяснения этого вопроса такова. Выберем какое-угодно целое число n и найдем самое большое число со знаменателем n, чтобы оно было все же меньше 1-го отношения (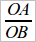 ). Для этого мы должны разделить отрезок OB на n равных частей и посмотреть, сколько таких частей уложится на отрезке OA. Пусть от O до K укладывается m таких частей, а конец следующей, (m + 1)-ой, части приходится уже за точкою A. Тогда самое большое число со знаменателем n, меньшее отношения
). Для этого мы должны разделить отрезок OB на n равных частей и посмотреть, сколько таких частей уложится на отрезке OA. Пусть от O до K укладывается m таких частей, а конец следующей, (m + 1)-ой, части приходится уже за точкою A. Тогда самое большое число со знаменателем n, меньшее отношения 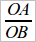 , есть дробь
, есть дробь 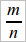 (уже дробь
(уже дробь 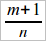 должна быть больше
должна быть больше 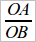 ). Построив ряд параллельных, мы убеждаемся, что это же число
). Построив ряд параллельных, мы убеждаемся, что это же число 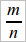 должно быть также меньше
должно быть также меньше 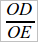 .
.
Итак, даже самое большое число со знаменателем n, меньшее 1-го отношения, должно быть меньше 2-го отношения; следовательно, всякое число со знаменателем n, меньшее 1-го отношения, должно быть также меньше и 2-го. Что значит: «со знаменателем n»? Это значит «с любым знаменателем», т. е. «любое число, меньшее 1-го отношения, должно быть меньше и второго». Так как мы могли бы отношения 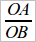 и
и 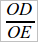 поменять местами, то приходим к заключению: любое число, меньшее одного из рассматриваемых отношений, должно быть меньше и другого. Итак, мы убедились, что в нашем примере нельзя найти числа, меньшего одного из наших отношений и большего другого, т. е. наши отношения должны считаться равными:
поменять местами, то приходим к заключению: любое число, меньшее одного из рассматриваемых отношений, должно быть меньше и другого. Итак, мы убедились, что в нашем примере нельзя найти числа, меньшего одного из наших отношений и большего другого, т. е. наши отношения должны считаться равными:
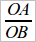 =
= 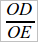 .
.
При повторении с учащимися подобных соображений следует брать другие комбинации отрезков. Например, 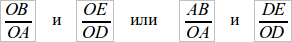 и т. д. Изменить предыдущее изложение и дать для этих комбинаций соответствующие чертежи – дело не трудное. Поэтому не останавливаемся на этом.
и т. д. Изменить предыдущее изложение и дать для этих комбинаций соответствующие чертежи – дело не трудное. Поэтому не останавливаемся на этом.
Важным побочным результатом здесь явится следующий: мы убеждаемся предыдущими соображениями в совместном существовании пропорций.
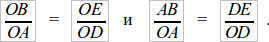
Это обстоятельство указывает на возможность получения одной пропорции производной при помощи вычитания 1 из обоих отношений, т. е. оправдывается следующая операция для отрезков, справедливость которой мы раньше знали лишь для чисел:
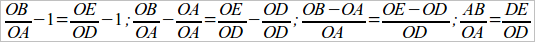
(центральный пункт этой операции лежит в переходе из 2-го равенства к 3-му).
Дальнейший, и крайне существенный, шаг в том же направлении состоял бы в выяснении возможности в пропорции, составленной из отрезков, переставлять средние (или крайние) члены. Даем выяснение этого, заимствованное из книги D. Hilbert’а – «Grundlagen der Geometrie». Впрочем, следует оговориться, что полезным это выяснение окажется лишь для немногих учащихся. По отношению же к большинству придется стать на упрощенную точку зрения: каждый из отрезков, входящий в пропорцию, может быть выражен числом, принимая за единицу какой-либо определенный отрезок, и тогда с этой пропорцией явится возможность оперировать так же, как и с числовою пропорциею.
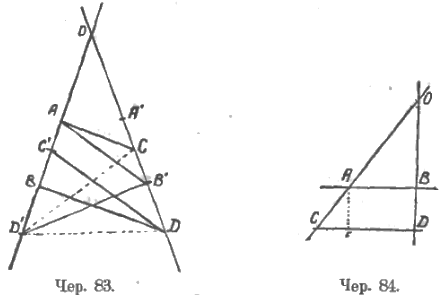
Вот выяснение Hilbert’а интересующего нас вопроса (чер. 83). Пусть AC || BD. Тогда 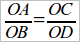 . Возникает вопрос, справедлива ли пропорция
. Возникает вопрос, справедлива ли пропорция 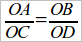 . Построим OA’ = OA, OB’ = OB, OC’ = OC и OD’ = OD. Интересующий нас вопрос сводится к другому: параллельны ли прямые AB’ и C’D. Рассмотрим четыреугольник ACB’D’. Так как ∠OCA = ∠ODB = ∠OD’B’ (последнее из равенства треугольников OBD и OB’D’), то ∠ACB’ + ∠OD’B’ = 2d, т. е. точки A, C, B’ и D’ лежат на одном круге. Отсюда следует, что ∠CAB’ = ∠CD’B’, а ∠СD’B = ∠C’DB (из равенства ∆CD’B’ и ∆C’DB). Поэтому: ∠OB’A = ∠OCA – ∠CAB’ и ∠ODC’ = ∠ODB – ∠C’DB и след. ∠OB’A = ∠ODC’, как разности попарно равных углов. Итак ∠OB’A = ∠ODC’ и, следовательно, AB’ || C’D. Отсюда вытекает справедливость пропорции:
. Построим OA’ = OA, OB’ = OB, OC’ = OC и OD’ = OD. Интересующий нас вопрос сводится к другому: параллельны ли прямые AB’ и C’D. Рассмотрим четыреугольник ACB’D’. Так как ∠OCA = ∠ODB = ∠OD’B’ (последнее из равенства треугольников OBD и OB’D’), то ∠ACB’ + ∠OD’B’ = 2d, т. е. точки A, C, B’ и D’ лежат на одном круге. Отсюда следует, что ∠CAB’ = ∠CD’B’, а ∠СD’B = ∠C’DB (из равенства ∆CD’B’ и ∆C’DB). Поэтому: ∠OB’A = ∠OCA – ∠CAB’ и ∠ODC’ = ∠ODB – ∠C’DB и след. ∠OB’A = ∠ODC’, как разности попарно равных углов. Итак ∠OB’A = ∠ODC’ и, следовательно, AB’ || C’D. Отсюда вытекает справедливость пропорции:
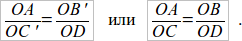
Переход к дальнейшему само собою намечается: мы имели дело с фигурой, изображенной на чертеже 84, где AB || CD, и знаем, что отношение двух отрезков на одной прямой равно отношению соответствующих отрезков на другой. Мы можем в этой фигуре увидеть треугольники ∆OAB и ∆OCD и увидать, что они находятся в определенном соотношении: 1) у них попарно равны углы и 2)отношение одной пары сторон этих треугольников (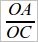 ) равно отношению другой пары (
) равно отношению другой пары (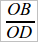 ). Возникает вопрос о третьей паре, т. е. об отношении
). Возникает вопрос о третьей паре, т. е. об отношении 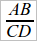 , – неравно ли оно каждому из предыдущих отношений? Для рассмотрения этого вопроса необходимо стороны AB и CD перенести на одну прямую. Для этого строим AE || OD; тогда ED = AB, и мы опять получаем 2 прямые CO и CD, пересеченные параллельными AE и OD, откуда и следует:
, – неравно ли оно каждому из предыдущих отношений? Для рассмотрения этого вопроса необходимо стороны AB и CD перенести на одну прямую. Для этого строим AE || OD; тогда ED = AB, и мы опять получаем 2 прямые CO и CD, пересеченные параллельными AE и OD, откуда и следует: 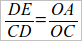 или
или 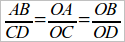 .
.
Построив где-либо еще ∆A’O’B’ = ∆AOB, мы можем рассматривать 2 треугольника: OCD и O’A’B’, и у них должны быть те же соотношения для углов и сторон. Здесь устанавливается понятие о подобии треугольников. Основной способ построения треугольника, подобного данному, состоит в том, что данный треугольник пересекается прямою, параллельною одной из сторон. У других подобных треугольников 1) углы попарно равны и 2) отношение одной пары сходственных сторон равно отношению другой пары и равно отношению 3-ей пары (с сокращенным словесным выражением этой зависимости – «сходственные стороны пропорциональны» – спешить не следует).
Основной признак подобия треугольника намечается само собою: наложим один ∆ на другой – если их расположение окажется таким же, как на одном из предыдущих чертежей (2 стороны одного идут по сторонам другого, а третьи стороны параллельны), то треугольники подобны, для того же, чтобы получить таковое расположение, необходимо и достаточно равенство двух углов одного треугольника двум углам другого. Последнее и есть основной признак подобия треугольников. Для курса средней школы вполне достаточно ограничиться лишь этим основным признаком, а остальные два, обычно вводимые в курс, признака («если 2 стороны одного пропорциональны двум сторонам другого и углы между ними равны, то …» и «если 3 стороны одного пропорц. трем сторонам другого, то …») являются ненужным балластом для этого курса и их следует выпустить.
Учащиеся взамен того должны получше укрепиться в применениях подобия треугольников. Свойство биссектора угла треугольника (хотя бы лишь внутреннего), свойства отрезков в прямоугольном треугольнике, получаемых от построения перпендикуляра из вершины прямого угла на гипотенузу, свойство отрезков хорд или секущих, проходящих через определенную точку – все это должно быть детально разобрано и сопровождаемо рядом упражнений.
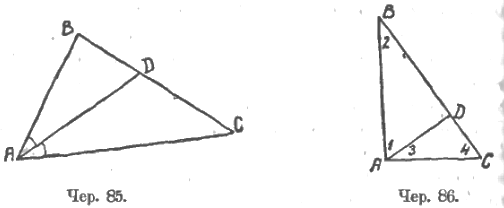
Полезною является и такая работа. Пусть начинаем исследовать свойство биссектора угла треугольника (чер. 85). Построив биссектор, например, для ∠A треугольника ABC, получим ∆ABD и ∆ADC. Возникает вопрос, не подобны ли они. Выяснение, почему их нельзя считать подобными, является чрезвычайно ценною работою.
При получении дальнейших свойств можно рекомендовать такой метод (чер. 86). Пусть имеем прямоугольный ∆ABC (∠A = d), строим AD ⊥ BC. Разбираем ∆ABD и ∆ADC. Пронумеровав острые углы этих треугольников, мы имеем возможность установить:
1) Мы видим: ∠1 + ∠3 = d.
2) мы знаем: ∠1 + ∠2 = d
отсюда заключаем: ∠3 = ∠2.
Установим, что ∆ABD подобен ∆ADC, мы имеем право написать:
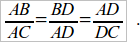
Желательно написать именно равенство отношений всех трех пар сторон. Рассматривая полученную запись, мы наблюдаем (и ученики это обычно подмечают и говорят об этом), что во 2-м и 3-м отношениях имеется особенность, а именно: повторяемость отрезка AD. Установив это, мы рассматриваем только равенство 2-го и 3-го отношений и приходим в конце концов к обычной формулировке теоремы о перпендикуляре из вершины прямого угла на гипотенузу.
Возможно было бы, рассматривая этот пример более внимательно, установить, что средний пропорциональный отрезок между двумя другими всегда должен появляться, когда имеется два подобных треугольника с общею стороною, причем эта сторона не сходственна сама себе. Если учащиеся хорошо освоятся с этою мыслью, то его можно в дальнейшем курсе (например, при рассмотрении секущей и касательной) пользоваться, сокращая свою работу.
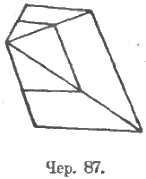
Подобие многоугольников следует рассматривать с точки зрения обобщения понятия о подобии треугольников. Прежде всего должно установить построение, аналогичное тому, какое имело место для получения подобных треугольников, чтобы при его помощи можно было получить 2 подобных многоугольника. Таковым построением является данное здесь на чер. 87 и, конечно, общеизвестное, почему оно и не требует пояснений. В обычном курсе средней школы учение о подобии многоугольников вряд ли может быть развито с большою подробностью и, быть может, даже следует выпустить обычно вводимые в курс прямую и обратную теоремы о связи между подобием многоугольников и подобием треугольников, получаемых построением диагоналей.
Теорема Фалеса и теорема о пропорциональных отрезках
ТЕОРЕМА ФАЛЕСА:
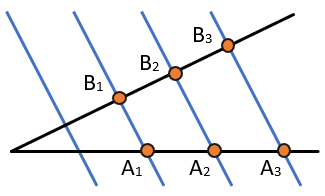
1. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
<>
Если (A_{1}B_{1} parallel A_{2}B_{2} parallel A_{3}B_{3}), (A_{1}A_{2} = A_{2}A_{3}), то (B_{1}B_{2} = B_{2}B_{3}).
2. Эта теорема применима также и к пересекающимся прямым:
Параллельные прямые, пересекающие две данные прямые и отсекающие на одной прямой равные отрезки, отсекает равные отрезки и на другой прямой.
3. Из теоремы Фалеса следуют определения средней линии треугольника и средней линии трапеции.
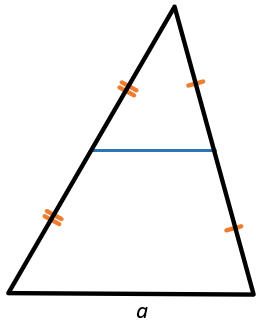
Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна её половине.
(a parallel m, m = frac{1}{2}a)
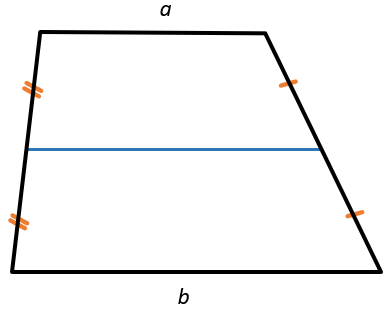
Средняя линия трапеции параллельна основаниям и равна их полусумме:
(m parallel a, b, m = frac{a + b}{2})
ТЕОРЕМА О ПРОПОРЦИОНАЛЬНЫХ ОТРЕЗКАХ:
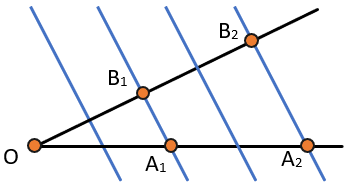
Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
Если (A_{1}B_{1} parallel A_{2}B_{2},) то (frac{OA_{1}}{OA_{2}} = frac{OB_{1}}{OB_{2}})