Как найти отрезок в треугольнике параллельный основанию

Отрезок параллельный основанию треугольника

Как найти среднюю линию треугольника?

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие треугольника

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

• Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
• Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
• Тупоугольный. Один угол тупой, два других — острые.

Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.

Треугольник, у которого все стороны равны, называется равносторонним или правильным.

Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.

Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Свойства треугольников:

• В треугольнике против большего угла лежит большая сторона — и наоборот.
• Сумма углов треугольника равна 180 градусов.
• Все углы равностороннего треугольника равны 60 градусам.
• В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Понятие средней линии треугольника

Определение средней линии треугольника подходит для любого вида этой фигуры.

​Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.

​Основанием считается сторона, которой параллельна средняя линия.

Как найти среднюю линию треугольника — расскажем дальше, а для начала еще немного разберемся со всеми определениями.

Понятие средней линии прямоугольного треугольника

Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.

Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.

В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.

Свойства средней линии треугольника

Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

Свойства:

1. Средняя линия равна половине длины основания и параллельна ему.
2. Средняя линия отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
3. Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным.
4. Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.

Теорема о средней линии треугольника

Теорема о средней линии треугольника звучит так:

Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:

Докажем теорему:

По условию нам дано, что MA = MB, NA = NC

Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.

(по второму признаку подобия треугольников).

△ABC, то Следовательно, ВС = 2МN. Значит, доказано, что средняя линия равна половине основания.

△ABC, то ∠1 = ∠2 . Так как ∠1 и ∠2 — соответственные углы, то по признаку параллельности прямых MN || BC.

Параллельность средней линии и соответствующего ей основания доказана.

Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.

Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:

Ответ: периметр треугольника ΔMNK равен 10.

Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.

Площадь треугольника равна половине произведения основания на высоту. Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:

Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:

Значит, AC = 2MN = 2 × 3 = 6.

Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:

Значит, BC = 2NP = 2 × 4 = 8.

Тогда найдем площадь большого треугольника, используя формулу, указанную выше:

S = ½ × 6 × 8 = ½ × 48 = 24.

Ответ: площадь большого прямоугольного треугольника равна 24.

Подобие треугольников и пропорциональные отрезки

Теорема 1:

Если на одной из сторон угла отметить равные между собой отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на второй стороне также равные между собой отрезки.

Доказательство:

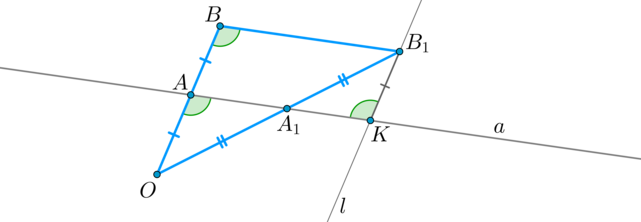
Докажем сначала лемму: Если в (triangle OBB_1) через середину (A) стороны (OB) проведена прямая (aparallel BB_1) , то она пересечет сторону (OB_1) также в середине.

Через точку (B_1) проведем (lparallel OB) . Пусть (lcap a=K) . Тогда (ABB_1K) — параллелограмм, следовательно, (B_1K=AB=OA) и (angle A_1KB_1=angle ABB_1=angle OAA_1) . Значит, по второму признаку (triangle OAA_1=triangle B_1KA_1 Rightarrow OA_1=A_1B_1) . Лемма доказана.

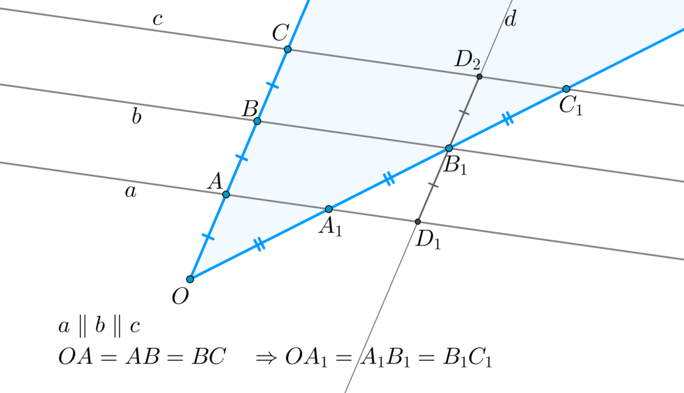
Перейдем к доказательству теоремы. Пусть (OA=AB=BC) , (aparallel bparallel c) и нужно доказать, что (OA_1=A_1B_1=B_1C_1) .

Таким образом, по данной лемме (OA_1=A_1B_1) . Докажем, что (A_1B_1=B_1C_1) . Проведем через точку (B_1) прямую (dparallel OC) , причем пусть (dcap a=D_1, dcap c=D_2) . Тогда (ABB_1D_1, BCD_2B_1) — параллелограммы, следовательно, (D_1B_1=AB=BC=B_1D_2) . Значит, по первому признаку (triangle A_1B_1D_1=triangle C_1B_1D_2 Rightarrow A_1B_1=B_1C_1) .

Теорема Фалеса:

Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.

Доказательство:

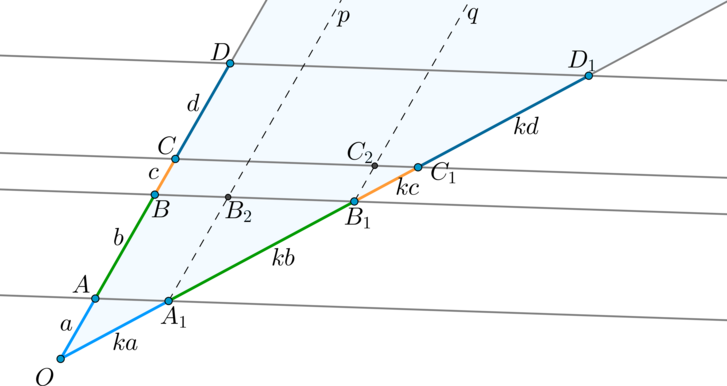
Пусть параллельные прямые (pparallel qparallel rparallel s) разбили одну из прямых на отрезки (a, b, c, d) . Тогда вторую прямую эти прямые должны разбить на отрезки (ka, kb, kc, kd) соответственно.

Проведем через точку (A_1) прямую (pparallel OD) ( (ABB_2A_1) — параллелограмм, следовательно, (AB=A_1B_2) ). Тогда (triangle OAA_1 sim triangle A_1B_1B_2) по двум углам. Следовательно, (dfrac =dfrac Rightarrow A_1B_1=kb) .

Аналогично проведем через (B_1) прямую (qparallel OD Rightarrow triangle OBB_1sim triangle B_1C_1C_2 Rightarrow B_1C_1=kc) и т.д.

Наиболее часто встречающиеся подобия треугольников:

Теорема 2.

Средняя линия треугольника отсекает от него подобный ему треугольник.

Доказательство:

Т.к. средняя линия — это отрезок, соединяющий середины двух сторон, то (dfrac=dfrac =2) .

Таким образом, по двум пропорциональным сторонам и углу между ними ( (angle B) — общий) (triangle A_1BC_1 sim triangle ABC) .

Теорема 3.

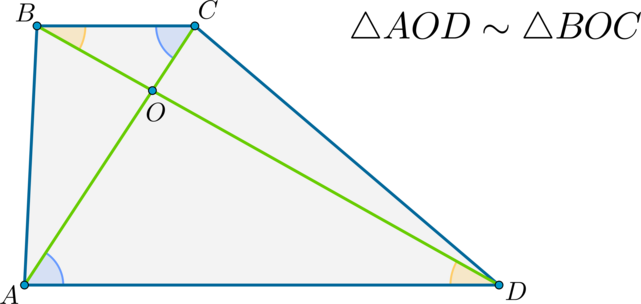
Треугольники, образованные диагоналями трапеции и основаниями, подобны.

Доказательство:

Т.к. (ADparallel BC Rightarrow angle OBC=angle ODA) . (angle BOC=angle AOD) как вертикальные. Следовательно, по двум углам (triangle BOCsim triangle AOD) .

Теорема 4.

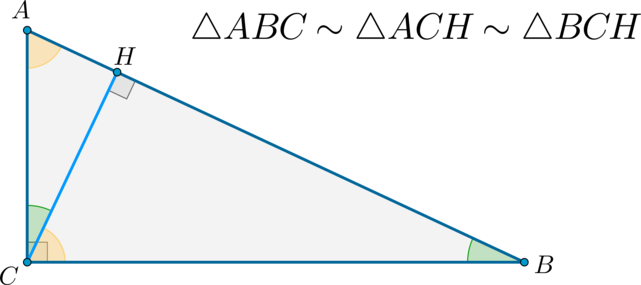
Высота прямоугольного треугольника, проведенная к гипотенузе, делит его на два подобных треугольника.

Доказательство:

Обозначим (angle ACH=alpha, angle BCH=beta) , т.е. (alpha+beta=90^circ) . Тогда (angle CAH=90^circ-alpha=beta, angle CBH=90^circ-beta=alpha) .

Следовательно, по двум углам (triangle ACHsim triangle BCHsim ABC) .

Теорема 5.

Отрезки, соединяющие основания высот треугольника, отсекают от него подобные ему треугольники.

Эти отрезки также являются биссектрисами углов треугольника, вершинами которого являются основания данных высот.

Доказательство:

1) Рассмотрим четырехугольник (AC_1A_1C) — около него можно описать окружность, т.к. (angle AC_1C=angle AA_1C) . Таким образом, (angle CAA_1=angle CC_1A_1=x) , т.к. опираются на одну и ту же хорду (A_1C) . Таким образом (angle ACA_1=90^circ-x, angle BC_1A_1=90^circ-x Rightarrow angle ACA_1=angle BC_1A_1) .

Значит, по двум углам (triangle A_1BC_1sim triangle ABC) ( (angle B) — общий).

Аналогично доказывается, что (triangle AB_1C_1sim triangle ABC, triangle A_1B_1Csim triangle ABC) .

2) Докажем, что (AA_1, BB_1, CC_1) – биссектрисы углов (A_1, B_1, C_1) в треугольнике (A_1B_1C_1) соответственно.

Обозначим (angle BC_1A_1=angle B_1C_1A=alpha) . Тогда (angle A_1C_1C=90^circ -alpha=angle B_1C_1C) . Значит, (CC_1) – биссектриса угла (C_1) .

Аналогично доказывается про (AA_1) и (BB_1) .

Теорема 6.

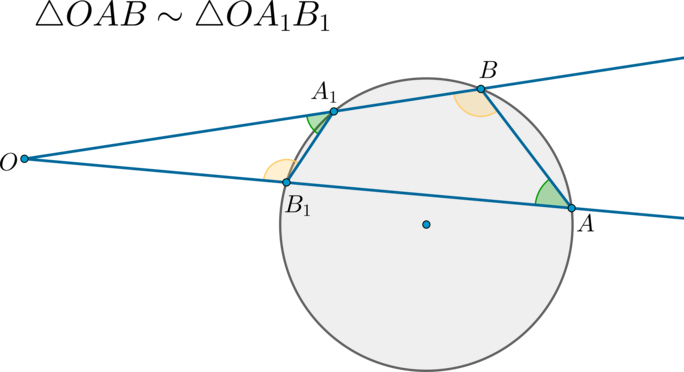
Если к окружности из одной точки вне окружности проведены две секущие, то:

Доказательство:

Четырехугольник (ABA_1B_1) описанный, следовательно, (angle BAB_1+angle BA_1B_1=180^circ Rightarrow angle OA_1B_1=180^circ-angle BA_1B_1=angle BAB_1) .

Таким образом, по двум углам ( (angle O) — общий) (triangle OABsim triangle OA_1B_1) .

Теорема 7.

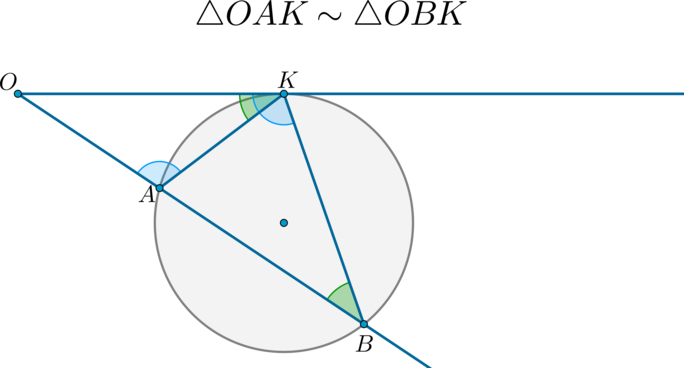
Если к окружности из одной точки проведены касательная и секущая, то:

Доказательство:

Т.к. угол между касательной и хордой, проведенной в точку касания, равен половине дуги, заключенной между ними, то (angle OKA=frac12 buildrelsmileover =angle KBA) .

Следовательно, по двум углам ( (angle O) — общий) (triangle OKAsim triangle OKB) .

Теорема 8.

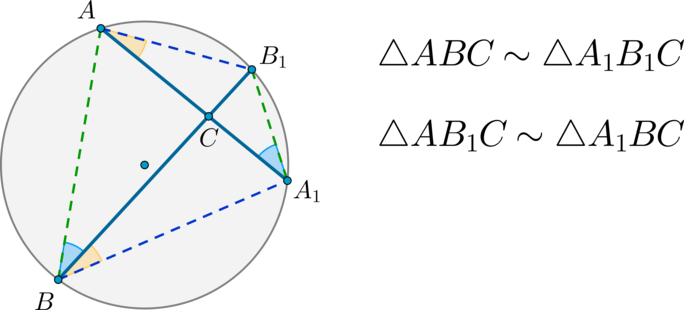
Если в окружности две хорды пересекаются, то:

Доказательство:

(angle A_1AB_1=angle A_1BB_1) , т.к. опираются на одну и ту же дугу. (angle A_1CB=angle B_1CA) , т.к. они вертикальные. Следовательно, по двум углам (triangle A_1BCsim triangle B_1C) .

Аналогично (triangle ABCsim triangle A_1B_1C) .

Отрезок параллельный основанию треугольника

Ключевые слова: основные линии треугольника, медиана, биссектриса, высота, средния линия, серединные перпендикуляры

Рассмотрим произвольный треугольник ABC:

a, b, c — стороны треугольника

$$m_a$$ — медиана к стороне a угла A

$$h_a$$ — высота к стороне a угла A

$$l_a$$ — биссектриса к стороне a угла A

Медиана треугольника — это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.

Свойства медиан треугольника

• Медиана разбивает треугольник на два треугольника одинаковой площади.
• Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
• Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.

Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам.
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.

Свойства биссектрис треугольника

• Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла.
• Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилегажащим сторонам.
• Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.

Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.

Свойства высот треугольника

• В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.
• В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.
• Если треугольник остроугольный, то все основания высот принадлежат сторонам треугольника, а у тупоугольного треугольника две высоты попадают на продолжение сторон
• Три высоты в остроугольном треугольнике пересекаются в одной точке и эту точку называют ортоцентром треугольника.

Свойства серединных перпендикуляров треугольника

• Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
• Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Свойство средней линии треугольника

• Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

Как найти среднюю линию треугольника?

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие треугольника

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

• Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
• Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
• Тупоугольный. Один угол тупой, два других — острые.

Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.

Треугольник, у которого все стороны равны, называется равносторонним или правильным.

Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.

Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Свойства треугольников:

• В треугольнике против большего угла лежит большая сторона — и наоборот.
• Сумма углов треугольника равна 180 градусов.
• Все углы равностороннего треугольника равны 60 градусам.
• В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Понятие средней линии треугольника

Определение средней линии треугольника подходит для любого вида этой фигуры.

​Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.

​Основанием считается сторона, которой параллельна средняя линия.

Как найти среднюю линию треугольника — расскажем дальше, а для начала еще немного разберемся со всеми определениями.

Понятие средней линии прямоугольного треугольника

Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.

Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.

В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.

Свойства средней линии треугольника

Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

Свойства:

1. Средняя линия равна половине длины основания и параллельна ему.
2. Средняя линия отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
3. Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным.
4. Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.

Теорема о средней линии треугольника

Теорема о средней линии треугольника звучит так:

Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:

Докажем теорему:

По условию нам дано, что MA = MB, NA = NC

Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.

(по второму признаку подобия треугольников).

△ABC, то Следовательно, ВС = 2МN. Значит, доказано, что средняя линия равна половине основания.

△ABC, то ∠1 = ∠2 . Так как ∠1 и ∠2 — соответственные углы, то по признаку параллельности прямых MN || BC.

Параллельность средней линии и соответствующего ей основания доказана.

Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.

Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:

Ответ: периметр треугольника ΔMNK равен 10.

Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.

Площадь треугольника равна половине произведения основания на высоту. Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:

Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:

Значит, AC = 2MN = 2 × 3 = 6.

Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:

Значит, BC = 2NP = 2 × 4 = 8.

Тогда найдем площадь большого треугольника, используя формулу, указанную выше:

S = ½ × 6 × 8 = ½ × 48 = 24.

Ответ: площадь большого прямоугольного треугольника равна 24.

Подобие треугольников и пропорциональные отрезки

Теорема 1:

Если на одной из сторон угла отметить равные между собой отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на второй стороне также равные между собой отрезки.

Доказательство:

Докажем сначала лемму: Если в (triangle OBB_1) через середину (A) стороны (OB) проведена прямая (aparallel BB_1) , то она пересечет сторону (OB_1) также в середине.

Через точку (B_1) проведем (lparallel OB) . Пусть (lcap a=K) . Тогда (ABB_1K) — параллелограмм, следовательно, (B_1K=AB=OA) и (angle A_1KB_1=angle ABB_1=angle OAA_1) . Значит, по второму признаку (triangle OAA_1=triangle B_1KA_1 Rightarrow OA_1=A_1B_1) . Лемма доказана.

Перейдем к доказательству теоремы. Пусть (OA=AB=BC) , (aparallel bparallel c) и нужно доказать, что (OA_1=A_1B_1=B_1C_1) .

Таким образом, по данной лемме (OA_1=A_1B_1) . Докажем, что (A_1B_1=B_1C_1) . Проведем через точку (B_1) прямую (dparallel OC) , причем пусть (dcap a=D_1, dcap c=D_2) . Тогда (ABB_1D_1, BCD_2B_1) — параллелограммы, следовательно, (D_1B_1=AB=BC=B_1D_2) . Значит, по первому признаку (triangle A_1B_1D_1=triangle C_1B_1D_2 Rightarrow A_1B_1=B_1C_1) .

Теорема Фалеса:

Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.

Доказательство:

Пусть параллельные прямые (pparallel qparallel rparallel s) разбили одну из прямых на отрезки (a, b, c, d) . Тогда вторую прямую эти прямые должны разбить на отрезки (ka, kb, kc, kd) соответственно.

Проведем через точку (A_1) прямую (pparallel OD) ( (ABB_2A_1) — параллелограмм, следовательно, (AB=A_1B_2) ). Тогда (triangle OAA_1 sim triangle A_1B_1B_2) по двум углам. Следовательно, (dfrac=dfrac Rightarrow A_1B_1=kb) .

Аналогично проведем через (B_1) прямую (qparallel OD Rightarrow triangle OBB_1sim triangle B_1C_1C_2 Rightarrow B_1C_1=kc) и т.д.

Наиболее часто встречающиеся подобия треугольников:

Теорема 2.

Средняя линия треугольника отсекает от него подобный ему треугольник.

Доказательство:

Т.к. средняя линия — это отрезок, соединяющий середины двух сторон, то (dfrac=dfrac=2) .

Таким образом, по двум пропорциональным сторонам и углу между ними ( (angle B) — общий) (triangle A_1BC_1 sim triangle ABC) .

Теорема 3.

Треугольники, образованные диагоналями трапеции и основаниями, подобны.

Доказательство:

Т.к. (ADparallel BC Rightarrow angle OBC=angle ODA) . (angle BOC=angle AOD) как вертикальные. Следовательно, по двум углам (triangle BOCsim triangle AOD) .

Теорема 4.

Высота прямоугольного треугольника, проведенная к гипотенузе, делит его на два подобных треугольника.

Доказательство:

Обозначим (angle ACH=alpha, angle BCH=beta) , т.е. (alpha+beta=90^circ) . Тогда (angle CAH=90^circ-alpha=beta, angle CBH=90^circ-beta=alpha) .

Следовательно, по двум углам (triangle ACHsim triangle BCHsim ABC) .

Теорема 5.

Отрезки, соединяющие основания высот треугольника, отсекают от него подобные ему треугольники.

Эти отрезки также являются биссектрисами углов треугольника, вершинами которого являются основания данных высот.

Доказательство:

1) Рассмотрим четырехугольник (AC_1A_1C) — около него можно описать окружность, т.к. (angle AC_1C=angle AA_1C) . Таким образом, (angle CAA_1=angle CC_1A_1=x) , т.к. опираются на одну и ту же хорду (A_1C) . Таким образом (angle ACA_1=90^circ-x, angle BC_1A_1=90^circ-x Rightarrow angle ACA_1=angle BC_1A_1) .

Значит, по двум углам (triangle A_1BC_1sim triangle ABC) ( (angle B) — общий).

Аналогично доказывается, что (triangle AB_1C_1sim triangle ABC, triangle A_1B_1Csim triangle ABC) .

2) Докажем, что (AA_1, BB_1, CC_1) – биссектрисы углов (A_1, B_1, C_1) в треугольнике (A_1B_1C_1) соответственно.

Обозначим (angle BC_1A_1=angle B_1C_1A=alpha) . Тогда (angle A_1C_1C=90^circ -alpha=angle B_1C_1C) . Значит, (CC_1) – биссектриса угла (C_1) .

Аналогично доказывается про (AA_1) и (BB_1) .

Теорема 6.

Если к окружности из одной точки вне окружности проведены две секущие, то:

Доказательство:

Четырехугольник (ABA_1B_1) описанный, следовательно, (angle BAB_1+angle BA_1B_1=180^circ Rightarrow angle OA_1B_1=180^circ-angle BA_1B_1=angle BAB_1) .

Таким образом, по двум углам ( (angle O) — общий) (triangle OABsim triangle OA_1B_1) .

Теорема 7.

Если к окружности из одной точки проведены касательная и секущая, то:

Доказательство:

Т.к. угол между касательной и хордой, проведенной в точку касания, равен половине дуги, заключенной между ними, то (angle OKA=frac12 buildrelsmileover=angle KBA) .

Следовательно, по двум углам ( (angle O) — общий) (triangle OKAsim triangle OKB) .

Теорема 8.

Если в окружности две хорды пересекаются, то:

Доказательство:

(angle A_1AB_1=angle A_1BB_1) , т.к. опираются на одну и ту же дугу. (angle A_1CB=angle B_1CA) , т.к. они вертикальные. Следовательно, по двум углам (triangle A_1BCsim triangle B_1C) .

Аналогично (triangle ABCsim triangle A_1B_1C) .

[spoiler title=”источники:”]

http://skysmart.ru/articles/mathematic/kak-najti-srednyuyu-liniyu-treugolnika

http://shkolkovo.net/theory/19

[/spoiler]

23
Янв 2014

Категория: Планиметрия

Задачи на подобие треугольников

2014-01-23
2022-01-11

Автор: egeMax |

комментариев 12

Знаете ответ?

Теорема 1:

Если на одной из сторон угла отметить равные между собой отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на второй стороне также равные между собой отрезки.

Доказательство:

Перейдем к доказательству теоремы. Пусть (OA=AB=BC), (aparallel
bparallel c) и нужно доказать, что (OA_1=A_1B_1=B_1C_1).

Таким образом, по данной лемме (OA_1=A_1B_1). Докажем, что (A_1B_1=B_1C_1). Проведем через точку (B_1) прямую (dparallel OC), причем пусть (dcap a=D_1, dcap c=D_2). Тогда (ABB_1D_1, BCD_2B_1) — параллелограммы, следовательно, (D_1B_1=AB=BC=B_1D_2). Значит, по первому признаку (triangle A_1B_1D_1=triangle C_1B_1D_2
Rightarrow A_1B_1=B_1C_1).

Теорема Фалеса:

Доказательство:

Пусть параллельные прямые (pparallel qparallel rparallel s) разбили одну из прямых на отрезки (a, b, c, d). Тогда вторую прямую эти прямые должны разбить на отрезки (ka,
kb, kc, kd) соответственно.

Проведем через точку (A_1) прямую (pparallel OD) ((ABB_2A_1) — параллелограмм, следовательно, (AB=A_1B_2)). Тогда (triangle OAA_1
sim triangle A_1B_1B_2) по двум углам. Следовательно, (dfrac{OA}{A_1B_2}=dfrac{OA_1}{A_1B_1} Rightarrow A_1B_1=kb).

Аналогично проведем через (B_1) прямую (qparallel OD Rightarrow
triangle
OBB_1sim triangle B_1C_1C_2 Rightarrow B_1C_1=kc) и т.д.

Наиболее часто встречающиеся подобия треугольников:

Теорема 2.

Доказательство:

Т.к. средняя линия — это отрезок, соединяющий середины двух сторон, то (dfrac{AB}{A_1B}=dfrac{CB}{C_1B}=2).

Таким образом, по двум пропорциональным сторонам и углу между ними ((angle B) — общий) (triangle A_1BC_1 sim triangle ABC).

Теорема 3.

Доказательство:

Т.к. (ADparallel BC Rightarrow angle OBC=angle ODA). (angle
BOC=angle AOD) как вертикальные. Следовательно, по двум углам (triangle BOCsim triangle AOD).

Теорема 4.

Доказательство:

Обозначим (angle ACH=alpha, angle BCH=beta), т.е. (alpha+beta=90^circ). Тогда (angle
CAH=90^circ-alpha=beta, angle CBH=90^circ-beta=alpha).

Следовательно, по двум углам (triangle ACHsim triangle BCHsim
ABC).

Теорема 5.

Отрезки, соединяющие основания высот треугольника, отсекают от него подобные ему треугольники.

Доказательство:

1) Рассмотрим четырехугольник (AC_1A_1C) — около него можно описать окружность, т.к. (angle AC_1C=angle
AA_1C). Таким образом, (angle CAA_1=angle CC_1A_1=x), т.к. опираются на одну и ту же хорду (A_1C). Таким образом (angle
ACA_1=90^circ-x, angle BC_1A_1=90^circ-x Rightarrow angle
ACA_1=angle BC_1A_1).

Значит, по двум углам (triangle A_1BC_1sim
triangle ABC) ((angle B) — общий).

Аналогично доказывается, что (triangle AB_1C_1sim triangle ABC,
triangle A_1B_1Csim triangle ABC).

2) Докажем, что (AA_1, BB_1, CC_1) – биссектрисы углов (A_1, B_1,
C_1) в треугольнике (A_1B_1C_1) соответственно.

Обозначим (angle BC_1A_1=angle B_1C_1A=alpha). Тогда (angle
A_1C_1C=90^circ -alpha=angle B_1C_1C). Значит, (CC_1) – биссектриса угла (C_1).

Аналогично доказывается про (AA_1) и (BB_1).

Теорема 6.

Доказательство:

Четырехугольник (ABA_1B_1) описанный, следовательно, (angle
BAB_1+angle BA_1B_1=180^circ Rightarrow
angle OA_1B_1=180^circ-angle BA_1B_1=angle BAB_1).

Таким образом, по двум углам ((angle O) — общий) (triangle
OABsim
triangle OA_1B_1).

Теорема 7.

Доказательство:

Т.к. угол между касательной и хордой, проведенной в точку касания, равен половине дуги, заключенной между ними, то (angle OKA=frac12 buildrelsmileover{KA}=angle KBA).

Следовательно, по двум углам ((angle O) — общий) (triangle
OKAsim triangle OKB).

Теорема 8.

Доказательство:

(angle A_1AB_1=angle A_1BB_1), т.к. опираются на одну и ту же дугу. (angle A_1CB=angle B_1CA), т.к. они вертикальные. Следовательно, по двум углам (triangle A_1BCsim
triangle B_1C).

Аналогично (triangle ABCsim triangle A_1B_1C).

План урока:

Пропорциональные отрезки

Определение подобных треугольников

Первый признак подобия треугольников

Второй и третий признаки подобия треугольников

Отношение площадей подобных треугольников

Пропорциональные отрезки

Если известна длина двух отрезков, то можно узнать, во сколько раз один из них больше другого. Например, если некоторый отрезок NM = 24 см, а другой отрезок KP = 4 см, то можно утверждать, что NM в 6 раз длиннее, так как

Величину NM/KP именуют отношением отрезков NM и KP. Надо заметить, что в ряде случаев отношение отрезков можно найти, не зная их длины. Пусть в ∆МКР проведена медиана МН. Очевидно, что отрезок КР будет вдвое длиннее КН, ведь Н – середина КР:

Другой пример – это отношение между диагональю квадрата и его стороной.

Используя теорему Пифагора, несложно показать, что в любом квадрате АВСD

Наконец, в прямоугольном треуг-ке, один из углов которого равен 30°, гипотенуза всегда вдвое длиннее меньшего из катетов:

Если отношение отрезка AB к А₁В₁ равно отношению отрезка СD к С₁D₁, то говорят, что отрезки AB и CD пропорциональны отрезкам А₁В₁ и С₁D₁. Например, пусть

Получается, AВ и CD пропорциональны А₁В₁ и С₁D₁. Важно отметить, что пропорциональны могут быть также сразу три и более отрезка.

Определение подобных треугольников

В жизни нередко можно наблюдать объекты, у которых совпадает форма, но отличаются размеры. В качестве примера можно привести мяч для настольного тенниса и баскетбольный мяч. Оба этих предмета имеют форму шара, на баскетбольный мяч значительно больше. Другой пример – настоящий танк и игрушка, изображающая его. Часто подобны друг другу матрешки, которые вкладываются друг в друга – все они выглядят одинаково, а отличаются только общим размером. Наконец, подобны и знаменитые египетские пирамиды:

Такие объекты в геометрии именуют подобными. Подобны друг другу любые две окружности и любые два квадрата. Но особо важную роль в геометрии играют подобные треугольники. Рассмотрим это понятие подробнее.

Пусть есть два треуг-ка, ∆AВС и ∆А₁В₁С₁, у которых соответственно равны углы:

Стороны, которые лежат против одинаковых углов в таких треуг-ках, именуют сходственными. Ими являются стороны AВ и А₁В₁, ВС и В₁С₁, АС и А₁С₁.

Можно дать такое определение подобных треугольников:

Таким образом, подобие треугольников (оно обозначается символом ∾) обозначает выполнение сразу нескольких равенств:

Отношение между сходственными сторонами подобных треуг-ков именуется коэффициентом подобия и обозначается буквой k:

Грубо говоря, подобие треуг-ков означает, что их форма одинакова, но один из них в несколько раз больше или меньше другого. Чтобы получить, из одного треуг-ка другой, равный ему по размерам, его надо просто «масштабировать». Например, на этом рисунке все стороны исходного треуг-ка просто увеличили в три раза:

Это значит, что коэффициент подобия в данном случае равен 3. Однако важно понимать, что в различных геометрических задачах подобные треуг-ки также могут быть повернуты друг относительно друга:

Задание. ∆AВС подобен ∆DEF. Известно, что

Найдите длину ЕF.

Решение. Как только в задаче появляются подобные треуг-ки, стоит сразу же определить их коэффициент подобия, а для этого надо разобраться, какие стороны будут сходственными. Так как∠А = ∠Е, то лежащие против них стороны DF и ВС– сходственные. Их отношение и будет равно коэффициенту подобия:

Получили, что стороны ∆DEF вдвое длиннее сходственных им сторон ∆AВС. У подобных треуг-ков углы одинаковы, поэтому∠С = ∠D. Отсюда следует, что стороны AВ и ЕF сходственны, а потому ЕF вдвое больше:

Задание. ∆AВС и∆DEF – подобные. Известно, что

Найдите длину ЕF.

Решение. По сравнению с предыдущей задачей изменилось только одно условие, теперь∠А = ∠D. Однако это меняет сходственные стороны. Из подобия треуг-ков следует, что∠С = ∠Е. Тогда сходственными оказываются уже стороны AВ и DF. Найдем коэффициент подобия треугольников:

Сходственными являются также стороны ВС и ЕF (ведь∠А = ∠D), поэтому ЕF в 1,25 раза длиннее:

Эти две задачи показывают, как важно правильно определять сходственные стороны подобных треугольников.

Естественно, что все равные друг другу треуг-ки являются одновременно и подобными, причем их коэффициент подобия равен единице.

Задание. Докажите, что у подобных треуг-ков отношение их периметров равно коэффициенту подобия.

Решение. Пусть подобны ∆ AВС и ∆А₁В₁С₁, причем

Периметр ∆AВС можно вычислить так:

Мы доказали утверждение, сформулированное в условии.

Первый признак подобия треугольников

Оказывается, для того, чтобы доказать подобие треуг-ков, не требуется сравнивать все их углы и находить соотношение всех сторон. Существуют три простых признака подобия треугольников.

Однако прежде, чем сформулировать их, нам придется доказать отдельное утверждение, которое известно как обобщенная теорема Фалеса («обычную», не обобщенную теорему мы уже изучали ранее).

Если прямые ВВ₁ и СС₁ (показаны красным цветом)параллельны, то отрезки AВ и АС пропорциональны отрезкам AВ₁ и АС₁, то есть справедливо соотношение:

Доказывать будем от противного. Пусть отрезки AВ и АС непропорциональны AВ₁ и АС₁. Тогда отметим наАС такую точку Н, которая разобьет АС на пропорциональные отрезки, то есть

Естественно, эта точка не будет совпадать с С₁. Рассмотрим случай, когда она окажется правее, чем С₁:

Теперь поступим следующим образом. Проведем через стороны угла большое число прямых, параллельных ВС, которые будут разбивать АС на одинаковые отрезки. По теореме Фалеса эти же прямые отсекут одинаковые отрезки и на AВ. При этом мы проведем настолько много параллельных прямых, что хотя бы одна из них пересечет отрезок С₁Н:

Пусть эта прямая пересечет отрезок С₁Н в некоторой точке С₂, а сторону AВ в точке В₂. Ясно, что отрезки AВ и АВ₂ пропорциональны отрезкам АС и АС₂, так как они состоят из одинакового количества одинаковых отрезков. Например, на построенном рисунке отношение AB₂ к AB равно 5/8, так как AB₂ состоит из 5 отрезков, отсеченных зелеными параллельными прямыми, а AB состоит из 8 таких отрезков. Аналогично и отношение АС₂ к АС также равно 5 к 8. Таким образом, можно записать:

Здесь мы рассмотрели случай, когда точка Н лежит правее С₁, то есть АН >C₁. Случай, когда АН <АС₁, рассматривается аналогично, и также получается противоречие. Эти противоречия означают, что на самом деле точка Н должна совпадать с С₁, то есть справедливо равенство

ч.т. д.

Теперь, доказав обобщенную теорему Фалеса, мы можем перейти к первому признаку подобия треугольников.

Действительно, пусть есть ∆AВС и ∆А₁В₁С₁, у которых

Так как сумма углов у любого треуг-ка постоянна и составляет 180°, то должны быть одинаковы и третьи углы:

При таком наложении прямые ВС и В₁С₁ окажутся параллельными, так как соответственные углы ∠В₁С₁А и ∠ВСА одинаковы. Но параллельные прямые должны отсекать на сторонах угла пропорциональные отрезки, то есть

У ∆AВС и ∆А₁В₁С₁ углы одинаковы, а лежащие напротив них стороны пропорциональны, следовательно, это подобные треуг-ки.

Задание. Прямая, параллельная стороне AВ ∆AВС, пересекает стороны ВС и АС в точках Е и Р. Известно, что ЕС = 2, ВЕ = 3, ЕР = 3,2. Какова длина AВ?

Решение. В данной задаче есть только два треуг-ка, ∆AВС и ∆РЕС. Докажем их подобие. У них есть общий∠С, а ∠СЕР = ∠СВА, ведь это односторонние углы при параллельных прямых ЕР и AВ. Отсюда следует, что ∆AВС∾∆РЕС. Значит, ∠А = ∠СРЕ.

Далее надо найти коэффициент подобия. Стороны СЕ и ВС лежат против равных углов∠А и ∠СРЕ, поэтому они сходственные.

Задание. По данным рисунка найдите длину КЕ:

Решение. На рисунке показано, что ∠ВСА = ∠СКЕ, а∠А = ∠Е = 90°. То есть у ∆AВС и ∆СКЕ есть два одинаковых угла, и, следовательно, они подобны. Сходственными будут являться стороны AВ и ЕС, с их помощью найдем коэффициент подобия:

Задание. Основания трапеции имеют длины 5 и 8 см. Длины ее боковых сторон составляют 3,6 и 3,9 см. Продолжения боковых сторон пересекаются в точке М. Определите расстояние от М до вершин меньшего основания.

Решение. Для начала выполним построение:

Отрезки ВС и АD параллельны, так как они являются основаниями трапеции. Отсюда получаем равенство соответственных углов:

Теперь посмотрим на ∆АМD и ∆ВМС. МЫ только что выяснили, что у них есть одинаковые углы (∠МВС и ∠МАD), а ∠М является общим для них. Тогда получаем, что эти треуг-ки подобны. Стороны ВС и AD будут сходственными, так как лежат против одного и того же ∠М, поэтому по их длине можно найти коэффициент подобия:

Для нахождения МВ обозначим его длину как х. Тогда отрезок АМ будет иметь длину х + 3,9. Но из подобия треуг-ков следует такое соотношение:

Подставив сюда значение k и выраженные через х длины АМ и МВ, получим уравнение:

МС можно найти таким же путем, обозначив его длину как у. Тогда отрезок МD будет равен у + 3,6, и можно составить уравнение:

Второй и третий признаки подобия треугольников

Существует ещё два признака подобия треуг-ков, которые в решении задач используются значительно реже. Они выводятся непосредственно из первого признака.

Докажем второй признак подобия. Пусть есть ∆AВС и ∆А₁В₁С₁, для которых выполняются соотношения:

Необходимо доказать, что они подобны. Для этого построим ещё один ∆AВС₂, который будет иметь общую сторону с ∆AВС, причем точку С₂ мы выберем так, что будут выполняться условия:

∆А₁В₁С₁ и ∆AВС₂ будут подобными, ведь у них одинаковы два угла. Значит, будет выполняться соотношение

Но тогда ∆AВС и ∆AВС₂ будут равными, ведь у них одинаковы две стороны и угол, образованный этими сторонами:

В итоге у ∆AВС и ∆А₁В₁С₁ оказываются два одинаковых угла, то есть они подобны друг другу

ч. т. д.

Задание. На стороне угла отмечены точки A и В так, что AВ = 5 см и АС = 16 см. На другой стороне этого же угла отмечены точки С и D так, что AD = 8 cм и AF = 10 см. Подобны ли ∆АСD и ∆AFB? 

Решение.

У рассматриваемых треуг-ков есть общий угол ∠А. Найдем отношение сторон, прилегающих к этому углу.

Отношения одинаковы, значит, треуг-ки подобны.

Примечание. В данном случае важно понимать, какие стороны надо делить друг на друга. У ∆АСD известны стороны АС и АD, равные 16 и 8 см. У ∆AFB известны AF и AB, которые составляют 10 и 5 см. Делить надо большую сторону одного треуг-ка на большую сторону другого треуг-ка, то есть 16 на 10. Потом же делим меньшие стороны, то есть 8 на 5.Если получили одно и тоже число, то это значит, что рассмотренные треуг-ки подобны, причем полученное число как раз и является коэффициентом подобия.

Рассмотрим третий признак подобия треуг-ков.

Докажем его. Пусть у ∆AВС и ∆А₁В₁С₁ пропорциональны их стороны:

Можно заметить, что ∆AВС₂ и ∆А₁В₁С₁ подобны, ведь у них совпадают два угла. Тогда верны соотношения:

Самая левая дробь в обоих случаях одинакова, а в других отличны лишь числители. Значит, эти числители одинаковы:

Но тогда у ∆AВС и ∆AВС₂ совпадают все стороны, то есть эти треуг-ки равные. Следовательно. Так как ∆AВС₂ подобен ∆А₁В₁С₁, то и равный ему ∆AВС также подобен ∆А₁В₁С₁

ч. т. д.

Задание. Подобны ли ∆AВС и ∆DEF, если их стороны имеют длины:

Решение.

Для проверки достаточно просто поделить длины сторон друг на друга. При этом большую сторону одного треуг-ка будем делить на большую сторону другого, а меньшую – на меньшую. Если в результате отношение всех трех сторон будет одинаково, то можно утверждать, что треуг-ки подобны:

Все три раза мы получали число 2, именно оно и является коэффициентом подобия треуг-ков.

Отношение площадей подобных треугольников

Если треуг-ки подобны, то их стороны отличаются в k раз, где k– коэффициент подобия. А как соотносятся друг с другом длины их высот, медиан и других характерных отрезков. Несложно догадаться, что они также отличаются в k раз.

Докажем это на примере высот. Пусть есть подобные ∆AВС и ∆А₁В₁С₁, причем их коэффициент подобия равен k:

Проведем в них высоты СН и С₁Н₁:

Теперь сравним ∆АСН и ∆А₁С₁Н₁. Из подобия ∆AВС и ∆А₁В₁С₁ следует, что

Аналогично можно доказать, что в k раз будут отличаться длины медиан и биссектрис.

А каким будет отношение площадей подобных треугольников?Оказывается, что они отличаются уже в k² раз. Докажем это.

Пусть ∆AВС и ∆А₁В₁С₁ подобны с коэффициентом подобия k. Снова проведем в них высоты СН и СН₁:

Запишем очевидные равенства:

В итоге получили, что площади подобных треугольников отличаются в k² раз.

Задание. Известно, у ∆AВС площадь составляет 10, а отрезок AВ имеет длину 5. ∆DEF подобен ∆AВС, причем сторона DE, сходственная AВ, равна 15. Вычислите площадь ∆DEF.

Решение. По условию задачи легко найти коэффициент подобия ∆AВС и ∆DEF, надо лишь поделить одну сходственную сторону на другую:

Задание. Площади двух подобных треуг-ков составляют 75 м² и 300 м². Одна из сторон второго треуг-ка равна 9 м. Вычислите сходственную ей сторону первого треуг-ка.

Решение. Зная площади треуг-ков, легко найдем коэффициент их подобия:

Если коэффициент равен 2, то стороны первого многоугольника вдвое меньше сторон второго, поэтому интересующая нас сторона равна

9:2 = 4,5 м

Ответ: 4,5 м.