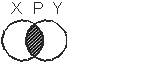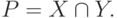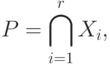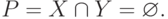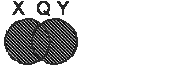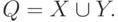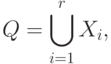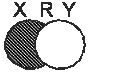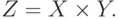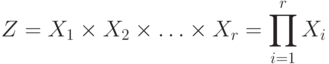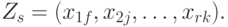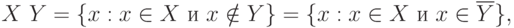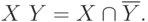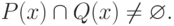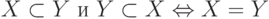Пересечение, объединение и разность множеств
- Пересечение множеств
- Объединение множеств
- Универсум и отрицание
- Свойства операций пересечения и объединения
- Разность множеств
- Формулы включений и исключений
- Примеры
Пересечение множеств
Пересечением множеств A и B называют множество, содержащее те и только те элементы, которые входят одновременно как в множество A, так и в множество B:
$$ A cap B = {x|x in Bbb A и x in Bbb B } $$
Если множества не пересекаются, то $A cap B = varnothing $ – пустое множество в пересечении. Если $B subseteq A$ – подмножество, то $A cap B = B$ – пересечением будет меньшее множество из двух.
Например:
Если A = {1;3;5;9}, Β = {3;7;11}, то $A cap B$ = {3;5}.
Если A = {f|f-прямоугольник}, B = {f|f-ромб}, то $A cap B$ = {f|f-квадрат}.
Если A = ${n|n⋮3, n in Bbb N }$ – натуральные числа, кратные 3, B = ${n|n⋮5, n in Bbb N }$ – натуральные числа, кратные 5, то $A cap B = {n|n⋮15, n in Bbb N}$ – натуральные числа, кратные 15.
Если A = {a│a-слон}, B = {a|a-птица}, то $A cap B = varnothing$.
Объединение множеств
Объединением – множеств A и B называют множество, содержащее те и только те элементы, которые входят хотя бы в одно из множеств, A или B:
$$ A cup B = { x|x in Bbb A или x in Bbb B } $$
Если $B subseteq A$ – подмножество, то $A cap B = A$ – объединением будет большее множество из двух.
Например:
Если A = {1;3;5;9}, Β = {3;7;11}, то $A cup B$ = {1;3;5;7;9;11}.
Если $A = {x|x^2-4 = 0, x in Bbb R}, B = {x|x+3 = 2, x in Bbb R }, то A cup$ B = {-2;-1;2}
Если $A = {n│n in Bbb Z }$- все целые числа, $B = {x|x = frac{a}{b}, a in Bbb Z, b in Bbb N }$ – все дроби, то $A cup B = {x│x in Bbb Q}$ – множество рациональных чисел. Заметим, что в данном случае $A subset B$.
Универсум и отрицание
Универсум (универсальное множество) – множество, включающее в себя все множества, рассматриваемые в данной задаче.
В литературе универсум обозначают U.
На диаграммах Эйлера универсум изображают как множество точек прямоугольника, в котором лежат остальные множества:
Примеры универсумов:
При рассмотрении целочисленных задач, универсум – это множество целых чисел.
При построении двумерных графиков, универсум – это множество всех точек координатной плоскости.
При решении вероятностных задач, универсум – это множество всех возможных исходов цепочек событий.
Отрицание (абсолютное дополнение) множества A – множество всех элементов универсума, не принадлежащих A:
$$ bar{A} = {x|x notin A } $$
Читается «не A».
У отрицания есть любопытное свойство: $bar{bar{Α}} = Α $(два раза «нет» – это «да»).
Например:
Если U = {1;2;3;4;5;6;7}, A = {3;4;5}, то $bar{A} = {1;2;6;7}$
Если U = ${x|x in Bbb R}$ – все действительные числа, A = ${x|x gt 0, x in Bbb R }$ – все положительные действительные числа, то $ bar{A} = {x|x le 0, x in Bbb R}$.
Свойства операций пересечения и объединения
$A cap B = B cap A$
$ A cup B = B cup A $
$(A cap B) cap C = A cap (B cap C)$
$ (A cup B) cup C = A cup ( B cup C) $
$(A cup B) cap C = (A cap C) cup (B cap C)$
$ (A cap B) cup C = (A cup C) cap (B cup C) $
$A cap A = A$
$ A cup A = 0 $
Взаимодействие с отрицанием, пустым множеством и универсумом
$A cap bar{A} = varnothing $
$A cap U = A$
$A cap varnothing = varnothing$
$A cup bar{A} = U $
$A cup U = U$
$A cup varnothing = A$
$ overline{(A cap B)} = bar{A} cup bar{B} $
$ overline{(A cup B)} = bar{A} cap bar{B} $
$ (A cup B) cap A = A $
$ (A cap B) cup A = A $
Разность множеств
Разностью двух множеств A и B называют множество, в которое входят все элементы из множества A, не принадлежащие множеству B:
$$ AB = {x|x in Bbb A , x notin B} $$
Читается «A без B».
На диаграммах Эйлера разности для пересекающихся множеств выглядят так:
Получается, что отрицание – частный случай разности: $ bar{A} = {x|x in Bbb U, x notin A } $= UA
«Не A» – это «универсум без A».
Формулы включений и исключений
Рассмотрим два конечных пересекающихся множества A и B.
Пусть число элементов во множествах равно n(A)и n(B) соответственно. А число элементов в пересечении $n(A cap B)$.
Вопрос: сколько всего элементов в обоих множествах, т.е. чему равно $n(A cup B)$?
Сумма n(A)и n(B) даст нам больше, чем общее количество, потому что мы два раза посчитаем то, что попадает в пересечение. Значит, если отнять одно пересечение, получится как раз то, что ищем:
$$n(A cup B) = n(A)+ n(B)-n(A cap B)$$
Выведем аналогичную формулу для трёх пересекающихся конечных множеств.
Сумма n(A)+ n(B)+n(C) учтёт каждое из парных пересечений по два раза. Поэтому, аналогично задаче с двумя множествами, нужно отнять всё, что попадает в парные пересечения, т.е. отнять сумму $(n(A cap B)+n(A cap C)+n(B cap C) )$. Но после этого получится, что мы лишний раз отняли $n(A cap B cap C)$; значит, его нужно «вернуть».
Получаем:
$$ n(A cup B cup C) = n(A)+ n(B)+n(C)- $$
$$ -(n(A cap B)+n(A cap C)+n(B cap C) )+n(A cap B cap C) $$
Примеры
Пример 1. Найдите пересечение данных множеств:
а) A = {0;5;8;10},
B = {3;6;8;9}
$A cap B$ = {8}
$б) A = {x|x lt 3, x in Bbb R}, $
$ B = {x|x gt 1, x in Bbb R} $
$A cap B = {x|1 lt x lt 3, x in Bbb R}$ – отрезок
$в) A = {x|x lt 3, x in Bbb R}, $
$ B = {x|x gt 1, x in Bbb N} $
$A cap B = {x|1 lt x lt 3, x in Bbb N } или A cap B = {2}$ – одна точка
г) A = {f|f-правильный многоугольник},
B = {f|f-четырехугольник}
$A cap B = {f|f-квадрат}$
Пример 2. Найдите объединение данных множеств:
а) A = {0;5;8;10}, B = {3;6;8;9}
$A cup B$ = {0;3;5;6;8;9;10}
б) A = {1;2}, B = {1;2;3;4}
$A subset B$ – строгое подмножество
$A cup B $ = B = {1;2;3;4}
$в) A = {x|x lt 1, x in Bbb R}, B = {x|x gt 1,x in Bbb R} $
$A cup B = {x|x neq 1, x in Bbb R }$
$г) A = {n│n⋮3, n in Bbb Z}, B = {n|n⋮9,n in Bbb N} $
$B subset A$ – строгое подмножество
$ A cup B = A = {n│n⋮3, n in Bbb Z} $
Пример 3. Найдите отрицание данного множества на данном универсуме:
а) U = {1;2;3;4;5}, A = {2;3}
$ bar{A} = {1;4;5}$
б) U = ${x│x in Bbb Q }$, A = ${ frac{4}{5}, frac{7}{8} }$
$ bar{A} = {x|x neq frac{4}{5}, x neq frac{7}{8}, x in Bbb Q} $
$в) U = {x│x in Bbb R}, A = {x|x ge 2, x in Bbb R} $
$bar{A} = {x|x lt 2, x in Bbb R}$
г) U = { 0;1}, A = { 0}
$ bar{A} = {1}$
Пример 4. Найдите обе разности данных множеств:
а) A = {0;1;2;3;4}, B = {2;4}
AB = {0;1;3}, $BA = {∅}$
б) A = {0;1;3}, B = {2;4;6}
AB = {0;1;3}, BA = {2;4;6}
$в) A = {x|x gt 1, x in Bbb R}, $
$ B = {x|x lt 3, x in Bbb R} $
AB $ = {x|x ge 3, x in Bbb R}$
BA $ = {x|x le 1,x in Bbb R} $
$ г*) A = {(x,y)|x gt 0, x in Bbb R, y in Bbb R} $
$ B = {(x,y)|x le 5, x in Bbb R, y in Bbb R} $
AB $ = {(x,y)|x gt 5, x in Bbb R, y in Bbb R} $
BA $ = {(x,y)|x le 0, x in Bbb R, y in Bbb R} $
Пример 5. Из 100 студентов умеют программировать на Python 28 человек, на Java 30 человек, на C# 42 человека, на Python и Java 8 человек, на Python и C# 10 человек, на Java и C# 5 человек. Все три языка знают 3 студента. А сколько студентов не умеют программировать на этих языках?
n(U) = 100
n(A) = 28, n(B) = 30, n(C) = 42
$ n(A cap B) = 8, n(B cap C) = 5, n(A cap C) = 10 $
$n(A cap B cap C) = 3$
Всего программистов:
$ n(A cup B cup C) = n(A)+n(B)+n(C)- $
$ (n(A cap B)+n(B cap C)+n(A cap C) )+n(A cap B cap C) $
$n(A cup B cup C) = 28+30+42-(8+5+10)+3 = 100-23+3 = 80$
Число не умеющих программировать:
$n(U)-n(A cup B cup C) = 100-80 = 20$
Ответ: 20 человек
На чтение 13 мин Просмотров 2к. Опубликовано 16.12.2021
Содержание
- Теория множеств
- Что такое множество в математике и как оно обозначается
- Множество натуральных чисел
- Множество целых чисел
- Множество рациональных чисел
- Операции над множествами
- Объединение
- Пересечение множеств
- Дополнение
- Универсум и отрицание
- Разность множеств
- Формулы включений и исключений
- Свойства операций над множествами
- Счетные и несчетные множества
- Исследование множеств с помощью координатной прямой
- Примеры из реальной жизни
- Геометрические фигуры
- Отрезки
- Еще пример
Теория множеств
Говоря простым языком, множество — это элементарный математический объект, который содержит определенный набор данных, предметов или чисел. Это исходное математическое понятие, которое невозможно представить другими терминами. Именно поэтому множество описывается как набор разрозненных элементов, мыслимое как единое целое. Понятие множества ввел немецкий математик Георг Кантор, который развил собственную теорию трансфинитных чисел, позволяющую оперировать вполне упорядоченными бесконечными множествами.
Георг Кантор разработал уникальную программу стандартизации всех математических знаний, согласно которой любой математический объект является тем или иным множеством. К примеру, согласно канторовской теории, любое натуральное число — это одноэлементное множество, принадлежащее надмножеству натурального ряда. Натуральный ряд, в свою очередь, считается подмножеством целого ряда, а целое множество — подмножеством действительного или вещественного ряда.
Теория Георга Кантора вызвала широкий резонанс в математических кругах. Многие современники негативно отзывались о его работах, особенно его учитель Леопольд Кронекер, который не принимал канторовского определения натурального числа. Несмотря на это, теория множеств получила признание позже, когда группа французских математиков под псевдонимом Никола Бурбаки предприняла попытку перевести весь математический аппарат на теоретико-множественный язык.
Что такое множество в математике и как оно обозначается
Множество – это количество предметов или чисел, обладающих общими свойствами.
Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.
В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A1, A2 и т. д.
Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a1, a2 и т. д.
Границы совокупности обозначаются фигурными скобками { }.
Пример:
А = {а, в, с, у} – А состоит из четырех элементов.
Записать совокупность Z согласных букв в слове «калькулятор»:
Z = {к, л, т, р}, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.
Принадлежность элементов множеству обозначается знаком – Є.
Пример: N = {a, b, c, y}, а Є N – элемент «а» принадлежит N.
Выделяют три вида множеств:
- конечные — совокупности, имеющие максимальный и минимальный предел (например, отрезок);
- бесконечные — не являющиеся конечными (например, числовые);
- пустые (обозначаются Ø) – не имеющие элементов.
Если две разные совокупности содержат одинаковые элементы, то одна из них (со всеми своими элементами) является подмножеством другой и обозначается знаком — ⊆.
Пример: А = {а, в, с, у} и В = {а, в, с, е, к} – все элементы А являются элементами совокупности В, следовательно А ⊆ В.
Если множества состоят из одинаковых элементов, их называют равными.
Пример: А = {23, 29, 48} и В = {23, 29, 48}, тогда А = В.
В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.
Множество натуральных чисел
К совокупности натуральных чисел (N) относятся цифры, используемые при счете — от 1 до бесконечности.
Натуральные числа используют для исчисления порядка предметов. Обязательное условие данной числовой группы — каждое следующее число больше предыдущего на единицу.
N = {9, 11, 13, 15……}.
Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.
Множество целых чисел
Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:
Z = {-112, -60, -25, 0, 36, 58, 256}.
Следовательно, N — подмножество Z, что можно записать как N ⊆ Z. Любое натуральное число можно назвать так же и целым.
Множество рациональных чисел
Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:
Q={-½; 0; ½, 5; 10}.
Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:
5 = 5/1 = 10/2 = 25/5;
0,45 = 45/100 = 9/20.
Следовательно, N и Z являются подмножествами Q.
Операции над множествами
Точно так же, как и все математические объекты, множества можно складывать и вычитать, то есть совершать операции.
Если две группы образуют третью, содержащую элементы исходных совокупностей – это называется суммой (объединением) множеств и обозначается знаком ∪.
Пример: В = {1, 6, 17} и С = {2, 13, 18}, В ∪ С= {1, 2, 6, 13, 17, 18}.
Если две группы совокупностей образуют третью, состоящую только из общих элементов заданных составляющих, это называется произведением (пересечением) множеств, обозначается значком ∩.
Пример: В = {36, 42, 53, 64} и С = {32, 42, 55, 66}, В ∩ С = {42}.
Если две совокупности образуют третью, включающую элементы одной из заданных групп и не содержащую элементы второй, получается разность (дополнение) совокупностей, обозначается значком /.
Пример: В = {12, 14, 16, 18} и С = {13, 14, 15, 17}, В / С = {14}.
В случае, когда В / С = С / В, получается симметричная разность и обозначается значком Δ.
Объединение
Пересечение множеств
Пересечением множеств A и B называют множество, содержащее те и только те элементы, которые входят одновременно как в множество A, так и в множество B:
$$ A cap B = {x|x in Bbb A и x in Bbb B } $$
Если множества не пересекаются, то $A cap B = varnothing $ — пустое множество в пересечении. Если $B subseteq A$ — подмножество, то $A cap B = B$ – пересечением будет меньшее множество из двух.
Например:
Если A = {1;3;5;9}, Β = {3;7;11}, то $A cap B$ = {3;5}.
Если A = {f|f-прямоугольник}, B = {f|f-ромб}, то $A cap B$ = {f|f-квадрат}.
Если A = ${n|n⋮3, n in Bbb N }$ — натуральные числа, кратные 3, B = ${n|n⋮5, n in Bbb N }$ — натуральные числа, кратные 5, то $A cap B = {n|n⋮15, n in Bbb N}$ — натуральные числа, кратные 15.
Если A = {a│a-слон}, B = {a|a-птица}, то $A cap B = varnothing$.
Дополнение
С помощью данных диаграмм можно разобраться с законами де Моргана по поводу логической интерпретации операций над множествами.
Универсум и отрицание
Универсум (универсальное множество) – множество, включающее в себя все множества, рассматриваемые в данной задаче.
В литературе универсум обозначают U.
На диаграммах Эйлера универсум изображают как множество точек прямоугольника, в котором лежат остальные множества:
Примеры универсумов:
- При рассмотрении целочисленных задач, универсум – это множество целых чисел.
- При построении двумерных графиков, универсум – это множество всех точек координатной плоскости.
- При решении вероятностных задач, универсум – это множество всех возможных исходов цепочек событий.
Отрицание (абсолютное дополнение) множества A — множество всех элементов универсума, не принадлежащих A:
$$ bar{A} = {x|x notin A } $$
Читается «не A».
У отрицания есть любопытное свойство: $bar{bar{Α}} = Α $(два раза «нет» — это «да»).
Например:
Если U = {1;2;3;4;5;6;7}, A = {3;4;5}, то $bar{A} = {1;2;6;7}$
Если U = ${x|x in Bbb R}$ — все действительные числа, A = ${x|x gt 0, x in Bbb R }$ — все положительные действительные числа, то $ bar{A} = {x|x le 0, x in Bbb R}$.
Разность множеств
Разностью двух множеств A и B называют множество, в которое входят все элементы из множества A, не принадлежащие множеству B:
$$ AB = {x|x in Bbb A , x notin B} $$
Читается «A без B».
На диаграммах Эйлера разности для пересекающихся множеств выглядят так:
Получается, что отрицание – частный случай разности: $ bar{A} = {x|x in Bbb U, x notin A } $= UA
«Не A» — это «универсум без A».
Формулы включений и исключений
Рассмотрим два конечных пересекающихся множества A и B.
Пусть число элементов во множествах равно n(A)и n(B) соответственно. А число элементов в пересечении $n(A cap B)$.
Вопрос: сколько всего элементов в обоих множествах, т.е. чему равно $n(A cup B)$?
Сумма n(A)и n(B) даст нам больше, чем общее количество, потому что мы два раза посчитаем то, что попадает в пересечение. Значит, если отнять одно пересечение, получится как раз то, что ищем:
$$n(A cup B) = n(A)+ n(B)-n(A cap B)$$
Выведем аналогичную формулу для трёх пересекающихся конечных множеств.
Сумма n(A)+ n(B)+n(C) учтёт каждое из парных пересечений по два раза. Поэтому, аналогично задаче с двумя множествами, нужно отнять всё, что попадает в парные пересечения, т.е. отнять сумму $(n(A cap B)+n(A cap C)+n(B cap C) )$. Но после этого получится, что мы лишний раз отняли $n(A cap B cap C)$; значит, его нужно «вернуть».
Получаем:
$$ n(A cup B cup C) = n(A)+ n(B)+n(C)- $$
$$ -(n(A cap B)+n(A cap C)+n(B cap C) )+n(A cap B cap C) $$
Свойства операций над множествами
Операции над множествами обладают свойствами, аналогичными правилу свойств сложения, умножения и вычитания чисел:
Коммутативность – переместительные законы:
- умножения S ∩ D = D ∩ S;
- сложения S ∪ D = D ∪ S.
Ассоциативность – сочетательные законы:
- умножения (S ∩ F) ∩ G = S ∩ (F ∩ G);
- сложения (S ∪ F) ∪ G = S ∪ (F ∪ G).
Дистрибутивность – законы распределения:
- умножения относительно вычитания S ∩ (F – G) = (S ∩ F) – (S ∩ G);
- умножения относительно сложения G ∩ (S ∪ F) = (G ∩ S) ∪ (G ∩ F);
- сложения относительно умножения G ∪ (S ∩ F) = (G ∪ S) ∩ (G ∪ F).
Транзитивность — законы включения:
- если S ⊆ Fи F ⊆ J, то S ⊆ J;
- если S ⊆ F и F ⊆ S, то S = F.
Идемпотентность объединения и пересечения:
- S ∩ S = S;
- S ∪ S = S.
О других свойствах операций можно узнать из картинки:
Счетные и несчетные множества
Если между элементами двух групп можно установить взаимное немногозначное соответствие, то эти группы чисел равномощны, при условии равного количества элементов.
Мощность данной математической единицы равна количеству элементов в ней. Например, множество всех нечетных положительных чисел равномощно группе всех четных чисел больше ста.
В случае, когда бесконечное множество равномощно натуральному ряду чисел, оно называется счетным, а если оно не равномощно — несчетным. Другими словами, счетная единица — это совокупность, которую мы можем представить в виде последовательности чисел по порядковым номерам.
Но не все группы действительных чисел счетные. Примером несчетной группы предметов является бесконечная десятичная дробь.
Теория множеств — достаточно широкая тема, которая требует глубокого изучения. Она затрагивает начальный курс математики, изучается в среднем звене школьной программы по алгебре. Высшая математика, математический анализ, логика – рассматривают законы, теоремы, аксиомы множеств, на которых основаны фундаментальные знания науки.
Исследование множеств с помощью координатной прямой
Исследовать и выражать пересечения и объединения числовых множеств удобно с помощью координатной прямой и выделяемых на ней числовых промежутков. Любая выбранная точка разбивает все расположенные на такой прямой числа на два открытых числовых луча. Например, точка с координатой $36,6$ создаст промежутки, записываемые как $(−∞, 36,6)$, $(36,6, +∞)$. Сама точка не входит в состав ни одного из них, поэтому числовая прямая, представляющая собой множество всех действительных чисел $R = (−∞, +∞)$, представляет собой в данном случае объединение $ (−∞, −36,6) cup {36,6} cup (36,6, +∞)$.
Если рассматриваемую точку со значением $36,6$ добавить к одному из открытых числовых лучей, т.е. промежутку $(−∞, 36,6)$ или $(36,6, +∞)$, то такой промежуток перестанет быть открытым. Это записывается как $(−∞, 36,6]$ или $[36,6, +∞)$, т.е. вхождение граничного числа в состав числового луча обозначается квадратной скобкой. Множество действительных чисел $R$ в этом случае будет выглядеть как
$(−∞, 36,6] cup (36,6, +∞)$ либо $(−∞, 36,6) cup [36,6, +∞)$.
Если разбить числовую прямую на части не точкой, а отрезком или лучом, то все рассмотренные закономерности будут соблюдаться и в этих случаях. Более того, они соблюдаются и при разбиении самих числовых промежутков (отрезков, лучей).
Например, точка с координатой $14$ на промежутке $(5, 51]$ разобьет его на промежутки $(5, 14) ∪ {14} ∪ (14, 51]$. Включив точку в один из промежутков, можно получить такие записи, как $(5, 14] cup (14, 51]$, $(5, 14) cup [14, 51]$. Приняв за разбивающую точку число $51$, ограничивающее рассматриваемый промежуток справа и входящее в его состав, получим объединение множества ${51}$ и интервала $(5, 51)$, т.е. $(5, 51] = (5, 51) cup {51}$.
Подобные закономерности справедливы и в случаях, когда координатная прямая разбивается на промежутки несколькими точками. Например, числа $−6$, $0$ и $7$ разобьют ее на промежутки $(−∞, −6)$, $(−6, 0)$, $(0, 7)$, $(7, +∞)$, а множество действительных чисел $R$ будет представлено как $(−∞, −6) ∪ {−6} ∪ (−6, 0) ∪ {0} ∪ (0, 7) ∪ {7} ∪ (7, +∞)$.
С помощью координатной прямой удобно анализировать пересечения и объединения множеств. Они изображаются друг под другом на координатных прямых с совпадающими точками и направлениями отсчета. Для отображения объединения множеств координатные прямые отмечают слева квадратной скобкой, для обозначения пересечения используется фигурная скобка.
На дополнительной координатной прямой, размещаемой под исходными, изображаются искомые пересечение или объединение. На ней все граничные точки исходных множеств отмечают поперечными чертами, а после уточнения — полыми или сплошными точками. Графически вхождение промежутка в пересечение или объединение изображается штриховкой, вхождение точки — сплошной точкой, невхождение – полой.
Пересечение множеств $A$ и $B$ графически отображается промежутками, над которыми есть штриховка, с добавлением отдельных точек, принадлежащих обоим множествам. Объединение графически проявляется там, где есть штриховка хотя бы у одного из множеств, а также всех сплошных точек.
Пример 1
Найти пересечение и объединение множеств $A = [-3, 4)$ и $B = [0, 7)$ .
Для решения применим графический метод:
Рисунок 1. Графическое решение задачи. Автор24 — интернет-биржа студенческих работ
Видно, что объединение множеств представляет собой диапазон от крайней левой точки $-3$ включительно до крайней правой $7$ исключая ее. Пересечение множеств начинается от числа $0$. Оно входит в оба множества и ограничивает пересечение слева. Правой границей пересечения является $4$, но оно не входит в первое множество, поэтому здесь граница интервала будет открытой.
Ответ:
$A cap B = [0, 4); A cup B = [-3, 7); $
Примеры из реальной жизни
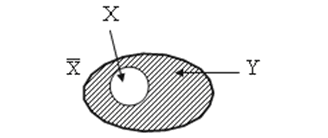
Геометрические фигуры
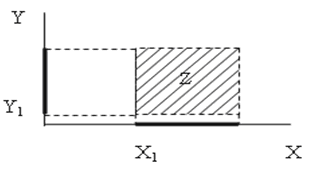
Допустим, существует множество X, которое содержит прямоугольники с разными длинами сторон. Также существует множество Y, содержащее ромбы с разными углами. Из курса геометрии мы знаем, что ромб — это параллелограмм, у которого все стороны равны, а прямоугольник — это параллелограмм, у которого равны все углы. В множествах X и Y могут встретиться ромбы с углами по 90 градусов или прямоугольники с одинаковыми сторонами. Фигура, у которой все углы прямые, а все стороны равны — это квадрат. Соответственно, пересечением множеств ромбов X и прямоугольников Y является множество квадратов Z.
Отрезки
Пусть у нас есть два отрезка, которые задаются координатами X = [1, 3] и Y = [2, 4]. Пересечением данных множеств будет отрезок [2, 3], так как именно эти числа входят в диапазон значений обоих отрезков на числовой оси.
Еще пример
Давайте попробуем узнать пересечение пятиэлементных множеств простых и четных чисел. Простое число — это число, которое делится только на себя и на единицу. Четное число — число, которое делится на 2 без остатка. Итак, наши множества S = {2, 3, 5, 7, 11} и E = {2, 4, 6, 8, 10}. Введем эти данные в онлайн-калькулятор и получим результат в виде P = {2}.
Введение
Среди всех наук
математика занимает особое место.
Математика определяется как наука о
пространственных формах и количественных
отношениях реального мира. Объектами
изучения в математике являются логические
модели, построенные для описания явлений
природы и общества. Математика изучает
соотношения между элементами этих
моделей. Если математическая модель
верно отражает суть данного явления,
то она позволяет вскрывать необнаруженные
вначале закономерности. В силу большой
абстрактности одна и та же модель может
описывать различные процессы. Например,
уравнение
описывает характер и радиоактивного
распада, и изменения температуры тела,
и протекания демографического процесса.
При изучении
явлений природы и общества мы на каждом
шагу сталкиваемся с изменением величины,
с зависимостью одной величины от другой.
Введение в математику понятий переменной
величины и функции позволило перейти
от решения отдельных разрозненных задач
к созданию общих методов их решения.
Развитие математического анализа,
создание которого является одним из
величайших достижений человеческого
разума, оказало огромное влияние на
общий прогресс науки и техники.
В предлагаемом
курсе лекций мы рассмотрим теорию
множеств, теорию пределов, дифференциальное
и интегральное исчисления. Изучение
материала следует проводить строго
последовательно, так как в математике
все понятия тесно связаны между собой.
Лекция 1. Теория
множеств.
1.1. Понятие
множества.
В математике все
понятия делятся на первичные
и определяемые
через
первичные или уже известные.
Понятие множества
является первичным, то есть не определяется
через более простые. Слова совокупность,
система, набор, объединение
являются синонимами слова множество.
Множество
– это совокупность некоторых объектов.
Объекты, которые образуют множество,
называются элементами
или точками этого множества.
Пример 1.1.
Примерами
множеств
служат множество натуральных чисел,
множество молекул в данном теле, множество
студентов и т.д.
Будем обозначать
множества большими латинскими буквами
A,B,…,X,Y,…,
а их элементы малыми – a,b,…,x,y,….
Запись
означает, что x
является элементом множества A,
принадлежит данному множеству.
Соответственно,
–
x
не является элементом множества A.
Запись
означает,
что A
является подмножеством B
(можно:
).
Запись
означает пустое множество. Верна запись:
.
Приведём пример пустого множества:
множество круглых квадратов.
Можно записывать
множества так:
,
.
Если множества A
и B
равны, пишут
.
Равенство множеств не всегда означает,
что
.
Например, если
,
,
где p
и q
– простые числа, большие 2. Ясно, что
,
но не установлено, верно ли, что
.
1.2. Операции над
множествами.
Для множеств можно
ввести арифметические операции сложения
и умножения, которые обладают свойствами,
аналогичными свойствам операций сложения
и умножения чисел.
Пусть даны два
произвольных множества A
и B.
Определение 1.1.
Суммой
(объединением)
множеств A
и B
называется множество C,
состоящее из элементов множеств A
или B.
|
Легко видеть,
|
|
Определение 1.2.
Произведением
(пересечением) множеств A
и B
называется множество C,
состоящее из элементов, одновременно
принадлежащих множествам A
и B.
|
Если |
|
Определение 1.3.
Разностью
множеств A
и B
называется множество C,
состоящее из элементов множества A,
которых нет в множестве B.
|
|
|
|
В общем случае |
|
Определение 1.4.
Дополнением
подмножества C
до множества A
называется подмножество D,
элементы которого не принадлежат С и
☼ Задание.
Привести примеры суммы, разности,
произведения двух или нескольких
множеств, примеры подмножеств.
☼
1.3. Символика
математической логики.
Импликация:
(из
следует β).
Эквивалентность:
(
и β
эквивалентны).
Квантор
всеобщности:
(для всякого x,
принадлежащего множеству A,
имеет место предположение
).
Квантор
существования:
(существует такой y,
принадлежащий множеству B,
что имеет место β).
или
означает существование единственного
элемента х.
Отрицание
:
.
На примере разберём, как работает эта
операция.
Пример 1.2.
Построим
отрицание:
,
.
Таким образом,
чтобы построить отрицание данной
логической формулы, содержащей кванторы
и
,
необходимо
заменить на
,
на
и на свойство, стоящее после двоеточия
поставить отрицание.
Пример 1.3.
.
Построим отрицание этого предложения:
.
Конъюнкция
«и»:
или
(
и β
– некоторые высказывания).
Дизъюнкция
«или»:
.
Операции конъюнкции
и дизъюнкции связаны следующим образом:
,
.
Логические операции
конъюнкции и дизъюнкции элементов
аналогичны соответственно операциям
пересечения и объединения множеств.
Составим таблицу истинности для
высказываний
и
.
1 означает истинное высказывание, 0 –
ложное высказывание.
Таблица истинности:
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
Для операций над
множествами можно составить аналогичную
таблицу.
1.4. Свойства
множеств.
Коммутативность:
1˚.
.
2˚.
.
Ассоциативность:
3˚.
.
4˚.
.
Доказательство
законов 1˚–4˚ следует из определений
1.1 и 1.2.
Дистрибутивность:
5˚.
.
6˚.
.
Дистрибутивные
законы доказываются с помощью таблицы
истинности.
Закон отрицания
отрицания:
7˚.
.
Законы де Моргана:
8˚.
.
9˚..
Докажем свойство
8˚:
Доказательство
свойства 9˚ проводится аналогичным
образом.
Законы де Моргана
можно доказать и при помощи таблицы
истинности.
10˚.
.
11˚.
.
12˚.
.
13˚.
.
14˚.
,
где I
– объединение всех множеств.
15˚.
.
16˚.
.
17˚.
.
Определение 1.5.
Множество
Х называется бесконечным,
если
в множестве Х имеется столько элементов,
что их количество больше n.
Определение 1.6.
Два множества
называются эквивалентными,
если между их элементами можно установить
взаимно однозначное соответствие (),
то есть существует такое правило, закон,
по которому
соответствует вполне определённый
элемент
.
При этом в силу этого правила двум разным
элементам
соответствуют
два разных элемента
,
и каждый элемент
соответствует некоторому элементу
.
Пример 1.4.
Если A
– множество точек на окружности радиуса
,
B
– множество точек на окружности радиуса
R
с тем же центром, то
.
Очевидно, что если
,
то
.
|
|
Определение 1.7.
Если
,
то множество X
называется счётным.
Естественно, само
множество натуральных чисел N
счётно
.
Множество всех
чётных натуральных чисел
счётно
.
,
Таким образом, подмножество множества
оказалось эквивалентным всему множеству.
Счётное множество
будем записывать в виде последовательности
его элементов:
.
♦ Предложение
1.1. Счётная
сумма
счётных множеств Ek
есть счётное множество.
Доказательство:
Перенумеруем
элементы счётных множеств Ek
в следующем порядке:
,
выбрасывая те элементы, которые были
до этого занумерованы: может случиться,
что Ek
и El
имеют общие элементы. В результате
получим бесконечную последовательность
элементов
,
исчерпывающих множество E.
Это доказывает, что Е
– счётное множество.
Аналогично
доказывается, что конечная сумма
счётных или
конечных множеств, среди которых есть
хотя бы одно счётное, счётна. ■
1.5. Мощность
множества.
Если два конечных
множества эквивалентны, то они состоят
из одного и того же числа элементов.
Если множества М
и N
эквивалентны, то они имеют одинаковую
мощность.
Мощность множества
натуральных чисел (то есть
счётного
множества) обозначается символом
(алеф
нуль) = Card N.
Мощность множества действительных
чисел отрезка [0,1] обозначается
или
С
и носит название мощность
континуума.
7
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
16.2. Действия над множествами
Над множествами, как и над другими математическими величинами, можно производить некоторые действия, например, выполнять пересечение множеств, их объединение, вычитание, находить дополнение, декартово произведение и прочее.
Пересечением множеств 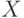




Рис.
16.1.
Пересечение множеств
Пересечение множеств 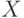
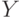
Это свойство носит название ” конъюнкция” или “логическое умножение”.
Если рассматривают пересечение нескольких множеств 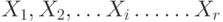
где 
Операция пересечения множеств подчиняется переместительному закону, т.е. 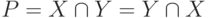
Если множества 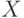
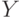
С помощью операции пересечения множеств можно, например, выявить множество типоразмеров конструктивных элементов, общих печатным платам 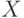

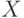

Объединение множеств X и Y приводит к образованию нового множества 
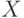

На рисунке это можно представить так:
Рис.
16.2.
Объединение множеств
Заштрихованная область – множество 
Математически объединение множеств 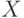
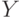
Это свойство носит название ” дизъюнкция” или “логическое сложение”.
Если рассматривать объединение нескольких множеств, то запись примет вид
где 
Операция объединения множеств, также как и операция пересечения, подчиняется переместительному закону.
С помощью этой операции можно подсчитать, например, число типоразмеров конструктивных элементов для печатных плат 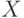
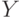
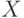

Разность множеств X и Y есть новое множество 


На рис. 16.3. 
Рис.
16.3.
Разность множеств
Математически разность множеств 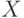
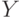
С помощью этой операции можно выявить сугубо индивидуальные признаки объекта, например, число типоразмеров конструктивных элементов, принадлежащих только плате 
Дополнением (или отрицанием) множества 




Схематически это изображается так (рис. 16.4):
Рис.
16.4.
Дополнение множеств
Множество 

С помощью операции дополнения множества можно выявить все дополнительные недостающие признаки проектируемого изделия и подвергнуть их анализу.
Декартовым произведением множеств 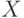
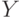
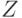



На рис. 16.5 декартово произведение множеств 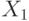

Рис.
16.5.
Декартово произведение множеств
Декартово произведение двух множеств используют для исследования всевозможных паросочетаний.
Декартово произведение нескольких множеств
представляет собой множество r – строчек, каждая из которых образуется упорядоченной композицией элементов исходных множеств, т.е.
Операция декартова произведения множеств не обладает переместительным свойством, т.е. 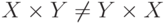
Разбиением множества 
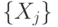

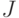

Это можно прочитать так:
Ряд прикладных задач разбиения множества конструктивных элементов высокого уровня на элементы более низкого уровня (например, задача разбиения множества микросхем блока РЭС на отдельные субблоки) сводится к операциям разбиения множеств.
Понятие пустого множества 

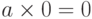
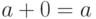
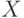

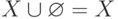
Существует понятие множества 


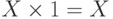
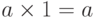
Множество 

В конкретных приложениях в качестве универсального множества могут использоваться различные общие подмножества.
Пример. Среди множества комплектов конструкторских документов на изготовление изделий РЭС полный комплект конструкторских документов на изготовление изделий является универсальным множеством этих документов или когда при рассмотрении множеств микросхем отдельных субблоков РЭС выделяют универсальное множество таких микросхем на всю данную радиоэлектронную систему в целом.
Универсальное множество обладает свойством, не имеющим аналога в алгебре чисел, а именно: для любого множества 
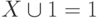
В объединение этих множеств должны входить как элементы множества 

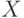



На основании этих рассуждений определяют дополнение множества 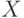
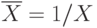
С помощью операции дополнения можно в удобном виде представить разность множеств
т.е.
Многие определения теории множеств записывают в виде математических выражений, содержащих некоторые логические символы.
К числу таких символов относится символ следствия (импликации) ” 
Например, запись 


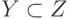
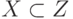
Другие символы связаны с применением кванторов общности и кванторов существования.
Квантор общности – это операция, которая сопоставляет 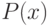
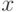
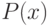
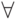
Например, запись 
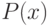
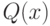
Квантор существования утверждает, что существует по крайней мере один объект 
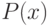
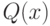
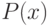
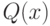
Квантор существования обозначается ” 
 |
( x) )) |
В теории множеств используется понятие логической эквивалентности (в смысле то же самое, что и …), обозначаемой ” 
нужно читать: ” Выполнение условий 
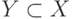
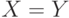

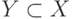
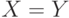
Дмитрий Михайлович Беляев
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Конъюнкция или логическое умножение (в теории множеств – это пересечение)
Конъюнкция является сложным логическим выражением, которое истинно в том и только том случае, когда оба простых выражения являются истинными. Такая ситуация возможно лишь в единственном случае, во всех остальных случаях конъюнкция ложна.
Обозначение: &, $wedge$, $cdot$.
Таблица истинности для конъюнкции
Рисунок 1.
Свойства конъюнкции:
- Если хотя бы одно из подвыражений конъюнкции ложно на некотором наборе значений переменных, то и вся конъюнкция будет ложной для этого набора значений.
- Если все выражения конъюнкции истинны на некотором наборе значений переменных, то и вся конъюнкция тоже будет истинна.
- Значение всей конъюнкции сложного выражения не зависит от порядка записи подвыражений, к которым она применяется (как в математике умножение).
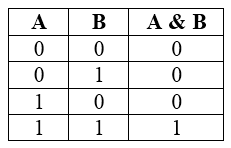
Дизъюнкция или логическое сложение (в теории множеств это объединение)
Дизъюнкция является сложным логическим выражением, которое истинно практически всегда, за исключением, когда все выражения ложны.
Обозначение: +, $vee$.
Таблица истинности для дизъюнкции
Рисунок 2.
Свойства дизъюнкции:
- Если хотя бы одно из подвыражений дизъюнкции истинно на некотором наборе значений переменных, то и вся дизъюнкция принимает истинное значение для данного набора подвыражений.
- Если все выражения из некоторого списка дизъюнкции ложны на некотором наборе значений переменных, то и вся дизъюнкция этих выражений тоже ложна.
- Значение всей дизъюнкции не зависит от порядка записи подвыражений (как в математике – сложение).
«Логические операции и их свойства» 👇
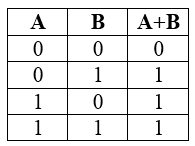
Отрицание, логическое отрицание или инверсия (в теории множеств это отрицание)
Отрицание – означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО и в итоге получаем, что если исходное выражение истинно, то отрицание исходного – будет ложно и наоборот, если исходное выражение ложно, то его отрицание будет истинно.
Обозначения: не $A$, $bar{A}$, $¬A$.
Таблица истинности для инверсии
Рисунок 3.
Свойства отрицания:
«Двойное отрицание» $¬¬A$ является следствием суждения $A$, то есть имеет место тавтология в формальной логике и равно самому значению в булевой логике.
Импликация или логическое следование
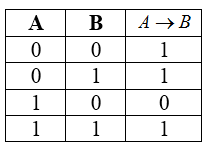
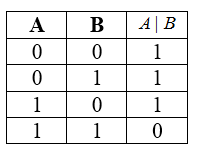
Импликация – это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть, данная логическая операция связывает два простых логических выражения, из которых первое является условием ($A$), а второе ($A$) является следствием условия ($A$).
Обозначения: $to$, $Rightarrow$.
Таблица истинности для импликации
Рисунок 4.
Свойства импликации:
- $A to B = ¬A vee B$.
- Импликация $A to B$ ложна, если $A=1$ и $B=0$.
- Если $A=0$, то импликация $A to B$ истинна при любом значении $B$, (из лжи может следовать истинна).
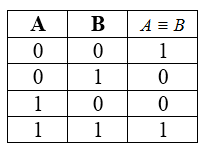
Эквивалентность или логическая равнозначность
Эквивалентность – это сложное логическое выражение, которое истинно на равных значениях переменных $A$ и $B$.
Обозначения: $leftrightarrow$, $Leftrightarrow$, $equiv$.
Таблица истинности для эквивалентности
Рисунок 5.
Свойства эквивалентности:
- Эквивалентность истинна на равных наборах значений переменных $A$ и $B$.
- КНФ $A equiv B = (bar{A} vee B) cdot (A cdot bar{B})$
- ДНФ $A equiv B = bar{A} cdot bar{B} vee A cdot B$
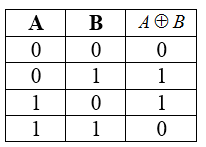
Строгая дизъюнкция или сложение по модулю 2 ( в теории множеств это объединение двух множеств без их пересечения)
Строгая дизъюнкция истинна, если значения аргументов не равны.
Для функции трёх и более переменных результат выполнения операции будет истинным только тогда, когда количество аргументов равных $1$, составляющих текущий набор — нечетное. Такая операция естественным образом возникает в кольце вычетов по модулю 2, откуда и происходит название операции.
Обозначения: $A oplus B$ (в языках программирования), $A≠B$, $A wedge B$ (в языках программирования).
Таблица истинности для операции сложения по модулю два
Рисунок 6.
Свойства строгой дизъюнкции:
- $a oplus 0 = a$(идемпотентность)
- $a oplus 1 = bar{a}$(отрицание)
- $a oplus a = 0$(получение 0)
- $a oplus b = b oplus a$(коммутативность)
- $(a oplus b) oplus c = a oplus (b oplus c)$(ассоциативность)
- $(a oplus b) oplus b = a$(поглощение)
- $bar{a} oplus b = a oplus bar{b} = (a equiv b)$(сравнения по модулю)
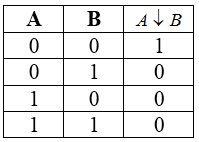
Стрелка Пирса
Бинарная логическая операция, булева функция над двумя переменными. Названа в честь Чарльза Пирса и введена в алгебру логики в $1880—1881$ гг.
Обозначения: $downarrow$ , ИЛИ-НЕ
Таблица истинности для стрелки Пирса
Рисунок 7.
Свойства:
Стрелка Пирса, как и конъюнкция, дизъюнкция, отрицание, образует базис для булевых функций двух переменных. При помощи стрелки Пирса, можно построить все остальные логические операции, например:
$X downarrow X = ¬X$— отрицание
$(X downarrow Y) downarrow (X downarrow Y) equiv X vee Y$ — дизъюнкция
$(X downarrow X) downarrow (Y downarrow Y) equiv X wedge Y$ — конъюнкция
$((X downarrow X) downarrow Y) downarrow ((X downarrow X) downarrow Y) = X to Y$ — импликация
В электронике стрелка Пирса представлена в виде элемента, который носит название «операция 2ИЛИ-НЕ» (2-in NОR).
Штрих Шеффера
Булева функция двух переменных или бинарная логическая операция. Введена в рассмотрение Генри Шеффером в 1913 г.
Обозначения: $|$, эквивалентно операции И-НЕ.
Таблицей истинности для функции штрих Шеффера
Рисунок 8.
Свойства:
Штрих Шеффера образует базис для всех булевых функций двух переменных. Применяя штрих Шеффера можно построить остальные операции, например,
$X mid X = ¬X$ — отрицание
$(X mid Y) mid (X mid Y) = (X wedge Y)$ — конъюнкция
$(X mid X) mid (Y mid Y) = X vee Y$ — дизъюнкция
$X mid ¬X$ — константа 1
Для электроники это означает, что реализация схем возможна с использованием одного типового элемента (правда это дорогостоящий элемент).
Порядок выполнения логических операций в сложном логическом выражении
- Инверсия(отрицание);
- Конъюнкция (логическое умножение);
- Дизъюнкция и строгая дизъюнкция (логическое сложение);
- Импликация (следствие);
- Эквивалентность (тождество).
Для того чтобы изменить указанный порядок выполнения логических операций, необходимо использовать скобки.
Общие свойства
Для набора из $n$ логических переменных существует ровно $2^n$ различных значений. Таблица истинности для логического выражения от $n$ переменных содержит $n+1$ столбец и $2^n$ строк.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме