Как найти отрицание предиката

Как найти отрицание предиката

Логические операции над предикатами

Над предикатами можно проделывать те же самые логические операции, что и над высказываниями: отрицание, конъюнкцию, дизъюнкцию, импликацию, эквивалентность. Рассмотрим эти операции в их связи с операциями над множествами.

Отрицание предиката

Определение 19.1. Отрицанием n-местного предиката P(x_1,x_2,ldots,x_n), определенного на множествах M_1,M_2,ldots,M_n, называется новый n-местный предикат, определенный на тех же множествах, обозначаемый lnot P(x_1,x_2,ldots,x_n) (читается: “неверно, что P(x_1,x_2,ldots,x_n), который превращается в истинное высказывание при всех тех и только тех значениях предметных переменных, при которых исходное высказывание превращается в ложное высказывание.

Другими словами, предикат lnot P(x_1,x_2,ldots,x_n) таков, что для любых предметов a_1in M_1,a_2in M_2,ldots,a_nin M_n высказывание lnot P(a_1,a_2,ldots,a_n) является отрицанием высказывания P(a_1,a_2,ldots,a_n).

Например, нетрудно понять, что отрицанием одноместного предиката “x leqslant 3“, определенного на множестве mathbb{R}, является одноместный предикат “x>3“, определенный на том же множестве mathbb{R}. Отрицанием предиката “Река x впадает в озеро Байкал” является предикат “Река x не впадает в озеро Байкал” (оба одноместных предиката определены на множестве названий рек). Отрицанием предиката “sin^2x+cos^2x=1” является предикат “sin^2x+cos^2xne1” (x,yin mathbb{R}).

Теорема 19.2. Для n-местного предиката P(x_1,x_2,ldots,x_n), определенного на множествах M_1,M_2,ldots,M_n, множество истинности его отрицания lnot P(x_1,x_2,ldots,x_n) совпадает с дополнением множества истинности данного предиката: (lnot P)^{+}= overline{P^{+}}.

Здесь следует понимать, что дополнение рассматривается в множестве

M_1times M_2times ldotstimes M_n, то есть (lnot P)^{+}= M_1times M_2times ldotstimes M_nsetminus P^{+}.

Доказательство. Согласно определениям 19.1, 18.3 и определению дополнения множества имеем

begin{aligned}(lnot P)^{+}&= bigl{(a_1,a_2, ldots, a_n)colon, lambda bigl(P(a_1,a_2,ldots, a_n)bigr)=0bigr}=\ &= bigl{(a_1,a_2,ldots,a_n)colon, (a_1,a_2,ldots,a_n)notin P^{+}bigr}=\ &= overline{P^{+}}= (M_1times M_2times ldotstimes M_n)setminus P^{+}, end{aligned}

что и требовалось доказать.

Следствие 19.3. Отрицание предиката будет тождественно истинным тогда и только тогда, когда исходный предикат тождественно ложен.

Доказательство. В предыдущей лекции (пункт “Множество истинности предиката”) тождественная истинность предиката выражена на языке множества истинности; она означает, что (lnot P)^{+}= M_1times M_2times ldotstimes M_n. Подставим в это равенство значение для (lnot P)^{+} из настоящей теоремы:

(M_1times M_2times ldotstimes M_n) setminus P^{+}= M_1times M_2times ldotstimes M_n,.

Вспоминая определение разности двух множеств и учитывая, что P^{+}subseteq M_1times M_2times ldotstimes M_n, заключаем, что P^{+}=varnothing. Значит, предикат P(x_1,x_2,ldots,x_n) тождественно ложен. Следствие доказано.

Рассмотрим еще один пример. Требуется выяснить, является ли предикат O(f)colon “f — нечетная функция” отрицанием предиката E(f)colon “f — четная функция” (оба одноместных предиката определены на множестве всех действительных функций одного действительного аргумента). Множество истинности O^{+} предиката O(f) не является дополнением множества истинности E^{+} предиката E(f), потому что не всякая функция, не являющаяся четной, будет непременно нечетной. Другими словами, существуют функции, не являющиеся одновременно ни четными, ни нечетными (приведите пример!). Следовательно, предикат O(f) не есть отрицание предиката E(f).

Замечание 19.4. В алгебре высказываний существенным было не содержание высказывания, а лишь его значение истинности, т.е. отождествлялись (не различались) между собой, с одной стороны, все истинные высказывания, а с другой — все ложные. В некотором смысле аналогичная ситуация имеется и в алгебре предикатов: здесь не различают равносильные предикаты. Подходя с такой точки зрения к определению 19.1 отрицания предиката, можем за отрицание данного предиката P(x_1,x_2,ldots,x_n) принять любой из равносильных предикатов, удовлетворяющих этому определению. Например, отрицанием предиката “|x|>2“, заданного на mathbb{R}, является каждый из следующих (равносильных между собой) предикатов:

|x|leqslant 2,qquad (x geqslant -2)lor (x leqslant 2),qquad xin[-2;2],

а отрицанием предиката “x^2 geqslant 0“, также определенного на mathbb{R} (этот предикат тождественно истинный), является каждый из следующих предикатов:

sin{x}=2,quad x^2<0,quad e^x<0,quad |x|<0 и т.д.

Сделанное замечание следует иметь в виду при рассмотрении и остальных логических операций в настоящем параграфе.

Конъюнкция двух предикатов

Определение 19.5. Конъюнкцией “-местного предиката P(x_1,x_2,ldots,x_n), определенного на множествах M_1,M_2,ldots,M_n, и m-местного предиката Q(y_1,y_2,ldots,y_m), определенного на множествах N_1,N_2,ldots,N_m, называется новый (n+m)-местный предикат, определенный на множествах

M_1,M_2,ldots,M_n,, N_1,N_2,ldots,N_m, обозначаемый P(x_1,x_2,ldots,x_n)land Q(y_1,y_2,ldots,y_m)

(читается “P(x_1,x_2,ldots,x_n) и Q(y_1,y_2,ldots,y_m)“), который превращается в истинное высказывание при всех тех и только тех значениях предметных переменных, при которых оба исходных предиката превращаются в истинные высказывания.

Другими словами, предикат P(x_1,x_2,ldots,x_n)land Q(y_1,y_2,ldots,y_m) таков, что для любых предметов a_1in M_1,a_2in M_2,ldots,a_nin M_n и b_1in N_1,b_2in N_2,ldots,b_min N_m высказывание P(a_1,a_2,ldots,a_n)land Q(b_1, b_2, ldots, b_n) является конъюнкцией высказываний P(a_1,a_2,ldots,a_n) и Q(b_1, b_2, ldots,b_m).

Например, конъюнкцией двух одноместных предикатов “x>-3” и “x<3“, определенных на mathbb{R}, будет одноместный предикат “(x>-3)lor (x<3)“, записываемый короче в виде: “-3<x<3“, который равносилен предикату “|x|<3” (см. замечание 19.4).

Другой пример. Конъюнкцией двух одноместных предикатов “x=0” и “y=0“, заданных на mathbb{R}, является двухместный предикат “(x=0)lor (y=0)“, заданный на mathbb{R}^2, который равносилен предикату “x^2+y^2=0“, определенному также на mathbb{R}^2.

Операцию конъюнкции можно применять к предикатам, имеющим общие переменные. В этом случае число переменных в новом предикате равно числу n+m-k, где n — число переменных первого предиката, m — число переменных второго предиката, k — число переменных общих для обоих предикатов. Именно таков первый из только что рассмотренных двух примеров. Более того, если оба предиката определены на одних и тех же множествах и зависят от одних и тех же переменных, то для них справедлива следующая теорема.

Теорема 19.6. Для n-местных предикатов P(x_1,x_2,ldots,x_n) и Q(x_1,x_2,ldots,x_n), определенных на множествах M_1,M_2,ldots,M_n, множество истинности конъюнкции P(x_1,x_2,ldots,x_n)land Q(x_1,x_2,ldots,x_n) совпадает с пересечением множеств истинности исходных предикатов:

(Pland Q)^{+}= P^{+}cap Q^{+}

Доказательство. Согласно определениям 19.5, 18.3 и определению пересечения множеств имеем

begin{aligned}(Pland Q)^{+}&= bigl{(a_1,a_2,ldots, a_n)colon, lambdabigl(P(a_1, a_2, ldots, a_n)land Q(a_1,a_2, ldots,a_nbigl)bigr)=1bigr}=\[2pt] &= bigl{(a_1,a_2,ldots,a_n)colon, lambdabigl(P(a_1,a_2,ldots,a_n)bigr)=1,, lambdabigl(Q(a_1,a_2, ldots,a_n)bigl)=1bigl}=\[2pt] &= bigl{(a_1,a_2,ldots,a_n)colon, lambdabigl(P(a_1, a_2,ldots, a_n)bigr)= 1bigr},cap\ &phantom{=~} cap bigl{(a_1,a_2,ldots,a_n)colon, lambdabigl(Q(a_1,a_2, ldots, a_n)bigr)=1bigr}=\[2pt] &= P^{+}cap Q^{+}.end{aligned}

Следствие 19.7. Конъюнкция двух предикатов тождественно истинна тогда и только тогда, когда оба данных предиката тождественно истинны.

Доказательство. Согласно пункту “Множество истинности предиката”, тождественная истинность предиката Pland Q означает, что

(Pland Q)^{+}= M_1times M_2times ldotstimes M_n,.

Тогда на основании теоремы P^{+}cap Q^{+}= M_1times M_2times ldotstimes M_n, т.е. пересечение двух подмножеств P^{+} и Q^{+} множества M_1times M_2times ldotstimes M_n совпадает с самим этим множеством. Следовательно,

P^{+}= Q^{+}= M_1times M_2times ldotstimes M_n,,

а это означает, что предикаты P и Q тождественно истинны.

Значительный раздел школьной математики составляют системы уравнений и неравенств. При их решении используется теорема 19.6. Пусть, например, требуется решить систему неравенств |x|<3,~ x geqslant 2. Для этого нужно найти множество истинности предиката “(|x|<3)land (x geqslant 2)“, определенного на mathbb{R}. Используем теорему 19.6:

bigl((|x|<3)land (x geqslant 2)bigr)^{+}= (|x|<3)^{+}cap (x geqslant 2)^{+}= (-3;3)cap [2;+infty)= [2;3).

Таким образом, решением данной системы является множество (полуинтервал) [2;3).

Следует отметить, что в предикаты P(x_1,x_2,ldots,x_n) и Q(x_1,x_2,ldots,x_n), о которых идет речь в теореме 19.6, некоторые предметные переменные могут в действительности не входить, т.е., как говорят, быть фиктивными. Это нужно понимать так, что значение истинности высказывания, в которое превращается данный предикат, не зависит от того, какие предметы подставляются вместо таких (фиктивных) переменных. При решении систем уравнений и неравенств данная ситуация встречается часто. Так, например, решения системы уравнений begin{cases}x+y=1,\[-2pt] y+z=2,\[-2pt] z+x=3end{cases} образуют множество, состоящее из одной упорядоченной тройки чисел (1;0;2), хотя первое уравнение не зависит от z, второе — от x, а третье — от y.

Дизъюнкция двух предикатов

Определение 19.8. Дизъюнкцией n-местного предиката P(x_1, x_2, ldots, x_n), определенного на множествах M_1,M_2,ldots,M_n, и m-местного предиката Q(y_1,y_2,ldots,y_m), определенного на множествах N_1,N_2,ldots,N_m, называется новый (n+m)-местный предикат, определенный на множествах M_1,M_2,ldots,M_n и N_1,N_2,ldots,N_m, обозначаемый

P(x_1, x_2, ldots, x_n)lor Q(y_1,y_2,ldots,y_m)

(читается “P(x_1, x_2, ldots, x_n) или Q(y_1,y_2,ldots,y_m)“), который превращается в истинное высказывание при всех тех и только тех значениях предметных переменных, при которых в истинное высказывание превращается по меньшей мере один из исходных предикатов.

Другими словами, предикат P(x_1, x_2, ldots, x_n)lor Q(y_1,y_2,ldots,y_m) таков, что для любых предметов

a_1in M_1,a_2in M_2,ldots,a_nin M_n и b_1in N_1,b_2in N_2,ldots,b_min N_m

высказывание P(a_1, a_2, ldots, a_n)lor Q(b_1,b_2, ldots, b_m) является дизъюнкцией высказываний P(a_1, a_2, ldots, a_n) и Q(b_1,b_2,ldots,b_m).

Операцию дизъюнкции, как и операцию конъюнкции (см. абзац перед теоремой 19.6), можно применять, в частности к предикатам, имеющим общие переменные. Например, дизъюнкцией двух одноместных предикатов “x — четное число” и “x — простое число”, определенных на mathbb{N}, является одноместный предикат, определенный на mathbb{N}: “x — четное или простое число”.

Дизъюнкцией одноместных предикатов “xne0” и “yne0“, определенных на mathbb{R}, является двухместный предикат “(xne0)lor (yne0)“, определенный на mathbb{R}^2, который равносилен предикату ” x^2+y^2ne0″ над mathbb{R}^2.

Следующая теорема аналогична теореме 19.6.

Теорема 19.9. Для n-местных предикатов P(x_1, x_2, ldots, x_n) и Q(x_1, x_2, ldots, x_n), определенных на множествах M_1,M_2,ldots,M_n, множество истинности дизъюнкции P(x_1, x_2, ldots, x_n)lor Q(x_1, x_2, ldots, x_n) совпадает с объединением множеств истинности исходных предикатов:

(Plor Q)^{+}= P^{+}cup Q^{+}.

Доказательство аналогично доказательству теоремы 19.6, поэтому предлагаем провести его самостоятельно.

Следствие 19.10. Дизъюнкция двух предикатов есть выполнимый предикат тогда и только тогда, когда по меньшей мере один из данных предикатов выполним.

Доказательство. Согласно § 18 (пункт”Множество истинности предиката”) выполнимость предиката Plor Q означает, что (Plor Q)^{+}ne varnothing. Отсюда на основании теоремы 19.9 имеем P^{+}cup Q^{+}ne varnothing. Последнее возможно в том и только в том случае, если P^{+}nevarnothing или Q^{+}ne varnothing, т.е. если выполним предикат P или выполним предикат Q.

Следствие 19.11. Дизъюнкция двух предикатов тождественно ложна тогда и только тогда, когда оба данных предиката тождественно ложны.

Доказательство предлагается провести самостоятельно.

Например, пусть требуется решить уравнение x^2-x-6=0, т. е. найти множество истинности этого предиката, определенного на mathbb{R}. Находим его, применяя теорему 19.9. Тогда

begin{aligned}bigl{xcolon, x^2-x-6=0bigr}&= bigl{xcolon, (x+2)(x-3)=0bigr}= bigl{xcolon, (x+2=0)lor (x-3=0)bigr}=\ &= {xcolon, x+2=0}cup {xcolon, x-3=0}= {-2}cup {3}= {-2;3}.end{aligned}

В другом примере дизъюнкция (x^2+y^2<0)lor (xy=0) двух двухместных предикатов, определенных на mathbb{R}, есть выполнимый предикат, потому что выполним один из них: xy=0 (проверьте).

Свойства отрицания, конъюнкции и дизъюнкции предикатов

После введения трех операций над предикатами возникают вопросы: как они влияют на равносильность предикатов и каковы закономерности образования с помощью этих операций равносильных предикатов? Аналогичны вопросы для следования предикатов. Ответ дает следующая теорема.

Теорема 19.12. Если во всех формулах теоремы 3.2 под P,,Q,,R понимать предикаты, определенные на соответствующих множествах, знак leftrightarrow всюду заменить знаком Leftrightarrow, а знак to — знаком Rightarrow, то получим верные утверждения о предикатах.

Доказательство. Рассмотрим, например, вторую из формул д) теоремы 3.2. Она превращается в следующее утверждение:

bigl(Plor (Qland R)bigr)~ Leftrightarrow~ bigl((Plor Q)land (Plor R)bigr)

означающее равносильность предикатов Plor (Qland R) и (Plor Q)land (Plor R) независимо от предикатов P,,Q,,R. Проверим, верно ли данное утверждение. В самом деле, каждый из двух предикатов при любой подстановке вместо предметных переменных конкретных предметов из соответствующих множеств превращается в такое высказывание, которое на основании тавтологии из теоремы 3.2 (пункт д) имеет одинаковые значения истинности. На основании определения равносильности предикатов это и означает, что данные предикаты равносильны.

Импликация и эквивалентность двух предикатов

Импликация P(x_1, x_2, ldots, x_n)to Q(y_1, y_2, ldots, y_m) определяется как такой предикат, что для любых предметов

a_1in M_1,~ a_2in M_2,~ ldots,~ a_nin M_n и b_1in M_1,~ b_2in M_2,~ ldots,~ b_min M_m

высказывание P(a_1, a_2, ldots, a_n)to Q(b_1, b_2, ldots, b_m) является импликацией высказываний P(a_1, a_2, ldots, a_n) и Q(b_1, b_2, ldots, b_m). Аналогично определяется эквивалентность двух предикатов. Нетрудно проверить, что импликация двух предикатов, зависящих от одних и тех же переменных, есть тождественно истинный предикат тогда и только тогда, когда ее заключение является следствием посылки, а эквивалентность тождественно истинна, если и только если исходные предикаты равносильны. Свойства этих операций над предикатами, подобно свойствам операций отрицания, конъюнкции и дизъюнкции над предикатами (см. теорему 19.12), получаются из соответствующих тавтологий теоремы 3.3. Так, если P,,Q,,R — предикаты, то, например,

а) bigl(Pto (Qto R)bigr)Rightarrow bigl((Pto Q)to (Pto R)bigr);
д) bigl(lnot Qland (Pto Q)bigr)Rightarrowlnot P;
п) (Pleftrightarrow Q)Leftrightarrow (Qleftrightarrow P)

и т.д. Аналогично, из тавтологий теоремы 3.4 получаются равносильности, выражающие одни логические операции над предикатами через другие. Например,

a) (Pto Q)Leftrightarrow (lnot Plor Q);
в) (Pland Q)Leftrightarrow lnot(lnot Plandlnot Q);
ж) (Pleftrightarrow Q)Leftrightarrow bigl((Pto Q)land (Qto P)bigr)

и так далее для любых предикатов P,,Q,,R.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Примеры:

S
(x,y):

S+
R

A(x):

Утверждения:

n-местный
предикат
,
заданный на множествах
будет:

  1. Тождественно-истинным
    тогда и только тогда, когда
    ;

  2. Тождественно-ложным
    тогда и только тогда, когда
    ;

  3. Выполнимым,
    тогда и только тогда, когда
    ;

  4. Опровержимым,
    тогда и только тогда, когда

Примеры:

P(x):
“x
– простое число” определен на множестве
N
(натуральных чисел), а множество
– множество всех простых чисел.

Q(x):
определен на множествеR,
множество истинности

F(x):
«диагонали параллелограмма x
перпендикулярны» определен на множестве
всех параллелограммов, множество
истинности
– множество всех ромбов.

§ 4. Равносильность предикатов

Определение.
Два n-местных предиката
,
и

заданных над одними и теми же множествами

называютсяравносильными
тогда и только тогда, когда их множества
истинности совпадают:

Равносильность
предикатов P
и Q
будем обозначать P↔Q.

Переход
от предиката
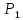к равносильномуназываетсяравносильным
преобразованием.

Определение.
Предикат
,
заданный на множествахназываетсяследствием
предиката
,
заданного над теми же множествами тогда
и только тогда, когда P+
Q+.

Q
– следствие P
записываем так: P
Q.

Теорема.
Каждые два тождественно истинных
предиката, заданных на одних и тех же
множествах, равносильны.

Обратно,
всякий предикат, равносильный тождественно
истинному предикату, сам является
тождественно истинным предикатом.

Пример 1

  1. –одноместный
    предикат P(x),
    P+={-4}.

  2. При
    выполняется равенство.
    Не является предикатом, это – ложное
    высказывание.

  3. .
    Предложение является одноместным
    предикатом P(x),
    P+={1}.

  4. Существует
    такое число x,
    что
    .
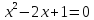    Не является предикатом. Истинное
    высказывание.

  5. –P(x),
    P+=
    (3,
    +∞).

  6. Однозначное
    число x
    кратно 3 – P(x),
    P+={0,
    3, 6 , 9}.

  7. –не
    предикат.

  8. –P(x,
    y)
    – двухместный предикат, P+=
    {(0; 0)}

Пример
2.
Какие предикаты тождественно истинные:

  5. при
    не тождественно истинный.

§ 5. Логические операции над предикатами Отрицание предиката

Определение.
Отрицанием предиката   P(x)   называется
новый предикат   ,  
который принимает значение «истина»
при всех значениях
,
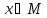при которых предикат  P(x)
принимает значение «ложь» и принимает
значение «ложь» при тех значениях
,
при которых предикат  P(x)  
принимает значение «истина».

Из
этого определения следует, что
.

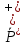Определение.
Отрицанием n-местного
предиката
,
определенного на множествахназываетсяn-местный
предикат, определенный на тех же
множествах, обозначаемый
,
который превращается в истинное
высказывание при всех тех значениях
предметных переменных, при которых
исходный предикат превращается в ложное
высказывание.

То
есть, предикат
таков, что для любыхвыказываниеявляется
отрицанием высказывания.

Примеры:

,
отрицанием одноместного предиката
является
,
определенного на множествеR.

,
.

Теорема.
Для n-местного
предиката
,
определенного на множествах,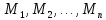
множество истинности его отрицаниясовпадает с дополнением множества
истинности данного предиката:.
Дополнение рассматривается в множествах,
то есть.

Доказательство

Согласно
определению:

Следствие.
Отрицание предиката будет тождественно
истинным тогда и только тогда, когда
исходный предикат будет тождественно
ложным.

Доказательство

–тождественно
истинный предикат, определен на множествах
,
тогда.

По
теореме имеем:

.

Отсюда
.

Так
как если
,
то,
значит предикаттождественно ложен.

Примеры:

есть
любой из равносильных (
)
предикатов:

–тождественнно
истинный предикат, задан на множестве
R.

Отрицание
предиката
также определенного наR:

и
т.д.

Конъюнкция двух предикатов

Определение.
Конъюнкцией двух предикатов P(x)
и Q(x)
называется новый предикат P(x)&Q(x),
который принимает значение истина при
тех и только тех значениях
,
при которых каждый из предикатов
принимает значение «истина» и принимает
значение «ложь» во всех остальных
случаях.

Пример
1.
Конъюнкцией двух одноместных предикатов

иопределенных наR,
будет одноместный предикат
,
который может быть записан:,
который равносилен предикату

Пример
2.
Конъюнкция двух одноместных предикатов
и,
заданных наR,
является двухместный предикат
,
заданный наR,
равносилен предикату
,
определенному наR.

Теорема.
Для n-местных
предикатов
и,
определенных на множествах,
множество истинности конъюнкциисовпадает с пересечением множеств
истинности исходных предикатов:

Доказательство:

Следствие.
Конъюнкция
двух предикатов тождественно истинна
тогда и только тогда, когда оба данных
предиката тождественно истинны.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник
Автор статьи

Татьяна Шкляр

Эксперт по предмету «Информатика»

Задать вопрос автору статьи

Понятие предиката

Определение 1

Предикат – утверждение, которое содержит переменные, принимающие значение $1$ или $0$ (истинно или ложно) в зависимости от значений переменных.

Пример 1

Например, выражение $x=x^5$ является предикатом, т.к. оно является истинным при $x=0$ или $x=1$ и ложным при всех остальных значениях $x$.

Определение 2

Множество, на котором предикат принимает только истинные значения, называется множеством истинности предиката $I_p$.

Замечание 1

Предикатом в программировании является функция, которая принимает один или более аргументов и возвращает значения булева типа.

Логотип baranka

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Предикат называется тождественно-истинным, если на любом наборе аргументов он принимает истинное значение:

$P (x_1, dots, x_n)=1$

Предикат называется тождественно-ложным, если на любом наборе аргументов он принимает ложное значение:

$P (x_1, dots, x_0)=0$

Предикат называется выполнимым, если хотя бы на одном наборе аргументов он принимает истинное значение.

Т.к. предикаты могут принимать только два значения (истинно/ложно или $0/1$), то к ним можно применять все операции алгебры логики: отрицание, конъюнкция, дизъюнкция и т.д.

Примеры предикатов

Пусть предикат $R(x, y)$: $«x = y»$ обозначает отношение равенства, где $x$ и $y$ принадлежат множеству целых чисел. В этом случае предикат R будет принимать истинное значение для всех равных $x$ и $y$.

Другой пример предиката — РАБОТАЕТ($x, y, z$) для отношения «$x$ работает в городе y в компании $z$».

Еще один пример предиката — НРАВИТСЯ($x, y$) для «x нравится y» для $x$ и $y$, которые принадлежат $M$ — множеству всех людей.

Таким образом, предикатом является все то, что утверждается или отрицается о субъекте суждения.

«Предикаты и кванторы» 👇

Операции над предикатами

Рассмотрим применение операций алгебры логики к предикатам.

Логические операции:

Определение 3

Конъюнкция двух предикатов $A(x)$ и $B(x)$ — предикат , который принимает истинное значение при тех и только тех значениях $x$ из $T$, при которых каждый из предикатов принимает истинное значение, а ложное значение — во всех остальных случаях. Множество истинности $T$ предиката — пересечение множеств истинности предикатов $A(x)$ и $B(x)$. Например: предикат $A(x)$: «$x$ — чётное число», предикат $B(x)$: «$x$ делится на $5$». Таким образом, предикатом будет выражение «$x$ — чётное число и делится на $5$» или «$x$ делится на $10$».

Определение 4

Дизъюнкция двух предикатов $A(x)$ и $B(x)$ — предикат , который принимает ложное значение при тех и только тех значениях $x$ из $T$, при которых каждый из предикатов принимает ложное значение и принимает истинное значение во всех остальных случаях. Множество истинности предиката — объединение областей истинности предикатов $A(x)$ и $B(x)$.

Определение 5

Отрицание предиката $A(x)$ — предикат, который принимает истинное значение при всех значениях $x$ из $T$, при которых предикат $A(x)$ принимает ложное значение и наоборот. Множество истинности предиката $A(x)$ — дополнение $T’$ к множеству $T$ в множестве $x$.

Определение 6

Импликация предикатов $A(x)$ и $B(x)$ — предикат , который является ложным при тех и только тех значениях $x$ из $T$, при которых $A(x)$ — истинно, а $B(x)$ — ложно, и принимает истинное значение во всех остальных случаях. Читается: «Если $A(x)$, то $B(x)$».

Пример 2

Пусть $A(x)$: «Натуральное число $x$ делится на $3$»;

$B(x)$: «Натуральное число $x$ делится на $4$».

Составим предикат: «Если натуральное число $x$ делится на $3$, то оно делится и на $4$».

Множество истинности предиката — объединение множества истинности предиката $B(x)$ и дополнения к множеству истинности предиката $A(x)$.

Над предикатами помимо логических операций можно выполнять квантовые операции: применение квантора всеобщности, квантора существования и т.д.

Кванторы

Определение 7

Кванторы — логические операторы, применение которых к предикатам превращает их в ложные или истинные высказывания.

Определение 8

Квантор — логические операции, которые ограничивают область истинности предиката и создают высказывание.

Чаще всего используют кванторы:

  • квантор всеобщности (обозначается символом $forall x$) — выражение «для всех $x$» («для любого $x$»);

  • квантор существования (обозначается символом $exists x$) — выражение «существует $x$ такое, что… »;

  • квантор единственности и существования (обозначается $exists !x$) — выражение «существует точно одно такое $x$, что… ».

В математической логике существует понятие связывание или квантификация, которые обозначают приписывание квантора к формуле.

Примеры применения кванторов

Пусть — предикат «$x$ кратно $7$».

С помощью квантора всеобщности можно записать следующие ложные высказывания:

  1. любое натуральное число делится на $7$;

  2. каждое натуральное число делится на $7$;

  3. все натуральные числа делятся на $7$;

который будет иметь вид:

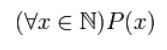
Рисунок 1.

Для записи истинных высказываний используем квантор существования:

  1. существуют натуральные числа, которые делятся на $7$;

  2. найдётся натуральное число, которое делится на $7$;

  3. хотя бы одно натуральное число делится на $7$.

Запись будет иметь вид:

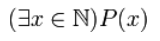
Рисунок 2.

Пусть на множестве $x$ простых чисел задан предикат : «Простое число является нечетным». Поставив перед предикатом слово «любое», получим ложное высказывание: «Любое простое число является нечетным» (например, $2$ является простым четным числом).

Поставим перед предикатом слово «существует» и получим истинное высказывание: «Существует простое число , которое является нечетным» (например, $x=3$ ).

Таким образом, предикат можно превратить в высказывание, если поставить перед предикатом квантор.

Операции над кванторами

Для построения отрицания высказываний, которые содержат кванторы, применяется правило отрицания кванторов:

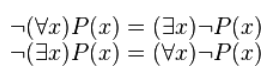
Рисунок 3.

Рассмотрим предложения и выделим среди них предикаты, указав область истинности каждого из них:

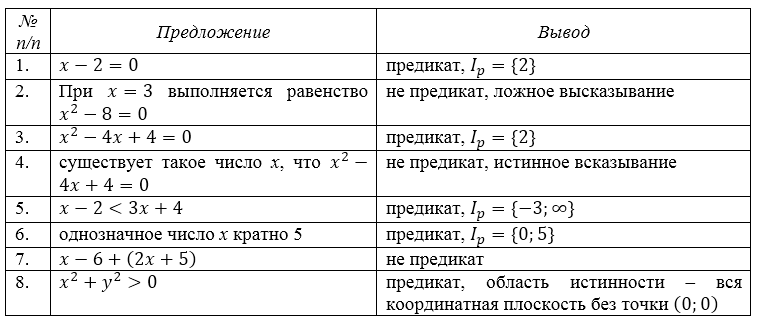
Рисунок 4.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Математическая логика — это раздел математики, изучающий математические обозначения, формальные системы, доказуемость математических суждений, природу математического доказательства в целом, вычислимость и прочие аспекты оснований математики.

Алгебра высказываний

Под высказыванием понимаем всякое утверждение (повествовательное предложение), про которое всегда определенно и объективно можно сказать, является оно истинным или ложным. Например, «5-3 = 2» или «В неделе семь дней» — истинные высказывания, а «5 > 8» или «В русском языке 35 букв» — ложные высказывания. Синонимами слова «высказывания» можно считать: логическое высказывание, булевское выражение, суждение, утверждение и т.п. Фразы: «Ура!», «Который час?» — не являются высказываниями.

Если высказывание истинное, то ему предписывается значение «истина» (другие обозначения: «1», «ДА» , «И», «+», «true»). Ложному высказыванию предписывается значение «ложь» (другие обозначения: «О», «НЕТ», «Л», «-«, «false»). Совокупность возможных значений высказывания образует множество истинности {0,1} и {И,Л}.

Есть два вида высказываний: простые и составные (сложные). Под простым будем понимать высказывание, которое не может быть разбито на более простые высказывания. Про него всегда однозначно можно сказать, что оно истинно или ложно, не интересуясь его структурой. Из простых высказываний при помощи логических операций можно строить сложные высказывания, которые всегда только истинны или только ложные. Высказывания обозначаются заглавными латинскими буквами: 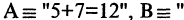Математическая логикасегодня вторникМатематическая логика если студент успешно сдал сессионные экзамены, то переводится на следующий курс и будет получать стипендию».

Логические операции

Операции над высказываниями задают в виде таблиц, называемых таблицами истинности.

Отрицание высказывания

Для каждого высказывания А может быть сформировано новое высказывание 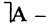Математическая логикаотрицание высказывания А, которое истинно, когда А ложно, и ложно, когда А истинно. Символ 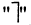Математическая логика соответствует логическому союзу «не». 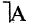Математическая логикачитается «не А» или «не верно, что А». Отрицание — одноместная (или унарная) операция. Последующие операции — двухместные (или бинарные). Например, если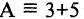 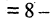Математическая логикаМатематическая логика истинное высказывание, то 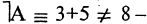Математическая логикаложное высказывание (отрицание А), или если 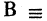Математическая логикав комнате холодно», 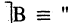Математическая логикав комнате не холодно». Отметим, что высказывание «в комнате жарко» не является отрицанием В.

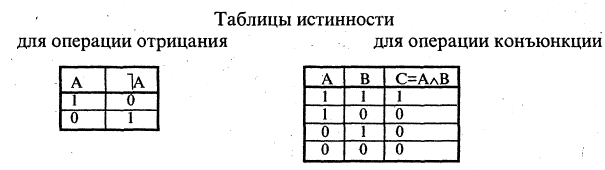
Математическая логика

Конъюнкция высказываний

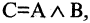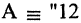Конъюнкцией высказываний А и В называется высказывание Математическая логика которое истинно только в том случае, когда и А, и В одновременно истинны. Выражение Математическая логика читается «А и В». Пример: пусть Математическая логикаделится на 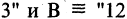Математическая логикаделится на 4″. Тогда формула Математическая логика имеет смысл: «12 делится на 3 и на 4».

Операцию конъюнкции можно определить и для нескольких высказываний как связку высказываний, объединенных союзом «и». Конъюнкция из п высказываний — новое высказывание, причем высказывание

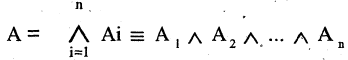
Математическая логика

имеет значение «истина», если 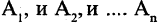Математическая логика истинны. Во всех других случаях эта конъюнкция имеет значение «ложь». Пусть, например, 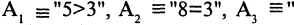Математическая логикаотец старше сына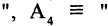Математическая логика Мурманск севернее Смоленска». Тогда высказывание 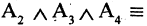Математическая логика («8=3 и отец старше сына, и

Мурманск севернее Смоленска») — ложное высказывание. В то время как 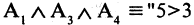Математическая логика и отец старше сына, и Мурманск севернее Смоленска» — истинное высказывание.

Дизъюнкция высказываний

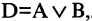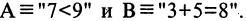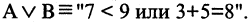
Дизъюнкцией высказываний А и В называется высказывание Математическая логикакоторое ложно только тогда, когда и А, и В ложны одновременно. Дизъюнкция имеет значение «истина», если хотя бы одно из высказываний, входящее в дизъюнкцию, является истинным. Выражение Математическая логикачитается «А или В». Пусть Математическая логика Тогда Математическая логика

Операцию дизъюнкции можно определить для нескольких высказываний как связку высказываний, объединенных союзом «или»,

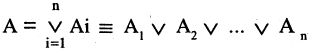
Математическая логика

В этом случае высказывание А истинно, если истинно хотя бы одно из высказываний, входящих в связку.

Импликация высказываний

Импликацией высказываний А и В называется высказывание 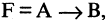Математическая логика которое ложно только в том случае, когда А — истинно, а В — ложно. Во всех других случаях импликация 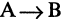Математическая логика имеет значение «истина». Символ 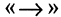Математическая логика соответствует логическому союзу: «если А, то В». Например, А — «целое число делится на 4, то оно делится на 2». 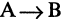Для иллюстрации содержательного смысла импликации рассмотрим следующий пример: А Математическая логика«папа завтра получит премию», В Математическая логика «папа завтра купит сыну велосипед». Тогда импликация Математическая логика может быть сформулирована так: «если папа завтра получит премию, то купит сыну велосипед».

Математическая логика

Пусть А и В истинны. Тогда папа, получив премию, покупает сыну велосипед. Естественно считать это истинным высказыванием. Когда же папа не купит сыну велосипед (В — ложно), получив премию (А — истинно), то это, мягко говоря, не логичный поступок, а импликация имеет значение «ложь». Если же папа не получит премию (А — ложно), но купит велосипед (В -истинно), то результат положителен. В том случае, если, не получив премии (А ложно), папа не купит велосипед (В — ложно) -обещание не нарушено, результат можно считать истинным.

Эквивалентность высказываний

Эквивалентностью высказываний А и В называется высказывание 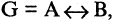Математическая логика которое истинно, когда высказывания и А, и В оба истинны или оба. ложны. Символ логической эквивалентности 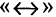Математическая логикасоответствует связке «тогда и только тогда». Пример. Пусть А Математическая логика «число ЗМатематическая логика является четным», В Математическая логика «число Математическая логика является четным». Высказывание «число ЗМатематическая логика является четным тогда и только тогда, когда Математическая логика -четное число» есть эквивалентность высказываний А и В. Эквивалентность высказываний может быть задана следующей таблицей истинности:

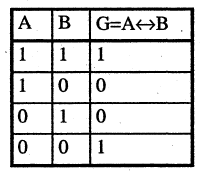
Математическая логика

Замечание. Характерной особенностью операций над высказываниями является введение логических союзов с точно определенным смыслом, не допускающим никакой двусмысленности в толковании этих символов. Таким образом, математическая логика применима не для любых высказываний, а только для таких, которые допуск кают четкую оценку в двоичной системе «истина — ложь». Для преодоления такого рода ограничений в рамках нечеткой математики разрабатывается нечеткая логика.

Если в выражении встречаются различные логические операции, то в качестве естественного порядка (выполняемого поочередно слева направо) используется следующая последовательность: 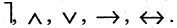Математическая логика Это означает, что сначала выполняются операции отрицания, затем конъюнкции и т. д. Для нарушения порядка служат скобки. Рассмотрим пример. Пусть высказывания А и В имеют значения «истина», а высказывания С и Б — «ложь». Тогда формула 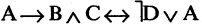Математическая логика имеет значение «ложь», т.к.:

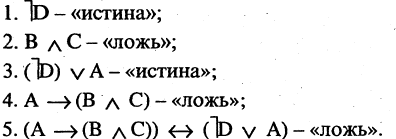
Математическая логика

Введя скобки, получим формулу 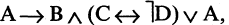Математическая логика которая уже имеет другое значение — «истина». Действительно:

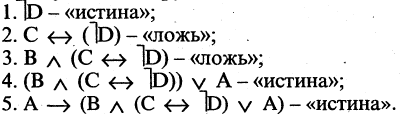
Математическая логика

Если в выражении присутствуют арифметические операции, операции сравнения и логические операции, то порядок старшинства операций следующий:

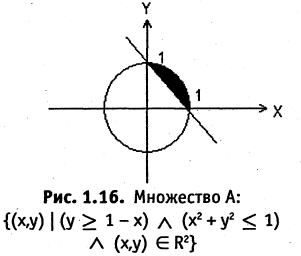
Использование различных операций позволяет в удобной аналитической форме задавать различные множества.

Например, множество точек А, заштрихованное на рис. 1.16, может быть задано следующей формулой:

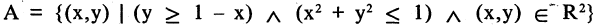
Математическая логика

Математическая логика

Система операций 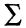Математическая логика называется полной, если всякая формула эквивалентна некоторой формуле, в которую входят только операции из системы 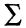Математическая логика. Система введенных пяти операций (отрицания, конъюнкции, дизъюнкции, импликации и эквивалентности) полная, хотя вообще говоря, избыточна, так как одни логические операции могут быть выражены через другие. Например, импликация и эквивалентность можно выразить через отрицание, конъюнкцию и дизъюнкцию следующим образом:

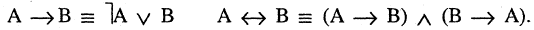
Математическая логика

Булевы функции

Всякую формулу логики высказываний можно рассматривать как некоторую функцию: каждая буква (высказывание) может принимать одно из двух значений — «истина» или «ложь», при этом сложное высказывание, заданное этой формулой, также может быть истинным или ложным. Так формула

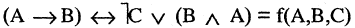
Математическая логика

выражает функцию от переменных А, В и С.

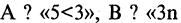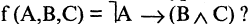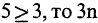Такого рода функции называются булевыми, а их аргументы — булевыми переменными. Аргументы булевых функций могут представлять собой, сокращенные обозначения некоторых конкретных высказываний. Тогда функция обозначает сокращенную запись некоторого сложного высказывания. Например, Математическая логика делится на 3», С ? «Мурманск севернее Смоленска». В этом случаеМатематическая логика «если Математическая логика делится на 3 и Мурманск севернее Смоленска». Сравните с известной формулой физики 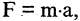Математическая логика где m — масса тела, а — его ускорение, а F — сила, вызвавшая это ускорение. Буквы в булевых функциях могут выступать в качестве переменных. Подставляя вместо них любые высказывания, можно по формуле вычислить соответствующее значение функции. Действительно, если в формуле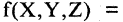 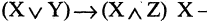Математическая логикаМатематическая логика «истина», Y — «ложь», Z — «истина», то 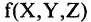Математическая логика — «истина». Если же Z будет иметь ложное значение, то 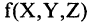Математическая логика поменяет значение на противоположное и будет «ложью».

Целый ряд булевых функций обладает тем свойством, что они принимают одни и те же значения при любых значениях истинности аргументов. Такие формулы называются тождественно истинными. Например, при любых X и Y истинны формулы 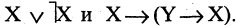Математическая логика Тождественно ложные функции при любых значениях аргументов имеют значение «ложь». Так формулы 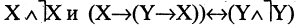Математическая логика всегда имеют значение «ложь».

Наиболее важные тождественно истинные формулы получили название Основные законы математической логики.

Основные законы математической логики

1.Коммутативность

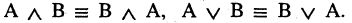
Математическая логика

2.Ассоциативность

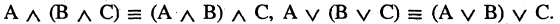
Математическая логика

3.Дистрибутивность

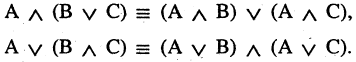
Математическая логика

4.Законы де Моргана

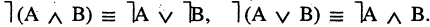
Математическая логика

5.Закон поглощения

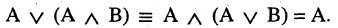
Математическая логика

6.Закон идемпотентности

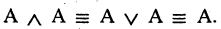
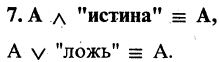
Математическая логика

Математическая логика

8.Закон противоречия

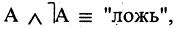
Математическая логика

9.Закон исключения третьего

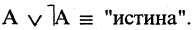
Математическая логика

10.Закон двойного отрицания

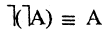
Математическая логика

Пример:

Упростить выражение, используя тождественны преобразования

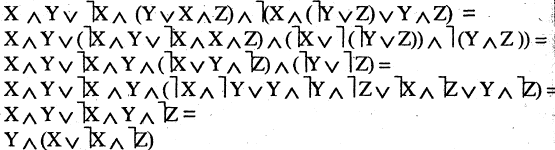
Математическая логика

Существует бесконечное множество тавтологий. Некоторы из них легли в основу методов доказательства.

Основные методы доказательств

При построении любой теории выделяется некоторый набор высказываний, так называемых аксиом, истинность которых постулируется. Из аксиом чисто логическим путем может был установлена истинность некоторых других высказываний называемых теоремами. Последовательность высказываний рассматриваемой теории, каждое из которых либо является аксиомой, либо выводится из одного или более предыдущих высказываний этой последовательности по логическим правилам вывода, называется доказательством. Высказывание, которое можно доказать, называется теоремой.

Формально каждая теорема может быть выражена в форме импликации 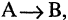Математическая логика где посылка А называется условием теоремы, а следствие В — заключением. Теорема верна, если выражающая ее импликация тождественно истинна, т. е. является тавтологией. Тавтологии рассматривают как некоторые логически истинные схемы рассуждений. В этой связи тавтологии играют роль законов, определяющих построение правильных умозаключений. Существует бесконечное множество тавтологий. Некоторые из них легли в основу методов доказательства. Основные методы доказательств.

Метод цепочек импликаций

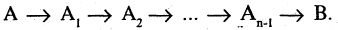
Метод цепочек импликаций состоит в том, что из посылки А страивается цепочка из Математическая логика-импликаций, последним высказыванием в которой является заключение теоремы В, т. е.

Математическая логика

В основе этого метода лежит закон цепного высказывания или закон силлогизма 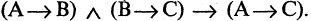Математическая логика

Метод от противного

Метод от противного. Используя этот метод, вместо доказательства прямого следствия «из А следует В» доказывают, что из «не В» следует «не А». Этот метод основан на законе контрапозиций, имеющем следующий вид:

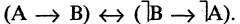
Математическая логика

Метод необходимого и достаточного

Метод необходимого и достаточного. Теорема формулируется так: «Чтобы имело место А, необходимо и достаточно выполнение В». Доказательство такого вида теоремы распадается на две части:

а) доказывается, что если имеет место А, то справедливо В (В необходимо для А);

б) если имеет место В, то имеет место и А (В достаточно для А).

Доказательство таким методом базируется на законе тавтологии:

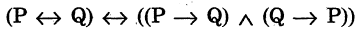
Математическая логика

Алгебра предикатов

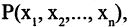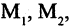
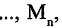
Предикатом Математическая логика заданным на множествах Математическая логикаМатематическая логика

называется функция Р, отображающая их прямое произведение на двоичное множество, т. е. 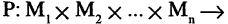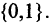Математическая логикаМатематическая логика Множество М называется предметной областью предиката, 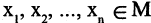Математическая логика называются предметными переменными или термами. Предикат представляет собой логическую функцию, принимающую, как и булевская функция, значение «истина» или «ложь», когда ее предметные переменные принимают определенные значения.

Рассмотрим примеры, 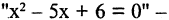Математическая логика одноместный предикат на множестве комплексных чисел, при этом, например, если 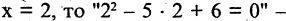Математическая логика истинное высказывание, а

положив 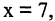Математическая логика получим 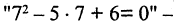Математическая логика «ложь». Выражение «X — брат Y» — двухместный предикат, заданный на множестве людей. Здесь термы X и Y указывают места, на которые нужна поставить имена двух людей, чтобы получить правильно построенное высказывание. Очевидно, что X — лицо мужского пола, а Y может выбираться из всего множества людей.

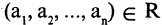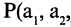
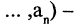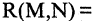Всякий предикат Математическая логика определяет отношение R, такое, что Математическая логика тогда и только тогда, когда Математическая логикаМатематическая логика«истина». В этом случае говорят, что отношение R задается областью истинности предиката Математическая логика. Например, отношение Математическая логика «расстояние на плоскости между точками 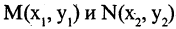Математическая логика больше величины 1″ можно задать предикатом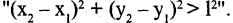 Математическая логика

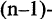Если в Математическая логика-местный предикат на место одного из термов подставить определенный элемент из соответствующего множества, то предикат станет Математическая логикаместным. Заменив все термы на конкретные значения из предметной области предиката, получим 0 — местный предикат, т. е. высказывание. Например, «Х- брат Y» — двухместный предикат, «X — брат Маши» — одноместный предикат, «Саша — брат Маши» — высказывание.

Логические операции над предикатами

Отрицание предиката

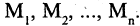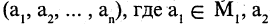
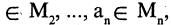Пусть предикат Математическая логика задан на множествах Математическая логика Предикат Математическая логика называется отрицанием предиката Математическая логика тогда и только тогда, если при одних и тех же кортежах Математическая логика Математическая логика высказывание 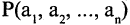Математическая логика истинно, когда 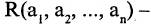Математическая логика ложно и наоборот. Обозначение

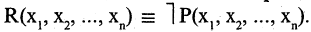
Математическая логика

Например, предикат «Математическая логика— четное число» есть отрицание предиката «Математическая логика— нечетное число» на множестве целых чисел.

Конъюнкция предикатов

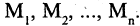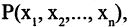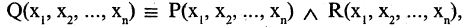
Пусть на множествах Математическая логика заданы два Математическая логика— местных предиката Математическая логика и Математическая логика. Конъюнкцией этих предикатов называется предикат

Математическая логика

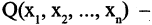который истинен для одних и тех же кортежей только тогда, когда оба предиката — и Математическая логика и Математическая логика истинны.

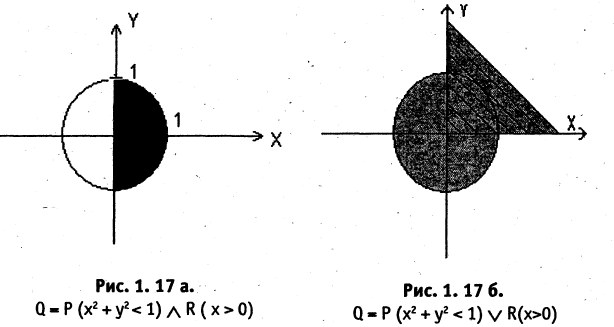
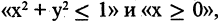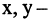Например, конъюнкция предикатов Математическая логика где Математическая логика вещественные числа, определяет предикат «точки правой половины единичного круга» (см. рис. 1.17а).

Дизъюнкция предикатов

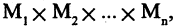Дизъюнкция предикатов Математическая логика и Математическая логика есть новый предикат Математическая логикакоторый имеет значение «ложь» для тех и только тех кортежей из Математическая логика для которых оба предиката — и Математическая логика и Математическая логика — имеют значение «ложь». На рис. 1.17 6 иллюстрируется дизъюнкция предиката 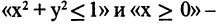Математическая логика(заштрихованная область).

Импликация предикатов

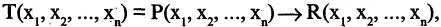Импликация предикатов Математическая логика и Математическая логика есть новый предикат Математическая логика который имеет значение «ложь» для тех и только тех кортежей из 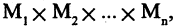Математическая логика для которых предикат Математическая логика имеет значение «истина», а предикат Математическая логика имеет значение «ложь».

Например, импликация «Математическая логика делится на 4″ —» » Математическая логика делится на 2″ есть предикат: «если Математическая логика делится на 4, то Математическая логика делится на 2″.

Математическая логика

Эквивалентность предикатов

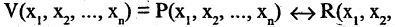
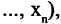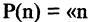Эквивалентность предикатов Математическая логика и Математическая логика есть новый предикат Математическая логикаМатематическая логика который имеет значение «истина» для тех и только тех кортежей из Математическая логика для которых предикат Математическая логика и предикат Математическая логика имеют одинаковые значение или оба «истина» или оба «ложь». Два предиката, заданные на одних и тех же множествах, называются равносильными, если при всех наборах входящих в них предметных переменных эти предикаты принимают одинаковые значения. Равносильность называют также логической эквивалентностью. 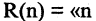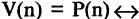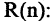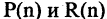Например, эквивалентность предикатов Математическая логика делится на 6» и Математическая логикаделится на 2 и Математическая логика делится на 3» есть предикат Математическая логикаМатематическая логика «если Математическая логика делится на 6, то Математическая логика делится на 2 и на 3». Предикаты Математическая логика логически эквивалентны.

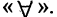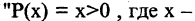Наряду с логическими операциями важную роль играют операции, называемые кванторами. Квантор всеобщности есть операция, которая предикат Математическая логика превращает в высказывание: «все Математическая логика обладают свойством Математическая логика». Знак квантора всеобщности Математическая логика Он заменяет фразы: «для всех», «каждый», «любой» и т.п. Обозначение Математическая логика читается так: «для всех Математическая логика таких, что Р от Математическая логика». Например, Математическая логика вещественное число», есть предикат «Математическая логика — положительное число». Тогда Математическая логика есть высказывание «каждое число — положительно». Это ложное высказывание. 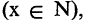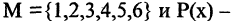Если же Математическая логика — любое натуральное число Математическая логика то Математическая логика есть выражение: «каждое натуральное число — положительно» — истинное высказывание. Квантор всеобщности есть обобщение серии конъюнкций единичных высказываний. Пусть М — множество очков, которое может выпасть при бросании игральной кости, т. е. 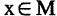Математическая логика предикат: «при бросании игральной кости один раз выпадает Математическая логика очков», где Математическая логика. Применение квантора всеобщности позволяет вместо сложного высказывания 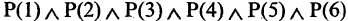Математическая логиказаписать равносильное ему компактное высказывание 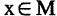Математическая логикаМатематическая логика: «при бросании игральной кости один раз может выпасть любое из шести первых натуральных чисел».

Квантор существования

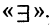Квантор существования есть операция, которая предикат Математическая логика превращает в высказывание: «существует хотя бы один Математическая логика

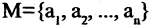из М, обладающий свойством Математическая логика». Знак квантора существования Математическая логика Он заменяет фразы: «существует хотя бы один», «найдется», «некоторый» и т.п. Обозначение Математическая логика читается так: «существует хотя бы один Математическая логика такой, что Р от Математическая логика». Например, Математическая логика — предикат: «Математическая логика — студент», где Математическая логика — элемент множества жителей Москвы. Тогда выражение Математическая логика есть высказывание «хотя бы один житель Москвы является студентом». Квантор существования есть обобщение серии дизъюнкций единичных высказываний. Если задано множество Математическая логика и на нем определен предикат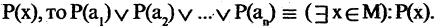 Математическая логика

Кванторы обладают свойствами, являющимися аналогами законов де Моргана:

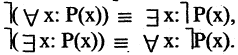
Математическая логика

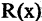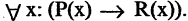
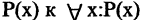С помощью кванторов можно выражать ряд часто используемых на практике отношений между множествами. Например, высказывание «все объекты Математическая логика из данного множества, обладающие свойством Математическая логика, обладают также и свойством Математическая логика» формально можно записать — Математическая логика

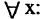
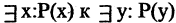Переход от Математическая логика или Математическая логика называется квантификацией или связыванием переменной Математическая логика. Связанная переменная фактически не является переменной, т. е. переход от Математическая логикаМатематическая логика или от Математическая логика не меняет истинности выражений. Навешивание переменной на многоместный предикат уменьшает в нем число свободных переменных и превращает его в предикат от меньшего числа переменных

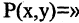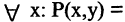Рассмотрим пример. На множестве чисел задан двухместный предикат Математическая логика число Математическая логика делится на число Математическая логика». Связывая одну переменную, можно получить следующие одноместные предикаты:

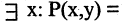Математическая логика«каждое число делится на Математическая логика» — ложь;

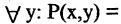Математическая логика«существует число, которое делится на Математическая логика» — истина;

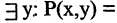Математическая логика«число Математическая логика делится на любое число» — ложь;

Математическая логика«существует число, на которое делится Математическая логика» — истина.

Связывая обе переменные данного предиката, получим высказывания:

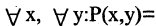Математическая логика«каждое число делится на любое число» -ложное высказывание,

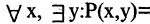Математическая логика«существует число, на которое делится любое число» — истина, т.к. такое число есть 1,

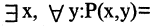Математическая логика«существует число, которое делится на любое число» — ложное высказывание,

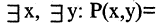Математическая логика«существует число, которое делится на какое-нибудь число» — истинное высказывание.

Решение заданий и задач по предметам:

  • Математика
  • Высшая математика
  • Математический анализ
  • Линейная алгебра

Дополнительные лекции по высшей математике:

  1. Тождественные преобразования алгебраических выражений
  2. Функции и графики
  3. Преобразования графиков функций
  4. Квадратная функция и её графики
  5. Алгебраические неравенства
  6. Неравенства
  7. Неравенства с переменными
  8. Прогрессии в математике
  9. Арифметическая прогрессия
  10. Геометрическая прогрессия
  11. Показатели в математике
  12. Логарифмы в математике
  13. Исследование уравнений
  14. Уравнения высших степеней
  15. Уравнения высших степеней с одним неизвестным
  16. Комплексные числа
  17. Непрерывная дробь (цепная дробь)
  18. Алгебраические уравнения
  19. Неопределенные уравнения
  20. Соединения
  21. Бином Ньютона
  22. Число е
  23. Непрерывные дроби
  24. Функция
  25. Исследование функций
  26. Предел
  27. Интеграл
  28. Двойной интеграл
  29. Тройной интеграл
  30. Интегрирование
  31. Неопределённый интеграл
  32. Определенный интеграл
  33. Криволинейные интегралы
  34. Поверхностные интегралы
  35. Несобственные интегралы
  36. Кратные интегралы
  37. Интегралы, зависящие от параметра
  38. Квадратный трехчлен
  39. Производная
  40. Применение производной к исследованию функций
  41. Приложения производной
  42. Дифференциал функции
  43. Дифференцирование в математике
  44. Формулы и правила дифференцирования
  45. Дифференциальное исчисление
  46. Дифференциальные уравнения
  47. Дифференциальные уравнения первого порядка
  48. Дифференциальные уравнения высших порядков
  49. Дифференциальные уравнения в частных производных
  50. Тригонометрические функции
  51. Тригонометрические уравнения и неравенства
  52. Показательная функция
  53. Показательные уравнения
  54. Обобщенная степень
  55. Взаимно обратные функции
  56. Логарифмическая функция
  57. Уравнения и неравенства
  58. Положительные и отрицательные числа
  59. Алгебраические выражения
  60. Иррациональные алгебраические выражения
  61. Преобразование алгебраических выражений
  62. Преобразование дробных алгебраических выражений
  63. Разложение многочленов на множители
  64. Многочлены от одного переменного
  65. Алгебраические дроби
  66. Пропорции
  67. Уравнения
  68. Системы уравнений
  69. Системы уравнений высших степеней
  70. Системы алгебраических уравнений
  71. Системы линейных уравнений
  72. Системы дифференциальных уравнений
  73. Арифметический квадратный корень
  74. Квадратные и кубические корни
  75. Извлечение квадратного корня
  76. Рациональные числа
  77. Иррациональные числа
  78. Арифметический корень
  79. Квадратные уравнения
  80. Иррациональные уравнения
  81. Последовательность
  82. Ряды сходящиеся и расходящиеся
  83. Тригонометрические функции произвольного угла
  84. Тригонометрические формулы
  85. Обратные тригонометрические функции
  86. Теорема Безу
  87. Математическая индукция
  88. Показатель степени
  89. Показательные функции и логарифмы
  90. Множество
  91. Множество действительных чисел
  92. Числовые множества
  93. Преобразование рациональных выражений
  94. Преобразование иррациональных выражений
  95. Геометрия
  96. Действительные числа
  97. Степени и корни
  98. Степень с рациональным показателем
  99. Тригонометрические функции угла
  100. Тригонометрические функции числового аргумента
  101. Тригонометрические выражения и их преобразования
  102. Преобразование тригонометрических выражений
  103. Комбинаторика
  104. Вычислительная математика
  105. Прямая линия на плоскости и ее уравнения
  106. Прямая и плоскость
  107. Линии и уравнения
  108. Прямая линия
  109. Уравнения прямой и плоскости в пространстве
  110. Кривые второго порядка
  111. Кривые и поверхности второго порядка
  112. Числовые ряды
  113. Степенные ряды
  114. Ряды Фурье
  115. Преобразование Фурье
  116. Функциональные ряды
  117. Функции многих переменных
  118. Метод координат
  119. Гармонический анализ
  120. Вещественные числа
  121. Предел последовательности
  122. Аналитическая геометрия
  123. Аналитическая геометрия на плоскости
  124. Аналитическая геометрия в пространстве
  125. Функции одной переменной
  126. Высшая алгебра
  127. Векторная алгебра
  128. Векторный анализ
  129. Векторы
  130. Скалярное произведение векторов
  131. Векторное произведение векторов
  132. Смешанное произведение векторов
  133. Операции над векторами
  134. Непрерывность функций
  135. Предел и непрерывность функций нескольких переменных
  136. Предел и непрерывность функции одной переменной
  137. Производные и дифференциалы функции одной переменной
  138. Частные производные и дифференцируемость функций нескольких переменных
  139. Дифференциальное исчисление функции одной переменной
  140. Матрицы
  141. Линейные и евклидовы пространства
  142. Линейные отображения
  143. Дифференциальные теоремы о среднем
  144. Теория устойчивости дифференциальных уравнений
  145. Функции комплексного переменного
  146. Преобразование Лапласа
  147. Теории поля
  148. Операционное исчисление
  149. Системы координат
  150. Рациональная функция
  151. Интегральное исчисление
  152. Интегральное исчисление функций одной переменной
  153. Дифференциальное исчисление функций нескольких переменных
  154. Отношение в математике
  155. Графы в математике
  156. Линейные пространства
  157. Первообразная и неопределенный интеграл
  158. Линейная функция
  159. Выпуклые множества точек
  160. Система координат

Источник

Предикаты. Операции над предикатами

При изучении высказываний мы отмечали, что утверждение с переменными не является высказыванием. Можно, например, рассмотреть предложение %%P(x) : x^2 + 1 > 2%% с переменной %%x in mathbb R%%. Это предлождение не является высказыванием, так как нельзя сказать истинно оно или ложно. Однако, если заменить переменную %%x%% на какое-либо значение, например, %%x = 1%%, получаем высказывание %%2 > 2%%, которое является ложным. Заменив переменную %%x%% на значение %%x = 2%%, получим истинное высказывание %%5 > 2%%. Итак есть выражение %%P(x)%% не являющиееся высказыванием, но превращающееся в него при замене переменной %%x%% на ее произвольное значение из соответствующего множества.

Определение

Одноместным предикатом, определенным на множестве %%D%%, называется предложение с переменной, которое превращается в высказывание при замене этой переменной на ее значение из множества %%D%%. Одноместный предикат будем называть унарным или предикатом от одной переменной.

Примеры

Следующие предложения являются одноместными предикатами:

  1. %%P(x): x^ 2 + 1 > 2%%, где %%D%% — множество действительных чисел.
  2. %%Q(x):%% Длина отрезка равна %%1%%, где %%D%% — множество всех отрезков прямой.

Следующие предложения не являются одноместными предикатами:

  1. %%1 > 2%%.
  2. Прямая %%x%% параллельна прямой %%y%%.

%%n%%-местный предикат

%%n%%-местым предикатом с областью определения %%D = D_1 times D_2 times ldots times D_n%% называется предикат %%P(x_1, x_2, ldots, x_n)%% от %%n%% переменных, который превращается в высказывание при замене переменных %%x_1, x_2, ldots, x_n%% на их значения из множеств %%D_1, D_2, ldots, D_n%% соответственно.

Тогда предложение прямая %%x%% параллельна прямой %%y%% является двуместным предикатом %%P(x, y)%%, где %%X, Y%% — множество всех прямых.

Область определения предиката

Рассмотрим %%n%%-местный предикат %%P(x_1, x_2, ldots, x_n)%%. В этом случае переменные берутся из множеств %%D_1, D_2, ldots, D_n%% соответственно. Можно рассмотреть множество %%D = D_1 times D_2 times ldots times D_n%% — декартово произведение множеств %%D_1, D_2, ldots, D_n%%, элементами которого являются всевозможные упорядоченные %%n%%-ки %%(d_1, d_2, ldots, d_n)%% элементов исходных множеств.

Множество %%D%% называется областью определения предиката.

Область истинности

Областью истинности предиката %%P(x_1, x_2, ldots, x_n)%% называется множество всех %%n%%-ок %%(d_1, d_2, ldots, d_n) in D%% таких, что при замене %%x_1%% на %%d_1%%, %%x_2%% на %%d_2%%, …, %%x_n%% на %%d_n%% получается истинное высказывание.

Пример

На множестве %%D = { 1, 2, 3, 4, 5, 6, 7, 8, 9}%% рассмотрим одноместный предикат %%P(x): x%% — простое число. Найти область истинности предиката %%P(x)%%.

Обозначим область истинности буквой %%A%%. Тогда %%A%% состоит из таких элементов, при которых выполняется предикат %%P(x)%%. Поэтому %%A = {2, 3, 5, 7}%%.

Операции над предикатами

Аналогично операциям для высказываний вводятся операции для предикатов.

Пусть %%P(x)%% и %%Q(x)%% — одноместные предикаты, определенные на множестве %%D%%.

Отрицанием предиката %%P(x)%% называется новый предикат, обозначаемый %%overline{P(x)}%% и являющийся ложным для тех и только тех %%x%%, для которых предикат %%P(x)%% истинный.

Конъюнкцией предикатов %%P(x)%% и %%Q(x)%% называется новый предикат, обозначаемый %%P(x) land Q(x)%% и являющийся истинным для тех и только тех %%x%%, для которых предикаты %%P(x)%% и %%Q(x)%% истинны.

Дизъюнкцией предикатов %%P(x)%% и %%Q(x)%% называется новый предикат, обозначаемый %%P(x) lor Q(x)%% и являющийся ложным для тех и только тех %%x%%, для которых предикаты %%P(x)%% и %%Q(x)%% ложны.

Импликацией предикатов %%P(x)%% и %%Q(x)%% называется новый предикат, обозначаемый %%P(x) rightarrow Q(x)%% и являющийся ложным для тех и только тех %%x%%, для которых предикаты %%P(x)%% истинный, а %%Q(x)%% ложный.

Эквиваленцией предикатов %%P(x)%% и %%Q(x)%% называется новый предикат, обозначаемый %%P(x) leftrightarrow Q(x)%% и являющийся истинным для тех и только тех %%x%%, для которых предикаты %%P(x)%% и %%Q(x)%% имеют одинаковые значения.

Применяя операции над предикатами, мы получаем составные предикаты, которые будем называть формулами алгебры предикатов.

Предикаты %%P(x)%% и %%Q(x)%% эквивалентные , если для любого значения переменной %%x%% их значения истинности совпадают. Обозначают $$P(x) equiv Q(x).$$

Законы алгебры предикатов

Для предикатов справедливы все законы, аналогичные законам алгебры логики высказываний1.

В случае тождественно истинных и тождественно ложных предикатов имеем следующие определения.

Предикат %%P(x_1, x_2, ldots, x_n)%% называется тождественно истинным если при любой замене переменных %%x_1, x_2, ldots, x_n%% на их значения предикат превращается в истинное высказывание.

Предикат %%P(x_1, x_2, ldots, x_n)%% называется тождественно ложным если при любой замене переменных %%x_1, x_2, ldots, x_n%% на их значения предикат превращается в ложное высказывание.

Высказывание является частным случаем предиката, когда в предикате нет переменных. То есть высказывание является предикатом %%0%% порядка (от %%0%% переменных).

1. Законы алгебры логики высказываний.

Источник

Добавить комментарий