производная отрицатеьная -при каких условиях? и как это понть если можно на конкретных примерах спасибо
Мастер
(2221),
закрыт
14 лет назад
Екатерина Н
Мудрец
(17300)
14 лет назад
На примерах.
1) Пусть задана функция у = х^2. Находим ее производную, будет: у’ = 2x
у’ будет отрицательным, если 2х < 0, значит x < 0. Таким образом, на промежутке от минус бесконечности до нуля производная отрицательна, а значит функция на этом промежутке убывает
2) у = 4х + 5
Находим производную: у’ = 4. Это число положительное, значит производная этой функции не может быть отрицательной, а так как у’ > 0, то функция возрастает.
3) у = х^3 – 3x
Находим производную: у ‘ = 3x^2 – 3
3x^2 -3 < 0
3(x^2 – 1) < 0
x^2 – 1 < 0
(x – 1)(x + 1) < 0
x є (-1;1) Значит производная отрицательна на промежутке (-1;1), поэтому на этом промежутке функция убывает
Производная положительна только тогда, когда функция возрастает. То есть, нам необходимо найти точки, в которых функция растет. Смотрим на график нашей функции: функция растет на промежутках: от (x=-7) до (x=0) и от (x = 6) до (x=12).
Так как по условию нам нужны только ЦЕЛЫЕ точки, в которых производная положительна, то это будут: (x=—6); (x=-5), (x=-4), (x=-3), (x=-2), (x=-1), (x=7), (x=8), (x=9), (x=10), (x=11). Всего точек получилось (11). Я отметил их зеленым цветом.
Обратите внимание, что точки (x=-7), (x=0), (x=6), (x=12) мы не считаем, так как в этих точках у нас будут минимумы и максимумы функции, а в них производная равна нулю, то есть не положительна.
Ответ: (11.)
Пример 2
На рисунке 6 изображен график функции, определенной на промежутке ((-10;12)). Найдите количество точек, в которых производная функции равна нулю.
|
Ответ на этот вопрос будет полезен всем, кто желает знать практическое применение производной функции (в данном случае от одной переменной). Если при исследовании функции получается отрицательная производная при любых значениях аргумента х, то можно сделать вывод, что данная функция убывает на всей области определения. Например, пусть у= -2х+3. Найдем ее производную, которая будет равна -2 (производная от -2х равна -2 умноженное на 1 и плюс производная постоянной величины 3, которая равна нулю). -2 меньше нуля для всех х из множества действительных чисел (области определения данной функции). Значит данная функция является убывающей для всех х. В частности, производная функции отрицательна на некотором отрезке тогда и только тогда, когда функция на этом отрезке убывает, т.е. меньшему значению аргумента из данного отрезка соответствует большее значение функции и наоборот, большему значению аргумента – меньшее значение функции.
Rafail 9 лет назад Во всех точках тех интервалов значений аргумента, в которых функция убывает. На графике при продвижении слева направо значение функции все меньше и меньше. Знаете ответ? |
Рассмотрим задания из №6 ЕГЭ, в которых по графику функции требуется определить точки, в которых производная положительна либо отрицательна.
№1
На рисунке изображён график дифференцируемой функции y=f(x). На оси абсцисс отмечены восемь точек: x1, x2 ,x3, x4, … , x8. Среди этих точек найдите все точки, в которых производная функции f(x) положительна. В ответе укажите количество найденных точек.
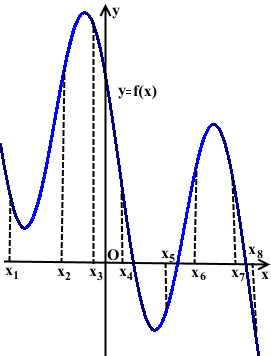
Решение:
Производная функции f'(x) положительна там, где функция y=f(x) возрастает:
f'(x)>0, если f(x) возрастает.
Выделяем промежутки возрастания функции y=f(x) и определяем количество точек, принадлежащих этим промежуткам.
Промежуткам возрастания функции y=f(x) принадлежат три точки: x2, x5 и x6.
Значит, производная функции в этих трёх точках положительна:
f'(x2)>0,
f'(x5)>0,
f'(x6)>0.
Ответ: 3.
№2
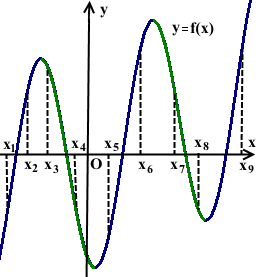На рисунке изображён график функции y=f(x) и отмечены девять точек на оси абсцисс: x1, x2 ,x3, x4 …x8, x9. В скольких из этих точек производная функции f(x) отрицательна?
Решение:
Производная функции f'(x) отрицательна там, где функция y=f(x) убывает:
f'(x)<0, если f(x) убывает.
Выделяем промежутки убывания функции y=f(x) и определяем количество точек, принадлежащих этим промежуткам.
Промежуткам убывания функции y=f(x) принадлежат четыре точки: x3, x4, x7 и x8. Значит, производная в этих четырёх точках отрицательна:
f'(x3)<0, f'(x4)<0, f'(x7)<0, f'(x8)<0.
Ответ: 4.
№3
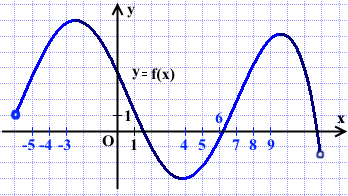На рисунке изображен график функции y=f(x), определенной на интервале (−6; 12). Определите количество целых точек, в которых производная функции положительна.
Решение:
Производная функции f'(x) положительна там, где функция y=f(x) возрастает.
Выделяем промежутки возрастания.
Целые точки, входящие в промежутки возрастания: -5; -4; -3; 4; 5; 6; 7; 8; 9.
Всего девять точек.
Ответ: 9.
было в ЕГЭ
в условии
в решении
в тексте к заданию
в атрибутах
Категория
Атрибут
Всего: 116 1–20 | 21–40 | 41–60 | 61–80 | 81–100 | 101–116
Добавить в вариант
Найдите точку минимума функции 
принадлежащую промежутку 
Найдите наибольшее значение функции 
на отрезке 
Найдите наибольшее значение функции 
на отрезке 
Найдите наибольшее значение функции 
на отрезке
На рисунке изображен график функции 
и отмечены точки −2, −1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку. 
На рисунке изображен график функции и отмечены точки −2, −1, 3, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
На рисунке изображен график функции и отмечены точки −1, 1, 2, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
На рисунке изображен график функции и отмечены точки -2, -1, 2, 3. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
На рисунке изображен график функции и отмечены точки −2, −1, 1, 3. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
На рисунке изображён график дифференцируемой функции y = f(x). На оси абсцисс отмечены девять точек: x1, x2, x3, …, x9. Среди этих точек найдите все точки, в которых производная функции f(x) отрицательна. В ответе укажите количество найденных точек.
На рисунке изображён график функции 
— производной функции f(x) определённой на интервале (1; 10). Найдите точку минимума функции f(x).
На рисунке изображён график функции y = f(x) и отмечены семь точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7. В скольких из этих точек производная функции f(x) отрицательна?
На рисунке изображён график производной y = f’(x) функции y = f(x), определённой на интервале (−4; 8). В какой точке отрезка [−3; 1] функция y = f(x) принимает наименьшее значение?
Функция y = f (x) определена и непрерывна на отрезке [−5; 5]. На рисунке изображён график её производной. Найдите точку x0, в которой функция принимает наименьшее значение, если f (−5) ≥ f (5).
Всего: 116 1–20 | 21–40 | 41–60 | 61–80 | 81–100 | 101–116
