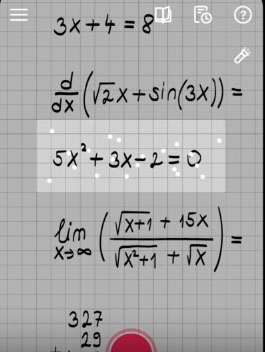Как найти ответ на пример

Не каждому ребенку успешно даются примеры и задачи по математике. Для них в сети есть программы и приложения, решающие примеры и задачи по фотографии онлайн. Их достаточно много, поэтому будут рассмотрены только лучшие. Из статьи вы узнаете, как ими пользоваться.

Как решить задачу по математике по фото в Photomath

Новая тема по школьным предметам далеко не каждым учеником сразу воспринимается. Ребёнку нужно решить несколько задач с примерами, объяснить принцип функций и тогда через какое-то время материал будет усвоен. Таким виртуальным репетитором может быть мобильное приложение Photomath для Android и Айфона. Программа не только решит задачу по картинке, но и подскажет все действия решения. Поможет понять пример, разложив его на действия.

1. Откройте учебник или любой другой источник примера;
2. Запустите приложение и откройте в нём камеру;
3. Наведите объектив камеры на задачу и сделайте снимок. Нажмите для этого на красную кнопку внизу экрана;
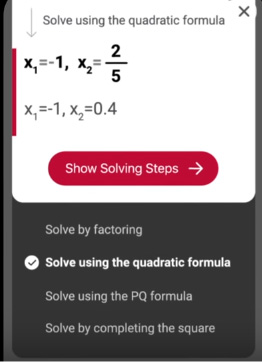
4. Затем нажмите на кнопку «Показать шаги решения». И на экране появятся действия, с помощью которых программа решала данную задачу.

Как видите, всё легко и просто работает. Любая самая сложная задача может быть разложена на простые шаги для решения. В приложении Photomath поддерживается более тридцати языков. Доступны разнообразные интерактивные графики. Камера приложения легко распознаются и текстовый текст из учебника, и рукописные записи конспекта. Кроме этого, в приложении доступно несколько методов решения одной и той же задачи.

Это интересно: решение уравнений по фото онлайн.

Решение задач в приложении Google Lens

Математические примеры научилось решать популярное приложение — Google Lens. До этого программа легко справлялась с поиском любых предметов в Интернете. Способно переводить на лету текст с одного языка на другой.

Разработчики из компании Гугл решили помочь студентам и школьникам и реализовали в своей программе настоящий онлайн-решебник. Теперь камера способна щёлкать математически примера в одну секунду. Запустив камеру Гугл, наведите её на задачу и сделайте фото.

Копия примера будет найдена в Интернете вместе с решением. Для того, чтобы пример был лучше рассмотрен объективом, сместите фиксирующее окно в место, где расположено условие в учебнике или конспекте.

Мобильное приложение Google Lens способно определять и другие предметы. Вы с лёгкостью сможете найти в сети по картинке любой костюм, платье. Узнать больше о достопримечательностях города, в который приехали на экскурсию. Перевести любые указатели и таблички с иностранного языка.

Google Lens умеет сканировать штрих и QR коды. По картинке определяет название блюд в кафе и ресторанах. Всё что ему нужно для полноценной работы — это подключение к сети Интернет. Приложение не сохраняет изображения, по которым вы ищите информацию. После загрузки и сканирования они удаляются с сервиса без индексирования. Подробнее об этом можно прочитать в пользовательском соглашении.

Читайте также: как написать корень на клавиатуре.

Поиск ответа на задачи в Mathway

Школьники давно мечтали о таких программах, которые бы делали домашнее задание за них. Наконец-то они появились. И способны сканировать любые примеры при помощи камеры на мобильном телефоне. Нужно лишь навести объектив смартфона на сложный пример и нажать кнопку для создания фото.

В приложении Mathway всё происходит в автоматическом режиме. Скачать программу можно для телефонов с Android и Айфона.

Программа Mathway легко решает математические задачи при помощи фотографии онлайн. Доступ в Интернет необходим, чтобы оно проверило свою базу и попыталось найти ответ.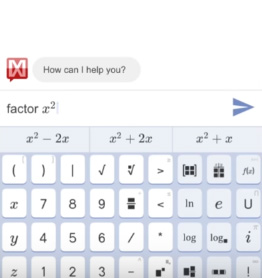 Офлайн доступны другие функции, но решение по изображению невозможно. Использование приложения бесплатно для всех пользователей. В нём также масса других возможностей.

• Решение примеров математики для начальных классов;
• Справляется с задачами по тригонометрии и алгебре;
• Выводит всю статистику решения и дополнительную информацию;
• Решает задачи по химии и линейной алгебре;
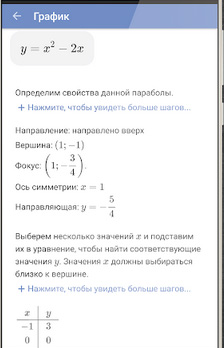
• Способно создавать графики любой сложности.

Приложение было высоко оценено различными западными СМИ и популярными Интернет-компаниями, в числе которых: Yahoo!, CNET, Lifehack и другие. Главными её качествами отмечают: простоту в использовании, эффективность в решении задач, быстрый поиск решения. Программа не просто выводит результат, но и помогает понять, какие действия для её решения предпринимались.

Mathway достепен онлайн

Кроме мобильного приложения Mathway есть ещё веб-сайт, на котором легко можно решать задачи по математике, сидя дома за компьютером. Попробуйте этот инструмент, если с другими возникли проблемы. Ресурс находится по адресу: Mathway.com.

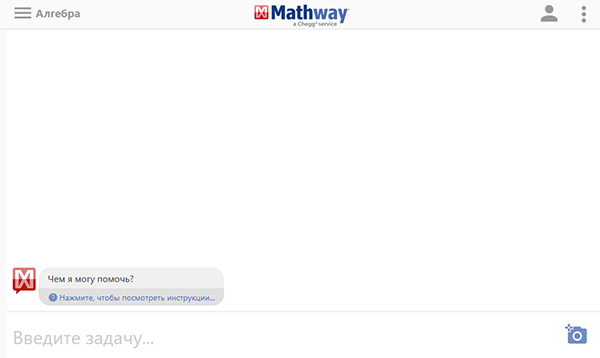
При переходе пользователь видит окно с приглашением к вводу данных. Программа уже готова решать примеры по фотографии или при вводе информации в текстовой форме.

Для учеников, которые впервые на сайте, предлагается текстовая инструкция по работе с сайтом. Найти её можно в нижней части, в левом углу.

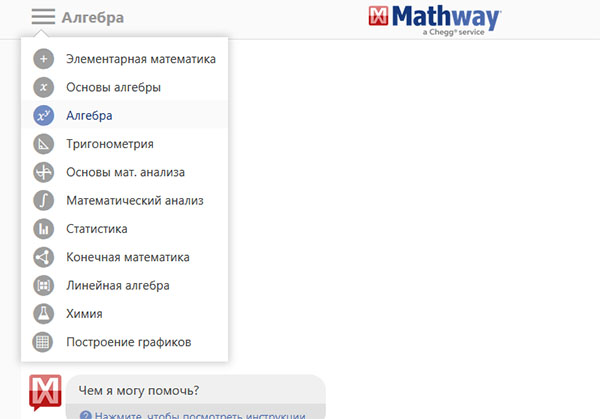
Стоит убедиться, что в данный момент выбрать нужный предмет. Нажмите на кнопку меню вверху и выберите другой, если это необходимо.

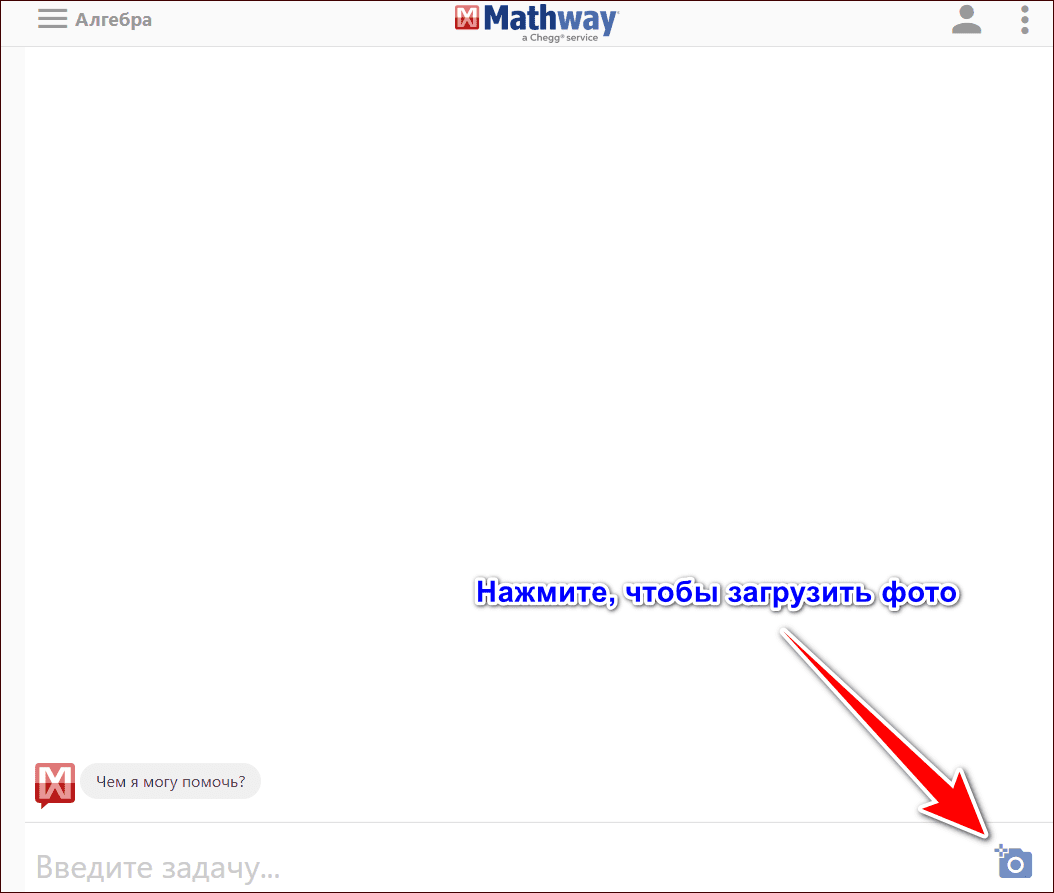
1. Чтобы сфотографировать пример, нажмите на иконку фотоаппарата с плюсом;
2. Затем наведите веб-камеру на пример или поднесите книгу к камере ноутбука. На экране будет виден результат;
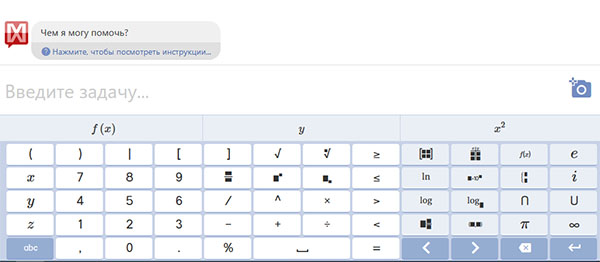
3. На виртуальной клавиатуре можно ввести текстовые данные для решения задачи;
4. Данные также можно набирать на обычной клавиатуре, а математически знаки добавлять из виртуальной;
5. Программе можно предоставить скан страницы с задачей, если камера на компьютере отсутствует.

Ресурс будет полезен всем учащимся, студентам и людям разных профессий. Помощь по сайту можно получить в разделе справки, которая находится в меню сайта. Для пользователей, которые не желают забивать память мобильного устройства разными приложениями, можно пользоваться онлайн сайтом Mathway даже через мобильный браузер. Все функции, которые доступны в приложении, можно применять в веб-версии.

Математический сканер по фото

Найден ещё один полезный инструмент для решения математических задач — Математический сканер. Эта программа умеет работать без подключения к сети Интернет. И выдавать решения не хуже остальных подобных программ из App Store или Google Play. Основным её инструментом является камера. Использовать в этом приложении лучше только печатный текст из учебников. Чтобы программа смогла определить сложность задачи и показать её решения. Иногда не справляется с написанным текстом от руки.

• Программа «Математический сканер» также способна отображать полное решения задач со схемой действий;
• Есть режим, в котором программа показывает каждый шаг детально, который она принимала для получения результата задачи;
• Решает любые примеры на вычитание, проценты, сложение, умножение и прочее;
• В ней есть возможность создавать графики и таблицы.

В программе встроен обычный калькулятор с дополнительными кнопками, который может быть использован из главного меню. А также имеет множество различных конвертеров. Для использования фото-сканера выберите его в приложении и сфотографируйте пример. Убедитесь в том, что все части его условия поместились в объектив. После чего можно увидеть результат решения математической задачи.

Видеоинструкция

Попробуйте использовать одно из описанных приложений, чтобы решить задачу по математике по картинке. Если возникли трудности с примерами на проценты, посмотрите это видео.

Поиск значений выражений — основное математическое действие. Им сопровождается каждый пример, задача. Поэтому чтобы вам было проще работать с различными математическими выражениями, подробно разберем способы и правила их решения в данной статье. Правила представлены в порядке увеличения сложности: от простейших выражений до выражений с функциями. Для лучшего понимания каждый пункт сопровождается подробным пояснением и расписанными примерами.

Поиск значения числовых выражений

Числовые выражения представляют собой математические задачи, состоящие, преимущественно, из чисел. Они подразделяются на несколько групп в зависимости от своей сложности: простейшие, со скобками, корнями, дробями и т.д. Каждый тип выражений подразумевает свои правила нахождения значения, порядок действий. Рассмотрим каждый случай подробнее.

Простейшие числовые выражения. К простейшим числовым выражениям относятся примеры, состоящие из двух элементов:

• Числа (целые, дробные и т.д.);
• Знаки: «+», «—», «•» и «÷».

Чтобы найти значение выражения в данном случае, необходимо выполнить все арифметические действия (которые подразумевают конкретные знаки). В случае отсутствия скобок решение примера производится слева направо. Первыми выполняются действия деления и умножения. Вторыми — сложение и вычитание.

Пример 1. Решение числового выражения

Задача. Решить:

20 — 2 • 10 ÷ 5 — 4 = ?

Решение. Чтобы решить выражение, нам необходимо выполнить все арифметические действия в соответствии с установленными правилами. Поиск значения начинается с решения деления и умножения. В первую очередь находим произведение цифр 2 и 10 (если рассматривать с левой стороны, данное действие является первым по значимости). Получаем 20. Теперь это число делим на 5. Итог — 4. Когда известно значение основных действий, можем подставить его в наш пример:

20 — 4 — 4 = ?

Упрощенный пример также решаем слева направо: 20 — 4 = 16. Второе действие: 16 — 4 = 12. Ответ 12.

Решение без пояснений. 20 — 2 • 10 ÷ 5 — 4 = 20 — (2 • 10 ÷ 5) — 4 = 20 — 4 — 4 = 12.

Ответ. 12

Пример 2. Решение числового выражения

Задача. Решить:

0,2 — 5 • (— 4) + 1/2 • 5 • 4 = ?

Решение. Начинаем решение с умножения и деления. Умножая 5 на (— 4) получаем (— 20), т.к. производное сохраняет знак множителя. Далее умножаем 1/2 на 5. Для этого преобразуем дробь: 1/2 = 5/10 = 0,5. 0,5 умножаем на 5. Ответ — 2,5. Далее умножаем полученное число на 4. 2,5 • 4 = 10. Получаем следующее выражение:

0,2 — (— 20) + 10

Теперь нам остается решить сложение и вычитание. В первую очередь раскрываем скобку и получаем:

0,2 + 20 + 10 = 30,2

Решение без пояснений. 0,2 — 5 • (— 4) + 1/2 • 5 • 4 = 0,2 — (— 20) + 10 = 0,2 + 20 + 10 = 30,2

Ответ. 30,2

Находим значение выражения со скобками

Скобки определяют порядок действий при решении примера. Выражения, находящиеся внутри скобок «()» имеют первостепенную значимость, независимо от того, какое математическое действие в них выполняется.

Пример 3. Значение числового выражения со скобками

Задача. Решить:

5 + (7 — 2 • 3) • (6 — 4) ÷ 2 = ?

Решение. Начинаем нахождение значения выражения с решения скобок. Порядок действий определяется слева направо. При этом не забываем, что после раскрытия скобок в первую очередь решаем умножение и деление и лишь потом — вычитание и сложение:

• 7 — 2 • 3 = 7 — 6 = 1
• 6 — 4 = 2

Когда скобки решены, подставляем полученные значения в наш пример:

5 + 1 • 2 ÷ 2

Снова решаем все по порядку, не забывая о том, что деление и умножение выполняется в первую очередь:

• 1 • 2 = 2
• 2 ÷ 2 = 1

Упрощенное выражение выглядит следующим образом:

5 + 1 = 6

Решение без пояснений. 5 + (7 — 2 • 3) • (6 — 4) ÷ 2 = 5 + (7 — 6) • 2 ÷ 2 = 5+ 1 • 2 ÷ 2 = 5 + 1 = 6

Ответ. 6

Значение числового выражения со скобками

Задача. Решить:

4 + (3 + 1 + 4 • (2+3)) = ?

Решение. Подобные примеры решаются поэтапно. Помним, что поиск выражения со скобками начинается с решения скобок. Поэтому в первую очередь решаем:

3 + 1 + 4 • (2+3)

В уже упрощенном примере снова встречаются скобки. Их будем решать в первую очередь:

2 + 3 = 5

Теперь можем подставить определенное значение в общую скобку:

3 + 1 + 4 • 5

Начинаем решение с умножения и далее слева направо:

• 4 • 5 = 20
• 3 + 1 = 4
• 4 + 20 = 24

Далее подставляем полученный ответ вместо большой скобки и получаем:

4 + 24 = 28

Решение без пояснений. 4 + (3 + 1 + 4 • (2+3)) = 4 + (3 + 1 + 4 • 5) = 4 + (3 + 1 + 20) = 4 + 24 = 28

Ответ. 28

Важно: Чтобы правильно определить значение числового выражения с множественными скобками, необходимо выполнять все действия постепенно. Скобки читаются слева направо. Приоритет в решении внутри скобок остается за делением и умножением.

Поиск значения выражения с корнями

Часто алгебраические задания основываются на нахождении значений из-под корня. И если определить √4 несложно (напомним, это будет 2), то с примерами, которые полностью расположены под корнем, возникает ряд вопросов. На самом деле в таких заданиях нет ничего сложного. В данном случае порядок действий следующий:

• Решаем все выражение, которое находится под корнем (не забываем о правильной последовательности: сперва скобки, деление и умножение, а лишь потом — сложение и вычитание);
• Извлекаем корень из числа, которое получили в результате решения обычного примера.

Если же и под корнем имеется корень (например: √ 4 + 8 — √4), то начинаем решение примера с его извлечения (в нашем примере это будет: √ 4 + 8 — 2). Если подкоренные числа возведены во вторую степень, то их квадратный корень будет равняться модулю подкоренного выражения.

Значение числового выражения с корнями

Задача. Решить:

√ 2² • 2² • 3² = ?

Решение. Все действия под корнем одинаковы — умножение. Это дает нам право разделить выражение на множители. Получаем:

√2² • √2² • √3² = ?

Т.к. под квадратным корнем у нас числа, возведенные во вторую степень, получаем:

2 • 2 • 3 = 12

Решение без пояснений. √ 2² • 2² • 3² = √2² • √2² • √3² = 2 • 2 • 3 = 12

Ответ. 12

Находим значение числовых выражений со степенями

Следующий математический знак, который имеет приоритет в процессе решения, — степени. Они представляют собой результат многократного умножения числа на себя. Само число является основанием степени. А количество операций умножения — ее показателем. Причем выражен он может быть не только целым числом, но и дробью, полноценным числовым выражением.

Начинается решение выражения со степенями с вычисления самих степеней. Если они представляют собой полноценное выражение (например: [3^{3 cdot 4-10}]), то его необходимо решить в нашем примере это будет: [3^{12-10}=3^{2}=9].

Задача. Решите:

[ 3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=? ]

Решение. Чтобы решить это выражение со степенями, воспользуемся равенством:

[(a cdot b)^{r}=a^{r} cdot b^{r}]

Рассматривая пример слева направо, видим, что у первых двух множителей одинаковые степени. Это позволяет нам упростить выражение:

[ (3 cdot 7)^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3} cdot 21^{2 / 3} ]

Зная, что при умножении степени с одинаковыми показателями складываются, получаем следующее выражение:

[ 21^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21 ]

Решение без пояснений: [3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=(3 cdot 7)^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21]

Ответ. 21

Интересно: Этот же пример можно решить и другим способом, преобразовав число 21 в степени ⅔ в два множителя. В данном случае решение будет выглядеть следующим образом:

[3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=3^{1 / 3} cdot 7^{1 / 3} cdot(3 cdot 7)^{2 / 3}=3^{1 / 3} cdot 7^{1 / 3} cdot 3^{2 / 3} cdot 7^{2 / 3}=3^{1 / 3+2 / 3} cdot 7^{1 / 3+2 / 3}=3^{1}+7^{1}=21]

Ответ. 21

Задача. Решить:

[ 2^{-2 sqrt{5}} cdot 4^{sqrt{5}-1}+left((sqrt{3})^{1 / 3}right)^{6} ]

Решение. В данном случает получить точные числовые значения показателей степеней не удастся. Поэтому искать значение выражения с дробями в виде степени будем снова через упрощение:

Ответ. 3,25

Выражения с дробями

Поиск значения выражения дробей начинается с их приведения к общему виду. В большинстве случаев проще представить все значения в виде обыкновенной дроби с числителем и знаменателем. После преобразования всех чисел необходимо привести все дроби к общему знаменателю.

Важно: Прежде чем найти выражение дробей, необходимо провести вычисления в их знаменателе и числителе отдельно. В данном случае действуют стандартные правила решения.

Когда дроби приведены к единому знаменателю можно переходить к решению. Вычисление значений верхней строки (числителя) и нижней (знаменателя) производятся параллельно.

Задача. Решить:

[ 6 frac{2}{13}+4 frac{1}{13}=? ]

Решение. Действуя по главному правилу, прежде чем найти значение числового выражения, преобразуем всего его части в простую дробь. Получаем:

[ frac{6 cdot 13+2}{13}+frac{4 cdot 13+1}{13} ]

Теперь выполняем вычисления в знаменателе и числителе и находим ответ:

[ frac{6 cdot 13+2}{13}+frac{4 cdot 13+1}{13}=frac{80}{13}+frac{53}{13}=frac{133}{13}=10 frac{3}{13} ]

Ответ. [10 frac{3}{13}]

Примеры(2):

Задача. Решить:

[ frac{2}{sqrt{5}-1}-frac{2 sqrt{5}-7}{4}-3=? ]

Решение. В данном примере мы не можем извлечь корень из пятерки. Но мы можем воспользоваться формулой разложения корней:

[ frac{2}{sqrt{5}-1}=frac{2(sqrt{5}+1)}{(sqrt{5}-1)(sqrt{5}+1)}=frac{2(sqrt{5}+1)}{5-1}=frac{2 sqrt{5}+2}{4} ]

Теперь можем придать нашему первоначальному выражению следующий вид:

[ frac{2 sqrt{5}+2}{4} frac{2 sqrt{5}-7}{4}-3=frac{2 sqrt{5}+2-2 sqrt{5}+7}{4}-3=frac{9}{4} 3=-frac{3}{4} ]

Ответ. [-frac{3}{4}].

Выражения с логарифмами

Как и степени, логарифмы (log), имеющиеся в выражении, вычисляются (если это возможно) в первую очередь. К примеру, зная, что [log _{2} 4=2] мы можем сразу упростить выражение  [log _{2} 4+5 cdot 6] до простого и понятного 2 + 5*6 = 32.

Со степенями логарифмы объединяет и порядок выполнения действий. Прежде чем искать значение выражения логарифмов, необходимо вычислить его основание (если оно представлено математическим выражением).

В случаях, когда полное вычисление логарифма невозможно, производится упрощение примера.

Задача. Решить:

[log _{27} 81+log _{27} 9=?]

Решение. Чтобы найти логарифм выражения, воспользуемся свойствами логарифмов и представим значение логарифмов со степенями:

Это позволит нам решить пример следующим образом:

Ответ. 2

Решаем выражения с тригонометрической функцией

Часто в выражениях встречаются тригонометрические функции. Всего их в математике шесть:

• Синус;
• Косинус;
• Котангенс;
• Тангенс;
• Секанс;
• Косеканс.

Изучение тригонометрии начинается в 9-м классе, когда ученики уже подготовлены к сложным задачам. Большинство заданий представляются с sin и cos. Остальные функции встречаются значительно реже.

В математических примерах, которые содержат sin, cos, tg и др. функции, вычисление тригонометрической функции производится в первую очередь. Если это невозможно — осуществляется упрощение выражения до получения краткой формулы.

Задача. Решить:

[ frac{24}{sin ^{2} 127+1+sin ^{2} 217} ]

Решение. Разложим 217 на 90 и 127. Т.к. по формуле приведения sin(90 + a) = cosa, получаем:

sin217 — sin (90 + 127) = cos127

Теперь заменяем полученной формулой наше слагаемое в знаменателе дроби:

[ frac{24}{sin ^{2} 127+cos ^{2} 127+1} ]

Вспоминаем, что по тригонометрическому тождеству sin²a+ cos² a= 1 (независимо от значения угла a). Поэтому одну часть слагаемого знаменателя (sin²127+ cos²127) преобразуем в единицу и получаем:

[ frac{24}{sin ^{2} 127+cos ^{2} 127+1}=frac{24}{1+1}=frac{24}{2}=2 ]

Ответ. 2

Задача. Решить:

[ sqrt{4} 8-sqrt{1} 92 sin ^{2} frac{19 pi}{12}=? ]

Решение. Начинаем решение с разбора второй дроби. Обращаем внимание, что 192 = 48 • 2. А значит, корень этого числа можно представить в виде 2√48. Зная это и используя формулу косинуса двойного угла, преобразим наше выражение:

Теперь по формуле приведения решаем наш пример:

[ sqrt{4} 8 cos left(3 pi+frac{pi}{6}right)=sqrt{4} 8left(-cos frac{pi}{6}right)=-sqrt{4} 8 cdot frac{sqrt{3}}{2}=-4 sqrt{3} cdot frac{sqrt{3}}{2}=-6 ]

Ответ. — 6.

Общий случай: находим значения выражений с дробями, функциями, степенями и не только

Самым сложным считается поиск числовых выражений общих случаев. Они представляют собой тригонометрические примеры, которые могут содержать:

• Степени;
• Скобки;
• Корни;
• Функции и т.д.

Общие числовые выражения сложны только длительностью решения. В остальном же они ничуть не сложнее, чем решение каждого примера (со скобкой, степенями, функциями и т.д.) по отдельности.

Чтобы найти значение выражения с логарифмами, тригонометрическими функциями, скобками и/или другими действиями, необходимо помнить три основных правила:

• Упрощение. Прежде чем приступать к решению внимательно изучите выражение. Особенно — его степени, корни, логарифмы, функции. В большинстве случаев их можно сократить или заменить простым числовым значением еще до решения.
• Скобки. Независимо от типа выражения, действий, начинать решение всегда необходимо со скобок. Часто именно игнорирование этого правила приводит к получению неверного ответа или отсутствию решения в принципе.
• Общий вид. Старайтесь привести выражение к общему виду. Особенно это касается дробей. Смешанные и десятичные дроби преобразуйте в обычные.
• Последовательность. Действия в скобках и действия после их решения выполняются слева направо. В первую очередь необходимо совершать умножение и деление. Когда все произведения и частные найдены, можно переходить к сложению и вычитанию.

Для удобства решения и устранения возможных ошибок рекомендуем расставлять порядок действий непосредственно над математическими знаками.

Задача. Решить:

[ -frac{sqrt{2} sin left(frac{pi}{6}+2left(frac{2 pi}{5}+frac{3 pi}{5}right)right)+3}{operatorname{Ln} e^{2}}+left(1+3^{sqrt{9}}right)=? ]

Решение. Чтобы решить этот пример, сначала найдем значение выражения числителя дроби, а точнее — подкоренного выражения. Для этого необходимо вычислить значение sin и общего выражения. Начинаем с раскрытия скобок в числителе:

Полученное значение можем подставить в подкоренное выражение для вычисления числителя дроби:

[ sqrt{2} sin cdotleft(frac{pi}{6}+2left(frac{2 pi}{5}+frac{3 pi}{5}right)+3=sqrt{4}=2right. ]

Со знаменателем дела обстоят куда проще:

[ ln e^{2}=2 ]

Числитель и знаменатель у нас одинаковые, что позволяет нам их сократить:

Теперь остается решить следующее выражение:

Ответ. 27

Как видите, при последовательном решении примеров с большим количеством действий нет ничего сложного. Главное — верно обозначить последовательность шагов и четко ей следовать.

Как найти значение выражения числителя дроби, подкорневого значения рационально?

Независимо от типа выражения решать его необходимо последовательно, руководствуясь стандартными правилами (описаны ранее). Но не стоит забывать, что во многих случаях поиск ответа может быть значительно упрощен за счет рационального подхода к решению. Основывается он на нескольких правилах.

Правило 1. Когда произведение равно нулю

Производное равно нулю в том случае, если хотя бы один из его сомножителей равен нулю. Если вы решаете пример из нескольких сомножителей, одним из которых является «0», то проводить многочисленные вычислительные действия не стоит.

Например, выражение [3 cdotleft(451+4+frac{18}{3}right)left(1-sin left(frac{3 pi}{4}right)right) cdot 0] будет равняться нулю.

Правило 2. Группировка и вынесение чисел

Ускорить процесс поиска ответа можно за счет группировки множителей, слагаемых или вынесения единого множителя за скобки. Также не стоит забывать о возможности сокращения дроби.

Например, выражение [frac{left(451+4+frac{18}{3}right)}{4left(451+4+frac{18}{3}right)}] решать не надо. Достаточно сократить скобки, чтобы получить ответ [=frac{1}{4}]

Решение примеров с переменными

Примеры с переменными отличаются от числовых только формой предоставления. В данном случае значения предоставляются дополнительно к выражению.

Пример задания: Найдите значение выражения 2x — y, если x = 2,5, а y = 2. В данном случае решение будет выглядеть следующим образом:

2x — y = 2 • 2,5 — 2 = 3

При этом в таких примерах сохраняются все описанные выше правила. Касается это и советов по рациональному решению примеров. Так, решать дробь [frac{sqrt{y}}{sqrt{y}}] бессмысленно, т.к. при любых значениях «y» ответ будет одинаковым — 1.

В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.

Как найти значение числового выражения?

Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.

Простейшие случаи

Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами. 

Если в выражении есть только числа и арифметические знаки “+”, “·”, “-“, “÷”, то действия выполняются слева направо в следующем порядке: сначала умножение и деление, затем сложение и вычитание. Приведем примеры.

Выражения со скобками

Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.

Значение выражений, содержащих скобки в скобках, находится по такому же принципу.

В нахождении значений выражений со скобками главное – соблюдать последовательность действий.

Выражения с корнями

Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.

Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.

Выражения со степенями

Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.

Также часто целесообразно бывает провести упрощение выражения  с использованием свойств степени.

Выражения с дробями

Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения. 

Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.

Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.

Выражения с логарифмами

Когда в выражении присутствуют логарифмы, их значение, если это возможно, вычисляется с самого начала. К примеру, в выражении log24+2·4 можно сразу вместо log24 записать значение этого логарифма, а потом выполнить все действия. Получим: log24+2·4=2+2·4=2+8=10.

Под самим знаком логарифма и в его основании также могут находится числовые выражения. В таком случае, первым делом находятся их значения. Возьмем выражение log5-6÷352+2+7. Имеем:

log5-6÷352+2+7=log327+7=3+7=10.

Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.

Выражения с тригонометрическими функциями

Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.

Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.

Общий случай числового выражения

В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.

Разберем пример.

В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.

Вычисление значений выражений рациональными способами

Вычислять значения числовых нужно последовательно и аккуратно. Данный процесс можно рационализировать и ускорить, используя различные свойства действий с числами. К примеру, известно, что произведение равно нулю, если нулю равен хотя бы один из множителей. С учетом этого свойства, можно сразу сказать, что выражение 2·386+5+58941-sin3π4·0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.

Также удобно использовать свойство вычитания равных чисел. Не выполняя никаких действий, можно заказать, что значение выражения 56+8-3,789lne2-56+8-3,789lne2 также равно нулю.

Еще один прием, позволяющий ускорить процесс – использование тождественных преобразований таких как группировка слагаемых и множителей и вынесение общего множителя за скобки. Рациональный подход к вычислению выражений с дробями – сокращение одинаковых выражений в числителе и знаменателе. 

Например, возьмем выражение 23-15+3·289·343·23-15+3·289·34. Не выполняя действий в скобках, а сокращая дробь, можно сказать, что значение выражения равно 13.

Нахождение значений выражений с переменными

Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных. 

Чтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.

Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.

Например, выражение х+3-х, очевидно, имеет значение 3, и для вычисления этого значения совсем необязательно знать значение переменной икс. Значение данного выражения равно трем для всех значений переменной икс из ее области допустимых значений. 

Еще один пример. Значение выражения xx равно единице для всех положительных иксов. 

Развитие информационных технологий здорово упростило жизнь во многих аспектах. В том числе и процесс образования. Сегодня в интернете можно найти ответ на любые вопросы из школьных и университетских учебников. Но до недавнего времени единственной сложностью оставались задачи фундаментальных предметов.

Сейчас, имея под рукой смартфон, можно найти решение по фото или картинке почти любого примера. Конечно, если установить правильно приложение. А те, что не поддаются машинной логике, доверить более опытным людям из интернета. А если вы еще не знаете, как решить пример по фото, но хотите научиться, то эта статья точно для вас.

Приложения для смартфона

Если открыть Play Market по соответствующему запросу, можно увидеть внушительный список приложений. К сожалению большинство из них не всегда корректно распознают пример на фото. Трудно сказать в чем проблема: то ли сканер плохо распознает пример, то ли почерк непонятный. Поэтому пришлось повозится, чтобы отобрать только качественные приложения, которые отлично справляются со всеми этапами работы.

Maple Калькулятор

Maple Калькулятор – отличный инструмент для работы с математическими примерами. Приложение решает задачи не только школьного уровня, но также и примеры университетского уровня. Оно русифицировано и полностью бесплатно и, как ни странно, в нем полностью отсутствует реклама. Такое еще поискать надо!

Чтобы найти решение примера по фото с помощью Maple Калькулятора, выполните следующее:

1. Запустите приложение и тапните по иконке камеры на главном экране (при первом запуске программа запросит доступ к фотокамере, нажмите «Подтвердить»).
2. Наведите окно сканера на пример, таким образом, чтобы он весь попал в окно и сделайте фото.
3. Дождитесь пока приложение отсканирует пример, при необходимости отредактируйте выражение, нажав на значок карандаша рядом с записью.

Если решаете пример из геометрии, можно посмотреть график функции. Для этого разверните пункт «Двухмерный график». Только он почему-то строится трехмерный, но общий смысл понятен.

Microsoft Math Solver

Приложение Math Solver не просто выдает готовый результат вычислений, но также показывает шаги решений и итоговый график. Что будет весьма полезно для решения домашних работ по математике и алгебре. А дополнительные функция подробного описания хода решения будет особенно полезна для решения задач таких предметов как физика и геометрия.

Чтобы решить пример по фото выполните следующие действия:

1. Запустите приложение (при первом запуске выберите язык и пролистайте ознакомление с основными функциями, при желании ознакомьтесь с ними).
2. Сфотографируйте пример.
3. После того как приложение выполнит сканирование, потяните появившееся окошко вверх, чтобы увидеть подробности решения и правильный ответ.
4. Если хотите посмотреть шаги решения, нажмите соответствующую кнопку на экране.

Math Solver отлично русифицировано, бесплатно и не содержит рекламы. От предыдущего отличается только тем, что не умеет строить трехмерные графики.

Math Scanner

Math Scanner бесплатное нерусифицированное приложение со встроенной рекламой. Но простота интерфейса и ненавязчивость рекламы никак не мешают пользоваться им при слабом знании английского. К тому же у него высокая точность сканирования.

Чтобы решить пример с помощью Math Scanner следуйте инструкции ниже:

1. Запустите приложение и пропустите рекламу, чтобы открыть основное меню.
2. Наведите сканер на пример, так, чтобы он целиком попал в окно и нажмите кнопку активации.
3. Дождитесь пока приложение выполнит сканирование и подтвердите полученный результат (если Math Scanner понял уравнение неверно, перепишите пример аккуратнее и повторно запустите сканирование).

В следующем окне вы увидите правильный ответ и этапы решения.

В отличии от описанных выше приложений, Math Scanner не строит графики. Зато с его помощью вы всегда сможете посмотреть похожие задачи.

Photomath

Photomath – это одно из двух самых известных приложений для решения примеров по фото. Это не просто удобное приложение, облегчающее подготовку домашнего задания для школьников и студентов, а полноценный обучающий портал с разделами для учеников, родителей и учителей.

Чтобы решить пример или уравнение с помощью Фотомач сделайте следующие действия:

1. При первом запуске укажите свой возраст и категорию (учитель, ученик, родитель). Это нужно, чтобы приложение правильно показывало рекомендации и по необходимости подбирало обучающий материал.Больше всего полезной информации Photomath показывает в категории «Ученик».
2. Отсканируйте записанный пример и дождитесь пока приложение решит его. Если хотите посмотреть шаги по решению, то нажмите соответствующую кнопку в окне программы.

Среди окон с результатами вы найдете не только шаги решения, но также график функции, разные способы записи уравнения и пояснения к каждому этапу вычислений. А для сложных примеров длинные и укороченные способы расчета.

Сервис Mathway для решения примеров по фото онлайн

Без сомнений, пользоваться смартфоном для решения примеров удобно. Но что делать, если доступа к гаджету нет, а пример решить нужно? На помощь придет онлайн сервис Mathway. А сфотографировать пример можно, например, на веб камеру. Главное, чтобы изображение было читаемым.

Принцип работы сервиса аналогичен приложениям для смартфона. Чтобы решить пример по фото выполните следующие действия:

1. Сфотографируйте пример и загрузите его на компьютер.
2. На сайте сервиса выберите необходимый раздел науки, которой соответствует пример (необязательное действие, если вам не нужны подробности вычислений).
3. Через форму загрузите пример на сайт.
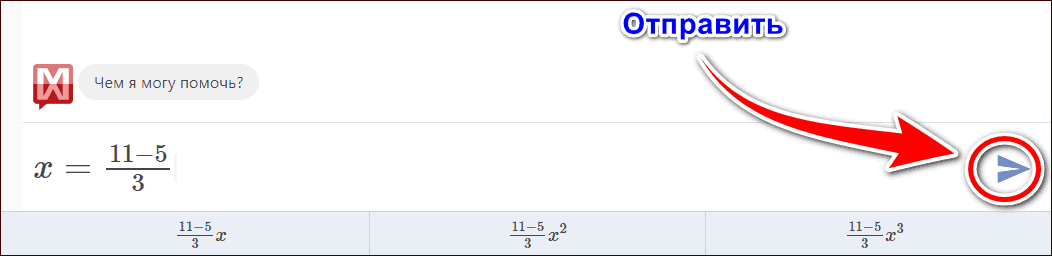
4. Если на фотографии записано несколько примеров или присутствует текст, выделите в специальном окне нужную задачу. А затем нажмите кнопку «Отправить» (иконка в форме бумажного самолетика).
5. Если сервис верно распознал выражение, еще раз нажмите кнопку «Отправить» в правом нижнем углу экрана.
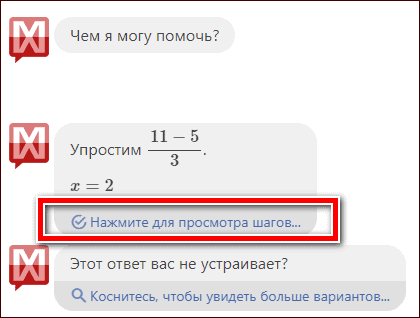
6. Дождитесь пока сервис выполнит расчет. Если нужны подробности решения, кликните по надписи: «Нажмите для просмотра шагов…».

Платные сервисы для решения задач

Как решать примеры по фото понятно. Описанных выше сервисов более чем достаточно, чтобы справиться с задачами по алгебре, физике и даже химии за 5-7 класс. Однако домашние задания для старших классов и тем более университетские по высшей математике могут быть настолько сложными, что даже правильно записать равенство не всегда получится. Конечно можно открыть решебник или повторить пройденный материал. И, в принципе, это правильное решение. Но не всегда найдется время.

В таком случае автоматизированные сервисы не помогут, а значит нужно обращаться к преподавателям по соответствующему предмету. И если среди знакомых таковых нет, можно воспользоваться услугами сервисов, где задачи решают люди.

Кампус

«Кампус» — это инновационный сервис, который предоставляет уникальную возможность решения задач и ответов на вопросы по фотографии. Пользователи могут легко загрузить фотографию задачи на платформу и ожидать быстрого и точного решения.

Процесс заказа:

1. Описываете задание.
2. Загружаете фото.

Загруженный заказ передается опытным математическим исполнителям, которые имеют глубокие знания и навыки в этой области.

1. Решение задания исполнителем.

Процесс решения начинается с тщательного анализа фотографии задачи специалистом. Исполнитель осуществляет не только распознавание и интерпретацию текста, но и осмысленное понимание сути задания. Затем, используя свои знания и методы, исполнитель решает задачу с высокой точностью и эффективностью.

1. Получение ответа.

После завершения решения задания, заказчик получает ответ, который содержит не только конечный результат, но и подробное объяснение примененных методов и шагов решения. Это позволяет заказчику не только получить правильный ответ, но и разобраться в процессе решения.

Сервис «Кампус» является надежным помощником для всех, кто сталкивается со сложными задачами. Он предлагает высококачественные услуги, оперативное решение и подробные объяснения, чтобы помочь пользователям достичь успеха в изучении знаний.

Ссылка на приложение Android

HomeWork

Сервис HomeWork устроен по принципу биржи. После регистрации вы оставляете задание с фотографией задачи из учебника и коротким описанием того, что нужно сделать. Далее сотрудник сервиса проведет предварительную оценку и передаст задачу на решение специалистам. Если цена вас устроит последний приступит к решению. Процесс не самый быстрый, в зависимости от сложности задачи может потребоваться от получаса до 3-4 часов и даже больше.

Чтобы воспользоваться услугами сервиса следуйте инструкции ниже:

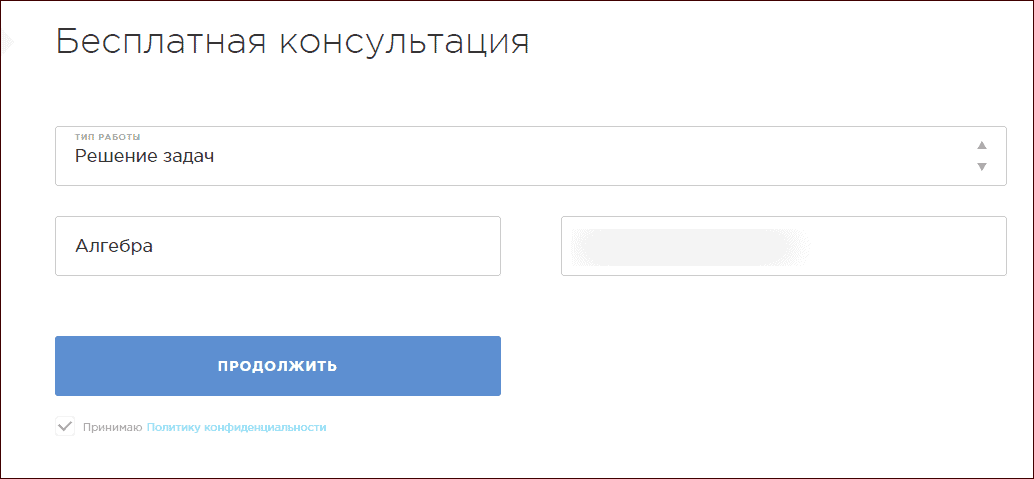
1. На главной странице сайта выберите тип работы и укажите адрес вашей электронной почты, а затем нажмите «Продолжить».
2. В следующем окне укажите предмет, кратко опишите что нужно сделать и загрузите фото задачи или примера, перетащив фото в специальное поле (цифра 3 на скриншоте ниже).
3. Самый неприятный момент. Для завершения регистрации необходимо указать свой номер телефона, куда будет направлена цена решения (спамить будут гарантированно, поэтому лучше указывать дополнительный номер, если таковой имеется).

Это же действие завершит создание аккаунта на сервисе. Спустя 10-15 минут менеджер пришлет смс с указанием стоимости решения. Она же появится в личном кабинете. Если цена вас устраивает, подтвердите выполнение работы и оплатите услуги.

Все сдал!

Принцип работы сервиса Все сдал! такой же, как и у предыдущего, только здесь не просят номер телефона. Что избавляет от головной боли со спам-звонками.

Чтобы оставить заявку на решение задачи, сделайте следующее:

1. Выполните регистрацию на сайте (укажите e-mail и установите пароль), либо воспользуйтесь упрощенной формой для входа.
2. В личном кабинете создайте задание.
3. Заполните поля формы, загрузите фото задачи или примера, а затем нажмите кнопку «Разместить заказ».
4. Дождитесь пока сервис пришлет уведомление о выполнении работы, который появится в разделе «Мои заказы».

После оплаты вы сможете увидеть решение и при необходимости скачать его.

Обложка: кадр из промо видео Maple Calculator

Где в интернете найти все эти математические символы, чтобы самому научиться делать задания по математике.

Задание 1.

Найти сумму, разность, произведение и частное комплексных чисел:

1. z1= 1 + 2 и z2= 1 – 2

2. z1= 4 – 3 и z2= 2 +

3. z1= 0,2 + 2 и z2= -0,3 +
4. z1= 5 – 6 и z2= -10 +8
5. z1= + и z2= –
6. z1= 2 + 2 и z2= 1 –
7. z1= 2 + и z2= 2 –
8. z1= 2 и z2= 1 +
9. z1= 4 – 5 и z2= -2 +7
10. z1 = 5 + 12 и z2 = 8 – 6

Задание 2.

Найти указанные пределы:

3×2 – 5x -2 2×2 – 3x +1

11 а) lim ————— b) lim —————-

x→ 2 2×2 – x – 6 x →∞ 3×2 + x + 4

12 2×2 + 15x +25 5×2 – 2x +1

а) lim ——————- b) lim —————-

x→ -5 5 – 4x – x2 x→∞ 2×2 + x – 3

4×2 + 7x +3 3 – 2x – x2

13 а) lim —————- b) lim —————-

x→ -1 2×2 + x – 1 x→ ∞ x2 + 4x + 1

2×2 – 9x + 9 3 x2 – 5x + 4

14 а) lim —————- b) lim —————-

x→ 3 x2 – 5x + 6 x→ ∞ x3 – x + 1

5x – x2 – 4 2×2 + x – 4

15 а) lim —————- b) lim —————-

x →4 x2 – 2x – 8 x→∞ 3 + x – 4×2

x2 – x – 6 3×2 – 7x + 3

16 а) lim —————- b) lim —————-

x →3 x2 – 6x + 9 x→∞ 2×2 -5x – 3

x2 – 4x + 4 5 – 2x – 3×2

17 а) lim —————- b) lim —————-

x→ -2 x2 – 4 x→∞ x2 + x + 3

x2 – 4 2×3 – 2x + 1

18 а) lim —————- b) lim —————-

x →-2 x2 + x – 2 x→ ∞ 3×2 + 4x + 2

x2 – 7x + 10 3×2 + 5x + 4

19 а) lim —————- b) lim —————-

x →5 x2 – 10x + 25 x →∞ 2×2 – x + 1

x2 – 2x – 8 x2 – 7x + 1

20 а) lim —————- b) lim —————-

x→ -2 2×2 + 5x + 2 x → ∞ 3×2 + x + 3

Задание 3. Найти производную следующих функций:

21 а) y = + – 4×6 +

б) y = (x3 + 4x) ∙ tg2 3x

c) y =

22 a) y = 4×4

б) y = (x – 2)4 ∙ sin 6x

с) y =

23 a) y = 5×3 – +

b) y = (2x – x2) ∙ tg4 x

c) y =

24 a) y = 2×5 –

b) y = (2x – x2) ∙ tg4 x

c) y =

25 a) y = 3×4 +

b) y = (x2 + 3x) ∙ tg

c) y =

1. a) y = 3×4

b) y = cos3 5x – x ∙ sin 3x

c) y =

1. a) y = 3×6

b) y = cos 2x ∙ ctg (x2)

c) y =

1. a) y = 8×2

b) y = ( x5 – 4×4 + 3×3 – 2×2)∙cos 7x

c) y =

1. a) y = 5×2 – +

b) y = (x – 7)6 ∙ ctg 3x

c) y =

30 . a) y = 3×5

b) y = (x + 5)3 ∙ sin2 x

c) y =

Задание 4. Найти частные производные функций

Задание 5. Выясните, является ли функция четной, нечетной или общего вида.

41) f(х) =3х2 – 2х

42) f(х) = х2 + х3

43) f(х) = х6 – 2х4 +4

44) f(х) = х5 – х

45) f(х) = х3 – 2

46) f(х) = 2х3 + 3

47) f(х) = х3 – 2х

48) f(х) = х4 – 2

49) f(х) = х2 : (х4 – 1)

50) f(х) = 3 – 2х – х2

Задание 6. Написать определения:

а) комплексного числа,

б) предела функции,

в) непрерывной функции,

г) функции двух независимых переменных,

д) частной производной функции нескольких переменных.