Как найти ответы на задачи по логике

Логика – это основа рационального мышления и фундамент для развития интеллекта ребенка. Решение различных логических задач дает возможность детям научиться анализировать ситуацию, находить взаимосвязи, отличать главное и второстепенное, формировать стратегию, применять в нужном месте свои знания и навыки.

Эти умения пригодятся не только в учебе, но и в реальной жизни. Рассуждая логически, ребенок может грамотно выразить свое мнение, подойти к решению той или иной задачи более осознанно, дать обоснование всевозможным явлениям, быстро сориентироваться в ситуации.

Поэтому решение логических задач должно быть неотъемлемой частью детского развития и образования. А для того, чтобы щелкать их как орешки, нужно понимать, какими приемами и методами пользоваться при решении.

Самое главное в решении логических задач

Почти у любой задачи есть несколько вариантов решения. Чтобы легко справляться даже с самыми непростыми заданиями, надо знать, какой способ будет наиболее подходящим в той или иной ситуации.

Понимание разных методов позволяет находить оптимальный вариант решения, что особенно важно в условиях ограниченного времени.

Все задачи на развитие логики можно разделить на группы:

• Математические ребусы;
• Задачи на истинность утверждений;
• Задачи на перемещение, взвешивание или переливание;
• Задачи, которые решаются с конца;
• Работа с множествами;
• Задачи на сопоставление «Кто есть кто?»

Выбор способа решения зависит от того, к какой группе относится задание.

Известные техники решения логических задач

1. Табличный метод (таблицы соответствий, истинности, совмещенные, кубические):
   таблицы создают наглядность, прозрачность рассуждений, помогают сделать верные выводы.
2. Применение законов из алгебры логики: вводятся обозначения для простых высказываний и преобразовываются в некую формулу.
3. Метод рассуждений: подходит для решения простых задач с небольшим количеством объектов. Последовательное рассуждение над каждым условием задачи приводит к правильному выводу.
4. Черчение блок-схем: способ, подходящий для решения задач на переливание, взвешивание. Рисуется схема, на которой отмечают последовательность действий и результат, полученный при их выполнении.
5. Графический метод: подходит для решения задач на объединение или пересечение множеств. Самый популярный графический метод называется «Круги Эйлера». Нарисованная геометрическая схема наглядно показывает отношение между множествами.
6. Метод «математический бильярд»: используется для решения задач на переливание жидкостей. Вычерчивается траектория движения бильярдного шара, который отталкивается от бортов стола в форме параллелограмма.

Рассмотрим подробно самые распространенные способы, которые могут использовать в решении логических задач ученики начальных классов:

Табличный метод

Условия задачи и результаты записываем в специальную таблицу. На пересечении строк и столбцов ставим «+», если утверждения не противоречат друг другу и «-», если они расходятся.

Задача:

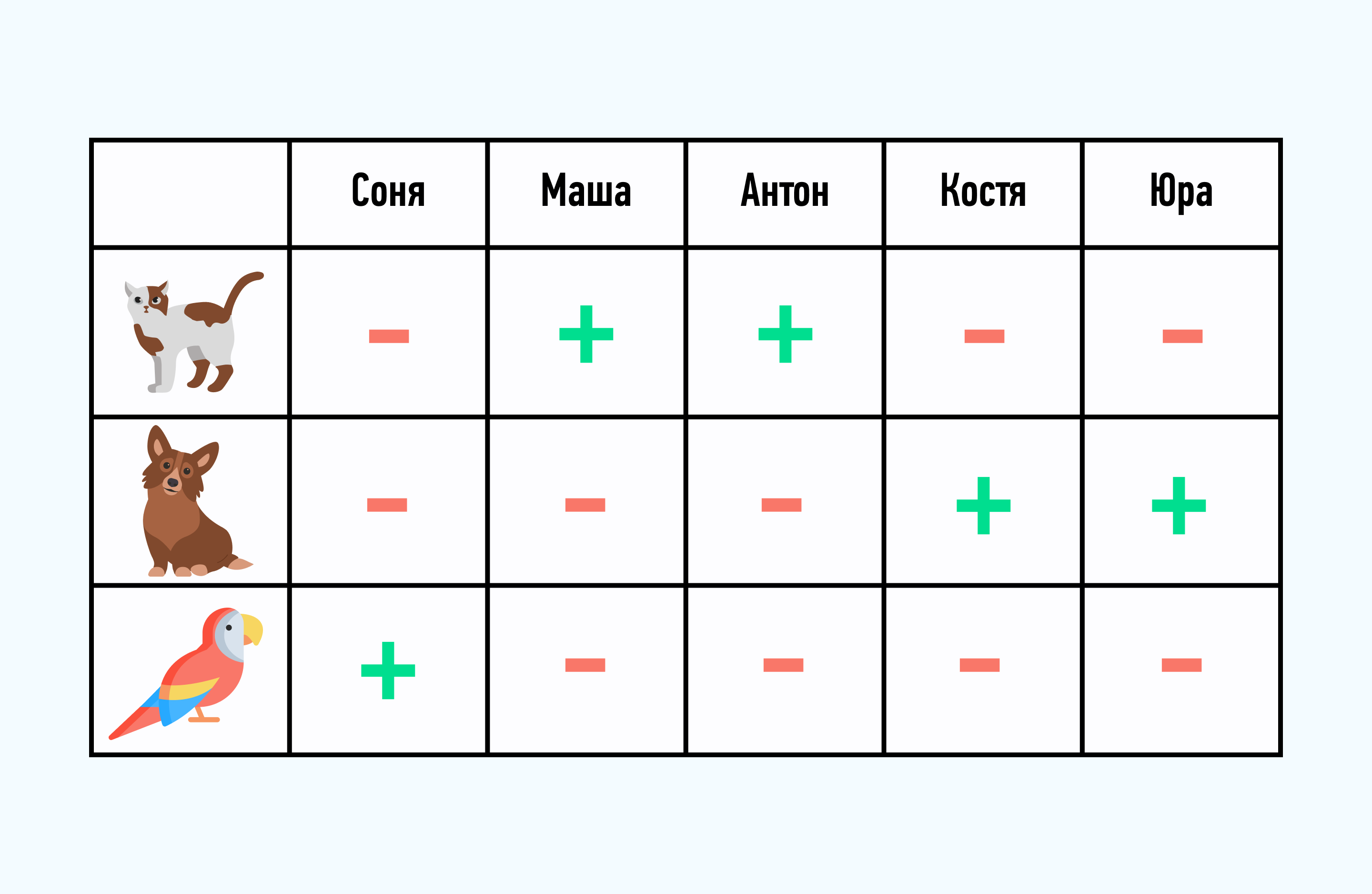
У Сони, Маши, Антона, Кости и Юры есть домашние животные. У каждого из ребят живет или собака, или кошка, или попугай. Вот только девочки собак не держат, а у мальчиков нет попугаев. У Сони и Маши разные питомцы, а вот у Маши с Антоном – одинаковые. У Сони нет кошки. У Кости с Юрой живут одинаковые животные, а у Антона с Костей – разные. Какие животные живут у каждого?

Решение:

Чертим таблицу, где названия столбцов – имена ребят, а названия строк – животные. Ставим в каждой ячейке знаки «+» или «-», опираясь на условия задачи:

1. Девочки собак не держат (ставим «-» на пересечении этих ячеек).
2. У мальчиков нет попугаев (в этих ячейках тоже ставим «-»).
3. У Сони нет кошки (ставим «-»).
4. Значит, у Сони есть попугай (ставим «+»).
5. У Сони и Маши разные питомцы. Получается, у Маши нет попугая (ставим «-»), зато есть кошка (ставим «+»).
6. У Маши с Антоном одинаковые животные. Значит, у Антона тоже живет кошка (ставим «+») и нет собаки (ставим «-»).
7. У Антона с Костей разные питомцы, выходит, что у Кости нет кошки (ставим «-»), зато есть собака (ставим «+»).
8. У Кости с Юрой одинаковые животные, значит у Юры тоже собака (ставим «+»), а не кошка (ставим «-»).

Так мы узнали, какие питомцы живут у каждого из ребят (ячейки со знаком «+»).

Ответ: У Сони попугай, у Маши и Антона кошки, у Кости и Юры собаки.

Круги Эйлера

Чтобы было легче разобраться в условиях задачи и найти решение, чертим круги, каждый из которых – отдельное множество.

Задача:

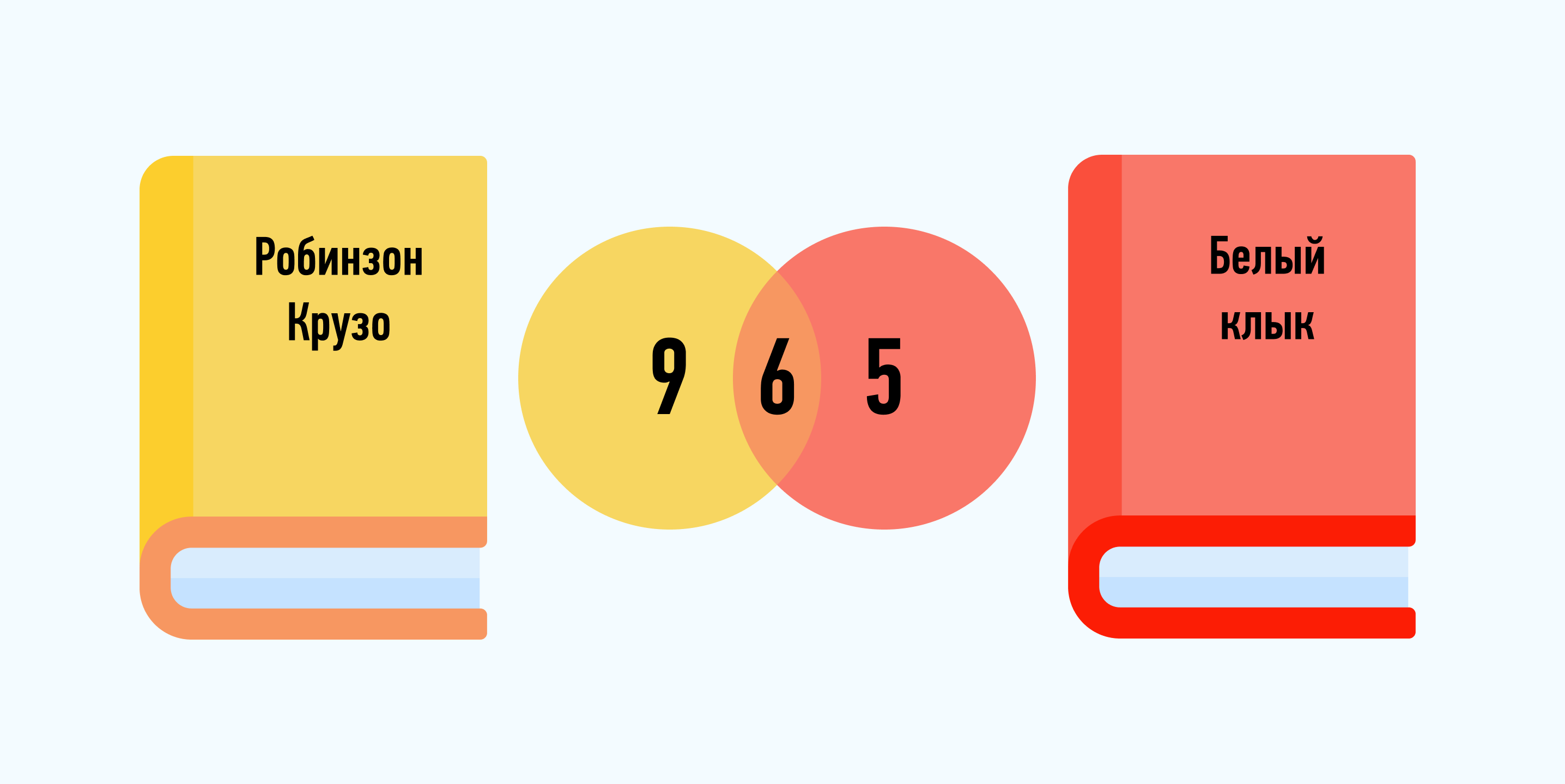
Всему классу задали на лето читать книжки. В списке литературы были такие произведения, как «Робинзон Крузо» Даниэля Дефо и «Белый клык» Джека Лондона. Известно, что 15 человек из класса прочитали «Робинзон Крузо», а остальные 11 – «Белый клык». Но среди них были 6 ребят, которые прочитали обе книги. Сколько человек прочитало только «Белый клык»?

Решение:

Чертим два круга, каждый из которых – множество детей, прочитавших определенную книгу, а пересечение кругов – дети, прочитавшие обе книги.

1. 15 – 6 = 9 – дети, которые прочитали только «Робинзон Крузо».
2. 11 – 6 = 5 – дети, которые читали лишь «Белый клык».

Ответ: 5 человек.

Метод рассуждений

Поочередно рассматриваем каждое из условий задачи и делаем логические выводы.

Задача:
На столе стоят вазы: голубая, зеленая, розовая и оранжевая. Третьей в ряду стоит та ваза, название цвета которой содержит больше всего букв. А зеленая стоит между оранжевой и розовой. Какая ваза стоит последней?

Решение:

1. Больше всего букв в слове «оранжевая», значит она третья по счету.
2. Если зеленая ваза стоит между оранжевой и розовой, значит, она будет второй в ряду, так как если ее поставить четвертой, то не останется места для розовой.
3. Соответственно, розовая будет стоять первой.
4. Остается голубая, она будет четвертой, то есть последней.

Ответ: голубая ваза.

Метод рассуждений «с конца»

Начинаем раскручивать клубок с конца, а затем сопоставляем результат с условиями задачи.

Задача:

Маме, папе и сыну вместе 125 лет. Когда родился сын, маме был 21 год. А папа старше мамы на 2 года. Сколько лет сейчас каждому из них?

Решение:

1. 21+2= 23 — было папе ( значит вместе родителям было 44 года)
2. (125 — 44) : 3 = 27 — возраст сына
3. 27 + 21 = 48 — возраст мамы
4. 48 + 2 = 50 — возраст папы

Ответ: 27, 48 и 50 лет.

---

Мы рассмотрели самые популярные и доступные методы, с помощью которых можно легко справиться с заданием. Главное – подобрать подходящий способ решения, который быстро приведет к правильному результату.

Для этого необходимо регулярно практиковаться и развивать свои способности. Отточить навыки решения подобных логических задач и многих других вы можете с помощью образовательной онлайн-платформы «Умназия».

Попробуйте решить вместе с ребенком задачу из раздела «логика» и переходите к регулярным занятиям на тренажере

Если вам понравилось, было весело интересно и полезно, то ждем вас на нашей онлайн платформе!
Умназия сегодня — это:

1. Онлайн тренажер развития навыков мышления — логики, внимания, эрудиции.
2. Программа «Культурный код» по развитию кругозора. Для самых любознательных и тех, кого кажется уже ничем не удивить!
3. Курсы развития памяти. Хотите чтобы Ваш ребенок без труда учил стихи, запоминал иностранные слова и всегда помнил про день рождения бабушки? На курсах покажем и расскажем как же этого достичь.
4. Пять ступеней финансовой грамотности. Увлекательная история героя, которая полностью зависит от действий ребенка и не имеет определенного результата. Сможет ли он пройти все финансовые ловушки и освоить пятую ступень?

Ждем вас, будет весело и интересно!

---

Читайте также:

• 15 сложных загадок на логику
• Загадки на логику с подвохом
• Логические загадки для детей
• Смешные логические загадки
• Загадки Эйнштейна на логику

---

Товарищи, приветствуем!

Нам регулярно поступают вопросы, касающиеся поисков ответов к заданиям, приведённым в замечательном учебнике В.М. Богуславского «Упражнения по Логике» (ПРИОБРЕСТИ)

Для удобства решения задач вы можете использовать электронную версию книги (СКАЧАТЬ).

К большому сожалению, подробного пособия или готовых ответов к этому учебнику нам найти не удалось.

Однако мы предлагаем всем, кому интересны логические задачи, присоединиться к чату

«Решение упражнений по логике», чтобы принять участие в обсуждениях, дискуссиях, потренировать логическое мышление. Итогом такой совместной работы мы видим создание сборника верных ответов, который будет важным пособием для читателей книги «Упражнения по Логике».

Наши ресурсы:
|

Сайт | ВКонтакте | Telegram |

#сталинскийбукварь
#задачи по логике
#логика
#логическое мышление
#советские учебники

Как решать логические и математические задачи

Решение задач на логику — отличная гимнастика для ума детей и взрослых на каждый день.
На ЛогикЛайк более 3500 заданий с ответами и пояснениями, полноценный учебный комплекс для развития логики и способностей к математике.

Решение задач по логике

Вариант I

1.
К какому виду относится следующее
понятие?

Безвластное
государство

Ответ

А) По объему:
(логически) пустое.

Б) По содержанию:
отрицательное.

В) По характеру
элементов объема: несобирательное,
конкретное.

2. Преобразуйте
следующее сложное суждение с внешним
отрицанием в эквивалентное ему суждение
без внешнего отрицания:

Неверно, что если
не знаешь ответ, то есть смысл задавать
вопрос.

Ответ

Символически:
(pq)
_Df
(p&q)
_Df
p&q
(не знаешь ответ и нет смысла задавать
вопрос).

3. Определите
правильность следующего силлогизма:

Все газы (М) –
твердые тела (Р). М⁺аР^–

Ксенон
(S) – газ (M).
S⁺aM^–

Ксенон
– твердое тело.S⁺aP^–

I-ая фигура, модус
ААА.

Силлогизм правильный.

Вариант II

1. Проверьте
правильность деления понятия, в случае
неправильности попробуйте

произвести деление
правильно:

ИМУЩЕСТВО:
ПРИОБРЕТЕННОЕ, ПОЛУЧЕННОЕ ПО НАСЛЕДСТВУ,
ПЕРЕДАННОЕ ВО ВРЕМЕННОЕ ПОЛЬЗОВАНИЕ,
ПОДАРЕННОЕ, УКРАДЕННОЕ.

Ответ

Деление неправильное,
так как деление ведется как минимум по
трем основаниям (отсюда и нарушение
других правил, как, например, включение
одних членов деления в другие).

«Исправить» его
можно, например, сначала осуществив
дихотомию по основанию «приобретение/отчуждение»,
а затем каждое полученное понятие
разделить по основанию «основание
приобретения/отчуждения»:

А) (Приобретенное)
имущество: полученное по наследству,
украденное.

Б) (Отчужденное)
имущество: переданное во временное
пользование, подаренное.

2. Преобразуйте следующее сложное суждение с внешним отрицанием в эквивалентное ему суждение без внешнего отрицания:

НЕВЕРНО, ЧТО
РЕВОЛЮЦИЯ МОЖЕТ НАЧАТЬСЯ ТОЛЬКО В ТОМ
СЛУЧАЕ, ЕСЛИ В СТРАНЕ СЛОЖИЛАСЬ
РЕВОЛЮЦИОННАЯ СИТУАЦИЯ.

Ответ

Символически:
(pq)
_Df
pq
(либо может начаться революция, либо в
стране сложилась революционная ситуация).

3. Проверьте по
логическому квадрату наличие отношения
следования:

Из истинности
высказывания «Не все книги интересны»
следует ложность высказывания «Ни одна
книга не интересна».

Ответ

Не все книги
интересны: SaP
_Df
SoP
(по квадрату в силу контрадикторности
SaP
и SoP).

Ни одна книга не
интересна: SeP.

Из SoP
логически не следует SeP,
поэтому при истинности SoP может быть
ложно SeP.

Вариант III

1.
К какому виду относится следующее
понятие?

Общенародное
государство

Ответ

А) По объему:
(фактически) пустое.

Б) По содержанию:
положительное.

В) По характеру
элементов объема: несобирательное,
конкретное.

2. Преобразуйте
отрицание следующего суждения с
отношениями в суждение без

внешнего отрицания:

НЕВЕРНО, ЧТО
КАКОЙ-НИБУДЬ РОССИЙСКИЙ ГОРОД БОЛЬШЕ
МОСКВЫ.

Ответ

Символически: SiP
_Df
SeP
(по квадрату в силу контрадикторности
SiP
и SeP;
ни один российский город не больше
Москвы)

3. Проверьте,
имеет ли место отношение
логического следования между указанными
посылками и
заключением:

Цезарь был в Германии
или в России; он не был в России; значит,
Цезарь был в Германии.

Ответ

Символически: pq,
q
=
p

p	q	pq	q
И	И	И	Л
И	Л	И	И
Л	И	И	Л
Л	Л	Л	И

В совместной таблице
таблице истинности для посылок и
заключения нет строки, где посылки
истинны, а заключение – ложно, поэтому
отношение логического следования есть.

Вариант IV

Соседние файлы в предмете Логика

• #
• #
• #
• #

Логика изучает абстрактное мышление как средство постижения мира, исследует формы и законы, по которым мир отражается в процессе мышления. Логика является философской дисциплиной и связана с теорией познания. Логика является философской дисциплиной и связана с теорией познания, поскольку процесс восприятия мира полностью изучается философией, а логика изучает лишь один из аспектов когнитивного мышления.

Логика происходит от греческого слова “логос”, что означает “мысль”, “слово”, “причина” или “закономерность”. Это слово используется, во-первых, для обозначения набора правил, которым должен следовать процесс мышления, и, во-вторых, для обозначения науки о правилах рассуждения и формах, в которых они осуществляются. Изучение мышления. Но мышление изучается не только логикой, но и различными другими науками, такими как психология, кибернетика, педагогика и т.д., каждая из которых изучает тот или иной аспект мышления.

Законы логики объективны и действуют независимо от воли или желания человека. Они имеют универсальный характер, заключающийся в том, что во все исторические периоды люди мыслят по одним и тем же законам. Законы, изучаемые в формальной логике, – это закон тождества, закон непротиворечия, закон достаточного основания и закон исключенной трети.

Если у вас нет времени на выполнение заданий по логике, вы всегда можете попросить меня, пришлите задания мне в whatsapp, и я вам помогу онлайн или в срок от 1 до 3 дней.

Ответы на вопросы по заказу заданий по логике:

Сколько стоит помощь?

• Цена зависит от объёма, сложности и срочности. Присылайте любые задания по любым предметам – я изучу и оценю.

Какой срок выполнения?

• Мне и моей команде под силу выполнить как срочный заказ, так и сложный заказ. Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые работы и задания раньше срока.

Если требуется доработка, это бесплатно?

• Доработка бесплатна. Срок выполнения от 1 до 2 дней.

Могу ли я не платить, если меня не устроит стоимость?

• Оценка стоимости бесплатна.

Каким способом можно оплатить?

• Можно оплатить любым способом: картой Visa / MasterCard, с баланса мобильного, google pay, apple pay, qiwi и т.д.

Какие у вас гарантии?

• Если работу не зачли, и мы не смогли её исправить – верну полную стоимость заказа.

В какое время я вам могу написать и прислать задание на выполнение?

• Присылайте в любое время! Я стараюсь быть всегда онлайн.

Ниже размещён теоретический и практический материал, который вам поможет разобраться в предмете “Логика“, если у вас есть желание и много свободного времени!

Содержание:

1. Ответы на вопросы по заказу заданий по логике:
2. Логические операции над высказываниями
3. Конъюнкция (логическое умножение)
4. Дизъюнкция (логическое сложение)
5. Импликация
6. Эквиваленция
7. Задача 1
8. Решение:
9. Задача 2
10. Решение:
11. Задача 3
12. Решение:
13. Задача 4
14. Решение:
15. Задача 5
16. Решение:
17. Задача 6
18. Решение:
19. Задача 7
20. Решение:
21. Задача 8
22. Решение:
23. Задача 9
24. Решение:
25. Задача 10
26. Решение:

Основным (неопределяемым) понятием математической логики является понятие «простого высказывания». Под высказыванием обычно понимают всякое повествовательное предложение, утверждающее что-либо о чем-либо, и при этом мы можем сказать, истинно оно или ложно в данных условиях места и времени. Логическими значениями высказываний являются «истина» и «ложь».

Приведем примеры высказываний.

• 1) Новгород стоит на Волхове.
• 2) Париж – столица Англии.
• 3) Карась не рыба.
• 4) Число 6 делится на 2 и на 3.
• 5) Если юноша окончил среднюю школу, то он получает аттестат зрелости.

Высказывания 1), 4), 5) истинны, а высказывания 2) и 3) ложны. Очевидно, предложение «Да здравствуют наши спортсмены!» не является высказыванием. Высказывание, представляющее собой одно утверждение, принято называть простым или элементарным. Примерами элементарных высказываний могут служить высказывания 1) и 2).

Высказывания, которые получаются из элементарных с помощью грамматических связок «не», «и», «или», «если …, то…», «тогда и только тогда», принято называть сложными или составными. Так, высказывание 3) получается из простого высказывания «Карась – рыба» с помощью отрицания «не», высказывание 4) образовано из элементарных высказываний «Число 6 делится на 2», «Число 6 делится на 3», соединенных союзом «и». Высказывание 5) получается из простых высказываний «Юноша окончил среднюю школу», «Юноша получает аттестат зрелости» с помощью грамматической связки «если …, то …». Аналогично сложные высказывания могут быть получены из простых высказываний с помощью грамматических связок «или», «тогда и только тогда». В алгебре логики все высказывания рассматриваются только с точки зрения их логического значения, а от их житейского содержания отвлекаются. Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.

В дальнейшем будем элементарные высказывания обозначать малыми буквами латинского алфавита: истинное значение высказывания — буквой или цифрой 1, а ложное значение – буквой или цифрой 0. Если высказывание а истинно, то будем писать а если ложно, то

Возможно, вас также заинтересует эта ссылка:

Логические операции над высказываниями

1. Отрицание. Отрицанием высказывания называется новое высказывание, которое является истинным, если высказывание ложно, и ложным, если высказывание истинно. Отрицание высказывания обозначается и читается «не » или «неверно, что ». Логические значения высказывания можно описать с помощью таблицы

Таблицы такого вида принято называть таблицами истинности. Пусть высказывание. Так как также является высказыванием, то можно образовать отрицание высказывания , то есть высказывание которое называется двойным отрицанием высказывания . Ясно, что логические значения высказываний и совпадают. Например, для высказывания «Река Волхов вытекает из озера Ильмень» отрицанием будет высказывание «Неверно, что река Волхов вытекает из озера Ильмень» или «Река Волхов не вытекает из озера Ильмень», а двойным отрицанием будет высказывание «Неверно, что река Волхов не вытекает из озера Ильмень»

Возможно, вас также заинтересует эта ссылка:

Конъюнкция (логическое умножение)

Конъюнкцией двух высказываний называется новое высказывание, которое считается истинным, если оба высказывания истинны, и ложным, если хотя бы одно из них ложно. Конъюнкция высказываний обозначается символом или читается Высказывания называются членами конъюнкции. Логические значения конъюнкции описываются следующей таблицей истинности:

Например, для высказываний «6 делится на 2», «6 делится на 3» их конъюнкцией будет высказывание «6 делится на 2 и 6 делится на 3», которое, очевидно, истинно.

Из определения операции конъюнкции видно, что союз «и» в алгебре логики употребляется в том же смысле, что и в повседневной речи. Но в обычной речи не принято соединять союзом «и» два высказывания далеких друг от друга по содержанию, а в алгебре логики рассматривается конъюнкция двух любых высказываний. Из определения операции конъюнкции и отрицания ясно, что высказывание всегда ложно.

Возможно, вас также заинтересует эта ссылка:

Дизъюнкция (логическое сложение)

Дизъюнкцией двух высказываний называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний истинно, и ложным, если они оба ложны. Дизъюнкция высказываний обозначается символом читается Высказывания называются членами дизъюнкции. Логические значения дизъюнкции описываются следующей таблицей истинности:

Например, высказывание «В треугольнике угол или угол острый» истинно, так как обязательно истинно хотя бы одно из высказываний: «В треугольнике угол острый», «В треугольнике угол острый». В повседневной речи союз «или» употребляется в различном смысле: исключающем и не исключающем. В алгебре логики союз «или» всегда употребляется в не исключающем смысле. Из определения операции дизъюнкции и отрицания ясно, что высказывание всегда истинно.

Возможно, вас также заинтересует эта ссылка:

Импликация

Импликацией двух высказываний называется новое высказывание, которое считается ложным, если истинно, а – ложно, и истинным во всех остальных случаях. Импликация высказываний обозначается символом читается «если то » или «из следует ». Высказывание называют условием или посылкой, высказывание – следствием или заключением, высказывание – следованием или импликацией.

Логические значения операции импликации описываются следующей таблицей истинности:

Например, высказывание «Если число 12 делится на 6, то оно делится на 3», очевидно, истинно, так как здесь истинна посылка «Число 12 делится на 6» и истинно заключение «Число 12 делится на 3». Употребление слов «если то …» в алгебре логики отличается от употребления их в обыденной речи, где мы, как правило, считаем, что, если высказывание ложно, то высказывание «Если , то » вообще не имеет смысла. Кроме того, строя предложение вида «если , то » в обыденной речи, мы всегда подразумеваем, что предложение вытекает из предложения . Употребление слов «если …, то …» в математической логике не требует этого, поскольку в ней смысл высказываний не рассматривается. Импликация играет важную роль в математических доказательствах, так как многие теоремы формулируются в условной форме «Если , то ». Если при этом известно, что истинно и доказана истинность импликации то мы вправе сделать вывод об истинности заключения .

Возможно, вас также заинтересует эта ссылка:

Эквиваленция

Эквиваленцей (или эквивалентностью) двух высказываний называется новое высказывание, которое считается истинным, когда оба высказывания либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях. Эквиваленция высказываний обозначается символом , читается «для того, чтобы , необходимо и достаточно, чтобы » или « тогда и только тогда, когда ». Высказывания называются членами эквиваленции.

Задача 1

Существуют ли три таких высказывания чтобы одновременно выполнялись для них следующие условия:

• Решение:

Из первого условия, по определению дизъюнкции, следует, что и т.е. Тогда второе данное условие, по определению импликации, влечет Отсюда Следовательно, что противоречит третьему данному условию. Значит, трех высказываний удовлетворяющих данным условиям, не существует.

Задача 2

Следующие составные высказывания расчлените на простые и запишите символически, введя буквенные обозначения для простых их составляющих: а) Если число делится на 2 и не делится на 3, то оно не делится на 6. б) Произведение трех чисел равно нулю тогда и только тогда, когда одно из них равно нулю. в) Если производная функции в точке равна нулю и вторая производная этой функции в той же точке отрицательна, то данная точка есть точка локального максимума функции. г) Если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна и линии их пересечения. д) Если прямая перпендикулярна двум прямым и лежащим в плоскости (утверждение ), и прямые и не параллельны (утверждение ), то прямая перпендикулярна всякой прямой лежащей в плоскости (утверждение ). е) Если прямая перпендикулярна двум прямым и лежащим в плоскости (утверждение ), и неперпендикулярна некоторой прямой лежащей в этой же плоскости (утверждение ), то прямые и параллельны ( — утверждение ). ж) Если две прямые и лежащие в плоскости , непараллельны (утверждение ) и прямая неперпендикулярна некоторой прямой лежащей в плоскости (утверждение ), то неперпендикулярна одной из прямых или (утверждение ). з) Если какие-либо два из трех векторов коллинеарны, то их смешанное произведение равно нулю и) Логарифм некоторого положительного числа будет положительным, если основание логарифма и логарифмируемое число будут больше 1 или если основание логарифма и логарифмируемое число будут заключены между 0 и 1. к) Если в параллелограмме не все углы прямые или не все стороны равны между собой, то этот параллелограмм не прямоугольник или не ромб. л) Если в треугольнике любая его медиана не является высотой и биссектрисой, то этот треугольник не равнобедренный и не равносторонний.

• Решение:

Выделим и следующим образом обозначим простейшие составляющие высказывания: А: «В треугольнике некоторая его медиана является высотой»; В: «В треугольнике некоторая его медиана является биссектрисой»; С: «Этот треугольник равнобедренный»; D: «Этот треугольник равносторонний». Тогда данное высказывание символически записывается так: будут формулами. Далее, формулами будут выражения Наконец выражение представляющее собой данную последовательность, также является формулой.

Задача 3

В следующей последовательности символов всевозможными способами расставьте скобки так, чтобы получилась формула:

• Решение:

л) Вот эти формулы (внешние скобки опущены):

Задача 4

Составьте таблицы истинности для следующих формул и укажите, какие из формул являются выполнимыми, какие — опровержимыми, какие — тождественно истинными (тавтологиями), какие — тождественно ложными (противоречиями):

• Решение:

Пользуясь определениями логических связок (операций над высказываниями), составим таблицу истинности данной формулы (логические значения этой формулы записаны в последнем столбце таблицы, где сама формула обозначена

Из построенной таблицы истинности видно, что данная формула выполнима, так как если, например, вместо пропозициональной переменной вставить в формулу ложное высказывание, а вместо — истинное, то вся формула превратится в истинное высказывание. Но эта формула является также и опровержимой, поскольку если, например, вместо пропозициональной переменной вставить в формулу истинное высказывание, а вместо переменной — ложное, то вся формула превратится в ложное высказывание. Следовательно, формула не является ни тавтологией, ни тождественно ложной формулой.

Возможно, вас также заинтересует эта ссылка:

• Решение задач

Задача 5

Докажите, что следующие формулы выполнимы, не составляя для них таблиц истинности, а указав какие-нибудь значения входящих в них пропозициональных переменных, при которых эти формулы обращаются в истинные высказывания:

• Решение:

л) Заключение второй импликации есть, очевидно, тождественно ложная формула. Поэтому если посылка второй импликации превратится при некоторой подстановке в ложное высказывание, то эта импликация станет истинным высказыванием и, следовательно, вся данная импликация превратится в истинное высказывание независимо от того, в какое высказывание обратится посылка всей данной импликации.

Посылка второй импликации обращается в ложное высказывание, когда вместо переменных и подставляются ложные высказывания.

Итак, данная формула выполнима, поскольку она обращается в истинное высказывание, если вместо и подставить ложные высказывания, а вместо — произвольное высказывание (его истинностное значение в данном случае не повлияет на истинностное значение всего высказывания).

Задача 6

Выясните, справедливы ли следующие утверждения (если утверждение несправедливо, то постарайтесь определить, обе его части «тогда» и «только тогда» не выполняются или только одна): а) тогда и только тогда, когда б) тогда и только тогда, когда в) тогда и только тогда, когда г) тогда и только тогда, когда д) тогда и только тогда, когда е) тогда и только тогда, когда ж) тогда и только тогда, когда з) тогда и только тогда, когда и) тогда и только тогда, когда к) тогда и только тогда, когда л) тогда и только тогда, когда м) тогда и только тогда, когда

• Решение:

л) Данное утверждение в полном объеме несправедливо: неверна его часть «тогда» (необходимость). Для подтверждения этого нужно указать такие конкретные формулы и чтобы по меньшей мере одна из них не была тавтологией, а формула тавтологией была бы. Вот пример таких формул: Ни одна из них не является тавтологией, но формула — тавтология. Еще пример: Проверьте, что этот пример действительно опровергает необходимость данного утверждения. Приведите самостоятельно аналогичный пример. Рассмотрим теперь часть «только тогда» (достаточность) данного утверждения. Оказывается, она верна. В самом деле, предположим, что и Это означает, что для любых высказываний высказывания будут истинными. Следовательно, для любых высказываний истинным будет и высказывание А это означает, что формула является тавтологией, т.е. м) Покажем, что данное утверждение справедливо. Необходимость. Пусть Следовательно, формула тождественно ложна. Но тогда, ввиду определения дизъюнкции, тождественно ложны обе формулы и А раз так, то отрицание каждой из этих формул будет всегда принимать лишь истинные значения, т. е. Докажите достаточность самостоятельно: убедитесь, что каждый логический шаг, сделанный при доказательстве необходимости, может быть проделан в обратном направлении.

Задача 7

Докажите, что справедливы следующие логические следования, руководствуясь определением этого понятия: Выясните, будут ли верны обратные следования, т.е. будет ли формула, стоящая слева, логическим следствием формулы, стоящей справа.

• Решение:

л) (Изучите сначала ход решения задачи 1.35, м.) Составим таблицу истинности для формул и участвующих в отношении следования:

Последовательный просмотр по строкам столбцов () и () показывает, что как только в какой-либо строке столбца () появляется 1, так сейчас же в этой строке и в столбце () обнаруживается 1. Значит, требуемое логическое следование действительно выполняется (алгоритм см. в Учебнике, с. 55). Обратное же следование неверно, поскольку, например, в первой же строке (т.е. при ) формула принимает значение 1 (столбец ()), а формула тем не менее принимает значение 0 (столбец ()).

Задача 8

Следующие формулы преобразуйте равносильным образом так, чтобы отрицание было отнесено только к пропозициональным переменным и не стояло перед скобками:

• Решение:

л) Проделаем требуемые равносильные преобразования:

Задача 9

Каждую из формул предыдущей задачи преобразуйте равносильным образом так, чтобы она содержала только логические связки

• Решение:

л) Воспользуемся результатом равносильных преобразований данной формулы, выполненных в предыдущей задаче, и продолжим преобразования для решения данной задачи:

Задача 10

Для каждой из следующих систем высказываний найдите логически эквивалентную ей, но более простую систему высказываний, если известно, что в данной системе по меньшей мере одно высказывание истинно:

• Решение:

л) По меньшей мере одно из высказываний данной совокупности будет истинным тогда и только тогда, когда истинна дизъюнкция всех этих высказываний. Поэтому, составив дизъюнкцию из данных высказываний и приведя ее с помощью равносильных преобразований к дизъюнкции более простого вида, можно получить более простую систему высказываний, эквивалентную данной. В нашем случае имеем следующую дизъюнкцию, которую затем упрощаем: Следовательно, по меньшей мере одно высказывание из данной системы будет истинным тогда и только тогда, когда будет истинным одно из высказываний или Поэтому данная система трех высказываний логически эквивалентна более простой системе из двух высказываний

Возможно, вас также заинтересует эта ссылка: