Падение напряжения
 На каждом сопротивлении r при прохождении тока I возникает напряжение U=I∙r, которое называется обычно падением напряжения на этом сопротивлении.
На каждом сопротивлении r при прохождении тока I возникает напряжение U=I∙r, которое называется обычно падением напряжения на этом сопротивлении.
Если в электрической цепи только одно сопротивление r, все напряжение источника Uист падает на этом сопротивлении.
Если в цепи имеются два сопротивления r1 и r2, соединенные последовательно, то сумма напряжений на сопротивлениях U1=I∙r1 и U2=I∙r2 т. е. падений напряжения, равна напряжению источника: Uист=U1+U2.
Напряжение источника питания равно сумме падений напряжения в цепи (2-й закон Кирхгофа).
1. Какое падение напряжения возникает на нити лампы сопротивлением r=15 Ом при прохождении тока I=0,3 А (рис. 1)?
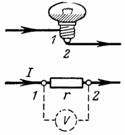
Падение напряжения подсчитывается по закону Ома: U=I∙r=0,3∙15=4,5 В.
Напряжение между точками 1 и 2 лампочки (см. схему) составляет 4,5 В. Лампочка светит нормально, если через нее проходит номинальный ток или если между точками 1 и 2 номинальное напряжение (номинальные ток и напряжение указываются на лампочке).
2. Две одинаковые лампочки на напряжение 2,5 В и ток 0,3 А соединены последовательно и подключены к карманной батарее с напряжением 4,5 В. Какое падение напряжения создается на зажимах отдельных лампочек (рис. 2)?
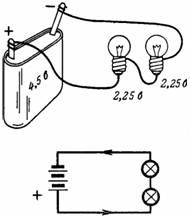
Одинаковые лампочки имеют равные сопротивления r. При последовательном включении через них проходит один и тот же ток I. Из этого следует, что на них будут одинаковые падения напряжения, сумма этих напряжений должна быть равна напряжению источника U=4,5 В. На каждую лампочку приходится напряжение 4,5:2=2,25 В.
Можно решить эту задачу и последовательным расчетом. Сопротивление лампочки рассчитываем по данным: rл=2,5/0,3=8,33 Ом.
Ток в цепи I = U/(2rл )=4,5/16,66=0,27 А.
Падение напряжения на лампочке U=Irл=0,27∙8,33=2,25 В.
3. Напряжение между рельсом и контактным проводом трамвайной линии равно 500 В. Для освещения используются четыре одинаковые лампы, соединенные последовательно. На какое напряжение должна быть выбрана каждая лампа (рис. 3)?
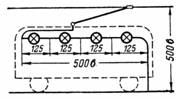
Одинаковые лампы имеют равные сопротивления, через которые проходит один и тот же ток. Падения напряжения на лампах будут тоже одинаковыми. Значит, на каждую лампу будет приходиться 500:4=125 В.
4. Две лампы мощностью 40 и 60 Вт с номинальным напряжением 220 В соединены последовательно и включены в сеть с напряжением 220 В. Какое падение напряжения возникает на каждой из них (рис. 4)?
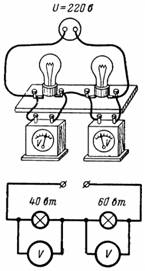
Первая лампа имеет сопротивление r1=1210 Ом, а вторая r2=806,6 Ом (в нагретом состоянии). Ток, проходящий через лампы, I=U/(r1+r2 )=220/2016,6=0,109 А.
Падение напряжения на первой лампе U1=I∙r1=0,109∙1210=132 В.
Падение напряжения на второй лампе U2=I∙r2=0,109∙806,6=88 В.
На лампе с большим сопротивлением большее падение напряжения, и наоборот. Накал нитей обеих ламп очень слаб, однако у лампы 40 Вт он несколько сильнее, чем у лампы 60 Вт.
5. Чтобы напряжение на электродвигателе Д (рис. 5) было равно 220 В, напряжение в начале длинной линии (на электростанции) должно быть больше 220 В на величину падения (потери) напряжения на линии. Чем больше сопротивление линии и ток в ней, тем больше падение напряжения на линии.
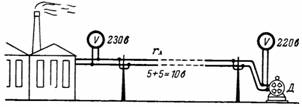
В нашем примере падение напряжения в каждом проводе линии равно 5 В. Тогда напряжение на шинах электростанции должно быть равно 230 В.
6. От аккумулятора напряжением 80 В потребитель питается током 30 А. Для нормальной работы потребителя допустимо 3% падения напряжения в проводах из алюминия с сечением 16 мм2. Каким может быть максимальное расстояние от аккумулятора до потребителя?
Допустимое падение напряжения в линии U=3/100∙80=2,4 В.
Сопротивление проводов ограничивается допустимым падением напряжения rпр=U/I=2,4/30=0,08 Ом.
По формуле для определения сопротивления подсчитаем длину проводов: r=ρ∙l/S, откуда l=(r∙S)/ρ=(0,08∙16)/0,029=44,1 м.
Если потребитель будет отдален от аккумулятора на 22 м, то напряжение на нем будет меньше 80 В на 3%, т.е. равным 77,6 В.
7. Телеграфная линия длиной 20 км выполнена из стального провода диаметром 3,5 мм. Обратная линия заменена заземлением через металлические шины. Переходное сопротивление между шиной и землей rз=50 Ом. Каким должно быть напряжение батареи в начале линии, если сопротивление реле на конце линии rр=300 Ом, а ток реле I=5 мА?
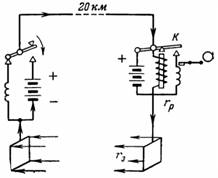
Схема включения показана на рис. 6. При нажатии телеграфного ключа в месте посылки сигнала реле в месте приема на конце линии притягивает якорь К, который в свою очередь включает своим контактом катушку записывающего аппарата. Напряжение источника должно компенсировать падение напряжения в линии, принимающем реле и переходных сопротивлениях заземляющих шин: U=I∙rл+I∙rр+I∙2∙rз; U=I∙(rл+rр+2∙rз).
Напряжение источника равно произведению тока на общее сопротивление цепи.
Сечение провода S=(π∙d^2)/4=(π∙3,5^2)/4=9,6 мм2.
Сопротивление линии rл=ρ∙l/S=0,11∙20000/9,6=229,2 Ом.
Результирующее сопротивление r=229,2+300+2∙50=629,2 Ом.
Напряжение источника U=I∙r=0,005∙629,2=3,146 В; U≈3,2 В.
Падение напряжения в линии при прохождении тока I=0,005 А будет: Uл=I∙rл=0,005∙229,2=1,146 В.
Сравнительно малое падение напряжения в линии достигается благодаря малой величине тока (5 мА). Поэтому в месте приема должно быть чувствительное реле (усилитель), которое включается от слабого импульса 5 мА и своим контактом включает другое, более мощное реле.
8. Как велико напряжение на лампах в схеме на рис. 28, когда: а) двигатель не включен; б) двигатель запускается; в) двигатель в работе.
Двигатель и 20 ламп включены в сеть с напряжением 110 В. Лампы рассчитаны на напряжение 110 В и мощность 40 Вт. Пусковой ток двигателя Iп=50 А, а его номинальный ток Iн=30 А.
Подводящий медный провод имеет сечение 16 мм2 и длину 40 м.
Из рис. 7 и условия задачи видно, что ток двигателя и ламп вызывает в линии падение напряжения, поэтому напряжение на нагрузке будет меньше 110 В.
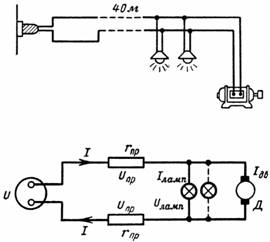
Отсюда напряжение на лампах Uламп=U-2∙Uл.
Надо определить падение напряжения в линии при различных токах: Uл=I∙rл.
Ток, проходящий через все лампы,
Падение напряжения в линии, когда включены только лампы (без двигателя),
Напряжение на лампах в этом случае равно:
При пуске двигателя лампы будут светить слабее, так как падение напряжения в линии больше:
2∙Uл=(Iламп+Iдв )∙2∙rл=(7,27+50)∙0,089=57,27∙0,089=5,1 В.
Минимальное напряжение на лампах при пуске двигателя будет:
Когда двигатель работает, падение напряжения в линии меньше, чем при пуске двигателя, но больше, чем при выключенном двигателе:
2∙Uл=(Iламп+Iном )∙2∙rл=(7,27+30)∙0,089=37,27∙0,089=3,32 В.
Напряжение на лампах при нормальной работе двигателя равно:
Даже небольшое снижение напряжения на лампах относительно номинального сильно влияет на яркость освещения.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Источник
Катушка индуктивности в цепи постоянного и переменного тока
Как ведет себя катушка индуктивности в цепи постоянного и переменного тока?
Катушка индуктивности в цепи постоянного тока
Итак, для этого опыта нам понадобится блок питания, который выдает постоянное напряжение, лампочка накаливания и собственно сама катушка индуктивности.
Чтобы сделать катушку индуктивности с хорошей индуктивностью, нам надо взять ферритовый сердечник:
Намотать на него лакированного медного провода и зачистить выводы:
Замеряем индуктивность нашей катушки с помощью LC метра:
Теперь собираем все это вот по такой схеме:
La — лампочка накаливания на напряжение 12 Вольт
Bat — блок питания, с выставленным напряжением 12 Вольт
Как вы помните из прошлой статьи, конденсатор у нас не пропускал постоянный электрический ток:
Делаем вывод: постоянный электрический ток почти беспрепятственно течет через катушку индуктивности. Сопротивлением обладает только сам провод, из которого намотана катушка.
Катушка индуктивности в цепи переменного тока
Для того, чтобы узнать, как ведет себя катушка индуктивности в цепи переменного тока, нам понадобится осциллограф, генератор частоты, собственно сама катушка индуктивности и резистор на 100 Ом. Чем больше сопротивление, тем меньше будет проседать напряжение с моего генератора частоты, поэтому я взял резистор на 100 Ом.Он у меня будет в качестве шунта. Падение напряжения на этом резисторе будет зависеть от тока, протекающего через него
Собираем все это дело по такой схеме:
Сразу договоримся, что у нас первый канал будет красным цветом, а второй канал — желтым. Следовательно, красная синусоида — это частота, которую нам выдает генератор частоты, а желтая синусоида — это сигнал, который снимается с резистора.
Мы с вами узнали, что при нулевой частоте (постоянный ток), катушка почти беспрепятственно пропускает через себя электрический ток. В нашем опыте мы будем подавать с генератора частоты синусоидальный сигнал с разной частотой и смотреть, меняется ли напряжение на резисторе.
Опыт N1
Для начала подаем сигнал с частотой в 1 Килогерц.
.jpg)
Давайте разберемся, что есть что. В зеленой рамочке я вывел автоматические замеры, которые делает осциллограф

Красный кружок с цифрой «1» — это замеры «красного»канала. Как мы видим, F (частота) =1 Килогерц, а Ма (амплитуда) = 1,96 Вольт. Ну грубо скажем 2 Вольта. Смотрим на кружочек с цифрой «2». F=1 Килогерц, а Ма=1,96 Вольт. То есть можно сказать, что сигнал на выходе точно такой же, как и на входе.
Увеличиваем частоту до 10 Килогерц
.jpg)
Амплитуда не уменьшилась. Сигнал какой есть, такой и остался.
Увеличиваем до 100 Килогерц
.jpg)
Заметили разницу? Амплитуда желтого сигнала стала меньше, да еще и график желтого сигнала сдвигается вправо, то есть запаздывает, или научным языком, появляется сдвиг фаз. Красный сигнал никуда не сдвигается, запаздывает именно желтый. Это имейте ввиду.
Сдвиг фаз — это разность между начальными фазами двух измеряемых величин. В данном случае напряжения. Для того, чтобы произвести замер сдвига фаз, должно быть условие, что у этих сигналов одна и та же частота. Амплитуда может быть любой. Ниже на рисунке приведен этот самый сдвиг фаз или, как еще его называют, разность фаз:

Увеличиваем частоту до 200 Килогерц
.jpg)
На частоте 200 Килогерц амплитуда упала вдвое, да и разность фаз стала больше.
Увеличиваем частоту до 300 Килогерц.
.jpg)
Амплитуда желтого сигнала упала уже до 720 милливольт. Разность фаз стала еще больше.
Увеличиваем частоту до 500 Килогерц
.jpg)
Амплитуда уменьшилась до 480 милливольт.
Добавляем еще частоту до 1 Мегагерц
.jpg)
Амплитуда желтого канала стала 280 милливольт.
Ну и добавляем частоту до предела, который позволяет выдать генератор частоты: 2 Мегагерца
.jpg)
Амплитуда «желтого» сигнала стала настолько маленькой, что мне пришлось ее даже увеличить в 5 раз.
И можно сказать, что сдвиг фаз стал почти 90 градусов или π/2.
Но станет ли сдвиг фаз больше, чем 90 градусов, если подать очень-очень большую частоту? Эксперименты говорят, что нет. Если сказать просто, то при бесконечной частоте сдвиг фаз будет равняться 90 градусов. Если совместить наши графики на бесконечной частоте, то можно увидеть примерно вот такой рисунок:

Так какой вывод можно сделать?
С увеличением частоты сопротивление катушки растет, а также увеличивается сдвиг фаз. И чем больше частота, тем больше будет сдвиг фазы, но не более, чем 90 градусов.
Опыт N2
Давайте же уменьшим индуктивность катушки. Прогоним еще раз по тем же самым частотам. Я убрал половину витков и сделал витки на край феррита, тем самым уменьшил индуктивность до 33 микрогенри.
Итак, прогоняем все по тем же значениям частоты
.jpg)
При частоте в 1 Килогерц у нас значение почти не изменилось.
.jpg)
Здесь тоже ничего не изменилось.
.jpg)
Тоже почти ничего не изменилось, кроме того, что желтый сигнал стал тихонько сдвигаться.
.jpg)
Здесь уже видим, что амплитуда на желтом сигнале начинает проседать и сдвиг фаз наращивает обороты.
.jpg)
Сдвиг фаз стал больше и амплитуда просела еще больше
.jpg)
Сдвиг стал еще больше и амплитуда желтого сигнала тоже просела.
.jpg)
Амплитуда желтого сигнала падает, сдвиг фаз прибавляется. 😉
2 Мегагерца, предел моего генератор частоты
.jpg)
Сдвиг фаз стал почти равен 90 градусов, а амплитуда стала даже меньше, чем пол Вольта.
Обратите внимание на амплитуду в Вольтах на тех же самых частотах. В первом случае у нас индуктивность была больше, чем во втором случае, но амплитуда желтого сигнала во втором случае больше, чем в первом.
Отсюда вывод напрашивается сам собой:
При уменьшении индуктивности, сопротивление катушки индуктивности также уменьшается.
Реактивное сопротивление катушки индуктивности
С помощью нехитрых умозаключений, физиками была выведена формула:

П — постоянная и равна приблизительно 3,14
В данном опыте мы с вами получили фильтр низких частот (ФНЧ). Как вы видели сами, на низких частотах катушка индуктивности почти не оказывает сопротивление напряжению, следовательно амплитуда и мощность на выходе такого фильтра будет почти такой же, как и на входе. Но с увеличением частоты у нас амплитуда гасится. Применив такой фильтр на динамик, можно с уверенностью сказать, что будет усиливаться только бас, то есть низкая частота звука.
Видео про катушку индуктивности:
Заключение
Постоянный ток протекает через катушку индуктивности без каких-либо проблем. Сопротивлением обладает только сам провод, из которого намотана катушка.
Сопротивление катушки зависит от частоты протекающего через нее тока и выражается формулой:
Источник
Токи в ветвях после разветвления:
![]() А,
А,
![]() А.
А.
Если разветвленный участок имеет только
две ветви, включенные параллельно, то
токи в ветвях после разветвления можно
определять без расчета U
ab,используя формулу
разброса. Эта формула использовалась
в примере 1.1 длярасчёта цепи
постоянного тока. В соответствии с этой
формулой
![]()
![]()
Модули показательной формы выражений
для токов есть действующие значения
реальных токов ветвей, которые фиксируют
приборами электромагнитной
системы. Следовательно, амперметр в
первой ветви покажет 8,3 А,
а во второй ветви – 5,86 А.
Вольтметр, включенный параллельно
катушке, покажет падение напряжения
на ней. Так как падение напряжения на
участке есть произведение тока участка
на значение его сопротивления, то
получаем:
![]() ,
,
где zV– полное сопротивление участка, на
котором определяется падение напряжения.
Так как в примере находится падение
напряжения на катушке индуктивности
с сопротивлением xL1,
то на основании выражения (2.25) полное
сопротивление участка
![]() Ом.
Ом.
Падение напряжения на катушке
![]() В.
В.
Показание вольтметра есть модуль
выражения UV,
т. е.UV= 83 В.
Ваттметр, включенный на входе цепи,
показывает активную мощность, потребляемую
всей схемой. Эта мощность будет
действительной частью выражения
комплекса полной мощности Sна входе, которое имеет вид
![]()
Активная мощность Р = 551 Вт , реактивная
мощностьQ = 620
вар.
Для проверки результатов расчета
необходимо составить баланс активных
и реактивных мощностей. Эти балансы
показывают, что активные и реактивные
мощности на входе должны быть равны
сумме соответственно активных и
реактивных мощностей всех потребителей.
Активная мощность на входе определена,
а активные мощности отдельных потребителей
рассчитывают как произведение активного
сопротивления участка на квадрат
действующего значения тока этого
участка. В рассматриваемой схеме только
два активных потребителя r1иr2.
Суммарная мощность этих потребителей
![]() Вт.
Вт.
Разница в мощностях получилась в 1 Вт,
что составляет несколько десятых долей
процента. Ошибка менее одного процента
допускается. Она возникает из-за
округления числовых данных при расчете.
Реактивную мощность потребителей
определяют как произведение квадрата
тока реактивного элемента на его
сопротивление. Причем мощность катушки
индуктивности положительна, а конденсатора
отрицательна.
Суммарная реактивная мощность всех потребителей
![]() .
.
Разница в реактивных мощностях также
составляет одну единицу, ошибка меньше
одного процента. Таким образом, баланс
активных и реактивных мощностей
соблюдается. Токи определены правильно.
Для возникновения в цепи резонанса
напряжений необходимо, чтобы полное
сопротивление всей цепи было активным.
Полное сопротивление
z = z1
+z23
= 3 +j4 + 5 +j5
= 8 +j9 Ом.
Из выражения для полного сопротивления
видно, что эквивалентное реактивное
сопротивление исходной цепи равно +9
Ом. Знак плюс указывает на индуктивный
характер эквивалентной реактивности.
Устранить эту реактивность можно
включением в первую ветвь конденсатора
с емкостным сопротивлением – 9
Ом (минус подчёркивает емкостный
характер реактивности). После такого
включения реактивные сопротивления
взаимно компенсируются, а полное
сопротивление становится активным и
равно 8 Ом. В цепи наступает резонанс
напряжений.
Н а
а
рисунке 2.5 приведена векторная диаграмма,
на которой относительно осей координат
комплексной плоскости +j
и +1 в масштабе построены векторы
напряжений и токов. Вектор строится
под углом к вещественной оси комплексной
плоскости +1. Значение этого угла равно
аргументу показательной формы
комплексного выражения. При положительном
значении аргумента угол откладывается
от вещественной оси против часовой
стрелки, а при отрицательном – по
часовой.
|
Рисунок 2.5 –
разветвлённой |
Длина вектора должна в масштабе
соответствовать модулю показательной
формы комплексного выражения. Например,
вектор входного напряжения (![]() )
)
должен иметь длину в десять масштабных
отрезков (U =
100 В, в масштабном отрезке – 10 В). Угол
между этим вектором и вещественной
осью равен 30 градусам и откладывается
против часовой стрелки. Аналогично
строятся и другие векторы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В этой статье объясняется, что такое падение напряжения и как рассчитать падение напряжения в последовательной цепи. Когда напряжение встречается с резистивным элементом в цепи, значение уменьшается или «падает».
В последовательной цепи имеется несколько сопротивлений или импедансов. Каждый раз, когда через них проходит ток, напряжение падает. Итак, нам нужно знать значение конкретного сопротивления и ток, проходящий через него, чтобы вычислить падение напряжения на нем. Падение напряжения – это ток, умноженный на сопротивление.
Что такое падение напряжения?
Допустим, мы соединяем батарею с резистором через провод. Электроны имеют тенденцию течь от отрицательной стороны батареи к положительной. Это похоже на электрический заряд, идущий от положительной клеммы к отрицательной.
Когда одна единица заряда встречает резистор, она на время останавливается. Когда он проходит мимо резистора, появляется другая единица заряда и останавливается. В любой момент количество заряда на конце резистора меньше заряда в начале резистора. Это явление создает «падение потенциала или напряжения».
Подробнее… ..Постоянно ли напряжение в серии: полная информация и ответы на часто задаваемые вопросы
Как рассчитать полное падение напряжения в последовательной цепи?
Общее падение напряжения в последовательной цепи – это сложение всех отдельных падений напряжения, вызванных параметрами импеданса. Кроме того, сумма равна общему напряжению, подаваемому в цепь, или напряжению до любого «падения».
Разберем явления с помощью схемы. В схеме ниже два резистора R1 100 Ом и R2 200 Ом, подключенный к источнику питания V 30 вольт. Ток i = В/(R1 + R2) = 30/(100+200) = 0.1 А. Следовательно, падение напряжения на резисторе R1 = икс р1 = 0.1 x 100 = 10 В и через R2 = икс р2 = 0.1 х 200 = 20 В.
Как рассчитать падение напряжения в последовательной цепи переменного тока?
переменного тока или переменный ток цепи – это электрические цепи с переменным напряжением питания. AC последовательная схема состоит из любой комбинации резистора, катушки индуктивности и конденсатора, соединенных последовательно.
Как и в случае с постоянным током, мы можем вычислить чистый импеданс последовательной цепи переменного тока, сложив их. Аналогичным образом можно найти и падения напряжения. Падение напряжения на любом элементе в последовательной цепи переменного тока равно V = iZ, где Z – полное сопротивление цепи, а i – полный ток, протекающий через нее.
Подробнее… ..Как рассчитать напряжение в последовательной цепи: подробные факты
Падение напряжения в последовательной цепи RLC:
Цепь RLC является частным случаем цепей переменного тока. Цепь RLC состоит из резисторов, конденсаторов и катушек индуктивности, соединенных последовательно. Давайте поймем падение напряжения в последовательной цепи RLC на примере.
Схема состоит из трех компонентов, показанных ниже: резистора R Ом, индуктивности L Генри и конденсатора C Фарад. Ранее мы знали, что падение напряжения на любом из них = импеданс × ток. Так,
Падение напряжения на резисторе = iR, катушка индуктивности = iXL и конденсатор = iXC, где XL = 2πfL и XC = 1/2πfC
Как рассчитать падение напряжения в последовательной цепи – численные примеры
Q1. Три резистора подключены последовательно со значениями R1= 4 Ом, R2= 5 Ом, а R3 = 6 Ом. Схема подключена к источнику питания 15 В. Узнайте падение напряжения на резисторах.
Для расчета капель потенциала на R1, R2и R3, нам сначала нужно получить ток в цепи. Мы знаем, ток = чистое напряжение/эквивалентное сопротивление
Эквивалентное сопротивление Req = R1 + R2 + R3 = 4 + 5 + 6 = 15 Ом
Следовательно, общий ток = 15 В / 15 Ом = 1 А.
Теперь мы можем использовать закон Ома (V = IR) для каждого резистора и найти падение напряжения на них.
Итак, V1 = я х р1 = 1 х 4 = 4 В
V2 = я х р2 = 1 х 5 = 5 В
V3 = я х р3 = 1 х 6 = 6 В
Q2. Для приведенной ниже схемы падение напряжения на резисторе 6 Ом составляет 12 В. Определите другие падения напряжения и вычислите общее падение напряжения или напряжение питания.
Мы знаем, что падение напряжения на любом резисторе в последовательная цепь = сопротивление × общий ток
Если в цепи протекает ток i, падение напряжения на резисторе 6 Ом составляет 6i.
6i = 12 или i = 2 ампер
Следовательно, падение напряжения на резисторе 2 Ом = 2 x 2 = 4 В.
Падение напряжения на резисторе 4 Ом = 2 x 4 = 8 В
Итак, сеть падение напряжения или напряжение питания = (12 + 4 + 8) = 24 В
Q3. На изображении ниже изображена последовательная цепь RLC со следующими компонентами: Источник переменного тока 120 В, 50 Гц, Резистор на 100 Ом, Конденсатор 20 мкФ, Индуктор 420 мГн. Рассчитайте падение напряжения на всех трех импедансах.
Раньше мы умели рассчитать падение напряжения для последовательной цепи RLC. Ток, умноженный на импеданс ( R или XL или XC) дает нам падение напряжения. Давайте узнаем XL и ХC первый.
XL= 2πfL (f – частота сети переменного тока)
Итак, ХL = 2 x π x 50 x 420 x 10^{-3} = 131.95 Ом
XC = 1/2 x π x 50 x 20 x 10^{-6} }= 159.15 Ом
Следовательно, полное сопротивление,

Теперь для цепей переменного тока существует объект, называемый фазовым углом. Он дает меру угла, на который ток отстает или опережает напряжение. Фазовый угол φ = arctan (XC – ИКСL/Р)
φ = арктангенс (27.2/100) = 15.22°
Итак, текущий

Следовательно,

Здесь ток опережает напряжение как XC > XL.


Подробнее….Что такое напряжение в последовательной цепи: подробные факты
ТОЭ › Расчет цепей синусоидального тока

Реальная катушка в отличии от идеальной имеет не только индуктивность, но и активное сопротивление, поэтому при протекании переменного тока в ней сопровождается не только изменением энергии в магнитном поле, но и преобразованием электрической энергии в другой вид. В частности, в проводе катушки электрическая энергия преобразуется в тепло в соответствии с законом Ленца — Джоуля.
Ранее было выяснено, что в цепи переменного тока процесс преобразования электрической энергии в другой вид характеризуется активной мощностью цепи Р, а изменение энергии в магнитном поле — реактивной мощностью Q.
В реальной катушке имеют место оба процесса, т. е. ее активная и реактивная мощности отличны от нуля. Поэтому одна реальная катушка в схеме замещения должна быть представлена активным и реактивным элементами.
Схема замещения катушки с последовательным соединением элементов
В схеме с последовательным соединением элементов реальная катушка характеризуется активным сопротивлением R и индуктивностью L.
Активное сопротивление определяется величиной мощности потерь
R = P/I2

а индуктивность — конструкцией катушки. Предположим, что ток в катушке (рис. 13.9, а) выражается уравнением i = Imsinωt. Требуется определить напряжение в цепи и мощность. При переменном токе в катушке возникает э. д. с. самоиндукции eL поэтому ток зависит от действия приложенного напряжения и эдс eL. Уравнение электрического равновесия цепи, составленное по второму закону Кирхгофа, имеет вид:
Приложенное к катушке напряжение состоит из двух слагаемых,одно из которых uR равно падению напряжения в активном сопротивлении, а другое uL уравновешивает эдс самоиндукции.
В соответствии с этим катушку в схеме замещения можно представить активным и индуктивным сопротивлениями, соединенными последовательно (рис. 13.9, б). Дополнительно заметим, что оба слагаемых в правой части равенства (13.12) являются синусоидальными функциями времени. Согласно выводам полученных в этих предыдущих двух (первая, вторая) статьях получим — uR совпадает по фазе с током, UL опережает ток на 90°.
Поэтому:
u = R*Imsinωt + ωLImsin(ωt+π/2).
Влияние числа витков и способа намотки
Катушка индуктивности – это спираль, созданная из проводящего материала. Рабочие параметры изделий будут зависеть от особенностей конструкции. Индуктивность увеличивают:
- большим количеством витков на единицу длины;
- укрупнением поперечного сечения;
- установкой в центральной части сердечника с ферромагнитными характеристиками.

Индуктивность одновиткового контура и индуктивность катушки
Для расчета элементарной конструкции подойдет преобразованная первая формула:
Ф = L * I.
Если рассматривается катушка, это выражение трансформируют в суммарное выражение магнитных потоков (Ψ), образованных отдельными витками:
Ψ = n * Ф.
Аналогичным образом:
Советуем изучить Векторная диаграмма токов и напряжений
Ln = L1 * n.
В действительности для точных расчетов учитывают различия силовых линий в центральной части и на краях конструкции. Для коррекции применяют более сложные выражения.
Индуктивность соленоида
Достаточно длинная электрическая катушка формирует внутри параллельные силовые линии. Для создания равномерного распределения энергии необходимо применять проводник с толщиной намного меньше, по сравнению с диаметром поперечного сечения. Разумеется, необходимо установить одинаковое расстояние между отдельными витками.
Такую конструкцию называют соленоидом. Плотность магнитного потока (B) в центральной рабочей части будет зависеть прямо пропорционально от длины (l) и следующих параметров:
- количества витков (N);
- тока (i);
- плотности намотки (n – число контуров на единицу длины);
- площади поперечного сечения (S);
- объема (V = S * l).
Ниже приведены основные формулы для вычислений при отсутствии сердечника с учетом магнитной постоянной (m ≈ 1,257 *10-6 Гн/ м):
- В = m0 * N * (i/l) = m0 * n * I;
- Ψ = m0 * N2 * (I * S/l) = m0 * n2 * i *V;
- L = m0 * N2 * (S/l) = m0 * n2 * V.
Индуктивность тороидальной катушки (катушки с кольцевым сердечником)
Для вычисления индукции катушки с сердечником в представленные выше формулы добавляют корректирующий множитель «m». С учетом особой формы изделия необходимо сделать следующие изменения:
L = N2 * ((m0 * m * S)/2π * rL), либо L = N2 * ((m0 * m * h)/2π) * ln(R/r),
где:
- 2π * rL – длина рабочего элемента со средним радиусом rL;
- R (r) и h – наружный (внутренний) радиус и высота тора, соответственно.
Коэффициентом «m» учитывают относительный показатель магнитной проницаемости определенного материала к значению для нейтральной среды (вакуума). Если m намного больше единицы, допускается не учитывать искажения поля, которые создает толстый проводник.
Векторная диаграмма реальной катушки и полное её сопротивление
Несовпадение по фазе слагаемых в выражении (13.12) затрудняет определение амплитуды и действующей величины приложенного к цепи напряжения U. Поэтому воспользуемся векторным способом сложения синусоидальных величин. Амплитуды составляющих общего напряжения
UmR = RIm; UmL = ωLIm ,
а действующие величины
UR = RI; UL = XLI .
Вектор общего напряжения
U = UR + UL
Для того чтобы найти величину вектора U, построим векторную диаграмму (рис. 13.10, а), предварительно выбрав масштабы тока Mi и напряжения Мu.
За исходный вектор диаграммы принимаем вектор тока I. Направление этого вектора совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза заданного тока Ψi =0). Как и ранее, эту ось удобно (но не обязательно) направить по горизонтали.
Вектор UR по направлению совпадает с вектором тока I, а вектор UL направлен перпендикулярно вектору I с положительным углом.
Из диаграммы видно, что вектор тока I общего напряжения U отражает вектор тока I на угол φ>0, но φ<90°, а по величине равен гипотенузе прямоугольного треугольника, катетами которого являются векторы падений напряжения в активном и индуктивном сопротивлениях UR и UL :
UR = Ucosφ

Проекция вектора напряжения U на направление вектора тока называется активной составляющей вектора напряжения и обозначается Ua. Для катушки по схеме рис. 13.9 при Ua = UR
U = Usinφ (13.14)
Проекция вектора напряжения U на направление, перпендикулярное вектору тока, называется реактивной составляющей вектора напряжения и обозначается Up. Для катушки Up = UL
При токе i = Imsinωtуравнение напряжения можно записать на основании векторной диаграммы в виде
U = Umsin(ωt+φ)
Стороны треугольника напряжений, выраженные в единицах напряжения, разделим на ток I. Получим подобный треугольник сопротивлений (рис. 13.10, б), катетами которого являются активное R = UR/I и индуктивное XL = UL/I, сопротивления, а гипотенузой величина Z = U/I.
Отношение действующего напряжения к действующему току данной цепи называется полным сопротивлением цепи. Стороны треугольника сопротивлений нельзя считать векторами, так как сопротивления не являются функциями времени. Из треугольника сопротивлений следует
Понятие о полном сопротивлении цепи Z позволяет выразить связь между действующими величинами напряжения и тока формулой, подобной формуле Ома:
Из треугольников сопротивления и напряжения определяются
cosφ = UR/U = R/Z; sinφ = UL/U = XL/Z; tgφ = UL/UR = XL/R. (13.18)
Мощность реальной катушки
Мгновенная мощность катушки
p = ui = Umsin(ωt+φ) * Imsinωt
Из графика мгновенной мощности (рис. 13.11) видно, что в течение периода мощность четыре раза меняет знак; следовательно, направление потока энергии и в данном случае в течение периода меняется. Относительно некоторой оси t’, сдвинутой параллельно оси t на величину Р, график мгновенно мощности является синусоидальной функцией двойной частоты. При положительном значении мощности энергия переходит от источника в приемник, а при отрицательном — наоборот. Нетрудно заметить, что количество энергии, поступившей в приемник (положительная площадь), больше возвращенной обратно (отрицательная площадь).
Следовательно, в цепи с активным сопротивлением и индуктивностью часть энергии, поступающей от генератора, необратимо превращается в другой вид энергии, но некоторая часть возвращается обратно. Этот процесс повторяется в каждый период тока, поэтому в цепи наряду с непрерывным превращением электрической энергии в другой вид энергии (активная энергия) часть ее совершает колебания между источником и приемником (реактивная энергия).
Скорость необратимого процесса преобразования энергии оценивается средней мощностью за период, или активной мощностью Р, скорость обменного процесса характеризуется реактивной мощностью Q.
Согласно выводам полученных в этих предыдущих (первая, вторая) статьях — в активном сопротивлении P = URI Q = 0; а в индуктивном Р = 0; Q = ULI.
Активная мощность всей цепи равна активной мощности в сопротивлении R, а реактивная — реактивной мощности в индуктивном сопротивлении XL. Подставляя значения UR = Ucosφ и UL = Usinφ, определяемые из треугольника напряжений по формулам (13.18), получим:
P = UIcosφ (13.19)
Q = UIsinφ (13.20)
Кроме активной и реактивной мощностей пользуются понятием полной мощности S, которая определяется произведением действующих величин напряжения и тока цепи;
S = UI = I2Z (13.21)
Величину полной мощности можно получить из выражения (13.22), которое легко доказать на основании формул (13.19) и (13.20):
(13.22)
Мощности S, Р, Q графически можно выразить сторонами прямоугольного треугольника (см. рис. 13.10, в). Треугольник мощностей получается из треугольника напряжений, если стороны последнего, выраженные в единицах напряжения, умножить на ток. Из треугольника мощностей можно определить
cosφ = P/S; sinφ = Q/S; tgφ = Q/P. (13.23)
Полная мощность имеет ту же размерность, что Р и Q, но для различия единицу полной мощности называют вольт-ампер (В · А).
Активная мощность Р меньше или равна полной мощности цепи. Отношение активной мощности цепи к ее полной мощности P/S = = cosφ называют коэффициентом мощности.
Назначение приемников электрической энергии — преобразование ее в другие виды энергии. Поэтому колебания энергии в цепи не только бесполезны, но и вредны, так как при этом в приемнике не совершается полного преобразования электрической энергии в работу или тепло, а в соединительных проводах она теряется.
Что такое индуктивность
Что такое индуктивность — это физическая величина, которая рассказывает нам о магнитных свойствах электрической цепи. Индуктивность измеряют в Гн (Генри).
Если вы вообще не понимаете о чём речь, то советую ознакомиться сначала с вот с этой статьей.
В электрических схемах например, нам встречаются какие-то непонятные катушки, дроссели и многие даже не знают их функциональную роль. В этой статье я постараюсь доступным языком рассказать, что такое индуктивность и как это явление применить на своей любимой работе.
Давайте посмотрим на рисунок

Давайте начнём движение проводника в магнитном поле таким образом, чтобы он пересек силовые линии постоянного магнита. Если это условие выполняется, то тогда в нашем проводнике появляется электродвижущая сила (ЭДС). Или наоборот проводник остаётся на месте, а магнит передвигают таким образом, чтобы силовые линии магнита пересекали проводник. Сейчас был пример электромагнитной индукции. Значение индуцированной электродвижущей силы в проводнике прямо пропорциональна магнитной индукции поля, скорости перемещения и длине проводника
Направление возникшей электродвижущей силы в проводнике определяют через правило правой руки.
Советуем изучить Варианты подсветки потолка в помещениях

Правая рука находится в таком положении чтобы силовые линии магнита заходили в ладонь. Следовательно, большой палец показывает нам направление перемещения проводника, а остальные пальцы покажут нам направление возникшей электродвижущей силы.
Для усиления электродвижущей силы индукции применяют электрические катушки
А если подать напряжение на катушку, то по её виткам потечёт ток, который создаёт своё магнитное поле.
