И снова приветствую всех тех, кто серьёзно готовится к профильному ЕГЭ и всерьёз претендует на решение самых сложных задач 19 (они же С6)! Как и обещал, продолжаем разбирать самые разнообразные и необычные задачи на теорию чисел и способы успешно расправляться с такими монстрами. Хотя для подготовленного ученика в задачах 19 страшного особо ничего и нету.)
Использование признаков делимости и перебора на ограниченном множестве. Задача про числа-палиндромы.
В данном материале я хотел бы разобрать очередную необычную и не самую сложную задачку про так называемые числа-палиндромы. Для начала, что это вообще за зверь такой (для тех, кто не в курсе)?
Палиндром — это слово, число или даже целый текст, одинаково читающееся в обоих направлениях. Как слева направо, так и справа налево.
Примеры:
Число 12321, слово «ротор», красивое женское имя Анна, словосочетание «искать такси», а также всем известная бородатая фраза «А роза упала на лапу Азора». В общем, идея понятна, я думаю. 🙂
В нашей задаче, разумеется, речь пойдёт о числах. Что ж, давайте теперь посмотрим на саму задачу.
Вот такая вот задачка. Как к ней подступиться? Ну, во-первых, в каждом из пунктов речь идёт о делимости на 15. Стало быть, нашей отправной точкой будут признаки делимости чисел нацело. Это тема 6-го класса средней школы. Других вариантов просто нет. И какие же это признаки, спросите вы?
Вспоминаем 6-й класс, ищем там признак делимости на 15 и… вы правы! Такого признака нету. Но! Зато есть признаки делимости чисел на 3 и на 5. А что такое 15? Это не что иное, как 3·5! Элементарно, Ватсон! 🙂 Стало быть, если какое-либо натуральное число одновременно делится нацело на тройку и пятёрку, то автоматически оно будет делиться и на пятнадцать. Поэтому давайте-ка быстренько освежим в памяти признаки делимости чисел на 3 и на 5. Вот они:
Признак делимости на 3
Натуральное число делится нацело на 3, если сумма его цифр делится на 3.
Скажем, число 12384 точно поделится на 3, так как сумма его цифр 1+2+3+8+4 = 18 делится на 3. А вот 23576 даже и пытаться не стоит, так как его сумма цифр 2+3+5+7+6 = 23 не делится на 3.
Признак делимости на 5
Натуральное число делится нацело на 5, если оно заканчивается цифрой 0 или 5.
Например, на 5 делится число 12345, так как оно заканчивается на пятёрку. Или 1234567890, так как оно заканчивается нулём. Ну, в общем, вы поняли. Признак очень простой.
Значит, натуральное число делится на 15 тогда и только тогда, когда оно одновременно делится на 3 (по сумме цифр) и на 5 (по последней цифре). Что ж, теоретическая база подготовлена, пора приступать к разбору нашей задачи. Итак,
а) Приведите пример числа-палиндрома, который делится на 15.
Прежде чем что-то решать, давайте посмотрим, как вообще устроены числа-палиндромы:
И так далее…
Здесь a, b, c и так далее — цифры натурального числа. В общем случае — различные. Черта сверху ставится для того, чтобы обозначить тот факт, что перед нами именно цифры, а не произведение типа a·b·c.
Скажем, запись
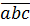
означает трёхзначное натуральное число, которое в десятичной форме запишется так:
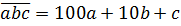
Что ж, давайте теперь искать числа-палиндромы, делящиеся на 15. Для начала поищем их среди двузначных чисел. Это числа 11, 22, 33, 44 и так далее до 99. Можно заметить, что все они делятся на простое число 11:
11=11·1
22=11·2
33=11·3
И так далее. Наименьшее число, которое делится как на 11, так и на 15 — это 11·3·5 = 165 – уже трёхзначное. Облом. Значит, среди двузначных чисел таковых нету.
Что ж, поехали шерстить трёхзначные числа. 🙂 Трёхзначное число-палиндром имеет вид
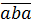
Раз оно делится на 15, то должно делиться как на 5 (по последней цифре), так и на 3 (по сумме цифр).
Значит, согласно признаку делимости на 5, последняя цифра (a) может быть только 0 или 5. Третьего не дано. 🙂
А теперь прикинем. Если a = 0, то наше число имеет вид
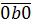
и никак не является трёхзначным. Значит, единственный устраивающий нас вариант – это
а = 5.
Поэтому трёхзначные числа-палиндромы, делящиеся на 5, имеют вид:
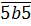
Что ж, кое-чего уже проясняется. 🙂
А теперь в игру дополнительно вступает признак делимости на 3. Составляем сумму цифр:
5 + b + 5 = 10 + b,
где b, будучи цифрой числа, принимает значения 0, 1, 2, 3, …, 9.
Теперь понятно, как расправиться с пунктом а). Подберём число b так, чтобы выражение для суммы цифр 10 + b делилось бы на 3. Например, при b = 2 получим:
10+b = 10+2 = 12 — делится на 3.
Следовательно, самое первое по счёту трёхзначное (и вообще глобально) число-палиндром, делящееся на 15, – это число 525.
Всё, этого вполне достаточно для ответа на вопрос пункта а).
Ответ: Например, 525.
Переходим к пункту б).
б) Сколько существует пятизначных чисел-палиндромов, делящихся на 15?
Все пятизначные числа-палиндромы имеют вид:
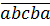
Здесь снова рулят признаки делимости чисел на пятёрку и на тройку. Как и в предыдущем пункте, начнём с признака делимости на 5. Это означает, что последняя цифра в нашем числе (т.е. а) может быть равна либо нулю, либо пятёрке.
Нулём цифра а быть никак не может, поскольку в таком случае наше число примет вид
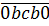
и попросту не будет пятизначным. Значит, а = 5 (и только 5).
Итак, наши пятизначные кандидаты предварительно обретают вот такой вид:
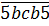
Теперь снова подключаем признак делимости чисел на 3 по сумме цифр. В нашем случае:
5 + b + c + b + 5 = 10 + 2b + c — должно делиться на 3.
В предыдущем пункте мы варьировали только одну единственную цифру b, добиваясь делимости на 3 суммы цифр (напомню, это было выражение 10+b). Здесь же нам надо варьировать уже две цифры — b и c. И как нам теперь быть? Ведь число всевозможных вариантов стало гораздо больше! Да, не спорю, больше. На первый взгляд может показаться, что вариантов и вправду довольно много и перебирать их все очень долго и муторно. Но давайте подумаем: ведь b и с — не просто числа, а цифры натурального числа. Которые могут принимать очень ограниченные значения — 0, 1, 2, 3, …, 9. Поэтому, если мы как-то зафиксируем b, последовательно придавая ему значения от 0 до 9, то в каждом из случаев варьировать уже придётся только одну цифру c. Давайте посмотрим, как это делается. Первый случай я разберу подробно, а остальные — кратко.
Итак, первый вариант b = 0. Тогда сумма цифр 10 + 2b + c нашего числа будет равна:
10+2·0+c = 10+c.
Когда выражение 10+c делится на 3? Очевидно, в трёх ситуациях:
10+c = 12 (тогда c = 2),
10+c = 15 (тогда c = 5),
10+c = 18 (тогда c = 2).
Всё. Больше, чем 8 (например, 11) число с быть уже никак не может. Ещё раз напоминаю, что наши буковки — это на самом деле циферки. 🙂 То есть, 0, 1, 2, …, 9. Этот случай дал нам три пятизначных числа-палиндрома делящихся на 15. Какие же это числа? Пожалуйста, вот они:
50205, 50505 и 50805 (3 числа).
Пусть теперь b = 1. В этом случае сумма цифр нашего числа будет такая:
10+2·1+c = 12+c
Добиваясь теперь, чтобы выражение 12+c делилось на 3, получим с = {0; 3; 6; 9}. Итого выплыли ещё 4 числа-палиндрома (51015, 51315, 51615, 51915).
Уловили закономерность? 🙂 Да! Надо разобрать оставшиеся 8 случаев. Не так уж и много, по большому счёту. Добрый вечер! Буду краток. 🙂
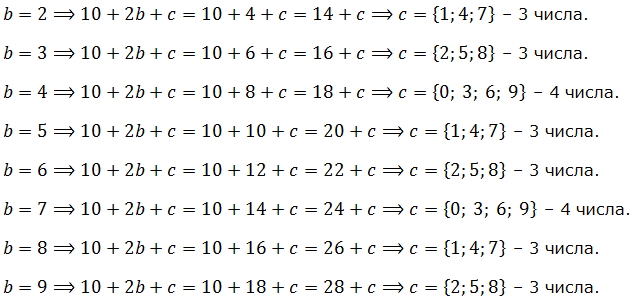
Подобная процедура в целочисленных задачах называется перебор на ограниченном множестве. Суть метода заключается в том, что, если число всевозможных вариантов не очень большое (в нашем случае — всего 10), то мы просто перебираем все-все возможные случаи и отбираем всё то, что нас устраивает. 🙂
А теперь подсчитываем наших цыплят палиндромов:
3 + 4 + 3 + 3 + 4 + 3 + 3 + 4 + 3 + 3 = 33
Итого тридцать три коровы пятизначных числа-палиндрома, делящихся на 15! 🙂
Ответ: 33.
Теперь, когда проведено столь масштабное исследование, самый сложный пункт в) многим ученикам может показаться совсем пустяковым. 🙂 Сейчас всё увидите!
в) Найдите 37-е по величине число-палиндром, которое делится на 15.
Для ответа на вопрос сначала подсчитаем все трёхзначные и четырёхзначные числа-палиндромы.
Одно из трёхзначных (самое первое вообще среди таких чисел) мы уже нашли — это 525. Давайте найдём все остальные. Для этого снова обратимся к нашей сумме цифр (см. пункт а)):
10 + b – делится на 3.
Тогда b = {2; 5; 8} — три трёхзначных числа-палиндрома (т.е. 525, 555 и 585).
Разбираемся теперь с четырёхзначными числами-палиндромами. Здесь всё аналогично. Они имеют вот такую запись:
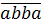
По признаку делимости на 5, последняя (и первая) цифры могут быть равны 0 или 5. Сразу, по понятным причинам, отметаем ноль и получаем:
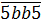
По признаку делимости на 3 составляем сумму цифр:
5 + b + b + 5 = 10 + 2b.
Чтобы эта штука делилась на 3, цифра b должна принимать лишь одно из трёх значений: b = {1; 4; 7}. Итого получаем три четырёхзначных числа-палиндрома (5115, 5445 и 5775).
Тогда получается, что всего трёх-, четырёх- и пятизначных чисел-палиндромов, делящихся на 15, будет:
3 (трёхзначные)+3 (четырёхзначные)+33 (пятизначные) = 39 чисел.
Тогда очевидно, что искомое 37-е число-палиндром — пятизначное. Гуд.) Идём дальше.
А теперь смотрим на результаты нашего исследования пятизначных чисел в пункте б). Я не стал для каждого случая выписывать их все, но зато можно заметить, что при росте b все наши получаемые числа располагаются в порядке возрастания. Это значит, что самое последнее, 39-е число будет соответствовать случаю b=9, c=8. Тогда искомое 37-е по величине число-палиндром, делящееся на 15, будет соответствовать случаю b=9, c=2, т.е. 59295.
Вот и всё! 🙂
Ответ: 59295.
Как видите, ничего сложного. Если знать пару признаков делимости и понимать суть задания (что такое число-палиндром и немного что такое десятичная запись числа). Да, в пункте б) надо разбирать 10 случаев, но все они совсем простые и решаются фактически в уме. Главное — не бояться!
Назовём натуральное число палиндромом
Задача. Назовём натуральное число палиндромом, если в его десятичной записи все цифры расположены симметрично (совпадают первая и последняя цифры, вторая и предпоследняя, и т.д.). Например, числа 121 и 953359 являются палиндромами, а числа 10 и 953359 не являются палиндромами.
а) Приведите пример числа-палиндрома, который делится на 15.
б) Сколько существует пятизначных чисел-палиндромов, делящихся на 15?
в) Найдите 37-е по величине число-палиндром, которое делится на 15.
Решение.
Так как наше число-палиндром должно делиться на 15, то оно должно делиться и на 5 и на 3. На 5 делятся числа, оканчивающиеся на 0 и на 5. Однако, число не может начинаться с нуля, а, значит, и не может оканчиваться нулём, поэтому искомые числа будут оканчиваться на 5 и начинаться тоже с цифры 5. Имеем в виду, что на 3 делится число, сумма цифр которого делится на 3.
а) Так как 55 не делится на 3, то среди двузначных чисел нет чисел-палиндромов, делящихся на 15. Из трёхзначных чисел наименьшим числом-палиндромом, делящимся на 15, будет число 525. Оно оканчивается на «5», поэтому делится на 5, а также число 525 делится на 3, так как сумма цифр этого числа 5+2+5=12 делится на 3.
Так как в пункте в) нам нужно будет указать 37-е по величине число-палиндром, которое делится на 15, то найдём все трёхзначные и четырёхзначные числа-палиндромы, которые делится на 15. Все наши числа начинаются и оканчиваются на «5», поэтому нам остаётся только позаботиться о том, чтобы сумма цифр каждого из чисел делилась на 3. Так как в любом искомом числе-палиндроме уже есть две пятерки (5+5=10), то общая сумма цифр трёхзначного числа-палиндрома может быть равна 12 или 15 или 18, т.е. в серединке между двумя «пятёрками» может стоять цифра 2 (число 525) или 5 (число 555) или 8 (число 585). Таким образом, среди трёхзначных чисел всего три числа-палиндрома, которые делятся на 15.
Переходим к четырёхзначным числам. Первая и последняя цифры – пятёрки, а сумма двух (одинаковых) цифр, стоящих в середине может быть равна 2 (число 5115) или 8 (число 5445) или 14 (число 5775). Других вариантов нет. Таким образом, среди четырёхзначных чисел тоже нашлись всего три числа-палиндрома, которые делятся на 15.
б) Приступаем к нахождению пятизначных чисел-палиндромов, делящихся на 15. Нас будет интересовать сумма трёх средних цифр каждого пятизначного числа. Так как общая сумма всех цифр пятизначного числа должна делиться на 3, то она может быть равна или 12 или 15 или 18 или 21 или 24 или 27 или 30 или 33 или 36. Учитывая сумму первой и последней цифр (5+5=10), заключаем, что сумма средних трёх цифр может быть равна 2 или 5 или 8 или 11 или 14 или 17 или 20 или 23 или 26. Выпишем в порядке возрастания эти трёхзначные числа-палиндромы, стоящие между двумя «пятёрками» в искомых пятизначных числах-палиндромах, делящихся на 15.
020, 050, 080, 101, 131, 161, 191, 212, 242, 272, 323, 353, 383, 404, 434, 464, 494, 515, 545, 575, 626, 656, 686, 707, 737, 767, 797, 818, 848, 878, 929, 959, 989. Пересчитываем. Их 33, и это числа:
50205, 50505, 50805, 5105, 51315, 51615, 51915, 52125, 52425, 52725, 53235, 53535, 53835, 54045, 54345, 54645, 54945, 55155, 55455, 55755, 56265, 56565, 56865, 57075, 57375, 57675, 57975, 58185, 58485, 58785, 59295, 59595, 59895.
в) Так как число 50205 уже 7-ое по счёту число-палиндром, делящееся на 15 (помните, были три трёхзначных числа и три четырёхзначных числа?), то на 37-ом месте стоит число 59295.
Ответ: а) 525; б) 33; в) 59295.
Навигация
2018-12-08 
Найдите среднее арифметическое всех пятизначных чисел-палиндромов (чисел, которые справа налево и слева направо читаются одинаково, например, 12421).
Решение:
Будем отдельно считать суммы единиц, десятков, сотен и т. д., встречающихся в этих палиндромах. Любой палиндром имеет вид $overline{abcba}$. Для каждой цифры в разряде сотен существует $90 = 9 cdot 10$ вариантов выбора $a$ и $b$ ($a neq 0$). Поэтому общее количество палиндромов равно $9 cdot 10 cdot 10 = 900$.
Сумма всех сотен в палиндромах равна
$(0 + 100 + 200 + cdots + 800 + 900) cdot 90 = (1 + 2 + cdots + 8 + 9) cdot 100 cdot 90 = 45 cdot 90 cdot 100$.
Аналогично, сумма всех тысяч и десятков равна
$(0 + 1010 + 2020 + cdots + 8080 + 9090) cdot 90 = (1 + 2 + cdots + 8 + 9) cdot 1010 cdot 90 = 45 cdot 90 cdot 1010$,
сумма всех десятков тысяч и единиц равна
$(10001 + 20002 + 30003 + cdots + 80008 + 90009) cdot 100 = (1 + 2 + 3 + cdots + 8 +9) cdot 10001 cdot 100 = 45 cdot 100 cdot 10001$.
Таким образом среднее арифметическое всех чисел-палиндромов равно
$frac{45 cdot 90 cdot 100 + 45 cdot 90 cdot 1010 + 45 cdot 100 cdot 10001}{900} = frac{45 cdot (9000 + 90900 + 1000100)}{900} = frac{1100000}{20} = 55 000$.
Ответ: 55000.
ОсновноеЗадачи на сайтеЗадачи из сказкиЗадачи про числа – палиндромы |
Числа – палиндромы и делимость. Ответы.
|
| А | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| В | 1, 4, 7 | 2, 5, 8 | 0,3,6,9 | 1, 4, 7 | 2, 5, 8 | 0,3,6,9 | 1, 4, 7 | 2, 5, 8 | 0,3,6,9 |
Итак, всего чисел – палиндромов 3*4+6*3=30.
в) для четырехзначных чисел задача решается аналогично. Ответ 30.
г) Для пятизначных чисел – палиндромов вида АВСВА первую и последнюю цифры моно выбрать из 9 – от 1 до 9, вторую и предпоследнюю – из 10 – от 0 до 10. Третья цифра будет определяться необходимостью делимости суммы 2*А+2*В+С на 3. Набор возможностей аналогичен пункту б) и при В=0, С может принимать 3 или 4 значения. Таким образом, всего чисел – палиндромов 6*33+3*34=300.
Задача 3.
Вычислить количество чисел – палиндромов, делящихся на 5
а) двузначных
б) трехзначных
в) четырехзначных
г) пятизначных
Число делится на 5, если оканчивается на 0 или 5. Это значит, поскольку у числа – палиндрома первая и последняя цифры одинаковые, что ими может быть только пятерка.
а) среди двузначных чисел такое число только одно – 55.
б) на втором месте в трехзначном числе, делящемся на 5 может стоять любая из 10 цифр от 0 до 9. Всего 1*10=10 трехзначных чисел – палиндромов вида 5А5.
в) четырехзначных чисел – палиндромов, делящихся на 5 также 10 (докажите сами!)
г) для пятизначных чисел количество чисел – палиндромов, делящихся на 5, будет 1*10*10 = 100 (смотри решение задачи 1).
ЗАДОМ НАПЕРЁД
Наука и жизнь // Иллюстрации
‹
›
Числовой палиндром — это натуральное число, которое читается слева направо и справа налево одинаково. Иначе говоря, отличается симметрией записи (расположения цифр), причём число знаков может быть как чётным, так и нечётным. Палиндромы встречаются в некоторых множествах чисел, удостоенных собственных названий: среди чисел Фибоначчи — 8, 55 (6-й и 10-й члены одноимённой последовательности); фигурных чисел — 676, 1001 (квадратное и пятиугольное соответственно); чисел Смита — 45454, 983389. Указанным свойством обладает также всякий репдиджит, например 2222222 и, в частности, репьюнит*.
Палиндром можно получить как результат операций над другими числами. Так, в книге «Есть идея!» известного популяризатора науки Мартина Гарднера в связи с этой задачей упоминается «гипотеза о палиндромах». Возьмём любое натуральное число и сложим его с обращённым числом, то есть записанным теми же цифрами, но в обратном порядке. Проделаем то же действие с получившейся суммой и будем повторять его до тех пор, пока не образуется палиндром. Иногда достаточно сделать всего один шаг (например, 312 + 213 = 525), но, как правило, требуется не менее двух. Скажем, число 96 порождает палиндром 4884 только на четвёртом шаге. В самом деле:
96 + 69 = 165,
165 + 561 = 726,
726 + 627 = 1353,
1353 + 3531 = 4884.
А суть гипотезы в том, что, взяв любое число, после конечного числа действий мы обязательно получим палиндром.
Можно рассматривать не только сложение, но и другие операции, включая возведение в степень и извлечение корней. Вот несколько примеров того, как при их помощи из одних палиндромов получаются другие:
ИГРЫ ЦИФР
До сих пор мы рассматривали в основном составные числа. Теперь обратимся к числам простым. В их бесконечном множестве имеются немало любопытных экземпляров и даже целые семейства палиндромов. Только среди первых ста миллионов натуральных чисел насчитывается 781 простой палиндром, причём двадцать приходятся на первую тысячу, из них четыре числа однозначные — 2, 3, 5, 7 и всего одно двузначное — 11. С такими числами связано немало интересных фактов и красивых закономерностей.
Во-первых, существует единственный простой палиндром с чётным числом цифр — 11. Другими словами, произвольный палиндром с чётным числом цифр, бóльшим двух, число составное, что нетрудно доказать на основе признака делимости на 11.
Во-вторых, первой и последней цифрами любого простого палиндрома могут быть только 1, 3, 7 или 9. Это следует из известных признаков делимости на 2 и на 5. Любопытно, что все простые двузначные числа, записанные с помощью перечисленных цифр (за исключением 19), можно разбить на пары чисел-«перевёртышей» (взаимно обращённых чисел) вида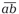 
и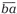 
, где цифры a и b различны. Каждая из них, независимо от того, какое число стоит на первом месте, читается одинаково слева направо и справа налево:
13 и 31, 17 и 71,
37 и 73, 79 и 97.
Заглянув в таблицу простых чисел, мы обнаружим аналогичные пары, в записи которых присутствуют и другие цифры, в частности, среди трёхзначных чисел подобных пар наберётся четырнадцать.
Кроме того, среди простых трёхзначных палиндромов встречаются пары чисел, у которых средняя цифра отличается всего на 1:
181 и 191, 373 и 383,
787 и 797, 919 и 929.
Аналогичная картина наблюдается и у бо`льших простых чисел, например:
94849 и 94949,
1177711 и 1178711.
Простые числа-палиндромы могут «задаваться» разными симметричными формулами, которые отражают особенности их записи. Это хорошо видно на примере пятизначных чисел:
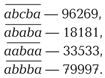
Кстати, простые многозначные числа вида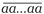 
встречаются, очевидно, только среди репьюнитов. Таких чисел известно пять. Примечательно, что у каждого из них количество цифр выражается простым числом: 2, 19, 23, 317, 1031. А вот среди простых чисел, у которых все цифры, кроме центральной, единицы, был обнаружен палиндром весьма внушительной длины — в нём 1749 цифр:
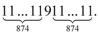
Вообще среди простых чисел-палиндромов встречаются удивительные экземпляры. Вот лишь один пример — числовой гигант
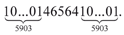
А интересен он тем, что содержит 11 811 цифр, которые можно разбить на три палидромические группы, причём в каждой группе количество цифр выражается простым числом (5903 или 5).
ПРИМЕЧАТЕЛЬНЫЕ ПАРЫ
Любопытные палиндромические закономерности просматриваются и в группах простых чисел, в записи которых присутствуют определённые цифры. Скажем, только цифры 1 и 3, причём в каждом числе. Так, двузначные простые числа составляют упорядоченные пары 13 — 31 и 31 — 13, из шести трёхзначных простые сразу пять чисел, среди которых есть два палиндрома: 131 и 313, а ещё два числа образуют пары «перевёртышей» 311 — 113 и 113 — 311. Во всех этих случаях составленные пары наглядно представляются в виде числовых квадратов (рис. 1).
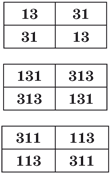
Рис. 1
Своими свойствами они напоминают магический и латинский квадраты. Например, у среднего квадрата сумма чисел, стоящих в каждой строке и в каждом столбце, равна 444, на диагоналях — 262 и 626. Сложив числа из всех клеток, получим 888. И что характерно, каждая сумма — палиндром. Даже просто выписывая без пробела несколько чисел из одной таблицы, получим новые палиндромы: 3113, 131313131 и т. д. Какое наибольшее число можно составить таким способом? Будет ли оно палиндромом?
Если в каждую из пар 311 — 113 и 113 — 311 добавить 131 или 313, образуются четыре палиндромические тройки. Запишем одну из них в столбик:
311
131
113
Как видим, и сами числа, и нужная их комбинация дают о себе знать при прочтении в разных направлениях. Кроме того, расположение цифр симметрично, а их сумма в каждой строке, каждом столбце и на одной из диагоналей выражается простым числом − 5.
Надо сказать, рассмотренные числа интересны и сами по себе. Например, палиндром 131 — простое циклическое число: при любых последовательных перестановках первой цифры на последнее место он порождает простые числа 311 и 113. Можете ли вы указать другие простые палиндромы, обладающие таким же свойством?
А вот пары чисел-«перевёртышей» 13 — 31 и 113 — 311 при возведении в квадрат дают также пары «перевёртышей»: 169 — 961 и 12769 — 96721. Любопытно, что даже суммы их цифр оказались связаны хитрым образом:
(1 + 3)2 = 1 + 6 + 9,
(1 + 1 + 3)2 = 1 + 2 + 7 + 6 + 9.
Добавим, что среди натуральных чисел имеются и другие пары «перевёртышей» с подобным свойством: 103 — 301, 1102 — 2011, 11113 — 31111 и др. Чем объясняется подмеченная закономерность? Чтобы ответить на этот вопрос, нужно понять, что особенного в записи указанных чисел, какие цифры и в каком количестве могут в ней присутствовать.
ЧИСЛОВОЙ КОНСТРУКТОР
Из простых чисел-палиндромов, располагая их определённым образом, скажем построчно, можно составить симметричные фигуры, отличающиеся оригинальным рисунком из повторяющихся цифр.
Вот, например, красивая комбинация из простых палиндромов, записанных с помощью 1 и 3 (кроме первого, рис. 2). Особенность этого числового треугольника в том, что один и тот же фрагмент повторяется трижды, не нарушая симметрию рисунка.
Рис. 2
Легко видеть, что общее количество строк и столбцов — число простое (17). К тому же простые числа и суммы цифр: выделенных красным фрагментов (17); каждой строки, за исключением первой (5, 11, 17, 19, 23); третьего, пятого, седьмого и девятого столбцов (7, 11) и «лесенки» из единиц, образующей боковые стороны треугольника (11). Наконец, если двигаться параллельно указанным «сторонам» и складывать по отдельности цифры третьего и пятого рядов (рис. 3), получим ещё два простых числа (17, 5).
Рис. 3
Продолжая построение, можно сконструировать на основе данного треугольника более сложные фигуры. Так, ещё один треугольник с аналогичными свойствами нетрудно получить, двигаясь с конца, то есть начать с последнего числа, вычёркивая на каждом шаге две одинаковые симметрично расположенные цифры и переставляя или заменяя другие — 3 на 1 и наоборот. При этом сами цифры следует выбирать с таким расчётом, чтобы образующееся в итоге число оказалось простым. Объединив обе фигуры, получим ромб с характерным узором из цифр, скрывающим в себе немало простых чисел (рис. 4). В частности, сумма выделенных красным цветом цифр равна 37.
Рис. 4
Другой пример — треугольник, полученный из исходного после добавления к нему шести простых палиндромов (рис. 5). Фигура сразу привлекает внимание своим изящным обрамлением из единиц. Её окаймляют два простых репьюнита одинаковой длины: 23 единицы составляют «основание» и ещё столько же — «боковые стороны» треугольника.
Рис. 5
Ещё несколько фигур
Можно составить также многоугольные фигуры из чисел, обладающие определёнными свойствами. Пусть требуется построить фигуру из простых палиндромов, записанных с помощью 1 и 3, у каждого из которых крайние цифры — единицы, а сумма всех цифр и общее количество единиц в строке — простые числа (исключение — однозначный палиндром). Кроме того, простым числом должно выражаться общее количество строк, а также цифр 1 либо 3, встречающихся в записи.
На рис. 6 приведено одно из решений задачи — «домик», сконструированный из 11 различных палиндромов.
Рис. 6
Конечно, не обязательно ограничиваться двумя цифрами и требовать наличия в записи каждого используемого числа всех указанных цифр. Скорее, наоборот: ведь именно их необычные сочетания придают своеобразие узору фигуры. В подтверждение этому приведём несколько примеров красивых палиндромических зависимостей (рис. 7−9).
Рис. 7
Рис. 8
Рис. 9
Теперь, вооружившись таблицей простых чисел, вы и сами сконструируете фигуры вроде предложенных нами.
А напоследок ещё одна диковинка — треугольник, буквально пронизанный вдоль и поперёк палиндромами (рис. 10). В нём 11 строк из простых чисел, а столбцы образованы репдиджитами. И главное: ограничивающий фигуру с боков палиндром 193111111323111111391 — число простое!
Рис. 10
Комментарии к статье
*Число Смита — составное число, сумма цифр которого равна сумме цифр его простых делителей.
Репдиджит — натуральное число, в записи которого все цифры одинаковые.
Репьюнит — натуральное число, записанное с помощью одних только единиц.
