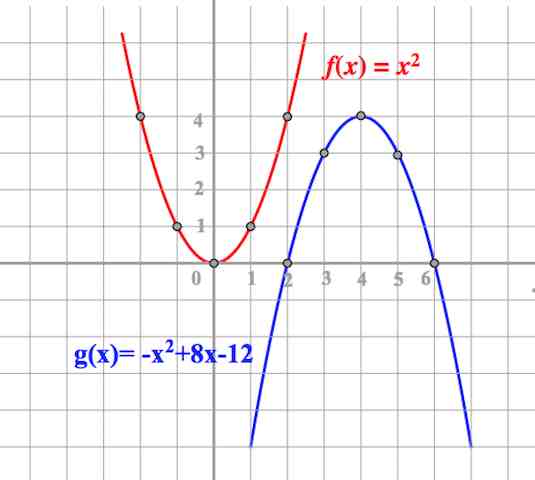
Здравствуйте, дорогие читатели, подписчики и гости канала. В этом выпуске рассмотрим построение графика функции у=|f(x)| и составим алгоритм на примере следующего задания:
1) Построим сначала график функции, который находится под модулем.
Графиком этой функции является парабола. Найдем координаты вершины параболы:
Для построения графика параболы, нам необходимо найти еще координаты точек. Для этого сделаем табличку. В центре таблички поместим координаты вершины параболы.
Построим график функции по координатам из таблицы. Точки будем соединять пунктирной линией, поскольку это не основной график, что нам нужно построить, а на экзамене есть только в распоряжении гелиевая черная паста (график слева).
2)Чтобы построить график, который требуется по заданию, отразим относительно прямой Ох те части параболы, что лежат ниже оси абсцисс. Получим искомый график, которые начерчен справа сплошной линией.
3)Ответим на второй вопрос задания: Наибольшее число общих точек график нашей построенной функции может иметь с прямой параллельной оси абсцисс ровно 4. На рисунке показано красной линией.
Спасибо что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
Каталог заданий.
Параболы
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 22 № 49
i
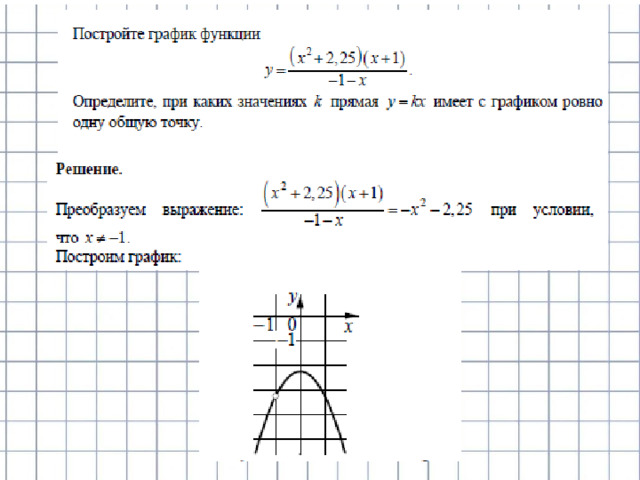
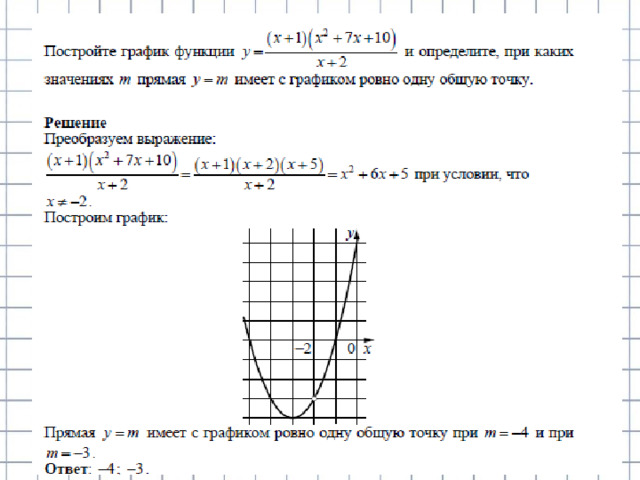
Постройте график функции и определите, при каких значениях параметра c прямая
имеет с графиком ровно одну общую точку.
2
При каком значении p прямая имеет с параболой
ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении p.
3
Известно, что парабола проходит через точку и её вершина находится в начале координат. Найдите уравнение этой параболы и вычислите, в каких точках она пересекает прямую
Источник: ГИА-2013. Математика. Тренировочная работа № 1 (1 вар.)
4
Парабола проходит через точки K(0; –5), L(3; 10), M( –3; –2). Найдите координаты её вершины.
Источник: Банк заданий ФИПИ
5
При каких значениях p вершины парабол и
расположены по разные стороны от оси x?
Источник: Банк заданий ФИПИ
Пройти тестирование по этим заданиям
на главную
Найти репетитора
Поддержать сайт
Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют
функцией в математике.
Если вы прочно закрепите общие знания о функции (способы задания, понятие графика)
дальнейшее изучение других
видов функций будет даваться значительно легче.
Что называют квадратичной функцией
Запомните!
Квадратичная функция — это функция вида
y = ax2 + bx + c,
где a,
b и с — заданные числа.
Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень,
в которой стоит «x» — это «2»,
то перед нами квадратичная функция.
Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты «a»,
«b» и «с».
| Квадратичная функция | Коэффициенты |
|---|---|
| y = 2x2 − 7x + 9 |
|
| y = 3x2 − 1 |
|
| y = −3x2 + 2x |
|
Как построить график квадратичной функции
Запомните!
График квадратичной функции называют параболой.
Парабола выглядит следующим образом.
Также парабола может быть перевернутой.
Существует четкий алгоритм действий при построении графика квадратичной функции.
Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.
Чтобы было проще понять этот алгоритм, сразу разберем его на примере.
Построим график квадратичной функции «y = x2 −7x + 10».
- Направление ветвей параболы
Запомните!
Если «a > 0», то ветви направлены вверх.
Если «a », то ветви направлены вниз.
В нашей функции «a = 1», это означает, что ветви параболы направлены вверх.
- Координаты вершины параболы
Запомните!
Чтобы найти «x0»
(координата вершины по оси «Ox»)
нужно использовать формулу:Найдем «x0» для нашей функции «y = x2 −7x + 10».
Теперь нам нужно найти «y0»
(координату вершины по оси «Oy»).
Для этого нужно подставить найденное значение «x0» в исходную функцию.
Вспомнить, как найти значение функции можно в уроке
«Как решать задачи на функцию» в подразделе
«Как получить значение функции».y0(3,5) =
(3,5)2 − 7 ·3,5 + 10 = 12,25 − 24,5 + 10 =−12,25 + 10 = −2,25
Выпишем полученные координаты вершины параболы.
(·) A (3,5; −2,25) — вершина параболы.
Отметим вершину параболы на системе координат.
Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график
относительно оси «Oy». - Нули функции
Для начала давайте разберемся, что называют нулями функции.
Запомните!
Нули функции — это точки пересечения графика функции с осью «Ox»
(осью абсцисс).Наглядно нули функции на графике выглядят так:
Свое название нули функции получили из-за того, что у этих точек координата
по оси «Oy» равна нулю.Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.
Запомните!
Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо
«y = 0».Подставим в заданную функцию «y = x2 −7x + 10»
вместо «y = 0» и решим полученное
квадратное уравнение
относительно
«x» .0 = x2 −7x + 10
x2 −7x + 10 = 0x1;2 =
7 ±
√49 − 4 · 1 · 102 · 1 x1;2 =
x1;2 =
x1 = x2 =
x1 = x2 =
x1 = 5 x2 = 2
Мы получили два корня в уравнении, значит, у нас две точки пересечения
с осью «Ox».
Назовем эти точки и выпишем их координаты.- (·) B (5; 0)
- (·) C (2; 0)
Отметим полученные точки («нули функции») на системе координат.
- Дополнительные точки для построения графика
Возьмем четыре произвольные числовые значения для «x».
Целесообразно брать целые числовые значения на оси «Ox»,
которые наиболее близки к оси
симметрии. Числа запишем в таблицу в порядке возрастания.Для каждого выбранного значения «x»
рассчитаем «y».- y(1) = 12 − 7 · 1 + 10 = 1 − 7 + 10 =
4 - y(3) = 32 − 7 · 3 + 10 = 9 − 21 + 10 =
−2 - y(4) = 42 − 7 · 4 + 10 = 16 − 28 + 10 =
−2 - y(6) = 62 − 7 · 6 + 10 = 36 − 42 + 10 =
4
Запишем полученные результаты в таблицу.
Отметим полученные точки графика на системе координат (зеленые точки).
Теперь мы готовы построить график.
На забудьте после построения подписать график функции. - y(1) = 12 − 7 · 1 + 10 = 1 − 7 + 10 =
Краткий пример построения параболы
Рассмотрим другой пример построения графика квадратичной функции.
Только теперь запишем алгоритм построения коротко без подробностей.
Пусть требуется построить график функции
«y = −3x2 − 6x − 4».
- Направление ветвей параболы
- Координаты вершины параболы
x0 =
x0 = == −1
y0(−1) = (−3) · (−1)2 − 6 · (−1) − 4 =
−3 · 1 + 6 − 4 = −1(·) A (−1; −1)
— вершина параболы.
- Нули функции
Точки пересечения с осью «Ox» (y = 0).
0 = −3x2 − 6x − 4
−3x2 − 6x − 4 = 0 |·(−1)
3x2 + 6x + 4 = 0
x1;2 =
−6 ±
√62 − 4 · 3 · 42 · 1 x1;2 =
x1;2 =
Ответ: нет действительных корней.
Так как корней нет, значит, график функции не пересекает ось
«Ox». - Вспомогательные точки для: «x = −3»;
«x = −2»;
«x = 0»;
«x = 1». Подставим в исходную функцию
«y = −3x2 − 6x − 4».- y(−3) = −3 · (−3)2 − 6 · (−3) − 4
= −3 · 9 + 18 − 4 = −27 + 14 = −13 - y(−2) = −3 · (−2)2 − 6 · (−2) − 4
= −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4 - y(0) = −3 · 02 − 6 · 0 − 4
= −4 - y(1) = −3 · 12 − 6 · 1 − 4
= −3 −6 − 4 = −13
x −3 −2 0 1 y −13 −4 −4 −13 - y(−3) = −3 · (−3)2 − 6 · (−3) − 4
«a = −3» — ветви параболы направлены вниз.
Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые
не выходят за масштаб нашей системы координат, то есть точки
«(−2; −4)» и «(0; −4)».
Построим и подпишем график функции.
Функция вида , где
называется квадратичной функцией.
График квадратичной функции – парабола.
Рассмотрим случаи:
I СЛУЧАЙ, КЛАССИЧЕСКАЯ ПАРАБОЛА
, то есть
,
,
Для построения заполняем таблицу, подставляя значения x в формулу:
Отмечаем точки (0;0); (1;1); (-1;1) и т.д. на координатной плоскости (чем с меньшим шагом мы берем значения х ( в данном случае шаг 1 ), и чем больше берем значений х, тем плавнее будет кривая), получаем параболу:
Нетрудно заметить, что если мы возьмем случай ,
,
, то есть
, то мы получим параболу, симметричную
относительно оси (ох). Убедиться в этом несложно, заполнив аналогичную таблицу:
II СЛУЧАЙ, «a» ОТЛИЧНО ОТ ЕДИНИЦЫ
Что же будет, если мы будем брать ,
,
? Как изменится поведение параболы? При
парабола
изменит форму, она “похудеет” по сравнению с параболой
(не верите – заполните соответствующую таблицу – и убедитесь сами):
На первой картинке (см. выше) хорошо видно, что точки из таблицы для параболы (1;1), (-1;1) трансформировались в точки (1;4), (1;-4), то есть при тех же значениях
ордината
каждой точки умножилась на 4. Это произойдет со всеми ключевыми точками исходной таблицы. Аналогично рассуждаем в случаях картинок 2 и 3.
А при парабола
«станет шире» параболы
:
Давайте подитожим:
III СЛУЧАЙ, ПОЯВЛЯЕТСЯ «С»
Теперь давайте введем в игру (то есть рассматриваем случай, когда
), будем рассматривать параболы вида
. Нетрудно догадаться (вы всегда можете обратиться к таблице), что будет происходить смещение параболы
вдоль оси
вверх или вниз в зависимости от знака
:

IV СЛУЧАЙ, ПОЯВЛЯЕТСЯ «b»
Когда же парабола “оторвется” от оси и будет, наконец, “гулять” по всей координатной плоскости? Когда
перестанет быть равным
.
Здесь для построения параболы нам понадобится формула для вычисления вершины:
,
.
Так вот в этой точке (как в точке (0;0) новой системы координат) мы будем строить параболу , что уже нам по силам. Если имеем дело со случаем
, то от вершины откладываем один единичный отрезок вправо, один вверх, – полученная точка – наша (аналогично шаг влево, шаг вверх – наша точка); если имеем дело с
, например, то от вершины откладываем один единичный отрезок вправо, два – вверх и т.д.
Например, вершина параболы :
,
. Теперь главное уяснить, что в этой вершине мы будем строить параболу по шаблону параболы
, ведь
в нашем случае.
При построении параболы после нахождения координат вершины очень удобно учитывать следующие моменты:
1) парабола обязательно пройдет через точку . Действительно, подставив в формулу
x=0, получим, что
. То есть ордината точки пересечения параболы с осью (оу), это
. В нашем примере (выше), парабола пересекает ось ординат в точке
, так как
.
2) осью симметрии параболы является прямая , поэтому все точки параболы будут симметричны относительно нее. В нашем примере, мы сразу берем точку (0; -2) и строим ей симметричную относительно оси симметрии параболы, получим точку (4; -2), через которую будет проходить парабола.
3) Приравнивая к
, мы узнаем точки пересечения параболы с осью (ох). Для этого решаем уравнение
. В зависимости от дискриминанта, будем получать одну (
,
), две (
,
) или нИсколько (
) точек пересечения с осью (ох). В предыдущем примере у нас корень из дискриминанта – не целое число, при построении нам особо нет смысла находить корни, но мы видим четко, что две точки пересечения с осью (ох) у нас будут (так как
), хотя, в общем, это видно и без дискриминанта.
Итак, давайте выработаем
Алгоритм для построения параболы, если она задана в виде 
1) определяем направление ветвей ( а>0 – вверх, a<0 – вниз)
2) находим координаты вершины параболы по формуле
,
.
3) находим точку пересечения параболы с осью (оу) по свободному члену , строим точку, симметричную данной относительно оси симметрии параболы (надо заметить, бывает, что эту точку невыгодно отмечать, например, потому, что значение
велико… пропускаем этот пункт…)
4) В найденной точке – вершине параболы (как в точке (0;0) новой системы координат) строим параболу . Если
, то парабола
становится у’же по сравнению с
, если
, то парабола расширяется по сравнению с
5) Находим точки пересечения параболы с осью (оу) (если они еще сами “не всплыли”), решая уравнение
Пример 1
Пример 2
Замечание 1. Если же парабола изначально нам задана в виде , где
– некоторые числа (например,
), то построить ее будет еще легче, потому что нам уже заданы координаты вершины
. Почему?
Возьмем квадратный трехчлен и выделим в нем полный квадрат:
Посмотрите, вот мы и получили, что
,
. Мы с вами ранее называли вершину параболы
, то есть теперь
,
.
Например, . Отмечаем на плоскости вершину параболы
, понимаем, что ветви направлены вниз, парабола расширена (относительно
). То есть выполняем пункты 1; 3; 4; 5 из алгоритма построения параболы (см. выше).
Замечание 2. Если парабола задана в виде, подобном этому (то есть
представлен в виде произведения двух линейных множителей), то нам сразу видны точки пересечения параболы с осью (ох). В данном случае – (0;0) и (4;0). В остальном же действуем согласно алгоритму, раскрыв скобки.
у
У=5
5
4
У=4
х
-3
0
1
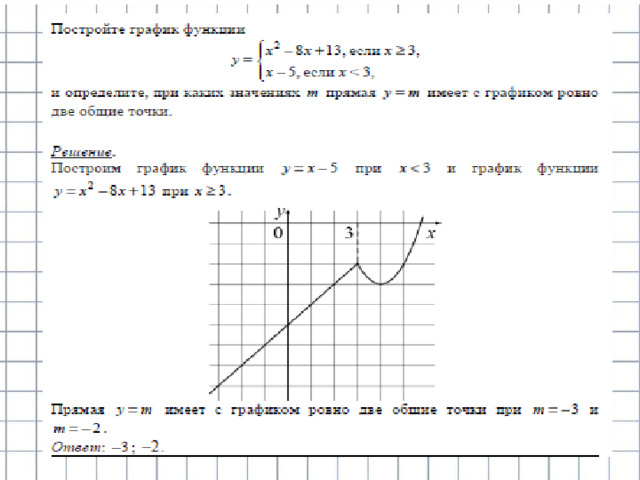
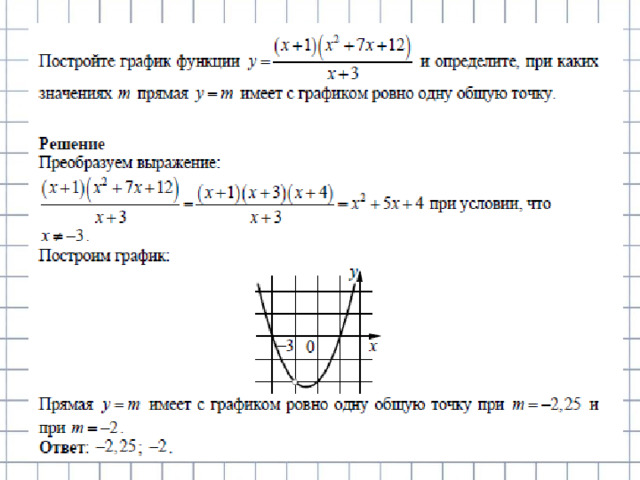
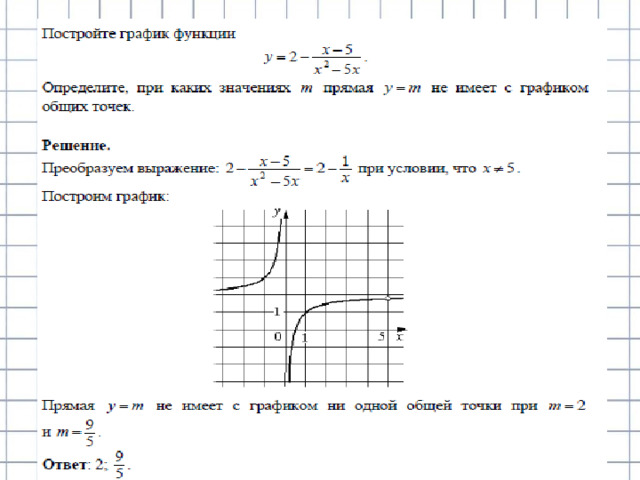
Прямая у=m имеет с графиком ровно две общие точки, если она проходит через вершину параболы или через точку (-2;3). Получаем, что m=4 или m= 3.
Ответ : 3;4
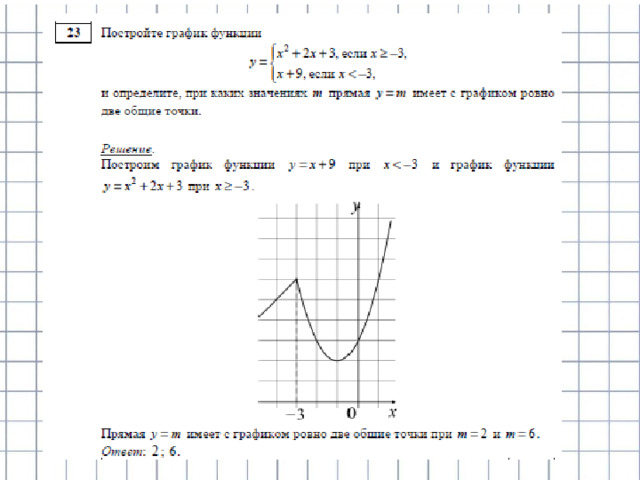
Постройте график функции и определите,
Решение:
при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Построим график функции y = 2,5 x при x
график функции y = x 2 − 6 x + 13 при x ≥ 2.
Прямая y = m имеет с графиком ровно
две общие точки при m = 4 и при m = 5 .
Ответ: 4; 5.
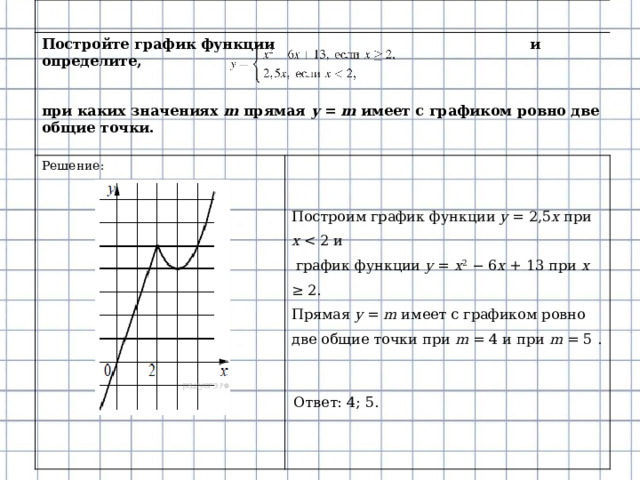
Постройте график функции и определите,
Решение:
при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Построим график функции y = 2,5 x при x
график функции y = x 2 − 6 x + 13 при x ≥ 2.
Прямая y = m имеет с графиком ровно
две общие точки при m = 4 и при m = 5 .
Построим график функции у=-х²-4 при х≠1
а) Координаты вершины параболы (0;-4)
б)Ось симметрии х=0
в) Дополнительные точки:
Х
У
-2
-1
-8
0
-5
1
-4
-5
2
-8
у
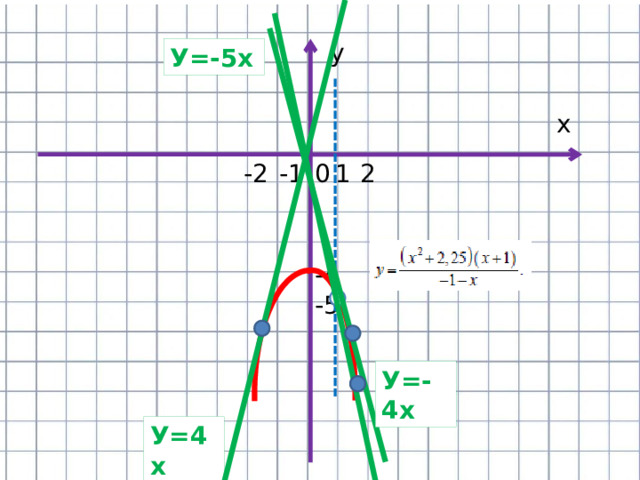
У=-5х
х
1
0
-2
-1
2
-4
-5
У=-4х
У=4х
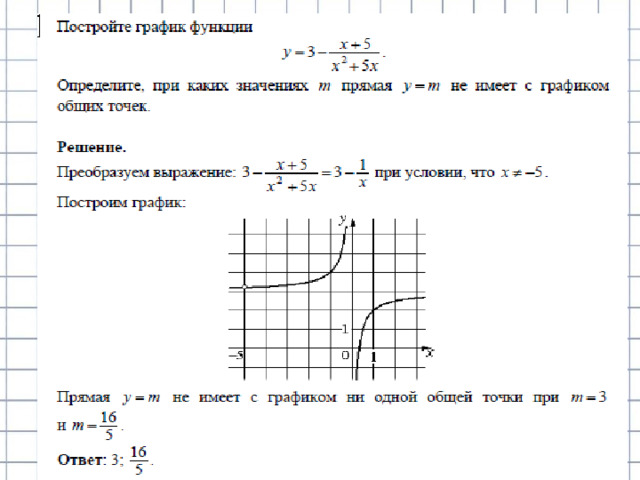
Прямая у=кх имеет с графиком ровно одну общую точку, если она проходит через точку (1;-5) или если уравнение –х²-4=кх имеет один корень.
Дискриминант уравнения х²+кх+4=0 равен к²-16. и он должен быть равен 0.Получаем , что к= -5, к=-4, к=4.
Ответ: -5;-4;4
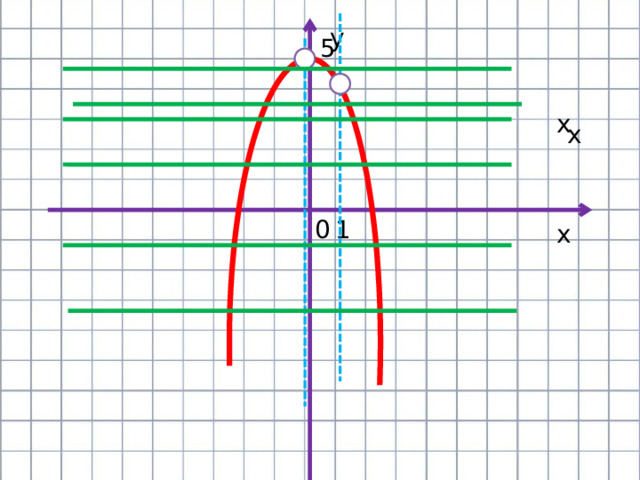
Построим график функции у=5-х²
а)Координаты вершины параболы: (0;5)
б) Ось симметрии : х=0
в)Дополнительные точки:
Х
У
-3
-2
-4
-1
1
0
4
1
5
2
4
3
1
-4
у
5
х
х
0
1
х
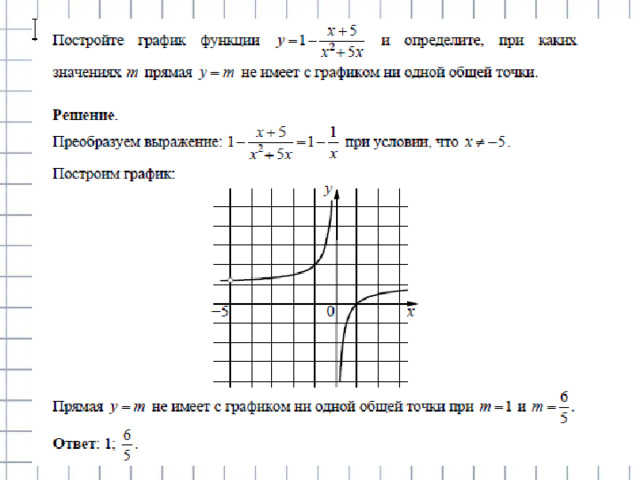
- Прямая у=m имеет с графиком ровно две общие точки при m
- Ответ при mє(-∞;4),(4;5)
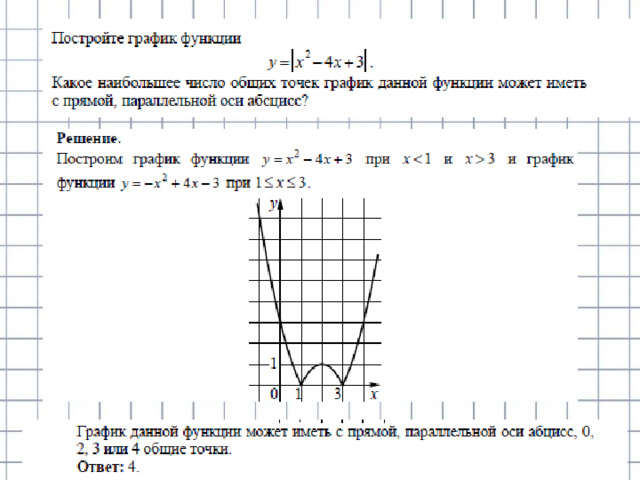
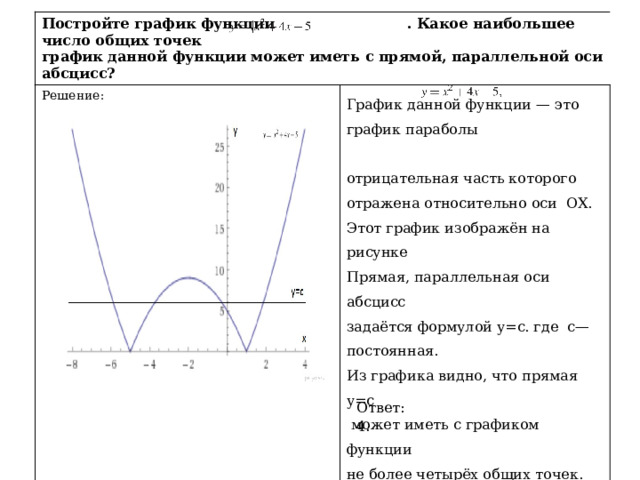
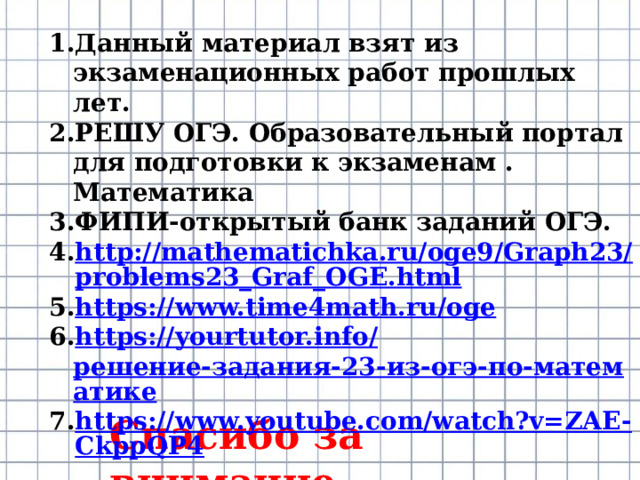
Постройте график функции . Какое наибольшее число общих точек
график данной функции может иметь с прямой, параллельной оси абсцисс?
Решение:
График данной функции — это график параболы
отрицательная часть которого отражена относительно оси ОХ.
Этот график изображён на рисунке
Прямая, параллельная оси абсцисс
задаётся формулой у=с. где с— постоянная.
Из графика видно, что прямая у=с
может иметь с графиком функции
не более четырёх общих точек.
Ответ: 4 .
- Данный материал взят из экзаменационных работ прошлых лет.
- РЕШУ ОГЭ. Образовательный портал для подготовки к экзаменам . Математика
- ФИПИ-открытый банк заданий ОГЭ.
- http://mathematichka.ru/oge9/Graph23/problems23_Graf_OGE.html
- https://www.time4math.ru/oge
- https://yourtutor.info/ решение-задания-23-из-огэ-по-математике
- https://www.youtube.com/watch?v=ZAE-CkppQP4
Спасибо за внимание.
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Декартова система координат
Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.
Координатные оси – прямые, образующие систему координат.
Ось абсцисс (ось x ) – горизонтальная ось.
Ось ординат (ось y ) – вертикальная ось.
Функция
Функция – это отображение элементов множества X на множество Y. При этом каждому элементу x множества X соответствует одно единственное значение y множества Y.
Прямая
Линейная функция – функция вида y = a x + b где a и b – любые числа.
Графиком линейной функции является прямая линия.
Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :
Если a > 0 , прямая будет проходить через I и III координатные четверти.
b – точка пересечения прямой с осью y .
Если a < 0 , прямая будет проходить через II и IV координатные четверти.
b – точка пересечения прямой с осью y .
Если a = 0 , функция принимает вид y = b .
Отдельно выделим график уравнения x = a .
Важно: это уравнение не является функцией так как нарушается определение функции (функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y. Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».
Парабола
Графиком функции y = a x 2 + b x + c является парабола.
Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a , b , c :
- Коэффициент a указывает на то, куда направлены ветки параболы.
- Если a > 0 , ветки параболы направлены вверх.
- Если a < 0 , ветки параболы направлены вниз.
- Коэффициент c указывает, в какой точке парабола пересекает ось y.
- Коэффициент b помогает найти x в – координату вершины параболы.
x в = − b 2 a
- Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .
- Если D > 0 – две точки пересечения.
- Если D = 0 – одна точка пересечения.
- Если D < 0 – нет точек пересечения.



Гипербола
Графиком функции y = k x является гипербола.
Характерная особенность гиперболы в том, что у неё есть асимптоты.
Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.
Ось x – горизонтальная асимптота гиперболы
Ось y – вертикальная асимптота гиперболы.
На графике асимптоты отмечены зелёной пунктирной линией.
Если коэффициент k > 0 , то ветви гиперолы проходят через I и III четверти.
Если k < 0, ветви гиперболы проходят через II и IV четверти.
Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y .
Квадратный корень
Функция y = x имеет следующий график:
Возрастающие/убывающие функции
Функция y = f ( x ) возрастает на интервале, если большему значению аргумента (большему значению x ) соответствует большее значение функции (большее значение y ) .
То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)
Примеры возрастающих функций:
Функция y = f ( x ) убывает на интервале, если большему значению аргумента (большему значению x ) соответствует меньшее значение функции (большее значение y ) .
То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).
Примеры убывающих функций:

Для того, чтобы найти наибольшее значение функции, находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наибольшим значением функции.
Для того, чтобы найти наименьшее значение функции, находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наименьшим значением функции.
Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.
Скачать домашнее задание к уроку 5.