Пример параллакса (видео)
Паралла́кс (греч. παράλλαξις, от παραλλαγή, «смена, чередование») — изменение видимого положения объекта относительно удалённого фона в зависимости от положения наблюдателя.
Зная расстояние между точками наблюдения L (базис) и угол смещения α, можно определить расстояние до объекта:
Для малых углов (α — в радианах)
Измерение расстояния при помощи параллакса
Параллакс используется в геодезии и астрономии для измерения расстояния до удалённых объектов (в частности в специальных единицах — парсеках). На явлении параллакса основано бинокулярное зрение.
Астрономия[править | править код]
Суточный параллакс[править | править код]
Суточный параллакс (геоцентрический параллакс) — разница в направлениях на одно и то же светило из центра масс Земли (геоцентрическое направление) и из заданной точки на поверхности Земли (топоцентрическое направление).
Этот угол зависит от высоты светила над горизонтом, максимальное его значение достигается при нулевой высоте (когда светило наблюдается прямо на горизонте).
Такая величина называется горизонтальным параллаксом[1]. База параллакса при этом равна радиусу Земли (около 6400 км).
Из-за вращения Земли вокруг своей оси положение наблюдателя относительно центра Земли и, соответственно, параллактический угол циклически изменяются.
При наблюдении Луны её кажущиеся смещения на фоне звёзд (по сравнению с расчётным орбитальным движением) достигают 2° (соответственно, параллакс равен 1°) и были замечены уже древнегреческими астрономами, что позволило им довольно точно определить расстояние до Луны[2].
Суточный параллакс планет довольно мал (для Марса 24″ во время великого противостояния), но тем не менее был единственным способом измерения абсолютных расстояний в Солнечной системе до появления радиолокации: наиболее удобными для этого были прохождения Венеры по диску Солнца и близко подходящие к Земле астероиды (относительные же расстояния легко определяются на основе законов Кеплера, так что достаточно абсолютного измерения какого-то одного расстояния, чтобы определить все).
Годичный параллакс[править | править код]
Параллактические эллипсы звёзд при различных расстояниях от плоскости эклиптики
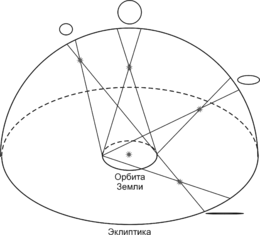
Годичный параллакс — изменение направления на объект (например, звезду), связанное с движением Земли вокруг Солнца. Величина параллакса равна углу, под которым со звезды видна большая полуось земной орбиты (перпендикулярная лучу зрения).
Годичные параллаксы являются показателями расстояний до звёзд. Расстояние до объекта, годичный параллакс которого равен 1 угловой секунде, называется парсек (1 парсек = 3,085678⋅1016 м). Ближайшая к нам звезда Проксима Центавра имеет параллакс 0,7687±0,0003″, следовательно, расстояние до неё составляет 1,3009±0,00015 пк.
Вековой параллакс[править | править код]
Вековым параллаксом обычно называется изменение видимого положения объекта на небесной сфере в результате комбинаций собственных движений этого объекта и Солнечной системы в галактике.
Параллакс в фотографии[править | править код]
Отражение солнца в воде находится на отражении фонаря, хотя в неотражённом виде оно находится на заметном удалении над фонарём
Параллакс видоискателя[править | править код]
Параллакс видоискателя — несовпадение границ изображения, видимых в оптическом видоискателе, с границами изображения, получаемого в кадровом окне[3]. Параллакс почти незаметен в случае съёмки удалённых объектов, и весьма значителен на небольших конечных дистанциях[4]. Он возникает из-за наличия расстояния (базиса) между оптическими осями съёмочного объектива и видоискателя. Величина параллакса 
где 


Параллакс прицела[править | править код]
Частным случаем является параллакс прицела.
Параллакс прицела — это угол между осью ствола и осью прицела с вершиной на цели. Чем ближе цель к стрелку, тем больше этот угол, тем больше надо корректировать прицел. Если прицел пристрелян на расстояние в 100 метров, а цель находится на расстоянии 50 метров, то пуля пролетит ниже цели. И чем ближе цель будет приближаться к 100 метрам от стрелка, тем ближе будет попадание к цели. При нахождении цели дальше 100 метров пуля пролетит выше цели. Баллистика в данном вопросе не учитывается.
Параллакс дальномера[править | править код]
Параллакс дальномера — угол, под которым виден объект во время наводки на резкость с помощью оптического дальномера.
Стереоскопический параллакс[править | править код]
Стереоскопический (бинокулярный) параллакс — это угол, под которым рассматривают объект двумя глазами или когда его фотографируют стереоскопическим фотоаппаратом.
Временно́й параллакс[править | править код]
Временной параллакс — искажение формы быстро движущихся объектов, возникающее при съёмке фотоаппаратом со шторно-щелевым фокальным затвором или видеокамерой со строчным переносом. Так как экспозиция происходит не единовременно по всей площади светочувствительного элемента, а последовательно по мере движения щели, то при съёмке быстро движущихся объектов их форма может искажаться. Например, если объект движется в ту же сторону, что и щель затвора, его изображение будет растянуто, а если в обратную, то сужено.
Примечания[править | править код]
- ↑ Параллакс Архивная копия от 26 апреля 2016 на Wayback Machine (Глоссарий astronet.ru)
- ↑ Еремеева А. И., Цицин Ф.А. История астрономии. — М.: Изд-во МГУ, 1989. — С. 89. — 349 с.
- ↑ Техника фотографии, 1973, с. 40.
- ↑ Выбор фотоаппарата, 1962, с. 26.
Литература[править | править код]
- Бунимович Д. З. Выбор фотоаппарата / Е. А. Иофис. — М.: «Искусство», 1962. — 128 с.
- Иофис Е. А. Техника фотографии. — М.: «Искусство», 1973. — 349 с.
- Яштолд-Говорко В. А. Фотосъёмка и обработка. Съёмка, формулы, термины, рецепты. Изд. 4-е, сокр. — М.: «Искусство», 1977.
- Hirshfeld, Alan w. Parallax: The Race to Measure the Cosmos. — New York: W.H. Freeman (англ.) (рус., 2001. — ISBN 978-0-7167-3711-7.
- Whipple, Fred L. Earth Moon and Planets. — Read Books, 2007. — ISBN 978-1-4067-6413-0.
- Zeilik, Michael A.; Gregory, Stephan A. Introductory Astronomy & Astrophysics. — 4th. — Saunders College Publishing (англ.) (рус., 1998. — ISBN 978-0-03-006228-5.
Ссылки[править | править код]
- The ABC’s of Distances — обзор об измерении расстояний до астрономических объектов (англ.)
Random converter
- Калькуляторы
- Астрономия
Калькулятор расстояния и годичного параллакса
Калькулятор определяет расстояние до недалекой звезды в световых годах и парсеках, если известен годичный параллакс этой звезды в угловых секундах. Можно также определить параллакс, если известно расстояние.
Пример: рассчитать расстояние в световых годах до самой яркой звезды звездного неба северного полушария Арктура (α Волопаса) в созвездии Волопаса, если известно что ее параллакс равен 88.83 угловым миллисекундам.
Параллакс
p
Расстояние
D
Поделиться ссылкой на этот калькулятор, включая входные параметры
Определение параллакса и формула для расчета расстояния
Параллакс — это изменение видимого кажущегося положения объекта, наблюдаемого с разных точек и измеренное как угол (или половинный угол) между направлениями от наблюдателя на объект. Годичный звездный параллакс — это изменение положения звезды, наблюдаемой с двух находящихся на большом расстоянии друг от друга точек. Эти две точки наблюдения расположены на земной орбите, как показано ниже. Параллакс небесного тела можно использовать для нахождения расстояния до него по формуле:
Здесь D — расстояние до небесного тела, измеренное в парсеках, и p — наблюдаемый годичный параллакс, измеренный в дуговых секундах. Эта формула и используется для расчетов в нашем калькуляторе. Парсек определяется как расстояние до объекта, годичный звездный параллакс которого равен 1 дуговой секунде. Иными словами, парсек — это расстояние, с которого диск размером в 1 а.е. будет иметь угловой размер в 1 угловую секунду.
Годичный параллакс звезды (чертеж не в масштабе); 1 — астрономическая единица (а.е.), то есть расстояние от Земли до Солнца; D — расстояние от центра земной орбиты до звезды S; p — параллакс, измеренный в угловых секундах (“)
Подробнее о длине и расстоянии: измерение расстояний в космосе
Общие сведения
Космос огромен — поэтому космические расстояния измеряются не так, как это делается на Земле. В статье о длине и расстояниях мы говорили главным образом об измерении относительно небольших расстояний, которые не трудно себе представить. Однако расстояния в космосе представить себе очень трудно из-за их огромной величины, а привычные метры и километры едва ли годятся для использования в космосе. Для измерения расстояний между планетами и галактиками вряд ли можно использовать измерительные приборы типа рулетки или линейки. Спутниковая навигация в космосе тоже не работает. Поэтому для космоса придется ввести не только новые единицы измерения, но и новые методы измерения этих расстояний.
Измерения с помощью радиолокации
Расположенная на Земле радиолокационная станция (РЛС) посылает СВЧ-излучение в сторону астрономического объекта, расстояние до которого нужно вычислить. Затем измеряется время, которое необходимо, чтобы сигнал достиг объекта и вернулся назад, к РЛС. Зная это время и скорость света в вакууме, можно определить расстояние, умножая скорость на время.
Использовать РЛС для этих измерений удобно не только для определения расстояния до нужного астрономического объекта, но и для оценки скорости изменения этого расстояния (ведь объекты во Вселенной движутся друг относительно друга!). Это, в свою очередь, полезно при слежении за перемещениями объектов в космосе, например, для оценки возможности столкновения астероида с Землей.
Этот метод ограничен астрономическими объектами, которые находятся на небольших расстояниях от Земли. Можно сказать, что он пригоден для объектов, находящихся в пределах Солнечной системы. Это связано с тем, что радиосигнал ослабляется и рассеивается на больших расстояниях. Кроме того, чем больше расстояние, тем больше должен быть объект для того, чтобы его могла «увидеть» радиолокационная станция.
Годичный звездный параллакс
В статье о длине и расстоянии мы уже обсуждали годичный звездный параллакс. Здесь мы кратко рассмотрим это явление, потому что именно параллакс используется для измерения расстояний в космосе. Параллакс — геометрические явление, используемое для определения расстояний. Он хорошо выражен, если наблюдать объект с разных точек зрения относительно удаленного фона. Познать суть параллакса достаточно легко: вытяните перед собой палец или карандаш и закройте один глаз. Отметьте насколько далеко этот палец от другого объекта (скажем, от дерева, если вы на улице, или от шкафа, если вы находитесь в помещении). Теперь закройте этот глаз и откройте другой. Заметили, что палец или карандаш переместился относительно удаленного объекта? Это перемещение и является параллаксом. Если проделать аналогичный эксперимент, удерживая палец ближе к глазам, можно заметить, что расстояние, на которое перемещается палец или карандаш относительно удаленного объекта, стало больше. Чем ближе палец к глазам, тем больше он сдвигается относительно удаленного объекта при рассматривании пальца обоими глазами. Понятно, что это явление можно использовать для измерения расстояния до объекта, в данном случае — пальца.
На этом рисунке два положения Земли обозначены голубыми кружками, а Солнце — оранжевое. А — реальное положение звезды, расстояние до которой необходимо измерить. А2 и А3 — кажущиеся положения этой звезды с двух точек наблюдения относительно удаленной белой звезды DS. Р — параллактический угол. Измеряемое расстояние между Солнцем и звездой, обозначенное оранжевой линией AS, равно одному парсеку, если угол Р равен одной дуговой секунде.
Более подробное математическое объяснение измерения расстояний с помощью параллакса приводится в статье о длине и расстоянии. В общем случае, можно сказать, что расстояния следует измерять, когда Земля находится в двух противоположных точках ее орбиты вокруг Солнца (с интервалом в шесть месяцев, так как Земля делает один оборот вокруг Солнца за один год). Мы используем известное расстояние от Земли до Солнца (точно измеренное и называемое астрономической единицей) и измерим угол, образованный линией, соединяющей Землю в точке первого измерения, звезду, расстояние до которой измеряется, и точкой, в которой находится Земля во время второго измерения. Фактически, нам нужно знать только половину этого угла, которая называется параллактическим углом и обозначена на рисунке буквой P. Таким образом, имеется достаточно информации, чтобы рассчитать расстояние от Земли до звезды с помощью тригонометрических уравнений.
С помощью описанного метода можно измерить расстояние в различных единицах длины, но астрономы предпочитают парсек. Один парсек — это расстояние от Солнца до рассматриваемой звезды, если параллактический угол равен 1 дуговой секунде. Другой единицей длины является световой год (1 парсек = 3,26 светового года), однако эту единицу чаще используют журналисты. Астрономы предпочитают парсеки.
Четыре звезды имеют один и тот же размер, но расположены на разных расстояниях от нас. Звезда в положении 1 находится ближе всего, а звезда в положении 4 на максимальном удалении от нас. В результате мы видим ближние к нам звезды как более яркие, а удаленные — как менее яркие. Если известная их реальная яркость, можно сравнить ее с их кажущейся яркостью и, таким образом, узнать расстояние до них
Как и при радиолокационных измерениях, этот метод ограничен расстоянием, на которое удалена звезда. Если она слишком далеко (более 500 парсеков), то угол, который нужно измерить, слишком мал и измерить его практически невозможно. Поэтому для больших расстояний данный метод не работает.
Цефеиды
Для измерения расстояний в космосе можно использовать определенные типы звезд, называемых Цефеидами. Цефеида — пульсирующая звезда с точной зависимостью светимости (яркости) от периода пульсации. Чем больше этот период, тем выше яркость Цефеид. Эта корреляция между периодом пульсации я светимостью хорошо известна и все Цефеиды ведут себя одинаково. Поэтому, если известен период пульсации, который несложно наблюдать, можно измерить светимость звезды. Мы знаем, что чем дальше звезда, тем меньше ее яркость. Таким образом, если сравнить реальную яркость с кажущейся, можно определить расстояние до звезды.
Пульсация цефеид обусловлена их сжатием и расширением. При этом их яркость изменяется, и для определения периода нужно измерить время между точками с максимальной яркостью. Ядро звезды не изменяет размеры, однако их внешние газовые слои расширяются и сжимаются вследствие флуктуаций давления газа в этих слоях. Сжатие и расширение происходит за счет двух сил: гравитационного притяжения, которое приводит к сближению молекул газа в направлении центра звезды, и давления газа, которое приводит к расширению внешнего слоя.
Схематическое изображение пульсирующей Цефеиды с периодом в два дня. Пики светимости 1 декабря 2010 г., когда звезда начинает постепенно терять яркость. 2 декабря яркость минимальная. Затем звезда снова достигает максимальной светимости 3 декабря и уменьшает светимость 4 декабря и так далее
Когда звезда находится в сжатом состоянии, ее фотоны имеют высокую энергию и в результате давление повышается, что приводит к расширению внешней оболочки звезды. Когда это давление падает и становится меньше гравитационных сил, сжимающих оболочку, звезда сжимается. Затем процесс повторяется.
Цефеиды можно использовать для измерения расстояний до 40 миллионов парсеков, то есть намного больших, чем позволяет метод параллакса. Недостаток метода — цефеиды не так уж часто встречаются.
Сверхновая типа Ia
Еще одним стандартным измерителем расстояния являются сверхновые типа Ia. Идея аналогичная использованию Цефеид: при известной реальной светимости сверхновой в момент взрыва, когда яркость максимальна, можно сравнить ее с видимой яркостью звезды и, таким образом, определить насколько далеко она от нас. Именно эта категория сверхновых интересует нас в связи с тем, что они наиболее хорошо изучены, а их поведение предсказуемо, поэтому максимальная светимость во время взрыва хорошо известна. Эти взрывы происходит с двумя астрономическими объектами — с белыми карликами и еще одним белым карликом или со звездой-гигантом. Белый карлик представляет собой звезду очень высокой плотности в конце ее жизненного цикла, когда эта звезда «всасывает» материю находящихся рядом звезд (в нашем случае — второй звезды) до тех пор, пока не взорвется. Эти взрывы сверхновых позволяет измерять расстояния до галактик, в которых они находятся.
Другие методы измерения расстояний
Имеется еще несколько методов измерения расстояний в космосе. Один из них основан на предположении, что вселенная расширяется с известной скоростью. Если известна скорость, с которой галактики удаляются от нашей галактики, то с помощью закона Хаббла можно рассчитать насколько далеко они от нас. Закон Хаббла гласит, что расстояние до галактики равно скорости галактики, деленной на постоянную Хаббла, которая является известной константой. Скорость галактики можно определить, изучая спектр галактики, а затем, учитывая эффект Доплера, можно определить расстояние. Эффект Доплера, более известный в астрономии как смещение Доплера — это изменение частоты электромагнитного излучения (в нашем случае — света), излучаемого объектом, который движется относительно наблюдателя. При движении в сторону от наблюдателя этот спектр сдвигается в сторону низких частот, то есть в красную сторону, причем степень сдвига зависит от скорости удаления галактики. По смещению можно рассчитать скорость, а затем вычислить расстояние.
Примеры расчета расстояния до некоторых звезд и их звездного параллакса
Параллакс в дуговых миллисекундах и расстояние в световых годах
Канопус (α Киля)
Ригель Кентаурус (α Центавра A)
Сириус (α Большого Пса)
Вега (α Лиры)
Капелла (α Возничего)
Ригель (β Ориона)
Альтаир (α Орла)
Альдебаран (α Тельца)
Антарес (α Скорпиона)
Арктур (α Волопаса)
Unit Converter articles were edited and illustrated by Анатолий Золотков
Параллакс: глубинное зрение
Время на прочтение
4 мин
Количество просмотров 18K
Как мы определяем глубину — расстояние от нашего местоположения до другого объекта? Для этого существует несколько способов, и один из самых распространённых и простых для понимания включает в себя такое геометрическое явление, как параллакс. Этот чрезвычайно простой принцип используется нашими глазами и мозгом для формирования нашего трёхмерного изображения мира, а астрономы столетиями используют его для определения расстояний (или относительных расстояний) от Земли до астрономических объектов.
Ещё один распространённый способ определять расстояния включает в себя отправку волны (звука, света, чего-то ещё), распространяющейся с известной скоростью, которая отражается от объекта и возвращается к нам; время, затраченное на возврат волны — эхо — сообщает нам расстояние до объекта. По этому принципу летучие мыши определяют расстояние до пищи и препятствий, а также работает радар.
Рис. 1
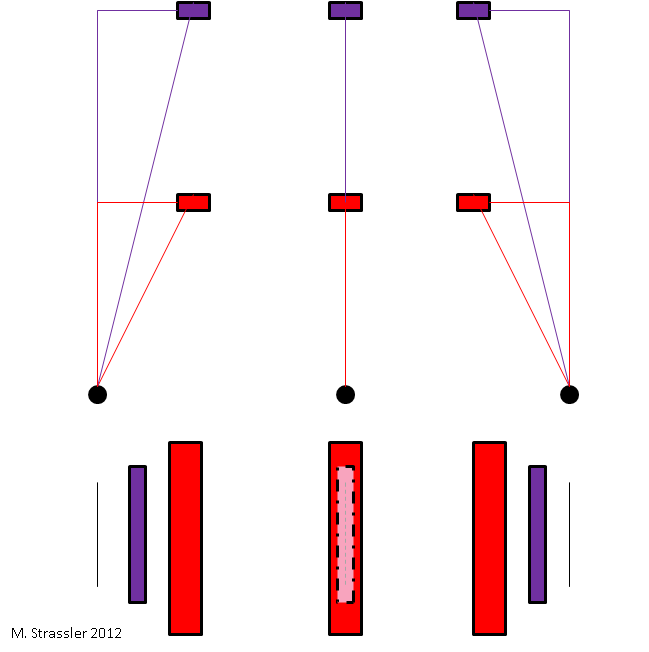
Мы воспринимаем параллакс, даже не думая о нём, каждый раз, когда двигаем головой. Представьте, что произойдёт, Если ваш друг спрячется от вас, встав в нескольких метрах за крупным деревом (рис. 1, в центре). Если вы достаточно далеко отодвинетесь влево или вправо, вашего друга станет видно (рис. 1, слева и справа). Мы знаем, что всё дело просто в перспективе; при определённом угле зрения дерево уже не будет загораживать вам вашего таинственного друга. Геометрически происходящее изображено на рис. 1. Когда вы двигаетесь влево и вправо, смотря вперёд, близлежащие объекты меняют свой угол по отношению к тому, что находится прямо перед вами, быстрее, чем объекты, расположенные дальше. Из скорости изменения угла при вашем движении — из параллакса движения — вы можете понять, насколько далеко расположен объект.
Каждый ребёнок это знает, поскольку, когда вы выглядываете из окна движущейся машины, фонарные столбы проносятся мимо очень быстро, удалённые здания проходят медленнее, а Луна, находящаяся настолько далеко, что угол зрения по отношению к наблюдателю не меняется на ощутимую величину, пока машина едет по шоссе, как будто бы двигается вместе с машиной. Именно небольшой параллакс, являющийся следствием огромного расстояния, заставляет луну «следовать за машиной».
Все, кто смотрел старые двумерные мультфильмы (и многие современные), такие, как Флинстоуны, знают, что этот факт используется, чтобы изобразить глубину. Когда персонажи путешествуют в автомобиле, двигаясь слева направо, автомобиль рисуют неподвижным, деревья рисуют в другом слое, который с высокой скоростью передвигается справа налево, а холмы в удалении рисуют на третьем слое, который двигается справа налево чуть медленнее (см. рис. 2).
Рис. 2
Наша способность воспринимать глубину, даже не двигая головой, основана на том же принципе. Левый и правый глаз видят мир с немного разных углов. Попробуйте разместить пару объектов — неважно, каких, пусть даже это будут большие пальцы рук — так, чтобы один из них был в два раза дальше другого, и находился прямо за ним. Закройте левый глаз и посмотрите на них правым; затем поменяйте глаза; потом снова поменяйте, и сделайте так несколько раз — и вы увидите, что объекты двигаются, как на рис. 1, только ваш левый глаз увидит ближайший объект справа от того, что дальше, а правый глаз увидит его чуть левее.
Так почему вы воспринимаете эти объекты при помощи обоих глаз так, будто они находятся один за другим? У вашей оптической системы есть очень хитрый обработчик информации — своего рода компьютер. Для вас он создаёт не такую картину мира, какую непосредственно видят ваши глаза, а выстроенную на её основе при помощи сложных преобразований картину. Воспринимать глубину вам позволяет информация, полученная от двух глаз и скомбинированная вместе (это в основном — хотя параллакс движения тоже вносит свою лепту). Ни один из ваших глаз не может определить глубину, если вы стоите неподвижно. Попробуйте закрыть глаза, повернуться в другую сторону и открыть один глаз. Можете ли вы точно описать расстояние до предметов? Мир выглядит более плоским, более двумерным, чем обычно. С обоими открытыми глазами у вас нет таких проблем. Это использование двух изображений для использования трёхмерной карты мира называется стереоэффектом.
Но даже с одним открытым глазом вы можете довольно быстро оценить глубину, если подвигаете головой. Ваш мозг способен использовать параллакс движения — более быстрое изменение угла зрения на близлежащие объекты по отношению к отдалённым при движении влево или вправо — чтобы помочь восстановить часть информации о глубине, которая обычно получается сравнением вида из двух разных глаз (рис. 2).
Рис. 3
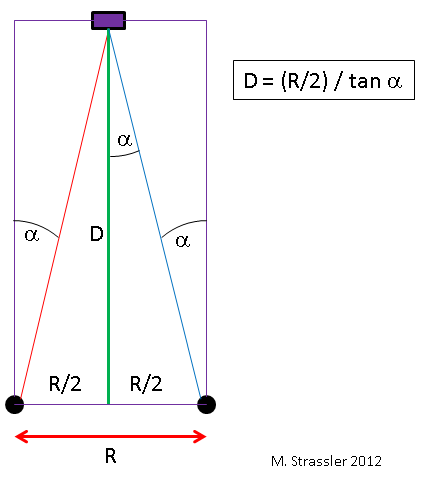
Какие основные подсчёты использует наша оптическая система? Простейший случай показан на рис. 3. Допустим, объект находится прямо перед вами. Если ваши глаза находятся на расстоянии R друг от друга, а ваш левый глаз видит объект под углом α правее по отношению ко взгляду прямо вперёд, а правый глаз видит объект под углом α левее, тогда согласно простейшей геометрии прямоугольных треугольников, расстояние D до объекта будет равняться
Из формулы видно, что когда D меньше, угол, на который линия взгляда на объект отстоит от прямого взгляда, становится больше. Именно этого мы и ожидаем от параллакса.
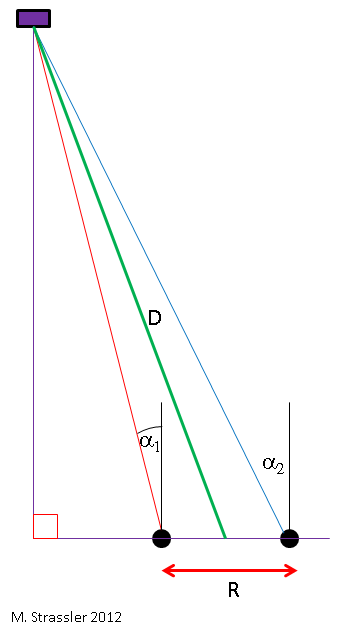
В более общем случае, показанном на рис. 4, когда объект находится не прямо перед вами, получается чуть более сложным, как и тригонометрические формулы, но в нём работает тот же самый основной принцип и в итоге его не так уж сложно подсчитать. Ваш мозг проделывает такие подсчёты так быстро (используя технику, которую мы пока ещё не раскрыли), что вы об этом и не подозреваете.
Для достаточно удалённых объектов угол α оказывается слишком малым для того, чтобы его восприняли ваши глаза и мозг. В этот момент ваше чувство глубины пропадает. Поэтому Луна не кажется расположенной ближе, чем звёзды; они находятся слишком далеко, чтобы ощутить глубину. Также вашего ощущения глубины обычно не хватает, чтобы понять, пройдёт ли самолёт перед или за горой вдалеке. Но это просто ограничение ваших глаз.
Рис. 4
Как определить расстояние до более удалённых объектов? Есть два варианта; разработать научный инструмент, способный измерять углы точнее, чем ваш глаз; увеличить R, чтобы сравнивать не вид из глаз, а, например, вид из двух камер, стоящих в нескольких метрах друг от друга, или даже в разных местах континента. А когда астрономы хотят измерить самые большие расстояния, какие только можно измерить при помощи параллакса, они сравнивают изображения удалённой звезды, сделанные с разницей в шесть месяцев, чтобы получить максимальное расстояние R на основании того, что Земля в течение года проходит довольно большое расстояние. Детали этих техник отличаются, но основной принцип тот же, что показа на рис. 3 и рис. 4 — принцип параллакса.
Как-то игрался с одним астрономическим приложением в смартфоне и рассказывал супруге про ближайшие к нам звезды.
И вышел у нас вот такой диалог:
— А как определяют все эти расстояния до звёзд?
— С помощью параллакса.
— Чего?
— Параллакса.
Ну что же, объясняю на пальцах: вытяните вперёд руку с поднятым большим пальцем, посмотрите на него по очереди сначала одним глазом, затем другим. Видно, что палец смещается относительно фоновых объектов. Это видимое смещение и называется параллаксом. Теперь, определив величину параллакса (смещения), и зная расстояние между глаз (расстояние между точками наблюдения называется базисом), можно определить расстояние до пальца (длину руки). Здорово, правда?
Первая ступенька
Но чтобы заметить смещения звезд, недостаточно смотреть на них поочередно правым и левым глазом. Расстояния до звезд так огромны, что для измерения параллакса приходится применить самый большой доступный базис — диаметр орбиты Земли.
Наблюдая звезду сначала из точки 1, а через полгода из точки 2, можно заметить параллакс относительно очень далеких тусклых звёзд.
Придумали даже специальную единицу измерения расстояний — парсек. Если параллакс объекта за год составит ровно одну угловую секунду, значит до объекта ровно один парсек (параллактическая секунда). Равен 3,26 световых года.
Но на небе не нашлось ни одной звезды, которая сместилась хотя бы на одну угловую секунду. Все параллаксы измеряются долями секунды. Именно поэтому долгое время астрономы не могли определить расстояния даже до ближайших звезд: техника не позволяла зафиксировать такие малые отклонения.
Но и на данный момент у этого метода есть ограничения из-за техники: примерно 1 килопарсек. У объектов, которые находятся дальше, не определить параллакс. Но откуда тогда известны расстояния до галактик? Это же мегапарсеки!
Вторая ступенька
Возьмём две одинаковые свечи. И зажжём одну рядом с нами, а другую — на неопределенном расстоянии от нас. Мы знаем, что свечи обладают одинаковой светимостью. Но видимая яркость у второй свечи из-за расстояния будет меньше. Определив, на какую величину снизилась яркость, мы можем точно определить расстояние до удалённой свечи.
Итак, к чему тут свечи? У астрономов просто тоже есть свои стандартные свечи. Это объекты, светимость которых известна независимо от их удаленности. Например, цефеиды — звезды переменной яркости. Светимость этих звезд зависит от периода изменения яркости. Узнав период, всегда можно определить светимость. А узнав расстояния до ближайших цефеид методом параллакса и сравнив яркость с удаленными цефеидами, можно найти и это удаленное расстояние.
Именно с помощью цефеид было впервые измерено расстояние до галактики Андромеды, которое составляет 2,5 млн световых лет.
Метод стандартных свечей — вторая ступенька космической измерительной лестницы, на которую мы поднимаемся благодаря первой — тригонометрическому методу параллакса.
Помимо цефеид в качестве объектов с известной светимостью используют красные гиганты, сверхновые.
Но со второй ступени всё же нельзя дотянуться до всех галактик: из-за сильного удаления можно просто не различить отдельные объекты в галактике. Поднимаемся дальше.
Третья ступенька
Метод основанный на зависимости Талли—Фишера. Суть зависимости в том, что чем быстрее галактика вращается, тем больше её общая светимость. Если галактика видна с Земли с ребра, или почти с ребра, можно определить скорость её вращения по доплеровскому смещению линий спектра. Определив скорость вращения, узнаём светимость. А по светимости находим расстояние.
Для проверки метода используют галактики с уже определенными по цефеидам расстояниями.
Но и тут есть предел: качество получаемого спектра с расстоянием уменьшается, скорость вращения галактики определяется не точно.
Четвертая ступенька
В основе метода лежит закон Хаббла, в котором говорится о зависимости скорости галактики от расстояния до неё. Скорость галактики можно определить по смещению линий спектра галактики из-за эффекта Доплера. И для того чтобы получить расстояние, необходимо разделить полученную скорость на некоторый коэффициент — постоянную Хаббла. А вот эту постоянную определяют исходя из известных расстояний до галактик, полученных одним из предыдущих методов.
Вот такая лестница, высотой в обозримую вселенную. Помимо описанных методов существуют в ступенях и другие. Но если описывать их все, статья получится просто огромной. Но для общего представления об измерении космических расстояний, я думаю, этого вполне достаточно.
Другие методы можно обсудить в комментариях.
Если статья интересна и полезна, ставьте лайк! И подписывайтесь, чтобы чаще видеть астрономию в ленте!
Определение расстояний по параллаксам космических объектов
В этой статье мы рассмотрим задачи, связанные с расчетом расстояний до небесных тел. При этом будем пользоваться понятием параллакс. О том, что такое параллактический угол, рассказывает иллюстрация. По тому, на сколько меняется видимое положение звезды на небесной сфере в связи с движением Земли по орбите, можно судить о расстоянии до нее. Если объект достаточно близко (по космическим меркам), то параллактический угол велик, если далеко – то совсем мал. Параллактический угол измеряют, как правило, в минутах или секундах.
Параллакс
Расстояния от Земли до тел Солнечной системы вычисляются по их горизонтальным экваториальным параллаксам
и экваториальному радиусу Земли
:
или
если параллакс выражен в минутах дуги () и
при параллаксе, выраженном в секундах дуги ()·
Если положить , то
получается в экваториальных радиусах Земли. При вычислении
в километрах следует принять
км.
Если угловые размеры небесного тела , то его линейные размеры
а при , вследствие пропорциональности
и
,
— в минутах дуги,
— в секундах дуги.
и
где и
— в одноименных единицах измерения.
Радиусы Солнца и планет обычно выражаются в радиусах Земли (реже — в километрах), причем полярный радиус , экваториальный радиус
и сжатие планеты
связаны зависимостью
а средний радиус
При совпадении направлений вращения и обращения небесного тела вокруг Солнца продолжительность его солнечных суток , период вращения
и период обращения
связаны зависимостью
а при противоположных направлениях одному из периодов приписывается знак минус.
Задача 1.
Вычислить средний радиус и сжатие Земли, если ее экваториальный радиус равен 6378 км, а полярный радиус— 6357 км.
Средний радиус найдем как:
Сжатие Земли:
Ответ: км,
.
Задача 2.
Радиоимпульс, направленный к Венере в ее нижнем соединении на среднем расстоянии от Солнца 0,7233 а. е., возвратился к Земле через 4м36с. Вычислить геоцентрическое расстояние планеты во время радиолокации, длину астрономической единицы в километрах и средний горизонтальный экваториальный параллакс Солнца.
Вспоминаем, что нижнее соединение – это такое расположение Венеры, когда она между Землей и Солнцем. Так как сигнал возвратился через 4 минуты 36 с, следовательно, в одну сторону он шел 2 минуты 18 секунд, или 138 секунд. Сигнал идет со скоростью света. Давайте найдем расстояние до планеты:
В километрах это км.
Так как расстояние от Земли до Солнца равно 1 астрономической единице, то
Где – расстояние от Венеры до Солнца.
Тогда:
Мы получили длину астрономической единицы сразу в миллионах км.
Вычислим горизонтальный экваториальный параллакс Солнца в секундах дуги:
Откуда
Ответ: км,
млн. км,
.
Задача 3.
При среднем противостоянии Марса посланный к нему радиосигнал возвратился к Земле через 522,6 с. Найти среднее гелиоцентрическое расстояние Земли и соответствующий ему горизонтальный экваториальный параллакс Солнца. Сидерический период обращения Марса равен 1,881 года.
Аналогично предыдущей задаче, противостояние – это положение Марса такое, что Земля расположена между Солнцем и Марсом. Средним его назвали потому, что при противостоянии Марс может находиться ближе или дальше от Земли, здесь взято среднее расстояние.
Так как сигнал возвратился через 522,6 с, следовательно, в одну сторону он шел 261,3 секунды. Сигнал идет со скоростью света. Давайте найдем расстояние до планеты:
В километрах это км.
Дальше для решения нам потребуется третий закон Кеплера
Где – расстояние от Солнца до Марса,
– расстояние от Солнца до Земли.
Тогда
Расстояние найдено в км.
Определяем параллакс Солнца:
Ответ: км,
.
Задача 4.
Чему равен горизонтальный экваториальный параллакс Луны при ее среднем (384 400 км), ближайшем (356 410 км) и наибольшем (406 740 км) геоцентрическом расстоянии? Экваториальный радиус Земли — 6378 км.
Ответ: ,
,
.
Задача 5.
По данным или результатам задачи 4 вычислить предельные значения диаметра лунного диска, который при среднем геоцентрическом расстоянии равен 31’05”.
Если угловые размеры небесного тела , вследствие пропорциональности
и
, его линейные размеры
— в минутах дуги.
Переведем размер лунного диска в минуты: .
Тогда линейный размер
Теперь используем это при расчете минимального и максимального размеров лунного диска:
Ответ: ,
.
Задача 6.
Пределы геоцентрического расстояния Луны, измеренного радиолокационным методом в 1975 г., были: 16 января —406 090 км; 28 января —357 640 км и 12 февраля— 406 640 км. Найти значения большой полуоси и эксцентриситета лунной орбиты в интервалах времени, заключенных между смежными датами.
Средним расстоянием планеты от Солнца является большая полуось ее орбиты
Где и
– перигельное и афелийное расстояния. То же и для Луны, только вместо перигельного будет перигейное расстояние, вместо афелийного – апогейное.
Тогда
Тогда
И эксцентриситет
Для второго периода времени
И эксцентриситет
Ответ: для периода времени от 16 января до 28 – км, эксцентриситет – 0,0634, для периода 28 января – 12 февраля
км, эксцентриситет – 0,0641.
Задача 7.
Радиосигнал, направленный к Меркурию при его наибольшем сближении с Землей, вернулся на Землю через 8м52с. Определить геоцентрическое расстояние планеты и эксцентриситет ее орбиты, если большая полуось орбиты равна 0,387 а. е.
Так как сигнал возвратился через 532 с, следовательно, в одну сторону он шел 266 секунд. Сигнал идет со скоростью света. Давайте найдем расстояние до планеты:
В километрах это км, а в астрономических единицах – 0,533 а.е.
Так как расстояние от Солнца до Земли равно 1 а.е., то расстояние от Солнца до Меркурия равно
Это больше, чем большая полуось орбиты, поэтому это – афелийное расстояние. Тогда
И эксцентриситет
Ответ: км,
.