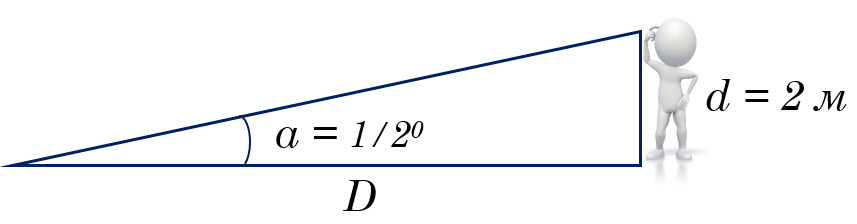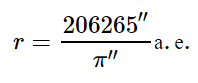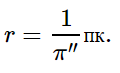Random converter
- Калькуляторы
- Астрономия
Калькулятор расстояния и годичного параллакса
Калькулятор определяет расстояние до недалекой звезды в световых годах и парсеках, если известен годичный параллакс этой звезды в угловых секундах. Можно также определить параллакс, если известно расстояние.
Пример: рассчитать расстояние в световых годах до самой яркой звезды звездного неба северного полушария Арктура (α Волопаса) в созвездии Волопаса, если известно что ее параллакс равен 88.83 угловым миллисекундам.
Параллакс
p
Расстояние
D
Поделиться ссылкой на этот калькулятор, включая входные параметры
Определение параллакса и формула для расчета расстояния
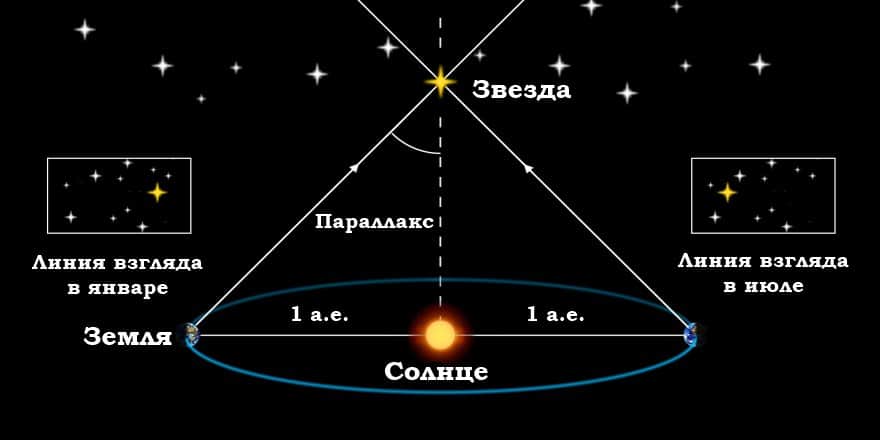
Параллакс — это изменение видимого кажущегося положения объекта, наблюдаемого с разных точек и измеренное как угол (или половинный угол) между направлениями от наблюдателя на объект. Годичный звездный параллакс — это изменение положения звезды, наблюдаемой с двух находящихся на большом расстоянии друг от друга точек. Эти две точки наблюдения расположены на земной орбите, как показано ниже. Параллакс небесного тела можно использовать для нахождения расстояния до него по формуле:
Здесь D — расстояние до небесного тела, измеренное в парсеках, и p — наблюдаемый годичный параллакс, измеренный в дуговых секундах. Эта формула и используется для расчетов в нашем калькуляторе. Парсек определяется как расстояние до объекта, годичный звездный параллакс которого равен 1 дуговой секунде. Иными словами, парсек — это расстояние, с которого диск размером в 1 а.е. будет иметь угловой размер в 1 угловую секунду.
Годичный параллакс звезды (чертеж не в масштабе); 1 — астрономическая единица (а.е.), то есть расстояние от Земли до Солнца; D — расстояние от центра земной орбиты до звезды S; p — параллакс, измеренный в угловых секундах (“)
Подробнее о длине и расстоянии: измерение расстояний в космосе
Общие сведения
Космос огромен — поэтому космические расстояния измеряются не так, как это делается на Земле. В статье о длине и расстояниях мы говорили главным образом об измерении относительно небольших расстояний, которые не трудно себе представить. Однако расстояния в космосе представить себе очень трудно из-за их огромной величины, а привычные метры и километры едва ли годятся для использования в космосе. Для измерения расстояний между планетами и галактиками вряд ли можно использовать измерительные приборы типа рулетки или линейки. Спутниковая навигация в космосе тоже не работает. Поэтому для космоса придется ввести не только новые единицы измерения, но и новые методы измерения этих расстояний.
Измерения с помощью радиолокации
Расположенная на Земле радиолокационная станция (РЛС) посылает СВЧ-излучение в сторону астрономического объекта, расстояние до которого нужно вычислить. Затем измеряется время, которое необходимо, чтобы сигнал достиг объекта и вернулся назад, к РЛС. Зная это время и скорость света в вакууме, можно определить расстояние, умножая скорость на время.
Использовать РЛС для этих измерений удобно не только для определения расстояния до нужного астрономического объекта, но и для оценки скорости изменения этого расстояния (ведь объекты во Вселенной движутся друг относительно друга!). Это, в свою очередь, полезно при слежении за перемещениями объектов в космосе, например, для оценки возможности столкновения астероида с Землей.
Этот метод ограничен астрономическими объектами, которые находятся на небольших расстояниях от Земли. Можно сказать, что он пригоден для объектов, находящихся в пределах Солнечной системы. Это связано с тем, что радиосигнал ослабляется и рассеивается на больших расстояниях. Кроме того, чем больше расстояние, тем больше должен быть объект для того, чтобы его могла «увидеть» радиолокационная станция.
Годичный звездный параллакс
В статье о длине и расстоянии мы уже обсуждали годичный звездный параллакс. Здесь мы кратко рассмотрим это явление, потому что именно параллакс используется для измерения расстояний в космосе. Параллакс — геометрические явление, используемое для определения расстояний. Он хорошо выражен, если наблюдать объект с разных точек зрения относительно удаленного фона. Познать суть параллакса достаточно легко: вытяните перед собой палец или карандаш и закройте один глаз. Отметьте насколько далеко этот палец от другого объекта (скажем, от дерева, если вы на улице, или от шкафа, если вы находитесь в помещении). Теперь закройте этот глаз и откройте другой. Заметили, что палец или карандаш переместился относительно удаленного объекта? Это перемещение и является параллаксом. Если проделать аналогичный эксперимент, удерживая палец ближе к глазам, можно заметить, что расстояние, на которое перемещается палец или карандаш относительно удаленного объекта, стало больше. Чем ближе палец к глазам, тем больше он сдвигается относительно удаленного объекта при рассматривании пальца обоими глазами. Понятно, что это явление можно использовать для измерения расстояния до объекта, в данном случае — пальца.
На этом рисунке два положения Земли обозначены голубыми кружками, а Солнце — оранжевое. А — реальное положение звезды, расстояние до которой необходимо измерить. А2 и А3 — кажущиеся положения этой звезды с двух точек наблюдения относительно удаленной белой звезды DS. Р — параллактический угол. Измеряемое расстояние между Солнцем и звездой, обозначенное оранжевой линией AS, равно одному парсеку, если угол Р равен одной дуговой секунде.
Более подробное математическое объяснение измерения расстояний с помощью параллакса приводится в статье о длине и расстоянии. В общем случае, можно сказать, что расстояния следует измерять, когда Земля находится в двух противоположных точках ее орбиты вокруг Солнца (с интервалом в шесть месяцев, так как Земля делает один оборот вокруг Солнца за один год). Мы используем известное расстояние от Земли до Солнца (точно измеренное и называемое астрономической единицей) и измерим угол, образованный линией, соединяющей Землю в точке первого измерения, звезду, расстояние до которой измеряется, и точкой, в которой находится Земля во время второго измерения. Фактически, нам нужно знать только половину этого угла, которая называется параллактическим углом и обозначена на рисунке буквой P. Таким образом, имеется достаточно информации, чтобы рассчитать расстояние от Земли до звезды с помощью тригонометрических уравнений.
С помощью описанного метода можно измерить расстояние в различных единицах длины, но астрономы предпочитают парсек. Один парсек — это расстояние от Солнца до рассматриваемой звезды, если параллактический угол равен 1 дуговой секунде. Другой единицей длины является световой год (1 парсек = 3,26 светового года), однако эту единицу чаще используют журналисты. Астрономы предпочитают парсеки.
Четыре звезды имеют один и тот же размер, но расположены на разных расстояниях от нас. Звезда в положении 1 находится ближе всего, а звезда в положении 4 на максимальном удалении от нас. В результате мы видим ближние к нам звезды как более яркие, а удаленные — как менее яркие. Если известная их реальная яркость, можно сравнить ее с их кажущейся яркостью и, таким образом, узнать расстояние до них
Как и при радиолокационных измерениях, этот метод ограничен расстоянием, на которое удалена звезда. Если она слишком далеко (более 500 парсеков), то угол, который нужно измерить, слишком мал и измерить его практически невозможно. Поэтому для больших расстояний данный метод не работает.
Цефеиды
Для измерения расстояний в космосе можно использовать определенные типы звезд, называемых Цефеидами. Цефеида — пульсирующая звезда с точной зависимостью светимости (яркости) от периода пульсации. Чем больше этот период, тем выше яркость Цефеид. Эта корреляция между периодом пульсации я светимостью хорошо известна и все Цефеиды ведут себя одинаково. Поэтому, если известен период пульсации, который несложно наблюдать, можно измерить светимость звезды. Мы знаем, что чем дальше звезда, тем меньше ее яркость. Таким образом, если сравнить реальную яркость с кажущейся, можно определить расстояние до звезды.
Пульсация цефеид обусловлена их сжатием и расширением. При этом их яркость изменяется, и для определения периода нужно измерить время между точками с максимальной яркостью. Ядро звезды не изменяет размеры, однако их внешние газовые слои расширяются и сжимаются вследствие флуктуаций давления газа в этих слоях. Сжатие и расширение происходит за счет двух сил: гравитационного притяжения, которое приводит к сближению молекул газа в направлении центра звезды, и давления газа, которое приводит к расширению внешнего слоя.
Схематическое изображение пульсирующей Цефеиды с периодом в два дня. Пики светимости 1 декабря 2010 г., когда звезда начинает постепенно терять яркость. 2 декабря яркость минимальная. Затем звезда снова достигает максимальной светимости 3 декабря и уменьшает светимость 4 декабря и так далее
Когда звезда находится в сжатом состоянии, ее фотоны имеют высокую энергию и в результате давление повышается, что приводит к расширению внешней оболочки звезды. Когда это давление падает и становится меньше гравитационных сил, сжимающих оболочку, звезда сжимается. Затем процесс повторяется.
Цефеиды можно использовать для измерения расстояний до 40 миллионов парсеков, то есть намного больших, чем позволяет метод параллакса. Недостаток метода — цефеиды не так уж часто встречаются.
Сверхновая типа Ia
Еще одним стандартным измерителем расстояния являются сверхновые типа Ia. Идея аналогичная использованию Цефеид: при известной реальной светимости сверхновой в момент взрыва, когда яркость максимальна, можно сравнить ее с видимой яркостью звезды и, таким образом, определить насколько далеко она от нас. Именно эта категория сверхновых интересует нас в связи с тем, что они наиболее хорошо изучены, а их поведение предсказуемо, поэтому максимальная светимость во время взрыва хорошо известна. Эти взрывы происходит с двумя астрономическими объектами — с белыми карликами и еще одним белым карликом или со звездой-гигантом. Белый карлик представляет собой звезду очень высокой плотности в конце ее жизненного цикла, когда эта звезда «всасывает» материю находящихся рядом звезд (в нашем случае — второй звезды) до тех пор, пока не взорвется. Эти взрывы сверхновых позволяет измерять расстояния до галактик, в которых они находятся.
Другие методы измерения расстояний
Имеется еще несколько методов измерения расстояний в космосе. Один из них основан на предположении, что вселенная расширяется с известной скоростью. Если известна скорость, с которой галактики удаляются от нашей галактики, то с помощью закона Хаббла можно рассчитать насколько далеко они от нас. Закон Хаббла гласит, что расстояние до галактики равно скорости галактики, деленной на постоянную Хаббла, которая является известной константой. Скорость галактики можно определить, изучая спектр галактики, а затем, учитывая эффект Доплера, можно определить расстояние. Эффект Доплера, более известный в астрономии как смещение Доплера — это изменение частоты электромагнитного излучения (в нашем случае — света), излучаемого объектом, который движется относительно наблюдателя. При движении в сторону от наблюдателя этот спектр сдвигается в сторону низких частот, то есть в красную сторону, причем степень сдвига зависит от скорости удаления галактики. По смещению можно рассчитать скорость, а затем вычислить расстояние.
Примеры расчета расстояния до некоторых звезд и их звездного параллакса
Параллакс в дуговых миллисекундах и расстояние в световых годах
Канопус (α Киля)
Ригель Кентаурус (α Центавра A)
Сириус (α Большого Пса)
Вега (α Лиры)
Капелла (α Возничего)
Ригель (β Ориона)
Альтаир (α Орла)
Альдебаран (α Тельца)
Антарес (α Скорпиона)
Арктур (α Волопаса)
Unit Converter articles were edited and illustrated by Анатолий Золотков
Меня часто спрашивают – как мы узнаем расстояния до далеких звезд? Вот например есть звезда на расстоянии 100 световых лет, как мы узнали, что расстояние именно такое? В этой статье я расскажу об очень старом методе, определения расстояния до звезд. Этот метод называется метод годичного звездного параллакса.
История
Параллакс (от греческого παραλλάξ – чередование) – это изменение местоположения неподвижного наблюдаемого объекта в зависимости от положения наблюдателя. Впервые использовать параллакс для определения дальности до звезд предложил еще древнегреческий ученый Аристарх Самосский, однако он используя доступные ему способы наблюдения не смог обнаружить видимого параллакса ни у одной из наблюдаемых звезд. Отсутствие параллакса он вполне справедливо объяснил тем, что звезды находятся очень далеко для того, чтобы их параллакс можно было обнаружить.
Сама идея о том, что параллакс можно использовать для этой цели явилась следствием идеи о том, что Земля вращается вокруг Солнца. К сожалению вскоре Европа погрузилась в темные века и почти две тысячи лет господствовала геоцентрическая система мира. Отсутствие параллакса считалось одним из доказательств того, что Земля НЕ вращается вокруг Солнца.
В 17-м веке некоторые астрономы заявляли о том, что им удалось засечь параллакс некоторых звезд, однако скорее всего это объясняется ошибками и неточностями измерений. Техника, которая была в их распоряжении была слишком неточна для того, чтобы с ее помощью можно было определить параллакс.
Первым точно определить параллакс звезд удалось русскому астроному Василию Яковлевичу Струве в 1837-м году. Вскоре его успех повторили немецкий астроном Фридрих Бессель и англичанин Томас Хендерсон. Однако на тот момент измерения были все еще очень не точны – разница в измерении параллакса одной и той же звезды могли отличаться на 20-30 процентов! С появлением фотографии наметился большой прогресс – до появления фотографии астрономы зарисовывали то, что видели в телескоп, это вело к ошибкам и неточностям. Сейчас для таких измерений используется метод сверхдальней радиоинтерферометрии что обеспечивает очень точные измерения.
Использование параллакса для определения расстояния до звезд
Зная расстояние между точками наблюдения и угол параллакса довольно легко определить расстояние до объекта.
С помощью геометрии школьного уровня это расстояние вычисляется как расстояние между точками наблюдения (L) деленное на удвоенный синус половины угла параллакса (α).
В качестве точек измерения параллакса обычно избираются противоположные точки орбиты Земли.
Как мы видим, позиции Земли по разные стороны от Солнца и исследуемая звезда образуют различные треугольники. Медиана этого треугольника (т.е. линия соединяющая исследуемую звезду и Солнце) и есть искомым расстоянием.
В общем случае вычисление расстояния r до звезды сводится к решению прямоугольного треугольника в котором расстояние от земли до солнца является катетом, а расстояние от Солнца до звезды либо вторым катетом (в случае если звезда расположена вблизи полюса эклиптики – рисунок справа) или гипотенузой (в случае если звезда близка к плоскости эклиптики – рисунок слева)
Благодаря методу параллакса появилась такая внесистемная единица измерения астрономических расстояний как парсек (сокращенно – паралкс-секунда). Парсек – это расстояние до звезды параллакс которой равен 1 угловой секунде, парсек примерно равен 3.26 световых лет.
P.S. Вообще существуют и другие методы измерения расстояний до звезд и галактик в частности с использованием спектрального анализа (так называемый спектральный параллакс), с использованием последовательностей Талли-Фишера и Фабер-Джексона и другие, но в этой статье я специально остановился на самом базовом и простом для понимания методе.
Подписывайтесь на мой канал здесь, а также на мой канал в телеграме. Там вы можете почитать большое количество интересных материалов, а также задать свой вопрос.
Наше Солнце справедливо называют типичной звездой, но среди огромного многообразия мира звёзд есть немало таких, которые значительно отличаются от него по физическим характеристикам. Поэтому более полное представление о звёздах даёт такое определение:
звезда — это пространственно обособленный, гравитационно связанный, непрозрачный для излучения космический объект, в котором в значительных масштабах происходили, происходят или будут происходить термоядерные реакции превращения водорода в гелий.
Солнце существует уже несколько миллиардов лет и мало изменилось за это время, поскольку в его недрах всё ещё происходят термоядерные реакции, в результате которых из четырёх протонов (ядер водорода) образуется альфа-частица (ядро гелия, состоящее из двух протонов и двух нейтронов). Более массивные звёзды расходуют запасы водорода значительно быстрее (за десятки миллионов лет). После того как водород израсходован, начинаются реакции между ядрами гелия с образованием устойчивого изотопа углерода-12 и другие реакции, продуктами которых являются кислород и тяжёлые элементы (натрий, сера, магний и т. д.). Таким образом, в недрах звёзд образуются ядра многих химических элементов, вплоть до железа.
У наиболее массивных звёзд прекращение всех возможных термоядерных реакций сопровождается мощным взрывом, который наблюдается как вспышка сверхновой звезды.
Все элементы, которые входят в состав нашей планеты и всего живого на ней, образовались в результате термоядерных реакций, происходивших в звёздах, поэтому звёзды не только самые распространённые во Вселенной объекты, но и самые важные для понимания происходящих в ней явлений и процессов.
Именно термоядерные реакции являются характерной отличительной особенностью звёзд от планет. Поэтому современное определение планеты формулируется так:
планета — небесное тело, обращающееся вокруг звезды или остатка звезды, достаточно массивное, чтобы приобрести сферическую форму под действием собственной гравитации, и своим воздействием удалившее малые тела с орбиты, близкой к собственной, но при этом в её недрах не происходят и никогда не происходили реакции термоядерного синтеза.
Мысли о том, что звёзды — это далёкие солнца, высказывались ещё в глубокой древности. Однако долгое время оставалось неясным, как далеко они находятся от Земли. Ещё Аристотель понимал, что если Земля движется, то, наблюдая положение какой-либо звезды из двух диаметрально противоположных точек земной орбиты, можно заметить, что направление на звезду изменится (рис. 5.12). Это кажущееся (параллактическое) смещение звезды будет служить мерой расстояния до неё: чем оно больше, тем ближе к нам расположена звезда. Но не только самому Аристотелю, но даже значительно позднее Копернику не удалось обнаружить это смещение. Только в конце первой половины XIX в., когда телескопы были оборудованы приспособлениями для точных угловых измерений, удалось измерить такое смещение у ближайших звёзд.
Рис. 5.12. Параллактическое смещение звезды
Рис. 5.13. Годичный параллакс звезды
Годичным параллаксом звезды p называется угол, под которым со звезды можно было бы видеть большую полуось земной орбиты (равную 1 а. е.), перпендикулярную направлению на звезду (рис. 5.13).
Расстояние до звезды
D = 
где a — большая полуось земной орбиты. Заменив синус малого угла величиной самого угла, выраженной в радианной мере, и приняв a = 1 а. е., получим следующую формулу для вычисления расстояния до звезды в астрономических единицах:
D = 
В 1837 г. впервые были осуществлены надёжные измерения годичного параллакса. Русский астроном Василий Яковлевич Струве (1793—1864) провёл эти измерения для ярчайшей звезды Северного полушария Веги (α Лиры). Почти одновременно в других странах определили параллаксы ещё двух звёзд, одной из которых была α Центавра. Эта звезда, которая с территории России не видна, оказалась ближайшей к нам. Даже у неё годичный параллакс составил всего 0,75ʺ. Под таким углом невооружённому глазу видна проволочка толщиной 1 мм с расстояния 280 м. Поэтому неудивительно, что столь малые угловые смещения так долго не могли заметить.
Расстояние до ближайшей звезды, параллакс которой p = 0,75ʺ, составляет D = 
Парсек — это такое расстояние, на котором параллакс звёзд равен 1ʺ. Отсюда и название этой единицы: пар — от слова «параллакс», сек — от слова «секунда». Расстояние в парсеках равно обратной величине годичного параллакса. Например, поскольку параллакс α Центавра равен 0,75ʺ, расстояние до неё равно 1,3 парсека.
Световой год — это такое расстояние, которое свет, распространяясь со скоростью 300 тыс. км/с, проходит за год. От ближайшей звезды свет идёт до Земли свыше четырёх лет, тогда как от Солнца около восьми минут, а от Луны немногим более одной секунды.
1 пк (парсек) = 3,26 светового года = 206 265 а. е. = 3•1013 км.
К настоящему времени с помощью специального спутника «Гиппаркос» измерены годичные параллаксы более 118 тыс. звёзд с точностью 0,001ʺ.
Таким образом, теперь измерением годичного параллакса можно надёжно определить расстояния до звёзд, удалённых от нас на 1000 пк, или 3000 св. лет. Расстояния до более далёких звёзд определяются другими методами.
После того как астрономы получили возможность определять расстояния до звёзд, выяснилось, что звёзды, находящиеся на одинаковом расстоянии, могут отличаться по видимой яркости (т. е. по блеску). Стало очевидно, что звёзды имеют различную светимость. Солнце кажется самым ярким объектом на небе только потому, что оно находится гораздо ближе всех остальных звёзд.
Светимостью называется полная энергия, излучаемая звездой в единицу времени.
Она выражается в абсолютных единицах (ваттах) или в единицах светимости Солнца.
В астрономии принято сравнивать звёзды по светимости, рассчитывая их блеск (звёздную величину) для одного и того же стандартного расстояния — 10 пк.
Видимая звёздная величина, которую имела бы звезда, если бы находилась от нас на расстоянии D0 = 10 пк, получила название абсолютной звёздной величины M.
Рассмотрим, как можно определить абсолютную звёздную величину M, зная расстояние до звезды D (или параллакс — p) и её видимую звёздную величину m. Напомним, что блеск двух источников, звёздные величины которых отличаются на единицу, отличается в 2,512 раза. Для звёзд, звёздные величины которых равны m1 и m2 соответственно, отношение их блесков I1 и I2 выражается соотношением:
I1 : I2 = 
Для видимой и абсолютной звёздных величин одной и той же звезды отношение блесков будет выглядеть так:
I : I0 = 2,512M – m,
где I0 — блеск этой звезды, если бы она находилась на расстоянии D0 = 10 пк.
В то же время известно, что блеск звезды меняется обратно пропорционально квадрату расстояния до неё. Поэтому
I : I0 = 
Следовательно,
2,512M – m = 
Логарифмируя это выражение, находим
0,4(M – m) = lg 102 – lg D2,
или
M = m + 5 – 5 lg D,
или
M = m + 5 + lg p.
Абсолютная звёздная величина Солнца M☉ = 5m. Иначе говоря, с расстояния 10 пк наше Солнце выглядело бы как звезда пятой звёздной величины.
Зная абсолютную звёздную величину звезды M, легко вычислить её светимость L. Считая светимость Солнца L☉ = 1, получаем:
L = 2,5125 – M,
или
lg L = 0,4(5 – M).
По светимости (мощности излучения) звёзды значительно отличаются друг от друга: некоторые излучают энергию в сотни тысяч раз больше, чем Солнце, другие — в десятки тысяч раз меньше. Абсолютные звёздные величины звёзд наиболее высокой светимости (гигантов и сверхгигантов) достигают M = –9m, а звёзды-карлики, обладающие наименьшей светимостью, имеют абсолютную звёздную величину M = +17m.
Всю информацию о звёздах можно получить только на основе исследования приходящего от них излучения. Наблюдая звёзды, можно заметить, что они имеют различный цвет. Хорошо известно, что цвет любого нагретого тела, в частности звезды, зависит от его температуры. Более полное представление об этой зависимости даёт изучение звёздных спектров. Для большинства звёзд это спектры поглощения, в которых на фоне непрерывного спектра наблюдаются тёмные линии.
Температуру наружных слоёв звезды, от которых приходит излучение, определяют по распределению энергии в непрерывном спектре (рис. 5.14), а также по интенсивности разных спектральных линий. Длина волны, на которую приходится максимум излучения, зависит от температуры излучающего тела. По мере увеличения температуры положение максимума смещается от красного к фиолетовому концу спектра. Количественно эта зависимость выражается законом Ви́на:
λmax = 
где λmax — длина волны (в см), на которую приходится максимум излучения, а T — абсолютная температура.
Рис. 5.14. Распределение энергии в непрерывном спектре Солнца и чёрного тела при различных температурах

Как оказалось, эта температура для различных типов звёзд заключена в пределах от 2500 до 50 000 К. Изменение температуры меняет состояние атомов и молекул в атмосферах звёзд, что отражается в их спектрах. По ряду характерных особенностей спектров звёзды разделены на спектральные классы, которые обозначены латинскими буквами и расположены в порядке, соответствующем убыванию температуры: O, B, A, F, G, K, M.
У наиболее холодных (красных) звёзд класса M в спектрах наблюдаются линии поглощения некоторых двухатомных молекул (например, оксидов титана, циркония и углерода). Примерами звёзд, температура которых около 3000 К, являются Антарес и Бетельгейзе.
В спектрах жёлтых звёзд класса G с температурой около 6000 К, к которым относится и Солнце, преобладают линии металлов: железа, натрия, кальция и т. д. По температуре, спектру и цвету сходна с Солнцем звезда Капелла.
Для спектров белых звёзд класса A, которые имеют температуру около 10 000 К (Вега, Денеб и Сириус), наиболее характерны линии водорода и множество слабых линий ионизованных металлов. В спектрах наиболее горячих звёзд появляются линии нейтрального и ионизованного гелия.
Различия звёздных спектров объясняются отнюдь не разнообразием их химического состава, а различием температуры и других физических условий в атмосферах звёзд. Изучение спектров показывает, что преобладают в составе звёздных атмосфер (и звёзд в целом) водород и гелий. На долю всех остальных химических элементов приходится не более нескольких процентов.
Измерение положения спектральных линий позволяет не только получить информацию о химическом составе звёзд, но и определить скорость их движения. Если источник излучения (звезда или любой другой объект) приближается к наблюдателю или удаляется от него со скоростью v, то наблюдатель будет регистрировать изменение длины волны принимаемого излучения. В случае уменьшения расстояния между наблюдателем и звездой длина волны уменьшается и соответствующая линия смещается к сине-фиолетовому концу спектра. При удалении звезды длина волны излучения увеличивается, а линия смещается в красную его часть. Это явление получило название эффекта Доплера, согласно которому зависимость разности длин волн от скорости источника по лучу зрения v и скорости света c выражается следующей формулой:


где λ0 — длина волны спектральной линии для неподвижного источника, а λ — длина волны в спектре движущегося источника.
Эффект Доплера наблюдается в оптической и других областях спектра и широко используется в астрономии.
Полученные данные о светимости и спектрах звёзд уже в начале XX в. были сопоставлены двумя астрономами — Эйнаром Герцшпрунгом (Голландия) и Генри Расселлом (США) — и представлены в виде диаграммы, которая получила название «диаграмма Герцшпрунга—Расселла». Если по горизонтальной оси отложены спектральные классы (температура) звёзд, а по вертикальной — их светимости (абсолютные звёздные величины), то каждой звезде будет соответствовать определённая точка на этой диаграмме (рис. 5.15). В результате обнаруживается определённая закономерность в расположении звёзд на диаграмме — они не заполняют всё её поле, а образуют несколько групп, названных последовательностями. Наиболее многочисленной (примерно 90% всех звёзд) оказалась главная последовательность, к числу звёзд которой принадлежит наше Солнце (его положение отмечено на диаграмме кружочком). Звёзды этой последовательности отличаются друг от друга по светимости и температуре, и взаимосвязь этих характеристик соблюдается весьма строго: самую высокую светимость имеют наиболее горячие звёзды, а по мере уменьшения температуры светимость падает. Красные звёзды малой светимости получили название красных карликов. Вместе с тем на диаграмме существуют и другие последовательности, где подобная закономерность не соблюдается. Особенно заметно это среди более холодных (красных) звёзд: помимо звёзд, принадлежащих главной последовательности и потому имеющих малую светимость, на диаграмме представлены звёзды высокой светимости, которая практически не меняется при изменении их температуры. Такие звёзды принадлежат двум последовательностям (гиганты и сверхгиганты), получившим эти названия вследствие своей светимости, которая значительно превосходит светимость Солнца. Особое место на диаграмме занимают горячие звёзды малой светимости — белые карлики.
Рис. 5.15. Диаграмма «спектр — светимость»
Лишь к концу XX в., когда объём знаний о физических процессах, происходящих в звёздах, существенно увеличился и стали понятными пути их эволюции, удалось найти теоретическое обоснование тем эмпирическим закономерностям, которые отражает диаграмма «спектр — светимость».
Какова светимость звезды ξ Скорпиона, если её звёздная величина 3m, а расстояние до неё 7500 св. лет?
|
Дано: m = 3m D = 7500 св. лет |
Решение: lg L = 0,4(5 – M). M = m + 5 – 5 lg D, где D = 7500 : 3,26 = 2300 пк. Тогда M = 3 + 5 – 5 lg 2300 = –8,8. lg L = 0,4•[5 – (–8,8)] = 5,52. |
|
L — ? |
Отсюда L = 330 000.
Ответ: L = 330 000.

Вопросы 1. Как определяют расстояния до звёзд? 2. От чего зависит цвет звезды? 3. В чём главная причина различия спектров звёзд? 4. От чего зависит светимость звезды?

Упражнение 18 1. Во сколько раз Сириус ярче, чем Альдебаран; Солнце ярче, чем Сириус? 2. Одна звезда ярче другой в 16 раз. Чему равна разность их звёздных величин? 3. Параллакс Веги 0,11ʺ. Сколько времени идёт свет от неё до Земли? 4. Сколько лет надо было бы лететь по направлению к созвездию Лиры со скоростью 30 км/с, чтобы Вега стала вдвое ближе? 5. Во сколько раз звезда 3,4 звёздной величины слабее, чем Сириус, имеющий звёздную величину –1,6? Чему равны абсолютные величины этих звёзд, если расстояние до каждой составляет 3 пк?
ПРАКТИЧЕСКАЯ РАБОТА
ОПРЕДЕЛЕНИЕ РАССТОЯНИЙ ДО ЗВЕЗД
МЕТОДОМ ГОДИЧНОГО ПАРАЛЛАКСА
Цели занятия:
1. Научится определять расстояния до звёзд с
помощью годичного параллакса.
2. Развить логического мышления, развитие умения
решать задачи.
3. Формировать научное мировоззрение и
диалектическое мышление.
Ключевые слова: звезды, годовой параллакс, астрономическая
единица, парсек.
Теоретический материал
Астрономические единицы.
Поскольку расстояние между астрономическими объектами
(планетами, звёздами, галактиками), огромны, пользоваться обычными единицами
длины – метры и километры – неудобно. Поэтому в астрономии приняты особые
единицы измерения расстояний: астрономическая единица, парсек и световой год.
Астрономическая единица (а.е.) равна среднему расстоянию от Земли до Солнца (149 600 000 км)
Парсек – расстояние, из которого а.е. (средний радиус орбиты
Земли) видна под углом 1” (секунда дуги): 1 пк = 206 265 а.е.
= 30 857 244 000 000 км = 3,08 ×
1013 км.
Световой год –
это расстояние, которое преодолеет световой поток за время, равное
календарному году:
1 св.год = 3 × 105 км/с × 365,25дней × 24часов × 3600 сек. = 9 467 280 000 000
км = 9,46 × 1012 км.
1 пс = 3,26 св.лет.
Годичный параллакс
Как измерить расстояние, если
до предмета не дотянуться ни линейкой, ни лучом локатора? На помощь приходит
метод триангуляции, широко применяемый в обычной земной геодезии.

длины – «базу»( на рисунке – точки А и С), измеряем из его концов углы, под
которыми видна недоступная по тем или иным причинам точка В, а затем простые
тригонометрические формулы дают искомое расстояние.
Когда мы переходим с одного
конца базы на другой, видимое направление на точку меняется, она сдвигается на
фоне далёких объектов. Это называется параллактическим смещением, или параллаксом.
Величина параллакса тем
меньше, чем дальше объект, и тем больше, чем длиннее база.
Для измерения
расстояний до звёзд приходится брать максимально доступную астрономам базу,
равную диаметру земной орбиты. Соответствующее параллактическое смещение звёзд
на небе (строго говоря, его половину) стали называть годичным параллаксом.

называется угол, под которым со звезды можно было бы видеть большую полуось
земной орбиты (равную 1 а. е.), перпендикулярную направлению на звезду.
Определить расстояние до
звезды можно, зная годовой параллакс ρ– угол, под которым со звезды был виден
радиус земной орбиты. Для этого звезду фотографируют с помощью телескопа через
каждые 6 месяцев, то есть из двух противоположных точек земной орбиты. На
фотографиях близкая звезда несколько меняет своё положение относительно других,
более удалённых. Если это смещение таково, что его можно измерить, то вычислив
соответствующий угол, можно рассчитать расстояние до звезды по формуле
где а – средний радиус земной
орбиты , D – расстояние до звезды ,
ρ – её годичный параллакс.
Если углы малые, то синус малого угла можно заменить
величиной самого угла в радианной мере:
sin p ≈ p’’/206265. Тогда получаем: D = a∙206265/p’’, или
в астрономических единицах.
Если расстояние нужно выразить в парсеках (1 пк = 206265
а.е.), то
Примеры решения
Задача №1:
Годичный
параллакс самой близкой к нам звезды Проксима из созвездия Кентавра – 0,762″.
Каково до неё расстояние (в пк, св.годах, км).
Дано: ρ = 0,762″ Решение: Dпс = 1 / ρ = 1 / 0,762 пк = 1,31 пк ,
Dпс – ? Dсвг = 3,26 св.лет × 1,31 = 4,27 св.лет ,
Dсв.г – ? Dr =
4,27 × 9,46 × 1012 км = 40,39 × 1012 км,
D – ? или D = 1,31 × 3,08 × 1013 км = 40,39 × 1012 км.
Задача
№2:
Найти расстояние до звезды Альдебаран (α созвездия Телец) , имеющей
годичный параллакс 0,05″. Выразите это расстояние в парсеках, световых годах и
километрах.
Дано: ρ = 0,05″ Решение: D пс = 1 / ρ =
1 / 0,05 пк = 20пк ,
D пс – ? D свг. = 3,26 св.лет × 20 = 65,2 св.лет ,
Dсв.г – ? D =
65,2 × 9,46 × 1012 км = 616,792 × 1012 км.
D – ?
ПРАКТИЧЕСКОЕ
ЗАДАНИЕ
Задача №1. Рассчитать расстояние в
световых годах до яркой звезды звёздного неба северного полушария Арктура (α в
созвездии Волопаса) если известно, что её параллакс равен 88.83 угловым
миллисекундам.
Задача №2. Рассчитать расстояние в
световых годах до яркой звезды звёздного неба северного полушария Канопус (α в
созвездии Киля) если известно, что её параллакс равен 10.55 угловым
миллисекундам.
Задача №3. Рассчитать расстояние в
световых годах до яркой звезды звёздного неба северного полушария Ригель
Кентаурус (α в созвездии Центавра A) если известно, что её параллакс равен
754,81 угловым миллисекундам
Задача №4. Рассчитать расстояние в
световых годах до яркой звезды звёздного неба северного полушария Сириус (α в
созвездии Большого Пса) если известно, что её параллакс равен 379,21 угловым
миллисекундам
Задача №5. Рассчитать расстояние в
световых годах до яркой звезды звёздного неба северного полушария Вега (α в
созвездии Лиры) если известно, что её параллакс равен 130,23 угловым миллисекундам
Задача №6. Рассчитать расстояние в
световых годах до яркой звезды звёздного неба северного полушария Капелла (α в
созвездии Возничего) если известно, что её параллакс равен 76,2 угловым
миллисекундам
Задача №7. Рассчитать расстояние в
световых годах до яркой звезды звёздного неба северного полушария Ригель (β в
созвездии Ориона) если известно, что её параллакс равен 3,78 угловым
миллисекундам.
Задача №8. Рассчитать расстояние в
световых годах до яркой звезды звёздного неба северного полушария Альтаир (α в созвездии Орла) если известно, что её параллакс
равен 194,95 угловым миллисекундам.
Задача №9. Рассчитать расстояние в
световых годах до яркой звезды звёздного неба северного полушария Антарес (α в
созвездии Скорпиона) если известно, что её параллакс равен 5,89 угловым
миллисекундам
Задача №10. Рассчитать расстояние в
световых годах до яркой звезды звёздного неба северного полушария Альдебаран
(α в созвездии Тельца) если известно, что её параллакс равен 49,97 угловым
миллисекундам.
Задача №11. Рассчитать расстояние в
световых годах до яркой звезды звёздного неба северного полушария Денеб (α в
созвездии Лебедь) если известно, что её параллакс равен 0,003 угловым
миллисекундам
Литература.
Астрономия.
Учебник для 10 класса средней школы. (Издание 15-ое). Издательство: Москва
“Просвещение” Год: 1983., 145 страниц.
Калькулятор
параллакса и расстояний онлайн _
https://www.translatorscafe.com/unit-converter/ru-RU/calculator/parallax-distance/
Ответы
|
1 |
11,257 |
36,72 СГ |
3,47*1014 |
|
2 |
94,787 |
309,15 СГ |
2,92*1015 |
|
3 |
1,325 |
4,32 СГ |
4,09*1013 |
|
4 |
2,637 |
8,6 СГ |
8,14*1013 |
|
5 |
7,679 |
25,04 СГ |
2,37*1014 |
|
6 |
13,123 |
42,8 СГ |
4,05*1014 |
|
7 |
264,55 |
862,85 СГ |
8,16*1015 |
|
8 |
5,13 парс |
16,73 СГ |
1,58*1014 |
|
9 |
169,779 |
553,75 СГ |
5,24*1015 |
|
10 |
20,012 |
65,27 СГ |
6,18*1014 |
|
11 |
333,333 |
1087,19 |
1,03*1016 |
Почему так трудно определить размеры небесных объектов и расстояния до них? Все дело в том, что размеры удаленных объектов мы можем определить только по сравнению размерами известных объектов, а на небе нам не с чем сравнивать. Мы видим на небе множество светящихся точек, но яркость точки может определяться как ее размером, абсолютной светимостью, так и расстоянием до нее.
Поэтому в астрономии практически невозможно определить оптическими методами линейный размер удаленного объекта, можно определить только его угловой размер.
Древние греки изобрели тригонометрию, которая позволяет определить количественные соотношения между углами, линейными размерами и линейными расстояниями. С помощью простых математических соотношений, включающих базовую тригонометрию, мы можем вычислить расстояния до удаленных объектов, размеры которых известны (или размеры, если расстояния известны).
Уравнение малых углов
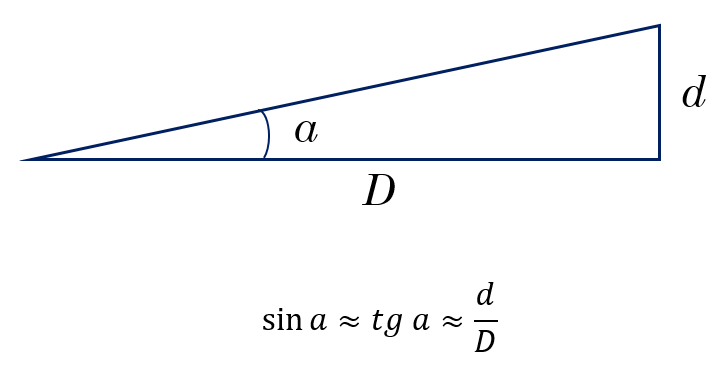
Если углы малые, то синус угла примерно равен тангенсу, который, в свою очередь примерно равен самому углу в радианной мере.
Уравнение малых углов включает в себя угловой размер объекта, его линейный размер и расстояние. Если известны какие-либо две из этих величин, можно вычислить третью. Обратимся к угловому размеру с символом a, выраженному в секундах дуги. Обозначим диаметр объекта как d, а расстояние до него как D. Тогда уравнение малого угла
a / 206 265 = d / D
Число 206 265 называется константой пропорциональности. Число 206 265 на самом деле является числом секунд дуги в угле 57,3°, который является специальным углом, называемым радианом. Радиан определяется как центральный угол дуги, длина которой равна радиусу окружности. Длина окружности равна 2πr, Радиан равен 360° / 2 π = 57,3° или около шестой части полного круга.
Вот пример использования уравнения малого угла. Предположим, что ваш друг ростом в 2 метра стоит через поле от вас, где он виден под углом ½°, или 1800″. Как он далеко от вас? Мы хотим найти расстояние D, выразим эту величину из уранения:
D = 206 265 d / a
Используя метрические единицы, найдем
D = (2.1 x 105 x 2) / (1.8 x 103) = 2.3 х 102 метра = 230 метров
Если ваш друг имеет рост 2 метра и угловой размер его составляет ½ ° (или 1800 угловых секунд), расстояние D составляет 230 метров. Обратите внимание, что мы округляем все наши оценки до двух значащих цифр, потому что измерение угла вряд ли будет очень точным.
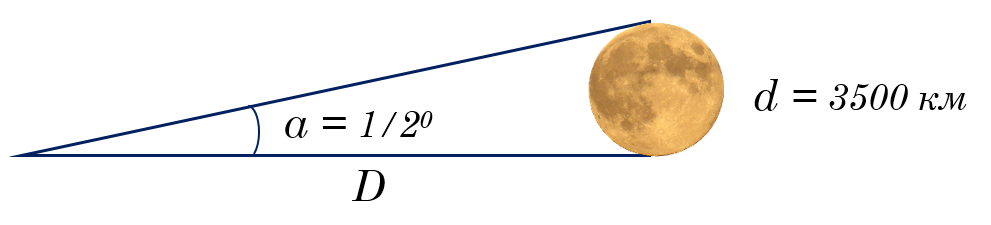
Как поняли древние греки, уравнение малого угла можно использовать для определения астрономических расстояний. Они не могли точно измерить диаметр Луны, но они знали ее угловой размер a, который также составляет примерно ½°, или 1800″.
Если мы используем современные знания о том, что диаметр Луны составляет около 3500 километров, мы можем оценить расстояние до нее так же, как мы это сделали для расстояния друга выше. В метрических единицах d будет 3,5 × 106 метров. Уравнение будет гласить:
D = (2.1 × 105 × 3.5 × 106) / (1.8 × 103) ≈ 4 х 108 метров ≈ 4 x 105 километров.
Реальное среднее расстояние до Луны 384 000 км. Неплохая точность!
Методы определения расстояний до звезд
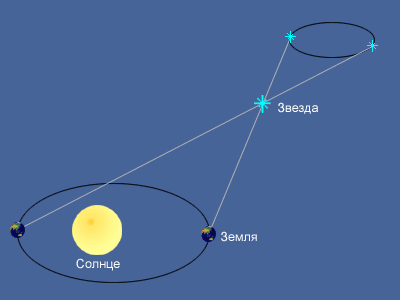
Годичный параллакс
Кажущееся перемещение более близкой звезды на фоне очень далеких звезд происходит по эллипсу с периодом в 1 год и отражает движение наблюдателя вместе с Землей вокруг Солнца. Маленький эллипс, описываемый звездой, называется параллактическим эллипсом. В угловой мере большая полуось этого эллипса равна величине угла, под которым со звезды видна большая полуось земной орбиты, перпендикулярная направлению на звезду. Этот угол называется годичным параллаксом (π).
Параллактические смещения звезд служат неопровержимым доказательством обращения Земли вокруг Солнца. Расстояния до звезд определяются по их годичному параллактическому смещению, которое обусловлено перемещением наблюдателя (вместе с Землей) по земной орбите.
Если CT = a есть средний радиус земной орбиты, SC = r – расстояние до звезды S от Солнца C, а угол π – годичный параллакс звезды, то
Так как годичные параллаксы звезд оцениваются десятичными долями секунды, а 1 радиан равен 206265′′, то расстояние до звезды можно определить из соотношения
При измерении расстояний до звезд астрономическая единица слишком мала. Поэтому для удобства определения расстояний до звезд в астрономии применяется специальная единица длины – парсек (пк), название которой происходит от слов «параллакс» и «секунда».
Парсек – это расстояние, с которого радиус земной орбиты был бы виден под углом в 1′′.
1 пк = 206 265 а. е. = 3,086 · 1013 км.
Таким образом, расстояние до звезд в парсеках будет определяться выражением
В астрономических единицах обычно выражаются расстояния до тел Солнечной системы. Расстояния до небесных тел, находящихся за пределами Солнечной системы, обычно выражаются в парсеках, килопарсеках (1 кпк = 103 пк) и мегапарсеках (1 Мпк = 106 пк), а также в световых годах (1 св. г. = 9,46 · 1012 км = 63 240 а. е. = 0,3067 пк или 1 пк = 3,26 св. г.).
Световой год – расстояние, которое электромагнитное излучение (в вакууме) проходит за 1 год.
Источник
Фотометрический метод определения расстояний
Освещенности, создаваемые одинаковыми по мощности источниками света, обратно пропорциональны квадратам расстояний до них. Следовательно, видимый блеск одинаковых светил (т.е. освещенность, создаваемая у Земли на единичной площадке, перпендикулярной лучам света) может служить мерой расстояний до них. Выражение освещенностей в звездных величинах (m – видимая, M – абсолютная звездная величина) приводит к следующей основной формуле фотометрических расстояний rф(пк):
Для светил, у которых известны тригонометрические параллаксы, можно, определив M по этой же формуле, сопоставить физические свойства с абсолютными звездными величинами. Это сопоставление показало, что абсолютные звездные величины многих классов светил (звезд, галактик и др.) можно оценивать по ряду их физических свойств.
Основным способом оценки абсолютных величин звезд является спектральный способ: в спектрах звезд одного и того же спектрального класса обнаружены особенности, указывающие на их абсолютные величины (чаще всего это усиление линий ионизованных атомов с возрастанием светимости звезд). По таким признакам звезды разделены на классы светимости. По классам и более мелким подклассам светимости, оцениваемым по спектрам звезд, можно находить абсолютные величины с погрешность до 0,5m. Эта погрешность соответствует относительной погрешности 30%.
Цефеиды (стандартные свечи)
Важный метод определения фотометрических расстояний в Галактике и до соседних звездных систем – галактик – основан на характерном свойстве переменных звезд – цефеид. Короткопериодические цефеиды (с периодами колебаний блеска менее суток) в среднем имеют абсолютную величину +0,5m. Они встречаются в шаровых звездных скоплениях, в центральной области и сферической короне Галактики и относятся к ее звездному населению II типа. По цефеидам в конечном счете найдены расстояния до шаровых звездных скоплений и установлено расстояние от Солнца до центра Галактики.
Для долгопериодических цефеид (периоды колебаний от 1 до 146 сут.), относящихся к звездному населению I типа (плоской составляющей Галактики), установлена важная зависимость период-светимость, согласно которой, чем короче период колебаний блеска, тем цефеида слабее по абсолютной величине. С помощью этой зависимости можно определить абсолютные величины цефеид по длительности их периодов колебаний блеска и, следовательно, фотометрические расстояния до цефеид и звездных скоплений, спиральных рукавов и звездных систем, где они наблюдаются (см. Период-светимость зависимость). Погрешность определения расстояний по цефеидам составляет для звездных скоплений в среднем 40% (в отдельных случаях меньше).

- Информация о материале
-
Просмотров: 15507
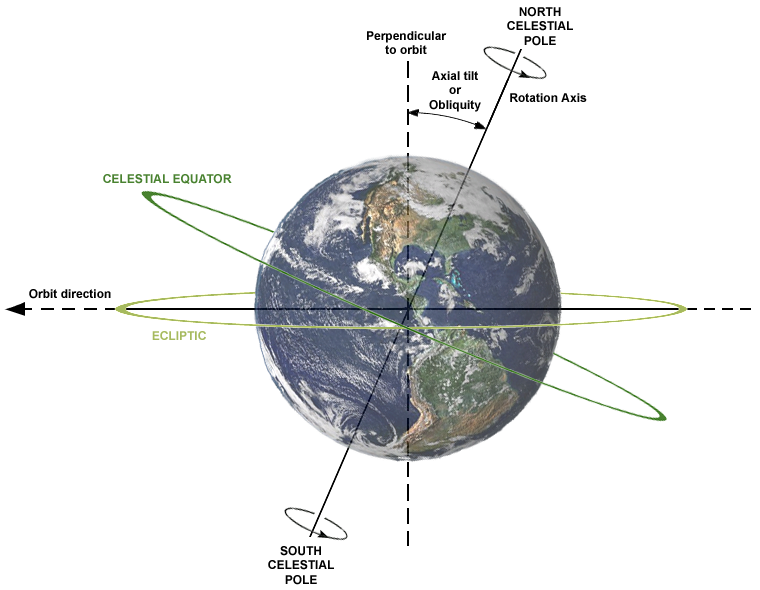
Смена времен года — вечное и неизменное явление природы. Причина его заключается в движении Земли вокруг Солнца.
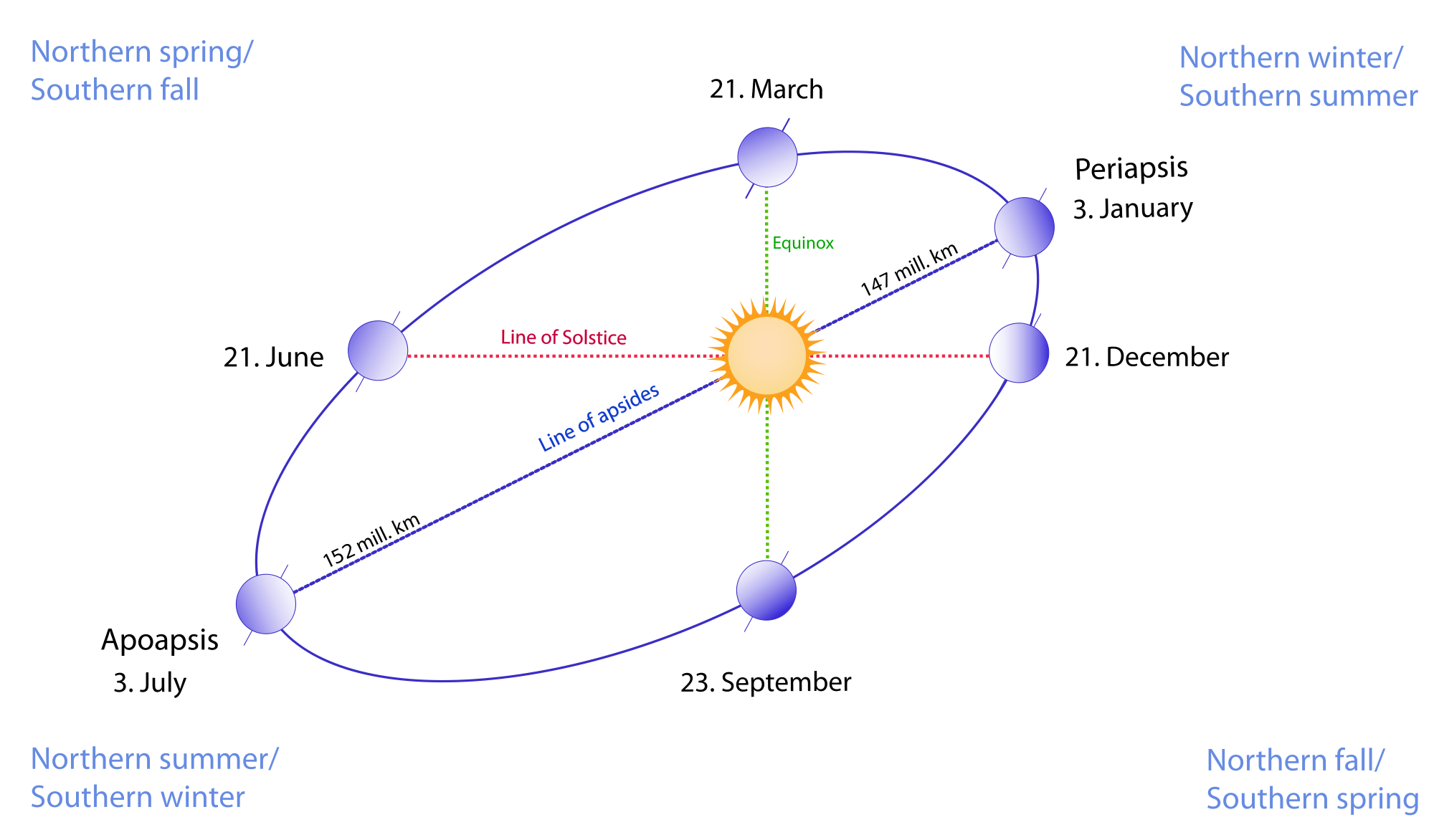
Путь, по которому в космическом пространстве движется земной шар, имеет форму вытянутого круга – эллипса. Солнце находится не в центре этого эллипса, а в одном из его фокусов. Поэтому на протяжении года расстояние от Солнца до Земли периодически меняется: от 147,1 млн. км (в начале января) до 152,1 млн. км (в начале июля). Переход от тёплого времени года (весна, лето) к холодному (осень, зима) происходит вовсе не потому, что Земля то приближается к Солнцу, то удаляется от него.
Истинная причина смены времен года — это наклон земной оси. Ось вращения, воображаемая линия, соединяющая северный и южный полюса Земли, не перпендикулярна плоскости земной орбиты, по которой она движется вокруг Солнца. И отклонение оси от перпендикуляра составляет 23,5°. Ось направлена на север в точку среди звезд возле Полярной звезды. (На самом деле, ось медленно меняет свое направление и со временем будет указывать не на Полярную, а на другую звезду.)
Лето приходит в Северное полушарие, когда ось, направленная через Северный полюс вверх, указывает примерно в сторону Солнца. В этой ситуации Солнце в полдень находится выше над горизонтом, чем во все остальные сезоны года, поэтому оно лучше освещает Северное полушарие и дает больше тепла. В это же самое время ось, проходящая вниз через Южный полюс, направлена от Солнца, поэтому Солнце в полдень находится ниже над горизонтом, чем в любое другое время года, и хуже освещает Южное полушарие. В это время в Австралии наступает зима.
Летом светлого времени суток больше, чем зимой, потому что Солнце находится выше над горизонтом. Поэтому ему требуется больше времени, чтобы сначала подняться на эту высоту, а потом — спуститься. И, поскольку день длится дольше, в это время года теплее.
По мере того как Земля движется по орбите вокруг Солнца, кажется, что Солнце перемещается по небу по некой окружности, которая называется эклиптикой. Плоскость эклиптики наклонена к плоскости экватора точно под таким же углом, как ось Земли — 23,5°.
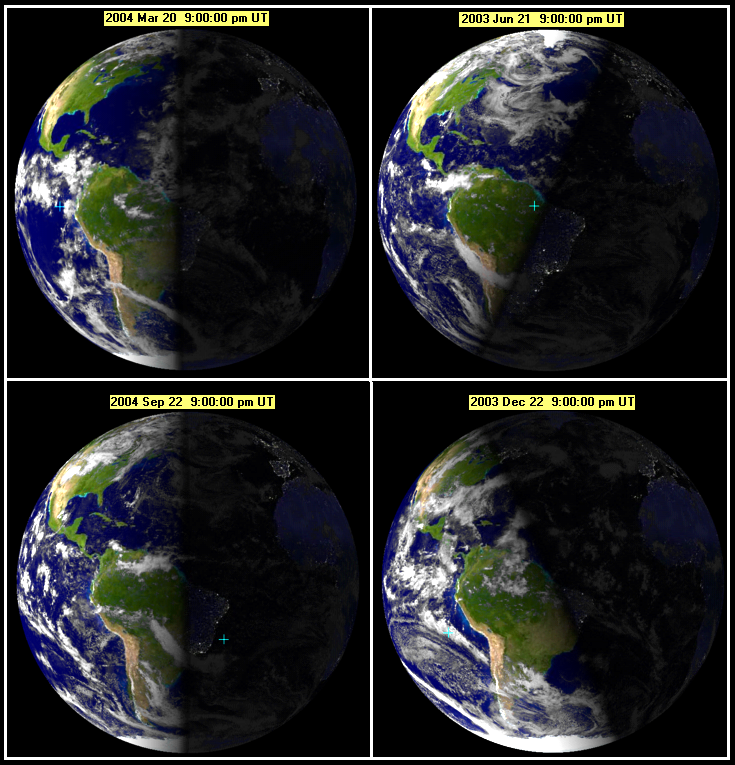
Равноденствие – момент пересечения небесного экватора центром видимого солнечного диска. Весеннее равноденствие наступает, когда Солнце переходит из южного полушария небесной сферы в северное и обычно происходит около 21 марта. Осеннее равноденствие бывает около 23 сентября. Вблизи равноденствия продолжительность дня в средних широтах примерно равна продолжительности ночи.
Когда Солнце переходит из южного полушария небесной сферы в северное, т. е. пересекает небесный экватор “снизу вверх”, наступает первый день весны, который называется днем весеннего равноденствия. Он приходится на 20–21 марта. В Южном полушарии Земли наступает астрономическая осень, а в Северном — астрономическая весна. Вблизи равноденствия продолжительность дня в средних широтах примерно равна продолжительности ночи.
Когда Солнце достигает самой высокой (северной) точки на эклиптике, это день летнего солнцестояния. Приходится примерно на 21–22 июня. С этого дня в Северном полушарии начинается астрономическое лето, а в Южном — астрономическая зима.
Когда Солнце переходит из северного полушария небесной сферы в южное, т. е. пересекает небесный экватор “сверху вниз”, это начало осени, день осеннего равноденствия. Обычно он приходится примерно на 23 сентября. В Южном полушарии Земли наступает астрономическая весна, а в Северном — астрономическая осень.
Когда Солнце достигает самой нижней (южной) точки на эклиптике, это день зимнего солнцестояния. Приходится примерно на 21–22 декабря. С этого дня в Северном полушарии начинается астрономическая зима, а в Южном — астрономическое лето.
Источник

- Информация о материале
-
Просмотров: 8814