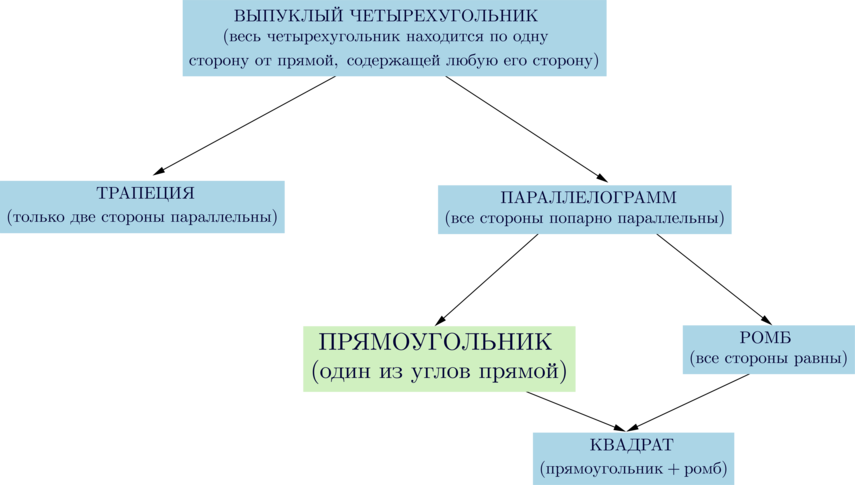
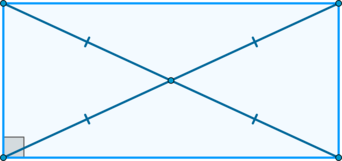
Сколько параллельных линий имеет прямоугольник?
Ответ: прямоугольник имеет 2 пары параллельных сторон.
Что такое параллельные прямые в прямоугольнике?
Резюме урока
А прямоугольник имеет две пары параллельных прямых. Квадрат также имеет две пары параллельных прямых. Параллелограмм также имеет две пары параллельных прямых. Чтобы найти параллельные линии, ищите линии, которые идут в одном направлении и никогда не пересекаются.
Как найти параллельную прямую прямоугольника?
Сколько параллельных линий имеет квадрат?
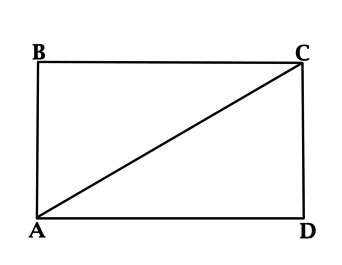
две пары Квадрат имеет две пары параллельных сторон, значит, это параллелограмм; на рисунке мы видим, что overline{AB} параллелен overline{CD}, а overline{AC} параллелен overline{BD}. Квадрат также имеет 4 прямых угла, следовательно, это прямоугольник.
См. также, какая техника используется для экспонирования изображений зубов.
Сколько линий в прямоугольнике?
Форма прямоугольника имеет четыре линии, две из которых являются вертикальными линиями. Две другие линии являются горизонтальными линиями.
Является ли прямоугольник параллельными прямыми?
Каждая пара внутренних углов является дополнительной, потому что два прямых угла складываются с прямым углом, поэтому противоположные стороны прямоугольника параллельны. Это означает, что прямоугольник является параллелограммом, поэтому: Его противоположные стороны равны и параллельны.
Все ли прямоугольники имеют 2 пары параллельных сторон?
Объяснение: Одно из определений параллелограмма — две пары параллельных сторон. Следовательно, любой параллелограмм ДОЛЖЕН иметь 2 пары параллельных сторон. Сюда входят все квадраты, ромбы и прямоугольники.
Сколько параллельных линий в прямоугольной призме?
Характеристики прямоугольной призмы
Прямоугольная призма имеет 12 ребер и 8 вершин. 12 ребер прямоугольной призмы находятся на 3 группы параллельных линии. Параллельные ребра равны по длине. Противоположные грани параллельны и конгруэнтны друг другу.
Какая фигура имеет 4 пары параллельных прямых?
Правильный восьмиугольник фигура, имеющая 4 пары параллельных сторон. Каждая сторона параллельна стороне, противоположной ей.
Какие фигуры имеют пары параллельных прямых?
Фигуры параллельны, если их линии всегда находятся на одинаковом расстоянии друг от друга и никогда не пересекаются и не соприкасаются. Некоторые фигуры с параллельными сторонами включают параллелограмм, прямоугольник, квадрат, трапеция, шестиугольник, и восьмиугольник. У трапеции одна пара параллельных сторон.
Сколько параллельных линий имеет пятиугольник?
Пятиугольник имеет пять сторон, а также не имеет наборов параллельных прямых.
Сколько осей симметрии у прямоугольника?
2
Сколько перпендикулярных прямых имеет прямоугольник?
4 прямых угла, но 2 пары перпендикулярных линий.
Какой прямоугольник имеет две линии симметрии?
В прямоугольнике две линии симметрии. Когда одна линия проводится через центр по его длине, а другая — по ширине (ширине), мы получаем две линии симметрии. Делая это, мы получаем четыре одинаковые и соответствующие формы.
Сколько углов у прямоугольника?
четыре
четырехугольник с четырьмя прямыми углами.
Сколько вершин у прямоугольника?
Прямоугольные призмы
Смотрите также, что означает денали
Он состоит из 6 прямоугольных граней. Когда вы соедините стороны вместе, она станет прямоугольной призмой с 8 вершин и 12 ребер.
Сколько параллельных и перпендикулярных прямых имеет прямоугольник?
Прямоугольники имеют четыре прямые стороны. Каждая пара противоположных сторон параллельна, а соседние стороны перпендикулярны. Это означает, что каждый угол в прямоугольнике является прямым (90∘) углом. Все синие фигуры на изображении ниже — прямоугольники.
Все ли прямоугольники имеют перпендикулярные и параллельные стороны?
Как мы упоминали ранее, прямоугольные треугольники имеют перпендикулярные стороны, прямоугольники имеют как перпендикулярные, так и параллельные стороны. стороны, но другие четырехугольники не могут. Правильный пятиугольник не имеет параллельных или перпендикулярных сторон, но неправильный пятиугольник может иметь параллельные и перпендикулярные стороны. Все зависит от полигона.
Сколько прямых сторон у прямоугольника?
Четыре прямые стороны У квадрата четыре равные стороны. У прямоугольника две пары равных сторон. Квадраты и прямоугольники имеют четыре прямые стороны и четыре прямых угла.
Что имеет только одну пару параллельных прямых?
трапеция четырехугольник, у которого ровно одна пара параллельных сторон.
Сколько прямоугольных граней у прямоугольной пирамиды?
5 граней Прямоугольная пирамида имеет 5 лиц. Его основание — прямоугольник или квадрат, а остальные 4 грани — треугольники. У него 8 ребер и 5 вершин.
Что такое косая прямоугольная призма?
Наклонная прямоугольная призма
Наклонная призма это призма, основания которой не перпендикулярны друг другу. Прямоугольная призма с основаниями, которые не выровнены одно над другим, является наклонной прямоугольной призмой.
Сколько параллельных прямых у прямоугольного параллелепипеда?
12 ребер прямоугольного параллелепипеда находятся в 3 группы параллельных линий. Параллельные ребра равны по длине. Любые пересекающиеся ребра перпендикулярны друг другу.
Какой формы прямоугольник?
Прямоугольник продолговатый. У него две пары параллельных сторон и четыре прямых угла. Прямоугольник также может быть известен как равноугольный четырехугольник. Это связано с тем, что прямоугольник представляет собой четырехугольник (четырехстороннюю форму), у которого стороны параллельны, равны друг другу, а все 4 угла имеют углы, равные 90º.
Является ли прямоугольник ромбом?
Прямоугольник ромб. Квадрат – это параллелограмм. Параллелограмм правильный.
Может ли квадрат быть прямоугольником?
Да, квадрат – это особый тип прямоугольника потому что он обладает всеми свойствами прямоугольника. Подобно прямоугольнику, квадрат имеет: внутренние углы, каждый из которых равен 90∘. противоположные стороны параллельны и равны.
Смотрите также, чем похожи равнины и плоскогорья.
Что имеет параллельные стороны, но не прямоугольник?
Другой четырехугольник, который вы можете увидеть, называется ромб. Все четыре стороны ромба равны. Его свойства включают в себя то, что каждая пара противоположных сторон параллельна, что также делает его параллелограммом. Таким образом, все квадраты являются прямоугольниками, но не все прямоугольники являются квадратами.
Сколько параллельных прямых у ромба?
две пары
Основные свойства Каждый ромб имеет две диагонали, соединяющие пары противоположных вершин, и две пары параллельных сторон.
Является ли треугольник параллельным?
Треугольник — это геометрическая фигура, которая всегда имеет три стороны и три угла. Треугольники имеют ноль пар параллельных прямых. Обычно они имеют нулевые пары перпендикулярных линий. Только один тип треугольника, прямоугольный, имеет две перпендикулярные линии.
Сколько параллелей в шестиугольнике?
3 пары
Правильный шестиугольник, что означает шестиугольник с равными сторонами и равными внутренними углами, представляет собой форму, которая имеет 3 пары параллельных сторон.
Сколько параллельных сторон у восьмиугольника?
4 пары Правильный восьмиугольник имеет 4 пары параллельные стороны.
Сколько параллельных прямых имеет параллелограмм?
две пары В евклидовой геометрии параллелограмм представляет собой простой (несамопересекающийся) четырехугольник с две пары параллельных стороны. Противоположные или обращенные стороны параллелограмма имеют одинаковую длину, а противоположные углы параллелограмма равны.
Почему прямоугольник имеет симметрию только по двум линиям?
Есть 2 линии симметрии прямоугольника, которые исходят из его длины и ширины. Эти две линии разрезают прямоугольник на две одинаковые половины, которые являются зеркальными отражениями друг друга. Если прямоугольник складывается по линии симметрии, он отлично накладывается.
Сколько параллельных линий в прямоугольной призме? : геометрия, алгебра и многое другое
3-й год – Определение перпендикулярных и параллельных линий в двухмерных фигурах – Объяснение
Сколько пар параллельных прямых в квадрате?
Что такое параллельные прямые и параллельные плоскости? | Не запоминай
Прямоугольник
Частным видом параллелограмма является прямоугольник.
Прямоугольником называют параллелограмм, у которого все углы прямые
ABCD – прямоугольник.
Особое свойство прямоугольника
Диагонали прямоугольника равны
Доказательство
Дано: ABCD – прямоугольник
Доказать: AC = DB
Доказательство:
Рассмотрим 







Теорема
Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник
Доказательство
Дано: ABCD – параллелограмм, AC = DB
Доказать: ABCD – прямоугольник
Доказательство:
Рассмотрим 

AC = DB (по условию), AD = BC (по свойству параллелограмма), AB – общая, 




















Теорема
Если один из углов параллелограмма прямой, то этот параллелограмм – прямоугольник
Доказательство
Дано: ABCD – параллелограмм, 
Доказать: ABCD – прямоугольник
Доказательство:
Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 0 , т.е. 



Противолежащие углы параллелограмма равны, 



Итак: ABCD – параллелограмм (по условию), и все его углы прямые (по доказанному выше), 
Две теоремы, доказанные выше, называют признаками прямоугольника.
Поделись с друзьями в социальных сетях:
Параллельность прямых
О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение параллельности прямых
Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.
Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.
Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.
Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.
На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Свойства и признаки параллельных прямых
Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.
Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.
Если секущая проходит через две параллельные прямые, то:
-
два внутренних односторонних угла образуют в сумме 180°:
∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.
два внутренних накрест лежащих угла равны между собой:
два соответственных угла равны между собой:
∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.
Если секущая образует перпендикуляр с одной из параллельных прямых, то она будет перпендикулярна и другой.
Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.
А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.
Задача 1
Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.
Решение
Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.
Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.
Задача 2
Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.
Решение
Поскольку а II b, значит ∠MKD + ∠KDN = 180°.
Соответственно, ∠MKD = 180° – ∠KDN = 180° – 150° = 30°.
Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.
Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.
Геометрия. 7 класс
Конспект урока
Признаки параллельности прямых
Перечень рассматриваемых вопросов:
- Параллельные прямые.
- Накрест лежащие, соответственные, односторонние углы.
- Признаки параллельности прямых.
- Решение задач на доказательство параллельности прямых.
Две прямые на плоскости называются параллельными, если они не пересекаются.
Признаки параллельности двух прямых:
1. Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.
2. Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.
3. Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
Вы уже знаете, что при пересечении двух прямых секущей образуются углы:
- накрест лежащие: 3 и 6, 4 и 5.
- односторонние: 3 и 5, 4 и 6.
- соответственные: 1 и 5, 3 и 7, 2 и 6; 4 и 8.
Прямая c называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.
Рассмотрим и докажем признаки параллельности прямых.
Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.
Дано: прямые a и b, секущая AB, ∠ 1 = ∠ 2 накрест лежащие.
В этом случае две прямые, перпендикулярные к третьей не пересекаются, т. е. параллельны.
2 случай: ∠ 1= ∠ 2 ≠ 90°
1) Из середины O отрезка AB проведём перпендикуляр OH к прямой а. На прямой b от точки B отложим отрезок BH1, равный отрезку AH и проведем отрезок OH1.
2) AO = OB т. к. O середина AB; AH = BH1 по построению; ∠1 = ∠2 по условию. Тогда ΔOHA = ΔOH1B по первому признаку равенства треугольников.
Далее следует из равенства треугольников: ∠3 = ∠4 и ∠5 = ∠6.
3) Из равенства углов ∠3 и ∠4 следует, что точка H1 лежит на продолжении луча OH. Это значит, что точки H1, O, H лежат на одной прямой.
4) Из равенства ∠5 и ∠6 следует, что ∠6 = 90°. Это значит, что прямые a и b перпендикулярны к третьей НН1, а значит, по теореме о двух прямых, перпендикулярных к третьей, не пересекаются, т. е. параллельны.
Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.
Дано: прямые a и b, секущая AB, ∠1 = ∠2 соответственные.
∠1 = ∠2 – по условию и ∠2 = ∠3 – по свойству вертикальных углов.
Значит, ∠1 = ∠3, это накрест лежащие углы, следовательно, a║b по теореме 1.
Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.
Прямые a и b, секущая AB, ∠1 + ∠2 = 180° ‑ односторонние.
∠3 +∠2 = 180°– по свойству смежных углов, откуда ∠3 = 180° – ∠2.
∠1 + ∠2 = 180 ° по условию, откуда ∠1 = 180° – ∠2.
Тогда ∠1 = ∠3, это накрест лежащие углы, следовательно, a║b по теореме 1.
Разбор заданий тренировочного модуля.
Дано: ∠1= 60°, ∠2 = 120°.
- ∠2 и ∠3 смежные, ∠3 = 180° – 120° = 60° по свойству смежных углов;
- ∠3 = ∠1, это накрест лежащие углы;
- Значит, прямые a и b параллельны по 1 признаку параллельности прямых.
Ответ: прямые a и b параллельны по 1 признаку параллельности прямых.
Дано: ΔABC – равнобедренный, ∠А = 60°. CD – биссектриса ∠BCK.
Докажите: AB ║ CD.
- ∠A = ∠C = 60° – углы при основании равнобедренного Δ–ка равны.
- ∠BCK и ∠С смежные. ∠BCK = 180° – 60°= 120° – по свойству смежных углов.
- ∠BCD = ∠CDK = 60° т. к. CD – биссектриса делит угол пополам.
- Значит, ∠A = ∠DCK = 60° ‑ соответственные, следовательно, AB║CD по 2 признаку параллельности прямых.
Ответ: AB║CD по 2 признаку параллельности прямых.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/parallelnost-pryamyh
http://resh.edu.ru/subject/lesson/7298/conspect/
[/spoiler]
Прямоугольник.
Приступаем к изучению разных видов параллелограмма.
Определение. Прямоугольником
называется параллелограмм, у которого все углы прямые.

– прямоугольник
Поскольку прямоугольник – это
параллелограмм, то он обладаем теми же свойствами, что и параллелограмм. Кроме
того, у него есть ещё свои, особые свойства.
Рассмотрим эти свойства.
ТЕОРЕМА (СВОЙСТВО I).
У прямоугольника диагонали равны.
Дано: – прямоугольник,
и
– диагонали.
Доказать:
Доказательство.
1.
Рассмотрим и
.

прямоугольных треугольников (или по I
признаку равенства треугольников) все соответствующие стороны
и углы у этих треугольников равны, т.е. , ч.т.д.
ТЕОРЕМА (СВОЙСТВО II).
У прямоугольника каждая диагональ делит его на два равных
прямоугольных треугольника.
Дано: – прямоугольник,
– диагональ.
Доказать:
Доказательство.
Рассмотрим
и
.

признаку равенства треугольников. по определению
прямоугольника. Значит, треугольники и
– равные и прямоугольные,
ч.т.д.
Итак, прямоугольник обладает следующими свойствами:
1. У
прямоугольника противолежащие стороны и углы равны.
2. У
прямоугольника диагонали пересекаются и точкой пересечения делятся пополам.
3. У
прямоугольника диагонали равны.
4. У
прямоугольника каждая диагональ делит его на два равных прямоугольных
треугольника.
5. Стороны
прямоугольника являются его высотами.
Выясним теперь, по
каким признакам можно утверждать, что геометрическая фигура является
прямоугольником.

Если у четырёхугольника три угла прямые, то такой
четырёхугольник является прямоугольником.
Дано: – четырёхугольник,
Доказать: – прямоугольник.
Доказательство.
Данный
четырёхугольник будет прямоугольником, если мы докажем, что четвёртый угол
также равен .
1.
Так как , то
. Так как
, то
.
2. 
3.

4.
Значит, – параллелограмм
(по определению). По свойству углов параллелограмма, .
5.
Итак, – параллелограмм,
у которого все углы прямые. По определению, такой параллелограмм является
прямоугольником, ч.т.д.
ТЕОРЕМА
(ПРИЗНАК II). Если
у параллелограмма диагонали равны, то такой параллелограмм является
прямоугольником.
Дано: – параллелограмм,
– диагонали.
Доказать: – прямоугольник.
Доказательство.
Данный
параллелограмм будет прямоугольником, если мы докажем, что у него все углы равны
.
1. Рассмотрим и
.

признаку равенства прямоугольных треугольников, следовательно, .
2. Так как – параллелограмм, то у него
стороны попарно параллельны, т.е. .
и
– внутренние односторонние
при параллельных прямых, значит, по свойству параллельных прямых, . Учитывая доказанное
равенство этих углов, получаем, что .
3. По свойству углов параллелограмма, и
.
4. Итак, у параллелограмма все углы прямые, значит, он
является прямоугольником (по определению), ч.т.д.

(ПРИЗНАК III). Если
у параллелограмма один угол прямой, то такой параллелограмм является
прямоугольником.
Дано: – параллелограмм,
.
Доказать: – прямоугольник.
Доказательство.
Данный
параллелограмм будет прямоугольником, если мы докажем, что у него все углы
равны .
1. Т.к.
– параллелограмм, то по
определению, т.е. и
.
По свойству углов параллелограмма, .
2. и
– внутренние односторонние
при параллельных прямых, значит, по свойству параллельных прямых, .
3. Т.к. , то
.
4. Итак, , значит, по определению,
параллелограмм является прямоугольником,
ч.т.д.
1. Периметр прямоугольника
равен см, а одна из его сторон
меньше другой на см. Найдите меньшую сторону
прямоугольника.
2. В прямоугольнике один
из углов, образованных диагоналями, равен . Меньшая сторона
прямоугольника равна см. Найдите диагональ
прямоугольника.
3. В прямоугольнике
перпендикуляры, проведённые из точки пересечения диагоналей к его сторонам,
равны соответственно см и
см. Найдите периметр
прямоугольника.
4.
 |
В прямоугольнике диагональ
составляет со стороной
угол, равный
. Найдите больший угол между
диагоналями прямоугольника.
5. В прямоугольнике один
из углов, образованных диагоналями, равен . Диагонали прямоугольника
равны см. Найдите меньшую сторону
прямоугольника.
6. В прямоугольнике диагонали пересекаются в
точке . Точка
– середина стороны
. Найдите
.
7. В прямоугольнике диагонали пересекаются в
точке . Отрезок
является высотой треугольника
. Найдите
.
8. В параллелограмме с острым углом
диагонали пересекаются в
точке . На отрезках
и
взяты точки
и
соответственно,
. Докажите, что
четырёхугольник является прямоугольником.
9. В прямоугольнике
– точка пересечения
диагоналей, и
– высоты треугольников
и
соответственно,
см. Найдите
.
10. В четырёхугольнике диагонали пересекаются в
точке . Найдите
.
11. В прямоугольнике
– точка пересечения
диагоналей, и
– перпендикуляры, проведённые
из вершин и
к прямой
. Известно, что
. Найдите
.
12. В четырёхугольнике диагонали пересекаются в
точке ,
. Найдите
.
13. В прямоугольнике точки
и
– середины сторон
и
соответственно. На прямой
взята точка
, на прямой
– точка
. Известно, что
. Найдите отношение сторон
.
14. На основании равнобедренного треугольника
взята точка
, а на сторонах
и
– соответственно точки
и
,
. Найдите
.
15. В прямоугольнике
– точка пересечения
диагоналей. Точки и
– середины сторон
и
соответственно. Точка
делит отрезок
в отношении
, считая от точки
Найдите отношение
.
16. Некая прямая,
параллельная основанию равнобедренного треугольника
, пересекает стороны
и
в отношении
, считая от точки
. Найдите
.
17. На диагонали прямоугольника
взята точка
. Известно, что
. Докажите, что
.
18. Дан параллелограмм с острым углом
. На отрезке
, как на диаметре построена
окружность, которая пересекает луч в точке
, лежащей вне параллелограмма.
. Найдите расстояние между
прямыми и
, если
см.
19. На отрезках и
в прямоугольнике
взяты точки
и
соответственно,
. Докажите, что
.
20. Дан параллелограмм с тупым углом
. На диагонали
, как на диаметре, построена
окружность, пересекающая отрезок в точке
– перпендикуляр к прямой
. Найдите
, если
см.
21. Биссектриса одного из
углов прямоугольника делит пересекаемую ею сторону на отрезки равной длины.
Найдите периметр этого прямоугольника, если длина меньшей стороны
прямоугольника равна см.
22. Периметр прямоугольника
равен см. Найдите сумму расстояний
от произвольной внутренней точки прямоугольника до его сторон.
23. Постройте
прямоугольник:
а)
по двум сторонам, имеющим общую вершину;
б)
по стороне и диагонали;
в)
по диагонали и углу между диагоналями;
г)
по диагонали и сумме прилежащих сторон.
24. Диагональ прямоугольника
равна
см. Найдите медиану
треугольника , проведённую к его большей
стороне.
25. Найдите острый угол
между диагоналями прямоугольника, если одна из них делит угол при вершине
прямоугольника в отношении .
26. Периметр прямоугольника
равен см. Найдите стороны
прямоугольника, если одна из них в раз больше другой.
27. Периметр прямоугольника
равен см. Найдите его стороны, если
одна из них на см меньше другой.
28. Диагонали
прямоугольника пересекаются в точке
. Найдите угол между
диагоналями, если .
29. В прямоугольнике проведена диагональ
. Известно, что
в 2 раза больше, чем
. Чему равны эти углы?
30. Одна из сторон
прямоугольника на см больше другой. Найдите
стороны прямоугольника, если его периметр равен см.
31. Меньшая сторона
прямоугольника см, угол между диагоналями
равен . Найдите диагонали
прямоугольника.
32. Дан прямоугольник – точка пересечения его
диагоналей. Докажите, что и
– равные равнобедренные
треугольники.
33. Найдите диагонали
прямоугольника, если его периметр равен см, а периметр одного из
треугольников, на которые диагональ разделила прямоугольник, равен см.
34. Докажите, что отрезок,
соединяющий точку пересечения диагоналей прямоугольника с серединой стороны,
перпендикулярен этой стороне.
35. В прямоугольнике диагональ
в
раз больше стороны
. Периметр треугольника
равен
см (
– точка пересечения
диагоналей). Найдите длину диагонали .
36. Из точки , взятой на стороне
прямоугольника
, опущен перпендикуляр
на сторону
. Докажите, что
четырёхугольник – прямоугольник.
37. Диагонали
прямоугольника пересекаются в точке
, его диагональ
равна
см. Найдите длины отрезков
и
.
38. Диагонали
прямоугольника пересекаются в точке
. Докажите, что
.
39. Диагонали
прямоугольника пересекаются в точке
. Найдите стороны
прямоугольника, если его периметр равен см, а периметры треугольников
и
равны
см и
см соответственно.
40. Дан прямоугольник – точка пересечения его
диагоналей. Найдите периметр треугольника , если
41. Диагонали
прямоугольника пересекаются в точке
. Найдите периметр
треугольника , если
.
42. Диагонали
прямоугольника пересекаются в точке
. Найдите периметр
треугольника , если
.
43. Диагонали
прямоугольника пересекаются в точке
. Найдите периметр
треугольника , если
.
44. Диагонали
прямоугольника пересекаются в точке
, сторона
равна
см, диагональ
равна
см. Определите вид
треугольника (ответ обоснуйте) и найдите
его периметр.
45. В прямоугольнике биссектриса угла
пересекает сторону
в точке
. Докажите, что треугольник
– равнобедренный.
46. В прямоугольнике диагональ
делит угол
в отношении
. Найдите углы треугольника
(
– точка пересечения
диагоналей).
47. Найдите диагональ
прямоугольника, если его периметр равен см, а периметр одного из
треугольников, на которые диагональ делит прямоугольник, равен см.
48.
 |
В прямоугольнике проведена биссектриса угла
. Найдите периметр
прямоугольника, если см,
см.
49. Расстояния от точки
пересечения диагоналей прямоугольника до его сторон равны см и
см. Найдите большую сторону
данного прямоугольника.
50. Диагонали
прямоугольника пересекаются под углом . Найдите угол между
диагональю прямоугольника и его меньшей стороной.
51. В прямоугольнике диагональ
в два раза больше стороны
. Найдите периметр
треугольника , если расстояние от точки
пересечения диагоналей
прямоугольника до стороны равно
см.
52. Диагонали
прямоугольника пересекаются в точке
, образуя тупой угол
. Определите, какое расстояние
больше: от точки до стороны
или от точки
до стороны
.
53.
 |
В прямоугольном треугольнике (
– прямой) через точку
, лежащую на гипотенузе,
проведены прямые и
, параллельные катетам
и
соответственно. Периметр
треугольника равен
см, а периметр треугольника
равен
см. Найдите периметр
треугольника .
54. На стороне равностороннего треугольника
взята точка
так, что сумма расстояний от
неё до сторон и
равна
см. Найдите высоту
треугольника, проведённую из вершины .
55. Периметр прямоугольника
равен
см, а его диагональ
равна
см. Найдите периметр
треугольника .
56.
 |
Найдите периметр прямоугольника , если биссектрисы
и
углов
и
делят сторону
на три отрезка, длина каждого
из которых равна см.
57. Точка пересечения
диагоналей прямоугольника отстоит от его сторон на расстояниях см и
см. Найдите меньшую сторону
данного прямоугольника.
58. В прямоугольнике диагональ
в два раза больше стороны
. Найдите острый угол между
диагоналями прямоугольника.
59. Меньшая сторона
прямоугольника равна см. Угол между его
диагоналями равен . Вычислите длину диагонали
прямоугольника.
60. Диагонали
прямоугольника пересекаются в точке
. Определите, какое расстояние
больше: от точки до стороны или от точки
до стороны
, если сторона
больше стороны
.
61.
 |
В прямоугольнике через точку
проведены прямая
, параллельная сторонам
и
, и прямая
, параллельная сторонами
и
. Периметр прямоугольника
равен
см, а периметр прямоугольника
равен
см. Найдите периметр
прямоугольника .
62. На продолжении стороны равностороннего треугольника
взята точка
так, что разность расстояний
от неё до сторон и
равна
см. Найдите высоту
треугольника, проведённую из вершины .
63. Диагонали
прямоугольника пересекаются в точке
. Периметр треугольника
равен
см, а периметр треугольника
равен
см. Найдите периметр
треугольника , если диагональ
прямоугольника равна см.
64.
 |
Найдите периметр прямоугольника , если биссектрисы
и
углов
и
делят сторону
на три отрезка, длина каждого
из которых равна см.
65. Сумма расстояний от
точки пересечения диагоналей прямоугольника до всех его вершин равна см. Найдите диагональ данного
прямоугольника.
66. Диагональ прямоугольника
образует угол
с одной из его сторон.
Найдите острый угол между диагоналями прямоугольника.
67. Диагональ
прямоугольника равна см. Угол между его
диагоналями равен . Вычислите длину меньшей
стороны прямоугольника.
68. Диагонали
прямоугольника пересекаются в точке
, образуя острый угол
. Определите, какое расстояние
больше: от точки до стороны
или от точки
до стороны
.
69.
 |
В прямоугольном равнобедренном треугольнике (
– прямой) через точки
и
, лежащие на гипотенузе,
проведены прямые и
, параллельные катету
, и прямые
и
, параллельные катету
. Сравните периметры
четырёхугольников и
.
70. На основании равнобедренного треугольника
взята точка
так, что сумма расстояний от
неё до сторон и
равна
см. Найдите высоту
треугольника, проведённую из вершины .
71. Диагонали
прямоугольника пересекаются в точке
. Периметр треугольника
равен
см, а сторона
равна
см. Найдите периметр
треугольника .
72.
 |
Биссектрисы углов и
прямоугольника
пересекаются на стороне
в точке
. Найдите периметр прямоугольника,
если длина равна
см.
73. Сумма расстояний от
точки пересечения диагоналей прямоугольника до всех его сторон равна см. Найдите периметр данного
прямоугольника.
74. Угол между диагоналями
прямоугольника равен
. Найдите угол
.
75. В прямоугольнике сторона
в два раза меньше диагонали
. Найдите расстояние от точки
пересечения диагоналей
прямоугольника до стороны , если периметр треугольника
равен
см.
76. Диагонали
прямоугольника пересекаются в точке
. Определите, какое расстояние
больше: от точки до стороны
или от точки
до стороны
, если сторона
меньше стороны
.
77.
 |
В прямоугольном равнобедренном треугольнике (
– прямой) через точку
, лежащую на гипотенузе,
проведены прямые и
, параллельные катетам
и
соответственно. Найдите
периметр прямоугольника , если катет треугольника
равен
см.
78. 
продолжении основания равнобедренного треугольника
взята точка
так, что разность расстояний
от неё до сторон и
равна
см. Найдите высоту
треугольника, проведённую из вершины .
79. 
прямоугольнике проведена диагональ
. Перпендикуляр к диагонали
составляет со стороной
угол, равный
и отсекает от диагонали
отрезок , равный
см. Найдите периметр
прямоугольника, если сторона см.
80. Дан прямоугольник со стороной
. К диагонали
проведён перпендикуляр
. Найдите периметр
прямоугольника, если диагональ составляет со стороной
угол, равный
.
81.
 |
В прямоугольнике
– точка пересечения его
диагоналей. Из точки к серединам сторон
и
проведены отрезки
и
соответственно. Найдите
периметр прямоугольника.
82.
 |
Биссектриса угла
прямоугольника
отсекает от стороны
отрезки
и
. Найдите периметр
прямоугольника.
83. В прямоугольнике проведена биссектриса
угла
. Найдите
.
 |
84. В прямоугольнике диагональ
составляет с его меньшей
стороной угол . Найдите углы
и
.
85. В прямоугольнике диагонали пересекаются в
точке . Найдите
и меньший угол между
диагоналями, если известно, что .
86.
 |
Диагонали прямоугольника пересекаются в точке
. Меньший угол между
диагоналями равен . Найдите углы треугольника
, если известно, что
.
87. В прямоугольнике диагонали пересекаются в
точке . Известно, что
. Найдите эти углы.
88. В прямоугольнике . Найдите стороны
прямоугольника, если его периметр равен .
89. В прямоугольнике из угла
проведён луч, который
пересекает сторону в точке
так, что
и
. Найдите стороны прямоугольника,
если известно, что периметр его равен .
90. Диагональ прямоугольника
составляет со стороной
угол, равный
. Перпендикуляр, опущенный из
вершины на эту диагональ отсекает от
неё отрезок . Периметр данного
прямоугольника равен . Найдите стороны
 |
прямоугольника.
91.
 |
Из вершины прямоугольника
, с периметром
, проведён луч, который
пересекает сторону под углом
. Разность отсекаемых отрезков
равна . Найдите стороны
прямоугольника.
Прямоугольник, свойства, признаки и формулы.
Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).
Прямоугольник (понятие, определение)
Видеоурок “Прямоугольник“
Свойства прямоугольника
Признаки прямоугольника
Формулы прямоугольника
Прямоугольник (понятие, определение):
Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).
Прямоугольник – это четырехугольник, у которого каждый угол является прямым.
Прямоугольник – это четырехугольник, у которого две противоположные стороны равны между собой и все четыре угла равны между собой и каждый из них составляет 90 градусов.
Рис. 1. Прямоугольник
В свою очередь четырёхугольник (греч. τετραγωνον) – это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), последовательно соединяющих эти точки.
Длинную сторону прямоугольника называют длиной прямоугольника, а короткую – шириной прямоугольника.
@ https://youtu.be/_EVDcbOydAI
Свойства прямоугольника:
1. Прямоугольник является параллелограммом – его противоположные стороны попарно параллельны.
Рис. 2. Прямоугольник
AB || CD, BC || AD
2. Противоположные стороны прямоугольника равны.
Рис. 3. Прямоугольник
AB = CD, BC = AD
3. Стороны прямоугольника являются его высотами.
4. Прилегающие стороны прямоугольника всегда перпендикулярны.
Рис. 4. Прямоугольник
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
5. Каждый угол прямоугольника прямой и равен 90 градусам. Сумма всех углов прямоугольника составляет 360 градусов.
Рис. 5. Прямоугольник
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°,
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
6. Диагонали прямоугольника равны.
Рис. 6. Прямоугольник
AC = BD
7. Каждая диагональ прямоугольника делит его на два одинаковых прямоугольных треугольника.
Рис. 7. Прямоугольник
△ABD = △BCD, △ABC = △ACD
8. Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (что вытекает из теоремы Пифагора).
Рис. 8. Прямоугольник
AC2 = AD2+ CD2
9. Диагонали прямоугольника делятся точкой пересечения пополам.
Рис. 9. Прямоугольник
AO = BO = CO = DO = АС / 2 = BD / 2
10. Около любого прямоугольника можно описать окружность. Диагональ прямоугольника является диаметром описанной окружности.
Рис. 10. Прямоугольник
АС и BD – диаметр описанной окружности и диагональ прямоугольника
11. Точка пересечения диагоналей называется центром прямоугольника и является центром описанной окружности.
12. Прямоугольник может содержать вписанную окружность и только одну, если все его стороны равны, т.е. он является квадратом.
Рис. 11. Квадрат
AВ = ВC = AD = CD
Признаки прямоугольника:
– если диагонали параллелограмма равны, то он является прямоугольником;
– если квадрат диагонали параллелограмма равен сумме квадратов смежных сторон, то он (параллелограмм) является прямоугольником;
– если углы параллелограмма равны, то он является прямоугольником.
Формулы прямоугольника:
Пусть a – длина прямоугольника, b – ширина прямоугольника, d – диагональ и диаметр описанной окружности прямоугольника, R – радиус описанной окружности прямоугольника, P – периметр прямоугольника, S – площадь прямоугольника.
Формула стороны прямоугольника (длины и ширины прямоугольника):
,
,
,
.
Формула диагонали прямоугольника:
,
d = 2R.
Формулы периметра прямоугольника:
P = 2a + 2b,
P = 2(a + b).
Формулы площади прямоугольника:
S = a · b.
Формула радиуса окружности, описанной вокруг прямоугольника:

Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Видео https://youtu.be/_EVDcbOydAI
Коэффициент востребованности
5 261
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Решение задач на прямоугольник
Сумма внутренних углов любого четырехугольника равна (360^circ).
Свойства прямоугольника:
(blacktriangleright) Те же, что и у параллелограмма:
(sim) Противоположные стороны попарно равны;
(sim) Диагонали точкой пересечения делятся пополам;
(sim) Противоположные углы попарно равны, а сумма соседних равна (180^circ);
(blacktriangleright) Диагонали равны;
(blacktriangleright) Все углы прямые.
Признаки прямоугольника.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – прямоугольник:
(blacktriangleright) все углы прямые;
(blacktriangleright) диагонали равны и он является параллелограммом.
Площадь прямоугольника
Площадь прямоугольника равна произведению двух его смежных сторон.
Задание
1
#281
Уровень задания: Равен ЕГЭ
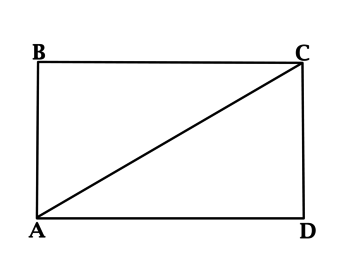
В прямоугольнике (ABCD): (AB = dfrac{2}{5}BC), периметр (ABCD) равен (42). Найдите площадь треугольника (ABC).
Так как прямоугольник является частным случаем параллелограмма, то у него противоположные стороны равны, тогда (2cdot AB + 2cdot BC = 42), что при (AB = dfrac{2}{5}BC) равносильно (dfrac{4}{5}BC + 2cdot BC = 42), откуда находим (BC = 15), значит, (AB = 6).
Треугольники (ABC) и (ADC) равны по двум катетам, тогда их площади равны, следовательно, площадь треугольника (ABC) равна половине площади (ABCD) и равна (0,5cdot 6cdot 15 = 45).
Ответ: 45
Задание
2
#283
Уровень задания: Равен ЕГЭ
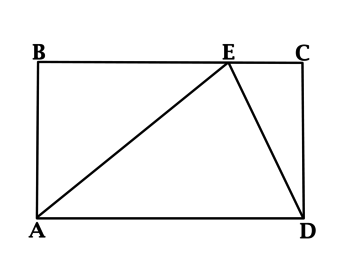
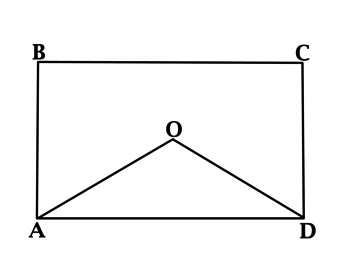
Точка (E) лежит на стороне (BC) прямоугольника (ABCD). Площадь треугольника (AED) равна 3. Найдите площадь прямоугольника (ABCD).
Площадь треугольника равна половине произведения основания на высоту, тогда площадь треугольника (AED) равна (0,5 cdot AD cdot h), где (h) – высота, опущенная из точки (E) на (AD). Пусть эта высота пересекает (AD) в точке (F), тогда (FECD) – параллелограмм ((EF parallel CD, EC parallel FD)), значит, (h = CD) и площадь прямоугольника (ABCD) равна (AD cdot h), то есть она в два раза больше, чем площадь треугольника (AED) и, следовательно, равна 6.
Ответ: 6
Задание
3
#284
Уровень задания: Равен ЕГЭ
(O) – точка пересечения диагоналей прямоугольника (ABCD), (angle OAD = 28^{circ}). Найдите (angle AOD). Ответ дайте в градусах.
В прямоугольнике диагонали пересекаются, точкой пересечения делятся пополам и равны, тогда (AO = OD), следовательно, (angle ADO = angle OAD = 28^{circ}), тогда (angle AOD = 180^{circ} – 2cdot 28^{circ} = 124^{circ}).
Ответ: 124
Задание
4
#1698
Уровень задания: Равен ЕГЭ
Точка (O) делит сторону (BC) прямоугольника (ABCD) на отрезки (7) и (1), а расстояние от точки (O) до стороны (AD) равно (3). Найдите периметр прямоугольника.
Расстояние от точки (O) до стороны (AD) совпадает с длиной смежных сторон к (AD), тогда (P_{ABCD} = 2cdot(7 + 1 + 3) = 22).
Ответ: 22
Задание
5
#2643
Уровень задания: Равен ЕГЭ
Расстояние от точки пересечения диагоналей прямоугольника до прямой, содержащей его большую сторону, равно (2,5). Найдите меньшую сторону прямоугольника.
(Задача от подписчиков.)
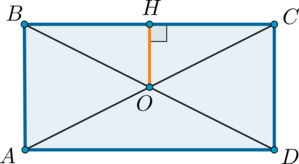
Рассмотрим прямоугольник (ABCD). Пусть (O) – точка пересечения диагоналей, (OH=2,5) – расстояние от точки (O) до большей стороны.
Т.к. диагонали прямоугольника равны и точкой пересечения делятся пополам, то (BO=CO). Следовательно, (triangle BOH=triangle COH) как прямоугольные по катету и гипотенузе. Следовательно, (BH=CH). Таким образом, (OH) – средняя линия в (triangle ABC), следовательно, она равна половине (AB). Значит, (AB=2cdot 2,5=5).
Ответ: 5
Задание
6
#2713
Уровень задания: Равен ЕГЭ
В прямоугольнике (ABCD) диагональ (AC = 2cdot CD). Найдите разность (angle BAC – angle CAD). Ответ дайте в градусах.
Треугольник (ACD) – прямоугольный, причём в нём катет равен половине гипотенузы, значит этот катет лежит против угла в (30^{circ}), то есть (angle CAD = 30^{circ}).
(angle BAC = 90^{circ} – angle CAD = 60^{circ}), тогда (angle
BAC – angle CAD = 60^{circ} – 30^{circ} = 30^{circ}).
Ответ: 30
Задание
7
#2714
Уровень задания: Равен ЕГЭ
Площадь прямоугольника равна (16). Найдите наименьшую из площадей треугольников, образующихся при пересечении диагоналей данного прямоугольника.
Диагонали разобьют прямоугольник на (4) равных по площади треугольника.
Действительно, т.к. (triangle ABC=triangle ADC), то и их площади равны. Т.к. медиана делит треугольник на два треугольника, равных по площади, то (S_{ABO}=S_{CBO}) и (S_{ADO}=S_{CDO}).
Площадь каждого треугольника равна (4).
Ответ: 4
Выпускники, которые готовятся к сдаче экзамена по математике и рассчитывают на получение достойных баллов, непременно должны справляться с задачами ЕГЭ на нахождение углов, сторон и площадей прямоугольника. Подобные планиметрические задания встречаются в аттестационном испытании каждый год.
Чтобы успешно решить задачи ЕГЭ по теме «Прямоугольник и его свойства», стоит вспомнить основные понятия из базового школьного курса. При этом рекомендуется следовать определенному алгоритму. Приступая к выполнению заданий ЕГЭ, к примеру, на нахождение сторон прямоугольника или геометрические свойства ромба, сделайте чертеж и отразите на нем все данные, которые известны согласно условию. Затем вспомните относящиеся к ним формулы и теоремы. Применив их, вы сможете найти правильный ответ.
Если задания ЕГЭ по теме «Прямоугольник и его свойства» вызывают у вас затруднения, обратитесь к образовательному порталу «Школково». Здесь вы сможете освежить в памяти базовый теоретический материал и попрактиковаться в выполнении упражнений. Наши специалисты собрали как простые, так и более сложные задания.
Для каждого из них на сайте представлен подробный алгоритм решения.
Оттачивать практический навык школьники могут в режиме онлайн, находясь в любом городе России.

УСТАЛ? Просто отдохни