Получение диагоналей в матрице. Алгоритм
Одна из причин, почему я захотел написать строчки насчет этого алгоритма, так как сам в большинстве случаев находил лишь вариант решения с numPy. Это, безусловно, отличная библиотека, но все же интересен сам алгоритм для использования в различных целях. Ну а начать, пожалуй, хочется с минимальным количеством воды, поэтому сразу начну с объяснения метода.

Очевидное, что приходит в голову, что если «продлить» диагонали, или же, другими словами, представить диагонали в виде набора элементов, то количество тех самых элементов будет равно, но не все матрицы будут заполнены «по максимуму». Посмотрим на изображение 1, в котором числами сверху отмечены номера диагоналей и они проведены через элементы таблицы чисел. Не трудно осознать, что количество таких диагоналей равно $inline$N + M – 1$inline$, где N — количество строк в таблице, а M — количество столбцов в таблице. Пускай номера диагоналей, чье начало начинается с отсутствия элементов, обозначим зеленым цветом для удобства понимания.
В голову напрашивается очевидный вариант, как можно получить все диагонали с их элементами. А точнее, перебрать $inline$N + M – 1$inline$, в начале пусто заполненных, диагоналей и заполнить их соответствующими элементами. Перебирать будем в диапазоне
$$display$$[-(N – 1); M)$$display$$
, поскольку все числа, какие будут «с минусом» в данном диапазоне будет, как раз, равно кол-ву диагоналям, чье начало идет с «пустыми элементами», а точнее вообще без ничего и будет равно кол-ву $inline$N – 1 = (N + M – 1 – M)$inline$. Удобно использовать в реализации.
diagonals = [[] for i in range(N + M - 1)]
for i in range(-(N - 1), M):
....
Изображение 1
Соображение №1
Давайте выясним, как можно заполнить нужными элементами. Для начала вспомним, что элементы главной диагонали подчиняются правилу, что индекс позиции элемента a (= a[i][i]), где i — номер столбца и строки соответственно. Теперь можно обратить внимание, что другие безымянные диагонали отличаются лишь позицией лишь началом «отсчёта». В общем виде каждый $inline$i$inline$-овый элемент дополнительных диагоналей, параллельных главной диагонали, можно выразить так: $inline$b[i] = a[i][i + j]$inline$, $inline$b$inline$ — набор элементов диагонали, где $inline$i$inline$ — номер элемента, $inline$j$inline$ — «коэффициент отклонения диагонали», то есть на сколько столбец уходит в сторону от нулевого. Влево, вправо — неважно. И также, безусловно, условия, чтобы не выходить за границы.
Получаем:
$$display$$begin{cases} b[i] = a[i][i + j], &text{где $i$ – это номер элемента в $j + N – 1$ диагонали, $a$ – исходная матрица} \ 0 <= i < n \ 0 <= i + j < m end{cases}$$display$$
То есть достаточно добавить до N элементов в набор каждой диагонали. Отметим, что если индекс выходит за границы размера таблицы, то элемент явно не является частью набор любой диагонали. Также поскольку номер позиции каждого элемента диагонали = номеру строки, в которой он находится, то значение некому row присвоим j. Столбец (col), можно понять, что равен i + j, исходя из соображения под номером (1). Нам остается лишь обязательно учитывать границы row и col, дабы избежать выхода из границ существующих элементов для наших диагоналей.
diagonals = [[] for i in range(N + M - 1)]
for i in range(-(N - 1), M):
for j in range(N):
row, col = j, i + j
if 0 <= row < len(matrix) and 0 <= col < len(matrix[0]):
diagonals[i + len(matrix) - 1].append(matrix[row][col])Также этот алгоритм можно немного изменить, чтобы проделать процесс относительно диагоналей, параллельных побочной диагонали, изменив лишь эту строчку таким образом:
diagonals[i + len(matrix) - 1].append(matrix[row][M - col - 1])
На этом в принципе все. Нетрудный для понимания алгоритм поможет найти все диагонали в матрице.
Я должен сделать программу, которая находит суммы элементов матрицы, которые расположены параллельно главной диагонали. Я понятия не имею, как найти элементы, которые параллельны главной диагонали. I == j работает только для главной диагонали. Допустим, у нас есть такая матрица:
22 5 6 4
32 45 7 9
1 21 43 6
7 5 9 11
Я должен найти суммы отдельно: 4; 6 + 9; 5 + 7 + 6; 22 + 45 + 43 + 11; 32 + 21 + 9; 1 + 5; 7
After the changes the code become like this:
#include <stdio.h>
#include <cmath>
#include <cstdlib>
#define N 50
void enter_matrix (float m[N][N],int n){
int i,j;
for(i=0;i<n;i++){
for(j=0;j<n;j++){
printf("Enter %d %d element of the matrix: ",i+1,j+1);
scanf("%f",&m[i][j]);
}
}
}
void show_matrix(float m[N][N],int n){
int i,j;
for(i=0;i<n;i++){
for(j=0;j<n;j++){
printf("%.2ft",m[i][j]);
}
printf("n");
}
}
int find_sums(float m[N][N],float sum[100],int n){
int j=0;
for(int offset = -n+1; offset < n; ++offset) {
float sum1 = 0;
for(int i = 0; i < n-fabs(offset); ++i) {
if(offset <= 0) {
sum1 += m[i][i-offset];
}
else {
sum1 += m[i+offset][i];
}
sum[j]=sum1;j++;printf("%.2f n",sum1);
}
}
return j;
}
int find_max(float sum, int j){
int i,maxn;float *s,max=0;s=∑
for(i=0;i<j;i++){
if(*(s+1)>max){
max=*(s+1);
maxn=i;
}
}
return maxn;
}
int find_min(float sum, int j){
int i,minn;
float *s;
s=∑float min=*(s+0);
for(i=0;i<j;i++){
if(*(s+1)<min){
min=*(s+1);
minn=i;
}
}
return minn;
}
void main(){
float matrix [N][N], sum[100],*s;
int n,j,maxn,minn;
s=sum;
do{
printf("Enter matrix dimension (between 1 and 50):");
scanf("%d",&n);
}
while(n<=0||n>50);
enter_matrix(matrix,n);
show_matrix(matrix,n);
j=find_sums(matrix,sum,n);
maxn=find_max(sum[100],j);
minn=find_min(sum[100],j);
printf("Maximum sum is equal to %.2f, at line %dn",sum[maxn],maxn+1);
printf("Minimum sum is equal to %.2f, at line %dn",sum[minn],minn+1);
}
И вывод такой:
Enter matrix dimension (between 1 and 50):3
Enter 1 1 element of the matrix: 1
Enter 1 2 element of the matrix: 2
Enter 1 3 element of the matrix: 3
Enter 2 1 element of the matrix: 4
Enter 2 2 element of the matrix: 5
Enter 2 3 element of the matrix: 6
Enter 3 1 element of the matrix: 7
Enter 3 2 element of the matrix: 8
Enter 3 3 element of the matrix: 9
1.00 2.00 3.00
4.00 5.00 6.00
7.00 8.00 9.00
3.00
2.00
8.00
1.00
6.00
15.00
4.00
12.00
7.00
Maximum sum is equal to 3.00, at line 1
Minimum sum is equal to 3.00, at line 1
Press any key to continue
Это делает некоторые дополнительные суммы не только полными строками. Какие-либо предложения?
-1
Решение
Не проверено и от макушки головы:
int n;
double A[n][n]
for(int offset = -n+1; offset < n; ++offset) {
double sum = 0;
for(int i = 0; i < n-std::abs(offset); ++i) {
if(offset <= 0) {
sum += A[i][i-offset];
else {
sum += A[i+offset][i];
}
}
std::cout << sum << std::endl;
}
Для отрицательного смещения это печатает суммы верхних параллельных диагоналей и для положительного смещения суммы нижних параллельных диагоналей. Первый цикл можно легко распараллелить, оператор print является единственной критической частью.
0
Другие решения
Для этих диагоналей считается, что j = i + z для z в зависимости от диагонали, достигающей от — (высота-1) до (ширина-1).
Это приводит к следующему алгоритму (с массивом решений, способным обрабатывать отрицательные индексы — вы должны изменить это с некоторым смещением):
Array<R> diagonalSums (Matrix<R> m)
initialize Array<R> solution in according size with all entries initialized to zero
for each cell i,j in m:
find z so that j = i + z (z = j - i)
solution[z] += m(i,j)
return solution
Я думаю, что вы делаете что-то подобное со своим смещением, но вы пытаетесь найти способ перейти от z к сумме, которая принадлежит этому z, что только излишне запутанно, по крайней мере, когда вы хотите вычислить все суммы в любом случае (ваш путь лучше, если нужна только одна сумма). Мой подход просто перебирает все ячейки, а затем добавляет его в соответствующем месте.
Я использовал массив с отрицательными индексами, и для повышения читабельности я бы посоветовал вам сделать это, то есть создать класс, который может это делать.
0
I have a problem to manage a two-dimensional matrix nxn in C++. My problem is create a function that control if exists any diagonal, parallel line at the principal diagonal, that is reverse to other. I controlled the two index, necessary for the rows and columns, if are different and maybe I could help me with support arrays, which reverse the elements. Perhaps it’s not a good idea with a huge matrix(such as 8×8, 14 arrays) so, I am asking your help.
Thanks

This is my code:
bool funct(short **M, int rows, int columns){
bool found = false;
for(int i = 0; i < rows; i++){
for(int j = 0; j < colums; j++){
if(i != j){
//control the reverse array
}
}
}
}
ps: my primary problem is general algorithm(nxn).
asked Dec 9, 2016 at 16:24
![]()
4
In a quadratic matrix, every diagonal has exactly one other diagonal with the same length (except the principal diagonal). So you just need to check this one:
for(int diagonal = 1; diagonal < cols - 1; ++diagonal)
{
//inspect the diagonal that starts at (0, diagonal)
//the other diagonal starts at (diagonal, 0)
int diagonalLength = cols - diagonal;
//Assume that this diagonal has a reverse counterpart
bool diagonalHasReverse = true;
//Now check if it really has
for(int i = 0; i < diagonalLength; ++i)
{
if(M[i][diagonal + i] !=
M[diagonal + diagonalLength - 1 - i][diagonalLength - 1 - i])
{
diagonalHasReverse = false;
break;
}
}
//do whatever you want with diagonalHasReverse
}
The outer loop does not process the very last (one-element) diagonal. If you want to include that, you have to modify the loop as follows:
for(int diagonal = 1; diagonal < cols; ++diagonal)
answered Dec 9, 2016 at 16:48
Nico SchertlerNico Schertler
31.9k4 gold badges38 silver badges67 bronze badges
7
Тем, кто знакомым с математическими матрицами, будет не трудно освоить и двумерные массивы в Pascal. Матрица – это математический объект, представляющий собой прямоугольную таблицу. Таблица состоит из элементов, которые находятся на пересечении строк и столбцов, определяющих их, то есть i-ая строка и j-ый столбец задают адрес k-ому элементу матрицы (kij). Двумерные массивы абсолютно аналогичны математическим матрицам.
В отличие от одномерных массивов, двумерные характеризуются в программе парой индексов, один из которых соответствует номеру строки, другой – столбца:
Mas[m, n], где Mas – имя массива, n – номер строки, а m – номер столбца.
Описать матрицу в программе можно несколькими способами:
1) В разделе описания переменных:
Var Mas: Array[1..n, 1..m] of <тип элементов>;
2) При помощи одномерного массива, элементами которого являются одномерные массивы.
Пример:
Const n = 5; m = 10; Type Arr1 = Array[1..m] of <тип элементов >; Arr2 = Array[1..n] of arr1; Var Mas: arr2;
Переменная Mas – матрица, состоящая из пяти строк, в каждую из которых включено по десять элементов.
3) Предыдущий способ можно упростить так:
Const n = 5; m = 10; Турe arr=Array[1..n] Of Аrrау[1..m] of <тип элементов>; Var Mas: arr;
4) И снова сократив запись, получим:
Const n = 5; m = 10; Type arr = Array[1..n,1..m] of <тип элементов>; Var Mas: arr;
Для обработки содержимого матрицы, удобно пользоваться вложенными циклами:
For i:= 1 To n Do For j:= 1 To m Do
Например, для заполнения массива случайнми числами:
for i:=1 to n do
for j:=1 to n do
x[i,j]:=random(100);
Для вывода двумерного массива вещественных чисел размером n строк, m столбцов:
for i:=1 to n do begin
for j:=1 to m do
write(x[i,j]:5:2);
writeln;
end;
В следующей программе массив сначала заполняется числами с клавиатуры, а затем выводиться на экран.
program input_and_output_array;
uses crt;
const n=3; m=3;
var i, j: integer;
mas: array[1..n, 1..m] of integer;
begin
{ввод массива}
for i:=1 to n do
for j:=1 to m do
begin
write(' Элемент ', i,' строки, ',j,' столбца = ');
readln(mas[i, j]);
end;
writeln(' Получившаяся матрица: ');
{вывод массива}
for i:=1 to n do
begin
for j:=1 to m do
begin
write(mas[i, j]:5);
end;
writeln
end;
end.
Количество элементов в массиве (его размерность) можно узнать, умножив количество строк на количество столбцов.
Сумма всех элементов квадратной матрицы:
sum:=0;
for i:=1 to n do
for j:=1 to n do
sum:=sum+x[i,j];
writeln('Сумма=',sum);
Сумма элементов главной диагонали квадратной матрицы (элементы главной диагонали имеют одинаковые индексы -x[1,1], x[2,2] и т.д.):
sum:=0;
for i:=1 to n do
sum:=sum+x[i,i];
writeln('Сумма=',sum);
Сумма элементов побочной диагонали (диагонали противоположной главной). Индексы элементов побочной диагонали в сумме равны n+1, т.е. i+j=n+1 или j=n+1-i:
sum:=0;
for i:=1 to n do
sum:=sum+x[i,n+1-i];
writeln('Сумма=',sum);
Сумма элементов ниже главной диагонали квадратной матрицы (строго ниже):
sum:=0;
for i:=1 to n do
for j:=1 to n do
if i>j then
sum:=sum+x[i,j];
writeln('Сумма=',sum);
Можно не просматривать весь массив, а брать только нужные элементы:
sum:=0;
for i:=2 to n do
for j:=1 to i-1 do
sum:=sum+x[i,j];
writeln('Сумма=',sum);
Сумма элементов выше и на главной диагонали квадратной матрицы:
sum:=0;
for i:=1 to n do
for j:=1 to n do
if i<=j then
sum:=sum+x[i,j];
writeln('Сумма=',sum);
Здесь также можно не просматривать весь массив, а брать только нужные элементы:
sum:=0;
for i:=1 to n do
for j:=i to n do
sum:=sum+x[i,j];
writeln('Сумма=',sum);
Сумма элементов ниже побочной диагонали квадратной матрицы (строго ниже) :
sum:=0;
for i:=1 to n do
for j:=1 to n do
if i+j>n+1 then
sum:=sum+x[i,j];
writeln('Сумма=',sum);
Можно не просматривать весь массив, а брать только нужные элементы:
sum:=0;
for i:=2 to n do
for j:=n+2-i to n do
sum:=sum+x[i,j];
writeln('Сумма=',sum);
Если надо посчитать сумму элемсентов ниже побочной диагонали и на ней, то в предыдущем примере, при просмотре всего массива в предыдущем примере надо заменить знак отношения > на >=, а при просмотре толко нужных элементов применить такой код:
sum:=0;
for i:=1 to n do
for j:=n+1-i to n do
sum:=sum+x[i,j];
writeln('Сумма=',sum);
При подсчете суммы элементов выше и на главной диагонали, выше и на побочной диагонали возможно применине такого кода:
sum:=0;
for i:=1 to n do
for j:=1 to n do
if (i<=j) and (i+j<=n+1) then
sum:=sum+x[i,j];
writeln('Сумма=',sum);
Подсчет сумм элементов по строкам:
for i:=1 to n do begin
sum:=0;
for j:=1 to n do
sum:=sum+x[i,j];
writeln('Сумма ',i,'-й строки',sum);
end;
Подсчет сумм элементов по столбцам:
for j:=1 to n do begin
sum:=0;
for i:=1 to n do
sum:=sum+x[i,j];
writeln('Сумма ',j,'-го столбца ',sum);
end;
Безусловно суммы по строкам и столбцам можно записывать в одномерный массив. Например, для сумм по столбцам:
for i:=1 to n do
sum[j]:=0;
for i:=1 to n do
for j:=1 to n do
zum[j]:=sum[j]+x[i,j];
{вывод сумм по столбцам}
for i:=1 to n do
write(sum[i]:4);
writeln;
Суммы элементов по диагоналям, параллельным главной диагонали.
Очевидно, что таких сумм будет 2n-1. Кроме того, разности индексов эдементов, стоящих на одной диагонали будут равны друг другу. Имеется в виду разность «номер строки минус номер столбца». Эти разности будут меняться от -n+1 для самой верхней диагонали s1, содержащей всего лишь один элемент, до n-1 для диагонали s2N-1, расположенной в самом низу матрицы и содержащей также всего один элемент. Таким образом, для подсчета сумм мы должны объявить массив:
Var sum:array[-n+1..n-1] of integer;
Число элементов в этом массиве будет 2n-1. Код для подсчета этих сумм:
for i:=-n+1 to n-1 do
sum[i]:=0;
for i:=1 to n do
for j:=1 to n do
sum[i-j]:=sum[i-j]+x[i,j];
for i:=-n+1 to n-1 do
write(sum[i]);
Суммы элементов по диагоналям, параллельным побочной диагонали.
for i:=2 to 2*n do
sum[i]:=0;
for i:=1 to n do
for j:=1 to n do
sum[i+j]:=sum[i+j]+x[i,j];
for i:=2 to 2*n do
write(sum[i]);
Суммы элементов по периметрам двумерного массива.
Cледует различать четный или нечетный порядок матрицы n. Число сумм будет равно k=n div 2 при четном n и k=n div 2 +1 при нечетном значении n.
Счет суммы начинается по строке i от столбца j равного i и заканчивается столбцом n-i+1, т.е. начинается с элемена находящегося на главной диагонали и заканчивается элементом на побочной диагонали.
Одновременно учитываются элементы из параллельной строки, индекс которой равен n-i+1.
Затем считаем элементы по двум паралельным столбцам i и n-i+1 (не учитывая элементы, стоящие в строках). Если n -нечетное число, то выводим значение центрального элемента массива x[k+1,k+1].
k:=n div 2;
for i:=1 to k do begin
sum:=0;
{строки}
for j:=i to n-i+1 do
sum:=sum+x[i,j]+x[n-i+1,j];
{столбцы}
for j:=i+1 to n-i do
sum:=sum+x[j,i]+x[j,n-i+1];
writeln(sum); {вывод суммы}
end;
if n mod 2=1 then
writeln(x[k+1,k+1]);
Дана целочисленная квадратная матрица. Определить:
- сумму элементов в тех столбцах, которые не содержат отрицательных элементов;
- минимум среди сумм модулей элементов диагоналей, параллельных побочной диагонали матрицы.
Код программы:
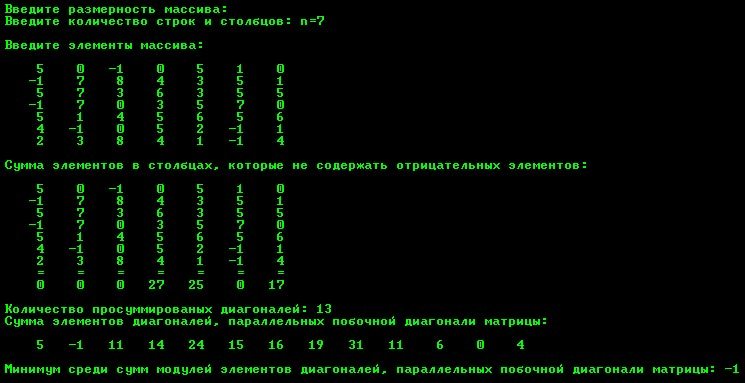
//--------------------------------------------------------------------------- #include<iostream.h> #include<conio.h> #include<math.h> #include<windows.h> #include<iomanip.h> #include<vcl.h> #pragma hdrstop #pragma argsused //--------------------------------------------------------------------------- char *rus(const char *text); int main(int argc, char* argv[]) { randomize(); int n,m,i,j,k,cnt=0,s1,q,w,minsum_of_diag; bool all_posit; cout<<rus("Введите размерность массива:")<<endl; cout<<rus("Введите количество строк и столбцов: n=");cin>>n; int **a=new int*[n]; for(i=0;i<n;i++)a[i]=new int[n]; int **buf_a=new int*[n]; for(i=0;i<n;i++)buf_a[i]=new int[n]; long unsigned *sum=new unsigned long[n]; int *sums_of_diag=new int[m]; //--------------------------------------------------------------------------- cout<<rus("nВведите элементы массива:nn"); for(i=0;i<n;i++) { for(j=0;j<n;j++) { a[i][j]=-1+random(10); cout<<setw(5)<<a[i][j]; } cout<<endl; } //--------------------------------------------------------------------------- cout<<rus("nСумма элементов в столбцах, которые не содержать отрицательных элементов:nn"); for(j=0;j<n;j++) { all_posit=true; sum[j]=0; for(i=0;i<n;i++) if(a[i][j]<0) { all_posit=false; sum[j]=0; break; } if(all_posit) { for(i=0;i<n;i++) sum[j]+=a[i][j]; } } for(i=0;i<n;i++) { for(j=0;j<n;j++) cout<<setw(5)<<a[i][j]; cout<<endl; } for(i=0;i<n;i++)cout<<setw(5)<<"=";cout<<endl; for(i=0;i<n;i++)cout<<setw(5)<<sum[i]; //--------------------------------------------------------------------------- for(i=q=0;i<n,q<n;i++,q++) //преобразование матрицы { //начало и конец for(j=n-1,w=0;j>=0,w<n;j--,w++) //каждой строки матрицы { //меняются местами buf_a[q][w]=a[i][j]; } } //------------------------- for(q=n-1,m=0;q>0;q--) { s1=0; for(w=0;w<n-1;w++) //сумма элементов диагоналей { //расположенных for(k=q+w;k<n;) //ниже главной диагонали { //матрицы s1+=buf_a[k][w]; break; } } sums_of_diag[m++]=s1; cnt++; } //------------------------- s1=0; for(q=0;q<n;q++) { //сумма элементов for(w=n-1;w>=0;w--) //расположенных на if(q==w) //главной диагонали s1+=buf_a[q][w]; } sums_of_diag[m++]=s1; cnt++; //------------------------- for(w=1,m=cnt;w<n;w++) { s1=0; for(q=0;q<n-1;q++) //сумма элементов диагоналей { //расположенных выше for(k=q+w;k<n;) //главной диагонали { //матрицы s1+=buf_a[q][k]; break; } } sums_of_diag[m++]=s1; cnt++; } cout<<rus("nnКоличество просуммированных диагоналей: ")<<cnt<<endl; cout<<rus("Сумма элементов диагоналей, параллельных побочной диагонали матрицы:nn"); for(m=cnt-1;m>=0;m--) cout<<setw(5)<<sums_of_diag[m]; //--------------------------------------------------------------------------- cout<<rus("nnМинимум среди сумм модулей элементов диагоналей, параллельных побочной диагонали матрицы: "); minsum_of_diag=sums_of_diag[0]; for(m=0;m<cnt;m++) { if(sums_of_diag[m]<minsum_of_diag) minsum_of_diag=sums_of_diag[m]; } cout<<minsum_of_diag; getch(); return 0; } //--------------------------------------------------------------------------- char bufrus[256]; char *rus(const char *text) { CharToOem(text, bufrus); return bufrus; } //---------------------------------------------------------------------------
Результат работы программы: