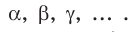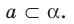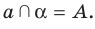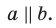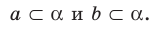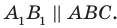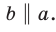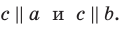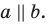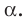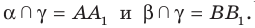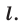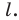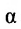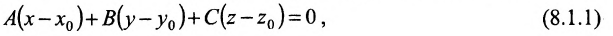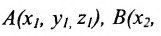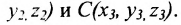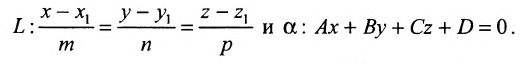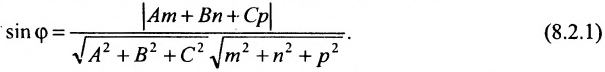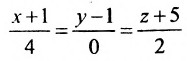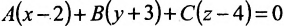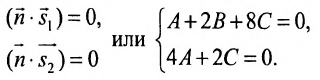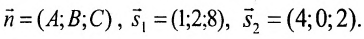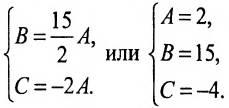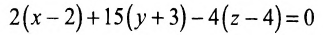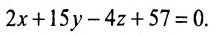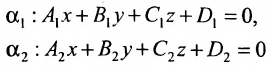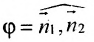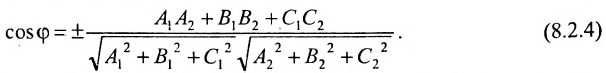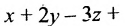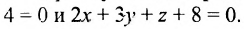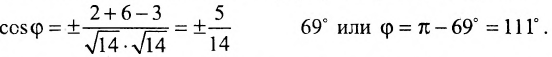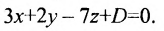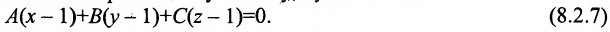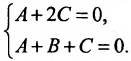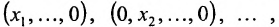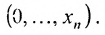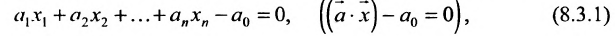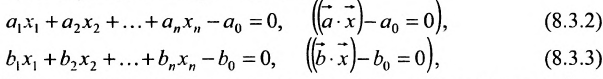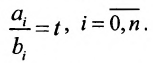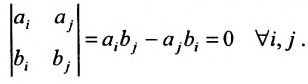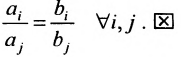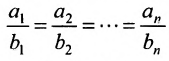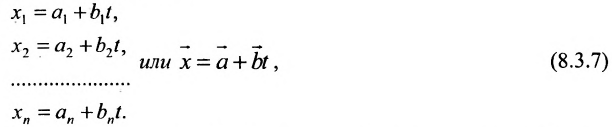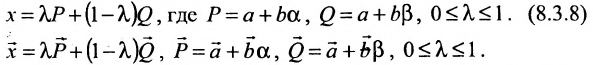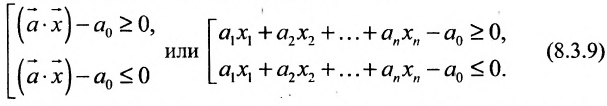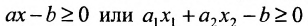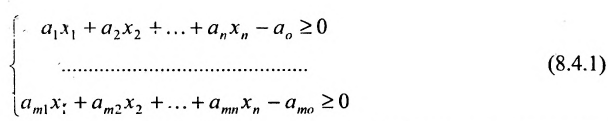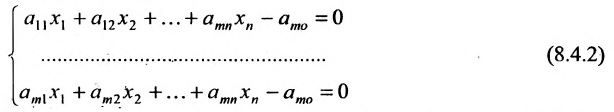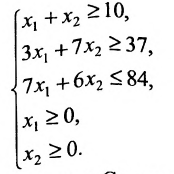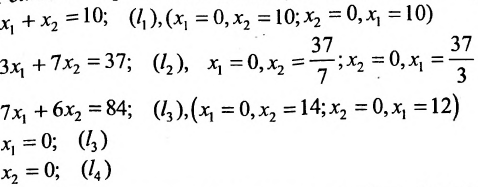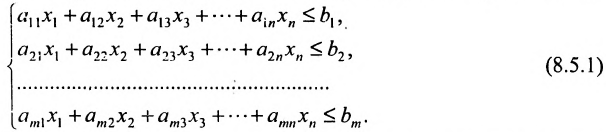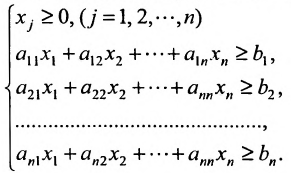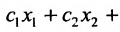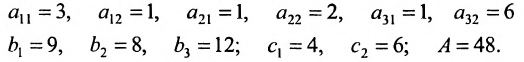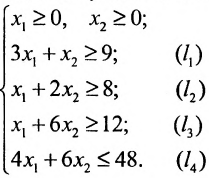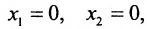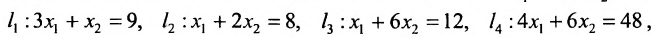Как известно из аксиом стереометрии, если плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Значит, две плоскости или пересекаются, или не пересекаются.
Плоскости, которые не пересекаются, называются параллельными.
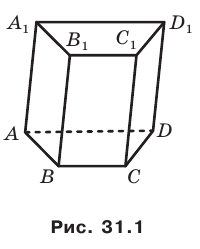
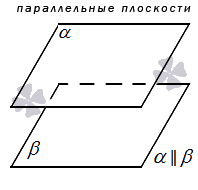
Параллельные плоскости
α
и
β
обозначаются
α∥β
.
Пример:
любая конструкция с полом, потолком и стенами даёт нам представление о параллельных плоскостях — пол и потолок как две параллельные плоскости, боковые стены как параллельные плоскости.
Рис. (1). Стены здания.
Признак параллельности плоскостей.
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
Рис. (2). Доказательство признака параллельности плоскостей.
Доказательство.
Пусть
α
и
β
— данные плоскости,
a1
и
a2
— пересекающиеся прямые в плоскости
α
, а
b1
и
b2
— соответственно параллельные им прямые в плоскости
β
.
Допустим, что плоскости
α
и
β
не параллельны, то есть, они пересекаются по некоторой прямой (c).
Прямая
a1
параллельна прямой
b1
, значит, она параллельна и самой плоскости
β
.
Прямая
a2
параллельна прямой
b2
, значит, она параллельна и самой плоскости
β
(признак параллельности прямой и плоскости).
Прямая (c) принадлежит плоскости
α
, значит, хотя бы одна из прямых —
a1
или
a2
— пересекает прямую (c), то есть имеет с ней общую точку. Но прямая (c) также принадлежит и плоскости
β
, значит, пересекая прямую (c), прямая
a1
или
a2
пересекает плоскость
β
, чего быть не может, так как прямые
a1
и
a2
параллельны плоскости
β
.
Из этого следует, что плоскости
α
и
β
не пересекаются, то есть, они параллельны.
Свойства параллельных плоскостей
Теорема 1. Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.
Рис. (3). Две параллельные плоскости пересечены третьей плоскостью..
Доказательство.
Пусть
α
и
β
— параллельные плоскости, а
γ
— плоскость, пересекающая их.
Плоскость
α
пересекается с плоскостью
γ
по прямой (a).
Плоскость
β
пересекается с плоскостью
γ
по прямой (b).
Линии пересечения (a) и (b) лежат в одной плоскости
γ
и потому могут быть либо пересекающимися, либо параллельными прямыми. Но, принадлежа двум параллельным плоскостям, они не могут иметь общих точек. Следовательно, они параллельны.
Теорема 2. Отрезки параллельных прямых, заключённых между двумя параллельными плоскостями, равны.
Рис. (4). Параллельные прямые пересекают две параллельные плоскости.
Доказательство.
Пусть
α
и
β
— параллельные плоскости, а (a) и (b) — параллельные прямые, пересекающие их.
Через прямые (a) и (b) можно провести плоскость — эти прямые параллельны, значит, определяют плоскость, причём только одну.
Проведённая плоскость пересекается с плоскостью
α
по прямой (AB), а с плоскостью
β
— по прямой (CD).
По предыдущей теореме прямые (AB) и (CD) параллельны. Четырёхугольник (ABCD) есть параллелограмм (у него противоположные стороны параллельны). А раз это параллелограмм, то противоположные стороны у него равны, то есть (BC = AD).
Источники:
Рисунки 2-4. Теоремы о параллельных плоскостях, © ЯКласс.
Содержание:
Параллельность в пространстве
В этом параграфе вы ознакомитесь с основными понятиями стереометрии, аксиомами стереометрии и следствиями из них. Расширите свои представления о многогранниках. Вы узнаете о взаимном расположении двух прямых, прямой и плоскости, двух плоскостей в пространстве. Ознакомитесь с правилами, по которым изображают пространственные фигуры на плоскости.
Основные понятия стереометрии. Аксиомы стереометрии
Изучая математику, вы со многими понятиями ознакомились с помощью определений. Так, из курса планиметрии вам хорошо знакомы определения четырехугольника, трапеции, окружности и др.
Определение любого понятия основано на других понятиях, содержание которых вам уже известно. Например, рассмотрим определение трапеции: «Трапецией называют четырехугольник, у которого две стороны параллельны, а две другие не параллельны». Видим, что определение трапеции основано на таких уже введенных понятиях, как четырехугольник, сторона четырехугольника, параллельные и непараллельные стороны и др. Итак, определения вводятся по принципу «новое основано на старом». Тогда ясно, что должны существовать первоначальные понятия, которым определений не дают. Их называют основными понятиями (рис. 27.1).
В изученном вами курсе планиметрии определения не давали таким фигурам, как точка и прямая. В стереометрии, кроме них, к основным понятиям отнесем еще одну фигуру — плоскость.
Наглядное представление о плоскости дают поверхность водоема в безветренную погоду, поверхность зеркала, поверхность полированного стола, мысленно продолженные во всех направлениях.
Используя понятие плоскости, можно считать, что в планиметрии мы рассматривали только одну плоскость, и все изучаемые фигуры принадлежали этой плоскости. В стереометрии же рассматривают бесконечно много плоскостей, расположенных в пространстве.
Как правило, плоскости обозначают строчными греческими буквами
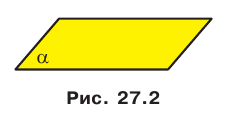
Плоскость, так же как и прямая, состоит из точек, то есть плоскость — это множество точек.
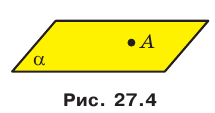
Существует несколько случаев взаимного расположения точек, прямых и плоскостей в пространстве. Приведем примеры.
На рисунке 27.4 изображена точка А, принадлежащая плоскости 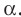
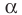
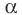
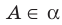
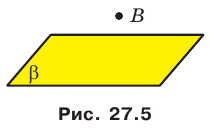
На рисунке 27.5 изображена точка В, не принадлежащая плоскости 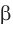
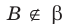
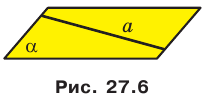
На рисунке 27.6 изображена прямая 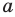
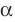
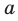
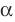
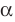
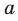
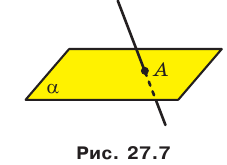
Если прямая и плоскость имеют только одну общую точку, то говорят, что прямая пересекает плоскость. На рисунке 27.7 изображена прямая 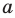
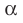
В дальнейшем, говоря «две точки», «три точки», «две плоскости» и т.п., будем иметь в виду, что это разные точки, разные прямые и разные плоскости. Если две плоскости имеют общую точку, то говорят, что эти плоскости пересекаются.
На рисунке 27.8 изображены плоскости 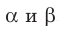
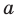
На начальном этапе изучения стереометрии невозможно доказывать теоремы, опираясь на другие утверждения, поскольку этих утверждений еще нет. Поэтому первые свойства, касающиеся точек, прямых и плоскостей в пространстве, принимают без доказательства и называют аксиомами. Отметим, что ряд аксиом стереометрии по формулировкам дословно совпадают со знакомыми вам аксиомами планиметрии.
Например:
- какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей;
- через любые две точки можно провести прямую, и притом только одну.
Мы не будем знакомиться со строгим аксиоматическим построением стереометрии. Рассмотрим лишь некоторые утверждения, выражающие основные свойства плоскостей пространства, основываясь на которых обычно строят курс стереометрии в школе.
Аксиома А1. В любой плоскости пространства выполняются все аксиомы планиметрии.
Если в любой плоскости пространства выполняются аксиомы планиметрии, то выполняются и следствия из этих аксиом, то есть теоремы планиметрии. Следовательно, в стереометрии можно пользоваться всеми известными нам свойствами плоских фигур.
Аксиома А2. Через любые три точки пространства, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Рисунки 27.9-27.11 иллюстрируют эту аксиому.


Из этой аксиомы следует, что три точки пространства, не лежащие на одной прямой, определяют единственную плоскость, про ходящую через эти точки. Поэтому для обозначения плоскости можно указать любые три ее точки, не лежащие на одной прямой.
Например, на рисунке 27.12 изображена плоскость АВС. Запись 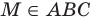
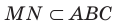
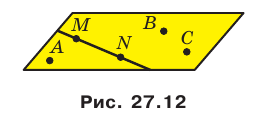
Аксиома АЗ. Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости.
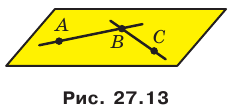
Например, на рисунке 27.13 точки А, В и С принадлежат плоскости АВС. Тогда можно записать: 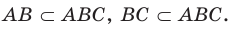
Утверждение, сформулированное в аксиоме АЗ, часто используют на практике, когда хотят проверить, является ли данная поверхность ровной (плоской). Для этого к поверхности в разных местах прикладывают ровную рейку и проверяют, есть ли зазор между рейкой и поверхностью (рис. 27.14).
Аксиома А4. Если две плоскости имеют общую точку, то они пересекаются по прямой.
Эту аксиому можно проиллюстрировать с помощью согнутого листа бумаги или с помощью вашего учебника (рис. 27.15).

Пример:
Докажите, что если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
Решение:
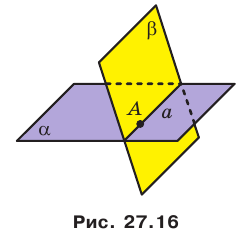
Пусть точка А является общей для двух плоскостей 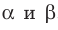
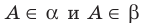
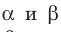
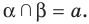
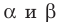
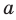
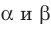

Теорема 27.1. Через прямую и не принадлежащую ей точку проходит плоскость, и притом только одна (рис. 27.17).
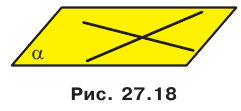
Теорема 27.2. Через две пересекающиеся прямые проходит плоскость, и притом только одна (рис. 27.18).
Из аксиомы А2 и теорем 27.1 и 27.2 следует, что плоскость однозначно определяется:
- тремя точками, не лежащими на одной прямой;
- прямой и точкой, не принадлежащей этой прямой;
- двумя пересекающимися прямыми.
Таким образом, мы указали три способа задания плоскости.
Пространственные фигуры
Начальные сведения о многогранниках. В стереометрии, кроме точек, прямых и плоскостей, рассматривают пространственные фигуры, то есть фигуры, не все точки которых лежат в одной плоскости. Некоторые из пространственных фигур вам уже знакомы. Так, на рисунке 28.1 изображены цилиндр, конус и шар. Подробно эти фигуры вы будете изучать в 11 классе.
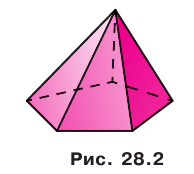
На рисунке 28.2 изображена еще одна знакомая вам пространственная фигура — пирамида. Эта фигура является частным видом многогранника. Примеры многогранников показаны на рисунке 28.3.
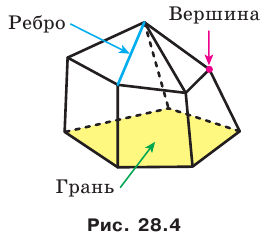
Поверхность многогранника состоит из многоугольников. Их называют гранями многогранника. Стороны многоугольников называют ребрами многогранника, а вершины — вершинами многогранника (рис. 28.4).
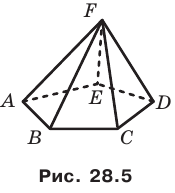
На рисунке 28.5 изображена пятиугольная пирамида FABCDE.
Поверхность этого многогранника состоит из пяти треугольников, которые называют боковыми гранями пирамиды, и одного пятиугольника, который называют основанием пирамиды. Вершину F, общую для всех боковых граней, называют вершиной пирамиды.
Ребра FA, FB, FC, FD и FE называют боковыми ребрами пирамиды, а ребра А В, ВС, CD, DE и ЕА — ребрами основания пирамиды.
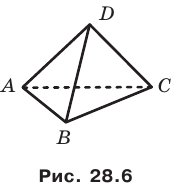
На рисунке 28.6 изображена треугольная пирамида DABC. Треугольную пирамиду называют также тетраэдром.
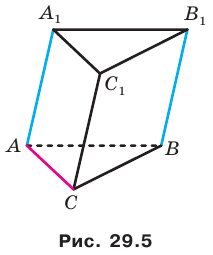
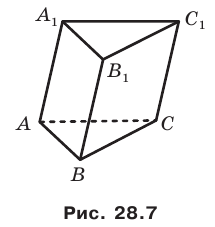
Еще одним частным видом многогранника является призма. На рисунке 28.7 изображена треугольная призма 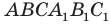
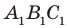
Остальные грани призмы — параллелограммы. Их называют боковыми гранями призмы. Ребра 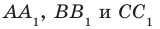
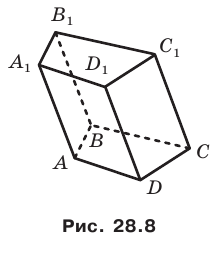
На рисунке 28.8 изображена четырехугольная призма 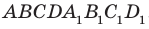
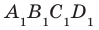
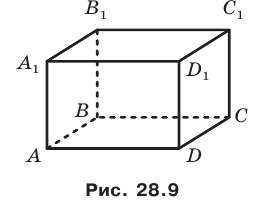
Вы знакомы также с частным видом четырехугольной призмы — прямоугольным параллелепипедом. На рисунке 28.9 изображен прямоугольный параллелепипед 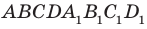
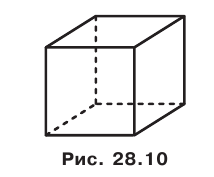
В свою очередь, частным видом прямоугольного параллелепипеда является куб. Все грани куба — равные квадраты (рис. 28.10).
Четырехугольную призму, основанием которой является параллелограмм, называют параллелепипедом.
В курсе геометрии 11 класса вы более подробно ознакомитесь с многогранниками и их частными видами.
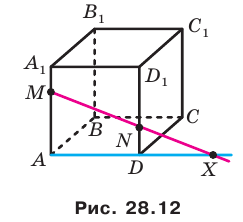
Пример:
На ребрах 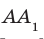
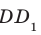
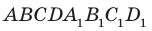
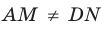
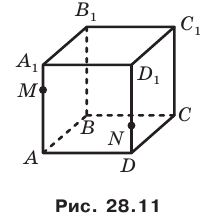
Решение:
Точки М и N принадлежат плоскости 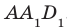
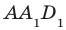
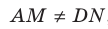
Взаимное расположение двух прямых в пространстве
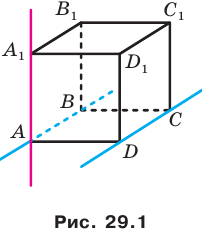
Из курса планиметрии вы знаете, что две прямые называют пересекающимися, если они имеют только одну общую точку. Такое же определение пересекающихся прямых дают и в стереометрии. Вам также известно, что две прямые называют параллельными, если они не пересекаются. Можно ли это определение перенести в стереометрию?
Обратимся к рисунку 29.1, на котором изображен куб 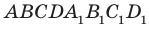
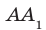
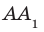
Определение. Две прямые в пространстве называют параллельным и, если они лежат в одной плоскости и не пересекаются. Если прямые 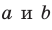
Определение. Две прямые в пространстве называют скрещивающимися, если они не лежат в одной плоскости. Например, на рисунке 29.1 прямые АВ и DC — параллельные, а прямые 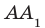
Наглядное представление о параллельных прямых дают колонны здания, корабельный лес, бревна сруба (рис. 29.2).
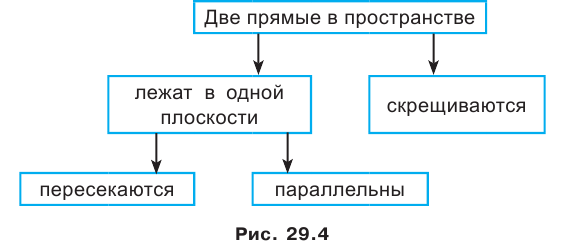
Наглядное представление о скрещивающихся прямых дают провода линий электропередачи, различные элементы строительных конструкций (рис. 29.3). Итак, существуют три возможных случая взаимного расположения двух прямых в пространстве (рис. 29.4):
- прямые пересекаются;
- прямые параллельны;
- прямые скрещиваются.
Два отрезка называют параллельными (скрещивающимися), если они лежат на параллельных (скрещивающихся) прямых. Например, ребра 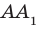
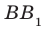
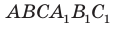
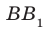
Теорема 29.1. Через две параллельные прямые проходит плоскость, и притом только одна.
Доказательство. Пусть даны параллельные прямые 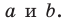
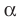
Существование плоскости 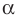
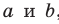
Если предположить, что существует еще одна плоскость, проходящая через прямые 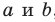
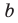
Существует три способа задания плоскости. Теорему 29.1 можно рассматривать как еще один способ задания плоскости — с помощью двух параллельных прямых.
Установить параллельность двух прямых, лежащих в одной плоскости, можно с помощью известных вам из курса планиметрии признаков параллельности двух прямых. А как установить, являются ли две прямые скрещивающимися? Ответить на этот вопрос позволяет следующая теорема.
Теорема 29.2 (признак скрещивающихся прямых). Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не принадлежащей первой прямой, то данные прямые — скрещивающиеся (рис. 29.6).
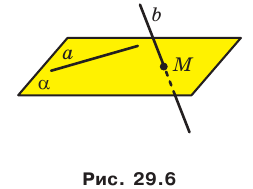
На рисунке 29.7 ребра АВ и DC тетраэдра DABC являются скрещивающимися. Действительно, прямая DC пересекает плоскость АВС в точке С, не принадлежащей прямой АВ. Следовательно, по признаку скрещивающихся прямых прямые АВ и DC являются скрещивающимися.
Параллельность прямой и плоскости
Вам уже известны два возможных случая взаимного расположения прямой и плоскости:
- прямая принадлежит плоскости, то есть все точки прямой принадлежат плоскости;
- прямая пересекает плоскость, то есть прямая имеет с плоскостью только одну общую точку.
Понятно, что возможен и третий случай, когда прямая и плоскость не имеют общих точек. Например, прямая, содержащая ребро 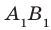
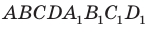
Определение. Прямую и плоскость называют параллельными, если они не имеют общих точек.
Если прямая 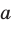
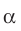
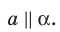
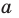
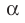
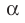
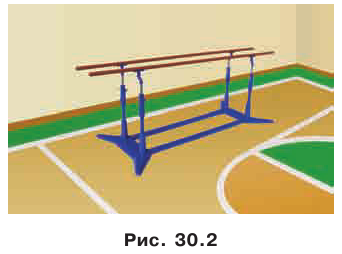
Наглядное представление о прямой, параллельной плоскости, дают некоторые спортивные снаряды. Например, брусья параллельны плоскости пола (рис. 30.2). Другой пример — водосточная труба: она параллельна плоскости стены (рис. 30.3).
Выяснять, параллельны ли данные прямая и плоскость, с помощью определения затруднительно. Гораздо эффективнее пользоваться следующей теоремой.
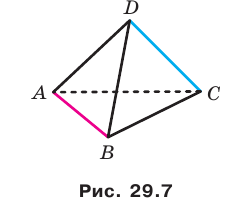
Теорема 30.1 (признак параллельности прямой и плоскости). Если прямая, не принадлежащая данной плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то данная прямая параллельна самой плоскости.
Например, на рисунке 30.1 прямые 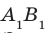
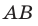
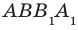
Поскольку 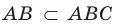
Отрезок называют параллельным плоскости, если он принадлежит прямой, параллельной этой плоскости. Например, ребро АВ куба параллельно плоскости 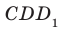
Вы умеете устанавливать параллельность двух прямых с помощью теорем-признаков, известных из планиметрии. Рассмотрим теоремы, описывающие достаточные условия параллельности двух прямых в пространстве.
Теорема 30.2. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то прямая пересечения плоскостей параллельна данной прямой.
На рисунке 30.4 прямая 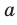
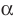
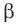
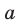
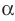
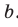
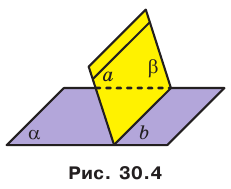
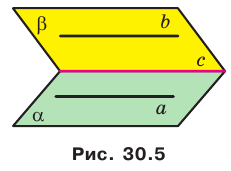
Теорема 30.3. Если через каждую из двух параллельных прямых проведена плоскость, причем эти плоскости пересекаются по прямой, отличной от двух данных, то эта прямая параллельна каждой из двух данных прямых.
На рисунке 30.5 прямые 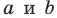
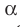
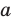
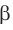
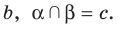
Теорема 30.4. Две прямые, параллельные третьей прямой, параллельны между собой.
Пример:
Докажите, что если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна прямой их пересечения.
Решение:
Пусть даны прямая 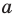
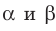
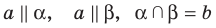
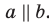
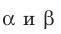
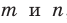
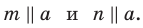
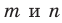
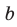
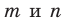
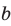
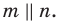
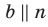
- Заказать решение задач по высшей математике
Параллельность плоскостей
Рассмотрим варианты возможного взаимного расположения двух плоскостей. Вы знаете, что две плоскости могут иметь общие точки, то есть пересекаться. Понятно, что две плоскости могут и не иметь общих точек. Например, плоскости АВС и 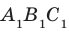
Определение. Две плоскости называют параллельны ми, если они не имеют общих точек.
Если плоскости 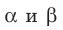
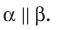
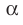
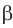
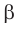
Наглядное представление о параллельных плоскостях дают потолок и пол комнаты; поверхность воды, налитой в аквариум, и его дно (рис. 31.2).
Из определения параллельных плоскостей следует, что любая прямая, лежащая в одной из двух параллельных плоскостей, параллельна другой плоскости.
В тех случаях, когда надо выяснить, являются ли две плоскости параллельными, удобно пользоваться следующей теоремой.
Теорема 31.1 (признак параллельности двух плоскостей). Если две пересекающиеся прямые одной плоскости параллельны соответственно двум прямым другой плоскости, то эти плоскости параллельны.
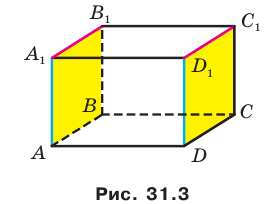
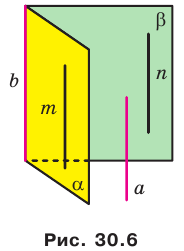
Например, на рисунке 31.3 изображен прямоугольный параллелепипед 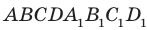
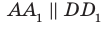
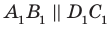
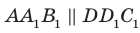
Будем говорить, что два многоугольника параллельны, если они лежат в параллельных плоскостях. Например, грани 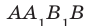
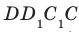
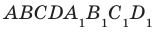
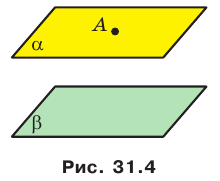
Теорема 31.2. Через точку в пространстве, не принадлежащую данной плоскости, проходит плоскость, параллельная данной плоскости, и притом только одна (рис. 31.4).
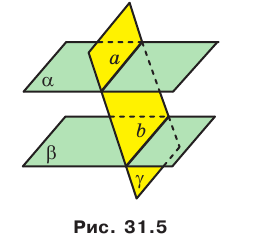
Теорема 31.3. Прямые пересечения двух параллельных плоскостей третьей плоскостью параллельны (рис. 31.5).
Пример:
Докажите, что отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Решение:
Пусть даны параллельные плоскости 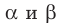
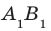
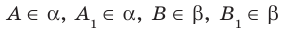
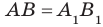
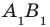
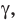
По теореме 31.3 получаем: 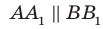
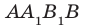
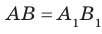
Параллельное проектирование
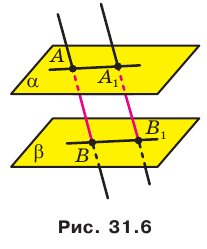
Многие явления и процессы, наблюдаемые нами в повседневной жизни, служат примерами преобразований, при которых образом пространственной фигуры является плоская фигура. Увидеть одно из таких явлений можно в солнечную погоду, когда предмет отбрасывает тень на плоскую поверхность (рис. 32.1). Этот пример иллюстрирует преобразование фигуры, которое называют параллельным проектированием. С помощью этого преобразования на плоскости создают изображения пространственных фигур.

Многие рисунки настоящего учебника, на которых изображены пространственные фигуры, можно рассматривать как тени, отбрасываемые на плоскость страницы предметами, освещенными параллельными лучами. Ознакомимся подробнее с параллельным проектированием.
Пусть даны плоскость 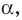
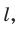
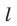
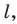
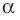
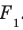
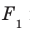
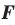
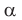
Выбирая выгодные положения плоскости 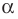
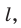
Пусть даны плоскость 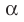
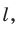
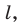
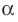
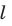
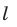
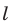
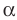
В следующих теоремах будем рассматривать прямые и отрезки, не параллельные прямой 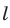
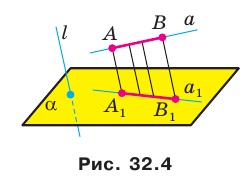
Теорема 32.1. Параллельной проекцией прямой является прямая; параллельной проекцией отрезка является отрезок (рис. 32.4).
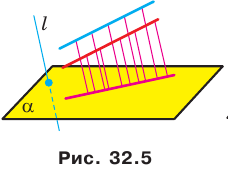
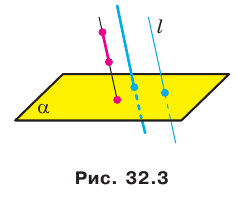
Теорема 32.2. Параллельной проекцией двух параллельных прямых являются или прямая (рис. 32.5), или две параллельные прямые (рис. 32.6). Параллельные проекции двух параллельных отрезков лежат на одной прямой или на параллельных прямых (рис. 32.6).
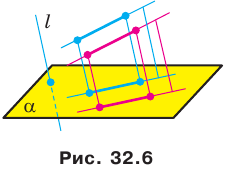
Теорема 32.3. Отношение параллельных проекций отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению самих отрезков (рис. 32.7).
Рассмотрим изображения некоторых многоугольников на плоскости 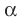
Если прямая 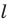
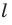
Из свойств параллельного проектирования следует, что параллельной проекцией треугольника является треугольник (рис. 32.8).
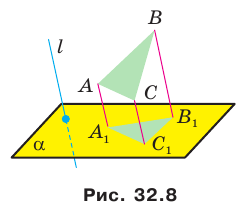
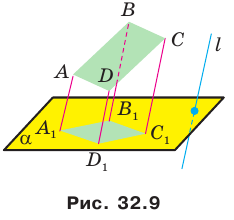
Поскольку при параллельном проектировании сохраняется параллельность отрезков, то изображением параллелограмма (в частности, прямоугольника, ромба, квадрата) является параллелограмм (рис. 32.9).
Также из свойств параллельного проектирования следует, что изображением трапеции является трапеция.
Параллельной проекцией окружности является фигура, которую называют эллипсом (рис. 32.10).
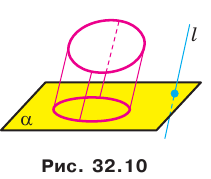
Изображения объектов с помощью параллельного проектирования широко используют в самых разных областях промышленности, например в автомобилестроении (рис. 32.11).

Основные аксиомы стереометрии
- А1. В любой плоскости пространства выполняются все аксиомы планиметрии.
- А2. Через любые три точки пространства, не лежащие на одной прямой, проходит плоскость, и притом только одна.
- АЗ. Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости.
- А4. Если две плоскости имеют общую точку, то они пересекаются по прямой.
Плоскость однозначно определяется:
- тремя точками, не лежащими на одной прямой;
- прямой и точкой, не принадлежащей этой прямой;
- двумя пересекающимися прямыми;
- двумя параллельными прямыми.
Взаимное расположение двух прямых в пространстве
- Две прямые называют пересекающимися, если они имеют только одну общую точку.
- Две прямые в пространстве называют параллельными, если они лежат в одной плоскости и не пересекаются.
- Две прямые в пространстве называют скрещивающимися, если они не лежат в одной плоскости.
Свойство параллельных прямых
Через две параллельные прямые проходит плоскость, и притом только одна.
Признак скрещивающихся прямых
Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не принадлежащей первой прямой, то данные прямые — скрещивающиеся.
Параллельность в пространстве
Прямую и плоскость называют параллельными, если они не имеют общих точек. Две плоскости называют параллельными, если они не имеют общих точек.
Признак параллельности прямой и плоскости
Если прямая, не принадлежащая данной плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то данная прямая параллельна самой плоскости.
Условия параллельности двух прямых в пространстве
- Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то прямая пересечения плоскостей параллельна данной прямой.
- Если через каждую из двух параллельных прямых проведена плоскость, причем эти плоскости пересекаются по прямой, от личной от двух данных, то эта прямая параллельна каждой из двух данных прямых.
- Две прямые, параллельные третьей прямой, параллельны между собой.
Признак параллельности двух плоскостей
Если две пересекающиеся прямые одной плоскости параллельны соответственно двум прямым другой плоскости, то эти плоскости параллельны.
Свойства параллельных плоскостей
Через точку в пространстве, не принадлежащую данной плоскости, проходит плоскость, параллельная данной плоскости, и притом только одна.
Прямые пересечения двух параллельных плоскостей третьей плоскостью параллельны.
Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
- Перпендикулярность в пространстве
- Векторы и координаты в пространстве
- Множества
- Рациональные уравнения
- Числовые последовательности
- Предел числовой последовательности
- Предел и непрерывность числовой функции одной переменной
- Функции, их свойства и графики
Геометрия, 10 класс
Урок №6. Параллельность плоскостей
Перечень вопросов, рассматриваемых в теме
- Определение параллельных плоскостей;
- Свойства параллельных плоскостей;
- Признак параллельности плоскостей.
Глоссарий по теме
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.
Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.
Определение. Плоскости, которые не пересекаются, называются параллельными.
Основная литература:
Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии 10 Москва «Просвещение» 2013 год. С. 1-4.
Дополнительная литература:
Зив Б. Г. Геометрия 10 класс Дидактические материалы Москва «Просвещение» 2013 год. С.4, 14, 24
Теоретический материал для самостоятельного изучения
Как известно из аксиом стереометрии, если плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Значит две плоскости или пересекаются, или не пересекаются.
Определение. Плоскости, которые не пересекаются, называются параллельными.
Параллельные плоскости α и β обозначаются α∥β.
Изображение:
Пример 1.
Любая конструкция с полом, потолком и стенами даёт нам представление о параллельных плоскостях – пол и потолок как две параллельные плоскости, боковые стены как параллельные плоскости.

Доказательство.
Пусть α и β – данные плоскости, a1 и a2 – пересекающиеся прямые в плоскости α, а b1 и b2 соответственно параллельные им прямые в плоскости β.
Допустим, что плоскости α и β не параллельны, то есть они пересекаются по некоторой прямой c.
Прямая a1 параллельна прямой b1, значит она параллельна и самой плоскости β.
Прямая a2 параллельна прямой b2, значит она параллельна и самой плоскости β (признак параллельности прямой и плоскости).
Прямая c принадлежит плоскости α, значит хотя бы одна из прямых a1 или a2 пересекает прямую c, то есть имеет с ней общую точку. Но прямая c также принадлежит и плоскости β, значит, пересекая прямую c, прямая a1 или a2 пересекает плоскость β, чего быть не может, так как прямые a1 и a2 параллельны плоскости β.
Из этого следует, что плоскости α и β не пересекаются, то есть они параллельны.
Теорема доказана.
Свойства параллельных плоскостей.

Доказательство.
Пусть α и β – параллельные плоскости, а γ- плоскость, пересекающая их.
Плоскость α пересекается с плоскостью γ по прямой a.
Плоскость β пересекается с плоскостью γ по прямой b.
Линии пересечения a и b лежат в одной плоскости γ и потому могут быть либо пересекающимися, либо параллельными прямыми. Но, принадлежа двум параллельным плоскостям, они не могут иметь общих точек. Следовательно, они параллельны.

Доказательство.
Пусть α и β – параллельные плоскости, а a и b – параллельные прямые, пересекающие их.
Через прямые a и b можно провести плоскость – эти прямые параллельны, значит определяют плоскость, причём только одну.
Проведённая плоскость пересекается с плоскостью α по прямой AB, а с плоскостью β по прямой CD.
По предыдущей теореме прямые AB и CD параллельны. Четырехугольник ABCD есть параллелограмм (у него противоположные стороны параллельны). А раз это параллелограмм, то противоположные стороны у него равны, то есть BC=AD.
Теорема 3. Если прямая пересекает одну из двух параллельных плоскостей, то она пересекает и другую.
Доказательство.
Пусть α||β, a пересекает α в точке А.
Выберем в плоскости любую точку C. Через эту точку и прямую a проведём плоскость.
Так как плоскость имеет с плоскостями α и β общие точки A и C соответственно, то она пересекает эти плоскости по некоторым прямым b и c, которые проходят соответственно через точки A и C. По предыдущей теореме прямые b и c параллельны. Тогда в плоскости прямая a пересекает (в точке A) прямую b, которая параллельна прямой c. Значит, прямая a пересекает и прямую c в некоторой точке B. Так как прямая c лежит в плоскости, то точка B является точкой пересечения прямой a и плоскости. Теорема доказана.

Доказательство.
Пусть α||β, α и γ пересекаются.
Докажем, что плоскости β и γ пересекаются.
Проведём в плоскости γ прямую a, пересекающую плоскость α в некоторой точке B. Тогда по теореме 3 прямая a пересекает и плоскость β в некоторой точке A. Следовательно, плоскости β и γ имеют общую точку A, т. е. пересекаются. Теорема доказана.
Теорема 5. Через точку, не лежащую в данной плоскости, можно провести плоскость, параллельную данной, и притом только одну.
Доказательство.
Пусть нам даны плоскость α и точка М, ей не принадлежащая.
Докажем, что существует плоскость β, которой принадлежит точка М, параллельная плоскости α.

Докажем методом от противного, что β — единственная плоскость, удовлетворяющая условию теоремы.
Допустим, что через точку M проходит другая плоскость, например β1, параллельная α.
Так как β1 пересекает плоскость β (они имеют общую точку M), то по теореме 4 плоскость β1 пересекает и плоскость α (β ‖ α). Мы пришли к противоречию. Таким образом, предположение о том, что через точку M можно провести плоскость, отличную от плоскости β и параллельную плоскости α, неверно. Значит, плоскость β — единственна. Теорема доказана.
Рассмотрим несколько примеров на применение данных свойств.
Пример 2.
Даны две пересекающиеся прямые a и b точка А, не лежащая в плоскости этих прямых. Докажите, что через точку А проходит плоскость, параллельная прямым a и b, и притом только одна.
Доказательство.
Прямые a и b пересекаются по условию, следовательно, по следствию из аксиомы А1, эти прямые единственным образом определяют плоскость α.
Известно, что через точку А, не принадлежащую плоскости α, проходит единственная плоскость, параллельная α, т.е. параллельная прямым a и b (по теореме 5) .
Пример 3.
Плоскости α и β параллельны, прямая m лежит в плоскости α. Докажите, что прямая m параллельна плоскости β.
Доказательство.
Предположим, что прямая m пересекает плоскость β в точке М. Тогда точка М принадлежит плоскости α (т.к. прямая m лежит в плоскости α) и М принадлежит плоскости β, значит, α и β пересекаются, но они параллельны по условию. Очевидно, m не пересекает плоскость α, т.е. параллельна ей.
Примеры и разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте

Доказательство.
Докажем параллельность А1В1 и А2В2.
Рассмотрим плоскость, проходящую через прямые А1А2 и В1В2
(она существует и единственная, т.к. прямые пересекаются).
В этой плоскости лежит четырехугольник А1В1А2В2, диагонали которого точкой пересечения делятся пополам. Следовательно, данный четырехугольник является параллелограммом (признак параллелограмма), значит, А1В1 и А2В2 параллельны.
Аналогично доказывается параллельность В1С1 и В2С2. Из вышеперечисленного следует, что плоскости А1В1С1 и А2В2С2 параллельны по признаку параллельности плоскостей.
Верное решение:
Докажем параллельность А1В1 и А2В2.
Рассмотрим плоскость, проходящую через прямые А1А2 и В1В2
(она существует и единственная, т.к. прямые пересекаются).
В этой плоскости лежит четырехугольник А1В1А2В2, диагонали которого точкой пересечения делятся пополам. Следовательно, данный четырехугольник является параллелограммом (признак параллелограмма), значит, А1В1 и А2В2 параллельны.
Аналогично доказывается параллельность В1С1 и В2С2. Из вышеперечисленного следует, что плоскости А1В1С1 и А2В2С2 параллельны по признаку параллельности плоскостей.
№2.
Тип задания: выделение цветом
Два равнобедренных треугольника FKС и FKD с общим основанием FK расположены так, что точка С не лежит в плоскости FKD. Определите взаимное расположение прямых, содержащих медианы треугольников, проведенных к сторонам KС и KD.
Решение:
Прямые, которые содержат медианы треугольников к KC и KD- выходят из одной точки F. Соответственно, можно сделать вывод, что данные прямые пересекаются.
Ответ:
1) они параллельны
2) скрещиваются
3) пересекаются
Одним из важнейших этапов в проведении ремонта является работа по выравниванию пола. Для этого, следует определить уровень пола, наличие неровностей на его поверхности и выбрать метод для устранения данных дефектов. Об особенностях определения уровня пола поговорим далее.
Блок: 1/9 | Кол-во символов: 286
Источник: http://strport.ru/poly/kak-opredelit-uroven-pola
Содержание
- 1 Проверка ровности пола
- 2 Вступление
- 3 Определяем перепад высот: шаг за шагом
- 4 Допустимые показатели кривизны для разных видов напольных покрытий
- 5 Методы вычисления ровности поверхности
- 5.1 Для более точного определения степени ровности пола используются лазерный уровень или гидроуровень
- 6 Проверяем уклон пола с помощью прави́ла с пузырьковым уровнем
- 7 Используем лазерный уровень
- 7.1 Как выставить уровень пола ротационным уровнем
- 7.2 Как измерить уровень пола с помощью оптического оборудования
Проверка ровности пола
Определить имеются ли на поверхности основания впадины или выступы можно при помощи специальной деревянной рейки, имеющей название – «правило».
Специфика задачи требует от такого инструмента соответствия двум характеристикам: длина от 2 метров, а также идеально ровная поверхность прикладываемых к полу частей.
Блок: 2/5 | Кол-во символов: 356
Источник: https://polspec.com/vyravnivanie-i-styazhka/kak-proverit-rovnost-pola-sposoby-proverki-na-praktike.html
Вступление
Для начала хочу отметить, что проверка пола на просвет или стяжки на просвет определяет только неровности основания и не является измерением его уклона. Для проверки пола «на просвет» достаточно длинного правила. Для измерения уклона необходим невилир, лазерный уровень или водный уровень. Проверка на просвет, она же проверка бугристости пола это самый простой и нужный способ измерений пола. Проверить ровный пол или нет можно двумя способами.
Блок: 2/4 | Кол-во символов: 463
Источник: https://opolax.ru/podgotovka-pola/proverka-pola-na-prosvet
Определяем перепад высот: шаг за шагом
Для начала давайте научимся определять кривизну пола при помощи обычного реечного уровня-линейки. Этот навык – бесценен, ведь вы не знаете, где и в каких условиях вам придется что-то измерять.
Итак, теперь шаг за шагом:
- Шаг 1. Наводим порядок в том помещении, где будем работать. Никакого строительного мусора или посторонних предметов там быть не должно – все это немало мешает поиску точной высоты будущей стяжки.
- Шаг 2. Проводим по стенам линию базового уровня – по всему периметру. Она должна быть строго параллельна полу, для чего мы рекомендуем вам использовать современный лазерный уровень или просто создать через две точки параллельный полу отрезок и продолжать его по стенам, пока не соедините его с началом.
- Шаг 3. Теперь проверяем от базового уровня высоту пола в разных частях помещения. Так мы найдем самую высокую точку покрытия, от которой и будем отталкиваться.
- Шаг 4. Теперь поднимаем линию (или чертим новую) так, чтобы она оказалась выше самой высокой точки ровно на метр.
- Шаг 5. Далее рисуем третью линию – линию чистового пола. Она будет ниже предыдущей по значению такой формулы: «100-х(толщина будущей стяжки)=?». Например, если стяжка у вас планируется 3 см высотой, тогда опускать уровень нужно на 97 см, а если 5 см – тогда на 95 см.
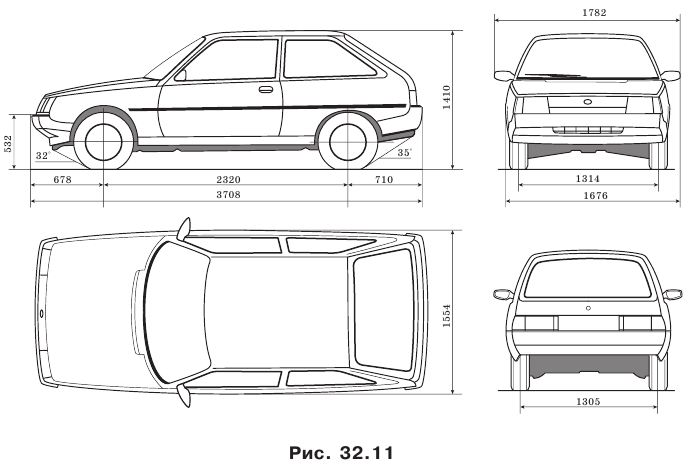
Если же у вас хороший прибор в наличии есть, тогда измеряем кривизну пола им. Важно правильно сделать и настройку уровня – это обеспечит нужную точность в замере кривизны. Так, если есть возможность выбрать определенный угол сканирования, то его стоит выбрать, а не довольствоваться тем, что и вертикальный луч для потолка вроде бы показывает ровную линию для чистового пола. Удобнее всего в этом плане работать с теми приборами, у которых есть функция самонастройки.
Итак, вот как выглядит работа с лазерным нивелиром:
- Шаг 1. Убираем с пола всю грязь и мусор, чтобы обеспечить точность результатов измерения.
- Шаг 2. Устанавливаем на пол прибор – желательно в самой высокой точке пола.
- Шаг 3. Направляем луч вдоль стены.
- Шаг 4. Как только лазерный уровень установлен окончательно, начинайте отмечать линии на всех стенах так, как это будет удобно вам. Насколько высоко или низко получается лазерные точки-линии – это не важно, их не сложно перенести на нужную высоту при помощи рулетки.
- Шаг 5. Когда обнаружите самый высокий участок пола, закрепите на нем малярный шнур, и натяните его вторым концом до отметок уровня на противоположных и соседних стенах. Если шнур свободно натянут в любом направлении – бугров нигде нет, и именно эту точку можно брать за точку отсчета. Если шнур наткнулся еще на что-то – внимательно осмотрите это место, возможно, выступающая площадь невелика и есть смысл просто сколоть этот выступ молотком с зубилом. Если нет – тогда переместите отметку самой высокой точки пола сюда.
- Шаг 6. Как только мы определились с самым высоким участком пола, поднимаем точку на 5 см – это и есть отметка будущей стяжки. Или еще проще: поднимаем на 100 см, т.е. на высоту всего правила, отмечаем на стенах и опускаем линии ровно на 95 см.
Совет: для глаз смотреть на лазер от нивелиров небезопасно – обязательно надевайте специальные очки. Обычно они идут в комплекте с нивелиром.
А теперь по отбитому уровню ставим маяки, по которым мы и будем выравнивать пол:
Блок: 3/4 | Кол-во символов: 3257
Источник: https://pol-master.com/viravniv-stazhka/vyravnivanie-pola-svoimi-rukami.html
Допустимые показатели кривизны для разных видов напольных покрытий
Согласно действующим в нашей стране нормативам допускаемая кривизна основания пола при использовании различных видов напольных покрытий может быть следующей:
- для полов с покрытием из мягких рулонных материалов, поливинилхлоридных плиток, паркета или ламината кривизна не должна превышать 0,2 см;
- для полов с покрытием из твёрдых плиточных материалов и мозаичных составов неровности могут быть в пределах 0,4 см.
На любом приобретаемом напольном покрытии должна указываться допустимая кривизна поверхности для укладки. Не пренебрегайте рекомендуемыми параметрами, поскольку укладка напольного покрытия на поверхности с неровностями, превышающими рекомендуемые, приведёт к преждевременной порче лицевого покрытия.
Блок: 3/3 | Кол-во символов: 778
Источник: http://mainstro.ru/kak-opredelit-rovnost-sushhestvuyushhego-pola-ili-monolitnoj-styazhki/
Методы вычисления ровности поверхности
В настоящее время существует два метода проверки ровности пола на просвет:
- Определение кривизны с использованием только рейки правила.
- Определение кривизны при помощи правила с деревянными брусками на концах.
Первый метод измерений проводится следующим образом:
- Для вычислений используется большое двухметровое правило.
- Инструмент укладывается на пол в любом месте.
- Затем нужно посмотреть, есть ли зазор между плоскостью пола и рейкой правила.
- При наличии зазора нужно измерять его высоту рулеткой. Для устройства качественных полов величина зазора не должна превышать 0,2 см. При зазорах большего размера основание пола нуждается в дополнительном выравнивании перед укладкой чистового слоя.
- После выполнения одного замера инструмент сдвигают в другое место на полу и проводят аналогичные измерения там. Двигая инструмент по всей плоскости пола в помещении, можно составить общее представление о степени ровности поверхности и о потребности проведения дальнейших работ по её выравниванию.
Может случиться ситуация, когда правило будет располагаться на большом выступе на плоскости пола. Тогда его невозможно расположить так, чтобы удобно было провести точный замер кривизны, поэтому данный способ измерений не является самым точным. Но в помещениях с небольшой неровностью пола он является достаточным для проведения измерительных работ.
Второй метод измерений позволяет вычислять кривизну пола даже с большими выступами и неровностями. Для предотвращения зависания инструмента на бугре на правило с обоих концов крепятся деревянные бруски. Но тогда измерения ведут несколько по-другому, поскольку просвет между полом и инструментом будет в любом случае. Вычисления проводят в таком порядке:
- На правило длиной два метра с обоих концов крепим небольшие бруски одинакового размера.
- Затем укладываем прибор на плоскость пола в нужном месте.
- Выполняем замеры величины зазора при помощи рулетки.
- Затем от этого числа нужно отнять величину высоты брусков. Так мы получим показатель кривизны пола.
Иногда при проведении измерений в одном месте показатель кривизны может быть в пределах нормы, а при сдвиге инструмента вправо или влево кривизна превышает допустимый показатель. Это значит, что пол в данном помещении нуждается в предварительном выравнивании перед укладкой отделочного слоя.
Блок: 2/3 | Кол-во символов: 2324
Источник: http://mainstro.ru/kak-opredelit-rovnost-sushhestvuyushhego-pola-ili-monolitnoj-styazhki/
Для более точного определения степени ровности пола используются лазерный уровень или гидроуровень
Лазерный уровень представляет собой довольно сложный и дорогостоящий прибор, в то время как гидроуровень можно изготовить самостоятельно (естественно, точность первого выше). Принцип действия гидроуровня основан на законе сообщающихся сосудов (уровень жидкости в них будет одинаковым, если кто не помнит). Таким образом, гидроуровень представляет собой довольно длинный шланг, на обоих концах которого размещены стеклянные или пластиковые колбы. Шланг заполняется жидкостью таким образом, чтобы она была видна в обеих колбах.
В обоих случаях (и при использовании лазерного уровня и при использовании гидроуровня) нам понадобится обозначить стартовую отметку на стене. Как правило, это обычная точка, обозначенная примерно на уровне груди. От стартовой точки выстраивается линия горизонта по всему периметру помещения (отметить ее можно как единичными метками, так и сплошной линией).
Работая с гидроуровнем, вам понадобится напарник: один конец шланга необходимо держать на стартовой метке, в то время, как вторым отмечаются точки линии горизонта.
После того как линия горизонта отчерчена, определить степень ровности пола не составит труда. Ваша задача заключается в том, чтобы замерить расстояние от линии до плоскости пола в разных точках периметра. Минимальное расстояние – наивысшая точка, максимальное – низшая. Разница между ними – перепад высот на полу. Если он больше 2 мм, то с укладкой ламината следует повременить до осуществления выравнивания.
Обратите внимание, что точные результаты данный метод обеспечивает вдоль стены. Оптимальный вариант, использование обоих изложенных методов, так как работа с рейкой может осуществляться и в глубине комнаты.
Блок: 3/3 | Кол-во символов: 1763
Источник: http://DekorMyHome.ru/remont-i-oformlenie/proverka-rovnosti-polov.html
Проверяем уклон пола с помощью прави́ла с пузырьковым уровнем
Необходимо прави́ло 1,5-2,5 м с пузырьковым уровнем или прави́ло и пузырьковый уровень отдельно, который который приложим к нему (на него) сверху. Или хотя бы метровый уровень, но это уже, если совсем ничего нет, точность будет приблизительная.
Правило с пузырьковым уровнем — прекрасный инструмент для проверки плоскостей на перепады
Прикладывая правило в разных точках пола можно определить её отклонения от горизонтали (в данном случае горизонтали, можно и нужно и вертикаль им мерить).
Начинать удобнее с углов. Первым делом нужно найти самую высокую точку (это может быть не точка, а некоторого размера плоскость) и от неё дальше найти самую низкую.
Блок: 4/5 | Кол-во символов: 719
Источник: https://chonemuzhik.ru/kak-proverit-izmerit-perepad-pola.html
Используем лазерный уровень
Лазерный уровень стоит дорого, и работать с ним на порядок сложнее, но затраты со временем будут компенсированы качеством измерений. Лазерный уровень имеет преимущество в том, что его функционал позволяет провести лазерными лучами и линию горизонта и линию пола при внесении соответствующих настроек.
Как уже говорилось выше, расхождение между измеренными участками не должно быть более 2 миллиметров. При таких показателях можно будет начинать процесс укладки напольного покрытия. Также стоит понимать, что строительные уровни позволяют произвести замеры только вдоль стен. Так как проверить ровность пола необходимо по всей площади основания, то применять уровень и правило необходимо совместно и тогда результаты измерений будут максимально точными.
Итог
Статья подробно описывает работу со строительным уровнем и правилом. Если возникают какие-либо трудности, то всегда можно обратиться к специалистам. Качество в этом случае будет неоспоримо самым лучшим и новенькую облицовку можно показать на фото или похвастаться ею перед гостями. Любая строительная компания начинает свою работу со стадии замером и расчетов, потому владельцу не придется выполнять какие-либо действия самостоятельно.
Блок: 5/5 | Кол-во символов: 1263
Источник: https://polspec.com/vyravnivanie-i-styazhka/kak-proverit-rovnost-pola-sposoby-proverki-na-praktike.html
Как выставить уровень пола ротационным уровнем
С помощью ротационного устройства удается не только измерять кривизну пола, но и выставлять и проектировать полученные результаты. Данное оборудование чаще всего используется профессионалами, из-за его дороговизны. В процессе вращения, происходит его превращение в линию, горизонтального или вертикального характера. Дальнейшие работы проводятся с помощью рейки.
У ротационных нивелиров присутствует довольно сложный механизм работы, в котором находятся светодиодные лампочки. В таком случае, удается одновременно осуществлять несколько проекций в одной плоскости. Различают несколько разновидностей ротационных инструментов для измерения уровня пола:
- ручной инструмент;
- маятниковые детали;
- электронное оборудование.
С помощью последнего варианта удается одновременно измерять более пяти плоскостей. Электронные механизмы очень чувствительны даже к самым маленьким погрешностям, так как у них имеется несколько датчиков. Кроме того, некоторые устройства являются комбинированными, например, маятниковый и электронный механизм.
Ротационный нивелир отличается небольшим спектром действий, однако он обладает самой высокой точностью, из всех вышеперечисленных устройств.
Блок: 5/9 | Кол-во символов: 1228
Источник: http://strport.ru/poly/kak-opredelit-uroven-pola
Как измерить уровень пола с помощью оптического оборудования
Оптические нивелирные устройства более распространены для измерений территориальных участков снаружи помещения. Однако, их использование в процессе определения кривизны пола вполне реально.
Принцип работы данного оборудования вполне схож с ротационным устройством. Однако, используя его в помещении с большой площадью, точность полученных результатов у него будет выше, нежели у ротационного.
Недостатком использования данного прибора вступает тот факт, что для его работы потребуется минимум два человека. Стоимость данного оборудования также очень высокая, более дешевые модели обойдутся минимум в двести долларов, а профессиональные установки будут стоить более тысячи долларов.
Блок: 6/9 | Кол-во символов: 744
Источник: http://strport.ru/poly/kak-opredelit-uroven-pola
Кол-во блоков: 14 | Общее кол-во символов: 16011
Количество использованных доноров: 8
Информация по каждому донору:
- https://polspec.com/vyravnivanie-i-styazhka/kak-proverit-rovnost-pola-sposoby-proverki-na-praktike.html: использовано 2 блоков из 5, кол-во символов 1619 (10%)
- http://DekorMyHome.ru/remont-i-oformlenie/proverka-rovnosti-polov.html: использовано 1 блоков из 3, кол-во символов 1763 (11%)
- https://tradinghub.ru/5-sposobov-proverit-osnovanie-pola-na-rovnost/: использовано 1 блоков из 2, кол-во символов 1156 (7%)
- https://chonemuzhik.ru/kak-proverit-izmerit-perepad-pola.html: использовано 2 блоков из 5, кол-во символов 2393 (15%)
- https://pol-master.com/viravniv-stazhka/vyravnivanie-pola-svoimi-rukami.html: использовано 1 блоков из 4, кол-во символов 3257 (20%)
- http://mainstro.ru/kak-opredelit-rovnost-sushhestvuyushhego-pola-ili-monolitnoj-styazhki/: использовано 2 блоков из 3, кол-во символов 3102 (19%)
- http://strport.ru/poly/kak-opredelit-uroven-pola: использовано 3 блоков из 9, кол-во символов 2258 (14%)
- https://opolax.ru/podgotovka-pola/proverka-pola-na-prosvet: использовано 1 блоков из 4, кол-во символов 463 (3%)
|
Поделитесь в соц.сетях: |
Оцените статью:
|
Параллельные плоскости, признак и условия параллельности плоскостей
В данной статье будут изучены вопросы параллельности плоскостей. Дадим определение плоскостям, которые параллельны между собой; обозначим признаки и достаточные условия параллельности; рассмотрим теорию на иллюстрациях и практических примерах.
Параллельные плоскости: основные сведения
Параллельные плоскости – плоскости, не имеющие общих точек.
Чтобы обозначить параллельность применяют такой символ: ∥ . Если заданы две плоскости: α и β , являющиеся параллельными, краткая запись об этом будет выглядеть так: α ‖ β .
На чертеже, как правило, плоскости, параллельные друг другу, отображаются как два равных параллелограмма, имеющих смещение относительно друг друга.
В речи параллельность можно обозначить так: плоскости α и β параллельны, а также – плоскость α параллельна плоскости β или плоскость β параллельна плоскости α .
Параллельность плоскостей: признак и условия параллельности
В процессе решения геометрических задач зачастую возникает вопрос: а параллельны ли заданные плоскости между собой? Для получения ответа на этот вопрос используют признак параллельности, который также является достаточным условием параллельности плоскостей. Запишем его как теорему.
Плоскости являются параллельными, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
Доказательство этой теоремы приводится в программе геометрии за 10 – 11 класс.
В практике для доказательства параллельности, в том числе, применяют две следующие теоремы.
Если одна из параллельных плоскостей параллельна третьей плоскости, то другая плоскость или также параллельна этой плоскости, или совпадает с ней.
Если две несовпадающие плоскости перпендикулярны некоторой прямой, то они параллельны.
На основе этих теорем и самого признака параллельности доказывается факт параллельности любых двух плоскостей.
Рассмотрим подробнее необходимое и достаточное условие параллельности плоскостей α и β , заданных в прямоугольной системе координат трехмерного пространства.
Допустим, что в некоторой прямоугольной системе координат задана плоскость α, которой соответствует общее уравнение A 1 x + B 1 y + C 1 z + D 1 = 0 , а также задана плоскость β , которую определяет общее уравнение вида A 2 x + B 2 y + C 2 z + D 2 = 0 .
Для параллельности заданных плоскостей α и β необходимо и достаточно, чтобы система линейных уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 не имела решения (являлась несовместной).
Предположим, что заданные плоскости, определяемые уравнениями A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 являются параллельными, а значит не имеют общих точек. Таким образом, не существует ни одной точки в прямоугольной системе координат трехмерного пространства, координаты которой отвечали бы условиям одновременно обоих уравнений плоскостей, т.е. система A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 не имеет решения. Если указанная система не имеет решений, тогда не существует ни одной точки в прямоугольной системе координат трехмерного пространства, чьи координаты одновременно отвечали бы условиям обоих уравнений системы. Следовательно, плоскости, заданные уравнениями A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 не имеют ни одной общей точки, т.е. они параллельны.
Разберем использование необходимого и достаточного условия параллельности плоскостей.
Заданы две плоскости: 2 x + 3 y + z – 1 = 0 и 2 3 x + y + 1 3 z + 4 = 0 . Необходимо определить, являются ли они параллельными.
Решение
Запишем систему уравнений из заданных условий:
2 x + 3 y + z – 1 = 0 2 3 x + y + 1 3 z + 4 = 0
Проверим, возможно ли решить полученную систему линейных уравнений.
Ранг матрицы 2 3 1 2 3 1 1 3 равен одному, поскольку миноры второго порядка равны нулю. Ранг матрицы 2 3 1 1 2 3 1 1 3 – 4 равен двум, поскольку минор 2 1 2 3 – 4 отличен от нуля. Таким образом, ранг основной матрицы системы уравнений меньше, чем ранг расширенной матрицы системы.
Совместно с этим, из теоремы Кронекера-Капелли следует: система уравнений 2 x + 3 y + z – 1 = 0 2 3 x + y + 1 3 z + 4 = 0 не имеет решений. Этим фактом доказывается, что плоскости 2 x + 3 y + z – 1 = 0 и 2 3 x + y + 1 3 z + 4 = 0 являются параллельными.
Отметим, что, если бы мы применили для решения системы линейных уравнений метод Гаусса, это дало бы тот же результат.
Ответ: заданные плоскости параллельны.
Необходимое и достаточное условие параллельности плоскостей возможно описать по-другому.
Чтобы две несовпадающие плоскости α и β были параллельны друг другу необходимо и достаточно, чтобы нормальные векторы плоскостей α и β являлись коллинеарными.
Доказательство сформулированного условия базируется на определении нормального вектора плоскости.
Допустим, что n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) являются нормальными векторами плоскостей α и β соответственно. Запишем условие коллинеарности данных векторов:
n 1 → = t · n 2 ⇀ ⇔ A 1 = t · A 2 B 1 = t · B 2 C 1 = t · C 2 , где t – некое действительное число.
Таким образом, чтобы несовпадающие плоскости α и β с заданными выше нормальными векторами были параллельны, необходимо и достаточно, чтобы имело место действительное число t , для которого верно равенство:
n 1 → = t · n 2 ⇀ ⇔ A 1 = t · A 2 B 1 = t · B 2 C 1 = t · C 2
В прямоугольной системе координат трехмерного пространства заданы плоскости α и β . Плоскость α проходит через точки: A ( 0 , 1 , 0 ) , B ( – 3 , 1 , 1 ) , C ( – 2 , 2 , – 2 ) . Плоскость β описывается уравнением x 12 + y 3 2 + z 4 = 1 Необходимо доказать параллельность заданных плоскостей.
Решение
Удостоверимся, что заданные плоскости не совпадают. Действительно, так и есть, поскольку координаты точки A не соответствуют уравнению плоскости β .
Следующим шагом определим координаты нормальных векторов n 1 → и n 2 → , соответствующие плоскостям α и β . Также проверим условие коллинеарности этих векторов.
Вектор n 1 → можно задать, взяв векторное произведение векторов A B → и A C → . Их координаты соответственно: ( – 3 , 0 , 1 ) и ( – 2 , 2 , – 2 ) . Тогда:
n 1 → = A B → × A C → = i → j → k → – 3 0 1 – 2 1 – 2 = – i → – 8 j → – 3 k → ⇔ n 1 → = ( – 1 , – 8 , – 3 )
Для получения координат нормального вектора плоскости x 12 + y 3 2 + z 4 = 1 приведем это уравнение к общему уравнению плоскости:
x 12 + y 3 2 + z 4 = 1 ⇔ 1 12 x + 2 3 y + 1 4 z – 1 = 0
Таким образом: n 2 → = 1 12 , 2 3 , 1 4 .
Осуществим проверку, выполняется ли условие коллинеарности векторов n 1 → = ( – 1 , – 8 , – 3 ) и n 2 → = 1 12 , 2 3 , 1 4
Так как – 1 = t · 1 12 – 8 = t · 2 3 – 3 = t · 1 4 ⇔ t = – 12 , то векторы n 1 → и n 2 → связаны равенством n 1 → = – 12 · n 2 → , т.е. являются коллинеарными.
Ответ: плоскости α и β не совпадают; их нормальные векторы коллинеарные. Таким образом, плоскости α и β параллельны.
Плоскость в трехмерном пространстве с примерами решения
Содержание:
Общее уравнение плоскости:
Пусть
которое называется уравнением плоскости, проходящей через точку 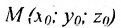
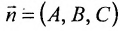

где 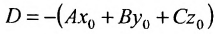
Приведём уравнение плоскости (8.1.2) к специальному виду. Для этого перенесём свободный член в правую часть уравнения: 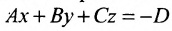
Разделим обе части уравнения на —D получим:
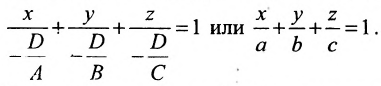
Это и есть специальный вид уравнения плоскости или уравнение плоскости “в отрезках”, где а, b, с – величины отрезков, которые отсекает плоскость на координатных осях.
Если плоскость проходит через точки 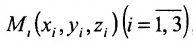
Разложив данный определитель по элементам первой строки, придём к уравнению вида (8.1.1).
Уравнения (8.1.1), (8.1.3), (8.1.4) можно привести к виду (8.1.2).
Пример:
Составить уравнение плоскости, проходящей через точки А(0, -2, -1), В(2, 4, -2) и С(3, 2, 0).
Решение:
Воспользуемся формулой (8.1.4), где
Подставив координаты точек A, В и С, получим: 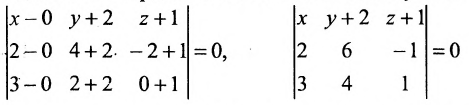
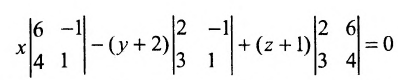
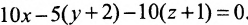
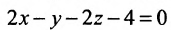
Взаимное расположение двух плоскостей, прямой и плоскости
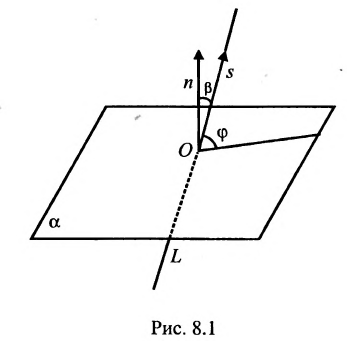
Углом между прямой и плоскостью будем называть угол, образованный прямой и ее проекцией на плоскость (рис. 8.1). Пусть прямая L и плоскость а заданы уравнениями:
Рассмотрим направляющий вектор 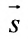
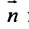
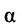
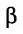
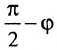
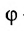
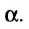
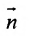
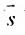
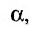
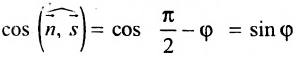
Если угол 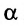
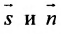
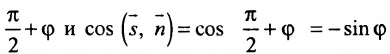
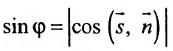
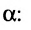
Условие перпендикулярности прямой и плоскости. Прямая и плоскость перпендикулярны тогда и только тогда, когда направляющий вектор 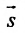
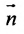
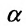
Условие параллельности прямой и плоскости. Прямая L и плоскость 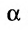
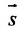
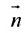
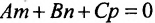
Пример:
Написать уравнение плоскости, проходящей через точку 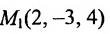
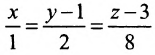
Решение:
Так как 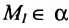
Применяя условие параллельности (8.2.3) прямой и плоскости, получим систему линейных уравнений
где
Решив систему, найдем:
Подставив найденные значения коэффициентов А,В,С, полУ
чим искомое уравнение плоскости:
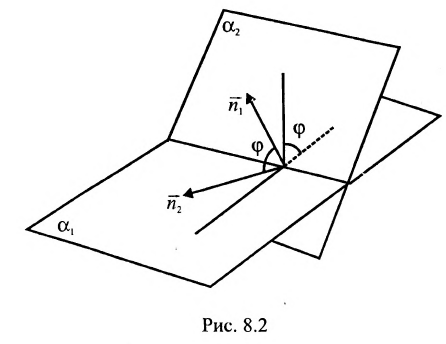
Угол между плоскостями. Рассмотрим две плоскости 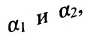
Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно,
что угол между нормальными векторами 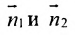
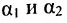
или 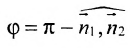
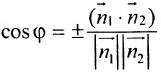
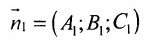
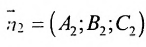
Пример:
Определить угол между плоскостями
Решение:
Воспользовавшись формулой (8.2.4), получим:
Условие параллельности двух плоскостей. Две плоскости 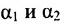
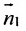
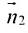
Векторы параллельны, если их координаты пропорциональны:
Две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы 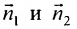
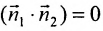
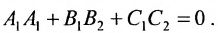
Пример:
Составить уравнение плоскости, проходящей через точку M(-2, 1, 4) параллельно плоскости 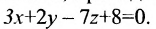
Решение:
Уравнение плоскости будем искать в виде 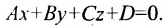
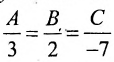
Так как 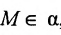
Пример:
Составить уравнение плоскости, проходящей через точки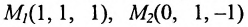
Решение:
Так как 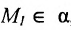
Далее, так как 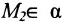
Учитывая, что заданная плоскость перпендикулярна искомой, составим еще одно уравнение: A+B+С=0. Получим систему:
Выразив коэффициенты А и В через С: А = -2 С, В=С и подставив их в уравнение (8.2.7), -2С (х-1)+С (у-1)+С (z-l)=0, определяем искомое уравнение: —2х + у +z = 0 .
Понятие гиперплоскости
Взаимное расположение гиперплоскостей:
Рассмотрим n-мерное векторное пространство Пусть вектор 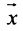
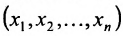
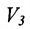
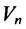
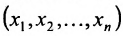
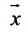
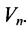
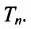
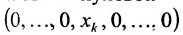
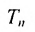
Совокупность точек 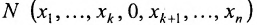
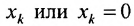
Определение 8.3.1. Гиперплоскостью в п-мериом пространстве 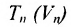
где 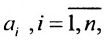
Заметим, что все 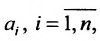
Рассмотрим две гиперплоскости:
Множество точек, принадлежащих как первой, так и второй гиперплоскости, называется их пересечением.
Теорема 8.3.1. Две гиперплоскости (8.3.2) и (8.3.3) не пересекаются в том и только в том случае, когда коэффициенты при соответствующих неизвестных пропорциональны, а свободные члены находятся в ином отношении:
Доказательство. Пусть гиперплоскости (8.3.2) и (8.3.3) не пересекаются. Следовательно, они не имеют общих точек и система
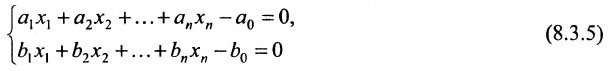
И наоборот, если система несовместна, то гиперплоскости (8.3.2) и (8.3.3) не пересекаются.
В силу теоремы Кронекера- Капелли система (8.3.5) несовместна, если ранг матрицы не равен рангу расширенной матрицы системы. А так как ранг расширенной матрицы системы не больше 2, то ранг матрицы системы должен ть равен 1. Эта возможность выражается условием (8.3.4).Поскольку для того, чтобы матрица 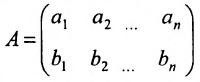
Ранг матрицы 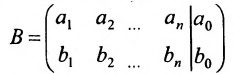
Теорема 8.3.2. Для того, чтобы уравнения (8.3.2) и (8.3.3) определят одну и ту же гиперплоскость, необходимо и достаточно, чтобы выполнялись условия:
Доказательство. Достаточность. Пусть условия (8.3.6) выполнены. Обозначим отношения через t, т.е.
Тогда уравнение (8.3.2) можно получить из (8.3.3) умножением всех его членов на t. Поэтому уравнения равносильны и, следовательно, определяют одну и ту же гиперплоскость.
Необходимость. Пусть уравнения (8.3.2) и (8.3.3) определяют одну и ту же гиперплоскость. Система (8.3.5) совместна и, следовательно, ранг матрицы системы равен рангу расширенной матрицы. И т.к. эта система определяет одну гиперплоскость, то каждое из уравнений можно рассматривать как систему. Поэтому ранг этой системы равен 1 и все миноры второго порядка равны нулю, т.е.
Откуда следует, что
Определение 8.3.2. Две гиперплоскости называются параллель-ными, если они не пересекаются или совпадают.
Тогда из теорем 8.3.1 и 8.3.2 вытекает
Теорема 8.3.3. Две гиперплоскости (8.3.2) и (8.3.3) параллельны тогда и только тогда, когда соответствующие коэффициенты
пропорциональны, т.е.
Введем понятие прямой в n мерном пространстве по аналогии с параметрическими уравнениями прямой в трехмерном пространстве.
Определение 8.3.3. Прямой в 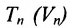
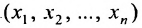
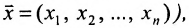
где 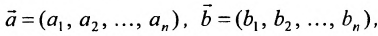
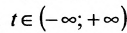
Определение 8.3.4. Отрезком в 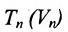
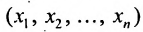
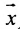
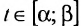
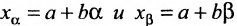
Теорема 8.3.4. Всякая точка отрезка может быть выражена линейной комбинацией его концов:
Если в трехмерном пространстве провести плоскость, то она разделит его на две части, называемые полупространствами. Очевидно, и гиперплоскость разделит n-мерное пространство на полупространства, т.е. справедливо.
Определение 8.3.5. Полупространствами, порождаемыми гиперплоскостью 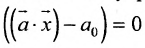
Гиперплоскость принадлежит обоим полупространствам, является их общей частью. Из (8.3.9) следует, что любое линейное неравенство геометрически определяет полупространство соответствующей размерности.
Определение 8.3.6. Множество точек 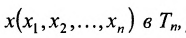
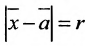
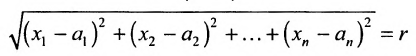
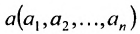
Системы m линейных неравенств с n неизвестными
В элементарной математике мы познакомились с линейными неравенствами одного или двух переменных:
Решением таких неравенств является промежуток числовой оси или полуплоскость.
Рассмотрим теперь линейное неравенство с n переменными:
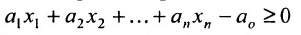
Несколько неравенств, рассматриваемых совместно, образуют систему:
Определение 8.4.1. Областью решений системы т неравенств с п неизвестными называется множество точек пространства 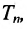
Из того факта, что областью решения линейного неравенства является полупространство, вытекает
Теорема 8.4.1. Область решений системы линейных неравенств есть пересечение некоторого числа полупространств.
Это пересечение является выпуклым множеством; оно ограничено гиперплоскостями
Так как линейные неравенства (8.4.1) независимы, то система (8.4.2) при m-n будет либо определённой, либо несовместной. И, следовательно, пересечение n гиперплоскостей в n-мерном пространстве либо даёт точку, либо не содержит ни одной точки.
Так как число систем по n уравнений с n неизвестными, которое может быть получено из (8.4.2) не может быть сколь угодно большим, и так как не всякая точка пересечения гиперплоскостей (является решением) принадлежит пересечению всех m гиперплоскостей, то число крайних точек, т.е. точек пересечения гиперплоскостей, принадлежащих данному множеству, ограничено. Следовательно, рассматриваемое множество будет многогранником, а крайние точки – его вершинами.
Итак, .областью решений совместной системы линейных нера-qchqtb является выпуклый многогранник, гранями которого служат некоторые части гиперплоскостей.
Пример:
Найти решение системы линейных неравенств
Решение:
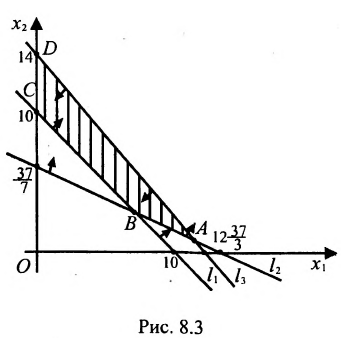
Строим на плоскости 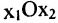
соответствующие заданным неравенствам (рис. 8.3). Каждая из них делит плоскость на две полуплоскости, одна из которых является решением соответствующего неравенства. Для выбора полуплоскости, являющейся решением неравенства, подставляем начало координат О (0, 0) в каждое неравенство. Если получаем верное неравенство, то полуплоскость, содержащая начало координат, является решением неравенства, в противном случае – полуплоскость, не содержащая начало координат, является решением неравенства.
Стрелки указывают полуплоскости, являющиеся областями решений данных неравенств. Пересечение отмеченных полуплоскостей- заштрихованный четырехугольник АВСД на рис. 8.3- область решения данной системы.
Применение систем линейных неравенств в экономических исследованиях
Рассмотрим систему m линейных неравенств с n переменными:
Каждое неравенство системы определяет полупространство. Решением системы (8.5.1) является пересечение этих полупространств.
Системы линейных неравенств широко применяются во многих экономических задачах, в частности, при построении линейной модели производства. Производственный способ описывает производство продукции и расход ресурсов в единицу времени. Он математически задается вектором выпуска или вектором валовой продукции 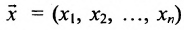
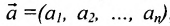
Если в производственной системе используется m видов производственных ресурсов, определены запасы ресурса i при использовании j-той технологии, то модель производственной системы математически приобретает вид системы линейных неравенств (8.5.1), в которой 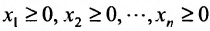
Пример:
Пусть известно содержание питательных веществ в единице каждого из имеющихся в хозяйстве кормов. Известна также цена каждого корма. Требуется определить все возможные рационы для кормления скота, которые удовлетворяли бы суточную потребность в каждом питательном веществе, а общая стоимость используемых кормов не превосходила бы A.
Решение:
Введем обозначения: m — число питательных веществ; n — число изменяющихся видов кормов; 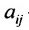
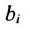
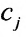
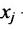
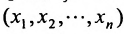
Задача рациона формулируется следующим образом: определить рацион 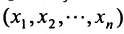
стоимость которого ограничена величиной А: 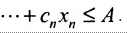
Например, пусть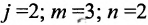
Тогда получаем систему:
Определим множество решений данной системы на плоскости 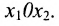
(рис. 8.4) соответствующие данным неравенствам. Каждая из них делит плоскость на две полуплоскости, одна из которых является решением соответствующего неравенства. Для выбора полуплоски являющейся решением неравенства, подставляем 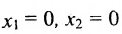
Если получаем верное неравенство, то полуплоскость, содержащая начало координат, является решением неравенства, в противном случае – полуплоскость, не содержащая начало координат, является решением неравенства.
Стрелки на прямых указывают полуплоскости, являющиеся областями решений данных неравенств. Заштрихованный четырехугольник 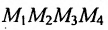
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Функция одной переменной
- Производная функции одной переменной
- Приложения производной функции одной переменной
- Исследование поведения функций
- Ранг матрицы – определение и вычисление
- Определители второго и третьего порядков и их свойства
- Метод Гаусса – определение и вычисление
- Прямая линия на плоскости и в пространстве
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Глава 32. Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей
Один из углов f между плоскостями A1x + B1y + C1z + D1 = 0 и
A2x +B2y + C2z + D2 = 0 (рис. 2.18.1) равен углу между их нормальными векторами 

Найти угол между плоскостями x – y + 21/2z + 2 = 0 и x + y +21/2z – 3 = 0.
Условие параллельности плоскостей
Две плоскости параллельны тогда и только тогда, когда их нормальные векторы 

Определить, параллельны ли плоскости 2x–3y–4z+11=0 и –4x+6y+8z+36=0.
Плоскости параллельны, так как
Условие перпендикулярности плоскостей
Если две плоскости заданы уравнениями A1x1 + B1y1 + C1z1 + D = 0, A2x2 + B2y2 + C2z2 + D = 0, то условием их перпендикулярности является
A1A2 + B1B2 + C1C2 = 0.
Если плоскости перпендикулярны, то перпендикулярны и их нормальные векторы N1 и N2.
Определить перпендикулярны ли плоскости 3x–2y–2z+7=0 и 2x+2y+z+4=0.
Так как 3×2+(–2)×2+(–2) ×1=0, то заданные плоскости перпендикулярны.
Плоскость, проходящая через данную точку параллельно данной плоскости
Плоскость, проходящая через точку M1(x1;y1;z1) и параллельная плоскости Ax+By+Cz+D=0, представляется уравнением
A(x–x1) + B(y–y1) + C(z–z1) = 0.
Написать уравнение плоскости, проходящей через точку (2;–1;6) параллельно плоскости x+y–2z+5=0.
(x–2) + (y+1) –2(z–6) = 0, т. е. x + y – 2z + 11 = 0.
Плоскость, проходящая через две точки перпендикулярно к данной плоскости
Плоскость P, проходящая через две точки M0(x0,y0,z0) и M1(x1,y1,z1) перпендикулярно к плоскости Q, заданной уравнением Ax+By+Cz+D=0, представляется уравнением
Написать уравнение плоскости, проходящей через две точки: M0(1;2;3) и M1(2;1;1) перпендикулярно к плоскости 3x+4y+z–6=0.
Плоскость представляется уравнением:

Расстояние от точки до плоскости
Расстояние от точки M1(x1;y1;z1) до плоскости Ax+By+Cz+D=0 равно
Найти расстояние от точки (3;9;1) до плоскости x–2y+2z–3=0.
[spoiler title=”источники:”]
http://www.evkova.org/ploskost-v-trehmernom-prostranstve
http://matica.org.ua/metodichki-i-knigi-po-matematike/vysshaia-matematika-uchebnoe-posobie/glava-32-ugol-mezhdu-dvumia-ploskostiami-usloviia-parallelnosti-i-perpendikuliarnosti-dvukh-ploskostei
[/spoiler]