Прямоугольник
Частным видом параллелограмма является прямоугольник.
Прямоугольником называют параллелограмм, у которого все углы прямые
ABCD – прямоугольник.
Особое свойство прямоугольника
Диагонали прямоугольника равны
Доказательство
Дано: ABCD – прямоугольник
Доказать: AC = DB
Доказательство:
Рассмотрим 
ABD иACB: ABCD – прямоугольник, 
А и B – прямые, ABD иACB – прямоугольные. AD = CB (по свойству параллелограмма). AB – общий катет, ABD =ACB (по двум катетам). А в равных треугольниках против соответственно равных углов лежат равные стороны, значит, AC = DB, что и требовалось доказать.
Теорема
Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник
Доказательство
Дано: ABCD – параллелограмм, AC = DB
Доказать: ABCD – прямоугольник
Доказательство:
Рассмотрим ABD иACB:
AC = DB (по условию), AD = BC (по свойству параллелограмма), AB – общая, ABD =ACB (по трем сторонам). А в равных треугольниках против соответственно равных сторон лежат равные углы, A = B. А в параллелограмме противоположные углы равны, значит A = C и В = D, A = В = C = D (1). A + В + C + D = 360 0 (2)(т.к. параллелограмм выпуклый четырёхугольник). Следовательно, из (2), учитывая (1), получаем, что A = В = C = D = 90 0 , ABCD – прямоугольник, что и требовалось доказать.
Теорема
Если один из углов параллелограмма прямой, то этот параллелограмм – прямоугольник
Доказательство
Дано: ABCD – параллелограмм, A = 90 0
Доказать: ABCD – прямоугольник
Доказательство:
Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 0 , т.е. A + В = 180 0 , В = 180 0 – A = 180 0 – 90 0 = 90 0
Противолежащие углы параллелограмма равны, A = C = 90 0 и В = D = 90 0
Итак: ABCD – параллелограмм (по условию), и все его углы прямые (по доказанному выше), ABCD – прямоугольник (по определению), что и требовалось доказать.
Две теоремы, доказанные выше, называют признаками прямоугольника.
Поделись с друзьями в социальных сетях:
Параллельность прямых
О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение параллельности прямых
Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.
Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.
Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.
Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.
На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Свойства и признаки параллельных прямых
Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.
Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.
Если секущая проходит через две параллельные прямые, то:
-
два внутренних односторонних угла образуют в сумме 180°:
∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.
два внутренних накрест лежащих угла равны между собой:
два соответственных угла равны между собой:
∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.
Если секущая образует перпендикуляр с одной из параллельных прямых, то она будет перпендикулярна и другой.
Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.
А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.
Задача 1
Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.
Решение
Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.
Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.
Задача 2
Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.
Решение
Поскольку а II b, значит ∠MKD + ∠KDN = 180°.
Соответственно, ∠MKD = 180° – ∠KDN = 180° – 150° = 30°.
Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.
Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.
Геометрия. 7 класс
Конспект урока
Признаки параллельности прямых
Перечень рассматриваемых вопросов:
- Параллельные прямые.
- Накрест лежащие, соответственные, односторонние углы.
- Признаки параллельности прямых.
- Решение задач на доказательство параллельности прямых.
Две прямые на плоскости называются параллельными, если они не пересекаются.
Признаки параллельности двух прямых:
1. Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.
2. Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.
3. Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
Вы уже знаете, что при пересечении двух прямых секущей образуются углы:
- накрест лежащие: 3 и 6, 4 и 5.
- односторонние: 3 и 5, 4 и 6.
- соответственные: 1 и 5, 3 и 7, 2 и 6; 4 и 8.
Прямая c называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.
Рассмотрим и докажем признаки параллельности прямых.
Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.
Дано: прямые a и b, секущая AB, ∠ 1 = ∠ 2 накрест лежащие.
В этом случае две прямые, перпендикулярные к третьей не пересекаются, т. е. параллельны.
2 случай: ∠ 1= ∠ 2 ≠ 90°
1) Из середины O отрезка AB проведём перпендикуляр OH к прямой а. На прямой b от точки B отложим отрезок BH1, равный отрезку AH и проведем отрезок OH1.
2) AO = OB т. к. O середина AB; AH = BH1 по построению; ∠1 = ∠2 по условию. Тогда ΔOHA = ΔOH1B по первому признаку равенства треугольников.
Далее следует из равенства треугольников: ∠3 = ∠4 и ∠5 = ∠6.
3) Из равенства углов ∠3 и ∠4 следует, что точка H1 лежит на продолжении луча OH. Это значит, что точки H1, O, H лежат на одной прямой.
4) Из равенства ∠5 и ∠6 следует, что ∠6 = 90°. Это значит, что прямые a и b перпендикулярны к третьей НН1, а значит, по теореме о двух прямых, перпендикулярных к третьей, не пересекаются, т. е. параллельны.
Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.
Дано: прямые a и b, секущая AB, ∠1 = ∠2 соответственные.
∠1 = ∠2 – по условию и ∠2 = ∠3 – по свойству вертикальных углов.
Значит, ∠1 = ∠3, это накрест лежащие углы, следовательно, a║b по теореме 1.
Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.
Прямые a и b, секущая AB, ∠1 + ∠2 = 180° ‑ односторонние.
∠3 +∠2 = 180°– по свойству смежных углов, откуда ∠3 = 180° – ∠2.
∠1 + ∠2 = 180 ° по условию, откуда ∠1 = 180° – ∠2.
Тогда ∠1 = ∠3, это накрест лежащие углы, следовательно, a║b по теореме 1.
Разбор заданий тренировочного модуля.
Дано: ∠1= 60°, ∠2 = 120°.
- ∠2 и ∠3 смежные, ∠3 = 180° – 120° = 60° по свойству смежных углов;
- ∠3 = ∠1, это накрест лежащие углы;
- Значит, прямые a и b параллельны по 1 признаку параллельности прямых.
Ответ: прямые a и b параллельны по 1 признаку параллельности прямых.
Дано: ΔABC – равнобедренный, ∠А = 60°. CD – биссектриса ∠BCK.
Докажите: AB ║ CD.
- ∠A = ∠C = 60° – углы при основании равнобедренного Δ–ка равны.
- ∠BCK и ∠С смежные. ∠BCK = 180° – 60°= 120° – по свойству смежных углов.
- ∠BCD = ∠CDK = 60° т. к. CD – биссектриса делит угол пополам.
- Значит, ∠A = ∠DCK = 60° ‑ соответственные, следовательно, AB║CD по 2 признаку параллельности прямых.
Ответ: AB║CD по 2 признаку параллельности прямых.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/parallelnost-pryamyh
http://resh.edu.ru/subject/lesson/7298/conspect/
[/spoiler]
Сколько параллельных линий имеет прямоугольник?
Ответ: прямоугольник имеет 2 пары параллельных сторон.
Что такое параллельные прямые в прямоугольнике?
Резюме урока
А прямоугольник имеет две пары параллельных прямых. Квадрат также имеет две пары параллельных прямых. Параллелограмм также имеет две пары параллельных прямых. Чтобы найти параллельные линии, ищите линии, которые идут в одном направлении и никогда не пересекаются.
Как найти параллельную прямую прямоугольника?
Сколько параллельных линий имеет квадрат?
две пары Квадрат имеет две пары параллельных сторон, значит, это параллелограмм; на рисунке мы видим, что overline{AB} параллелен overline{CD}, а overline{AC} параллелен overline{BD}. Квадрат также имеет 4 прямых угла, следовательно, это прямоугольник.
См. также, какая техника используется для экспонирования изображений зубов.
Сколько линий в прямоугольнике?
Форма прямоугольника имеет четыре линии, две из которых являются вертикальными линиями. Две другие линии являются горизонтальными линиями.
Является ли прямоугольник параллельными прямыми?
Каждая пара внутренних углов является дополнительной, потому что два прямых угла складываются с прямым углом, поэтому противоположные стороны прямоугольника параллельны. Это означает, что прямоугольник является параллелограммом, поэтому: Его противоположные стороны равны и параллельны.
Все ли прямоугольники имеют 2 пары параллельных сторон?
Объяснение: Одно из определений параллелограмма — две пары параллельных сторон. Следовательно, любой параллелограмм ДОЛЖЕН иметь 2 пары параллельных сторон. Сюда входят все квадраты, ромбы и прямоугольники.
Сколько параллельных линий в прямоугольной призме?
Характеристики прямоугольной призмы
Прямоугольная призма имеет 12 ребер и 8 вершин. 12 ребер прямоугольной призмы находятся на 3 группы параллельных линии. Параллельные ребра равны по длине. Противоположные грани параллельны и конгруэнтны друг другу.
Какая фигура имеет 4 пары параллельных прямых?
Правильный восьмиугольник фигура, имеющая 4 пары параллельных сторон. Каждая сторона параллельна стороне, противоположной ей.
Какие фигуры имеют пары параллельных прямых?
Фигуры параллельны, если их линии всегда находятся на одинаковом расстоянии друг от друга и никогда не пересекаются и не соприкасаются. Некоторые фигуры с параллельными сторонами включают параллелограмм, прямоугольник, квадрат, трапеция, шестиугольник, и восьмиугольник. У трапеции одна пара параллельных сторон.
Сколько параллельных линий имеет пятиугольник?
Пятиугольник имеет пять сторон, а также не имеет наборов параллельных прямых.
Сколько осей симметрии у прямоугольника?
2
Сколько перпендикулярных прямых имеет прямоугольник?
4 прямых угла, но 2 пары перпендикулярных линий.
Какой прямоугольник имеет две линии симметрии?
В прямоугольнике две линии симметрии. Когда одна линия проводится через центр по его длине, а другая — по ширине (ширине), мы получаем две линии симметрии. Делая это, мы получаем четыре одинаковые и соответствующие формы.
Сколько углов у прямоугольника?
четыре
четырехугольник с четырьмя прямыми углами.
Сколько вершин у прямоугольника?
Прямоугольные призмы
Смотрите также, что означает денали
Он состоит из 6 прямоугольных граней. Когда вы соедините стороны вместе, она станет прямоугольной призмой с 8 вершин и 12 ребер.
Сколько параллельных и перпендикулярных прямых имеет прямоугольник?
Прямоугольники имеют четыре прямые стороны. Каждая пара противоположных сторон параллельна, а соседние стороны перпендикулярны. Это означает, что каждый угол в прямоугольнике является прямым (90∘) углом. Все синие фигуры на изображении ниже — прямоугольники.
Все ли прямоугольники имеют перпендикулярные и параллельные стороны?
Как мы упоминали ранее, прямоугольные треугольники имеют перпендикулярные стороны, прямоугольники имеют как перпендикулярные, так и параллельные стороны. стороны, но другие четырехугольники не могут. Правильный пятиугольник не имеет параллельных или перпендикулярных сторон, но неправильный пятиугольник может иметь параллельные и перпендикулярные стороны. Все зависит от полигона.
Сколько прямых сторон у прямоугольника?
Четыре прямые стороны У квадрата четыре равные стороны. У прямоугольника две пары равных сторон. Квадраты и прямоугольники имеют четыре прямые стороны и четыре прямых угла.
Что имеет только одну пару параллельных прямых?
трапеция четырехугольник, у которого ровно одна пара параллельных сторон.
Сколько прямоугольных граней у прямоугольной пирамиды?
5 граней Прямоугольная пирамида имеет 5 лиц. Его основание — прямоугольник или квадрат, а остальные 4 грани — треугольники. У него 8 ребер и 5 вершин.
Что такое косая прямоугольная призма?
Наклонная прямоугольная призма
Наклонная призма это призма, основания которой не перпендикулярны друг другу. Прямоугольная призма с основаниями, которые не выровнены одно над другим, является наклонной прямоугольной призмой.
Сколько параллельных прямых у прямоугольного параллелепипеда?
12 ребер прямоугольного параллелепипеда находятся в 3 группы параллельных линий. Параллельные ребра равны по длине. Любые пересекающиеся ребра перпендикулярны друг другу.
Какой формы прямоугольник?
Прямоугольник продолговатый. У него две пары параллельных сторон и четыре прямых угла. Прямоугольник также может быть известен как равноугольный четырехугольник. Это связано с тем, что прямоугольник представляет собой четырехугольник (четырехстороннюю форму), у которого стороны параллельны, равны друг другу, а все 4 угла имеют углы, равные 90º.
Является ли прямоугольник ромбом?
Прямоугольник ромб. Квадрат – это параллелограмм. Параллелограмм правильный.
Может ли квадрат быть прямоугольником?
Да, квадрат – это особый тип прямоугольника потому что он обладает всеми свойствами прямоугольника. Подобно прямоугольнику, квадрат имеет: внутренние углы, каждый из которых равен 90∘. противоположные стороны параллельны и равны.
Смотрите также, чем похожи равнины и плоскогорья.
Что имеет параллельные стороны, но не прямоугольник?
Другой четырехугольник, который вы можете увидеть, называется ромб. Все четыре стороны ромба равны. Его свойства включают в себя то, что каждая пара противоположных сторон параллельна, что также делает его параллелограммом. Таким образом, все квадраты являются прямоугольниками, но не все прямоугольники являются квадратами.
Сколько параллельных прямых у ромба?
две пары
Основные свойства Каждый ромб имеет две диагонали, соединяющие пары противоположных вершин, и две пары параллельных сторон.
Является ли треугольник параллельным?
Треугольник — это геометрическая фигура, которая всегда имеет три стороны и три угла. Треугольники имеют ноль пар параллельных прямых. Обычно они имеют нулевые пары перпендикулярных линий. Только один тип треугольника, прямоугольный, имеет две перпендикулярные линии.
Сколько параллелей в шестиугольнике?
3 пары
Правильный шестиугольник, что означает шестиугольник с равными сторонами и равными внутренними углами, представляет собой форму, которая имеет 3 пары параллельных сторон.
Сколько параллельных сторон у восьмиугольника?
4 пары Правильный восьмиугольник имеет 4 пары параллельные стороны.
Сколько параллельных прямых имеет параллелограмм?
две пары В евклидовой геометрии параллелограмм представляет собой простой (несамопересекающийся) четырехугольник с две пары параллельных стороны. Противоположные или обращенные стороны параллелограмма имеют одинаковую длину, а противоположные углы параллелограмма равны.
Почему прямоугольник имеет симметрию только по двум линиям?
Есть 2 линии симметрии прямоугольника, которые исходят из его длины и ширины. Эти две линии разрезают прямоугольник на две одинаковые половины, которые являются зеркальными отражениями друг друга. Если прямоугольник складывается по линии симметрии, он отлично накладывается.
Сколько параллельных линий в прямоугольной призме? : геометрия, алгебра и многое другое
3-й год – Определение перпендикулярных и параллельных линий в двухмерных фигурах – Объяснение
Сколько пар параллельных прямых в квадрате?
Что такое параллельные прямые и параллельные плоскости? | Не запоминай
Представим
себе такую историю…
–
Паша, что ты читаешь? – спросил у друга Саша.
–
Я читаю книгу о поездах, – ответил другу Паша. – В ней очень много интересного
написано. Например, я узнал, когда появились первые поезда и как они были
устроены, когда и где появилась первая железная дорога.
–
Знаешь, Паша, мне всегда было интересно, как расположены железнодорожные рельсы,
– сказал Саша.
–
В книге написано, что рельсы можно сравнить с параллельными прямыми, – рассказал
Паша.
–
А что это за параллельные прямые? – спросил Саша.
–
Даже не знаю, – ответил Паша. – А давай спросим у Мудряша.
–
Ребята, прежде чем мы с вами поговорим, давайте немного разомнёмся и выполним
устные задания, – предложил Мудряш.
–
Теперь сверимся! – сказал Мудряш. –
Посмотрите, что у вас должно было получиться!
–
А сейчас вернёмся к вашему вопросу, – начал Мудряш. – Ребята, давайте
разберёмся, какие же прямые называют параллельными. Пусть на плоскости есть
прямая и
точка , которая не лежит
на этой прямой.
Проведём
через точку несколько прямых.
Обратите внимание, каждая из этих прямых, кроме прямой , пересекает
прямую . Тогда про прямые
и
мы можем сказать,
что они параллельны. Записывают это так: . И говорят: «Прямые
и
параллельны» или «прямая
параллельна
прямой ».
Запомните!
Две прямые на плоскости, которые не пересекаются, называют параллельными.
Паша,
Саша, может, вы приведёте примеры геометрических фигур, элементы которых лежат
на параллельных прямых?
–
Думаю, что стороны прямоугольника лежат на параллельных прямых, – предположил
Паша.
–
Да. Но только противолежащие стороны прямоугольника лежат на параллельных
прямых. Его соседние стороны перпендикулярны, – сказал Мудряш. – У прямоугольного
параллелепипеда на
параллельных прямых лежат, например, рёбра и
;
и
;
и
. А как вы думаете,
рёбра и
тоже лежат на
параллельных прямых?
–
Да, ведь они не пересекаются, – сказал Саша.
–
Но они не лежат в одной плоскости, – заметил Паша.
–
Верно, – сказал Мудряш. – Запомните! Прямые, которые не
пересекаются, но не лежат в одной плоскости, называют скрещивающимися.
На
следующем рисунке изображены отрезки и
, которые лежат на
параллельных прямых и
. Такие отрезки
также называют параллельными.
Лучи
и
, лежащие на
параллельных прямых и
, также
параллельны.
–
Тогда у прямоугольника параллельны
противолежащие стороны и
,
и
, – догадались мальчишки.
–
Молодцы! – похвалил ребят Мудряш. – В прямоугольном параллелепипеде
параллельными являются, например, рёбра и
;
и
.
Ребята,
а теперь посмотрите на рисунок. Здесь прямые и
перпендикулярны
прямой , так как соседние
стороны прямоугольника перпендикулярны. Причём прямая параллельна
прямой , так как
противолежащие стороны прямоугольника параллельны. Тогда можем сформулировать
следующее свойство.
Запомните!
Если две прямые, лежащие в одной плоскости, перпендикулярны третьей прямой, то
они параллельны.
Построить
параллельные прямые мы можем с помощью угольника и линейки.
Давайте
проведём прямую, параллельную прямой , через точку
. Для этого мы совместим
сторону прямого угла угольника с прямой . К другой стороне
прямого угла угольника прикладываем линейку. Теперь двигаем наш угольник вдоль
линейки до тех пор, пока точка не окажется на
стороне прямого угла угольника. Затем проводим прямую . Прямые
и
параллельны.
Итак,
мы с вами познакомились с параллельными прямыми и умеем их строить.
–
Теперь понятно, почему рельсы сравнивают с параллельными прямыми. Ведь они
никогда не пересекаются, – разобрались мальчишки.
–
Кроме рельсов, представление о параллельных прямых дают нам также провода воздушных
линий электропередач, линии дорожной разметки, линии в тетради в линейку,
следы, оставленные автомобилем на снегу, который двигался прямолинейно.
–
Паша, Саша, а сейчас давайте выполним несколько заданий, – предложил ребятам
Мудряш.
Задание
первое: проведите через точки и
прямые,
параллельные прямой .
Решение: строить
прямые, параллельные прямой , будем с помощью
угольника и линейки. Сначала проведём прямую, параллельную прямой , через точку
. Для этого совместим
сторону прямого угла угольника с прямой . К другой стороне
прямого угла угольника приложим линейку. Затем будем двигать наш угольник вдоль
линейки, пока точка не окажется на
стороне прямого угла угольника. Проведём прямую. Назовём её . Прямые
и
параллельны.
Теперь
проведём прямую, которая будет параллельна прямой , через точку
. Совместим
сторону прямого угла угольника с прямой . К другой стороне
прямого угла угольника приложим линейку и будем двигать угольник вдоль линейки
до тех пор, пока точка не окажется на
стороне прямого угла угольника. Теперь проведём прямую. Назовём её . Прямые
и
параллельны.
Задание
второе: проверьте с помощью угольника и линейки, параллельны
ли прямые и
,
и
.
Решение: проверить,
параллельны ли прямые, можно с помощью угольника и линейки. Возьмём угольник и
совместим сторону его прямого угла с прямой . К другой стороне
его прямого угла прикладываем линейку. Теперь двигаем угольник вдоль линейки до
прямой . Видим, что
сторона угольника совместилась с прямой . Значит, прямая
параллельна
прямой .
Продолжим
двигать наш угольник вдоль линейки до прямой . Видим, что
сторона угольника не совместилась с прямой . А значит, прямая
не параллельна
прямой .
Следующее
задание: проведите через каждую вершину треугольника прямую,
параллельную противоположной стороне.
Решение:
проведём
через вершину прямую,
параллельную противоположной стороне . Возьмём угольник
и совместим сторону его прямого угла с прямой . К другой стороне
его прямого угла приложим линейку и будем двигать угольник вдоль линейки до тех
пор, пока точка не окажется на
стороне прямого угла угольника. Проведём прямую , параллельную
стороне .
Теперь
проведём через вершину прямую,
параллельную противоположной стороне . Возьмём угольник
и совместим сторону его прямого угла с прямой . К другой стороне
его прямого угла приложим линейку и будем двигать угольник вдоль линейки до тех
пор, пока точка не окажется на
стороне прямого угла угольника. Проведём прямую , параллельную
стороне .
И
проведём через вершину прямую,
параллельную противоположной стороне . Возьмём угольник
и совместим сторону его прямого угла с прямой . К другой стороне
его прямого угла приложим линейку и будем двигать угольник вдоль линейки до тех
пор, пока точка не окажется на
стороне прямого угла угольника. Проведём прямую , параллельную стороне
.
Таким
образом, мы через каждую вершину треугольника провели прямые,
параллельные противолежащим сторонам.
И
ещё одно задание: начертите угол , градусная мера
которого равна . Отметьте между
сторонами угла точку и проведите через
эту точку прямые, параллельные сторонам угла.
Решение: в
первую очередь мы с вами построим угол, равный . Для этого
отметим произвольную точку . Затем начертим
луч с началом в этой
точке . Теперь приложим
к этому лучу транспортир так, чтобы его центр совпал с точкой , а сам луч прошёл
через начало отсчёта на шкале. Найдём на шкале транспортира штрих, который
соответствует шестидесяти градусам, и проведём через него луч . Таким образом,
мы построили угол , который равен
.
Отметим
точку между
сторонами построенного угла. Возьмём угольник и совместим сторону его прямого
угла со стороной . К другой стороне
его прямого угла приложим линейку и будем двигать угольник вдоль линейки до тех
пор, пока точка не окажется на
стороне прямого угла угольника. Проведём прямую , параллельную
стороне угла
.
Затем
сторону прямого угла угольника совместим со стороной . К другой стороне
прямого угла угольника приложим линейку и будем двигать его вдоль линейки до
тех пор, пока точка не окажется на
стороне прямого угла угольника. Проведём прямую , параллельную
стороне угла
.
Итак,
мы провели через точку прямые
и
, параллельные
соответственно сторонам и
угла
.
В этой статье мы расскажем о параллельных прямых, дадим определения, обозначим признаки и условия параллельности. Для наглядности теоретического материала будем использовать иллюстрации и решение типовых примеров.
Параллельные прямые: основные сведения
Параллельные прямые на плоскости – две прямые на плоскости, не имеющие общих точек.
Параллельные прямые в трехмерном пространстве – две прямые в трехмерном пространстве, лежащие в одной плоскости и не имеющие общих точек.
Необходимо обратить внимание, что для определения параллельных прямых в пространстве крайне важно уточнение «лежащие в одной плоскости»: две прямые в трехмерном пространстве, не имеющие общих точек и не лежащие в одной плоскости, являются не параллельными, а скрещивающимися.
Чтобы обозначить параллельность прямых, общепринято использовать символ ∥. Т.е., если заданные прямые a и b параллельны, кратко записать это условие нужно так: a ‖ b. Словесно параллельность прямых обозначается следующим образом: прямые a и b параллельны, или прямая а параллельна прямой b, или прямая b параллельна прямой а.
Сформулируем утверждение, играющее важную роль в изучаемой теме.
Через точку, не принадлежащую заданной прямой проходит единственная прямая, параллельная заданной. Это утверждение невозможно доказать на базе известных аксиом планиметрии.
В случае, когда речь идет о пространстве, верна теорема:
Через любую точку пространства, не принадлежащую заданной прямой, будет проходить единственная прямая, параллельная заданной.
Эту теорему просто доказать на базе вышеуказанной аксиомы (программа геометрии 10-11 классов).
Параллельность прямых: признаки и условия параллельности
Признак параллельности есть достаточное условие, при выполнении которого гарантирована параллельность прямых. Иначе говоря, выполнения этого условия достаточно, чтобы подтвердить факт параллельности.
В том числе, имеют место необходимые и достаточные условия параллельности прямых на плоскости и в пространстве. Поясним: необходимое – значит то условие, выполнение которого необходимо для параллельности прямых; если оно не выполнено – прямые не являются параллельными.
Резюмируя, необходимое и достаточное условие параллельности прямых – такое условие, соблюдение которого необходимо и достаточно, чтобы прямые были параллельны между собой. С одной стороны, это признак параллельности, с другой – свойство, присущее параллельным прямым.
Перед тем, как дать точную формулировку необходимого и достаточного условия, напомним еще несколько дополнительных понятий.
Секущая прямая – прямая, пересекающая каждую из двух заданных несовпадающих прямых.
Пересекая две прямые, секущая образует восемь неразвернутых углов. Чтобы сформулировать необходимое и достаточное условие, будем использовать такие типы углов, как накрест лежащие, соответственные и односторонние. Продемонстрируем их на иллюстрации:
Если две прямые на плоскости пересекаются секущей, то для параллельности заданных прямых необходимо и достаточно, чтобы накрест лежащие углы были равными, либо были равными соответственные углы, либо сумма односторонних углов была равна 180 градусам.
Проиллюстрируем графически необходимое и достаточное условие параллельности прямых на плоскости:
Доказательство указанных условий присутствует в программе геометрии за 7-9 классы.
В общем, эти условия применимы и для трехмерного пространства при том, что две прямые и секущая принадлежат одной плоскости.
Укажем еще несколько теорем, часто используемых при доказательстве факта параллельности прямых.
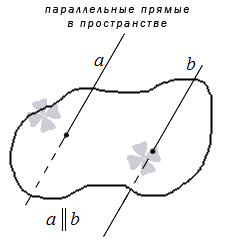
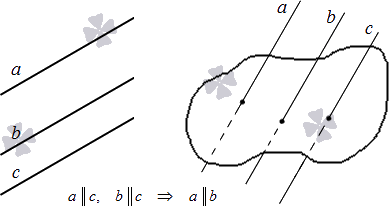
На плоскости две прямые, параллельные третьей, параллельны между собой. Этот признак доказывается на основе аксиомы параллельности, указанной выше.
В трехмерном пространстве две прямые, параллельные третьей, параллельны между собой.
Доказательство признака изучается в программе геометрии 10 класса.
Дадим иллюстрацию указанных теорем:
Укажем еще одну пару теорем, являющихся доказательством параллельности прямых.
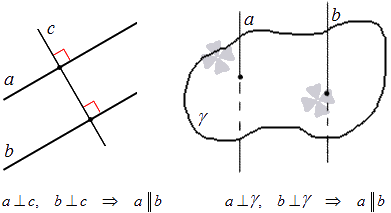
На плоскости две прямые, перпендикулярные третьей, параллельны между собой.
Сформулируем аналогичное для трехмерного пространства.
В трехмерном пространстве две прямые, перпендикулярные третьей, параллельны между собой.
Проиллюстрируем:
Все указанные выше теоремы, признаки и условия позволяют удобно доказать параллельность прямых методами геометрии. Т.е., чтобы привести доказательство параллельности прямых, можно показать, что равны соответственные углы, или продемонстрировать факт, что две заданные прямые перпендикулярны третьей и т.д. Но отметим, что зачастую для доказательства параллельности прямых на плоскости или в трехмерном пространстве удобнее использовать метод координат.
Параллельность прямых в прямоугольной системе координат
В заданной прямоугольной системе координат прямая определяется уравнением прямой на плоскости одного из возможных видов. Так и прямой линии, заданной в прямоугольной системе координат в трехмерном пространстве, соответствуют некоторые уравнения прямой в пространстве.
Запишем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от типа уравнения, описывающего заданные прямые.
Начнем с условия параллельности прямых на плоскости. Оно базируется на определениях направляющего вектора прямой и нормального вектора прямой на плоскости.
Чтобы на плоскости две несовпадающие прямые были параллельны, необходимо и достаточно, чтобы направляющие векторы заданных прямых были коллинеарными, или были коллинеарными нормальные векторы заданных прямых, или направляющий вектор одной прямой был перпендикулярен нормальному вектору другой прямой.
Становится очевидно, что условие параллельности прямых на плоскости базируется на условии коллинеарности векторов или условию перпендикулярности двух векторов. Т.е., если a→=(ax, ay) и b→=(bx, by) являются направляющими векторами прямых a и b;
и nb→=(nbx, nby) являются нормальными векторами прямых a и b, то указанное выше необходимое и достаточное условие запишем так: a→=t·b→⇔ax=t·bxay=t·by или na→=t·nb→⇔nax=t·nbxnay=t·nby или a→, nb→=0⇔ax·nbx+ay·nby=0, где t – некоторое действительное число. Координаты направляющих или прямых векторов определяются по заданным уравнениям прямых. Рассмотрим основные примеры.
- Прямая a в прямоугольной системе координат определяется общим уравнением прямой: A1x+B1y+C1=0; прямая b – A2x+B2y+C2=0. Тогда нормальные векторы заданных прямых будут иметь координаты (А1, В1) и (А2, В2) соответственно. Условие параллельности запишем так:
A1=t·A2B1=t·B2
- Прямая a описывается уравнением прямой с угловым коэффициентом вида y=k1x+b1. Прямая b – y=k2x+b2. Тогда нормальные векторы заданных прямых будут иметь координаты (k1, -1) и (k2, -1) соответственно, а условие параллельности запишем так:
k1=t·k2-1=t·(-1)⇔k1=t·k2t=1⇔k1=k2
Таким образом, если параллельные прямые на плоскости в прямоугольной системе координат задаются уравнениями с угловыми коэффициентами, то угловые коэффициенты заданных прямых будут равны. И верно обратное утверждение: если несовпадающие прямые на плоскости в прямоугольной системе координат определяются уравнениями прямой с одинаковыми угловыми коэффициентами, то эти заданные прямые параллельны.
- Прямые a и b в прямоугольной системе координат заданы каноническими уравнениями прямой на плоскости: x-x1ax=y-y1ay и x-x2bx=y-y2by или параметрическими уравнениями прямой на плоскости: x=x1+λ·axy=y1+λ·ay и x=x2+λ·bxy=y2+λ·by.
Тогда направляющие векторы заданных прямых будут: ax, ay и bx, by соответственно, а условие параллельности запишем так:
ax=t·bxay=t·by
Разберем примеры.
Заданы две прямые: 2x-3y+1=0 и x12+y5=1. Необходимо определить, параллельны ли они.
Решение
Запишем уравнение прямой в отрезках в виде общего уравнения:
x12+y5=1⇔2x+15y-1=0
Мы видим, что na→=(2, -3) – нормальный вектор прямой 2x-3y+1=0, а nb→=2, 15- нормальный вектор прямой x12+y5=1.
Полученные векторы не являются коллинеарными, т.к. не существует такого значения t, при котором будет верно равенство:
2=t·2-3=t·15⇔t=1-3=t·15⇔t=1-3=15
Таким образом, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, а значит заданные прямые не параллельны.
Ответ: заданные прямые не параллельны.
Заданы прямые y=2x+1и x1=y-42. Параллельны ли они?
Решение
Преобразуем каноническое уравнение прямой x1=y-42 к уравнению прямой с угловым коэффициентом:
x1=y-42⇔1·(y-4)=2x⇔y=2x+4
Мы видим, что уравнения прямых y = 2x + 1 и y = 2x + 4 не являются одинаковыми (если бы было иначе, прямые были бы совпадающими) и угловые коэффициенты прямых равны, а значит заданные прямые являются параллельными.
Попробуем решить задачу иначе. Сначала проверим, совпадают ли заданные прямые. Используем любую точку прямой y = 2x + 1, например, (0, 1), координаты этой точки не отвечают уравнению прямой x1=y-42, а значит прямые не совпадают.
Следующим шагом определим выполнение условия параллельности заданных прямых.
Нормальный вектор прямой y = 2x + 1 это вектор na→=(2, -1), а направляющий вектором второй заданной прямой является b→=(1, 2). Скалярное произведение этих векторов равно нулю:
na→, b→=2·1+(-1)·2=0
Таким образом, векторы перпендикулярны: это демонстрирует нам выполнение необходимого и достаточного условия параллельности исходных прямых. Т.е. заданные прямые параллельны.
Ответ: данные прямые параллельны.
Для доказательства параллельности прямых в прямоугольной системе координат трехмерного пространства используется следующее необходимое и достаточное условие.
Чтобы две несовпадающие прямые в трехмерном пространстве были параллельны, необходимо и достаточно, чтобы направляюще векторы этих прямых были коллинеарными.
Т.е. при заданных уравнениях прямых в трехмерном пространстве ответ на вопрос: параллельны они или нет, находится при помощи определения координат направляющих векторов заданных прямых, а также проверки условия их коллинеарности. Иначе говоря, если a→=(ax, ay, az) и b→=(bx, by, bz)являются направляющими векторами прямых a и b соответственно, то для того, чтобы они были параллельны, необходимо существование такого действительного числа t, чтобы выполнялось равенство:
a→=t·b→⇔ax=t·bxay=t·byaz=t·bz
Заданы прямые x1=y-20=z+1-3 и x=2+2λy=1z=-3-6λ. Необходимо доказать параллельность этих прямых.
Решение
Условиями задачи заданы канонические уравнения одной прямой в пространстве и параметрические уравнения другой прямой в пространстве. Направляющие векторы a→ и b→ заданных прямых имеют координаты: (1, 0, -3) и (2, 0, -6).
Так как:
1=t·20=t·0-3=t·-6⇔t=12, то a→=12·b→.
Следовательно, необходимое и достаточное условие параллельности прямых в пространстве выполнено.
Ответ: параллельность заданных прямых доказана.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо – в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ – раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности – включая административные, технические и физические – для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
На плоскости прямые называются параллельными, если у них нет общих точек, то есть они не пересекаются. Для обозначения параллельности используют специальный значок || (параллельные прямые a || b).
Для прямых, лежащих в пространстве, требования отсутствия общих точек недостаточно – чтобы они в пространстве были параллельными, они должны принадлежать одной плоскости (иначе они будут скрещивающимися).
За примерами параллельных прямых далеко идти не надо, они сопровождают нас повсюду, в комнате – это линии пересечения стены с потолком и полом, на тетрадном листе – противоположные края и т.д.
Совершенно очевидно, что, имея параллельность двух прямых и третью прямую, параллельную одной из первых двух, она будет параллельна и второй.
Параллельные прямые на плоскости связаны утверждением, которое не доказывается с помощью аксиом планиметрии. Его принимают как факт, в качестве аксиомы: для любой точки на плоскости, не лежащей на прямой, существует единственная прямая, которая проходит через нее параллельно данной. Эту аксиому знает каждый шестиклассник.
Ее пространственное обобщение, то есть утверждение, что для любой точки в пространстве, не лежащей на прямой, существует единственная прямая, которая проходит через нее параллельно данной, легко доказывается с помощью уже известной нам аксиомы параллельности на плоскости.
Свойства параллельных прямых
- Если любая из параллельных двух прямых параллельна третьей, то они взаимно параллельны.
Этим свойством обладают параллельные прямые и на плоскости, и в пространстве.
В качестве примера рассмотрим его обоснование в стереометрии.
Допустим параллельность прямых b и с прямой a.
Случай, когда все прямые лежат в одной и той же плоскости оставим планиметрии.
Предположим, a и b принадлежат плоскости бетта, а гамма – плоскость, которой принадлежат a и с (по определению параллельности в пространстве прямые должны принадлежать одной плоскости).
Если допустить, что плоскости бетта и гамма различные и отметить на прямой b из плоскости бетта некую точку B, то плоскость, проведенная через точку B и прямую с должна пересечь плоскость бетта по прямой (обозначим ее b1).
Если бы полученная прямая b1 пересекала плоскость гамма, то, с одной стороны, точка пересечения должна была бы лежать на a, поскольку b1 принадлежит плоскости бетта, а с другой, она должна принадлежать и с, поскольку b1 принадлежит третьей плоскости.
Но ведь параллельные прямые a и с пересекаться не должны.
Таким образом, прямая b1 должна принадлежать плоскости бетта и при этом не иметь общих точек с a, следовательно, согласно аксиоме параллельности, она совпадает с b.
Мы получили совпадающую с прямой b прямую b1, которая принадлежит одной и той же плоскости с прямой с и при этом ее не пересекает, то есть b и с – параллельны
- Через точку, которая не лежит на заданной прямой, параллельная данной может проходить лишь одна единственная прямая.
- Лежащие на плоскости перпендикулярно третьей две прямые параллельны.
- При условии пересечения плоскости одной из параллельных двух прямых, эту же плоскость пересекает и вторая прямая.
- Соответствующие и накрест лежащие внутренние углы, образованные пересечением параллельных двух прямых третьей, равны, сумма у образовавшихся при этом внутренних односторонних равна 180°.
Верны и обратные утверждения, которые можно принять за признаки параллельности двух прямых.
Условие параллельности прямых
Сформулированные выше свойства и признаки представляют собой условия параллельности прямых, и их вполне можно доказать методами геометрии. Иначе говоря, для доказательства параллельности двух имеющихся прямых достаточно доказать их параллельность третьей прямой либо равенство углов, будь то соответствующих или накрест лежащих, и т.п.
Для доказательства в основном используют метод «от противного», то есть с допущения, что прямые непараллельны. Исходя из этого допущения, легко можно показать, что в этом случае нарушаются заданные условия, например, накрест лежащие внутренние углы оказываются неравными, что и доказывает некорректность сделанного допущения.
Эта статья о параллельных прямых и о параллельности прямых. Сначала дано определение параллельных прямых на плоскости и в пространстве, введены обозначения, приведены примеры и графические иллюстрации параллельных прямых. Далее разобраны признаки и условия параллельности прямых. В заключении показаны решения характерных задач на доказательство параллельности прямых, которые заданы некоторыми уравнениями прямой в прямоугольной системе координат на плоскости и в трехмерном пространстве.
Навигация по странице.
Параллельные прямые – основные сведения.
Определение.
Две прямые на плоскости называются параллельными
, если они не имеют общих точек.
Определение.
Две прямые в трехмерном пространстве называются параллельными
, если они лежат в одной плоскости и не имеют общих точек.
Обратите внимание, что оговорка «если они лежат в одной плоскости» в определении параллельных прямых в пространстве очень важна. Поясним этот момент: две прямые в трехмерном пространстве, которые не имеют общих точек и не лежат в одной плоскости не являются параллельными, а являются скрещивающимися.
Приведем несколько примеров параллельных прямых. Противоположные края тетрадного листа лежат на параллельных прямых. Прямые, по которым плоскость стены дома пересекает плоскости потолка и пола, являются параллельными. Железнодорожные рельсы на ровной местности также можно рассматривать как параллельные прямые.
Для обозначения параллельных прямых используют символ «». То есть, если прямые а
и b
параллельны, то можно кратко записать а
b
.
Обратите внимание: если прямые a
и b
параллельны, то можно сказать, что прямая a
параллельна прямой b
, а также, что прямая b
параллельна прямой a
.
Озвучим утверждение, которое играет важную роль при изучении параллельных прямых на плоскости: через точку, не лежащую на данной прямой, проходит единственная прямая, параллельная данной. Это утверждение принимается как факт (оно не может быть доказано на основе известных аксиом планиметрии), и оно называется аксиомой параллельных прямых.
Для случая в пространстве справедлива теорема: через любую точку пространства, не лежащую на заданной прямой, проходит единственная прямая, параллельная данной. Эта теорема легко доказывается с помощью приведенной выше аксиомы параллельных прямых (ее доказательство Вы можете найти в учебнике геометрии 10-11 класс, который указан в конце статьи в списке литературы).
Для случая в пространстве справедлива теорема: через любую точку пространства, не лежащую на заданной прямой, проходит единственная прямая, параллельная данной. Эта теорема легко доказывается с помощью приведенной выше аксиомы параллельных прямых.
Параллельность прямых – признаки и условия параллельности.
Признаком параллельности прямых
является достаточное условие параллельности прямых, то есть, такое условие, выполнение которого гарантирует параллельность прямых. Иными словами, выполнение этого условия достаточно для того, чтобы констатировать факт параллельности прямых.
Также существуют необходимые и достаточные условия параллельности прямых на плоскости и в трехмерном пространстве.
Поясним смысл фразы «необходимое и достаточное условие параллельности прямых».
С достаточным условием параллельности прямых мы уже разобрались. А что же такое «необходимое условие параллельности прямых»? По названию «необходимое» понятно, что выполнение этого условия необходимо для параллельности прямых. Иными словами, если необходимое условие параллельности прямых не выполнено, то прямые не параллельны. Таким образом, необходимое и достаточное условие параллельности прямых
– это условие, выполнение которого как необходимо, так и достаточно для параллельности прямых. То есть, с одной стороны это признак параллельности прямых, а с другой стороны – это свойство, которым обладают параллельные прямые.
Прежде чем сформулировать необходимое и достаточное условие параллельности прямых, целесообразно напомнить несколько вспомогательных определений.
Секущая прямая
– это прямая, которая пересекает каждую из двух заданных несовпадающих прямых.
При пересечении двух прямых секущей образуются восемь неразвернутых . В формулировке необходимого и достаточного условия параллельности прямых участвуют так называемые накрест лежащие, соответственные
и односторонние углы
. Покажем их на чертеже.
Теорема.
Если две прямые на плоскости пересечены секущей, то для их параллельности необходимо и достаточно, чтобы накрест лежащие углы были равны, или соответственные углы были равны, или сумма односторонних углов равнялась 180
градусам.
Покажем графическую иллюстрацию этого необходимого и достаточного условия параллельности прямых на плоскости.
Доказательства этих условий параллельности прямых Вы можете найти в учебниках геометрии за 7
-9
классы.
Заметим, что эти условия можно использовать и в трехмерном пространстве – главное, чтобы две прямые и секущая лежали в одной плоскости.
Приведем еще несколько теорем, которые часто используются при доказательстве параллельности прямых.
Теорема.
Если две прямые на плоскости параллельны третьей прямой, то они параллельны. Доказательство этого признака следует из аксиомы параллельных прямых.
Существует аналогичное условие параллельности прямых в трехмерном пространстве.
Теорема.
Если две прямые в пространстве параллельны третьей прямой, то они параллельны. Доказательство этого признака рассматривается на уроках геометрии в 10
классе.
Проиллюстрируем озвученные теоремы.
Приведем еще одну теорему, позволяющую доказывать параллельность прямых на плоскости.
Теорема.
Если две прямые на плоскости перпендикулярны к третьей прямой, то они параллельны.
Существует аналогичная теорема для прямых в пространстве.
Теорема.
Если две прямые в трехмерном пространстве перпендикулярны к одной плоскости, то они параллельны.
Изобразим рисунки, соответствующие этим теоремам.
Все сформулированные выше теоремы, признаки и необходимые и достаточные условия прекрасно подходят для доказательства параллельности прямых методами геометрии. То есть, чтобы доказать параллельность двух заданных прямых нужно показать, что они параллельны третьей прямой, или показать равенство накрест лежащих углов и т.п. Множество подобных задач решается на уроках геометрии в средней школе. Однако следует отметить, что во многих случаях удобно пользоваться методом координат для доказательства параллельности прямых на плоскости или в трехмерном пространстве. Сформулируем необходимые и достаточные условия параллельности прямых, которые заданы в прямоугольной системе координат.
Параллельность прямых в прямоугольной системе координат.
В этом пункте статьи мы сформулируем необходимые и достаточные условия параллельности прямых
в прямоугольной системе координат в зависимости от вида уравнений, определяющих эти прямые, а также приведем подробные решения характерных задач.
Начнем с условия параллельности двух прямых на плоскости в прямоугольной системе координат Oxy
. В основе его доказательства лежит определение направляющего вектора прямой и определение нормального вектора прямой на плоскости.
Теорема.
Для параллельности двух несовпадающих прямых на плоскости необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, или нормальные векторы этих прямых были коллинеарны, или направляющий вектор одной прямой был перпендикулярен нормальному вектору второй прямой.
Очевидно, условие параллельности двух прямых на плоскости сводится к (направляющих векторов прямых или нормальных векторов прямых) или к (направляющего вектора одной прямой и нормального вектора второй прямой). Таким образом, если и – направляющие векторы прямых a
и b
, а 
и 
– нормальные векторы прямых a
и b
соответственно, то необходимое и достаточное условие параллельности прямых а
и b
запишется как 
, или 
, или , где t
– некоторое действительное число. В свою очередь координаты направляющих и (или) нормальных векторов прямых a
и b
находятся по известным уравнениям прямых.
В частности, если прямую a
в прямоугольной системе координат Oxy
на плоскости задает общее уравнение прямой вида 
, а прямую b
– 
, то нормальные векторы этих прямых имеют координаты и соответственно, а условие параллельности прямых a
и b
запишется как .
Если прямой a
соответствует уравнение прямой с угловым коэффициентом вида , а прямой b
– , то нормальные векторы этих прямых имеют координаты и , а условие параллельности этих прямых примет вид 
. Следовательно, если прямые на плоскости в прямоугольной системе координат параллельны и могут быть заданы уравнениями прямых с угловыми коэффициентами, то угловые коэффициенты прямых будут равны. И обратно: если несовпадающие прямые на плоскости в прямоугольной системе координат могут быть заданы уравнениями прямой с равными угловыми коэффициентами, то такие прямые параллельны.
Если прямую a
и прямую b
в прямоугольной системе координат определяют канонические уравнения прямой на плоскости вида 
и 
, или параметрические уравнения прямой на плоскости вида 
и 
соответственно, то направляющие векторы этих прямых имеют координаты и , а условие параллельности прямых a
и b
записывается как .
Разберем решения нескольких примеров.
Пример.
Параллельны ли прямые 
и ?
Решение.
Перепишем уравнение прямой в отрезках в виде общего уравнения прямой: 
. Теперь видно, что – нормальный вектор прямой , а – нормальный вектор прямой . Эти векторы не коллинеарны, так как не существует такого действительного числа t
, для которого верно равенство (
). Следовательно, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, поэтому, заданные прямые не параллельны.
Ответ:
Нет, прямые не параллельны.
Пример.
Являются ли прямые и параллельными?
Решение.
Приведем каноническое уравнение прямой к уравнению прямой с угловым коэффициентом: . Очевидно, что уравнения прямых и не одинаковые (в этом случае заданные прямые были бы совпадающими) и угловые коэффициенты прямых равны, следовательно, исходные прямые параллельны.
В разделе на вопрос как доказать что прямые параллельны???? заданный автором Алёнка Яковлева
лучший ответ это Свойства параллельных прямых
Теорема
Две прямые, параллельные третьей, параллельны.
Доказательство.
Пусть прямые a и b параллельны прямой с. Допустим, что прямые a и b не параллельны. Тогда они пересекаются в некоторой точке С. Получается, что через точку С проходит две прямые параллельные прямой с. Но это противоречит аксиоме «Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной» . Теорема доказана.
Теорема
Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны.
Доказательство.
Пусть есть параллельные прямые a и b, которые пересекаются секущей прямой с. Прямая с пересекает прямую а в точке A и прямую b в точке B. Проведем чрез точку A прямую a1 так, что бы прямые a1 и b с секущей с образовали равные внутренние накрест лежащие углы. По признаку параллельности прямых прямые a1 и b параллельны. А так как через точку A можно провести только одну прямую параллельную b, то a и a1 совпадают.
Значит, внутренние накрест лежащие углы, образованные прямой a и b, равны. Теорема доказана.
На основании теоремы доказывается:
Если две параллельные прямые пересечены третьей прямой, то соответствующие углы равны.
Если две параллельные прямые пересечены третьей прямой, то сумма внутренних односторонних углов равна 180 º
Инструкция
Перед началом доказательства убедитесь, что прямые лежат в одной плоскости и их можно изобразить на ней. Наиболее простым способом доказательства является метод измерения линейкой. Для этого при помощи линейки измерьте расстояние между прямыми в нескольких местах как можно дальше друг от друга. Если расстояние остается неизменным, данные прямые параллельны. Но такой метод недостаточно точен, поэтому лучше используйте другие способы.
Проведите третью прямую, так, чтобы она пересекала обе параллельные прямые. Она образует с ними четыре внешних и четыре внутренних угла. Рассмотрите внутренние углы. Те, которые лежат через секущую прямую называются накрестлежащими. Те, что лежат по одной стороне называются односторонними. При помощи транспортира измерьте два внутренних накрестлежащих угла. Если они равны между собой, то прямые будут параллельными. Если остались сомнения, измерьте односторонние внутренние углы и сложите получившиеся значения. Прямые будут параллельными, если сумма односторонних внутренних углов будет равна 180º.
Если нет транспортира, возьмите угольник с углом 90º. С его помощью постройте перпендикуляр к одной из прямых. После этого продолжите этот перпендикуляр таким образом, чтобы он пересек другую прямую. С помощью того же угольника проверьте, под каким углом этот перпендикуляр пересекает ее. Если этот угол тоже равен 90º, то прямые параллельны между собой.
В том случае, если прямые заданы в декартовой системе координат, найдите их направляющие или нормальные векторы. Если эти векторы, соответственно, между собой коллинеарны, то прямые параллельны. Приведите уравнение прямых к общему виду и найдите координаты нормального вектора каждой из прямых. Его координаты равны коэффициентам А и В. В том случае, если отношение соответствующих координат нормальных векторов одинаково, они коллинеарны, а прямые параллельны.
Например, прямые заданы уравнениями 4х-2у+1=0 и х/1=(у-4)/2. Первое уравнение – общего вида, второе – канонического. Приведите второе уравнение к общему виду. Используйте для этого правило преобразования пропорций, в результате получите 2х=у-4. После приведения к общему виду получите 2х-у+4=0. Поскольку уравнение общего вида для любой прямой записывается Ах+Ву+С=0, то для первой прямой: А=4, В=2, а для второй прямой А=2, В=1. Для первой прямой координаты нормального вектора (4;2), а для второй – (2;1). Найдите отношение соответствующих координат нормальных векторов 4/2=2 и 2/1=2. Эти числа равны, а значит вектора коллинеарны. Поскольку вектора коллинеарны, прямые параллельны.
