
Тетра́эдр (др.-греч. τετράεδρον «четырёхгранник»[1] ← τέσσαρες / τέσσερες / τέτταρες / τέττορες / τέτορες «четыре» + ἕδρα «седалище, основание») — простейший многогранник, гранями которого являются четыре треугольника[2].
Тетраэдр является треугольной пирамидой при принятии любой из граней за основание.
У тетраэдра 4 грани, 4 вершины и 6 рёбер.
Тетраэдр, у которого все грани — равносторонние треугольники, называется правильным. Правильный тетраэдр является одним из пяти правильных многогранников.
Свойства[править | править код]
- Параллельные плоскости, проходящие через три пары скрещивающихся рёбер тетраэдра, определяют описанный около тетраэдра параллелепипед.
- Плоскость, проходящая через середины двух скрещивающихся рёбер тетраэдра, делит его на две равные по объёму части[3]:216-217.
- Бимедианы тетраэдра пересекаются в той же самой точке, что и медианы тетраэдра.
- Бимедианами тетраэдра называют отрезки, соединяющие середины его скрещивающихся рёбер (не имеющих общих вершин).
- Центры сфер, которые проходят через три вершины и инцентр, лежат на сфере, центр которой совпадает с центром описанной сферы.
- Также это утверждение верно и для внешних инцентров.
- Плоскости, которые проходят через середину ребра и перпендикулярны противоположному ребру,пересекаются в одной точке (ортоцентр).
- Ортоцентр в симплексе определяется как пересечение гиперплоскостей, которые перпендикулярны ребру и проходят через центр тяжести противоположного элемента.
- Центр сферы(F),которая проходит через центры тяжести граней тетраэдра, центр тяжести тетраэдра(M), центр описанной сферы(R) и ортоцентр (H) лежат на одной прямой. При этом
.
- Центр сферы (S) вписанный в дополнительный тетраэдр,центр сферы (N) вписанный в антидополнительный тетраэдр, центр тяжести тетраэдра (M) и центр вписанной сферы (I) лежат на одной прямой.
- Пусть точка G1 делит отрезок соединяющий ортоцентр(H) и вершину 1 в отношении 1:2. Опустим перпендикуляр с точки G1 на грань противолежащей вершине 1. Перпендикуляр пересекает грань в точке W1. Точки G1 и W1 лежат на сфере (сфере Фейербаха), которая проходит через центры тяжести граней тетраэдра.
- Сечение плоскостью, проходящей через середины четырёх рёбер тетраэдра, является параллелограммом.
Типы тетраэдров[править | править код]
Равногранный тетраэдр[править | править код]

Развёртка равногранного тетраэдра
Все грани его представляют собой равные между собой треугольники. Развёрткой равногранного тетраэдра является треугольник, разделённый тремя средними линиями на четыре равных треугольника. В равногранном тетраэдре основания высот, середины высот и точки пересечения высот граней лежат на поверхности одной сферы (сферы 12 точек) (Аналог окружности Эйлера для треугольника).
Свойства равногранного тетраэдра:
- Все его грани равны (конгруэнтны).
- Скрещивающиеся рёбра попарно равны.
- Трёхгранные углы равны.
- Противолежащие двугранные углы равны.
- Два плоских угла, опирающихся на одно ребро, равны.
- Сумма плоских углов при каждой вершине равна 180°.
- Развёртка тетраэдра — треугольник или параллелограмм.
- Описанный параллелепипед прямоугольный.
- Тетраэдр имеет три оси симметрии.
- Общие перпендикуляры скрещивающихся рёбер попарно перпендикулярны.
- Средние линии попарно перпендикулярны.
- Периметры граней равны.
- Площади граней равны.
- Высоты тетраэдра равны.
- Отрезки, соединяющие вершины с центрами тяжести противоположных граней, равны.
- Радиусы описанных около граней окружностей равны.
- Центр тяжести тетраэдра совпадает с центром описанной сферы.
- Центр тяжести совпадает с центром вписанной сферы.
- Центр описанной сферы совпадает с центром вписанной.
- Вписанная сфера касается граней в центрах описанных около этих граней окружностей.
- Сумма внешних единичных нормалей (единичных векторов, перпендикулярных к граням) равна нулю.
- Сумма всех двугранных углов равна нулю.
- Центры вневписанных сфер лежат на описанной сфере.
Ортоцентрический тетраэдр[править | править код]
Все высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке.
- Высоты тетраэдра пересекаются в одной точке.
- Основания высот тетраэдра являются ортоцентрами граней.
- Каждые два противоположных ребра тетраэдра перпендикулярны.
- Суммы квадратов противоположных рёбер тетраэдра равны.
- Отрезки, соединяющие середины противоположных рёбер тетраэдра, равны.
- Произведения косинусов противоположных двугранных углов равны.
- Сумма квадратов площадей граней вчетверо меньше суммы квадратов произведений противоположных рёбер.
- У ортоцентрического тетраэдра окружности 9 точек (окружности Эйлера) каждой грани принадлежат одной сфере (сфере 24 точек).
- У ортоцентрического тетраэдра центры тяжести и точки пересечения высот граней, а также точки, делящие отрезки каждой высоты тетраэдра от вершины до точки пересечения высот в отношении 2:1, лежат на одной сфере (сфере 12 точек).
Прямоугольный тетраэдр[править | править код]
Все рёбра, прилежащие к одной из вершин, перпендикулярны между собой.
Прямоугольный тетраэдр получается отсечением тетраэдра плоскостью от прямоугольного параллелепипеда.
Каркасный тетраэдр[править | править код]
Это тетраэдр, отвечающий любому из следующих условий[4]:
- существует сфера, касающаяся всех рёбер,
- суммы длин скрещивающихся рёбер равны,
- суммы двугранных углов при противоположных рёбрах равны,
- окружности, вписанные в грани, попарно касаются,
- все четырёхугольники, получающиеся на развёртке тетраэдра, — описанные,
- перпендикуляры, восставленные к граням из центров вписанных в них окружностей, пересекаются в одной точке.
Соразмерный тетраэдр[править | править код]
У этого типа бивысоты равны.
Свойства соразмерного тетраэдра:
Инцентрический тетраэдр[править | править код]
У этого типа отрезки, соединяющие вершины тетраэдра с центрами окружностей, вписанных в противоположные грани, пересекаются в одной точке.
Свойства инцентрического тетраэдра:
- Отрезки, соединяющие центры тяжести граней тетраэдра с противоположными вершинами (медианы тетраэдра), всегда пересекаются в одной точке. Эта точка — центр тяжести тетраэдра.
- Замечание. Если в последнем условии заменить центры тяжести граней на ортоцентры граней, то оно превратится в новое определение ортоцентрического тетраэдра. Если же заменить их на центры вписанных в грани окружностей, называемых иногда инцентрами, мы получим определение нового класса тетраэдров — инцентрических.
- Отрезки, соединяющие вершины тетраэдра с центрами окружностей, вписанных в противоположные грани, пересекаются в одной точке.
- Биссектрисы углов двух граней, проведённому к общему ребру этих граней, имеют общее основание.
- Произведения длин противоположных рёбер равны.
- Треугольник, образованный вторыми точками пересечения трёх рёбер, выходящих из одной вершины, с любой сферой, проходящей через три конца этих рёбер, является равносторонним.
Правильный тетраэдр[править | править код]
Это равногранный тетраэдр, у которого все грани — правильные треугольники. Является одним из пяти платоновых тел.
Свойства правильного тетраэдра:
- все рёбра тетраэдра равны между собой,
- все грани тетраэдра равны между собой,
- периметры и площади всех граней равны между собой.
- Правильный тетраэдр является одновременно ортоцентрическим, каркасным, равногранным, инцентрическим и соразмерным.
- Тетраэдр является правильным, если он принадлежит к двум любым видам тетраэдров из перечисленных: ортоцентрический, каркасный, инцентрический, соразмерный, равногранный.
- Тетраэдр является правильным, если он является равногранным и принадлежит к одному из следующих видов тетраэдров: ортоцентрический, каркасный, инцентрический, соразмерный.
- В правильный тетраэдр можно вписать октаэдр, притом четыре (из восьми) грани октаэдра будут совмещены с четырьмя гранями тетраэдра, все шесть вершин октаэдра будут совмещены с центрами шести рёбер тетраэдра.
- Правильный тетраэдр состоит из одного вписанного октаэдра (в центре) и четырёх тетраэдров (по вершинам), причём рёбра этих тетраэдров и октаэдра вдвое меньше рёбер правильного тетраэдра.
- Правильный тетраэдр можно вписать в куб двумя способами, притом четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба.
- Правильный тетраэдр можно вписать в додекаэдр, притом, четыре вершины тетраэдра будут совмещены с четырьмя вершинами додекаэдра.
- Скрещивающиеся рёбра правильного тетраэдра взаимно перпендикулярны.
Объём тетраэдра[править | править код]
или
где 

- Объём тетраэдра через длины рёбер выражается с помощью определителя Кэли-Менгера:
- Эта формула имеет плоский аналог для площади треугольника в виде варианта формулы Герона через аналогичный определитель.
- Объём тетраэдра через длины двух противоположных рёбер a и b, как скрещивающихся линий, которые удалены на расстояние h друг от друга и образуют друг с другом угол
, находится по формуле:

- Объём тетраэдра через длины трёх его рёбер a, b и c, выходящих из одной вершины и образующих между собой попарно соответственно плоские углы
, находится по формуле[5]
где
- Аналогом для плоскости последней формулы является формула площади треугольника через длины двух его сторон a и b, выходящих из одной вершины и образующих между собой угол
:
где

Замечание[править | править код]
Есть аналог формулы Герона для объёма тетраэдра [6]
Формулы тетраэдра в декартовых координатах в пространстве[править | править код]
Обозначения:


- Объём тетраэдра (с учётом знака):

- Координаты центра тяжести (пересечение медиан):

- Координаты центра вписанной сферы:

где 

Соответственно уравнение вписанной сферы:

Уравнение вневписанной сферы, противолежащей первой вершине:

Уравнение вневписанной сферы, противолежащей первой и второй вершинам (количество таких сфер может варьироваться от нуля до трёх):

- Уравнение описанной сферы:

Формулы тетраэдра в барицентрических координатах[править | править код]
Обозначения:

- Объём тетраэдра (с учётом знака): Пусть
— координаты вершин тетраэдра.
Тогда


- Координаты центра тяжести (пересечение медиан):
- Координаты центра вписанной сферы:
- Координаты центра описанной сферы:

- Расстояние между точками
:
Пусть 
Тогда расстояние между двумя точками: 
Сравнение формул треугольника и тетраэдра[править | править код]
| Площадь(Объём) | |
|---|---|
 |
 , где , где  — расстояние между вершинами 1 и 2 — расстояние между вершинами 1 и 2
|
 |

|
 |
 , ,
где |
| Длина(площадь) биссектрисы | |
 |

|
| Длина медианы | |
 |

|
| Радиус вписанной окружности(сферы) | |
 |

|
| Радиус описанной окружности(сферы) | |
 |
 , где , где  — площадь треугольника со сторонами — площадь треугольника со сторонами 
|
| Теорема косинусов | |
 |
 , ,
где |
| Теорема синусов | |
 |
 , ,
где |
| Теорема о сумме углов треугольника(соотношение между двугранными углами тетраэдра) | |
 |
 , ,
где |
| Расстояние между центрами вписанной и описанной окружностей (сфер) | |
 |
 , ,
где Другая запись выражения: |
Тетраэдр в неевклидовых пространствах[править | править код]
Объём неевклидовых тетраэдров[править | править код]
Существует множество формул нахождения объёма неевклидовых тетраэдров. Например, формула Деревнина — Медных[7] для гиперболического тетраэдра и формула Дж. Мураками[8] для сферического тетраэдра. Объём тетраэдра в сферическом пространстве и в пространстве Лобачевского, как правило, не выражается через элементарные функции.
Соотношение между двугранными углами тетраэдра[править | править код]


Где 

Теорема косинусов[править | править код]



Где





Теорема синусов[править | править код]

Радиус описанной сферы[править | править код]

Другая запись выражения: 

Или с координатами вершин тетраэдра: 

Радиус вписанной сферы[править | править код]

Другая запись выражения: 


Расстояние между центрами вписанной и описанной сфер[править | править код]

Формулы тетраэдра в барицентрических координатах[править | править код]
- Координаты центра вписанной сферы:

- Координаты центра описанной сферы:

Тетраэдры в микромире[править | править код]
- Правильный тетраэдр образуется при sp3-гибридизации атомных орбиталей (их оси направлены в вершины правильного тетраэдра, а ядро центрального атома расположено в центре описанной сферы правильного тетраэдра), поэтому немало молекул, в которых такая гибридизация центрального атома имеет место, имеют вид этого многогранника.
- Молекула метана СН4.
- Ион аммония NH4+.
- Сульфат-ион SO42-, фосфат-ион PO43-, перхлорат-ион ClO4– и многие другие ионы.
- Алмаз C — тетраэдр с ребром, равным 2,5220 ангстрем.
- Флюорит CaF2, тетраэдр с ребром, равным 3,8626 ангстрем.
- Сфалерит, ZnS, тетраэдр с ребром, равным 3,823 ангстрем.
- Оксид цинка, ZnO.
- Комплексные ионы [BF4] –, [ZnCl4]2-, [Hg(CN)4]2-, [Zn(NH3)4]2+.
- Силикаты, в основе структур которых лежит кремнекислородный тетраэдр [SiO4]4-.
Тетраэдры в живой природе[править | править код]

Тетраэдр из грецких орехов
Некоторые плоды, находясь вчетвером на одной кисти, располагаются в вершинах тетраэдра, близкого к правильному. Такая конструкция обусловлена тем, что центры четырёх одинаковых шаров, касающихся друг друга, находятся в вершинах правильного тетраэдра. Поэтому похожие на шар плоды образуют подобное взаимное расположение. Например, таким образом могут располагаться грецкие орехи.
Тетраэдры в технике[править | править код]
- Тетраэдр образует жёсткую, статически определимую конструкцию. Тетраэдр, выполненный из стержней, часто используется в качестве основы для пространственных несущих конструкций пролётов зданий, перекрытий, балок, ферм,Стержни испытывают только продольные нагрузки.
- Прямоугольный тетраэдр используется в оптике. Если грани, имеющие прямой угол, покрыть светоотражающим составом или весь тетраэдр выполнить из материала с сильным светопреломлением, чтобы возникал эффект полного внутреннего отражения, то свет, направленный в грань, противоположную вершине с прямыми углами, будет отражаться в том же направлении, откуда он пришёл. Это свойство используется для создания уголковых отражателей, катафотов.
- Граф четверичного триггера представляет собой тетраэдр[9].
Тетраэдры в философии[править | править код]
«Платон говорил, что наименьшие частицы огня суть тетраэдры»[10].
См. также[править | править код]
- Симплекс — n-мерный тетраэдр
- Тетраэдр Мейсснера
- Тетраэдр Рёло
- Треугольник
Примечания[править | править код]
- ↑ Древнегреческо-русский словарь Дворецкого «τετρά-εδρον». Дата обращения: 20 февраля 2020. Архивировано из оригинала 28 декабря 2014 года.
- ↑ Селиванов Д. Ф.,. Тело геометрическое // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- ↑ Гусятников П.Б., Резниченко С.В. Векторная алгебра в примерах и задачах. — М.: Высшая школа, 1985. — 232 с. Архивная копия от 10 января 2014 на Wayback Machine
- ↑ В. Э. МАТИЗЕН Равногранные и каркасные тетраэдры «Квант» № 7, 1983 г.
- ↑ Моденов П.С. Задачи по геометрии. — М.: Наука, 1979. — С. 16.
- ↑ Маркелов С. Формула для объема тетраэдра// Математическое просвещение. Вып. 6. 2002. С. 132
- ↑ Источник. Дата обращения: 31 марта 2018. Архивировано 30 августа 2017 года.
- ↑ Источник. Дата обращения: 31 марта 2018. Архивировано 31 марта 2018 года.
- ↑ http://knol.google.com/k/триггер#view Архивная копия от 23 ноября 2010 на Wayback Machine Триггер
- ↑ Вернер Гейзенберг. У истоков квантовой теории. М. 2004 г. стр.107
Литература[править | править код]
- Матизен В. Э., Дубровский. Из геометрии тетраэдра «Квант», № 9, 1988 г. С.66.
- Заславский А. А. Сравнительная геометрия треугольника и тетраэдра // Математическое просвещение, сер. 3 (2004), № 8, стр. 78-92.
- Понарин Я. П. Элементарная геометрия. Том 3. Треугольники и тетраэдры.2009 г.
План урока:
Тетраэдр
Параллелепипед
Построение сечений
Тетраэдр
Пусть в пространстве есть точки М, Н, К, которые образуют ∆МНК и, таким образом, задают плоскость. Отметим в пространстве ещё одну точку Р, которая НЕ находится в плоскости МНК. Если мы соединим Р с вершинами ∆МНК, то получится объемная фигура. Её как раз именуют тетраэдром. Можно дать несколько различных определений тетраэдра, мы остановимся на следующем:

Такое название связано с тем, что в древнегреческом языке слово «тетра» означает «четыре». У тетраэдра ровно 4 грани и ровно 4 вершины. Приведем пример тетраэдра:

Легко увидеть, что гранями тетраэдра являются треугольники, в данном случае это ∆МРН, ∆МКР, ∆МНК и ∆РКН. Иногда одну из граней выделяют особенно и называют ее основанием тетраэдра. В этом случае три остальные грани именуют боковыми гранями тетраэдра.
Легко видеть, что есть всего 6 ребер тетраэдра. Действительно, назовем ∆МКН основанием тетраэдра. Оно, как и всякий треугольник, имеет 3 стороны. Ещё три ребра – это отрезки, соединяющие каждую из трех вершин ∆МКН с точкой Р. Перечислим грани, показанные на рисунке: МК, КН, МН, МР, НР и КР.
Заметим, что каждое ребро пересекается с четырьмя другими ребрами, и лишь с одним ребром скрещивается. Пары скрещивающихся ребер именуют противоположными ребрами. На рисунке противоположны друг другу грани РК и МН, МК и РН, МР и КН.
Тетраэдр называют простейшим многогранником. Действительно, у него всего 4 вершины, а меньшего количества вершин у многогранника быть не может (ведь любые три точки располагаются в одной плоскости). В этом тетраэдр во многом похож на треугольник – простейший из многоугольников. Как и треугольник, тетраэдр является очень жесткой конструкцией, поэтому его нередко используют в технике. Встречается тетраэдр и во многих научных дисциплинах, в том числе и в физике. Так, кристаллическая решетка алмаза, наиболее твердого материала на Земле, состоит из множества тетраэдров.
Наконец, отметим, есть особый, так называемый правильный тетраэдр. Его особенность заключается в том, что все его ребра имеют одинаковую длину.
Рассмотрим несколько задач.
Задание. Известно, что в тетраэдре АВСD:

Найдите длины ребер АВ, ВС и АС этого тетраэдра, а также площадь ∆АВС. Ответы округлите с точностью до целых.
Решение.

Неизвестные стороны можно вычислить, применяя теорему косинусов для каждой грани тетраэдра. Запишем ее для ∆ADB:

Далее используем ∆ADC. Так как ∠ADC = 90°, то вместо теоремы косинусов можно записать ее частный случай – теорему Пифагора:

Осталось найти площадь ∆АВС. Так как нам известны длины всех его сторон, то удобнее всего воспользоваться формулой Герона. Напомним, что для ее использования надо предварительно рассчитать полупериметр треугольника:

Задание. На ребрах АВ и АС тетраэдра ABCD отмечены их середины – точки M и N соответственно. Верно ли, что плоскость BCD и прямая MN параллельны?
Решение.

Так как отрезок MN соединяет середины сторона АС и АВ, то он является средней линией в ∆АВС. Это значит, что NM||ВС. Получается, что в плоскости ВСD есть прямая, параллельная NM. Ранее мы изучали теорему, согласно которой из этого факта следует, что MN либо параллельна BCD, либо полностью находится в ней. Очевидно, что MN не располагается в BCD, ведь в противном случае в BCD полностью находились бы прямые АС и АВ (в том числе и точка А), а по определению тетраэдра А находиться в плоскости BCD не может. Значит, остается один вариант – NM и BCD параллельны.
Задание. Верно ли, что плоскость, проходящая через середины трех ребер тетраэдра, обязательно будет параллельна одной из граней тетраэдра?
Решение. Обозначим вершины тетраэдра буквами М, Н, К, Р. Пусть плоскость будет проходить по точкам N, T и L, которые являются серединами ребер MP, HP и КР соответственно:

Ясно, что плоскость NTL пересекает как минимум три грани: РМН, РНК и РКМ, то есть она может быть параллельна только грани МНК.
Заметим, что TL – это средняя линия в ∆НРК, а NT – средняя линия в ∆РМН. Поэтому TL||НК и NT||МН.
Получается, что в плоскостях NTL и МНК есть по две пересекающихся прямых, которые попарно параллельны. В NTL ими являются NTи TL, а в МНК– МН и НК. Напомним, что по признаку параллельности плоскостей этого факта как раз достаточно, чтобы NTL и МНК считались параллельными плоскостями. То есть утверждение, приведенное в условии задачи, верно.
Параллелепипед
Построим в плоскости параллелограмм АВСD. Далее через каждую его вершину проведем прямые, которые пересекут плоскость параллелограмма и при этом будут параллельны. Отложим на каждой такой прямой точки А1, В1, С1 и D1 так, чтобы все они находись по одну сторону от плоскости АВСD и выполнялось равенство:

Заметим, что в таком случае четырехугольники АА1D1D, АВВ1А1, ВСС1В1 и СDD1C1 будут параллелограммами, ведь у каждого из них две противоположные стороны одинаковы и параллельны. Также можно убедиться, что отрезки А1D1 и В1С1 тоже параллельны и одинаковы по свойству транзитивности:

Это значит, что и А1D1C1B1– параллелограмм. Получается, что мы смогли построить многогранник с 6 гранями, каждая из которых является параллелограммом. Такой многогранник именуется параллелепипедом.

Легко подсчитать, что у параллелепипеда ровно 8 вершин и 12 ребер. Если у граней параллелепипеда есть общее ребро, то их называют смежными гранями. В противном случае грани именуются противоположными. Также противоположными могут быть и вершины параллелепипеда, если они не находятся на одной грани. Так, в приведенном выше примере противоположны вершины А и С1, В и D1, C и А1, D и B1.
Существуют также и диагонали параллелепипеда. Это прямые, соединяющие его противоположные вершины:

Иногда в параллелепипеде выбирают две противоположные грани и называют их основаниями параллелепипеда. В таком случае остальные четыре грани именуются боковыми гранями.
Сформулируем важное свойство параллелепипеда.

Действительно, рассмотрим параллелепипед АВСDА1В1С1D1:

Сравним грани АВВ1А1 и CDD1C1. СD||АВ как стороны в параллелограмме АВСD, а DD1||А1A уже как стороны в параллелограмме АА1D1D. По признаку параллельности плоскостей выходит, что грани АВВ1А1 и CDD1C1 параллельны, ведь они содержат пересекающиеся прямые (СDи DD1 в CDD1C1, АВ и АА1 в АВВ1А1), которые друг другу попарно параллельны.
Теперь продемонстрируем, что эти грани ещё и равны. Отрезки АВ и СD одинаковы, так как входят в состав параллелограмма АВСD. По той же причине одинаковы и отрезки АА1 и DD1 (они находятся в другом параллелограмме, в АА1D1D). Также одинаковы ∠СDD1 и ∠ВАА1, так как у этих углов стороны являются сонаправленными лучами. Равенства двух сторон и находящегося между ними угла достаточно для доказательства равенства параллелограммов АВВ1А1 и CDD1C1, ч. т. д.
Второе важное свойство параллелепипеда связано с его диагоналями.

Доказательство.

Всего в параллелепипеде есть 4 диагонали. Докажем сначала утверждение только для двух диагоналей, например, для А1С и В1D. Рассмотрим четырехугольник А1В1СD. Две его стороны, А1В1 и СD, равны и параллельны третьему отрезку – D1C1. Тогда, по свойству транзитивности, можно утверждать, что они также параллельны и равны друг другу. Значит, А1В1СD – параллелограмм, причем А1С и В1D – его диагонали. Но мы знаем, что диагонали параллелограмма пересекаются, а точка их пересечения (обозначим ее как О) делит их пополам.
Теперь возьмем диагонали В1D и, например, АС1. Аналогично и для них можно доказать, что у них есть общая точка, делящая их пополам (для этого надо рассмотреть параллелограмм В1С1D1A).Но мы уже знаем, что В1D1 делится пополам точкой О. Значит, именно она – общая для В1Dи АС1.
Наконец, рассмотрим также диагонали В1D и ВD1. И снова для них можно показать (используя параллелограмм BDD1B1), что они пересекаются в точке, делящей их пополам. И снова этой точкой будет О. Получается, что все четыре диагонали проходят через О, которая является для каждой из них серединой, ч. т. д.
Задание. Сумма длин всех ребер в параллелепипеде АВСDА1В1С1D1 составляет 120 см. Известно, что ВС больше АВ в 1,25 раза, а ВВ1 больше ВС в 1,2 раза. Найдите длину каждого ребра данного параллелепипеда.
Решение.

Заметим важный факт – хотя у параллелепипеда 12 ребер, их длины принимают всего три различных значения. Действительно, по свойству параллелограммов, являющихся его гранями, мы можем записать равенства:

Таким образом, сумма трех взаимно пересекающихся ребер (например, АВ, ВС и ВВ1) будет ровно в 4 раза меньше суммы длин всех ребер:

Используя условие задачи, выразим длины ВС и ВВ1 через АВ:

Задание. В параллелепипеде АВСDА1В1С1D1 отметили точки М, М1, N и N1, которые являются серединами АВ, А1В1, СD и С1D1 соответственно. Докажите, что многогранник МВNDM1B1N1D1– это также параллелепипед.
Решение.

Заметим, что ребра АВ, СD, А1В1 и С1D1 одинаковы. Значит, одинаковы и их половины:

Отрезки ND и N1D1 лежат на параллельных ребрах СD и С1D1, значит, они сами параллельны. Если учесть, что они ещё и одинаковы, то получается, что DNN1D1 – параллелограмм. Аналогично МВ||DN, МВ||М1В1 и М1В1||N1D1, поэтому четырехугольники МВND, МВВ1М1 и М1В1N1D1– параллелограммы.Теперь нам осталось показать, что грани М1D1DМи В1N1NB– тоже параллелограммы.
Отметим, что ММ1 = ВВ1 (из параллелограмма МВВ1М1) и ВВ1 = DD1 (это параллельные грани параллелепипеда), поэтому отрезки ММ1 и DD1 одинаковы. Также они и параллельны, так как ММ1||ВВ1 и ВВ1||DD1. Это значит, что М1D1DМ – параллелограмм. Аналогично, сравнивая NN1и ВВ1 с отрезком DD1, можно показать, что и В1N1NB– параллелограмм. В итоге получается, что у многогранника MBNDМ1B1N1D1 каждая из 6 граней – параллелограмм. То он по определению является параллелепипедом, ч. т. д.
Построение сечений
Любую объемную фигуру можно условно «разрезать» на две части, если провести через нее плоскость. Такая плоскость, проходящая через объемную фигуру, называется секущей плоскостью.

При пересечении плоскости и объемной фигуры образуется какая-нибудь плоская фигура, ее называют сечением. На рисунке выше сечение – это ∆NTL. Ещё раз отметим разницу между понятиями «секущая плоскость» и «сечение». Плоскость – это безграничная фигура, то есть она не имеет границ. Сечение же – это плоская фигура, имеющая границы.
Один из вопросов, который исследует стереометрия – это форма сечений тех или иных фигур.
Секущая плоскость пересекается с каждой гранью многогранника по отрезку, причем концы этих отрезков располагаются на ребрах многогранника. В результате сечение тетраэдра, параллелепипеда и вообще любого многогранника представляет собой плоский многоугольник. В тетраэдре всего 4 грани, поэтому его сечение не может иметь более 4 сторон. Другими словами, сечение тетраэдра – это либо четырехугольник, либо треугольник. У параллелепипеда уже шесть граней, а потому его сечения также могут быть даже шестиугольниками.
Важно уметь строить сечения, зная лишь несколько общих точек объемной фигуры и секущей плоскости. В случае многогранников достаточно просто найти все общие точки секущей плоскости и ребер, после чего их надо соединить отрезками. Заметим, что каждая сторона сечения должна находиться на одной из граней многогранника. Если с учетом этого ограничения построить сечение не получается, это значит, что сечение пересекает ещё какие-то ребра многогранника, и соответствующие точки пересечения надо найти. Рассмотрим несколько примеров задач на построение сечений.
Задание. Постройте сечение тетраэдра АВСD, проходящее через точки M, N и P:

Решение. Мы уже имеем три точки сечения. Однако просто соединить их нельзя, ведь точки M и P находятся на разных гранях. Значит, надо найти ещё одну общую точку сечения, находящуюся на каком-нибудь ребре.
Заметим, что плоскость MNP имеет с плоскостью BCD две общие точки – N и P. Значит, они пересекаются по прямой NP. Это значит, что если прямая ВС пересекается с NP, то эта точка пересечения будет принадлежать секущей плоскости. Продолжим ВС и NP, они пересекутся в некоторой точке Е, которая, как мы только что выяснили, находится на секущей плоскости:

Е находится на ВС, а ВС – это часть плоскости АВС. Значит, точка Е располагается на плоскости АВС. С другой стороны, и М находится на АВC. Получается, что у прямой ЕМ две точки принадлежат плоскости АВС, а потому она вся принадлежит АВС. Тогда мы можем найти ее точку пересечения с прямой АС, просто продлив прямую ЕМ:

Здесь мы обозначили точку пересечения ЕМ и АС буквой К. В итоге мы можем построить сечение MNPK, ведь каждая сторона этого многоугольника будет принадлежать одной из граней тетраэдра:

На картинке слева показано сечение MNPK. Именно это построение и необходимо выполнить, решая данную задачу. Справа для наглядности показан исходный тетраэдр, от которого секущая плоскость «отсекла» лишнее. Правую картинку строить при решении подобных задач не надо, она показана только для наглядности.
Заметим, что в этой задаче нам в качестве исходных данных были указаны три точки секущей плоскости, и этого хватило для построения сечения. Действительно, одна из аксиом стереометрии говорит, что три точки (если это не точки одной прямой) однозначно определяют плоскость, поэтому, зная только три точки, с помощью построений можно найти и все остальные точки.
Задание. В тетраэдре АВСD на грани АВD отмечена точка М. Постройте такое сечение тетраэдра, которое проходит через М и при этом параллельно грани АВС.

Решение. Секущая плоскость и плоскость АВС параллельны, при этом они пересекаются третьей плоскостью АВD. Тогда, по одной из изученных нами теорем, линии их пересечения с ABD будут параллельны. То есть чтобы построить отрезок, по которому секущая плоскость и грань ABD пересекаются, надо просто провести через M отрезок, параллельный ребру АВ:

Удалось получить две точки, Q и P, которые лежат на гранях. Теперь, чтобы найти линию пересечения секущей плоскости и грани АСD, надо провести через Р отрезок, параллельный АС. В итоге на грани CD мы получим ещё одну точку K:

Теперь у нас есть три точки сечения, при этом все отрезки, соединяющие их, лежат на гранях тетраэдра. Значит, мы уже можем построить сечение:

Обратите внимание, что отрезок QK также получился параллельным ребру СD, что говорит о правильности построения.
Задание. Постройте сечение параллелепипеда, проходящее через точки M, N и P, отмеченные на его гранях:

Решение. Здесь у задачи очень простое решение. Точки M, N, Р уже можно соединить так, что все соединяющие их отрезки будут находиться на гранях. Значит, никаких других точек искать не надо:

Задание. Решите предыдущую задачу, но при другом расположении точек М, N и Р:

Решение. Для начала мы можем построить отрезки MN и MР, по которым секущая плоскость пересекает грани АВВ1А1 и ВСС1В1:

Напомним, что противоположные грани у параллелепипеда параллельны. Поэтому и отрезки, которые образуются при их пересечении с секущей плоскостью, также должны быть параллельными. Значит, мы можем через N провести отрезок, параллельный MP, а через Р– отрезок, параллельный MN:

Теперь мы можем соединить KH (ведь K и H находятся на одной грани АВСD) и получить искомое сечение:

Задание. Решите предыдущую задачу при следующем расположении точек M, N и P:

Решение. На первом шаге мы можем построить отрезки MN и РМ. Секущая плоскость и плоскость АВВ1А1 пересекаются по прямой РМ. Найдем вспомогательную точку Е, в которой с РМ пересекается. Эта точка Е должна находиться в плоскости нижней грани АВСD, также она принадлежит секущей плоскости:

Так как верхняя и нижняя грани параллельны, то должны быть параллельны и линии их пересечения с секущей плоскостью. Но мы уже знаем, что секущая плоскость проходит через Е. Значит, линии пересечения секущей плоскости и нижней грани проходит через Е и параллельна MN. Этой информации достаточно для ее построения:

В результате нам удалось найти ещё две точки Q и F. Далее через F проводим отрезок, параллельный РМ:

В итоге мы получили 6 точек, которых достаточно для построения сечения:

Задание. В параллелепипеде АВСAА1В1С1D1 отрезок АС – это диагональ грани АВСD, а BD1 – диагональ параллелепипеда. Постройте сечение, проходящее через АС и при этом параллельное диагонали BD1.

Решение. Проведем на нижней грани диагональ BD. Она пересечется с АС в некоторой точке О:

Теперь мы можем в плоскости BDD1 построить через точку О прямую, параллельную BD1. Так как в этой же плоскости находится и DD1, то DD1 обязательно пересечется с этой прямой в какой-нибудь точке H:

Теперь проанализируем расположение плоскости АНСи диагонали BD1. Так как BD1||ОН, а ОН полностью принадлежит АНС, то получается, что BD1||АНС. При этом АНС проходит через диагональ АС. Значит, АНС удовлетворяет условиям задачи и является искомым сечением:

В рамках сегодняшнего урока мы познакомились с простейшими объемными фигурами – тетраэдром и параллелепипедом. Также мы узнали о сечениях и способах их построения.
Сообщения без ответов | Активные темы | Избранное
Сечение тетраэдра – параллелограмм
|
lvbealr |
Сечение тетраэдра – параллелограмм
|
|
13/03/22 |
|
|
|
|
|
Ende |
Posted automatically
|
||||
02/02/19 |
|
||||
|
|
|||||
|
Ende |
Posted automatically
|
||||
02/02/19 |
|
||||
|
|
|||||
|
iifat |
Re: Сечение тетраэдра – параллелограмм
|
||
16/02/13 |
Может, попробовать начать с уравнений? Ну, поместить начало координат в точку
|
||
|
|
|||
|
TOTAL |
Re: Сечение тетраэдра – параллелограмм
|
||
23/08/07 |
Через каждую из этих точек проведите прямую (в грани соответствующей точки), которая параллельна ребру, соединяющему грани этих точек. Так получите параллелограмм.
|
||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Тетраэдр. Виды тетраэдров

Тетраэдр (четырёхгранник) — многогранник, гранями которого являются четыре треугольника (от греческого tetra — четыре и hedra — грань).

Рис. 1
У тетраэдра (4) грани, (4) вершины и (6) рёбер (Рис. 1).
Один из треугольников называется основанием тетраэдра, а три остальные — боковыми гранями тетраэдра.
В зависимости от видов треугольников и их расположения выделяют разные виды тетраэдров.
В школьном курсе чаще говорят о следующих видах тетраэдра:
– равногранный тетраэдр, у которого все грани — равные между собой треугольники;
– правильная треугольная пирамида — основание — равносторонний треугольник, все боковые грани — одинаковые равнобедренные треугольники (Рис. 3);
– правильный тетраэдр, у которого все четыре грани — равносторонние треугольники (Рис. 2).


Рис. 2 Рис. 3
Свойство правильного тетраэдра:
из определения правильного многогранника следует, что все рёбра тетраэдра имеют равную длину, а грани — равную площадь.
Параллелепипед. Виды параллелепипедов


Параллелепипедом называется многогранник, у которого (6) граней — параллелограммы.

Рис. 4
У параллелепипеда, как отмечено, (6) граней, (8) вершин и (12) рёбер (Рис. 4).
Две грани параллелепипеда, имеющие общее ребро, называются смежными, а не имеющие общих рёбер — противоположными.
Обычно выделяют какие-нибудь две противоположные грани и называют их основаниями, а остальные грани — боковыми гранями параллелепипеда.
Рёбра параллелепипеда, не принадлежащие основаниям, называют боковыми рёбрами.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю параллелепипеда (Рис. 5).

Рис. 5
В зависимости от видов параллелограммов и их расположения выделяют разные виды параллелепипедов:
параллелепипеды могут быть прямые и наклонные.
У прямых параллелепипедов боковые грани — прямоугольники (Рис. 5),
у наклонных — параллелограммы (Рис. 4).
Прямой параллелепипед, у которого основанием тоже является прямоугольник, называется прямоугольным параллелепипедом.

Рис. 6
Длины непараллельных рёбер прямоугольного параллелепипеда называются его линейными размерами (измерениями).
У прямоугольного параллелепипеда — три линейных размера:
DA
,
DC
,
DD1
(Рис. 6).
Свойства параллелепипеда:
– противоположные грани параллелепипеда равны и параллельны.
– Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
– Боковые грани прямого параллелепипеда — прямоугольники.
Построение сечения тетраэдра и параллелепипеда
Плоскостью сечения многогранника можно назвать любую плоскость, по обе стороны которой находятся точки многогранника.
Секущая плоскость пересекает грани многогранников по отрезкам.
Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.
Так как у тетраэдра (4) грани, то сечением тетраэдра может быть треугольник (Рис. 7) или
четырёхугольник (Рис. 8).


Рис. 7 Рис. 8
У параллелепипеда (6) граней, поэтому сечением этого многогранника может быть треугольник (Рис. 9), четырёхугольник ( Рис. 10), пятиугольник (Рис. 11) или шестиугольник (Рис. 12).
При построении сечения надо вспомнить следующие знания из предыдущих тем:
1. если две точки прямой принадлежат плоскости, то прямая находится в этой плоскости.
2. Если две плоскости имеют общую точку, то эти плоскости пересекаются по прямой.
3. Если плоскость пересекает две параллельные плоскости, то линии пересечения параллельны.
Пример:
Задача
Построить сечение параллелепипеда плоскостью, которая проходит через точки (K), (M) и (N).

1. Проводим (MK), так как обе точки находятся в одной плоскости;
2.
MK∩CC1=X
— непараллельные прямые в одной плоскости пересекаются;

3. проводим (XN), так как обе точки находятся в одной плоскости;

5. проводим (MP), так как обе точки находятся в одной плоскости;
6. через точку (N) в плоскости основания
NL∥MP
, так как линии пересечения параллельных плоскостей с третьей плоскостью должны быть параллельны;

7. соединяем (N) и (L) и получаем сечение (MPNLK).


Тема:
« Тетраэдр
и его сечение ».
Урок №2 10 класс стереометрия
10 класс

Актуализация опорных знаний
Вопросы:
1) Что такое многогранник? Какие многогранники вы знаете?
МНОГОГРАННИК – это поверхность геометрического тела, составленная из многоугольников.
Мы познакомимся с двумя из них – ТЕТРАЭДРОМ и ПАРАЛЛЕЛЕПИПЕДОМ.

Актуализация опорных знаний
2) Дайте определение тетраэдра.
Поверхность, составленная из четырех треугольников АВС , ADC, ADB и BDC , называется тетраэдром и обозначается: DABC .
D
A
B
C

Актуализация опорных знаний
3) Назовите элементы тетраэдра
Треугольники, из которых состоит тетраэдр, называются гранями.
ABC, ADC, ADB и BDC – грани тетраэдра DABC.
Стороны треугольников называются ребрами тетраэдра , а вершины треугольника – вершинами тетраэдра.
AB,AC,AD,DC,DB и BC – ребра,
A,B,C, и D – вершины тетраэдра.
D
A
B
C

Задача по готовому чертежу
M
Укажите все грани, ребра, вершины, противоположные ребра, скрещивающиеся ребра тетраэдра.
L
N
K

1) Определение секущей плоскости тетраэдра
Секущей плоскостью тетраэдра называют такую плоскость, по обе стороны от которой имеются точки тетраэдра.
Секущая плоскость пересекает грани тетраэдра по отрезкам .
Многоугольник, сторонами которого являются эти отрезки, называется сечением тетраэдра .

2) Сечение тетраэдра
Т.к. тетраэдр имеет четыре грани, то его сечениями могут быть только треугольники и четырёхугольники .

3) Правила построения сечений ТЕТРАЭДРА
а)Проводим прямые через точки, лежащие в одной плоскости;
б) Ищем прямые пересечения плоскости сечения с гранями многогранника, для этого:
— ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);
— параллельные грани плоскость сечения пересекает по параллельным прямым.

Построение сечения тетраэдра через точки M, N, K
D
Построение:
1. KM
2. NM
K
А
C
M
N
B

Построение сечения тетраэдра через точки M, N, K
D
Построение:
3. NM ∩ АС = F
K
F
А
C
N
M
B

Построение сечения тетраэдра через точки M, N, K
D
Построение:
4. KF ∩ АС = L
5. KL
K
L
F
А
C
M
N
B

Построение сечения тетраэдра через точки M, N, K
D
Построение:
1. KM
2. NM
K
3. NM ∩ АС = F
4. KF ∩ АС = L
L
5. KL
6. LN
F
А
7. KLNM – искомое сечение
C
N
M
B

Объясните, как построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K
D
Найдите периметр сечения, если
M, N, K – середины ребер и каждое ребро тетраэдра
равно а.
M
K
N
А
C
B

Объясните, как построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K
D
Найдите периметр сечения, если M, N, K – середины ребер и каждое ребро тетраэдра равно а .
K
N
А
C
M
B

Индивидуальное задание
Построить сечение тетраэдра по данным точкам

























 “, а еще лучше “сторона
“, а еще лучше “сторона 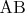 ” (наведите курсор на формулу, чтобы увидеть ее код). (краткие инструкции:
” (наведите курсор на формулу, чтобы увидеть ее код). (краткие инструкции:  , обозначим
, обозначим  и так далее. Подозреваю грандиозный объём, но таки систем линейных векторных уравнений, так что муторно, но подъёмно.
и так далее. Подозреваю грандиозный объём, но таки систем линейных векторных уравнений, так что муторно, но подъёмно. ,
, 
