Как найти параметр 8 класс

Задачи с параметрами играют важную
роль в формировании логического мышления и
математической культуры учащихся. Они имеют
принципиально исследовательский характер, и с
этим связаны как методическое значение таких
задач, так и трудности выработки навыков их
решения.

Важность понятия параметра связана с
тем, что, как правило, именно в терминах
параметров происходит описание свойств
математических объектов: функций, уравнений,
неравенств. Под параметрами мы понимаем входящие
в алгебраические выражения величины, численные
значения которых явно не заданы, однако
считаются принадлежащими определенным числовым
множествам. Учащимся 8 класса известны линейная
функция и ее частный случай – прямая
пропорциональность:

(параметры и определяют расположение
графика функции на плоскости и точки пересечения
с осями), а также линейное и квадратное уравнение
и соответствующие неравенства:

(параметры , и определяют, вообще говоря,
не только существование и количество корней, но и
степень уравнения).

Решение задач с параметрами требует
исследования, даже если это слово не упомянуто в
формулировке задачи. Недостаточно механического
применения формул, необходимо понимание
закономерностей, навыки анализа конкретного
случая на основе известных общих свойств
объекта, системность и последовательность в
решении, умение объединить рассматриваемые
частные случаи в единый результат. Этим
обусловлены трудности, возникающие у учащихся
при решении таких задач, и этим же объясняется
справедливое включение задач с параметрами в
экзаменационные работы в школе и на
вступительных экзаменах в вузы.

Таким образом, очевидна необходимость
отработки приемов решения различных задач с
параметрами. Ниже приводится система упражнений
по решению и исследованию квадратных уравнений и
неравенств с одним параметром в курсе 8 класса.

 Квадратные уравнения с параметром

1. При каких значениях
уравнение имеет единственное решение?

Решение.

Ошибочно считать данное уравнение
квадратным. На самом деле это уравнение степени
не выше второй. Исходя из этого соображения,
рассмотрим следующие случаи:

а) . При этом уравнение принимает вид , откуда , т.е.
решение единственно.

б) , тогда – квадратное уравнение, дискриминант . Для того,
чтобы уравнение имело единственное решение,
нужно, чтобы , откуда .

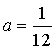Ответ: или .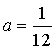

2. При каких значениях
уравнение имеет единственное решение?

Решение.

1) При исходное уравнение не имеет решения.

2) , тогда данное уравнение является
квадратным и принимает вид 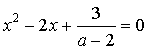. Искомые значения
параметра – это корни дискриминанта, который
обращается в нуль при .

Ответ: .

3. При каких значениях
уравнение имеет более одного корня?

Решение.

1) При уравнение имеет единственный корень .

2) При исходное уравнение, будучи квадратным,
имеет два корня, если его дискриминант
положителен, т.е. . Решая неравенство, получаем . Из этого

промежутка следует исключить число нуль.

Ответ: или .

4. При каких значениях уравнения
и
равносильны?

Решение.

1) При : имеет два различных корня, имеет один
корень. Равносильности нет.

2) При решения уравнений совпадают.

3) При ни первое, ни второе уравнения решений
не имеют. Как известно, такие уравнения считаются
равносильными.

Ответ: .

5. При каких значениях уравнения и
равносильны?

6. При каких значениях параметра уравнение
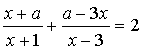имеет
одно решение?

7. При каких значениях ровно
один из корней уравнения равен нулю?

8. При каких значениях корни
уравнения равны по модулю, но противоположны по
знаку:

9. При каких значениях оба
корня уравнения равны нулю?

а) ;
б)

10. Решите уравнения:

I.

II.

III.

IV.

V.

11. При каких значениях
произведение корней квадратного уравнения равно
нулю?

12. При каких значениях сумма корней квадратного
уравнения равна нулю?

13. В уравнении сумма квадратов корней
равна 16. Найти .

14. В уравнении квадрат разности корней
равен 16. Найти .

15. При каких значениях сумма корней уравнения равна
сумме квадратов корней?

16. При каком значении параметра сумма
квадратов корней уравнения
наименьшая?

17. При каком значении параметра сумма
квадратов корней уравнения
наибольшая?

18. При каких значениях параметра один из
корней квадратного уравнения в два
раза больше другого?

19. Известно, что корни уравнения на 1 меньше
корней уравнения . Найдите и корни каждого из
уравнений.

20. Найдите наименьшее целое значение
, при
котором уравнение имеет два различных
действительных корня.

21. При каких значениях уравнение имеет
более двух корней?

22. При каких значениях
уравнение имеет хотя бы один общий корень с
уравнением ?

23. При каком соотношении между , , уравнение

имеет один корень? Может ли данное уравнение
иметь два действительных различных корня?

24. При каком значении параметра уравнение

имеет три корня?

 Неравенства с параметром

1. Решите неравенство, где –
параметр:

2. Найдите все значения , при
которых квадратное уравнение имеет два
действительных различных корня:

3. Найдите все значения , при
которых квадратное уравнение не имеет
действительных корней:

4. При каких значениях
уравнение имеет положительное решение?

5. При каких значениях
уравнение имеет отрицательное решение?

6. При каких значениях
уравнение имеет одно положительное решение?

7. При каких значениях
уравнение имеет решения, удовлетворяющее условию ?

8. При каких значениях система
неравенств имеет хотя бы одно решение:

9. При каких значениях система
неравенств не имеет решений:

10. При каких значениях система неравенств имеет
хотя бы одно решение?

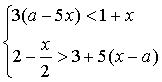
11. При каких значениях уравнение имеет
корни разных знаков?

12. При каких значениях уравнение имеет
корни
и
такие, что ?

13. Найдите все значения , при
которых корни уравнения меньше, чем 1.

14. Найдите все значения , при
которых один из корней уравнения меньше
1, а другой больше 1.

15. При каких значениях система уравнений

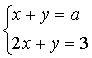
имеет решение ?

16. При каких значениях система уравнений

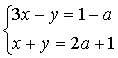
имеет решение ?

17. Для каждого решите неравенство:

I.

II.

III.

IV.

Урок 33. Уравнения с параметром. Контрольный урок

Тема: Уравнения с параметром

Содержание модуля (краткое изложение модуля):

Рассмотрим уравнение
ax + b = 0
Приведем уравнение к виду
ax = –b
Найдём корни уравнения, рассмотрев различные вариант значений параметров a и b.
Рассмотрим случаи

1. a = 0, b = 0 → 0x = 0 → 0 = 0 → x – любое число
2. a = 0, b ≠ 0 → 0x = b → 0 = b → корней нет
3. a ≠ 0 → x = (-b)/a

Решить уравнение с параметром – это значит показать, каким образом для любого значения параметра можно найти соответствующее множество корней уравнения, если корни существуют, или установить, что при этом значении параметра корней нет.

Алгебра. 8 класс: учеб. для общеобразоват. организаций / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. – 6-е изд. – М.: Просвещение, 2017.

• 
  1
  
• 
  2
  
• 
  3
  

Понятие уравнения с параметром и его решения

Часто на практике создаётся такая математическая модель, в которой приходится решать не одно, а целое «семейство» похожих уравнений.

Рассмотрим несложный пример.

Пусть нам дан прямоугольный участок площадью a. С точки зрения практической, мы хотим обнести участок забором, т.е. нас интересует зависимость периметра от длины x при некоторой площади a (ширина будет равна $frac{a}{x}$):

$$ P(x,a) = 2 Biggl(x+frac{a}{x} Biggr) $$

Допустим, у нас есть материалы, чтобы соорудить забор длиной 100 м.

Получаем уравнение:

$$ 2 Biggl(x+frac{a}{x} Biggr) = 100 Rightarrow x+frac{a}{x} = 50 overset{x neq 0}Rightarrow x^2-50x+a = 0 $$

Это – простейшее уравнение с параметром, в котором один из коэффициентов не задан конкретным числом.

Решим наше уравнение. Найдём дискриминант:

$$ D = 50^2-4a = 2500-4a = 4(625-a) $$

Чтобы решения существовали, потребуем:

$$ D ge 0 Rightarrow 625-a ge 0 Rightarrow a le 625 $$

Тогда: $x = frac{50 pm sqrt{D}}{2} = frac{50 pm sqrt{4(625-a)}}{2} = 25 pm sqrt{625-a}$.

Запишем ответ:

При $a lt 625$ два корня $x_{1,2} = 25 pm sqrt{625-a}$

При a = 625 один корень $x_0 = 25$

При $a gt 625$ решений нет

Наша модель немного усложнится, если мы поставим условия, чтобы площадь и длина были строго положительными:

$$ {left{ begin{array}{c} x^2-50x+a = 0 \ a gt 0 \ x gt 0 end{array} right.} $$

Исследуем решение. Полученный корень $x_2 = 25+ sqrt{625-a} ge 25 gt 0$ – положительный. И $x_1 = 25- sqrt{625-a}$ при $0 lt a lt 625$ меняется в пределах $0 lt x_1 lt 25$, т.е. также положительный.

Запишем ответ для модели с условиями:

При $0 lt a lt 625$ два корня $x_{1,2} = 25 pm sqrt{625-a}$

При a = 625 один корень $x_0$ = 25

При $a gt 625$ решений нет

Ответ изменился незначительно, но чтобы его записать, нам пришлось провести дополнительное исследование.

Решить уравнение с параметром F(x,a) при дополнительных условиях на переменную x и параметр a – это найти допустимое множество корней ${x_i }$ для любого допустимого значения параметра a.

Заметим, что согласно полученным результатам, максимальная площадь, которую мы можем огородить нашим забором длиной 100 м, равна a = 625 $м^2$. Участок при этом представляет собой квадрат с длиной $x_0 = 25$ м и шириной $ frac{a}{x_0} = 25$ м.

Примеры

Пример 1. При каких p квадрат разности корней уравнения $x^2-4x+p = 0$ равен 32?

Пусть $x_1, x_2$ – корни уравнения. По теореме Виета и условию задачи:

$$ {left{ begin{array}{c} x_1+x_2 = 4 \ x_1 x_2 = p \ x_1^2-x_2^2 = 32 end{array} right.} Rightarrow {left{ begin{array}{c} x_1+x_2 = 4 \ x_1 x_2 = p \ (x_1+x_2 )(x_1-x_2 ) = 32 end{array} right.} Rightarrow {left{ begin{array}{c} x_1+x_2 = 4 \ x_1-x_2 = 8 \ x_1 x_2 = p end{array} right.} Rightarrow $$

$$ Rightarrow {left{ begin{array}{c} 2x_1 = 4+8 = 12 \ 2x_2 = 4-8 = -4 \ x_1 x_2 = p end{array} right.} Rightarrow {left{ begin{array}{c} x_1 = 6 \ x_2 = -2 \ p = 6 cdot (-2) = -12 end{array} right.} $$

Ответ: p = -12

Пример 2. При каких значениях a уравнение

$$ x^2-(a+2)x+a+5 = 0 $$

имеет один корень? Найдите этот корень.

Найдём дискриминант:

$$ D = (a+2)^2-4(a+5) = a^2+4a+4-4a-20 = a^2-16 $$

Уравнение имеет один корень, если D = 0:

$$ a^2-16 = 0 Rightarrow a = pm 4 $$

При a = -4 уравнение имеет вид $x^2+2x+1 = 0$, т.е. $(x+1)^2 = 0$, $x_0 = -1$

При a = 4 уравнение имеет вид $x^2-6x+9 = 0$, т.е. $(x-3)^2 = 0, x_0 = 3$

Ответ:

При a = -4, $x_0$ = -1

При a = 4, $x_0$ = 3

Пример 3. Найдите такое p, чтобы уравнения

$$ x^2+x+p = 0 и x^2+px+1 = 0 $$

имели общий корень. Найдите этот корень.

Общий корень означает, что параболы пересекаются в точке, лежащей на оси OX.

$$ x^2+x+p = x^2+px+1 $$

$$ x(1-p) = 1-p Rightarrow left[ begin{array}{cc} {left{ begin{array}{c} p = 1 \ x in Bbb R – любой end{array} right.} \ {left{ begin{array}{c} p neq 1 \ x = 1 end{array} right.} end{array} right. $$

При p = 1 уравнения совпадают $x^2+x+1 = 0$, но решений не имеют, т.к. $D lt 0$.

При x = 1 уравнения парабол имеют вид: $p+2 = 0 Rightarrow p = -2$.

Ответ:

При p = 2 уравнения имеют общий корень x = 1.

Пример 4. Найдите все целые значения a, при которых уравнение $frac{4-a}{x^2-2x+4} = frac{1}{a}$ имеет решение.

$$ frac{4-a}{x^2-2x+4} = frac{1}{a} iff {left{ begin{array}{c} a(4-a) = x^2-2x+4 \ a neq 0 end{array} right.} $$

Особая точка: a = 4. Уравнение $x^2-2x+4 = 0$ решений не имеет, т.к. $D lt 0$.

Решаем уравнение в общем виде:

$$ x^2-2x+4-a(4-a) = 0 $$

$$ x^2-2x+a^2-4a+4 = 0 $$

$$ x^2-2x+(a-2)^2 = 0 $$

$$ D = 2^2-4(a-2)^2 = 4(1-(a-2) )(1+a-2) = 4(3-a)(a-1) = $$

$$ = -4(a-3)(a-1) $$

Потребуем $D ge 0$

$$ -4(a-3)(a-1) ge 0 Rightarrow (a-3)(a-1) le 0 $$

При a = 1 и a = 3 D = 0, уравнение имеет вид $x^2-2x+1 = 0$ и одно решение $x_0 = 1$.

При a = 2 уравнение имеет вид: $x^2-2x = 0 Rightarrow x(x-2) = 0 Rightarrow left[ begin{array}{cc} x_1 = 0 \ x_2 = 2 end{array} right. $

Ответ:

При a = 1 и a = 3 один корень $x_0 = 1$

При a = 2 два корня $x_1 = 0, x_2 = 2$

При всех других целых a уравнение решений не имеет.

Пример 5. При каких b и c уравнение $x^2+bx+c = 0$ имеет корнями b и c?

По условию $x_1 = b, x_2 = c$

По теореме Виета:

$$ {left{ begin{array}{c} x_1+x_2 = b+c = -b \ x_1 x_2 = bc = c end{array} right.} Rightarrow {left{ begin{array}{c} c = -2b = -2 \ b = 1end{array} right.} $$

Уравнение $x^2+x-2 = 0$ имеет корнями 1 и -2.

Ответ: b = 1, c = -2

Пример 6. Найдите все значения параметра a, при которых уравнения

$$ x^2+(a^2+3a+7)x = 0 и x^2+(4a+19)x+(a^2+7a-44) = 0 $$

имеют один и те же решения.

Старшие коэффициенты парабол одинаковы и равны 1.

Параболы будут иметь одинаковые решения в том случае, если будут полностью совпадать, т.е.:

$$ {left{ begin{array}{c} a^2+3a+7 = 4a+19 \ 0 = a^2+7a-44 end{array} right.} Rightarrow {left{ begin{array}{c} a^2-a-12 = 0 \ a^2+7a-44 = 0 end{array} right.} Rightarrow {left{ begin{array}{c} (a-4)(a+3) = 0 \ (a-4)(a+11) = 0 end{array} right.} Rightarrow a = 4 $$

Кроме того, они могли бы совпадать, если бы все переменные коэффициенты одновременно стали равны 0:

$$ {left{ begin{array}{c} a^2+3a+7 = 0 \ 4a+19 = 0 \ a^2+7a-44 = 0 end{array} right.} Rightarrow {left{ begin{array}{c} D lt 0, a in varnothing \ a = – frac{19}{4} \ a = {-11;4 } end{array} right.} Rightarrow a in varnothing $$

Таких a нет.

Ответ: a = 4

Пример 7. Решите уравнение:

$$ x^2-(a-1)x+(a+2)(a-1) = 0$$

Дискриминант:

$$ D = (a-1)^2-4(a+2)(a-1) = $$

$$ = (a-1)(a-1-4(a+2) ) = (a-1)(-3a-9) = -3(a-1)(a+3) $$

Ответ:

При a = -3 один корень $x_0 = -2$

При a = 1 один корень $x_0 = 0$

При $-3 lt a lt 1$ два корня $x_{1,2} = frac{a-1 pm sqrt{-3(a-1)(a+3)}}{2}$

При других a решений нет.

МИНИСТЕРСТВО ОБОРОНЫ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ
ГОСУДАРСТВЕННОЕ КАЗЁННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«ОРЕНБУРГКОЕ
ПРЕЗИДЕНТСКОЕ КАДЕТСКОЕ УЧИЛИЩЕ»

РЕШЕНИЕ КВАДРАТНЫХ
УРАВНЕНИЙ С ПАРАМЕТРАМИ

(методическое
пособие для воспитанников и преподавателей)

Составила
преподаватель математики

высшей
квалификационной категории

Зевина Елена Петровна

2013г.

УДК 372.

Зевина Е.П.: РЕШЕНИЕ  КВАДРАТНЫХ
УРАВНЕНИЙ С ПАРАМЕТРАМИ.

Методическое
пособие для воспитанников и преподавателей.

–
Оренбург: ФГКОУ  Оренбургское ПКУ, 2013. –32с.

В
пособии представлен опыт практической деятельности преподавателя училища по
методике обучения решению квадратных уравнений с параметрами.

Методическое
пособие содержит задачи с параметрами, при решении которых возникают наибольшие
затруднения во время обучения. Методами решения таких задач уделяется минимум
внимания, и целью данного пособия является помощь учащимся в устранении данного
пробела.

Данное
методическое пособие составлено по итогам многолетней практики работы и
подготовки учащихся к сдаче экзамена по математике в формате ЕГЭ и ГИА.

Рассмотрено
на заседании методического совета ФГКОУ Оренбургское ПКУ.

ФГОУ «Оренбургское
президентское кадетское училище», 2013

Содержание

1.                
Введение. . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

2.                
§1. Квадратные уравнения  с параметром . .
. . . . . . . . . . . . . . . . . . . . . .  5

1.1           
Понятие уравнения с параметром . . . .. .
. .  . . . . . .
. . . . . . . . . . . . . 5

1.2           
Квадратные уравнения . . . . . . . . . . .
. . . . . . . . . . . . . .  . . . . . . . . . . 5

1.3           
Теорема Виета . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . .. . . . . . . . . . 6

3.                
§2. Примеры
решения квадратных уравнений с параметром . . . . . . . . . 7

4.                
§3.
Задачи для самостоятельной работы по решению квадратных  

               
уравнений с параметром . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . 14

5.                
§4. Решение уравнений
с параметром, приводимых к квадратным. . . .15

6.                
§5. Задачи для
самостоятельной работы по решению уравнений,

          
приводимых к квадратным . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . .17

7.                
§6. Задачи, связанные с расположением
корней квадратного трехчлена.

              
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . 18

8.                
§7. Задачи для
самостоятельного решения, связанные с

          
расположением корней квадратного трехчлена . . . . . . . . . . .  . . . . . . .
25

9.                
Заключение. . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26

10.           
Список использованной литературы . . . . .
. . . . . . . . . . . . . . . . . . . . . . . 27

Введение

У большинства выпускников
и абитуриентов задачи с параметрами вызывают серьезные затруднения (как решать
задачу и как довести решение до правильного ответа). Трудности при решении
таких задач обусловлены во-первых: решением не по шаблону, во- вторых:
рассмотрением различных случаев, в которых методы решения существенно
отличаются друг от друга; в-третьих: хорошими знаниями свойств функций и
правильным выделением тех свойств, которые нужно применить.

Предлагаемое пособие
построено так, чтобы учащиеся самостоятельно могли понять логику решения задач
с параметрами, и научились их решать.

Пособие разбито на
параграфы, в конце которых приведены упражнения для самостоятельного решения.
Разобраны примеры, которые расположены в последовательности «от простого к
сложному», при этом предполагается, что учащийся имеет хорошие знания по
математике и изучает пособие последовательно.

Пособие может быть
использовано как для самостоятельной подготовки к вступительным экзаменам, так
и в качестве пособия на индивидуальных и групповых занятиях.

Функции вида , где   –
квадратный трехчлен, в школьном курсе математики придается большое значение.
Для нее строго доказываются все свойства, нужные в теории и для решения задач. Безукоризненное
знание необходимых свойств квадратного трехчлена требуется от каждого
абитуриента, так как квадратный трехчлен с параметром часто включается в
варианты письменных работ и в тесты для собеседования на вступительных
экзаменах в ВУЗы. Как правило, большая часть абитуриентов с этими задачами не
справляется. Значит, им надо уделять больше внимания на факультативных занятиях
в школе, на страницах печати.

§1.
Квадратные уравнения с параметром

1.1 Понятие уравнения с
параметром

Определение.
Пусть задано уравнение , если ставится задача,
для каждого действительного значения  решить уравнение
относительно , то это уравнение
называют уравнением с переменной  и параметром
.

Решить уравнение с параметром
– это значит, для каждого действительного значения  найти значение , удовлетворяющее данному
уравнению.

Назовем
контрольными значениями параметра (КЗП) те его значения, при
которых обращается в нуль: 1) старший коэффициент в уравнении или неравенстве; 2)
знаменатель дроби; 3) дискриминант квадратного уравнения.

1.2 Квадратные уравнения

Определение. Квадратным
уравнением называют уравнение вида

,

(1)

где  – переменная,  и , ,  – некоторые
действительные числа или выражения, зависящие от параметров.

Левая
часть уравнения является квадратным трехчленом, то есть многочленом второй
степени.

Корни
квадратного уравнения (1) находят по формуле

.

(2)

Выражение  называют дискриминантом
квадратного уравнения (1).

В
случае, когда второй коэффициент квадратного уравнения четное число , корни удобно находить
по формуле

.

(3)

Число корней квадратного уравнения
зависит от дискриминанта:

если
, то уравнение имеет два
различных действительных корня;

если , то уравнение имеет два
равных действительных корня

 

или
один корень, но двойной кратности.

если , то уравнение не
имеет действительных корней.

При
решении неполного квадратного уравнения , где  удобно пользоваться
разложением на множители левой части уравнения:

.

1.3 Теорема Виета

При
решении полных квадратных уравнений применяют теорему Виета: если  и  – корни
квадратного уравнения , где , то справедливы формулы
для суммы и произведения этих корней:

,  .

(4)

Формулы (4) называют формулами
Виета.

Верно и обратное
утверждение: если числа  и  удовлетворяют равенствам
(4), то эти числа являются корнями квадратного уравнения.

Формулы
Виета верны и для приведенного квадратного уравнения . В этом случае они
приобретают вид:

,  .

Квадратный
трехчлен можно разложить на линейные множители:

1)   если
, то ;

2)   если
, то .

§2.
Примеры решения квадратных уравнений с параметром

Пример 1.
Найти все значения параметра а, для которых квадратное уравнение

1)               
имеет два различных корня;

2)               
не имеет корней;

3)               
имеет один корень.

Решение. Так как по
условию старший коэффициент , то уравнение является
квадратным. Найдем его дискриминант: .

Контрольными
значениями параметра будут те значения, при которых дискриминант равен нулю.

КЗП:   или .

Далее определим знак дискриминанта,
а для этого заметим, что он представляет собой квадратичную функцию, графиком
которой является парабола, причем ветви её направлены вверх.

Знак
:                      
1)     +      2)         3)       2)     +    1)

                             
               – 4       
      –            4                   а

Возможны
три случая.

1)
Если , то  и уравнение имеет два различных
действительных корня

.

2)       
Если  или , то  и уравнение имеет один двукратный
корень , причем если , то , а если , то .

3) Если , то  и уравнение не имеет
действительных корней.

Ответ:
при   ;

при
  корней нет;

при
  ;

при
  .

Пример 2. Решить уравнение .

Решение. Поскольку старший
коэффициент данного уравнения зависит от параметр , то это уравнение нельзя
считать квадратным. Поэтому найдем первое контрольное значение параметра, приравняв
старший коэффициент к нулю.

КЗП:
.

1)       
Если , то исходное уравнение
принимает вид:

,

то
есть становится линейным и его корнем является .

2)       
Если , то исходное уравнение
является квадратным, поэтому вычислим его дискриминант :

.

Найдём
другие контрольные значения параметра, из условия, что дискриминант
квадратного уравнения равен нулю.

КЗП: 
 или .

Определим знак
дискриминанта. Поскольку он представляет собой квадратичную функцию, то графиком
его является парабола c ветвями
направленными вниз.

Знак                 а)              б) 
+   в)    б)       а)

 
                               –      1                      6     –      b

Возможны
следующие три подслучая.

а)
Если , то , а значит, уравнение не имеет
корней.

б)
Если  или , то  и найти значение корня
уравнения можно по формуле , то есть

при
 получим ,

при
 получим .

в)
Если , то  и уравнение имеет два различных
корня

.

В
ходе решения данного квадратного уравнения получили три контрольных значения
параметра b, которые наносим на
числовую прямую для удобства записи ответа.

                                   
               1            2             6              b

Ответ:
при   корней нет;

при  ;

при
  ;

при
  ;

при
  .

Пример 3. Найти все значения
параметра, для которых квадратное уравнение  имеет хотя бы один общий
корень с уравнением .

Решение. В первом
уравнении старший коэффициент – это выражение, содержащее параметр с.
Поэтому первым контрольным значением параметра с будет то, при
котором старший коэффициент уравнения равен нулю.

КЗП:
.

Возможны
два случая.

1)       
Если , то получим уравнение , которое не имеет
решений.

2)       
Если , уравнение является
квадратным и найдём его дискриминант:

Дискриминант представляет собой выражение
первой степени. Найдем второе контрольное значение параметра, приравняв  к нулю.

КЗП:
.

Определим
знак .

                     
                                      а)                           б)    
+ 

                              
                              –           –1                            с

Итак,
возможны два подслучая.

а)
Если , то  и уравнение корней не
имеет.

б)
Если , то  уравнение имеет два
различных корня

.

Рассмотрим
второе уравнение . Его корнями являются
числа  и .

По
условию задачи хотя бы один из найденных корней должен быть также корнем уравнения
, то есть при подстановке
найденного корня в это уравнение должно получиться тождество.

Если
, то получаем равенство:

,

,

откуда
. Аналогично найдём значение
с, при котором корнем уравнения  является .

Имеем

,

,

=0,

.

Значит,
при  и  уравнение  имеет, по крайней мере,
один общий корень с уравнением .

Ответ:
  и  .

Пример 4. Дано уравнение . Доказать, что если , ,  – попарно различные
действительные корни этого уравнения, то

.

Решение. По условию , ,  – попарно различные
действительные корни уравнения , поэтому одновременно выполняются
следующие равенства:

0,

0,

0.

Почленно
вычитая из первого равенства сначала второе, а затем третье равенство, получим:

Поскольку по условию корни уравнения , ,  – попарно различные, то  и , следовательно,

 и .

Тогда
и разность этих выражений также равна нулю:

,

.

Так
как , то .

Подставив
 в равенство , найдем, что .

Тогда
из исходного уравнения следует, что . Что требовалось
доказать.

Пример 5. При каких
значениях параметра с уравнение

имеет
более двух корней?

Решение. Квадратное
уравнение имеет более двух корней, если все его коэффициенты равны нулю (см. пример
4), поэтому

Первое
уравнение имеет корни  и ; корнями второго
уравнения являются числа  и , а третьего –  и .

Общим
для всех является корень .

Ответ:
.

Пример 6. Решить
относительно х уравнение .

Решение. Раскрыв скобки,
получим уравнение вида:

.

Приравняв
старший коэффициент к нулю, найдем контрольное значение параметра.

КЗП:

                 
                                 –        2)          0            3)    +  а

                   
                                                      1)

Возможны
три случая:

1)       
Если , то уравнение примет вид
. Это уравнение решений не имеет.

2)       
Если , то разделив обе части
исходного уравнения на а, получим уравнение вида:

.

Преобразуем его,
выделив в левой части уравнения полный квадрат:

,

,

корнями этого
уравнения являются  и .

3)       
Если , то  и уравнение  корней не имеет.

Ответ: при   ,  ,

при
  корней нет.

Пример 7.  При каких
значениях параметра m
корни уравнения

 равны по модулю и
противоположны по знаку?

Решение. 1 способ –
найти все значения параметра т, при которых уравнение имеет два корня, найти
эти корни, а затем определить при каких значениях параметра m
корни уравнения противоположные числа.

2 способ. Сначала найти
при каких значениях параметра т уравнение имеет два корня, затем по
теореме Виета найти их сумму

.

Так
как корни уравнения противоположные числа, то их сумма равна нулю,
следовательно, , откуда .

Ответ:
.

Пример 8. Решите уравнение
 относительно
х.

Решение. Данное
уравнение является неполным квадратным, поэтому приведём его к виду: .

Рассмотрим
следующие случаи в зависимости от знака параметра .

1)       
Если , то , следовательно,
уравнение имеет два корня

 и
.

2)       
Если , то уравнение примет вид
 и имеет один двукратный
корень  .

3)       
Если , то , следовательно, уравнение
 корней не имеет.

Ответ:
при   ,  ,

при
  ;

при
 корней нет.

Пример 9. При каких
значениях параметра а уравнение

имеет
более одного корня?

Решение. Найдем
контрольные значения параметра, приравняв старший коэффициент к нулю.

КЗП:
,   или .

1)       
Если ,
то данное уравнение примет вид

 или , откуда .

2)       
Если , то уравнение
примет вид

 или ,

решением
последнего уравнения является любое действительное число.

3)       
Если  и , то данное уравнение является
квадратным, поэтому найдём дискриминант:

.

По условию данное
уравнение должно иметь более одного корня, поэтому найдём, при каких значениях
параметра а дискриминант , то есть

.

Так как , то , тогда  или .

Ответ: при  и при  уравнение имеет более
одного корня.

§3.
Задачи для самостоятельной работы

по решению квадратных
уравнений с параметром

1.    
Найти все значения параметра а, при
каждом из которых уравнение

 не имеет решений.  .

2.     Найти
все значения параметра а, при каждом из которых уравнение

 имеет два различных
корня.

.

3.     При
каких значениях параметра m
оба корня уравнения

 равны нулю?  .

4.     При
каких значениях параметра а сумма квадратов величин, обратных корням
уравнения , меньше обоих корней
уравнения

?  .

5.    
Найти все значения параметра а, при
которых уравнения

 и

имеют хотя бы один общий корень?  .

6.     Найти
все значения параметра а, при которых один корень квадратного уравнения  в два раза больше
другого.  .

7.    
Для каждого значения параметра a решить
относительно х следующие уравнения:

§4.
Решение уравнений с параметром,
приводимых к квадратным.

Пример 1.  Решите
уравнение  .

Решение. Дробь равна нулю тогда,
когда числитель дроби равен нулю, а знаменатель отличен от нуля. Найдём сначала
допустимые значения для переменной: .

Тогда
, это квадратное уравнение,
так как его старший коэффициент равен 1. Найдём дискриминант:

.

Определим
контрольное значение параметра, приравняв дискриминант к нулю.

КЗП:
.

1)          
Если , то  и уравнение имеет один
двукратный корень , который принадлежит
области допустимых значений.

2)          
Если , то  и уравнение имеет два
корня

  и  .

Выясним,
при каких значениях параметра с эти корни удовлетворяют условию .

Если
, то  при условии, что  или .

Если
, то  при условии, что  или .

Найдём
корни уравнения при значениях параметра  и .

Если
, то корень уравнения
находим по формуле

,

а
если , то по формуле .

Ответ:
при  и   ;

при
 и   ;

при
  ;

при
  ;

при
  .

Пример 2.  Решите
относительно х уравнение  .

Решение. Преобразуем данное уравнение
следующим образом:

;

;

.

Определим
контрольное значение параметра, при котором знаменатель дроби равен нулю.

КЗП:
.

1)       
Если , то уравнение решений не
имеет.

2)       
Если , то  при условии, что  или .

Решим
квадратное уравнение .

Найдем
дискриминант

КЗП:
.

а)
Если , то  и уравнение имеет один
двукратный корень, который находим по формуле . Так как , то  и он удовлетворяет
условию .

б)
Если , то  и уравнение  имеет
два корня

  и  .

Так
как , то определим, при каких
значениях параметра а найденные корни удовлетворяют этому условию.

Если
, то  при условии, что , то есть .

Если
, то  при условии, что  или .

Найдём
корни уравнения при значениях параметра  и .

При
 корнем уравнения будет , а при  по формуле  находим, что .

Ответ:
при ,  и   ;

при
,  и   ;

при
  ;

при
  решений нет.

§5.
Задачи для самостоятельной работы

по решению уравнений,
приводимых к квадратным

1.          
Решить уравнение

(–6,
при     –5, при     2, при;

3,
при ;      или  во всех остальных
случаях)

2.                
При каких значениях параметра а
уравнение

имеет единственное
решение?  (при , , )

3.                
Найдите все значения а, при которых
вершины парабол

 и

лежат по разные
стороны от прямой .

§6. Задачи, связанные с расположением
корней квадратного трехчлена.

При
решении задач с параметрами приходится работать с тремя типами моделей:

1)    вербальная
модель – словесное описание задачи;

2)    геометрическая
модель – график квадратичной функции;

3)    аналитическая
модель – система неравенств, при помощи которой описывается геометрическая
модель.

Важно
уметь устанавливать связь между этими моделями. Это означает, что для любого
свойства, сформулированного на алгебраическом языке, нужно уметь давать
геометрическую интерпретацию и, наоборот, по поведению графика параболы дать
общую оценку коэффициентов квадратного трехчлена и его корней. Например,

если
старший коэффициент квадратного трехчлена меньше нуля, то ветви параболы
направлены вниз;

если
, то трехчлен имеет
различные действительные корни и парабола пересекает ось абсцисс в двух точках;

если
график функции  находится выше оси
абсцисс, то  и .

Последнюю
геометрическую модель можно описать еще тремя способами: неравенство  выполняется
при любом х; неравенство  не
имеет решений; трехчлен  не
имеет действительных корней и его старший коэффициент положителен.

Многие
задачи решают по следующему алгоритмическому предписанию:

1)       
уравнение записывают в виде ;

2)               
находят контрольные значения параметра и для
каждого случая строят параболу (геометрическую модель);

3)               
геометрическую модель описывают системой
неравенств (аналитическая модель);

4)               
решают систему неравенств.

Рассмотрим
несколько примеров теоретического плана, показывающих некоторые общие подходы к
решению задач о расположении корней квадратного трехчлена.

Пусть  – квадратный трёхчлен. Рассмотрим
случай, когда старший коэффициент  .

Обозначим корни
квадратного уравнения  через  и , причём .

Пусть  и В – некоторые
числа на оси Ох.

Задача 1.
При каких условиях оба корня квадратного уравнения, не
обязательно различные, меньше некоторого числа ?

Решение.
Обозначим через  абсциссу вершины
параболы, .

Так
как графиком квадратного трёхчлена является парабола, то построим
геометрическую модель данной задачи.

Оба
корня  и  квадратного уравнения меньше
некоторого числа  тогда
и только тогда, когда выполняются следующие условия:

  или 

2)
Корни  и  квадратного уравнения лежат
по разные стороны от числа  тогда и только тогда,
когда выполняются следующие условия:

  или 

3) Оба корня  и  квадратного уравнения больше
некоторого числа  тогда
и только тогда, когда выполняются следующие условия:

  или 

4) Оба корня  и  квадратного уравнения лежат
между числами  и В тогда и
только тогда, когда выполняются следующие условия:

  или 

5)
Корни  и  квадратного уравнения лежат
по разные стороны отрезка  на оси Ох тогда
и только тогда, когда выполняются следующие условия:

  или 

6) Квадратное уравнение
имеет два различных корня  и  и только один из
них принадлежит интервалу  или, другими словами,
для
того, чтобы парабола пересекала интервал  оси Ох только
в одной точке, необходимо и достаточно, чтобы значения
квадратного трехчлена

 в точках А и В
были разных знаков, то есть искомое условие имеет вид:

.

Очевидно,
что если

то
в рассматриваемом интервале лежит больший корень, а если

то
рассматриваемому интервалу принадлежит меньший корень.

7) Квадратное уравнение
имеет два отрицательных корня при условиях:

  Û 

8) Квадратное уравнение
имеет два положительных корня при условиях:

  Û 

Из приведенных примеров достаточно
ясно виден общий подход к решению задач рассматриваемого вида. Как правило,
задачи с ограничениями на корни квадратного трехчлена сводятся к системе
рациональных неравенств, которая легко решается методом интервалов. При этом
для определения условий, накладываемых на коэффициенты квадратного трехчлена,
рассматриваются следующие его свойства:

·              
расположение параболы относительно оси Ох;

·              
значения квадратного трехчлена в некоторых
заданных точках;

·              
положение оси симметрии параболы
относительно некоторых заданных точек.

Пример 1.
Найдите все значения параметра а, при которых корни уравнения  действительные,
различные и оба больше а.

Решение. Графическая
интерпретация задачи показана на рисунке. Обозначим через

.

Уравнение
 будет
иметь
два различных действительных корня, которые
одновременно больше а, тогда и только тогда, когда выполняются следующие
условия:

  Û 

Решая
полученную систему методом интервалов, найдем .

Ответ:
.

Пример 2. Найдите все
значения параметра а, при которых корни квадратного уравнения  неположительные.

Решение. Так как уравнение
квадратное, то . Обозначим через .

Рассмотрим
два случая.

1) 
Пусть . Для того чтобы
уравнение

имело
неположительные корни, необходимо и

достаточно
выполнение следующих условий:

  Û 

Применив
к системе метод интервалов, получим .

2)       
Пусть . Тогда положение
параболы определяется условиями:

  Û 

Решением этой системы является пустое
множество.

Ответ:
.

Пример 3. При каких
значениях а уравнение

имеет
корни разных знаков?

Решение. Для того чтобы парабола
– график

функции
,

пересекала
ось Ox,
в точках, между которыми

лежит
начало координат, необходимо и достаточно,

чтобы
квадратный трехчлен  принимал в точке  отрицательное значение,
поэтому искомое условие имеет вид:

 или .

Ответ:
.

Пример 4. При каких значениях
параметра  оба корня уравнения  принадлежат отрезку ?

Решение. Так как оба корня уравнения

 принадлежат отрезку ,

то
положение параболы

определяется
условиями:

  Û 

Данную
систему решаем методом интервалов, получаем .

Ответ:
.

Пример 5. При каких
значениях параметра а больший корень уравнения  принадлежит промежутку ?

Решение. Положение параболы,
являющейся графиком квадратного трехчлена , при котором только лишь
её правая ветвь пересекает промежуток  оси Оx определяется условиями:

  Û 
 

 Û 
  Û    Û 

Ответ:
.

Пример 6. При каких
значениях параметра а все корни уравнения  лежат
вне отрезка ?

Решение. При  данное уравнение имеет
вид  и,
следовательно, корней не имеет.

Если , то квадратный трехчлен

 всегда имеет два корня
разных знаков, так как .

Положение
параболы показано на рисунке.

Необходимые
и достаточные условия имеют

вид:

           

Ответ:
.

Пример 7. Найти все
значения параметра m,
при которых один из корней уравнения  находится между числами
0 и 2, а второй между 3 и 5.

Решение. Найдём дискриминант
квадратного уравнения

.

Так
как , то уравнение имеет два
корня:  и . Очевидно, что , поэтому

            .

Ответ:
 

§7.
Задачи для самостоятельного решения,

связанные с расположением
корней квадратного трехчлена.

1.                
Найдите все значения параметра а,
при каждом из которых все корни уравнений  и  различны и между двумя
корнями одного из них находится ровно один корень другого.  

2.                
Найдите все значения параметра а,
при которых корни уравнения

 неотрицательны.  

3.                
При каких значениях параметра а
существует единственный корень уравнения , удовлетворяющий условию
?

.

4.                
Найдите все значения параметра k,
при которых корни уравнения

 имеет два корня, причем
один из них меньше 1, а другой больше 2. 

5.        
Сколько решений, удовлетворяющих условию , имеет уравнение  в зависимости от значений
параметра а?

Заключение

Параметр – это величина,
значения которой служат для различения элементов некоторого множества между
собой, при этом он требует к себе осторожного и вдумчивого отношения. Ведь,
являясь фиксированным, но неизвестным числом, параметр ограничивает степень свободы
общения с ним. Задачи с параметром – это задачи исследовательского характера,
которые требуют хорошего понимания изучаемого теоретического материала.

Автор надеется, что данное
методическое пособие будет полезно кадетам как в процессе изучения рассмотренных
тем, так и для успешной сдачи экзаменов.

Список использованной литературы:

1.     Математика
для старшеклассников. Методы решения задач с параметрами /А.И. Азаров,С.А.
Барвенков-Мн.:»Аверсэв»,2003-272с.

2.     Большой
энциклопедический словарь. Математика. – М.: Научное издательство «Большая Российская
Энциклопедия», 1998.

3.     Задачи
с параметрами. Горнштейн П.И., Полонский В.Б., Якир М.С.  – М.: Илекса,
Харьков: Гимназия, 2003.

4.      Задачи
с параметрами. Егерман Е – Математика №2, 2003.

5.     Задачи
с параметром, сводящиеся к квадратным уравнениям/ Мещерякова Г.П.. – Математика
в школе №5, 2001.

6.     Математика:
интенсивный курс подготовки к экзамену. Черкасов О.Ю., Якушев А.Г.  – М.:
Рольф, 1997.

7.     .
Задачи с параметром. Линейные уравнения и их системы: 8-9 классы. Шевкин А.В –
М.: ТИД «Русское слово – РС», 2003.