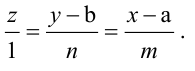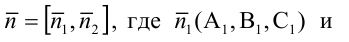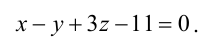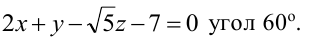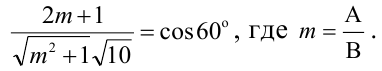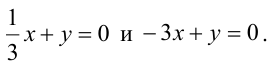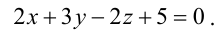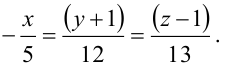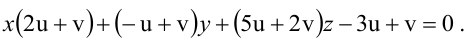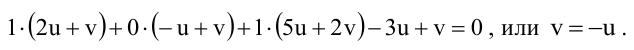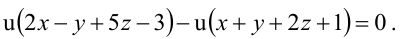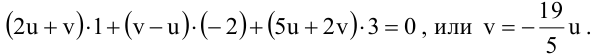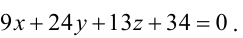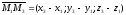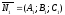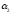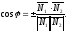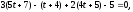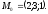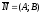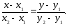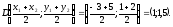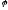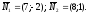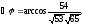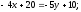Содержание:
Плоскость в пространстве
Общее уравнение плоскости
Определение: Уравнение вида
Определение: Порядок поверхности определяется по высшему показателю степени переменных х, у и z или по сумме показателей степени в произведении этих величин.
Определение: Уравнение вида Ax+By+Cz+D=O называется общим уравнением плоскости.
Рассмотрим частные случаи приведенного уравнения:
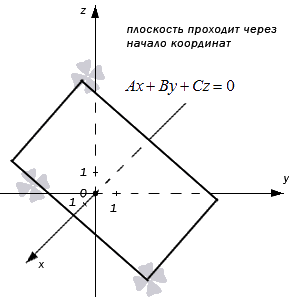
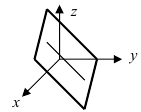
1. D = 0; Ах + By + Сz = 0. Из этого уравнения видно, что точка О(0; 0; 0) удов- летворяет этому уравнению, следовательно, это уравнение описывает плоскость, проходящую через начало координат (Рис. 36).
Рис. 36. Плоскость, проходящая через начало координат.
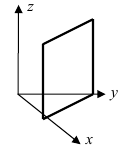
2. С = 0; Ах + Ву + D = 0. Этому уравнению удовлетворяет любое значение переменной z, поэтому данное уравнение описывает плоскость, которая параллельна оси аппликат (Oz) (Рис. 37).
Рис. 37. Плоскость, проходящая параллельно оси аппликат.
– плоскость параллельна оси ординат (Оу);
– плоскость параллельна оси абсцисс (Ох).
Замечание: При отсутствии в уравнении плоскости одной из переменных величин говорит о том, что плоскость параллельна соответствующей координатной оси.
3. С=0; D=0; Ах+ By=0 – плоскость проходит через начало отсчета параллельно оси аппликат (Рис. 38).
Рис. 38. Плоскость, проходящая через начало координат параллельно оси аппликат.
– плоскость проходит через начало координат параллельно оси ординат;
– плоскость проходит через начало координат параллельно оси абсцисс.
4. 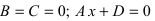
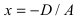
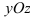
Рис. 39. Плоскость, проходящая параллельно координатной плоскости
5. В = С = D = 0; Ах = 0=>х = 0 – уравнение описывает плоскость 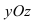
Рис. 40. Координатная плоскость 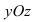
Другие уравнения плоскости
1. Уравнение плоскости в отрезках. Пусть в уравнении 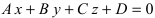
Введем следующие обозначения 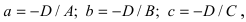
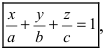
Откладывая на координатных осях точки М, N и Р, соединяя их прямыми лучим изображение данной плоскости (для определенности принято, что параметры а, b, с положительные) (Рис. 41):
Рис. 41. Отрезки, отсекаемые плоскостью на координатных осях.
Из рисунка видно, что числа а, b, с показывают отрезки, отсекаемые плоскостью на координатных осях, считая от начала координат.
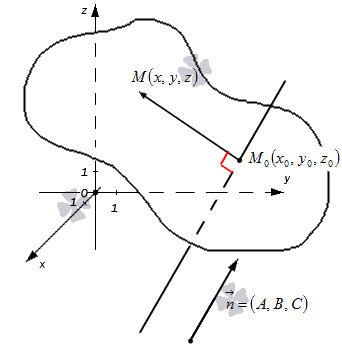
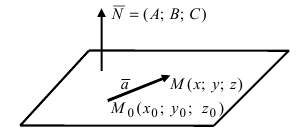
2. Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданному вектору. Пусть задана точка 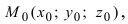
Возьмем на плоскости произвольную точку 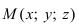
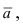
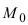
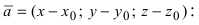
Рис. 42. Плоскость, проходящая через заданную точку перпендикулярно к нормальному вектору.
В силу того, вектор 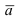
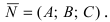
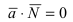
Пример:
Составить уравнение плоскости, проходящей через т. 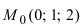
Решение:
Так как искомая плоскость параллельна плоскости (Q), то нормальный вектор этой плоскости 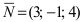
Пример:
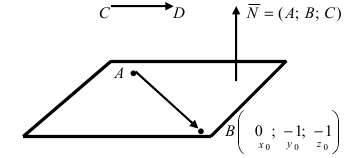
Составить уравнение плоскости, проходящей через точки А(—1; 1 ;2) и В(0; —1; —1) параллельно вектору 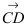
Решение:
Построим на искомой плоскости вектор 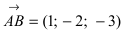
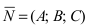
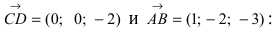
Уравнение плоскости, проходящей через заданную точку 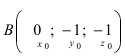
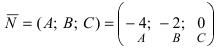
Отметим, что при выборе точки, через которую проходит искомая плоскость из точек 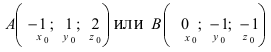
3. Уравнение плоскости, проходящей через три заданные точки. Пусть плоскость проходит через 3 известные точки 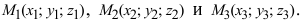
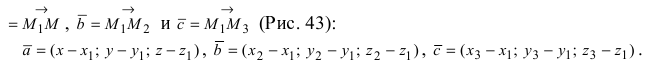
Рис. 43. Плоскость, проходящая через три заданные точки.
Вектора 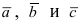
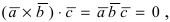
Замечание: Полученный определитель третьего порядка раскрывается по элементам первой строки.
Пример:
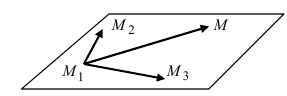
Составить уравнение плоскости, проходящей через три заданные точки
Решение:
Составим определитель третьего порядка 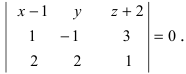
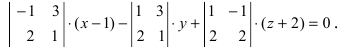
Основные задачи о плоскости в пространстве
1. Угол между пересекающимися плоскостями. Пусть даны две пересекающиеся плоскости 
Пусть линия пересечения плоскостей определяется прямой (l). Из одной точки этой прямой проведем два перпендикулярных к прямой вектора 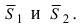
Рис.44. Угол между плоскостями.
В силу того, что 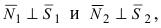
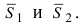
Следствие: Если плоскости перпендикулярны (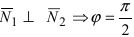
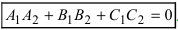
Следствие: Если плоскости параллельны, то нормальные вектора коллинеарны, следовательно, условие параллельности плоскостей:
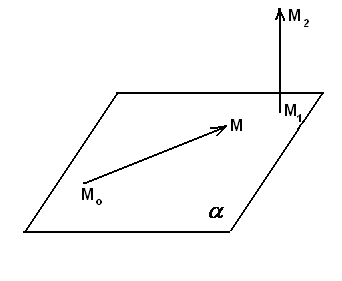
2. Расстояние от данной точки до заданной плоскости. Расстояние от данной точки 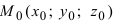
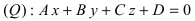
Пример:
На каком расстоянии от плоскости 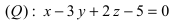
Решение:
Воспользуемся приведенной формулой:
Прямая в пространстве
Общее уравнение прямой
Прямая в пространстве может быть задана как пересечение двух плоскостей:
Определение: Геометрическое место точек пространства, удовлетворяющих системе уравнений (1), называется прямой в пространстве, а система уравнений (1) называется общим уравнением прямой.
Замечание: Для того чтобы система уравнений (1) определяла прямую в пространстве необходимо и достаточно, чтобы нормальные вектора плоскостей, определяющих прямую, 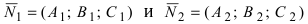
Пусть прямая проходит через точку 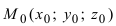
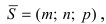
Замечание: Если в уравнении (2) одна из проекций направляющего вектора равна 0, то это означает, что прямая перпендикулярна соответствующей координатной оси.
Пример:
Как расположена прямая 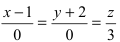
Решение:
Согласно замечанию эта прямая будет перпендикулярна осям абсцисс и ординат (параллельна оси аппликат) и будет проходить через точку 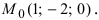
Пример:
Записать уравнение прямой 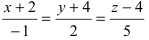
Решение:
Приравняем каждую дробь к параметру t: 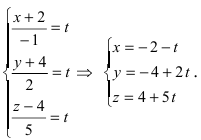
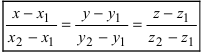
Пример:
Составить канонические и параметрические уравнения прямых, проходящих через точки А (— 1; 1; 2 ), В (0; -1; -1) И С (1; 0; -1), D (l; 0; 1 ).
Решение:
Составим каноническое уравнение прямой линии, проходящей через точки
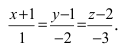
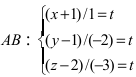
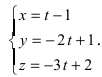
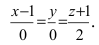
Основные задачи о прямой в пространстве
1. Переход от общего уравнения прямой к каноническому. Пусть прямая задана общим уравнением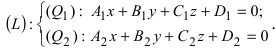
Пример:
Записать уравнение прямой 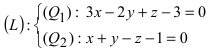
Решение:
Положив х = 0, получим СЛАУ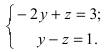
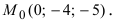
Запишем каноническое 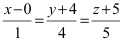
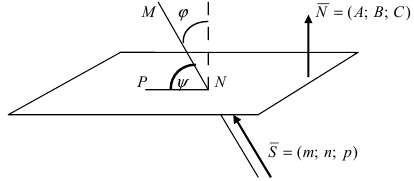
Угол между пересекающимися прямыми
Угол между двумя пересекающимися прямыми определяется как угол между их направляющими векторами. Если прямые 
соответственно, то угол между прямыми определяется по формуле:
Следствие: Если прямые перпендикулярны (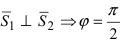
Следствие: Если прямые параллельны, то направляющие вектора коллинеарны, следовательно, условие параллельности прямых:
Координаты точки пересечения прямой и плоскости
Пусть прямая (L) задана общим уравнением 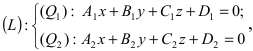
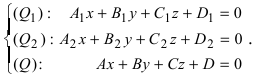
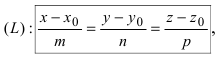
Рассмотрим возможные случаи:
- если выполняются условия
, то прямая не пересекает плоскость (прямая параллельна плоскости);
- при условиях
прямая лежит на плоскости;
- если
, прямая пересекает плоскость в одной точке.
Пример:
Найти координаты точки пересечения прямой (L), заданной уравнением 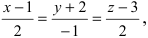
Решение:
Перепишем уравнение прямой (L) в параметрическом виде 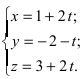
Найденное значение параметра 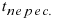
- Заказать решение задач по высшей математике
Угол между прямой и плоскостью
Пусть дана плоскость (Q) с нормальным вектором 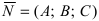
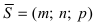
Рис. 45. Угол между прямой и плоскостью.
Угол 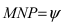
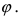
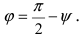
Следствие: Если прямая перпендикулярна плоскости (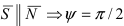
Следствие: Если прямая параллельна плоскости (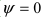
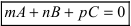
Плоскость и прямая в пространстве
Всякое уравнение первой степени относительно координат 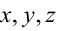

Вектор 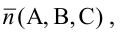
Особые случаи уравнения (3.1):
- D = 0, Ах + By + Cz = 0 – плоскость проходит через начало координат.
- С = 0, Ах + By + D = 0 – плоскость параллельна оси Oz.
- С = D = 0, Ах + By = 0 – плоскость проходит через ось Oz.
- С = В = 0, Ах + D = 0 – плоскость параллельна плоскости Oyz.
Уравнения координатных плоскостей:
Прямая в пространстве может быть задана:
- как линия пересечения двух плоскостей, т.е. системой уравнений:
- двумя своими точками
тогда прямая, через них проходящая, задается уравнениями:
- точкой
ей принадлежащей, и вектором
ей коллинеарным.
Тогда прямая определяется уравнениями:
Уравнения (3.4) называются каноническими уравнениями прямой.
Вектор 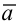
Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t: 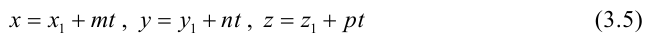
От уравнений (3.6) можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения:
От общих уравнений (3.2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор 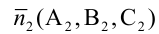
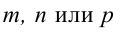
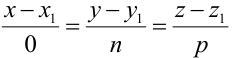
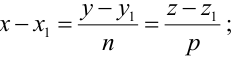
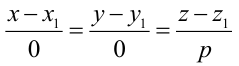
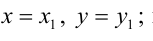
Пример:
Составьте уравнение плоскости, зная, что точка А(1,-1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.
Решение:
По условию задачи вектор 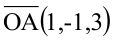
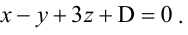
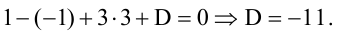
Пример:
Составьте уравнение плоскости, проходящей через ось Oz и образующей с плоскостью
Решение:
Плоскость, проходящая через ось Oz, задается уравнением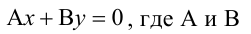
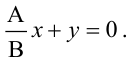
Решая квадратное уравнение 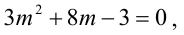
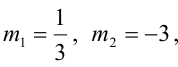
Пример:
Составьте канонические уравнения прямой: 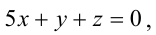
Решение:
Канонические уравнения прямой имеют вид:
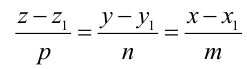
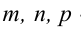
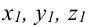
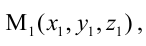
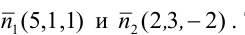
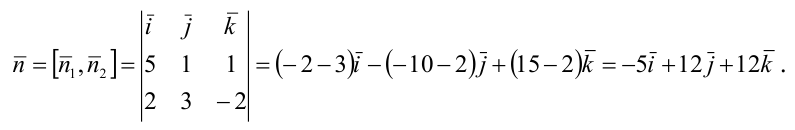
Пример:
В пучке, определяемом плоскостями 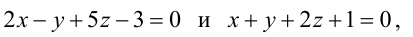
Решение:
Уравнение пучка, определяемого данными плоскостями, имеет вид 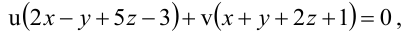
Для того, чтобы из пучка выделить плоскость, проходящую через точку М, подставим координаты точки М в уравнение пучка. Получим:
Тогда уравнение плоскости, содержащей М, найдем, подставив 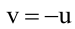
Т.к. и 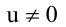
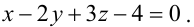
Значит, уравнение второй плоскости имеет вид: 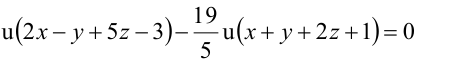
- Определитель матрицы
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Производная сложной функции
- Пределы в математике
- Функции многих переменных
- Уравнения прямых и кривых на плоскости
Пусть
задан вектор

перпендикулярный к плоскости

плоскости. Возьмем на плоскости
нефиксированную точку
(текущая точка) (рис.8).
Рис.8
Вектор

лежащий в плоскости
перпендикулярен вектору нормали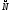
значит их скалярное произведение
следовательно
Полученное
уравнение – уравнение
плоскости, проходящей через точку

вектору

Пример.
Составить уравнение плоскости, проходящей
через точку

если

Решение.
Пусть


Найдем координаты векторов

Вектор



значит их скалярное произведение
–
уравнение плоскости

Рис.9
Рассмотрим
плоскость, проходящую через три точки,
не лежащие на
одной прямой:

Точка
текущая точка плоскости.
Рис.10
Три
вектора:

лежат
в одной плоскости, значит компланарны,
и их смешанное произведение равно нулю:
Запишем
смешанное произведение в координатной
форме, получим:

уравнение
плоскости, проходящей
через
три точки.
Пример.
Найти уравнение плоскости, проходящей
через три точки

Рис.11
Решение.
Пусть точка

координаты трех компланарных векторов:
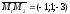

Смешанное
произведение векторов равно нулю:

уравнение плоскости

Пусть
плоскость

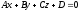
Расстояние
от точки


вычисляют по формуле

Рис.12
Пример.
Найти расстояние от точки


Решение.
Воспользуемся
формулой расстояния от точки до плоскости,
получим:

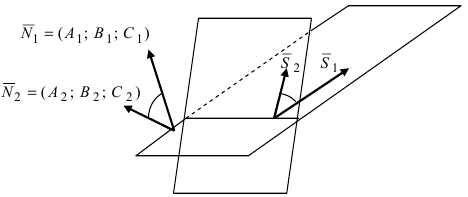
Угол
между плоскостями
равен углу
между их
векторами нормалей (рис.13).
Пусть
даны две плоскости:
плоскость
плоскость
с нормалью
Рис.13
Косинус
угла между плоскостями вычисляется по
формуле:
Пример.
Найти угол между плоскостями


Решение.
Векторы нормалей имеют координаты:

Уравнения
прямой в пространстве
Рассмотрим
в пространстве прямую a,
проходящую через точку

вектору
который называется направляющим вектором
прямойа
(рис.14).
Рис.14
Пусть
точка
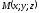


Из условия коллинеарности двух векторов,
имеем:
Эти
уравнения – канонические
уравнения прямой в пространстве.
Если
в канонических уравнениях ввести
параметр t:

получимпараметрические
уравнения прямой:
Прямую
можно задать как линию пересечения двух
плоскостей (рис.15):
Рис.15

общие
уравнения прямой в пространстве.
Уравнения
прямой, проходящей через две точки


Угол
между прямыми
равен острому углу между их направляющими
векторами (рис.16) и вычисляется по
формуле:
Рис.16
Пример.
Прямая

а)
Написать для этой прямой канонические
и параметрические уравнения;
б)
Найти угол между прямой

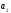
уравнениями
Решение.
а)
Выберем
одну из точек, через которую пройдет
указанная прямая, заданная пересечением
плоскостей. Исходная система имеет
бесчисленное множество решений, одно
из которых получим придавая одной из
переменных конкретное значение. Пусть

тогда значения других неизвестных
находим из системы
Решением
этой системы является пара чисел

В
результате получим точку

через которую проходит искомая прямая.
В качестве направляющего вектора прямой
можно взять вектор
где
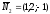
нормальные векторы плоскостей, линией
пересечения которых является прямая.
Таким образом,

Запишем
канонические уравнения прямой

Получим
из канонических параметрические
уравнения прямой:
б)
Направляющий вектор прямой

направляющий вектор прямой
между прямыми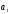

векторами:
Угол
между прямой и плоскостью
Пусть
заданы прямая a
и плоскость

Прямая
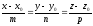
направляющим вектором
Плоскость
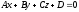
Рис.17
Угол
между прямой
а
и плоскостью

по формуле:
Чтобы
найти точку
пересечения прямой и плоскости,
нужно параметрические уравнения прямой

в уравнение плоскости
найти параметр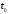
соответствующий точке пересечения.
Пример.
Найти а)
угол между прямой и плоскостью;
б)
точку пересечения прямой и плоскости.

Решение.

нормаль к плоскости;
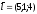
направляющий вектор прямой.
а)
Отсюда,
б)
Подставим параметрические уравнения
прямой



параметр точки пересечения прямой и
плоскости.
Подставим
значение параметра
в
параметрические уравнения, получим:

Уравнение
прямой на плоскости
Каноническое
уравнение прямой на плоскости:

где
направляющий вектор прямой.
Общее
уравнение прямой на плоскости:

где
– вектор
нормали прямой.
Уравнение
прямой с угловым коэффициентом

где

угол между прямой и осьюОХ;
b
– отрезок, отсекаемый прямой на оси OY.
Рис.18
Уравнение
прямой, проходящей через две точки


Пример
Даны точки
А(2;5),
В(-3;1),
С(5;2).
Найти:
уравнение медианыAD;
б)
уравнение высоты AE;
в)
угол между медианой AD
и высотой AE;
г)
уравнение прямой, проходящей через
точку С,
параллельно прямой АВ
(рис19).
Рис.19
Решение.
а)
Точка D
– середина
отрезка ВС,
найдем ее координаты:
Прямая
AD
проходит через две точки. Её уравнение
имеет вид:

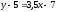

уравнение прямой AD.
б)
Высота
перпендикулярна ВС.
Пусть точка Е
имеет координаты

векторы
следовательно,
их скалярное произведение

в)
Угол
между
медианой AD
и высотой АЕ
– это угол между их векторами нормалей
Отсюда,
г)
Прямая СК
параллельна прямой АВ.
Пусть точка K
имеет координаты

векторы
и

Отсюда,



уравнение прямой СК,
параллельной АВ.
Соседние файлы в папке 1 семестр
- #
- #
- #
27.03.20162.06 Mб19Metodich_posobie_Khimia.doc
- #
- #
В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.
Общее уравнение плоскости: основные сведения
Перед началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат Oxyz в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x, y, и z, которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным.
Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.
Любую плоскость, заданную в прямоугольной системе координат Oxyz трехмерного пространства, можно определить уравнением Ax + By + Cz + D = 0. В свою очередь, любое уравнение Ax + By + Cz + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A, B, C, D – некоторые действительные числа, и числа A, B, C не равны одновременно нулю.
Теорема состоит из двух частей. Разберем доказательство каждой из них.
- Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида Ax + By + Cz + D = 0. Допустим, задана некоторая плоскость и точка M0(x0, y0, z0), через которую эта плоскость проходит. Нормальным вектором этой плоскости является n→= (A, B, C). Приведем доказательство, что указанную плоскость в прямоугольной системе координат Oxyz задает уравнение Ax + By + Cz + D = 0.
Возьмем произвольную точку заданной плоскости M(x, y, z).В таком случае векторы n→= (A, B, C) и M0M→=(x-x0, y-y0, z-z0) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:
n→, M0M→=Ax-x0+B(y-y0)+C(z-z0)=Ax+By+Cz-(Ax0+By0+Cz0)
Примем D=-(Ax0+By0+Cz0) , тогда уравнение преобразуется в следующий вид: Ax + By + Cz + D = 0. Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.
- Во второй части теоремы утверждается, что любое уравнение вида Ax + By + Cz + D = 0 задает некоторую плоскость в прямоугольной системе координат Oxyz трехмерного пространства. Докажем это.
В теореме также указано, что действительные числа А, B, C одновременно не являются равными нулю. Тогда существует некоторая точка M0(x0, y0, z0), координаты которой отвечают уравнению Ax + By + Cz + D = 0, т.е. верным будет равенство Ax0 + By0 + Cz0 + D = 0. Отнимем левую и правую части этого равенства от левой и правой частей уравнения Ax + By + Cz + D = 0. Получим уравнение вида
A(x-x0) + B(y-y0) + C(z-z0) + D = 0, и оно эквивалентно уравнению Ax + By + Cz + D = 0. Докажем, что уравнение A(x-x0) + B(y-y0) + C(z-z0) + D = 0 задает некоторую плоскость.
Уравнение A(x-x0) + B(y-y0) + C(z-z0) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n→=(A, B, C) и M0M→=x-x0, y-y0, z-z0. Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A(x-x0) + B(y-y0) + C(z-z0) + D = 0 множество точек M(x, y, z) задает плоскость, у которой нормальный вектор n→=(A, B, C). При этом плоскость проходит через точку M(x0, y0, z0). Иначе говоря, уравнение A(x-x0) + B(y-y0) + C(z-z0) + D = 0 задает в прямоугольной системе координат Oxyz трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение Ax + By + Cz + D = 0 также определяет эту плоскость. Теорема доказана полностью.
Уравнение вида Ax + By + Cz + D = 0 называют общим уравнением плоскости в прямоугольной системе координат Oxyz трехмерного пространства.
Допустим, задано некоторое общее уравнение плоскости λ·Ax+λ·By+λ·Cz+λ·D=0, где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением Ax+By+Cz+D=0, поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x-2·y+3·z-7=0 и -2·x+4·y-23·z+14=0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства.
Раскроем чуть шире смысл теорем.
В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида Ax+By+Cz+D=0( при конкретных значениях чисел A, B, C, D). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат.
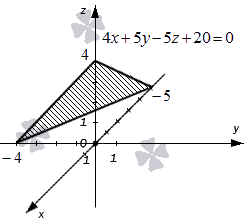
Укажем пример как иллюстрацию этих утверждений.
Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4x + 5y – 5z + 20 = 0, и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4x + 5y – 5z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость.
Общее уравнение плоскости, проходящей через точку
Повторимся: точка M0(x0, y0, z0) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением Ax+By+Cz+D=0 в том случае, когда подставив координаты точки M0(x0, y0, z0) в уравнение Ax+By+Cz+D=0, мы получим тождество.
Заданы точки M0(1, -1, -3) и N0(0, 2, -8) и плоскость, определяемая уравнением 2x+3y-z-2=0. Необходимо проверить, принадлежат ли заданные точки заданной плоскости.
Решение
Подставим координаты точки М0 в исходной уравнение плоскости:
2·1+3·(-1)-(-3)-2=0⇔0=0
Мы видим, что получено верное равенство, значит точка M0(1, -1, -3) принадлежит заданной плоскости.
Аналогично проверим точку N0. Подставим ее координаты в исходное уравнение:
2·0+3·2-(-8)-2=0⇔12=0
Равенство неверно. Таким, образом, точка N0(0, 2, -8) не принадлежит заданной плоскости.
Ответ: точка М0 принадлежит заданной плоскости; точка N0 – не принадлежит.
Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n→=(A, B, C) – нормальный вектор для плоскости, определяемой уравнением Ax+By+Cz+D=0. Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.
В прямоугольной системе координат задана плоскость 2x+3y-z+5=0. Необходимо записать координаты всех нормальных векторов заданной плоскости.
Решение
Мы знаем, что заданные общим уравнением коэффициенты при переменных x, y, z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n→ исходной плоскости имеет координаты 2, 3, -1 . В свою очередь, множество нормальных векторов запишем так:
λ·n→=λ·2, λ·3, -λ, λ∈R, λ≠0
Ответ: λ·2, λ·3, -λ, λ∈R, λ≠0
Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.
Очевидным фактом является то, что нормальный вектор n→=(A, B, C)является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M0(x0, y0, z0), принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.
Общее уравнение плоскости с нормальным вектором n→=(A, B, C) будет выглядеть так: Ax+By+Cz+D=0. По условию задачи точка M0(x0, y0, z0) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство:Ax0+By0+Cz0+D=0
Вычитая соответственно правые и левые части исходного уравнения и уравнения Ax0+By0+Cz0+D=0, получим уравнение вида A(x-x0)+B(y-y0)+C(z-z0)=0. Оно и будет уравнением плоскости, проходящей через точку M0(x0, y0, z0) и имеющей нормальный вектор n→=(A, B, C).
Возможно получить это уравнение другим способом.
Очевидным фактом является то, что все точки М (x, y, z) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n→=(A, B, C) и M0M→=(x-x0, y-y0, z-z0) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:
n→, M0M→=A(x-x0)+B(y-y0)+C(z-z0)=0
Задана точка М0(-1, 2, -3), через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n→=(3, 7, -5). Необходимо записать уравнение заданной плоскости.
Решение
Рассмотрим два способа решения.
- Исходные условия позволяют получить следующие данные:
x0=-1, y0=2, z0=-3, A=3, B=7, C=-5
Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A(x-x0)+B(y-y0)+C(z-z0)=0
И получим:
3(x-(-1))+7(y-2)-5(z-(-3))=0⇔3x+7y-5z-26=0
- Допустим, М (x, y, z) – некоторая точки заданной плоскости. Определим координаты вектора M0M→ по координатам точек начала и конца:
M0M→=(x-x0, y-y0, z-z0)=(x+1, y-2, z+3)
Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:
n→, M0M→=0⇔3(x+1)+7(y-2)-5(z+3)=0⇔⇔3x+7y-5z-26=0
Ответ: 3x+7y-5z-26=0
Неполное общее уравнение плоскости
Выше мы говорили о том, что, когда все числа А, B, C, D отличны от нуля, общее уравнение плоскости Ax+By+Cz+D=0 называют полным. В ином случае общее уравнение плоскости является неполным.
Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.
- В случае, когда D = 0, мы получаем общее неполное уравнение плоскости: Ax+By+Cz+D=0⇔Ax+By+Cz=0
Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О (0, 0, 0), то придем к тождеству:
A·0+B·0+C·0=0⇔0≡0
- Если А = 0, В ≠ 0, С ≠ 0, или А ≠ 0, В = 0, С ≠0, или А ≠ 0, В ≠ 0, С = 0, то общие уравнения плоскостей имеют вид соответственно: By+Cz+D=0, или Ax+Cz+D=0, или Ax+By+D=0. Такие плоскости параллельны координатным осям Оx, Oy, Oz соответственно. Когда D=0, плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей By+Cz+D=0, Ax+Cz+D=0 и Ax+By+D=0 задают плоскости, которые перпендикулярны плоскостям Oyz, Oxz, Ozy соответственно.
- При А=0, В=0, С≠0, или А=0, В≠0, С=0, или А≠0, В=0, С=0 получим общие неполные уравнения плоскостей: Cz+D=0 ⇔z+DC=0⇔z=-DC⇔z=λ, λ∈R или By+D=0⇔y+DB=0⇔y=-DB⇔y=λ, λ∈R или Ax+D=0⇔x+DA=0⇔x=-DA⇔x=λ, λ∈R соответственно.
Эти уравнения определяют плоскости, которые параллельны координатным плоскостям Oxy, Oxz, Oyz соответственно и проходят через точки 0, 0, -DC, 0, -DB, 0 и -DA, 0, 0 соответственно. При D=0 уравнения самих координатных плоскостей Oxy, Oxz, Oyz выглядят так: z=0, y=0, x=0
соответственно.
Задана плоскость, параллельная координатной плоскости Oyz и проходящая через точку М0(7, -2, 3). Необходимо составить общее уравнение заданной плоскости.
Решение
Условием задачи определено, что заданная плоскость параллельна координатной плоскости Oyz, а, следовательно, может быть задана общим неполным уравнением плоскости Ax+D=0, A≠0⇔x+DA=0. Поскольку точка M0(7, -2, 3) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x+DA=0, иначе говоря, должно быть верным равенство 7+DA=0 . Преобразуем: DA=-7, тогда требуемое уравнение имеет вид: x-7=0.
Задачу возможно решить еще одним способом.
Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости Oyz. Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости Oyz: i→=(1, 0, 0). Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:
A(x-x0)+B(y-y0)+C(z-z0)=0⇔⇔1·(x-7)+0·(y+2)+0·(z-3)=0⇔⇔x-7=0
Ответ: x-7=0
Задана плоскость, перпендикулярная плоскости Oxy и проходящая через начало координат и точку М0(-3, 1, 2).
Решение
Плоскость, которая перпендикулярна координатной плоскости Oxy определяется общим неполным уравнением плоскости Ax+By+D=0 (А≠0, В≠0). Условием задачи дано, что плоскость проходит через начало координат, тогда D=0 и уравнение плоскости принимает вид Ax+By=0⇔x+BAy=0.
Найдем значение BA. В исходных данных фигурирует точка М0(-3, 1, 2), координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: -3+BA·1=0, откуда определяем BA=3.
Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x+3y=0.
Ответ: x+3y=0.
Основные понятия и формулы по теме “Плоскость”.
Всякое уравнение первой степени между тремя переменными определяет плоскость. Обратно, всякая плоскость определяется уравнением первой степени относительно текущих координат.
1. Общее уравнение плоскости имеет вид:
Ах + By +Cz + D = 0. (1)
Особые случаи уравнения (1).
а) Пусть в уравнении (1) свободный член D=О, тогда получим уравнение
Ах + By + Сz = 0 (2)
плоскости, проходящей через начало координат.
б) Пусть в уравнении (1) один из коэффициентов А, В и С равен 0.
Тогда получим уравнения плоскостей, параллельных соответствующим координатным осям:
By + Cz + D = 0 — уравнение плоскости, параллельной оси Ох; (3)
Ax + Cz + D = 0 — уравнение плоскости, параллельной оси Оу; (4)
Аx + By + D = 0 — уравнение плоскости, параллельной оси Oz. (5)
в) Пусть в уравнениях (3), (4), (5) свободный член D = 0. Тогда получим уравнения плоскостей, проходящих через соответствующие оси координат:
By + Cz = 0 — уравнение плоскости, проходящей через ось Ох; (6)
Ax + Cz = 0 — уравнение плоскости, проходящей через ось Оу; (7)
Ах + Ву = 0 — уравнение плоскости, проходящей через ось Oz. (8)
г) Пусть в уравнении (1) два коэффициента В = С = 0 или А = С = 0, или А = В = 0. Тогда получим уравнения плоскостей, параллельных соответствующим координатным плоскостям:
Ax + D = 0, или х = а — уравнение плоскости, параллельной координатной плоскости yOz; (9)
By + D = 0, или у = b — уравнение плоскости, параллельной координатной плоскости xOz; (10)
Сz + 0 = 0, или z = c — уравнение плоскости, параллельной координатной плоскости хОу. (11)
д) Пусть в уравнении (1) три коэффициента В, С и D или А, С и D, или A, В и D равны нулю. Тогда получим уравнения координатных плоскостей
Ах = 0, или x = 0 — уравнение плоскости yOz; (12)
Ву = 0, или у = 0 — уравнение плоскости xOz; (13)
Cz = 0, или z = 0 — уравнение плоскости хОу. (14)
2. Общее уравнение плоскости в векторной форме имеет вид:
— вектор, перпендикулярный к данной плоскости;
— текущий радиус-вектор.
3. Нормальное уравнение плоскости.
а) Нормальное уравнение плоскости в координатной форме имеет вид:
За параметры, определяющие плоскость, приняты: длина перпендикуляра (нормали) р, опущенного из начала координат на плоскость, и направляющие косинусы этого перпендикуляра .
б) Нормальное уравнение плоскости в векторной форме имеет вид:
– единичный вектор, перпендикулярный к данной плоскости;
— направляющие косинусы вектора; р — расстояние плоскости от начала координат.
4. Для приведения общего уравнения плоскости (1) к нормальному виду (16), нужно умножить его на нормирующий множитель
выбрав знак перед корнем, противоположный знаку свободного члена D в уравнении (1).
Направляющие косинусы и параметр р определяются по формулам:
При этом, если D<0, то берутся верхние знаки; если D>0, то берутся нижние знаки.
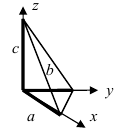
5. Уравнение плоскости в отрезках имеет вид:
где за параметры, определяющие плоскость, приняты отрезки a, b и с, отсекаемые этой плоскостью на осях координат.
6. Уравнение плоскости, проходящей через данную точку.
а) Уравнение плоскости, проходящей через данную точку, в координатной форме имеет вид:
Рис.1
б) Уравнение плоскости, проходящей через данную точку, в векторной форме имеет вид:
— данная точка, заданная радиусом-вектором
,
— радиус-вектор любой точки плоскости;
— нормальный вектор (рис.1)
7. Угол между двумя плоскостями.
а) Угол между двумя плоскостями, заданными уравнениями в координатной форме
определяется по формуле:
б) Угол между двумя плоскостями, заданными уравнениями в векторной форме
где определяется по формуле
8. Условие параллельности двух плоскостей имеет вид:
9. Условие перпендикулярности двух плоскостей имеет вид:
10. Расстояние от точки до плоскости.
Отклонением данной точки от данной плоскости называется число , равное длине перпендикуляра, опущенного из этой точки на плоскость, взятое со знаком плюс, если точка и начало координат лежат по разные стороны от этой плоскости, и со знаком минус, если они лежат по одну сторону от плоскости.
Отклонение получается в результате подстановки координат данной точки в нормальное уравнение данной плоскости
или в векторной форме
Расстояние d от точки до плоскости Ax + By + Cz + D = 0 равно абсолютной величине отклонения:
или
в векторной форме:
11. Уравнение плоскости, проходящей через три данные точки
не лежащие на одной прямой, имеет вид:
а) в координатной форме:
б) в векторной форме:
Уравнения прямых и плоскостей
Поверхности и линии первого порядка.
Уравнение первой степени, или линейное уравнение, связывающее координаты точки в пространстве, имеет вид
$$
Ax+By+Cz+D = 0,label
$$
причем предполагается, что коэффициенты при переменных не равны нулю одновременно, то есть (A^<2>+B^<2>+C^ <2>neq 0). Аналогично, линейное уравнение, связывающее координаты точки на плоскости, — это уравнение
$$
Ax+By+C = 0,label
$$
при условии (A^<2>+B^ <2>neq 0).
В школьном курсе доказывается, что в декартовой прямоугольной системе координат уравнения eqref и eqref определяют соответственно плоскость и прямую линию на плоскости. Из теорем о порядке алгебраических линий и поверхностей следует, что то же самое верно и в общей декартовой системе координат. Точнее, имеют место следующие теоремы.
В общей декартовой системе координат в пространстве каждая плоскость может быть задана линейным уравнением
$$
Ax+By+Cz+D = 0.nonumber
$$
Обратно, каждое линейное уравнение в общей декартовой системе координат определяет плоскость.
В общей декартовой системе координат на плоскости каждая прямая может быть задана линейным уравнением
$$
Ax+By+C = 0,nonumber
$$
Обратно, каждое линейное уравнение в общей декартовой системе координат на плоскости определяет прямую.
Эти теоремы полностью решают вопрос об уравнениях плоскости и прямой линии на плоскости. Однако ввиду важности этих уравнений мы рассмотрим их в других формах. При этом будут получены независимые доказательства теорем этого пункта.
Параметрические уравнения прямой и плоскости.
Мы будем предполагать, что задана декартова система координат в пространстве (или на плоскости, если мы изучаем прямую в планиметрии). Это, в частности, означает, что каждой точке сопоставлен ее радиус-вектор относительно начала координат.
Рис. 6.1
Вектор (overrightarrowM> = boldsymbol-boldsymbol_<0>), начало которого лежит на прямой, параллелен прямой тогда и только тогда, когда (M) также лежит на прямой. В этом и только этом случае для точки (M) найдется такое число (t), что
$$
boldsymbol-boldsymbol_ <0>= tboldsymbol.label
$$
Наоборот, какое бы число мы ни подставили в формулу eqref в качестве (t), вектор (boldsymbol) в этой формуле определит некоторую точку на прямой.
Уравнение eqref называется векторным параметрическим уравнением прямой, а переменная величина (t), принимающая любые вещественные значения, называется параметром.
Векторное параметрическое уравнение выглядит одинаково и в планиметрии, и в стереометрии, но при разложении по базису оно сводится к двум или трем скалярным уравнениям, смотря по тому, сколько векторов составляют базис.
Получим теперь параметрические уравнения плоскости. Обозначим через (boldsymbol
) и (boldsymbol) ее направляющие векторы, а через (boldsymbol_<0>) — радиус-вектор ее начальной точки (M_<0>). Пусть точка (M) с радиус-вектором (boldsymbol) — произвольная точка пространства (рис. 6.2).
Рис. 6.2
Вектор (overrightarrowM> = boldsymbol-boldsymbol_<0>), начало которого лежит на плоскости, параллелен ей тогда и только тогда, когда его конец (M) также лежит на плоскости. Так как (boldsymbol
) и (boldsymbol) не коллинеарны, в этом и только этом случае (boldsymbol-boldsymbol_<0>) может быть по ним разложен. Поэтому, если точка (M) лежит в плоскости (и только в этом случае), найдутся такие числа (t_<1>) и (t_<2>), что
$$
boldsymbol-boldsymbol_ <0>= t_<1>boldsymbol
+t_<2>boldsymbol.label
$$
Это уравнение называется параметрическим уравнением плоскости. Каждой точке плоскости оно сопоставляет значения двух параметров (t_<1>) и (t_<2>). Наоборот, какие бы числа мы ни подставили как значения (t_<1>) и (t_<2>), уравнение eqref определит некоторую точку плоскости.
Пусть ((x, y, z)) и ((x_<0>, y_<0>, z_<0>)) — координаты точек (M) и (M_<0>) соответственно, а векторы (boldsymbol
) и (boldsymbol) имеют компоненты ((p_<1>, p_<2>, p_<3>)) и ((q_<1>, q_<2>, q_<3>)). Тогда, раскладывая по базису обе части уравнения eqref, мы получим параметрические уравнения плоскости
$$
x-x_ <0>= t_<1>p_<1>+t_<2>q_<1>, y-y_ <0>= t_<1>p_<2>+t_<2>q_<2>, z-z_ <0>= t_<1>p_<3>+t_<2>q_<3>.label
$$
Отметим, что начальная точка и направляющий вектор прямой образуют на ней ее внутреннюю декартову систему координат. Значение параметра (t), соответствующее какой-то точке, является координатой этой точки во внутренней системе координат. Точно так же на плоскости начальная точка и направляющие векторы составляют внутреннюю систему координат, а значения параметров, соответствующие точке, — это ее координаты в этой системе.
Прямая линия на плоскости.
Поэтому мы можем сформулировать следующее утверждение.
В любой декартовой системе координат на плоскости уравнение прямой с начальной точкой (M_<0>(x_<0>, y_<0>)) и направляющим вектором (boldsymbol(a_<1>, a_<2>)) может быть записано в виде eqref.
Уравнение eqref линейное. Действительно, после преобразования оно принимает вид (a_<2>x-a_<1>y+(a_<1>y_<0>-a_<2>x_<0>) = 0), то есть (Ax+By+C = 0), где (A = a_<2>), (B = -a_<1>) и (C = a_<1>y_<0>-a_<2>x_<0>).
Вектор с координатами ((-B, A)) можно принять за направляющий вектор прямой с уравнением eqref в общей декартовой системе координат, а точку eqref за начальную точку.
Если система координат декартова прямоугольная, то вектор (boldsymbol(A, B)) перпендикулярен прямой с уравнением eqref.
Действительно, в этом случае ((boldsymbol, boldsymbol) = -BA+AB = 0).
Пусть в уравнении прямой (Ax+By+C = 0) коэффициент (B) отличен от нуля. Это означает, что отлична от нуля первая компонента направляющего вектора, и прямая не параллельна оси ординат. В этом случае уравнение прямой можно представить в виде
$$
y = kx+b,label
$$
где (k = -A/B), а (b = -C/B). Мы видим, что к равно отношению компонент направляющего вектора: (k = a_<2>/a_<1>) (рис. 6.3).
Рис. 6.3. k=-1. Прямая y=-x+1/2
Отношение компонент направляющего вектора (a_<2>/a_<1>) называется угловым коэффициентом прямой.
Угловой коэффициент прямой в декартовой прямоугольной системе координат равен тангенсу угла, который прямая образует с осью абсцисс. Угол этот отсчитывается от оси абсцисс в направлении кратчайшего поворота от (boldsymbol_<1>) к (boldsymbol_<2>) (рис. 6.4).
Рис. 6.4. (k=operatornamevarphi = -1). Прямая (y=-x+1/2)
Положив (x = 0) в уравнении eqref, получаем (y = b). Это означает, что свободный член уравнения (b) является ординатой точки пересечения прямой с осью ординат.
Если же в уравнении прямой (B = 0) и ее уравнение нельзя представить в виде eqref, то обязательно (A neq 0). В этом случае прямая параллельна оси ординат и ее уравнению можно придать вид (x = x_<0>), где (x_ <0>= -C/A) — абсцисса точки пересечения прямой с осью абсцисс.
Векторные уравнения плоскости и прямой.
Параметрическое уравнение плоскости утверждает, что точка (M) лежит на плоскости тогда и только тогда, когда разность ее радиус-вектора и радиус-вектора начальной точки (M_<0>) компланарна направляющим векторам (boldsymbol
) и (boldsymbol). Эту компланарность можно выразить и равенством
$$
(boldsymbol-boldsymbol_<0>, boldsymbol
, boldsymbol) = 0.label
$$
Вектор (boldsymbol = [boldsymbol
, boldsymbol]) — ненулевой вектор, перпендикулярный плоскости. Используя его, мы можем записать уравнение eqref в виде
$$
(boldsymbol-boldsymbol_<0>, boldsymbol) = 0.label
$$
Уравнения eqref и eqref называют векторными уравнениями плоскости. Им можно придать форму, в которую не входит радиус-вектор начальной точки. Например, положив в eqref (D = -(boldsymbol_<0>, boldsymbol)), получим
$$
(boldsymbol, boldsymbol)+D = 0.label
$$
Для прямой на плоскости можно также написать векторные уравнения, аналогичные eqref и eqref,
$$
(boldsymbol-boldsymbol_<0>, boldsymbol) = 0 mbox<или> (boldsymbol, boldsymbol)+C = 0.nonumber
$$
Первое из них выражает тот факт, что вектор (boldsymbol-boldsymbol_<0>) перпендикулярен ненулевому вектору (boldsymbol), перпендикулярному направляющему вектору (boldsymbol), и потому коллинеарен (boldsymbol).
Пусть (x, y, z) — компоненты вектора (boldsymbol) в общей декартовой системе координат. Тогда скалярное произведение ((boldsymbol-boldsymbol_<0>, boldsymbol)) при (boldsymbol neq 0) записывается линейным многочленом (Ax+By+Cz+D), где ((A^<2>+B^<2>+C^ <2>neq 0)).
Обратно, для любого линейного многочлена найдутся такие векторы (boldsymbol_<0>) и (boldsymbol neq 0), что в заданной общей декартовой системе координат (Ax+By+Cz+D = (boldsymbol-boldsymbol_<0>, boldsymbol)).
Первая часть предложения очевидна: подставим разложение вектора (boldsymbol) по базису в данное скалярное произведение:
$$
(xboldsymbol_<1>+yboldsymbol_<2>+zboldsymbol_<3>-boldsymbol_<0>, boldsymbol),nonumber
$$
раскроем скобки и получим многочлен (Ax+By+Cz+D), в котором (D = -(boldsymbol_<0>, boldsymbol)) и
$$
A = (boldsymbol_<1>, boldsymbol), B = (boldsymbol_<2>, boldsymbol), C = (boldsymbol_<3>, boldsymbol)label
$$
(A), (B) и (C) одновременно не равны нулю, так как ненулевой вектор (boldsymbol) не может быть ортогонален всем векторам базиса.
Для доказательства обратного утверждения найдем сначала вектор (boldsymbol) из равенств eqref, считая (A), (B) и (C) заданными. Из ранее доказанного утверждения 10 следует, что
$$
boldsymbol = frac_<2>, boldsymbol_<3>]><(boldsymbol_<1>, boldsymbol_<2>, boldsymbol_<3>)>+frac_<3>, boldsymbol_<1>]><(boldsymbol_<1>, boldsymbol_<2>, boldsymbol_<3>)>+frac_<1>, boldsymbol_<2>]><(boldsymbol_<1>, boldsymbol_<2>, boldsymbol_<3>)>.label
$$
Вектор (boldsymbol_<0>) должен удовлетворять условию (D = -(boldsymbol_<0>, boldsymbol)). Один из таких векторов можно найти в виде (boldsymbol_ <0>= lambda boldsymbol). Подставляя, видим, что (-lambda(boldsymbol, boldsymbol) = D), откуда (boldsymbol_ <0>= -Dboldsymbol/|boldsymbol|^<2>).
Итак, мы нашли векторы (boldsymbol) и (boldsymbol_<0>) такие, что линейный многочлен записывается в виде
$$
x(boldsymbol_<1>, boldsymbol)+y(boldsymbol_<2>, boldsymbol)+z(boldsymbol_<3>, boldsymbol)-(boldsymbol_<0>, boldsymbol),nonumber
$$
который совпадает с требуемым ((boldsymbol-boldsymbol_<0>, boldsymbol)).
Если система координат декартова прямоугольная, то вектор с компонентами (A), (B), (C) является нормальным вектором для плоскости с уравнением (Ax+By+Cz+D = 0).
Это сразу вытекает из формул eqref и доказанного ранее утверждения о нахождении компонент в ортогональном базисе.
Любые два неколлинеарных вектора, удовлетворяющие уравнению eqref, можно принять за направляющие векторы плоскости.
Утверждение 5 нетрудно доказать и непосредственно, рассматривая координаты вектора, параллельного плоскости, как разности соответствующих координат двух точек, лежащих в плоскости.
Все, сказанное о плоскостях, почти без изменений может быть сказано и о прямых на плоскости. В частности, верно следующее утверждение.
Действительно, (alpha_<1>, alpha_<2>), должны быть пропорциональны компонентам — (B), (A) направляющего вектора прямой.
Параллельность плоскостей и прямых на плоскости.
Ниже, говоря о параллельных прямых или плоскостях, мы будем считать, что параллельные плоскости (или прямые) не обязательно различны, то есть что плоскость (прямая) параллельна самой себе.
Прямые линии, задаваемые в общей декартовой системе координат уравнениями
$$
Ax+By+C = 0, A_<1>x+B_<1>y+C_ <1>= 0,nonumber
$$
параллельны тогда и только тогда, когда соответствующие коэффициенты в их уравнениях пропорциональны, то есть существует такое число (lambda), что
$$
A_ <1>= lambda A, B_ <1>= lambda B.label
$$
Прямые совпадают в том и только том случае, когда их уравнения пропорциональны, то есть помимо уравнения eqref выполнено (с тем же (lambda)) равенство
$$
C_ <1>= lambda C.label
$$
Первая часть предложения прямо следует из того, что векторы с компонентами ((-B, A)) и ((-B_<1>, A_<1>)) — направляющие векторы прямых.
Докажем вторую часть. В равенствах eqref и eqref (lambda neq 0), так как коэффициенты в уравнении прямой одновременно нулю не равны. Поэтому, если эти равенства выполнены, уравнения эквивалентны и определяют одну и ту же прямую.
Обратно, пусть прямые параллельны. В силу первой части предложения их уравнения должны иметь вид (Ax+By+C = 0) и (lambda(Ax+By)+C_ <1>= 0) при некотором (lambda). Если, кроме того, существует общая точка (M_<0>(x_<0>, y_<0>)) обеих прямых, то (Ax_<0>+By_<0>+C = 0) и (lambda(Ax_<0>+By_<0>)+C_ <1>= 0). Вычитая одно равенство из другого, получаем (C_ <1>= lambda C), как и требовалось.
Плоскости, задаваемые в общей декартовой системе координат уравнениями
$$
Ax+By+Cz+D = 0, A_<1>x+B_<1>y+C_<1>z+D_ <1>= 0nonumber
$$
параллельны тогда и только тогда, когда соответствующие коэффициенты в их уравнениях пропорциональны, то есть существует такое число (lambda), что
$$
A_ <1>= lambda A, B_ <1>= lambda B, C_ <1>= lambda C.label
$$
Плоскости совпадают в том и только том случае, когда их уравнения пропорциональны, то есть помимо уравнений eqref выполнено (с тем же (lambda)) равенство
$$
D_ <1>= lambda D.label
$$
Если плоскости параллельны, то их нормальные векторы (boldsymbol) и (boldsymbol_<1>) коллинеарны, и существует такое число (lambda), что (boldsymbol_ <1>= lambdaboldsymbol). В силу уравнений eqref (A_ <1>= (boldsymbol_<1>, boldsymbol_<1>) = lambda(boldsymbol_<1>, boldsymbol) = lambda A). Аналогично доказываются и остальные равенства eqref. Обратно, если равенства eqref выполнены, то из формулы eqref следует, что (boldsymbol_ <1>= lambdaboldsymbol). Это доказывает первую часть предложения. Вторая его часть доказывается так же, как вторая часть предложения 7.
Условия eqref выражают не что иное, как коллинеарность векторов с компонентами ((A, B)) и ((A_<1>, B_<1>)). Точно так же условия eqref означают коллинеарность векторов с компонентами ((A, B, C)) и ((A_<1>, B_<1>, C_<1>)). Поэтому согласно ранее доказанным этому и этому утверждениям условие параллельности прямых на плоскости можно записать в виде
$$
begin
A& B\
A_<1>& B_<1>
end
= 0,label
$$
а условие параллельности плоскостей — в виде
$$
begin
B& C\
B_<1>& C_<1>
end =
begin
C& A\
C_<1>& A_<1>
end =
begin
A& B\
A_<1>& B_<1>
end
= 0.label
$$
Утверждению 7 можно придать чисто алгебраическую формулировку, если учесть, что координаты точки пересечения прямых — это решение системы, составленной из их уравнений.
При условии eqref система линейных уравнений
$$
Ax+By+C = 0, A_<1>x+B_<1>y+C_ <1>= 0,nonumber
$$
не имеет решений или имеет бесконечно много решений (в зависимости от (C) и (C_<1>). В последнем случае система равносильна одному из составляющих ее уравнений. Если же
$$
begin
A& B\
A_<1>& B_<1>
end
neq 0.nonumber
$$
то при любых (C) и (C_<1>) система имеет единственное решение ((x, y)).
Уравнения прямой в пространстве.
Прямая линия в пространстве может быть задана как пересечение двух плоскостей и, следовательно, в общей декартовой системе координат определяется системой уравнений вида
$$
left<begin
Ax+By+Cz+D = 0,\
A_<1>x+B_<1>y+C_<1>z+D_ <1>= 0.
endright.label
$$
Пересечение плоскостей — прямая линия тогда и только тогда, когда они не параллельны, что согласно eqref означает, что хоть один из детерминантов отличен от нуля:
$$
begin
B& C\
B_<1>& C_<1>
end^ <2>+
begin
C& A\
C_<1>& A_<1>
end^ <2>+
begin
A& B\
A_<1>& B_<1>
end^<2>
neq 0.label
$$
Разумеется, систему eqref можно заменить на любую, ей эквивалентную. При этом прямая будет представлена как пересечение двух других проходящих через нее плоскостей.
Вспомним параметрические уравнения прямой eqref. Допустим, что в них ни одна из компонент направляющего вектора не равна нулю. Тогда
$$
t = frac><alpha_<1>>, t = frac><alpha_<2>>, t = frac><alpha_<3>>,nonumber
$$
и мы получаем два равенства
$$
frac><alpha_<2>> = frac><alpha_<3>>, frac><alpha_<1>> = frac><alpha_<3>>,label
$$
или, в более симметричном виде,
$$
frac><alpha_<1>> = frac><alpha_<2>> = frac><alpha_<3>>,label
$$
Уравнения eqref представляют прямую как линию пересечения двух плоскостей, первая из которых параллельна оси абсцисс (в ее уравнение не входит переменная (x)), а вторая параллельна оси ординат.
Если обращается в нуль одна из компонент направляющего вектора, например, (alpha_<1>), то уравнения прямой принимают вид
$$
x = x_<0>, frac><alpha_<2>> = frac><alpha_<3>>,label
$$
Эта прямая лежит в плоскости (x = x_<0>) и, следовательно, параллельна плоскости (x = 0). Аналогично пишутся уравнения прямой, если в нуль обращается не (alpha_<1>), а другая компонента.
Когда равны нулю две компоненты направляющего вектора, например, (alpha_<1>) и (alpha_<2>), то прямая имеет уравнения
$$
x = x_<0>, y = y_<0>.label
$$
Такая прямая параллельна одной из осей координат, в нашем случае — оси аппликат.
Важно уметь находить начальную точку и направляющий вектор прямой, заданной системой линейных уравнений eqref. По условию eqref один из детерминантов отличен от нуля. Допустим для определенности, что (AB_<1>-A_<1>B neq 0). В силу утверждения 9 при любом фиксированном (z) система уравнений будет иметь единственное решение ((x, y)), в котором (x) и (y), разумеется, зависят от (z). Они — линейные многочлены от (z): (x = alpha_<1>z+beta_<1>), (y = alpha_<2>z+beta_<2>).
Не будем доказывать этого, хотя это и не трудно сделать. Для ясности, заменяя (z) на (t), получаем параметрические уравнения прямой
$$
x = alpha_<1>t+beta_<1>, y = alpha_<2>t+beta_<2>, z = t.nonumber
$$
Первые две координаты начальной точки прямой (M_<0>(beta_<1>, beta_<2>, 0)) можно получить, решая систему eqref при значении (z = 0).
Из параметрических уравнений видно, что в этом случае направляющий вектор имеет координаты ((alpha_<1>, alpha_<2>, 1)). Найдем его компоненты в общем виде. Если система координат декартова прямоугольная, векторы с компонентами ((A, B, C)) и (A_<1>, B_<1>, C_<1>) перпендикулярны соответствующим плоскостям, а потому их векторное произведение параллельно прямой eqref, по которой плоскости пересекаются. Вычисляя векторное произведение в ортонормированном базисе, мы получаем компоненты направляющего вектора
$$
begin
B& C\
B_<1>& C_<1>
end,
begin
C& A\
C_<1>& A_<1>
end,
begin
A& B\
A_<1>& B_<1>
end.label
$$
Вектор с компонентами eqref есть направляющий вектор прямой с уравнениями eqref, какова бы ни была декартова система координат.
Согласно утверждению 5 каждый ненулевой вектор, компоненты которого ((alpha_<1>, alpha_<2>, alpha_<3>)) удовлетворяют уравнению (Aalpha_<1>+Balpha_<2>+Calpha_ <3>= 0), параллелен плоскости с уравнением (Ax+By+Cz+D = 0). Если, кроме того, он удовлетворяет уравнению (A_<1>alpha_<1>+B_<1>alpha_<2>+C_<1>alpha_ <3>= 0), то он параллелен и второй плоскости, то есть может быть принят за направляющий вектор прямой. Вектор с компонентами eqref ненулевой в силу неравенства eqref. Непосредственно легко проверить, что его компоненты удовлетворяют обоим написанным выше условиям. На этом доказательство заканчивается.
Уравнения плоскости, компланарной двум неколлинеарным векторам
Напомним, что три или более векторов называются компланарными , если существует плоскость, которой они параллельны. Эту плоскость будем называть компланарной заданным векторам .
Направляющими векторами плоскости называются два неколлинеарных вектора, компланарных этой плоскости, т.е. принадлежащих плоскости или параллельных ей.
Пусть в координатном пространстве заданы:
б) два неколлинеарных вектора (рис.4.15).
Требуется составить уравнение плоскости, компланарной векторам и проходящей через точку
Выберем на плоскости произвольную точку . Обозначим — радиус-векторы точек и (рис.4.16).
Условие компланарности векторов (рис.4.16) можно записать, используя свойства смешанного произведения Применяя формулу (1.17), получаем уравнение плоскости, проходящей через заданную точку и компланарной двум неколлинеарным векторам:
Параметрическое уравнение плоскости
Пусть в координатном пространстве заданы:
б) два неколлинеарных вектора (рис.4.15).
Требуется составить параметрическое уравнение вида (4.10) плоскости, компланарной векторам и проходящей через точку
Выберем на плоскости произвольную точку . Обозначим -радиус-векторы точек и (рис.4.16).
Точка принадлежит заданной плоскости тогда и только тогда, когда векторы и компланарны (см. разд. 1.3.2). Запишем условие компланарности: где — некоторые действительные числа (параметры). Учитывая, что получим векторное параметрическое уравнение плоскости :
где — направляющие векторы плоскости, а — радиус-вектор точки, принадлежащей плоскости.
Координатная форма записи уравнения (4.19) называется параметрическим уравнением плоскости:
где и — координаты направляющих векторов и соответственно. Параметры в уравнениях (4.19),(4.20) имеют следующий геометрический смысл: величины пропорциональны расстоянию от заданной точки до точки принадлежащей плоскости. При точка совпадает с заданной точкой . При возрастании (или ) точка перемещается в направлении вектора (или ), а при убывании (или ) — в противоположном направлении.
1. Поскольку направляющие векторы плоскости неколлинеарны, то они ненулевые.
2. Любой вектор , коллинеарный плоскости, ортогонален нормальному вектору для этой плоскости. Поэтому их скалярное произведение равно нулю:
Следовательно, координаты и направляющих векторов и плоскости и ее нормали связаны однородными уравнениями:
3. Направляющие векторы плоскости определяются неоднозначно.
4. Для перехода от общего уравнения плоскости (4.15) к параметрическому (4.20) нужно выполнить следующие действия:
1) найти любое решение уравнения определяя тем самым координаты точки принадлежащей плоскости;
2) найти любые два линейно независимых решения однородного уравнения определяя тем самым координаты решения и направляющих векторов и плоскости;
3) записать параметрическое уравнение (4.20).
5. Чтобы перейти от параметрического уравнения плоскости к общему , достаточно либо записать уравнение (4.18) и раскрыть определитель, либо найти нормаль как результат векторного произведения направляющих векторов:
и записать общее уравнение плоскости в форме (4.14):
6. Векторное параметрическое уравнение плоскости (4.19), полученное в прямоугольной системе координат, имеет тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнении остается прежним.
Пример 4.8. В координатном пространстве (в прямоугольной системе координат) заданы точки и (см. рис.4.11). Требуется:
а) составить параметрическое уравнение плоскости, перпендикулярной отрезку и проходящей через его середину;
б) составить общее уравнение плоскости, проходящей через середину отрезка и компланарной радиус-векторам и
Решение. а) Общее уравнение искомой плоскости было получено в примере 4.5: Составим параметрическое уравнение:
1) находим любое решение уравнения , например, следовательно, точка принадлежит плоскости;
2) находим два линейно независимых (непропорциональных) решения однородного уравнения например и следовательно, векторы являются направляющими для плоскости;
3) записываем параметрическое уравнение плоскости (4.20):
б) Координаты середины отрезка были найдены в примере 4.5. Нормаль к искомой плоскости получим как векторное произведение ее направляющих векторов и
Составляем уравнение (4.14):
Тот же результат можно получить, записывая уравнение (4.18):
Общее уравнение плоскости : описание, примеры, решение задач
В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.
Общее уравнение плоскости: основные сведения
Перед началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат O x y z в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x , y , и z , которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным.
Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.
Любую плоскость, заданную в прямоугольной системе координат O x y z трехмерного пространства, можно определить уравнением A x + B y + C z + D = 0 . В свою очередь, любое уравнение A x + B y + C z + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A , B , C , D – некоторые действительные числа, и числа A , B , C не равны одновременно нулю.
Теорема состоит из двух частей. Разберем доказательство каждой из них.
- Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида A x + B y + C z + D = 0 . Допустим, задана некоторая плоскость и точка M 0 ( x 0 , y 0 , z 0 ) , через которую эта плоскость проходит. Нормальным вектором этой плоскости является n → = ( A , B , C ) . Приведем доказательство, что указанную плоскость в прямоугольной системе координат O x y z задает уравнение A x + B y + C z + D = 0 .
Возьмем произвольную точку заданной плоскости M ( x , y , z ) .В таком случае векторы n → = ( A , B , C ) и M 0 M → = ( x – x 0 , y – y 0 , z – z 0 ) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:
n → , M 0 M → = A x – x 0 + B ( y – y 0 ) + C ( z – z 0 ) = A x + B y + C z – ( A x 0 + B y 0 + C z 0 )
Примем D = – ( A x 0 + B y 0 + C z 0 ) , тогда уравнение преобразуется в следующий вид: A x + B y + C z + D = 0 . Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.
- Во второй части теоремы утверждается, что любое уравнение вида A x + B y + C z + D = 0 задает некоторую плоскость в прямоугольной системе координат O x y z трехмерного пространства. Докажем это.
В теореме также указано, что действительные числа А , B , C одновременно не являются равными нулю. Тогда существует некоторая точка M 0 ( x 0 , y 0 , z 0 ) , координаты которой отвечают уравнению A x + B y + C z + D = 0 , т.е. верным будет равенство A x 0 + B y 0 + C z 0 + D = 0 . Отнимем левую и правую части этого равенства от левой и правой частей уравнения A x + B y + C z + D = 0 . Получим уравнение вида
A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) + D = 0 , и оно эквивалентно уравнению A x + B y + C z + D = 0 . Докажем, что уравнение A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) + D = 0 задает некоторую плоскость.
Уравнение A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n → = ( A , B , C ) и M 0 M → = x – x 0 , y – y 0 , z – z 0 . Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) + D = 0 множество точек M ( x , y , z ) задает плоскость, у которой нормальный вектор n → = ( A , B , C ) . При этом плоскость проходит через точку M ( x 0 , y 0 , z 0 ) . Иначе говоря, уравнение A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) + D = 0 задает в прямоугольной системе координат O x y z трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение A x + B y + C z + D = 0 также определяет эту плоскость. Теорема доказана полностью.
Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства.
Допустим, задано некоторое общее уравнение плоскости λ · A x + λ · B y + λ · C z + λ · D = 0 , где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением A x + B y + C z + D = 0 , поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x – 2 · y + 3 · z – 7 = 0 и – 2 · x + 4 · y – 2 3 · z + 14 = 0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства.
Раскроем чуть шире смысл теорем.
В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида A x + B y + C z + D = 0 ( при конкретных значениях чисел A , B , C , D ). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат.
Укажем пример как иллюстрацию этих утверждений.
Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4 x + 5 y – 5 z + 20 = 0 , и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4 x + 5 y – 5 z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость.
Общее уравнение плоскости, проходящей через точку
Повторимся: точка M 0 ( x 0 , y 0 , z 0 ) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением A x + B y + C z + D = 0 в том случае, когда подставив координаты точки M 0 ( x 0 , y 0 , z 0 ) в уравнение A x + B y + C z + D = 0 , мы получим тождество.
Заданы точки M 0 ( 1 , – 1 , – 3 ) и N 0 ( 0 , 2 , – 8 ) и плоскость, определяемая уравнением 2 x + 3 y – z – 2 = 0 . Необходимо проверить, принадлежат ли заданные точки заданной плоскости.
Решение
Подставим координаты точки М 0 в исходной уравнение плоскости:
2 · 1 + 3 · ( – 1 ) – ( – 3 ) – 2 = 0 ⇔ 0 = 0
Мы видим, что получено верное равенство, значит точка M 0 ( 1 , – 1 , – 3 ) принадлежит заданной плоскости.
Аналогично проверим точку N 0 . Подставим ее координаты в исходное уравнение:
2 · 0 + 3 · 2 – ( – 8 ) – 2 = 0 ⇔ 12 = 0
Равенство неверно. Таким, образом, точка N 0 ( 0 , 2 , – 8 ) не принадлежит заданной плоскости.
Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.
Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n → = ( A , B , C ) – нормальный вектор для плоскости, определяемой уравнением A x + B y + C z + D = 0 . Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.
В прямоугольной системе координат задана плоскость 2 x + 3 y – z + 5 = 0 . Необходимо записать координаты всех нормальных векторов заданной плоскости.
Решение
Мы знаем, что заданные общим уравнением коэффициенты при переменных x , y , z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n → исходной плоскости имеет координаты 2 , 3 , – 1 . В свою очередь, множество нормальных векторов запишем так:
λ · n → = λ · 2 , λ · 3 , – λ , λ ∈ R , λ ≠ 0
Ответ: λ · 2 , λ · 3 , – λ , λ ∈ R , λ ≠ 0
Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.
Очевидным фактом является то, что нормальный вектор n → = ( A , B , C ) является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M 0 ( x 0 , y 0 , z 0 ) , принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.
Общее уравнение плоскости с нормальным вектором n → = ( A , B , C ) будет выглядеть так: A x + B y + C z + D = 0 . По условию задачи точка M 0 ( x 0 , y 0 , z 0 ) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство: A x 0 + B y 0 + C z 0 + D = 0
Вычитая соответственно правые и левые части исходного уравнения и уравнения A x 0 + B y 0 + C z 0 + D = 0 , получим уравнение вида A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) = 0 . Оно и будет уравнением плоскости, проходящей через точку M 0 ( x 0 , y 0 , z 0 ) и имеющей нормальный вектор n → = ( A , B , C ) .
Возможно получить это уравнение другим способом.
Очевидным фактом является то, что все точки М ( x , y , z ) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n → = ( A , B , C ) и M 0 M → = ( x – x 0 , y – y 0 , z – z 0 ) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:
n → , M 0 M → = A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) = 0
Задана точка М 0 ( – 1 , 2 , – 3 ) , через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n → = ( 3 , 7 , – 5 ) . Необходимо записать уравнение заданной плоскости.
Решение
Рассмотрим два способа решения.
- Исходные условия позволяют получить следующие данные:
x 0 = – 1 , y 0 = 2 , z 0 = – 3 , A = 3 , B = 7 , C = – 5
Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) = 0
3 ( x – ( – 1 ) ) + 7 ( y – 2 ) – 5 ( z – ( – 3 ) ) = 0 ⇔ 3 x + 7 y – 5 z – 26 = 0
- Допустим, М ( x , y , z ) – некоторая точки заданной плоскости. Определим координаты вектора M 0 M → по координатам точек начала и конца:
M 0 M → = ( x – x 0 , y – y 0 , z – z 0 ) = ( x + 1 , y – 2 , z + 3 )
Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:
n → , M 0 M → = 0 ⇔ 3 ( x + 1 ) + 7 ( y – 2 ) – 5 ( z + 3 ) = 0 ⇔ ⇔ 3 x + 7 y – 5 z – 26 = 0
Ответ: 3 x + 7 y – 5 z – 26 = 0
Неполное общее уравнение плоскости
Выше мы говорили о том, что, когда все числа А , B , C , D отличны от нуля, общее уравнение плоскости A x + B y + C z + D = 0 называют полным. В ином случае общее уравнение плоскости является неполным.
Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.
- В случае, когда D = 0 , мы получаем общее неполное уравнение плоскости: A x + B y + C z + D = 0 ⇔ A x + B y + C z = 0
Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О ( 0 , 0 , 0 ) , то придем к тождеству:
A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0
- Если А = 0 , В ≠ 0 , С ≠ 0 , или А ≠ 0 , В = 0 , С ≠ 0 , или А ≠ 0 , В ≠ 0 , С = 0 , то общие уравнения плоскостей имеют вид соответственно: B y + C z + D = 0 , или A x + C z + D = 0 , или A x + B y + D = 0 . Такие плоскости параллельны координатным осям О x , O y , O z соответственно. Когда D = 0 , плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей B y + C z + D = 0 , A x + C z + D = 0 и A x + B y + D = 0 задают плоскости, которые перпендикулярны плоскостям O y z , O x z , O z y соответственно.
- При А = 0 , В = 0 , С ≠ 0 , или А = 0 , В ≠ 0 , С = 0 , или А ≠ 0 , В = 0 , С = 0 получим общие неполные уравнения плоскостей: C z + D = 0 ⇔ z + D C = 0 ⇔ z = – D C ⇔ z = λ , λ ∈ R или B y + D = 0 ⇔ y + D B = 0 ⇔ y = – D B ⇔ y = λ , λ ∈ R или A x + D = 0 ⇔ x + D A = 0 ⇔ x = – D A ⇔ x = λ , λ ∈ R соответственно.
Эти уравнения определяют плоскости, которые параллельны координатным плоскостям O x y , O x z , O y z соответственно и проходят через точки 0 , 0 , – D C , 0 , – D B , 0 и – D A , 0 , 0 соответственно. При D = 0 уравнения самих координатных плоскостей O x y , O x z , O y z выглядят так: z = 0 , y = 0 , x = 0
Задана плоскость, параллельная координатной плоскости O y z и проходящая через точку М 0 ( 7 , – 2 , 3 ) . Необходимо составить общее уравнение заданной плоскости.
Решение
Условием задачи определено, что заданная плоскость параллельна координатной плоскости O y z , а, следовательно, может быть задана общим неполным уравнением плоскости A x + D = 0 , A ≠ 0 ⇔ x + D A = 0 . Поскольку точка M 0 ( 7 , – 2 , 3 ) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x + D A = 0 , иначе говоря, должно быть верным равенство 7 + D A = 0 . Преобразуем: D A = – 7 , тогда требуемое уравнение имеет вид: x – 7 = 0 .
Задачу возможно решить еще одним способом.
Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости O y z . Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости O y z : i → = ( 1 , 0 , 0 ) . Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:
A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) = 0 ⇔ ⇔ 1 · ( x – 7 ) + 0 · ( y + 2 ) + 0 · ( z – 3 ) = 0 ⇔ ⇔ x – 7 = 0
Ответ: x – 7 = 0
Задана плоскость, перпендикулярная плоскости O x y и проходящая через начало координат и точку М 0 ( – 3 , 1 , 2 ) .
Решение
Плоскость, которая перпендикулярна координатной плоскости O x y определяется общим неполным уравнением плоскости A x + B y + D = 0 ( А ≠ 0 , В ≠ 0 ) . Условием задачи дано, что плоскость проходит через начало координат, тогда D = 0 и уравнение плоскости принимает вид A x + B y = 0 ⇔ x + B A y = 0 .
Найдем значение B A . В исходных данных фигурирует точка М 0 ( – 3 , 1 , 2 ) , координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: – 3 + B A · 1 = 0 , откуда определяем B A = 3 .
Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x + 3 y = 0 .
[spoiler title=”источники:”]
http://mathhelpplanet.com/static.php?p=uravneniya-ploskosti-komplanarnoi-dvum-nekollinyearnym-vektoram
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/obschee-uravnenie-ploskosti/
[/spoiler]
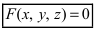
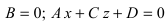 – плоскость параллельна оси ординат (Оу);
– плоскость параллельна оси ординат (Оу);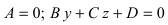 – плоскость параллельна оси абсцисс (Ох).
– плоскость параллельна оси абсцисс (Ох).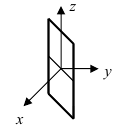
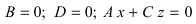 – плоскость проходит через начало координат параллельно оси ординат;
– плоскость проходит через начало координат параллельно оси ординат;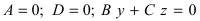 – плоскость проходит через начало координат параллельно оси абсцисс.
– плоскость проходит через начало координат параллельно оси абсцисс.
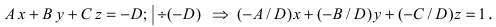
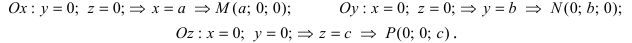
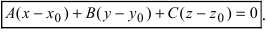
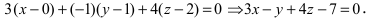
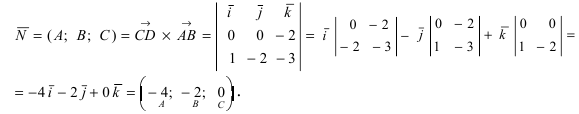
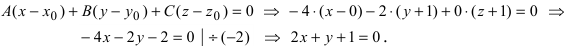
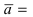

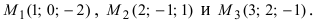
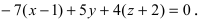
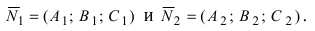
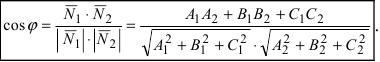
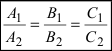
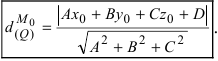
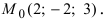
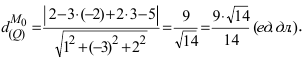
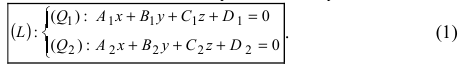
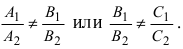

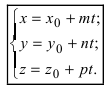
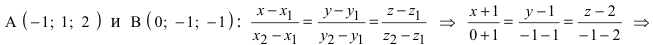
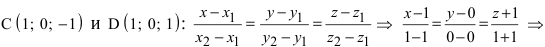
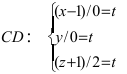
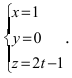
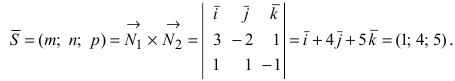
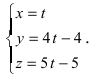
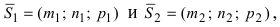

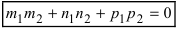
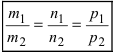
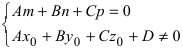 , то прямая не пересекает плоскость (прямая параллельна плоскости);
, то прямая не пересекает плоскость (прямая параллельна плоскости);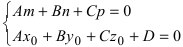 прямая лежит на плоскости;
прямая лежит на плоскости;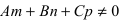 , прямая пересекает плоскость в одной точке.
, прямая пересекает плоскость в одной точке.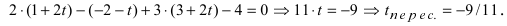
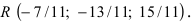
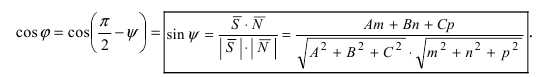
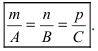
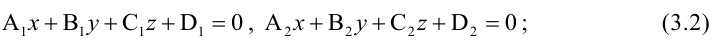
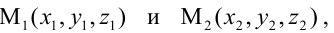 тогда прямая, через них проходящая, задается уравнениями:
тогда прямая, через них проходящая, задается уравнениями: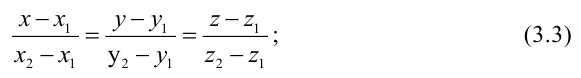
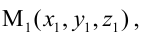 ей принадлежащей, и вектором
ей принадлежащей, и вектором 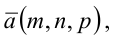 ей коллинеарным.
ей коллинеарным.