Как найти параметр круга

Как найти параметр круга

Информация по назначению калькулятора

В евклидовой геометрии круг – это множество всех точек на плоскости на фиксированном расстоянии, называемом радиусом, от заданной точки, центра. Длина круга называется его окружностью, а любая непрерывная часть окружности называется дугой.

Окружность – это простая замкнутая кривая, которая делит плоскость на внутреннюю и внешнюю. Внутренняя часть круга называется диском. Математически круг можно понимать и несколькими другими способами. Например, это частный случай эллипса, в котором два фокуса совпадают (то есть они являются одной и той же точкой). Альтернативно, окружность можно рассматривать как коническое сечение, достигаемое, когда прямой круговой конус пересекается плоскостью, перпендикулярной оси конуса.

Число π (ПИ) равно 3,141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375…

Все круги обладают одинаковыми свойствами. Некоторые из них отмечены далее:

⇒ Для любого круга заключенная площадь и квадрат его радиуса находятся в фиксированной пропорции, равной математической константе π (ПИ).

⇒ Для любого круга длина окружности и радиус находятся в фиксированной пропорции, равной 2π.

⇒ Круг – это фигура с наибольшей площадью для заданной длины периметра.

⇒ Круг имеет очень симметричную форму. Каждая линия, проходящая через центр, образует линию симметрии отражения. Кроме того, существует вращательная симметрия вокруг центра для каждого угла.

⇒ Окружность с центром в начале координат радиусом 1 называется единичной окружностью.

Онлайн калькулятор поможет найти параметры круга, такие как:

  • Диаметр

    • – равен двум радиусам или длине окружности поделенной на число π (d=r*2=P/π)

  • Радиус

    • – равен половине диаметра или длине окружности поделенной на 2π (r=d/2=P/2π)

  • Длина окружности

    • – (или периметр круга) равна диаметру умноженному на число π (P=d*π=2π*r)

  • Площадь

    • – равна радиусу в квадрате умноженному на число π (S=πr2=¼πd2)

Источник


1. Вспоминай формулы по каждой теме


2. Решай новые задачи каждый день


3. Вдумчиво разбирай решения

Решение задач с окружностями


Задание
1

#3079

Уровень задания: Равен ЕГЭ

Найдите все значения (a), при каждом из которых система уравнений [begin{cases}
x(x^2+y^2-2y-8)=|x|cdot (2y-8)\
y=x+a end{cases}]

имеет ровно три решения.

(Задача от подписчиков)

1) Изобразим график первого уравнения.

а) При (x>0) уравнение принимает вид: [x(x^2+y^2-2y-8)=x(2y-8) quadRightarrowquad x^2+(y-2)^2=4] Мы получили уравнение окружности (назовем ее (s)) с центром в точке ((0;2)) и радиусом (2).

б) При (x=0) уравнение принимает вид: [0cdot (0+y^2-2y-8)=0cdot (2y-8) quadRightarrowquad 0=0] Таким образом, мы получили верное равенство. Следовательно, мы получили множество точек, абсцисса (x) которых равна нулю.

в) При (x<0) уравнение принимает вид: [x(x^2+y^2-2y-8)=-x(2y-8) quadRightarrowquad x^2+y^2=16] Мы получили уравнение окружности (назовем ее (S)) с центром в точке ((0;0)) и радиусом (4).

2) Уравнение (y=x+a) задает множество прямых, параллельных прямой (y=x) (это прямые, угол наклона которых к положительному направлению оси (Ox) равен (45^circ)).
Таким образом, получаем такую картинку (голубым цветом изображен график первого уравнения):

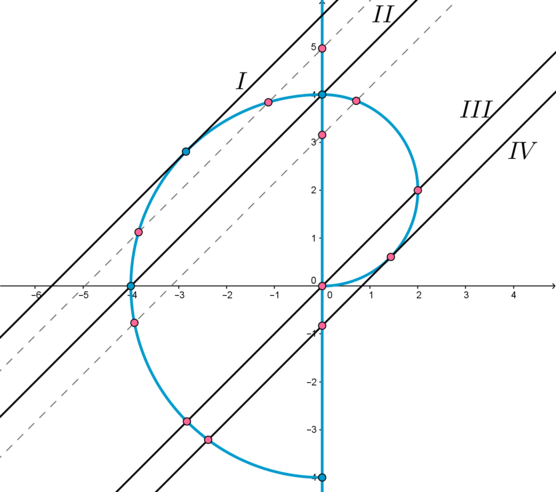
3) Для того, чтобы система имела 3 решения, нужно, чтобы при некотором фиксированном (a) прямая (y=x+a) пересекала “голубой график” ровно в трех точках.
Таким образом, нам подходят следующие случаи:
— когда прямая (y) находится между (I) и (II) (не включая эти случаи). Случай (I) – касание прямой (y) и окружности (S). Случай (II) – прохождение прямой (y) через точку пересечения окружности (S) и прямой (x=0).
— когда прямая (y) находится между (II) и (III) (не включая (II) и включая (III)). Случай (III) – прохождение прямой (y) через точку пересечения окружности (s) и прямой (x=0).
— когда прямая (y) находится в положении (IV) – касается окружности (s).

Рассмотрим каждый из этих случаев по отдельности.

Между (I) и (II).
– Найдем значение (a), при котором прямая (y) находится в положении (I). В этом случае (a>0).

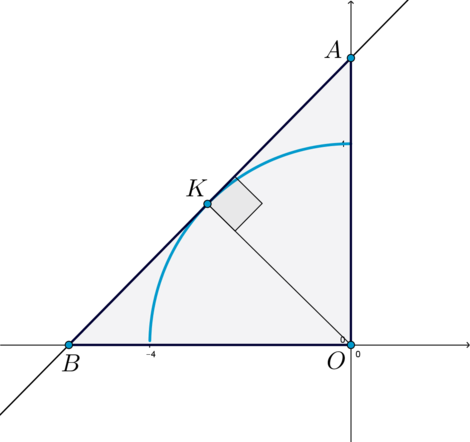
Пусть (A(0;a), B(-a;0)) – точки пересечения (y) с осями координат, (K) – точка касания. Тогда (OKperp AB) (как радиус, проведенный в точку касания). Длина (OA=a), (OB=a), (OK=4), (triangle AOB) прямоугольный. Тогда (AB=asqrt2). Тогда [S_{triangle AOB}=dfrac12 OKcdot AB=dfrac12 OBcdot OA
quadRightarrowquad a=4sqrt2.] – Найдем значение (a), при котором прямая (y) находится в положении (II). В этом случае (y) проходит через точку ((0;4)), следовательно, [4=0+a quadRightarrowquad a=4]

Таким образом, нам подходят значения (ain (4;4sqrt2)).

Между (II) и (III).
– Найдем (a), при котором прямая (y) находится в положении (III). В этом случае она проходит через точку ((0;0)), то есть (a=0).

Таким образом, нам подходят (ain [0;4)).

Положение (IV).

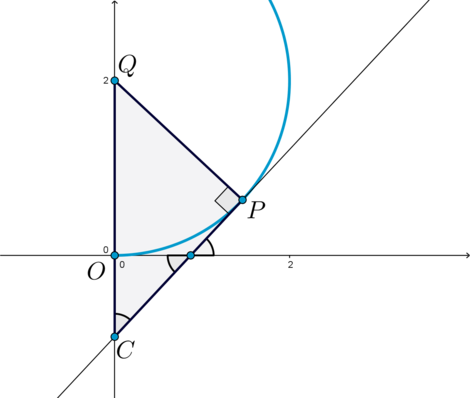
В этом случае (a<0). Пусть (Q) – центр окружности (s), (P) – точка касания, (C) – точка пересечения (y) с осью ординат. Тогда (triangle QPC) – прямоугольный. Ранее мы говорили, что прямая (y) наклонена к положительному направлению оси (Ox) под углом (45^circ), откуда будет следовать, что и (angle QCP=45^circ). Радиус (QP=2), отрезок (OC=-a) (так как (a<0)), (QO=2). Следовательно, [sinangle QCP=sin 45^circ=dfrac{sqrt2}2=dfrac{QP}{QC}=
dfrac{2}{2-a}
quadRightarrowquad a=-2sqrt2+2.]

Таким образом, обобщая все решение, находим ответ: [ain {-2sqrt2+2}cup[0;4)cup(4;4sqrt2).]

Ответ:

({-2sqrt2+2}cup[0;4)cup(4;4sqrt2))


Задание
2

#3202

Уровень задания: Равен ЕГЭ

Найдите все значения параметра (a), при каждом из которых система [begin{cases}
(x-2a+3)^2+(y-a)^2=2,25\
(x+3)^2+(y-a)^2=a^2+2a+1 end{cases}]

имеет единственное решение.

(Задача от подписчиков)

Оба уравнения системы при (ane -1) задают окружности: первое уравнение – окружность с центром в точке (O(2a-3; a)) и радиуса (R_1=1,5); второе – окружность с центром в точке (Q(-3;a)) и радиуса (R_1=|a+1|).
При (a=-1) второе уравнение задает точку (A(-3;-1)), которая не является решением первого уравнения. Следовательно, при (a=-1) система не имеет решений, значит, (a=-1) – не подходит.

Рассмотрим случай, когда (ane-1).
Система будет иметь единственное решение, когда окружности будут касаться друг друга (внутренним или внешним образом). Заметим, что центры обеих окружностей находятся на прямой (y=a). То есть линия центров окружностей параллельна оси абсцисс.

1) Пусть окружности касаются внешним образом в точке (K). Это одна из двух картинок:

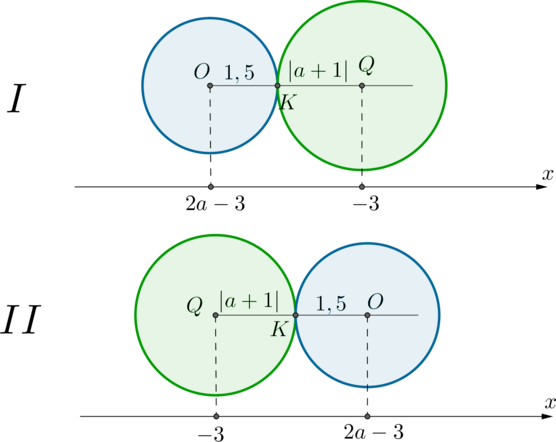
Заметим, что, с одной стороны, расстояние между центрами окружностей равно сумме радиусов: (OQ=|a+1|+1,5), а с другой стороны, равно (|-3-(2a-3)|=2|a|). Получаем уравнение: [|a+1|+1,5=2|a|quadLeftrightarrowquad
left[begin{gathered}begin{aligned} &begin{cases} a< -1\
-2a=-a-1+1,5end{cases}\
&begin{cases} -1<a<0\
-2a=a+1+1,5 end{cases}\
&begin{cases} ageqslant 0\
2a=a+1+1,5 end{cases} end{aligned}end{gathered}right. quad
Leftrightarrowquad a=-dfrac56; dfrac52]

2) Пусть окружности касаются внутренним образом в точке (K). Это также одна из двух картинок (а также симметричные картинки, то есть когда точка касания находится слева):

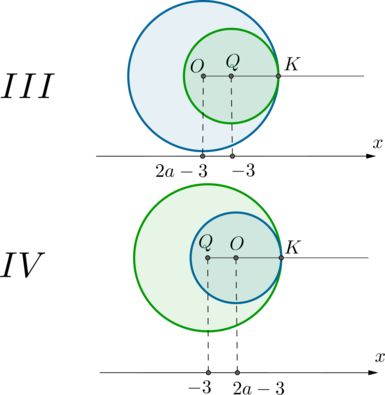
В этих случаях длина отрезка (OQ), с одной стороны, равна (|-3-(2a-3)|=2|a|), а с другой стороны, она равна разности радиусов: (big|1,5-|a+1|big|) (ставим модуль, потому что неизвестно, какой радиус больше, то есть как окружность с центром (O) может быть вписана в окружность с центром (Q), так и наоборот). Получаем уравнение: [2|a|=big|1,5-|a+1|big| quadLeftrightarrowquad
left[begin{gathered}begin{aligned} & 2a=|a+1|-1,5\
&2a=1,5-|a+1| end{aligned}end{gathered}right.
quadLeftrightarrowquad a=-dfrac12; dfrac16]

Таким образом, окончательный ответ: [ain left{-dfrac56;
-dfrac12; dfrac16; dfrac52right}]

Ответ:

(left{-dfrac56; -dfrac12; dfrac16; dfrac52right})


Задание
3

#3977

Уровень задания: Равен ЕГЭ

Найдите все значения параметра (a), при которых система [begin{cases} (2x^2-4x+3y^2+6y+5)(8-|2x+y|)leqslant 0\
x^2-4x+y^2=a end{cases}]

имеет единственное решение.

(Задача от подписчиков)

1) Преобразуем неравенство системы:

((2x^2-4x+2+3y^2+6y+3-2-3+5)(8-|2x+y|)leqslant 0
quadLeftrightarrow)
 

(Leftrightarrowquad (2(x-1)^2+3(y+1)^2)(8-|2x+y|)leqslant
0quadLeftrightarrow)
 

(Leftrightarrowquad left[begin{gathered}begin{aligned}
&begin{cases} 2(x-1)^2+3(y+1)^2leqslant 0\
8-|2x+y|geqslant 0end{cases}\[2ex]
&begin{cases} 2(x-1)^2+3(y+1)^2geqslant 0\
8-|2x+y|leqslant 0end{cases} end{aligned}end{gathered}right.)

Т.к. сумма квадратов всегда неотрицательна, то данная совокупность равносильна:

[left[begin{gathered}begin{aligned}
&begin{cases}
2(x-1)^2+3(y+1)^2=0\
|2x+y|leqslant 8
end{cases}\[2ex]
&begin{cases}
2(x-1)^2+3(y+1)^2geqslant 0\
|2x+y|geqslant 8
end{cases}
end{aligned}end{gathered}right.
quadLeftrightarrowquad
left[begin{gathered}begin{aligned} &begin{cases}
x=1\
y=-1\
|2cdot 1+1|leqslant 8
end{cases}\[2ex]
&begin{cases}
x,yinmathbb{R}\
|2x+y|geqslant 8
end{cases}
end{aligned}end{gathered}right.
quadLeftrightarrowquad
left[begin{gathered}begin{aligned}
&begin{cases}
x=1\
y=-1
end{cases}\[2ex]
&|2x+y|geqslant 8
end{aligned}end{gathered}right.]

Т.к. (|2x+y|geqslant 8) равносильно (2x+ygeqslant 8) или (2x+yleqslant -8), то данная совокупность задает область, состоящую из части плоскости, находящейся не ниже прямой (y=-2x+8), из части плоскости, находящейся не выше прямой (y=-2x-8), а также из точки ((1;-1)):

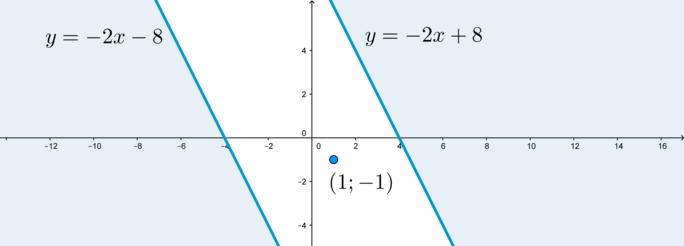
2) Преобразуем уравнение системы: [x^2-4x+y^2=aquadLeftrightarrowquad x^2-4x+4+y^2=a+4quadLeftrightarrowquad
(x-2)^2+y^2=a+4]

Данное уравнение при (a+4>0) задает окружность с центром в точке (O(2;0)) и радиусом (R=sqrt{a+4}); при (a+4=0) задает точку ((2;0)); при (a+4<0) – пустое множество.

Т.к. точка ((2;0)) не попадает в область, заданную неравенством, то при (a+4leqslant 0) система точно не будет иметь решений.

3) Рассмотрим случай (a+4>0).

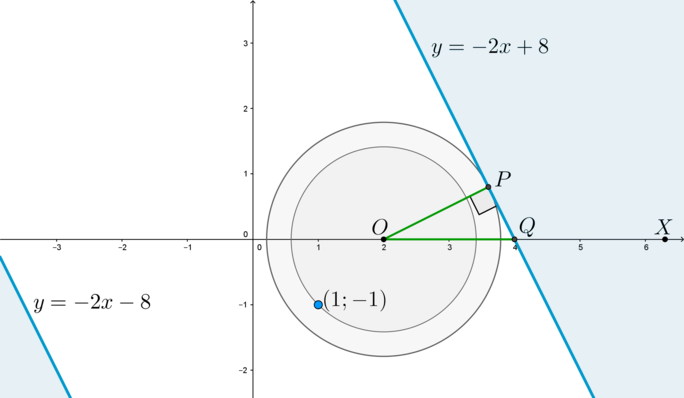
Система будет иметь единственное решение тогда и только тогда, когда окружность будет иметь ровно одну общую точку с областью. Это возможно в одном из двух случаев:

(1) Если окружность коснется границы области (y=-2x+8).
Пусть (P) – точка касания (то есть (OPperp y=-2x+8)). Рассмотрим прямоугольный (triangle OPQ), где (Q=(4;0)) – точка пересечения прямой (y=-2x+8) с осью абсцисс.

Т.к. угловой коэффициент прямой (y=-2x+8) равен (-2), то (mathrm{tg},angle PQX=-2), следовательно, (mathrm{tg},angle
PQO=2). Тогда [sin angle PQO=dfrac{2}{sqrt5}
quadRightarrowquad dfrac{OP}{OQ}=dfrac2{sqrt5} quad
Rightarrowquad OP=OQcdot dfrac2{sqrt5}=dfrac4{sqrt5}.]

Т.к. (OP) и есть радиус окружности, то [dfrac4{sqrt5}=sqrt{a+4} quad Rightarrowquad a=-dfrac45.]

(2) Если окружность проходит через точку ((1;-1)).
Это значит, что расстояние между точками (O) и ((1;-1)) равно радиусу окружности, следовательно, [sqrt{a+4}=sqrt{(2-1)^2+(0+1)^2}quad Leftrightarrowquad a=-2.]

Ответ:

(big{-2;-frac45big})


Задание
4

#3980

Уровень задания: Равен ЕГЭ

Найдите все значения параметра (a), при которых система [begin{cases}
left(|x|-3right)^2+left(|y|-2right)^2=1\
y=ax+1\xy<0end{cases}] имеет ровно два решения.

Рассмотрим первое уравнение системы. Оно задает 4 окружности. Действительно, пусть (x>0, y>0). Тогда уравнение примет вид ((x-3)^2+(y-2)^2=1) – это окружность с центром в точке (O_1(3;2)) и (r=1).
Если (x<0, y>0), то уравнение примет вид ((x+3)^2+(y-2)^2=1) – и это уравнение окружности с центром (O_2(-3;2)) и (r=1). И т.д.
Таким образом, получаем:


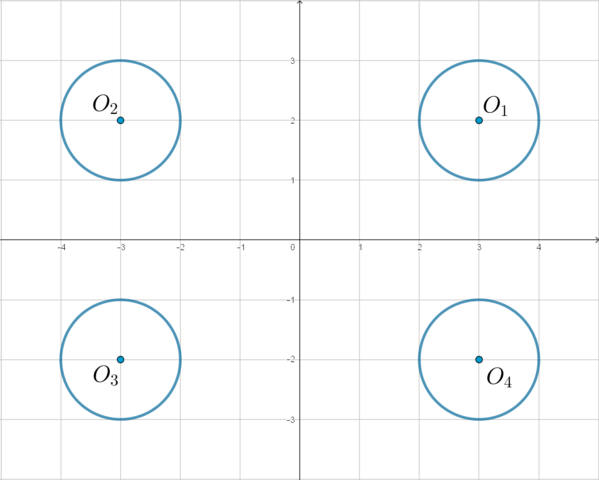
Рассмотрим третье неравенство системы (xy<0). Следовательно, либо (x>0, y<0), либо (x<0, y>0). Таким образом, учитывая это неравенство, остаются только две окружности: в (IV) и (II) четвертях. Уравнение (y=ax+1) задает прямую, у которой неизвестен угловой коэффициент, и которая проходит через точку ((0;1)):


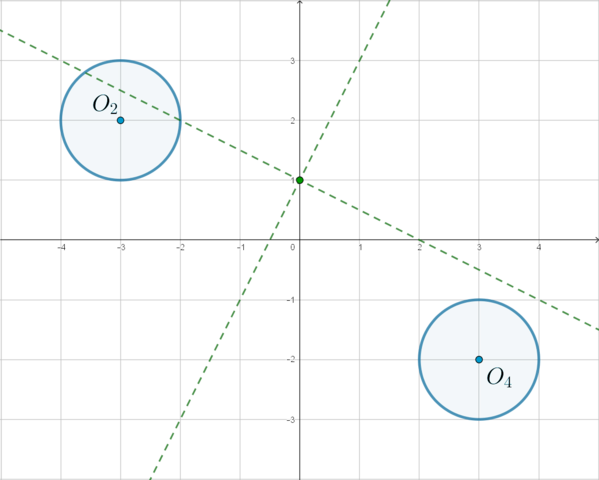
Какие у нас могут быть случаи пересечения прямой с этими окружностями так, чтобы в итоге было ровно две точки пересечения?
а) прямая пересекает одну окружность, а вторую – нет;
б) прямая касается обеих окружностей.
Заметим, что так как окружности расположены симметрично относительно начала координат, то для того, чтобы прямая могла одновременно касаться обеих окружностей, она должна проходить через начало координат (то есть она тоже должна быть симметрична относительно начала координат). Наша прямая через начало координат не проходит. Следовательно, она не может касаться обеих окружностей сразу. Значит, случай б) невозможен. Остается только случай а).
Таким образом, нам нужно для начала рассмотреть все ситуации, когда прямая будет касаться какой-то из окружностей.


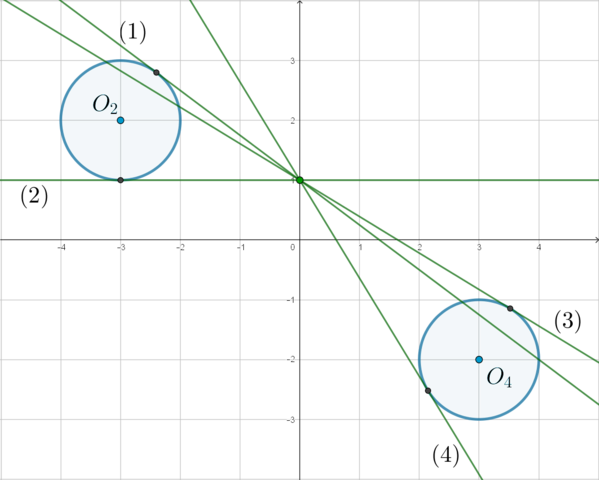
((1)) и ((2)) – случаи, когда прямая касается второй окружности (будем ее так называть, потому что у нее центр в (O_2)); ((3)) и ((4)) – случаи, когда прямая касается четвертой окружности.
Заметим, что эти случаи по возрастанию параметра (a) можно упорядочить так: ((4)rightarrow(1)rightarrow(3)rightarrow(2)).
Таким образом, нам нужны будут значения параметра, принадлежащие ((a_{4}; a_{1})) и ((a_{3}; a_{2})) (здесь (a_{i}) – значения параметра (a), которое соответствует расположению прямой в случае ((i))).
Значит, найдем (a_{1}, a_{2}, a_{3}, a_{4}).
Найдем значения (a), когда прямая (y=ax+1) касается второй окружности: [begin{cases} (x+3)^2+(y-2)^2=1\
y=ax+1end{cases}quadRightarrowquad (a^2+1)x^2+2(3-a)x+9=0] Так как прямая и окружность касаются, то есть имеют одну точку пересечения, то полученное уравнение должно иметь один корень, следовательно, его дискриминант должен быть равен нулю: [D=0quadRightarrowquad a=-dfrac34; 0] Значит, (a_2=0; a_1=-frac34).
Аналогично найдем, что (a_3=frac{-9+sqrt{17}}8), (a_4=frac{-9-sqrt{17}}8).
Следовательно, ответ: [ain left(dfrac{-9-sqrt{17}}8; -dfrac34right)cupleft(dfrac{-9+sqrt{17}}8;
0right)]

Ответ:

(ain left(frac{-9-sqrt{17}}8;
-frac34right)cupleft(frac{-9+sqrt{17}}8; 0right))

УСТАЛ? Просто отдохни

Источник

Материалы к занятию по теме “Параметр в уравнении окружности”

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Материалы для занятия по теме

«Параметр в уравнении окружности»

1. Уравнение окружности.

(х ‒ х 0 )² + (у ‒ у 0 )² = R ², где А(х 0 ; у 0 ) ‒ центр окружности, R ‒ радиус.

х² + у² = R ² ‒ уравнение окружности с центром в начале координат.

2. Параметр – радиус.

Если а = 0, то (х ‒ х 0 )² + (у‒ у 0 )² = 0, то есть А(х 0 ; у 0 ) – точка.

Если а ˂ 0, то ни окружность, ни точка не существуют.

Если а > 0, то R =, на плоскости – концентрические окружности с центром (х 0 ; у 0 ).

Пример. (х ‒ 2)² + (у + 2)² = а (а > 0)

3. Параметр в одной из координат центра.

Одна координата с параметром: (х ‒ 2а)² + (у + 3)² = 9. У центра окружности меняется абсцисса, ордината постоянна. Значит, центры окружностей зафиксированы на прямой у = ‒3.

Задание : подставляя разные значения параметра а, определите координаты центров нескольких окружностей и выполните построение.

Аналогично: (х‒3)² +(у ‒ 2а)² = 9. У центра окружности меняется ордината, абсцисса постоянна. Центры окружностей зафиксированы на прямой х=3.

Задание: построить несколько окружностей, удовлетворяющих последнему уравнению.

4. Параметр в обеих координатах центра.

(х ‒ а)² + (у ‒ а)² = 1. Обе координаты с параметром.

Центр окружности ‒ точка А (а ; а). Так как абсцисса и ордината равны, то все точки такие находятся на прямой у = х. Тогда данное уравнение задает множество окружностей , центры которых лежат на прямой у = х , а радиус равен 1.

Задание : построить несколько окружностей, удовлетворяющих следующему уравнению (х ‒ а)² + (у + 2а)² = 4.

Подсказка. Найдем координаты центра окружности: (х ‒ а)² + (у ‒ (‒2а))² = 4

А(а;-2а), значит центры окружностей лежат на прямой у = ‒2х, радиус равен 2.

5. Параметр в координатах центра и в радиусе.

( х ‒ а)² + (у‒ 2а ‒1 )² = а². Это окружности с центрами на прямой у = 2а + 1, радиус равен а. При а=0 – точка.

Задания для самостоятельной работы.

№ 1. Указать центр, радиус и построить каждую окружность , заданную уравнением:

а) (х ‒ 3)² + (у + 2)² = 16; б) (х + 1)² + (у ‒ 4)² = 10.

№ 2. Выяснить, какие из данных уравнений являются уравнениями окружности. Найти координаты центра и радиус каждой окружности:

а) х² + у² + 8х ‒ 4у + 40 = 0;

б) х² + у² ‒ 2х + 4у ‒ 20 = 0;

в) х² + у² ‒ 4х ‒ 2у + 1 = 0.

№ 3. Выделить уравнение окружности, указать ее центр и радиус в задачах с параметром. Описать расположение графика уравнения на координатной плоскости. Выполнить построение:

а) х² + у² + 2ах ‒ 4у + а² ‒ 1 = 0;

б) х² + у² ‒ 6х + 4ау + 4а² = 0;

в) х² + у² ‒ 2а( х ‒ у ) = 4 ‒ 2а².

1.Геометрия. 7-9 классы : учебник для общеобразовательных организаций с приложением на электронном носителе / [Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.]. – 3-е изд.-М. : Просвещение, 2014.-383 с.

2.Шестаков С.А. ЕГЭ 2014. Математика. Задача С5. Задачи с параметром / Под ред. А.Л.Семенова и И.В.Ященко. – М.:МЦМНО. 2014.-240 с.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

  • Сейчас обучается 949 человек из 80 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

  • Сейчас обучается 325 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

  • Сейчас обучается 698 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 483 045 материалов в базе

Дистанционные курсы для педагогов

Другие материалы

  • 15.02.2020
  • 215
  • 15.02.2020
  • 111
  • 15.02.2020
  • 759
  • 15.02.2020
  • 877
  • 15.02.2020
  • 204
  • 15.02.2020
  • 174
  • 15.02.2020
  • 156
  • 15.02.2020
  • 285

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

  • 15.02.2020 553 –> –> –> –>
  • DOCX 68.3 кбайт –> –>
  • Оцените материал:

Настоящий материал опубликован пользователем Сергеева Татьяна Владиславовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

  • На сайте: 2 года
  • Подписчики: 1
  • Всего просмотров: 1832
  • Всего материалов: 3

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

548 курсов от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

В местах сдачи ЕГЭ будут применены антиковидные меры

Время чтения: 1 минута

Свободное движение повышает креативность

Время чтения: 1 минута

В Петербурге дали рекомендации по переводу школьников на дистант

Время чтения: 3 минуты

Федеральный перечень учебников будет дополнен новыми учебниками

Время чтения: 3 минуты

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Графический метод решения задач с параметрами

Теперь вы узнали, что такое параметр, и увидели решение самых простых задач.

Но подождите — рано успокаиваться и говорить, что вы все знаете. Есть множество типов задач с параметрами и приемов их решения. Чтобы чувствовать себя уверенно, мало посмотреть решения трех незатейливых задач.

Вот список тем, которые стоит повторить:

1. Элементарные функции и их графики. Парабола, синус, логарифм, арктангенс и все остальные — всех их надо знать «в лицо».

Только после этого можно переходить к самому простому и наглядному способу решения задач с параметрами — графическому. Конечно, он не единственный. Но начинать лучше всего именно с него.

Мы разберем несколько самых простых задач, решаемых графическим методом. Больше задач — в видеокурсе «Графический метод решения задач с параметрами» (бесплатно).

1. При каких значениях параметра a уравнение имеет ровно 2 различных решения?

Дробь равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель не равен нулю.

В первом уравнении выделим полный квадрат:

Это уравнение окружности с центром в точке и радиусом равным 2. Обратите внимание — графики будем строить в координатах х; а.

Уравнение задает прямую, проходящую через начало координат. Нам нужны ординаты точек, лежащих на окружности и не лежащих на этой прямой.

Для того чтобы точка лежала на окружности, ее ордината а должна быть не меньше 0 и не больше 4.

Кроме того, точка не должна лежать на прямой , которая пересекает окружность в точках и Координаты этих точек легко найти, подставим в уравнение окружности.

Точка С также не подходит нам, поскольку при мы получим единственную точку, лежащую на окружности, и единственное решение уравнения.

2. Найдите все значения a, при которых уравнение имеет единственное решение.

Уравнение равносильно системе:

Мы возвели обе части уравнения в квадрат при условии, что (смотри тему «Иррациональные уравнения»).

Раскроем скобки в правой части уравнения, применяя формулу квадрата трехчлена. Получаем систему.

Приводим подобные слагаемые в уравнении.

Заметим, что при прибавлении к правой и левой части числа 49 можно выделить полные квадраты:

Решим систему графически:

Уравнение задает окружность с центром в точке , где радиус

Неравенство задает полуплоскость, которая расположена выше прямой , вместе с самой этой прямой.

Исходное уравнение имеет единственное решение, если окружность имеет единственную общую точку с полуплоскостью. Другими словами, окружность касается прямой, заданной уравнением

Пусть С — точка касания.

На координатной плоскости отметим точки и , в которых прямая пересекает оси Y и Х.

Рассмотрим треугольник ABP. Он прямоугольный, и радиус окружности PC является медианой этого треугольника. Значит по свойству медианы прямоугольного треугольника, проведенной к гипотенузе.

Из треугольника ABP найдем длину гипотенузы AB по теореме Пифагора.

Решая это уравнение, получаем, что

3. Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение.

График уравнения – окружность с центром и радиусом равным 2.

График уравнения – две симметричные окружности и радиуса 2 c центрами в точках и

Второе уравнение при задает окружность с центром в точке и радиусом a.

Вот такая картинка, похожая на злую птицу. Или на хрюшку. Кому что нравится.

Система имеет единственное решение в случаях, когда окружность , задаваемая вторым уравнением, касается только левой окружности или только правой

Если a – радиус окружности , то это значит, что (только правая) или (только левая).

Пусть А – точка касания окружности и окружности

, (как гипотенуза прямоугольного треугольника МNР с катетами 3 и 4),

В — точка касания окружности и окружности

длину MQ найдем как гипотенузу прямоугольного треугольника KMQ с катетами 7 и 4; Тогда для точки В получим:

Есть еще точки С и D, в которых окружность касается окружности или окружности соответственно. Однако эти точки нам не подходят. В самом деле, для точки С:

, но и это значит, что окружность с центром в точке М, проходящая через точку С, будет пересекать левую окружность и система будет иметь не одно, а три решения.

Аналогично, для точки D:

и значит, окружность с центром М, проходящая через точку D, будет пересекать правую окружность и система будет иметь три решения.

4. При каких значениях a система уравнений имеет 4 решения?

Конечно же, решаем графически. Только непуганый безумец возьмется решать такую систему аналитически : -)

И в первом, и во втором уравнении системы уже можно разглядеть известные «базовые элементы» (ссылка) — в первом ромбик, во втором окружность. Видите их? Как, еще нет? — Сейчас увидите!

Просто выделили полный квадрат во втором уравнении.

Сделаем замену Система примет вид:

Вот теперь все видно! Рисовать будем в координатах

Графиком первого уравнения является ромб, проходящий через точки с координатами и

Графиком второго уравнения является окружность с радиусом и центром в начале координат.

Когда же система имеет ровно 4 решения?

1) В случае, когда окружность вписана в ромб, то есть касается всех сторон ромба.

Запишем площадь ромба двумя способами — как произведение диагоналей пополам и как произведение стороны на высоту, проведенную к этой стороне.

Диагонали нашего ромба равны 8 и 6. Значит,

Сторону ромба найдем по теореме Пифагора. Видите на рисунке прямоугольный треугольник со катетами 3 и 4? Да, это египетский треугольник, и его гипотенуза, то есть сторона ромба, равна 5. Если h — высота ромба, то

При этом Мы помним, что если окружность вписана в ромб, то диаметр этой окружности равен высоте ромба. Отсюда

Мы получили ответ:

2) Есть второй случай, и мы его найдем.

Давайте посмотрим — если уменьшить радиус окружности, сделав , окружность будет лежать внутри ромба, не касаясь его сторон. Система не будет иметь решений, и нам это не подходит.

Пусть радиус окружности больше, чем , но меньше 3. Окружность дважды пересекает каждую из четырех сторон ромба, и система имеет целых 8 решений. Опять не то.

Пусть радиус окружности равен 3. Тогда система имеет 6 решений.

А что, если ? Окружность пересекает каждую сторону ромба ровно 1 раз, всего 4 решения. Подходит!

Значит, Объединим случаи и запишем ответ:

Больше задач и методов решения — на онлайн-курсе Анны Малковой. И на интенсивах ЕГЭ-Студии в Москве.

Вебинар по задачам 18: модуль и окружности

Всем, кто не смог прийти на вебинар (или не смог подключиться — такое тоже бывает), предлагаю просмотреть запись всего, что происходило в эти 2 часа. От себя добавлю: вебинар получился очень содержательным и вообще одним из лучших за все время проведения подобных мероприятий.

Благодарю всех, кто пришел на этот вебинар. В следующий раз мы разберем задачи C4 — постараюсь, чтобы было еще лучше.:)

Друзья! Приглашаю вас на вебинар по задачам C5, который состоится в воскресенье, 17 ноября, в 18:00 по московскому времени. Мы научимся работать с модулем, уравнением окружности, строить пересечения и грамотно выбирать значения параметров.

Ориентировочная продолжительность вебинара — 1 час, не более. Наш предыдущий вебинар растянулся на 3 часа — это слишком много, таких долгих уроков больше не будет.

Участие в вебинаре абсолютно бесплатное — достаточно заполнить заявку, которая находится в конце этой страницы.

Для кого этот вебинар?

  1. Для всех учеников 11-х классов, которым в этом году предстоит сдавать ЕГЭ по математике;
  2. Материал также будет полезен ученикам 10-х классов, которые сейчас изучают графики функций и задачи с параметрами.

Что будет на вебинаре?

  1. Основные прием работы с графиками: сдвиги по вертикали и горизонтали, а также растяжение вдоль осей;
  2. Модуль и окружность: их графики и «хитрости» для быстрого построения;
  3. Грамотная работа с касательными и нахождение расстояний на плоскости;
  4. Быстрый переход от геометрических построений к алгебраической интерпретации.

Чего точно не будет?

  1. Задач, рассчитанных на решение с помощью алгебраических методов;
  2. Метод областей — это вообще отдельная тема, для нее будет свой вебинар;
  3. Супернавороченных задач C5, в которых, например, координаты центра окружности являются функцией от параметра. Такие задачи, безусловно, интересны, но на настоящем ЕГЭ по математике не встречаются.

Как попасть на вебинар?

Очень просто. Заполните предложенную ниже форму — и через несколько секунд вы получите уведомление о регистрации. Если по каким-то причинам письмо к вам не пришло — ничего страшного. Я вышлю все данные за сутки до начала вебинара и еще раз — за час до начала.

[spoiler title=”источники:”]

Графический метод решения задач с параметрами

http://www.berdov.com/ege/parametr/parametr-moduli-okrujnosti/

[/spoiler]

Источник
Параметрическая касательная к окружности (задача за 9 класс)

Приветствую вас, друзья! В этой заметке подробно разберем задачу из ОГЭ по математике. Получается, что уровень сложности задачи: ~ 9 класс.

Задание

Прямая y  =  2•x + b касается окружности x²  +  y² =  5 в точке с положительной абсциссой. Определите координаты точки касания.

Решение:

В самом начале я привел рисунок, который описывает как может располагаться прямая и окружности (рисунок не подходит к нашей задаче, это сделано специально для того, чтобы бы вы подумали на начальном этапе).

Итак, прямая может:
1. Не иметь с окружностью общих точек (не пересекаться)
2. Иметь с окружностью одну общую точку (касаться окружности)
3. Иметь с окружностью две общих точкий (пересекать окружность, образуя хорду).

В нашей задаче нужно рассмотреть именно 2-й случай (обратите внимание на условие задачи).

Способ 1

Допустим, нам необходимо решить задачу со знаниями 9 класса. Найдем точку пересечения функций. Для этого решим совместную систему:

Параметрическая касательная к окружности (задача за 9 класс)

Решение последнего уравнения определяет количество точек пересечения прямой с окружностью и координаты этих точек. Так как в задании сказано, что прямая является касательной, то квадратное уравнение должно давать одно решение, зависящее от параметра. То есть в нашем уравнении должен быть нулевой дискриминант. Учтем это:

Параметрическая касательная к окружности (задача за 9 класс)

Если мы представим графическое решение, то поймем, что касание может происходит сверху и снизу. Нам же нужно выбрать ту точку, у которой будет положительное значение абсциссы.

Ответ: x₀ = 2 при значении параметра b = – 5

Способ 2

Если мы уже знакомы с производными, то можно написать уравнение для касательной к окружности. Анализ функций дает нам подсказку, что касание должно происходить в области, где x > 0 и y < 0, это значит, что функцию можем выразить явно. Это может понадобиться для дальнейшего нахождения производной этой функции. Производная в точке касания будет определять коэффициент наклона касательной.

Параметрическая касательная к окружности (задача за 9 класс)

Данное уравнение совпадает с уравнением касательной в условии задачи. Поэтому, приравняв соответствующие коэффициенты, мы сможем найти как абсциссу касания, так и значения параметра:

Параметрическая касательная к окружности (задача за 9 класс)

Выбираем положительное значение, получаем тот же ответ:

Ответ: x₀ = 2 при значении параметра b = – 5

Общий ответ: точка касания M(2; -1) при значение параметра b = -5

А теперь правильный график, иллюстрирующий касание параметрической прямой к окружности
А теперь правильный график, иллюстрирующий касание параметрической прямой к окружности

Понравилась заметка ? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно 🙂

Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в telegram

Источник

Геометрия круга

Круг, его части, их размеры и соотношения — вещи, с которыми ювелир постоянно сталкивается. Кольца, браслеты, касты, трубки, шары, спирали — много всего круглого приходится делать. Как же всё это посчитать, особенно если тебе посчастливилось в школе прогулять уроки геометрии?..

Давайте сначала рассмотрим, какие у круга бывают части и как они называются.Круг и его части

  • Окружность — линия, ограничивающая круг.
  • Дуга — часть окружности.
  • Радиус — отрезок, соединяющий центр круга с какой-либо точкой окружности.
  • Хорда — отрезок, соединяющий две точки окружности.
  • Сегмент — часть круга, ограниченная хордой и дугой.
  • Сектор — часть круга, ограниченная двумя радиусами и дугой.

Интересующие нас величины и их обозначения:

Теперь посмотрим, какие задачи, связанные с частями круга, приходится решать.

  • Найти длину развертки какой-либо части кольца (браслета). Задан диаметр и хорда (вариант: диаметр и центральный угол), найти длину дуги.
  • Есть рисунок на плоскости, надо узнать его размер в проекции после сгибания в дугу. Заданы длина дуги и диаметр, найти длину хорды.
  • Узнать высоту детали, полученной сгибанием плоской заготовки в дугу. Варианты исходных данных: длина дуги и диаметр, длина дуги и хорда; найти высоту сегмента.

Жизнь подскажет и другие примеры, а эти я привел только для того, чтобы показать необходимость задания каких-нибудь двух параметров для нахождения всех остальных. Вот этим мы и займемся. А именно, возьмем пять параметров сегмента: D, L, X, φ и H. Затем, выбирая из них все возможные пары, будем считать их исходными данными и путем мозгового штурма находить все остальные.

Чтобы зря не грузить читателя, подробных решений я приводить не буду, а приведу лишь результаты в виде формул (те случаи, где нет формального решения, я оговорю по ходу дела).

И еще одно замечание: о единицах измерения. Все величины, кроме центрального угла, измеряются в одних и тех же абстрактных единицах. Это значит, что если, к примеру, вы задаёте одну величину в миллиметрах, то другую не надо задавать в сантиметрах, а результирующие значения будут измеряться в тех же миллиметрах (а площади — в квадратных миллиметрах). То же самое можно сказать и про дюймы, футы и морские мили.

И только центральный угол во всех случаях измеряется в градусах и ни в чём другом. Потому что, как показывает практика, люди, проектирующие что-нибудь круглое, не склонны измерять углы в радианах. Фраза «угол пи на четыре» многих ставит в тупик, тогда как «угол сорок пять градусов» — понятна всем, так как это всего на пять градусов выше нормы. Однако, во всех формулах будет присутствовать в качестве промежуточной величины еще один угол — α. По смыслу это половина центрального угла, измеренная в радианах, но в этот смысл можно спокойно не вникать.

1. Даны диаметр D и длина дуги L

alpha~=~L/D;     длина хорды X~=~D~*~sin alpha;
высота сегмента H~=~D~*~{1~-~cos alpha}/2;    центральный угол varphi~=~alpha~*~{360/pi}.

2. Даны диаметр D и длина хорды X

alpha~=~arcsin X/D;     длина дуги L~=~D~*~alpha;
высота сегмента H~=~D~*~{1~-~cos alpha}/2;    центральный угол varphi~=~alpha~*~ {360/pi}.

Поскольку хорда делит круг на два сегмента, у этой задачи не одно, а два решения. Чтобы получить второе, нужно в приведенных выше формулах заменить угол α на угол alpha_1~=~pi~-~alpha.

3. Даны диаметр D и центральный угол φ

alpha~=~varphi~*~{pi/360};     длина дуги L~=~D~*~alpha;
длина хорды X~=~D~*~sin alpha;    высота сегмента H~=~D~*~{1~-~cos alpha}/2.

4. Даны диаметр D и высота сегмента H

alpha~=~arccos(1~-~{{2H}/D});     длина дуги L~=~D~*~alpha;
длина хорды X~=~D~*~sin alpha;    центральный угол varphi~=~alpha~*~{360/pi}.

6. Даны длина дуги L и центральный угол φ

alpha~=~varphi~*~{pi/360};     диаметр D~=~L/alpha;
длина хорды X~=~D~*~sin alpha;    высота сегмента H~=~D~*~{1~-~cos alpha}/2.

8. Даны длина хорды X и центральный угол φ

alpha~=~varphi~*~{pi/360};     длина дуги L~=~X~*~alpha/{sin alpha};
диаметр D~=~L/alpha;    высота сегмента H~=~D~*~{1~-~cos alpha}/2.

9. Даны длина хорды X и высота сегмента H

alpha~=~2~*~arctg~{2H}/X;     длина дуги L~=~X~*~alpha/{sin alpha};
диаметр D~=~L/alpha;    центральный угол varphi~=~alpha~*~{360/pi}.

10. Даны центральный угол φ и высота сегмента H

alpha~=~varphi~*~{pi/360};     диаметр D~=~{2 H}/{1~-~cos alpha};
длина дуги L~=~D~*~alpha;    длина хорды X~=~D~*~sin alpha.

Внимательный читатель не мог не заметить, что я пропустил два варианта:

5. Даны длина дуги L и длина хорды X
7. Даны длина дуги L и высота сегмента H

Это как раз те два неприятных случая, когда у задачи нет решения, которое можно было бы записать в виде формулы. А задача-то не такая уж редкая. Например, у вас есть плоская заготовка длины L, и вы хотите согнуть ее так, чтобы ее длина стала X (или высота стала H). Какого диаметра взять оправку (ригель)?

Задача эта сводится к решению уравнений:
L~*~sin alpha~=~X~*~alpha; — в варианте 5
L~*~(1~-~cos alpha)~=~2 H~*~alpha; — в варианте 7
и хоть они и не решаются аналитически, зато легко решаются программным способом. И я даже знаю, где взять такую программу: на этом самом сайте, под именем Segment. Всё то, что я тут длинно рассказываю, она делает за микросекунды.

Для полноты картины добавим к результатам наших вычислений длину окружности и три значения площадей — круга, сектора и сегмента. (Площади нам очень помогут при вычислении массы всяких круглых и полукруглых деталей, но об этом — в отдельной статье.) Все эти величины вычисляются по одним и тем же формулам:

длина окружности C~=~pi~*~D;
площадь круга S~=~pi~*~D^2/4;
площадь сектора S_sect~=~S~*~{varphi/360};
площадь сегмента S_segm~=~S_sect~-~{X~*~D~*~cos alpha}/4;

И в заключение еще раз напомню о существовании абсолютно бесплатной программы, которая выполняет все перечисленные вычисления, освобождая вас от необходимости вспоминать, что такое арктангенс и где его искать.

Программа Segment

Источник

Добавить комментарий