Парабола: определение, свойства, построение
Параболой называется геометрическое место точек плоскости, равноудаленных от заданной точки и заданной прямой
, не проходящей через заданную точку. Это геометрическое определение выражает директориальное свойство параболы.
Директориальное свойство параболы
Точка называется фокусом параболы, прямая
— директрисой параболы, середина
перпендикуляра, опущенного из фокуса на директрису, — вершиной параболы, расстояние
от фокуса до директрисы — параметром параболы, а расстояние
от вершины параболы до её фокуса — фокусным расстоянием (рис.3.45,а). Прямая, перпендикулярная директрисе и проходящая через фокус, называется осью параболы (фокальной осью параболы). Отрезок
, соединяющий произвольную точку
параболы с её фокусом, называется фокальным радиусом точки
. Отрезок, соединяющий две точки параболы, называется хордой параболы.
Для произвольной точки параболы отношение расстояния до фокуса к расстоянию до директрисы равно единице. Сравнивая директориальные свойства эллипса, гиперболы и параболы, заключаем, что эксцентриситет параболы по определению равен единице .
Геометрическое определение параболы, выражающее её директориальное свойство, эквивалентно её аналитическому определению — линии, задаваемой каноническим уравнением параболы:
(3.51)
Действительно, введем прямоугольную систему координат (рис.3.45,б). Вершину параболы примем за начало системы координат; прямую, проходящую через фокус перпендикулярно директрисе, примем за ось абсцисс (положительное направление на ней от точки
к точке
); прямую, перпендикулярную оси абсцисс и проходящую через вершину параболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат
оказалась правой).
Составим уравнение параболы, используя её геометрическое определение, выражающее директориальное свойство параболы. В выбранной системе координат определяем координаты фокуса и уравнение директрисы
. Для произвольной точки
, принадлежащей параболе, имеем:
где — ортогональная проекция точки
на директрису. Записываем это уравнение в координатной форме:
Возводим обе части уравнения в квадрат: . Приводя подобные члены, получаем каноническое уравнение параболы
т.е. выбранная система координат является канонической.
Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.51), и только они, принадлежат геометрическому месту точек, называемому параболой. Таким образом, аналитическое определение параболы эквивалентно его геометрическому определению, выражающему директориальное свойство параболы.
Уравнение параболы в полярной системе координат
Уравнение параболы в полярной системе координат (рис.3.45,в) имеет вид
где
— параметр параболы, а
— её эксцентриситет.
В самом деле, в качестве полюса полярной системы координат выберем фокус параболы, а в качестве полярной оси — луч с началом в точке
, перпендикулярный директрисе и не пересекающий её (рис.3.45,в). Тогда для произвольной точки
, принадлежащей параболе, согласно геометрическому определению (директориальному свойству) параболы, имеем
. Поскольку
, получаем уравнение параболы в координатной форме:
что и требовалось доказать. Заметим, что в полярных координатах уравнения эллипса, гиперболы и параболы совпадают, но описывают разные линии, поскольку отличаются эксцентриситетами ( для эллипса,
для параболы,
для гиперболы).
Геометрический смысл параметра в уравнении параболы
Поясним геометрический смысл параметра в каноническом уравнении параболы. Подставляя в уравнение (3.51)
, получаем
, т.е.
. Следовательно, параметр
— это половина длины хорды параболы, проходящей через её фокус перпендикулярно оси параболы.
Фокальным параметром параболы, так же как для эллипса и для гиперболы, называется половина длины хорды, проходящей через её фокус перпендикулярно фокальной оси (см. рис.3.45,в). Из уравнения параболы в полярных координатах при получаем
, т.е. параметр параболы совпадает с её фокальным параметром.
Замечания 3.11.
1. Параметр параболы характеризует её форму. Чем больше
, тем шире ветви параболы, чем ближе
к нулю, тем ветви параболы уже (рис.3.46).
2. Уравнение (при
) определяет параболу, которая расположена слева от оси ординат (рис. 3.47,a). Это уравнение сводится к каноническому при помощи изменения направления оси абсцисс (3.37). На рис. 3.47,a изображены заданная система координат
и каноническая
.
3. Уравнение определяет параболу с вершиной
, ось которой параллельна оси абсцисс (рис.3.47,6). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36).
Уравнение , также определяет параболу с вершиной
, ось которой параллельна оси ординат (рис.3.47,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36) и переименования координатных осей (3.38). На рис. 3.47,б,в изображены заданные системы координат
и канонические системы координат
.
4. График квадратного трехчлена является параболой с вершиной в точке
, ось которой параллельна оси ординат, ветви параболы направлены вверх (при
) или вниз (при
). Действительно, выделяя полный квадрат, получаем уравнение
которое приводится к каноническому виду , где
, при помощи замены
и
.
Знак выбирается совпадающим со знаком старшего коэффициента . Эта замена соответствует композиции: параллельного переноса (3.36) с
и
, переименования координатных осей (3.38), а в случае
еще и изменения направления координатной оси (3.37). На рис.3.48,а,б изображены заданные системы координат
и канонические системы координат
для случаев
и
соответственно.
5. Ось абсцисс канонической системы координат является осью симметрии параболы, поскольку замена переменной на
не изменяет уравнения (3.51). Другими словами, координаты точки
, принадлежащей параболе, и координаты точки
, симметричной точке
относительно оси абсцисс, удовлетворяют уравнению (3.S1). Оси канонической системы координат называются главными осями параболы.
Пример 3.22. Изобразить параболу в канонической системе координат
. Найти фокальный параметр, координаты фокуса и уравнение директрисы.
Решение. Строим параболу, учитывая её симметрию относительно оси абсцисс (рис.3.49). При необходимости определяем координаты некоторых точек параболы. Например, подставляя в уравнение параболы, получаем
. Следовательно, точки с координатами
принадлежат параболе.
Сравнивая заданное уравнение с каноническим (3.S1), определяем фокальный параметр: . Координаты фокуса
, т.е.
. Составляем уравнение директрисы
, т.е.
.
Общие свойства эллипса, гиперболы, параболы
1. Директориальное свойство может быть использовано как единое определение эллипса, гиперболы, параболы (см. рис.3.50): геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки (фокуса) к расстоянию до заданной прямой
(директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету
, называется:
а) эллипсом, если ;
б) гиперболой, если ;
в) параболой, если .
2. Эллипс, гипербола, парабола получаются в сечениях кругового конуса плоскостями и поэтому называются коническими сечениями. Это свойство также может служить геометрическим определением эллипса, гиперболы, параболы.
3. К числу общих свойств эллипса, гиперболы и параболы можно отнести биссекториальное свойство их касательных. Под касательной к линии в некоторой её точке понимается предельное положение секущей
, когда точка
, оставаясь на рассматриваемой линии, стремится к точке
. Прямая, перпендикулярная касательной к линии и проходящая через точку касания, называется нормалью к этой линии.
Биссекториальное свойство касательных (и нормалей) к эллипсу, гиперболе и параболе формулируется следующим образом: касательная (нормаль) к эллипсу или к гиперболе образует равные углы с фокальными радиусами точки касания (рис.3.51,а,б); касательная (нормаль) к параболе образует равные углы с фокальным радиусом точки касания и перпендикуляром, опущенным из нее на директрису (рис.3.51,в). Другими словами, касательная к эллипсу в точке является биссектрисой внешнего угла треугольника
(а нормаль — биссектрисой внутреннего угла
треугольника); касательная к гиперболе является биссектрисой внутреннего угла треугольника
(а нормаль — биссектрисой внешнего угла); касательная к параболе является биссектрисой внутреннего угла треугольника
(а нормаль — биссектрисой внешнего угла). Биссекториальное свойство касательной к параболе можно сформулировать так же, как для эллипса и гиперболы, если считать, что у параболы имеется второй фокус в бесконечно удаленной точке.
4. Из биссекториальных свойств следуют оптические свойства эллипса, гиперболы и параболы, поясняющие физический смысл термина “фокус”. Представим себе поверхности, образованные вращением эллипса, гиперболы или параболы вокруг фокальной оси. Если на эти поверхности нанести отражающее покрытие, то получаются эллиптическое, гиперболическое и параболическое зеркала. Согласно закону оптики, угол падения луча света на зеркало равен углу отражения, т.е. падающий и отраженный лучи образуют равные углы с нормалью к поверхности, причем оба луча и ось вращения находятся в одной плоскости. Отсюда получаем следующие свойства:
– если источник света находится в одном из фокусов эллиптического зеркала, то лучи света, отразившись от зеркала, собираются в другом фокусе (рис.3.52,а);
– если источник света находится в одном из фокусов гиперболического зеркала, то лучи света, отразившись от зеркала, расходятся так, как если бы они исходили из другого фокуса (рис.3.52,б);
– если источник света находится в фокусе параболического зеркала, то лучи света, отразившись от зеркала, идут параллельно фокальной оси (рис.3.52,в).
5. Диаметральное свойство эллипса, гиперболы и параболы можно сформулировать следующим образом:
– середины параллельных хорд эллипса (гиперболы) лежат на одной прямой, проходящей через центр эллипса (гиперболы);
– середины параллельных хорд параболы лежат на прямой, коллинеарной оси симметрии параболы.
Геометрическое место середин всех параллельных хорд эллипса (гиперболы, параболы) называют диаметром эллипса (гиперболы, параболы), сопряженным к этим хордам.
Это определение диаметра в узком смысле (см. пример 2.8). Ранее было дано определение диаметра в широком смысле, где диаметром эллипса, гиперболы, параболы, а также других линий второго порядка называется прямая, содержащая середины всех параллельных хорд. В узком смысле диаметром эллипса является любая хорда, проходящая через его центр (рис.3.53,а); диаметром гиперболы является любая прямая, проходящая через центр гиперболы (за исключением асимптот), либо часть такой прямой (рис.3.53,6); диаметром параболы является любой луч, исходящий из некоторой точки параболы и коллинеарный оси симметрии (рис.3.53,в).
Два диаметра, каждый их которых делит пополам все хорды, параллельные другому диаметру, называются сопряженными. На рис.3.53 полужирными линиями изображены сопряженные диаметры эллипса, гиперболы, параболы.
Касательную к эллипсу (гиперболе, параболе) в точке можно определить как предельное положение параллельных секущих
, когда точки
и
, оставаясь на рассматриваемой линии, стремятся к точке
. Из этого определения следует, что касательная, параллельная хордам, проходит через конец диаметра, сопряженного к этим хордам.
6. Эллипс, гипербола и парабола имеют, кроме приведенных выше, многочисленные геометрические свойства и физические приложения. Например, рис.3.50 может служить иллюстрацией траекторий движения космических объектов, находящихся в окрестности центра притяжения.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Параметры параболы
Точка F(p/2, 0) называется фокусомпараболы, величина p – параметром, точка О(0, 0) – вершиной (рис. 9.15). При этом прямая OF, относительно которой парабола симметрична, задает ось этой кривой.

Величина 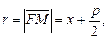 где M(x, y) – произвольная точка параболы, называется фокальным радиусом, прямая D: x = –p/2 – директрисой (она не пересекает внутреннюю область параболы). Величина
где M(x, y) – произвольная точка параболы, называется фокальным радиусом, прямая D: x = –p/2 – директрисой (она не пересекает внутреннюю область параболы). Величина 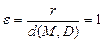 называется эксцентриситетомпараболы.
называется эксцентриситетомпараболы.
Основное характеристическое свойство параболы: все точки параболы равноудалены от директрисы и фокуса (рис. 9.15).
Существуют иные формы канонического уравнения параболы, которые определяют другие направления ее ветвей в системе координат (рис. 9.16):
а) 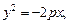 б)
б) 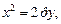 в)
в) 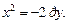

Для параметрического задания параболы в качестве параметра t может быть взята величина ординаты точки параболы:
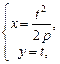
где t – произвольное действительное число.
Пример 1.Определить параметры и форму параболы по ее каноническому уравнению:
1) 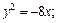 2)
2) 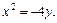
Решение.1) Уравнение y 2 = –8x определяет параболу с вершиной в точке О(0; 0), симметричную относительно оси Оx. Ее ветви направлены влево. Сравнивая данное уравнение с уравнением y 2 = –2px, находим: 2p = 8, p = 4, p/2 = 2. Следовательно, фокус находится в точке F(–2; 0), уравнение директрисы D: x = 2 (рис. 9.17).
2) Уравнение x 2 = –4y задает параболу с вершиной в точке O(0; 0), симметричную относительно оси Oy. Ее ветви направлены вниз. Сравнивая данное уравнение с уравнением x 2 = –2py, находим: 2p = 4, p = 2, p/2 = 1. Следовательно, фокус находится в точке F(0; –1), уравнение директрисы D: y = 1 (рис. 9.18).

Пример 2.Определить параметры и вид кривой x 2 + 8x – 16y – 32 = 0. Сделать рисунок.
Решение. Преобразуем левую часть уравнения, используя метод выделения полного квадрата:
(x + 4) 2 – 16 – 16y – 32 = 0;
В результате получим:
Это каноническое уравнение параболы с вершиной в точке (–4; –3), параметром p = 8, ветвями, направленными вверх 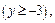 осью x = –4. Фокус находится в точке F(–4; –3 + p/2), т. е. F(–4; 1) Директриса D задается уравнением y = –3 – p/2 или y = –7 (рис. 9.19).
осью x = –4. Фокус находится в точке F(–4; –3 + p/2), т. е. F(–4; 1) Директриса D задается уравнением y = –3 – p/2 или y = –7 (рис. 9.19).
Пример 3. Написать уравнение кривой, все точки которой равноудалены от прямой y = –3 и точки F(0; 3).
Решение. Точка F(0; 3) лежит на оси Oy и находится с прямой y = –3 по разные стороны от начала координат, причем на одинаковом расстоянии (d = 3). Это позволяет заключить, что искомой кривой является парабола x 2 = 2py с параметром p = 2 × 3 = 6, т. е. x 2 = 12y (рис. 9.20).
Пример 4.Составить уравнение параболы с вершиной в точке V(3; –2) и фокусом в точке F(1; –2).
Решение. Вершина и фокус данной параболы лежат на прямой, параллельной оси Ox (одинаковые ординаты), ветви параболы направлены влево (абсцисса фокуса меньше абсциссы вершины), расстояние от фокуса до вершины равно p/2 = 3 – 1 = 2, p = 4. Следовательно, искомое уравнение
Дата добавления: 2015-09-29 ; просмотров: 8117 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Квадратичная функция. Построение параболы

О чем эта статья:
8 класс, 9 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ: наглядно.
- Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
График функции — это объединение всех точек, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.
Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.
Построение квадратичной функции
Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:
- a — старший коэффициент, который отвечает за ширину параболы. Большое значение a — парабола узкая, небольшое — парабола широкая.
- b — второй коэффициент, который отвечает за смещение параболы от центра координат.
- с — свободный член, который соответствует координате пересечения параболы с осью ординат.
График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 :
Точки, обозначенные зелеными кружками называют базовыми точками. Чтобы найти их координаты для функции y = x 2 , нужно составить таблицу:
x
y
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов.
График функции y = –x 2 выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
x
y
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:
- Если старший коэффициент больше нуля a > 0, то ветви параболы напрaвлены вверх.
- Если старший коэффициент меньше нуля a 2 + bx + c, для построения которой нужно решить квадратное уравнение ax 2 + bx + c = 0. В процессе найдем дискриминант D = b 2 – 4ac, который даст нам информацию о количестве корней квадратного уравнения.
Рассмотрим три случая:
- Если D 0,то график выглядит так:
- Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
- Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:
Если a > 0, то график выглядит как-то так:
0″ height=”671″ src=”https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=”602″>
На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:

Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.
Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.
Разберем общий алгоритм на примере y = 2x 2 + 3x – 5.
Как строим:
- Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
- Найдем дискриминант квадратного трехчлена 2x 2 + 3x – 5.
D = b 2 – 4ac = 9 – 4 * 2 * (-5) = 49 > 0
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
2x 2 + 3x – 5 = 0 2 + 3x – 5 = 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAPoAAAAyCAYAAAB1V8bkAAAJyElEQVR4Ae2c16sUwRLGfdRX/wXFB30QFFQUQUyIKCIGBEEQzCCoKIgB01ExZwVz4JpzztljwJxzzjlnrcuvL33unD2zOzO7OzvuThU0u5N6uuvrr7u6unrKiYpqQDVQ8BooV/A11AqqBlQDokTXRqAaiIEGlOgxAFmrqBpQomsbUA3EQANK9BiArFVUDSjRtQ2oBmKgASV6DEDWKqoGlOjaBlQDMdBAQRH9z58/8vv3b5P+/v2bMXy/fv0S8kxMGWesGRgNpIMXz7jhkg28CxmWgiH69+/f5dSpU7JixQpZtmyZXLx4UX7+/JkUOxoGjSaVTJw4UVatWiUbNmwoSYcPH071iF7zqYGgeNlsT58+LZMnTy7BA2y2bNkib9++tbfor4sGCobogD19+nR5/fq1nDx5Upo0aSLHjh2TZD39x48f5ebNmy4q+d8pRo327dtLo0aNTF6NGzeWevXqCeRXyVwDQfHijXTMmzZtMjiAL6lu3brSuXNnuXfvXuaFKuAcCobojOQDBgwwgD948EAg5ubNm42Z54bfjRs3ZMqUKW6XzDk6jP379wsjD/LmzRtZt26dvHr1KukzesG/BoLiRc5gceXKFZM4/vbtmxw6dEguXbokP3788P/yGN5ZMET/8uWLvHv3Tt6/f2/Muh49esj169eTQupF9MQHIfm1a9cST+txmhoIipfba86fPy9Hjx4VrDOV1BooGKJTTYh++fJlGTt2rCxevNgcJ6t+EKIz3587d26yrPR8mhoIglfiK549e2Y6dHBU8dZA3hH9+PHjYhNmnFO+fv1qTOwDBw5Ily5dhF+nQ47ndu/ebdLChQule/fuJcecp9E477d5d+zYUW7fvm0P9TeABixW/AbBCz+LffbChQtl3rh69WpZsmSJjuZlNON+Iu+IDkGZW+N427Ztm6nVp0+f5MiRI6Zh2Dl1hw4dZOjQoaVGdebc1oM+a9Ys48Sxx/y6zfUePnwoVapUcdeenvXUQLp4LV261OA8bdo0g5nzRR8+fJBhw4YJeav400DeEf3Ro0dmZGD+/fLlS1NLzLjhw4fLmDFjhEaA4DHv16+fGeHdVOHXdKczqVy5slsWes6HBtLF6/HjxwZn/CLPnz8v9aZbt25Jt27dlOiltJL6IO+I7lYdTPY1a9bIjBkz5M6dO7Jjxw5hRN++fXtSb6xfos+ZM0cqVark9trQzrEmXFxc7LnOH1oBQs44HbycRTpz5oy0a9funyA6DkGW/NavX19mauIsc+J/OkCmJliRL168ME7FVM7jxOeDHhcE0ak05KD3P3v2rFkWO3HihHz+/DmpPlh3XbRoUdLr9gL5LF++3B6G+nv//n3ZuHGjDBw4UDp16pS0kwq1EDnKPChezmI9efJEtm7dmnJVxXl/WP8PHjxopoxXr141RG3Tpo0JsPLzPqaaLVq0kDp16kjDhg2lb9++JgbEz7Pp3FMwRKfyBLkwX2fpxivqjbm8Nf1TKY77WK/NhVBuGvGoUaNMHID1N+Ti3VG8IwhezvIR5gwm/EYlrBgMGTJE9u3bZxy4YDV69Gjf/py9e/fKypUrjSVKLEDYqwcFRfSoQM/2e2fOnGmivgqd6NnWWy7zI3CqefPmUlRUVOIXgrzly5cXfEZewr2Y/XTuyaI3vfIIcj1tolM4lpyIBZ83b56MGzdO9uzZY0YjwkSfPn0apBx6r0MDYRBd8XIoOAt/sRiZU0N4az2OHz9eKlSo4MvSgOgs6RKIBYdIYUraRMfsYpkL84m5cc+ePY1DYv78+dKnTx/B2eAlmKldu3b1TISy5luII8s/XnWbNGmSMC9PlDCIrniJcXB6YcJ15s9+JHEkrlq1qixYsMDPowLRcRqzSgSHiOkI0xeUNtHpxXBUIQQ3tGrVKnLniC8N58FNYRBd8QoOPES2Php8Agw2dvR25gZRcaaNHDnSeTrlf/JxdhTsuMQacJ5LmUHAi2kT3b6HyrNBoXXr1uYUBXVThr3f+YuCcGp4JZRsFYAV8K8lt1hremqveuE4RAeJEgbR7Tvigpfb1JG6e2HCde5DCJbCM16rVi2T2D9BiLVT6Agwv3GsgSXPumHqfAZ+sLqCNWfbNQ455ve8MwxJm+gsXeF0YFcXPRlRaAiebD/OCO5l/XDQoEGeCTPHhqZWq1ZN/rVElF2iTJ061bNemHkEhiRKGESPG141atRIVKtZevXT3tjz7kcYgIioZDRmtyM6Zk09sf0zbYIndkBgabFt27ZmeZeYAgQzvmLFimWe9VMOP/ekTXTWMXv37m16uF69esmECRNMZdgDzgcgVIJrwLm8Vr9+fSECjM4wG6J4ZUOL/8+DgQdSwwGccIRkk4jITBRGaZZM8V/ZlRRGdIJlwJzBsX///gKPwpK0iY7HkArSgKgwu8XYMnju3LmkgSr0ZNZUCatCfvLFtKIHtj2sn2dycY8NmCGcF6cQIwXx+dmQfMMLfEj/qjA1Yx29ZcuWpRLmfaLcvXtXBg8eLCNGjChxUoM1mBAdt3btWmP9ZatTT3w/x2kTHcKytAB5EeYmyYiDecpWz9mzZyf9EIRb4cI6Rw/KikGcLI98w4vlWkKYC0Uw5xkEMeGt4A/Akc28P+wBMG2i28L6+WV7IruRmjVrVmK6+HkujHuYL+3atcuUhbm/SlkNRI0Xn/iqWbOmaTNlS5d/ZzDzITOhslFJTohO5Rg98WDaOUoUFabXpBExV2JThBI9OQpR4YX1x3SQb/UxOBSCYO2yA48RPCqJFdGZmxN8w/q/Ej11k4uK6ERXMqflw4+FQvTUms7N1VgRnYgndq2RlOipG1gURCf2myhLpldNmzZVoqeGKNDV2BAdj+bOnTuNcpTo3m0k10THrCVohCAiRInujVGQO2JDdJYA8bQTpIJHt3bt2mZtk1FEpawGck10PrRB4BEf4QQjgqIIK2UbqErmGsgJ0fE2AmL16tWFj/oRwpprYcRgVCcR+URsPkELBCyolNZAFHgRVcZyrcWoQYMGwtd97KfBSpdQj4JqICdEZ3kBkwwQIZZXLHDQSvi9H687G/wJgyREkl+7McdvHnG4L0q8WG9mUOCDnASf4DxVyVwDOSF65sXMXg6QnYbMMh+/fjfgZK8EmlMqDYAPzji7WyyqQSFVGfPxWuyIno8gaZlVA5lqQImeqQb1edVAHmhAiZ4HIGkRVQOZakCJnqkGI3m+WIrKlZOi45G8XF+ahxpQouchaKbIx4uU6PmKXQTlVqJHoPTMX/lM/tOuSIozz0hziIkGlOgxAVqrGW8NKNHjjb/WPiYaUKLHBGitZrw1oESPN/5a+5hoQIkeE6C1mvHWwH8BSUfSiO3XWNEAAAAASUVORK5CYII=”>
- Координаты вершины параболы:
- Точка пересечения с осью OY находится: (0; -5) и ей симметричная.
- Нанести эти точки на координатную плоскость и построить график параболы:
2 + 3x – 5 = 0″ height=”671″ src=”https://lh6.googleusercontent.com/TYyA5dFfh0ZKINaPSps3Y_X1mCv8Mhv_8bNG3_dPbZud1AEsvo7UBFmVQNm1GcR1CQFo6HE1lNjYaAgepQUTQiK_ay_Fnuv7LEsB53woHkFO66W0R1PP8QfGsFcYzaR_h4AJdLxC” width=”602″>
Уравнение квадратичной функции имеет вид y = a * (x – x₀) 2 + y₀
Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x 2 + 3x – 5 при а = 1, то второй коэффициент является четным числом.
Рассмотрим пример: y = 2 * (x – 1) 2 + 4.
Как строим:
- Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:
- построить y = x 2 ,
- умножить ординаты всех точек графика на 2,
- сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- сдвинуть его вдоль оси OY на 4 единицы вверх.
- Построить график параболы для каждого случая. 2 + y₀” height=”431″ src=”https://lh5.googleusercontent.com/_zgF-CXWf4Yy0p2OnBYSJkUm0zO-mNetq5feU6LIPEbIgSrO9kdr2ti_tr7Gg3yTMOlJVnuZgG0HleAFfAzG7yr7ELHT6KSMqMrRHkHqt-VcgIiSZx80cVj0zlPMBzEM0wAWQ-L6″ width=”602″>
Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
Рассмотрим следующий пример: y = (x − 2) × (x + 1).
Как строим:
Данный вид уравнения позволяет быстро найти нули функции:
(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.
Определим координаты вершины параболы:

Найти точку пересечения с осью OY:
с = ab = (−2) × (1) = −2 и ей симметричная.
Отметим эти точки на координатной плоскости и соединим плавной прямой.
Парабола
Вы будете перенаправлены на Автор24
Парабола — это кривая, образованная геометрическим множеством точек, равноудалённых от точки $F$, не лежащей на параболе, и прямой $d$, не проходящей через точку $F$.
Рисунок 1. Парабола в прямоугольной системе координат
Парабола наряду с окружностью, эллипсом и гиперболой является одним из сечений конуса.
Парабола симметрична относительно своей оси, и поэтому можно построить сначала одну половину параболы, а затем, отложив симметричные этой половине точки, уже другую.
Классическая парабола описывается уравнением, оно имеет следующий вид:
$y^2 = 2px$, где число $p$ должно быть больше нуля.
Это уравнение является каноническим уравнением параболы и описывает вид параболы в прямоугольной системе координат.
Чаще всего приходится иметь дело с уравнениями параболы с вершиной, располагающейся не на пересечении осей координат, их общий вид представлен формулой: $y = ax^2 + bx + c$.
Кто придумал параболу
Парабола известна математикам уже очень давно, а название этой функции дал древнегреческий математик Аполлоний Пергский в III в. до н.э., изучавший свойства сечений конуса.
Также изучением параболы занимались Архимед и Папп Александрийский.
В дальнейшем разные учёные показали, что многие явления можно описать параболой, так, например, была открыта траектория движения снаряда.
Основные определения и строение параболы
Вершина параболы — это точка, находящаяся на минимальном расстоянии от директрисы параболы $d$.
Готовые работы на аналогичную тему
Фокус $F$ параболы — это точка, через которую проходит ось симметрии параболы, перпендикулярная прямой, находящаяся на расстоянии $d$. Фокус расположен на расстоянии $frac
<2>$ от вершины. Координаты фокуса классической параболы можно определить из её уравнения.
Фокус и вершина являются основными точками, характеризующими параболу.
Параметр $p$ параболы иначе называется фокальным параметром и является расстоянием между фокусом и директрисой. Чтобы найти фокальный параметр параболы, нужно выразить $p$ из формулы канонического уравнения параболы:
$p = frac<2x>$, где $x$ и $y$ — координаты точки, лежащей на параболе. Координаты фокуса параболы определяются через значение фокального параметра и равны ($frac
<2>;0)$.
Анализ уравнения и описание параболы
Сначала необходимо обратить внимание на коэффициент $a$ при $x^2$. Если он отрицательный, то парабола перевёрнутая по отношению к обычной и её ветви смотрят вниз, а если положительный – то её ветви смотрят вверх. Также модуль коэффициента $a$ влияет на степень пологости (ширину) параболы, чем меньше модуль $a$, тем парабола более широкая (пологая), и чем больше модуль $a$, тем она более узкая (крутая).
Далее необходимо посмотреть на коэффициент $c$. Коэффициент $c$ обозначает смещение по оси $OY$ относительно пересечения осей координат. Это легко проверить, если приравнять $x$ к нулю в имеющемся уравнении. Если коэффициент $c$ – положительный, то парабола смещена вверх относительно точки $(0;0)$, а если отрицательный – то вниз. В случае если $c=0$ — парабола проходит через точку начала координат.
Теперь можно найти вершину параболы, её координаты вычисляются по формуле:
$x = – frac<2a>$ (1).
Чтобы найти $y$, нужно подставить полученный по формуле $x$ в уравнение.
Рассмотрим уравнение параболы $y = x^2 + 2x + 3$
Рисунок 2. Анализ уравнения параболы, график и примеры решения
- Коэффициент при $a$ положительный, значит, ветви параболы смотрят вверх.
- Теперь смотрим на коэффициент $c$, он равен 3, значит, парабола пересекается с осью ординат в точке $(0; 3)$.
- Найдём координату $x$ вершины параболы по формуле (1), она равна $x = – frac<2><2>= -1$. Теперь найдём значение $y$, подставив значение $x$ в уравнение: $y = 1^2 +(-1) cdot 2 + 3 = 2$. Координаты вершины равны $(-1; 2)$.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 04 12 2021
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/kvadratichnaya-funkciya-parabola
http://spravochnick.ru/matematika/parabola/
[/spoiler]
оксана николаевна кузнецова
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение 1
Парабола — это кривая, образованная геометрическим множеством точек, равноудалённых от точки $F$, не лежащей на параболе, и прямой $d$, не проходящей через точку $F$.
Рисунок 1. Парабола в прямоугольной системе координат
Парабола наряду с окружностью, эллипсом и гиперболой является одним из сечений конуса.
Парабола симметрична относительно своей оси, и поэтому можно построить сначала одну половину параболы, а затем, отложив симметричные этой половине точки, уже другую.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Определение 2
Классическая парабола описывается уравнением, оно имеет следующий вид:
$y^2 = 2px$, где число $p$ должно быть больше нуля.
Это уравнение является каноническим уравнением параболы и описывает вид параболы в прямоугольной системе координат.
Чаще всего приходится иметь дело с уравнениями параболы с вершиной, располагающейся не на пересечении осей координат, их общий вид представлен формулой:
$y = ax^2 + bx + c$.
Кто придумал параболу
Парабола известна математикам уже очень давно, а название этой функции дал древнегреческий математик Аполлоний Пергский в III в. до н.э., изучавший свойства сечений конуса.
Также изучением параболы занимались Архимед и Папп Александрийский.
В дальнейшем разные учёные показали, что многие явления можно описать параболой, так, например, была открыта траектория движения снаряда.
Основные определения и строение параболы
Вершина параболы — это точка, находящаяся на минимальном расстоянии от директрисы параболы $d$.
«Парабола» 👇
Фокус $F$ параболы — это точка, через которую проходит ось симметрии параболы, перпендикулярная прямой, находящаяся на расстоянии $d$. Фокус расположен на расстоянии $frac{p}{2}$ от вершины.
Координаты фокуса классической параболы можно определить из её уравнения.
Фокус и вершина являются основными точками, характеризующими параболу.
Параметр $p$ параболы иначе называется фокальным параметром и является расстоянием между фокусом и директрисой.
Чтобы найти фокальный параметр параболы, нужно выразить $p$ из формулы канонического уравнения параболы:
$p = frac{y^2}{2x}$, где $x$ и $y$ — координаты точки, лежащей на параболе.
Координаты фокуса параболы определяются через значение фокального параметра и равны ($frac{p}{2};0)$.
Анализ уравнения и описание параболы
-
Сначала необходимо обратить внимание на коэффициент $a$ при $x^2$. Если он отрицательный, то парабола перевёрнутая по отношению к обычной и её ветви смотрят вниз, а если положительный – то её ветви смотрят вверх.
Также модуль коэффициента $a$ влияет на степень пологости (ширину) параболы, чем меньше модуль $a$, тем парабола более широкая (пологая), и чем больше модуль $a$, тем она более узкая (крутая). -
Далее необходимо посмотреть на коэффициент $c$. Коэффициент $c$ обозначает смещение по оси $OY$ относительно пересечения осей координат.
Это легко проверить, если приравнять $x$ к нулю в имеющемся уравнении.
Если коэффициент $c$ – положительный, то парабола смещена вверх относительно точки $(0;0)$, а если отрицательный – то вниз.
В случае если $c=0$ — парабола проходит через точку начала координат. -
Теперь можно найти вершину параболы, её координаты вычисляются по формуле:
-
$x = – frac{b}{2a}$ (1).
Чтобы найти $y$, нужно подставить полученный по формуле $x$ в уравнение.
Пример 1
Рассмотрим уравнение параболы $y = x^2 + 2x + 3$
Рисунок 2. Анализ уравнения параболы, график и примеры решения
- Коэффициент при $a$ положительный, значит, ветви параболы смотрят вверх.
- Теперь смотрим на коэффициент $c$, он равен 3, значит, парабола пересекается с осью ординат в точке $(0; 3)$.
- Найдём координату $x$ вершины параболы по формуле (1), она равна $x = – frac{2}{2} = -1$. Теперь найдём значение $y$, подставив значение $x$ в уравнение:
$y = 1^2 +(-1) cdot 2 + 3 = 2$. Координаты вершины равны $(-1; 2)$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Парабола — это график функции описанный определённой формулой. Чтобы построить параболу нужно следовать формуле, определениям и уравнениям.
Парабола
Парабола – это множество точек плоскости, которые равноотделённые от заданной точки, что называется фокусом и заданной прямой под названием директриса.
Чтобы получить каноническое уравнение параболы, расположим директрису перпендикулярно оси , а фокус
на оси
так, чтобы начало координат
помещался на одинаковом расстоянии от них (см. рис. 1). Обозначим через
расстояние от фокуса к директрисе, тогда у фокуса будут координаты
,
.
Для произвольной точки параболы расстояний
, а расстояние к директрисе
. По определению
из рис. 1 видим, что
, а
и поэтому:
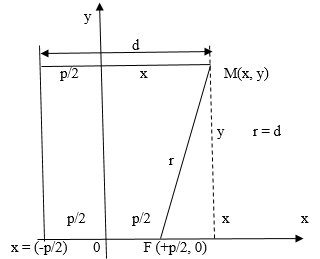
Рис. 1
(1)
– каноническое уравнение параболы.
Нужна помощь в написании работы?

Мы – биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Цена работы
Что такое вершина параболы
Вершина параболы – это парабола, которая проходит через точки . Если точка
принадлежит параболе, то и
тоже принадлежит параболе, так как из:
.
Значит, парабола симметрична относительно оси , её график достаточно построить в первой четверти, где из канонического уравнения параболы получается, что:
Чтобы найти вершину параболы, необходимо знать формулу: .
Давайте посмотрим, как данная формула действует, допустим дано уравнение:
Тогда:
,
,
. Чтобы найти величины
,
и
, в квадратном уравнении коэффициент при
, при
, постоянная (коэффициент без переменной) =
. Если взять тот же пример,
, получается, что:
,
,
.
Форма и характеристики параболы
Исследуем за каноническим уравнением форму и расположение параболы:
1. В уравнении переменная входит в парной степени откуда получается, что парабола симметрична относительно оси
. Ось
– это ось, которая симметрична параболе.
2. Так как , тогда
, откуда получается, что парабола расположена справа от оси
.
3. При мы имеем
, то есть парабола проходит через начало координат. Точка
– это вершина параболы.
4. При увеличении значений переменной модуль
тоже возрастает. Изобразим параболу на рисунке:
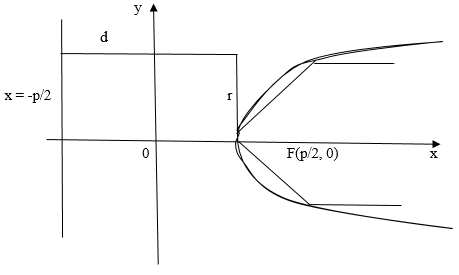
Рис. 2
5. В полярной системе координат, у канонического уравнения параболы такой вид:
6. Уравнение ,
,
, тоже описывают параболы:
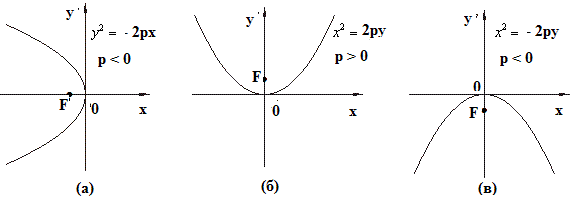
Рис. 3
Оптическое свойство параболы
У параболы “оптическое” свойство, если: в фокусе параболы поместить источник света, тогда отбитые от параболы лучи будут параллельными оси . Это свойство учитывают при изготовлении прожекторов, зеркальных телескопов, теле- и радио антенн.
При положительном уравнении:
описывают параболу симметричную относительно с вершиной в точке
, ветви которой направлены влево (рис. 3 (а)).
Аналогично изложенному, уравнение и
описывают параболы с вершиной в точке
симметрично относительно
, ветви которой направлены соответственно вверх и вниз (см. рис. 3 (б) и (в)). Если например, уравнение
решить относительно
и обозначить
, тогда получим известное со школьного курса уравнение параболы
. Теперь её фокусное расстояние
.
Примеры решения
Задача
Найти координаты фокуса и составить уравнение директрисы параболы .
Решение
Сравнивая каноническое уравнение и данное
, получим
,
, тогда
. Так как уравнение директрисы
, тогда в данном случае
.
Ответ
координаты фокуса: , а уравнение директрисы параболы:
.
Задача
Составить каноническое уравнение параболы:
а) с фокусом в точке ;
б) с фокусом в точке .
Решение
а). Так как фокус на положительной полуоси
, тогда парабола симметрична относительно
с вершиной в точке
и
, поэтому
и согласно формуле (1)
.
б). Фокус лежит на отрицательной полуоси
с вершиной в точке
, ветви направлены вниз, каноническое уравнение следует искать в виде
. Фокусное расстояние параболы
и уравнение запишется
.
Ответ
а) каноническое уравнение параболы с фокусом в точке :
;
б) каноническое уравнение с фокусом в точке :
.
Задача
Показать путём выделения полного квадрата, что уравнение – это уравнение параболы. Привести его к каноническому виду. Найти вершину, фокус, ось и директрису этой параболы.
Решение
Выделим относительно переменной полный квадрат
=
=
=
=
=
=
.
Обозначим ,
. Тогда в результате параллельного переноса координатных осей в новое начало, то есть в точку
, получим каноническое уравнение параболы
.
Ветви этой параболы направлены вниз симметрично относительно оси ,
,
– фокусное расстояние. В новой системе координат фокус находится в точке
, уравнение директрисы в новой системе
.
Повернёмся к старым координатам при помощи замены ,
. Уравнение оси в новой системе
, а в старой
– уравнение оси параболы.
Уравнение директрисы в новой системе координат , а в старой
.
В новой системе для фокуса
,
, а в старой системе
,
, то есть
.
Ответ
Каноническое уравнение параболы – ;
вершина – ветви параболы направлены вниз;
,
,
– фокусное расстояние, а фокус находится в точке
;
уравнение оси ;
уравнение директрисы .
вершина которой находится в начале координат,
зная, что:
расположена в правой полуплоскости, симметрично
относительно оси Ох и ее параметр р=3;
расположена в левой полуплоскости симетрично
относительно оси Ох и ее параметр р=0,5.
расположена в верхней полуплоскости симметрично
относительно оси Оу и ее параметр р=1/4.
расположена в нижней полуплоскости симметрично
оси Оу и ее параметр р=3.
величину параметра и расположение относительно
координатных осей следующих парабол:
уравнение параболы, вершина которой находится в
начале координат, зная, что:
расположена симметрично относительно оси Ох и
проходит через точку А(9; 6);
расположена симметрично относительно оси Ох и
проходит через точку В(-1; 3);
расположена симметрично относительно оси Оу и
проходит через точку С(1; 1);
расположена симметрично относительно оси Оу и
проходит через точку D(4; -8).
подвешен за два конца; точки крепления
расположены на одинаковой высоте; расстояние
между ними равно 20 см. Величина его прогиба на
расстоянии 2 м от точки крепления, считая по
горизонтали, равна 14,4 см. Определить величину
прогиба этого троса в середине между точками
крепления, приближенно считая, что трос имеет
форму дуги параболы.
уравнение параболы, которая имеет фокус Е(0; -3) и
проходит через начало координат, зная, что ее
осью служит ось Оу.
линии определяются следующими уравнениями.
Изобразить эти линии на чертеже.
уравнение директрисы параболы
фокальный радиус точки М параболы
абсцисса точки М равна 7.
фокальный радиус точки М параболы
ордината точки М равна 6.
которых равен 13.
уравнение параболы, если дан фокус F(-7; 0) и
уравнение директрисы
уравнение параболы, зная, что ее вершина
совпадает с точкой (
Ох и парабола простирается в бесконечность:
направлении оси Ох;
направлении оси Ох.
уравнение параболы, зная, что ее вершина
совпадает с точкой (
Оу и парабола простирается в бесконечность:
направлении оси Оу (т.е. парабола является
восходящей);
направлении оси Оу (т.е. парабола являетя
нисходящей).
каждое из следующих уравнений определяет
параболу, и найти ее вершины А, величину
параметра р и уравнение директрисы:
каждое из следующих уравнений определяет
параболу, и найти координаты ее вершины А и
величину параметра р:
каждое из следующих уравнений определяет
параболу, и найти ее вершины А и величину
параметра р:
линии определяются следующими уравнениями:
уравнение параболы, если даны ее фокус F(4; 3) и
директриса
уравнение параболы, если даны ее фокус F(4; 3) и
директриса
уравнение параболы, если даны ее фокус F(2; -1) и
директриса
параболы А(6; -3) и уравнение ее директрисы
параболы А(-2; -1) и уравнение е директрисы
пересечения прямой
пересечения прямой
пересечения прямой
определить, как расположена данная прямая
относительно данной параболы – пересекает ли,
касается или проходит вне ее:
каких значениях углового коэффициента k прямая
параболу
параболы.
при котором прямая
параболе
только одну касательную с угловым коэффициентом
уравнение касательной к параболе
точке М1(x1; y1).
уравнение прямой, которая касается параболы
уравнение прямой, которая касается параболы
касательную к параболе
прямой
касательной и данной прямой.
вычислить расстояние d от точки М1 до этой прямой.
уравнения касательных к параболе
из точки А(2; 9).
вершина этой параболы лежит посередине между
точкой пересечения касательной с осью Ох и
проекцией точки касания на ось Ох.
проведены касательные к параболе
уравнение хорды, соединяющей точки касания.
проведены касательные к параболе
расстояние d от точки Р до хорды параболы,
соединяющей точки касания.
пересечения эллипса
параболы
пересечения гиперболы
параболы
пересечения парабол
прямая, касающаяся параболы в некоторой точке М,
составляет равные углы с фокальным радиусом
точки М и с лучом, который, исходя из М, идет
параллельно оси параболы в ту сторону, куда
парабола бесконечно простирается.
Ох направлен луч света. Известно, что
до параболы, луч от нее отразился. Составить
уравнение прямой, на которой лежит отраженный
луч.
параболы, имеющую общую ось и общий фокус,
расположенный между ее вершинами, пересекаются
под прямым углом.
две параболы со взаимно перпендикулярными осями
пересекаются в четырех точках, то эти точки лежат
на одной окружности.



