Как найти параметр ребра

Как найти параметр ребра

Для
определения истинных размеров ребер
многогранников и углов наклона ребер
к плоскости проекций можно воспользоваться
тремя способами:

  • способом
    прямоугольного треугольника;

  • способом
    перемены плоскостей проекции;

  • способом
    вращения вокруг оси, перпендикулярной
    к плоскости

проекции.

Рассмотрим
применение данных способов на примере
определения натуральных величин ребер
и их углов наклона к плоскостям проекций
для треугольной пирамиды SABC
(рис. 6а).

Основание
АВС
пирамиды лежит в горизонтальной плоскости
уровня. Поэтому его стороны па П1
проецируются в натуральную величину.
Ребра SА, SB,
SC пирамиды
относительно плоскостей проекций
изображены с искажением, так как это
отрезки прямых общего положения.
Определим натуральные величины ребер
и углы наклона этих ребер к плоскостям
проекций.

Способ
прямоугольного треугольника.

Для
установления зависимости между
натуральной величиной отрезка прямой
и его проекциями на комплексном чертеже
достаточно построить прямоугольный
треугольник, взяв за один его катет
горизонтальную (фронтальную, профильную)
проекцию отрезка, а за другой катет
разницу – расстояний концов отрезка
до горизонтальной (или соответственно
фронтальной, профильной) плоскости
проекций.

На
рис. 6а
показано определение натуральной
величины ребра SС
и его угла наклона к плоскости проекций
П1.
Приняв S1С1
за катет прямоугольного треугольника,
и восстановив из точки S1
перпендикуляр S1S0,
равный по величине разности ZS
– ZC
=
Z
(разницу
замеряем на фронтальной проекции),
получим на горизонтальной плоскости
проекций прямоугольный
S1C1S0.
Гипотенуза этого треугольника равна
натуральной величине ребра SC,
а угол, образованный гипотенузой C1S
0 с катетом
S1C1
– 
натуральная величина угла наклона ребра
SC
к плоскости проекций П1.

а)
б)

Рис.6


Способ перемены
плоскостей проекций.

Особенностью
способа перемены плоскостей проекций,
является переход от одной системы
(старой), в которой заданы проекции
объекта, к новой системе взаимно-перпендикулярных
плоскостей, выбранных определенным
образом.

Например,
для определения натуральной величины
ребра SА
пирамиды SABC
(рис. 6б) новая плоскость проекций П4
должна быть расположена параллельно
ему (П4
||
SА)
и перпендикулярно плоскости проекций
П1
(П4

П1).
Новая ось проекций Х14
располагается параллельно проекции S1
А1.
Затем через проекции А1
и S1
точек А
и S
проводим новые линии связи и откладываем
на них высоты точек А
и S
(ZА,
ZS),
строим новые проекции А4
и S4.
Соединим эти точки, получим новую
проекцию ребра А4S4,
которое в новой системе плоскостей
проекции (П1
/ П4)
стало линией уровня. Следовательно,
проекция ребра А4S4
равна
натуральной величине ребра АS,
а угол 
равен углу наклона ребра к плоскости
проекций П1.

Для
определения натуральной величины ребра
SА
пирамиды SABC
(рис. 6б) может быть применена новая
плоскость проекций П5.
Плоскость проекций П5
должна
быть расположена параллельно SА
(П5
||
SА)
и перпендикулярно плоскости проекций
П2
(П5

П2).
Новая ось проекций Х25
располагается параллельно проекции
S2А2.
Далее построения выполняются аналогично,
рассмотренным выше.

Способ
вращения вокруг оси, перпендикулярной
к плоскости проекций.

Способ
вращения нагляден и в ряде случаев
наиболее удобен для определения
натуральных величин отрезков и углов
наклона прямой к плоскости. Отрезок
проецируется без искажения, если в
результате перемещения он станет
параллельным какой-либо из плоскостей
проекций. При этом вращение отрезка
должно осуществляться таким образом,
чтобы угол наклона прямой к одной из
плоскостей проекций не изменялся.
Последнее требование вынуждает вращать
отрезок вокруг осей, перпендикулярных
к плоскостям проекций.

Пусть,
например, требуется определить натуральную
величину ребра SА
пирамиды SABC
(рис. 6а).

Сокращая
количество построений, проведем ось
i(i1,i2)
через один из концов ребра – через точку
S.
Из точки S1
радиусом S1А1
описываем дугу окружности до пересечения
с прямой, проведенной из точки S1
параллельно оси Х12
. Точка пересечения А1
– новая
горизонтальная проекция точки А.
Фронтальную проекцию А1
точки А
находим, проведя вертикальную линию
связи из точки
до пересечения с прямой, проведенной
из точки А2
параллельно оси Х12.
Соединив точки А2
и S2
на плоскости П2,
получим натуральную величину длины
S2А2
ребра SА,
а угол 
есть угол наклона ребра к плоскости П2.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Взвешенные графы

В классических графах все рёбра считаются равноценными и длина пути
соответствует количеству рёбер, которые он содержит. Однако часто
в задаче каждому ребру соответствует некоторый параметр – длина
ребра или стоимость прохождения по нему. В терминологии графов такой
параметр называется весом ребра, а граф, содержащий взвешенные
рёбра, взвешенным.

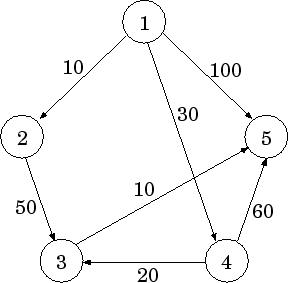
Взвешенный граф

Типичная задача для таких графов – поиск кратчайшего пути. Например,
в этом графе кратчайший путь между вершинами (1) и (5): (1 – 4 – 3 – 5), так
как его вес равен (30 + 20 + 10 = 60), а вес ребра (1 – 5) равен (100).

Алгоритм Дейкстры

Классический алгоритм для поиска кратчайших путей во взвешенном графе –
алгоритм Дейкстры (по имени автора Эдгара Дейкстры). Он позволяет найти
кратчайший путь от одной вершины графа до всех остальных за (O(M log N))
((N, M) – количество вершин и рёбер соответственно).

Принцип работы алгоритма напоминает принцип работы BFS: на каждом шаге
обрабатывается ближайшая ещё не обработанная вершина (расстояние до неё
уже известно). При её обработке все ещё не посещённые соседи добавляются
в очередь для посещения (расстояние до каждой из них рассчитывается как
расстояние до текущей вершины + длина ребра). Главное отличие от BFS
заключается в том, что вместо классической очереди используется очередь с
приоритетом. Она позволяет нам выбирать ближайшую вершину за (O(log N)).

Анимация выполнения алгоритма Дейкстры для поиска кратчайшего пути из вершины
(a) в вершину (b):

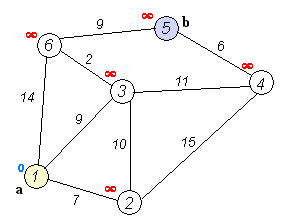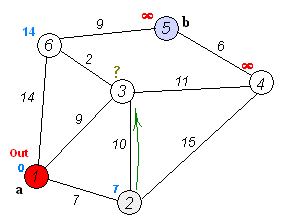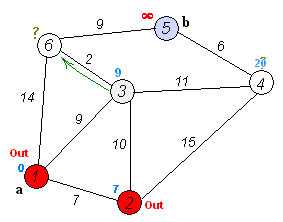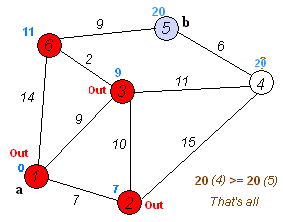
Анимация алгоритма Дейкстры

С помощью псевдокода алгоритм Дейкстры описывается следующим образом:

ans = массив расстояний от начальной вершины до каждой.
      изначально заполнен бесконечностями (ещё не достигнута).

ans[start] = 0

q = очередь с приоритетом, хранящая пары (v, dst),
    где dst - предполагаемое расстояние до v

добавить (start, 0) в q

пока q не пуста:
    (v, dst) = первая вершина в очереди (с минимальным расстоянием), и расстояние до неё
    извлечь (v, dst) из очереди

    если ans[v] < dst:   //мы уже обработали эту вершину, используя другой путь
        перейти к следующей вершине

    для каждой v -> u:
        n_dst = dst + len(v -> u)   //расстояние до u при прохождении через v
        если n_dst < ans[u]:        //если мы можем улучшить ответ
            ans[u] = n_dst
            добавить (u, n_dst) в q

Как видите, в очереди с приоритетом хранится не только номер вершины, но
и вычисленное расстояние до неё, по которому и ведётся сортировка. Также
возможна ситуация, при которой одна и та же вершина будет помещена в очередь
несколько раз с разным расстоянием (так как она достижима по нескольким рёбрам).
В такой ситуации обрабатываем её только один раз (с минимальным возможным
расстоянием).

Реализация

В нашей очереди с приоритетом должны храниться пары (вершина, расстояние до неё),
причём отсортированы они должны быть по уменьшению расстояния. Для этого нужно
использовать тип
std::priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>>:
первым элементом пары будет расстояние, а вторым – номер вершины.

Для хранения взвешенного графа в виде списка смежности для каждой вершины мы
храним вектор пар (соседняя вершина, длина ребра до неё).

Реализация на C++:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47





#include <bits/stdc++.h>

using namespace std;

const int INF = 1e9 + 7;

vector<pair<int, int>> graph[100000];
int ans[100000];

int main() {
    //Ввод графа и вершины start.

    for (int i = 0; i < n; i++) {
        ans[i] = INF;
    }

    ans[start] = 0;

    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;

    q.push({0, start});

    while (!q.empty()) {
        pair<int, int> c = q.top();
        q.pop();

        int dst = c.first, v = c.second;

        if (ans[v] < dst) {
            continue;
        }

        for (pair<int, int> e: graph[v]) {
            int u = e.first, len_vu = e.second;

            int n_dst = dst + len_vu;
            if (n_dst < ans[u]) {
                ans[u] = n_dst;
                q.push({n_dst, u});
            }
        }
    }

    for (int i = 0; i < n; i++) {
        cout << "Shortest path from " << start + 1 << " to " << i + 1 << " has length " << ans[i] << endl;
    }
}











Реализация с восстановлением пути


Восстановление пути для алгоритма Дейкстры реализуется точно так же, как и для

BFS: при успешном улучшении пути в вершину (u) через вершину (v), мы запоминаем,

что (prev[v] = u). После окончания работы алгоритма используем массив (prev) для

восстановления пути в обратном направлении.


Реализация на C++:


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64





#include <bits/stdc++.h>

using namespace std;

const int INF = 1e9 + 7;

vector<pair<int, int>> graph[100000];
int ans[100000];
int pr[100000];     //prev

int main() {
    //Ввод графа и вершин start и end.

    for (int i = 0; i < n; i++) {
        ans[i] = INF;
        pr[i] = -1;   //Значение, обозначающее что из этой вершины возвращаться некуда
    }

    ans[start] = 0;

    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;

    q.push({0, start});

    while (!q.empty()) {
        pair<int, int> c = q.top();
        q.pop();

        int dst = c.first, v = c.second;

        if (ans[v] < dst) {
            continue;
        }

        for (pair<int, int> e: graph[v]) {
            int u = e.first, len_vu = e.second;

            int n_dst = dst + len_vu;
            if (n_dst < ans[u]) {
                ans[u] = n_dst;
                pr[u] = v;
                q.push({n_dst, u});
            }
        }
    }

    vector<int> path;

    int cur = end;
    path.push_back(cur);

    while (pr[cur] != -1) {
        cur = pr[cur];
        path.push_back(cur);
    }

    reverse(path.begin(), path.end());

    cout << "Shortest path between vertices " << start + 1 << " and " << end + 1 << " is: " << endl;

    for (int v: path) {
        cout << v + 1 << ", ";
    }
}











Область применения алгоритма Дейкстры


Алгоритм Дейкстры является оптимальным для поиска пути практически в любых

графах, но он имеет одно ограничение. Алгоритм Дейкстры неприменим для графов,

содержащих рёбра с отрицательным весом. Для поиска кратчайшего пути в таких

графах обычно используют алгоритм Форда-Беллмана.
Источник

Что такое граф?

Граф — абстрактный математический объект, представляющий собой множество вершин графа и набор рёбер, то есть соединений между парами вершин. Вершиной графа могут быть города, а ребрами дорога между городами. Или, например, вершинами могут быть аккаунты в VK. А ребра между ними означает, что два аккаунта находятся в друзьях друг у друга.

Графы бывают разные. На этом семинаре нам важно, что они бывают:

  1. Ориентированные – ребро(дуга) позволяет добраться из вершины i в вершину j.
  2. Неориентированные – ребро позволяет добраться из вершины i в вершину j, и наоборот.

Способы задания графа:

  1. Матрица смежности
  2. Матрица инцидентности
  3. Список смежности
  4. Список рёбер

Нам понадобится только матрица смежности. Важно помнить, что для неориентированных графов она симметрична.

Матрицы в R

Давайте вспомним как пользоваться матрицами в R.

Способы задания матриц

Для этого нам понадобится функция ‘matrix’. У неё есть 3 главных аргумента:

  • data – то чем заполняем матрицу, это может быть число или массив.
  • nrow – количество строк в матрице.
  • ncol – количество столбцов в матрице.

Давайте попробуем создать матрицу, состоящую из 0 размером 3 на 4.

matrix(data = 0, nrow = 3, ncol = 4)
##      [,1] [,2] [,3] [,4]
## [1,]    0    0    0    0
## [2,]    0    0    0    0
## [3,]    0    0    0    0

А теперь давайте попробуем заполнить матрицу с помощью массива.

matrix(data = 1:12, nrow = 3, ncol = 4)
##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12

Как видим массив заполнялся по столбцам, сначала первый, потом второй и так далее. Если вы хотите заполнить его построчно, то вы можете воспользоваться еще одним параметром byrow. Давайте попробуем.

matrix(data = 1:12, nrow = 3, ncol = 4, byrow = TRUE)
##      [,1] [,2] [,3] [,4]
## [1,]    1    2    3    4
## [2,]    5    6    7    8
## [3,]    9   10   11   12

Обращение к матрице и изменение ее значений

Матрица – это двумерный массив, поэтому обращаться к ней можно так же, но при этом нужно указывать уже 2 индекса(строка и столбец). Давайте зададим случайную матрицу 4 на 5 и найдем ее значение, которое находится в 3 строчке, 4 столбце.

(M <- matrix(sample(-100:100, 20), nrow = 4, ncol = 5))
##      [,1] [,2] [,3] [,4] [,5]
## [1,]    6  -80   26   90 -100
## [2,]   78   62  -43   69   44
## [3,]    1  -62  -18   89   56
## [4,]   -4  -79    9   49  -40
M[3,4]
## [1] 89

Также указав один индекс мы можем получить целую строчку или целый столбец.

M[3,]
## [1]   1 -62 -18  89  56
M[,4]
## [1] 90 69 89 49

Если мы хотим присвоить какое-то значение, то мы указываем какой элемент матрицы хотим поменять.Ставим знак присвоения и пишем новое значение. Давайте поменяем значение в 3 строчке,4 столбце матрицы M.

M[3,4] <- 25
print(M)
##      [,1] [,2] [,3] [,4] [,5]
## [1,]    6  -80   26   90 -100
## [2,]   78   62  -43   69   44
## [3,]    1  -62  -18   25   56
## [4,]   -4  -79    9   49  -40

Основные функции для работы с графами

При реализации алгоритмов нам нужно будет каждый раз создавать граф, добавлять и удалять ребра. Поэтому напишем готовые функции для этого.

Создание графа

Чтобы создать граф достаточно создать матрицу из нулей размера n на n.

newGraph <- function(n){
  G <- matrix(data = 0, nrow = n, ncol = n)
  return(G)
}

Давайте попробуем использовать функцию. Создадим граф из 6 вершин.

R <- newGraph(6)
print(R)
##      [,1] [,2] [,3] [,4] [,5] [,6]
## [1,]    0    0    0    0    0    0
## [2,]    0    0    0    0    0    0
## [3,]    0    0    0    0    0    0
## [4,]    0    0    0    0    0    0
## [5,]    0    0    0    0    0    0
## [6,]    0    0    0    0    0    0

Добавление ребра

Пустой граф нам не очень интересен, поэтому нужно заполнить его ребрами. Представим, что мы работаем с неориентированным графом и нам не важен вес. Чтобы добавить ребро, нужно знать в какой граф мы хотим это сделать, а также вершины между которыми будет ребро. На выходе у нас будет обновленная матрица.

addEdge <- function(G, i, j){
  G[i, j] <- 1
  G[j, i] <- 1
  return(G)
}

Добавим несколько ребер в наш граф R.

R <- addEdge(R, 1, 2)
R <- addEdge(R, 2, 5)

У ребер бывает вес, поэтому при добавлении ребра хотелось бы иметь параметр w, который отвечает за вес. Улучшим нашу функцию.

addEdge <- function(G, i, j, w = 1){
  G[i, j] <- w
  G[j, i] <- w
  return(G)
}

Если мы не хотим добавлять вес, то он будет по дефолту равен 1. Добавим еще ребер в граф R.

R <- addEdge(R, 1, 2, 10)
R <- addEdge(R, 2, 5)

Граф бывает ориентированный. В этом случае мы должны поменять только 1 значение, а не 2. Введем еще один бинарный параметр directed для обозначения типа графа. С помощью if можно удостовериться в типе графа и изменить либо 1, либо 2 значения.

addEdge <- function(G, i, j, w = 1, directed = FALSE){
  if(directed == FALSE){
    G[i, j] <- w
    G[j, i] <- w
  }else{
    G[i, j] <- w
  }
  return(G)
}

Давайте добавим в граф R ориентированое ребро из вершины 5 в вершину 6 с весом 19.

R <- addEdge(R, 5, 6, 19, directed = TRUE)
print(R)
##      [,1] [,2] [,3] [,4] [,5] [,6]
## [1,]    0   10    0    0    0    0
## [2,]   10    0    0    0    1    0
## [3,]    0    0    0    0    0    0
## [4,]    0    0    0    0    0    0
## [5,]    0    1    0    0    0   19
## [6,]    0    0    0    0    0    0

Наша функция почти идеальна, оптимизируем ее немного. Во – первых, вне зависимости от типа графа мы выполним операцию G[i, j] <- w. Поэтому вынесем ее за if. Когда if небольшой можно использовать функцию ifelse.

addEdge <- function(G, i, j, w = 1, directed = FALSE){
  G[i, j] <- w
  ifelse(directed == FALSE, G[j, i] <- w)
  return(G)
}

Удаление ребра

Удаление ребра эквивалентно добавлению ребра с весом 0. Поэтому можно взять код оттуда и удалить переменную w

removeEdge <- function(G, i, j, directed = FALSE){
  if(directed == FALSE){
    G[i, j] <- 0
    G[j, i] <- 0
  }else{
    G[i, j] <- 0
  }
  return(G)
}

Удалим в графе R недавно созданное ребро из вершины 5 в вершину 6.

R <- removeEdge(R, 5, 6)
print(R)
##      [,1] [,2] [,3] [,4] [,5] [,6]
## [1,]    0   10    0    0    0    0
## [2,]   10    0    0    0    1    0
## [3,]    0    0    0    0    0    0
## [4,]    0    0    0    0    0    0
## [5,]    0    1    0    0    0    0
## [6,]    0    0    0    0    0    0
Источник

Определение параметров элементарной кристаллической ячейки в виде параллелепипеда с параметрами длины рёбер a, b, c и с углами между рёбрами

α, β, γ

Постоя́нная решётки, или параметр решётки — размеры элементарной кристаллической ячейки кристалла. В общем случае элементарная ячейка представляет собой параллелепипед с различными длинами рёбер, обычно эти длины обозначают как a, b, c. Но в некоторых частных случаях кристаллической структуры дли́ны этих рёбер совпадают. Если к тому же выходящие из одной вершины рёбра равны и взаимно перпендикулярны, то такую структуру называют кубической. Структуру с двумя равными рёбрами, находящимися под углом 120 градусов, и третьим ребром, перпендикулярным им, называют гексагональной.

Принято считать что, параметры элементарной ячейки описываются 6 числами: 3 длинами рёбер и 3 углами между рёбрами, принадлежащими одной вершине параллелепипеда.

Например, элементарная ячейка алмаза — кубическая и имеет параметр решётки 0,357 нм при температуре 300 К.

В литературе обычно не приводят все шесть параметров решётки, только среднюю длину рёбер ячейки и тип решётки.

Размерность параметров решётки a, b, c в СИ — длина. Величину, ввиду малости, обычно приводят в нанометрах или ангстремах (1 Å = 0,1 нм).

Параметры решётки могут быть экспериментально определены методами рентгеноструктурного анализа (исторически первый метод, развитый в начале XX века) или, начиная с конца XX века, — атомно-силовой микроскопией. Параметр кристаллической решётки может использоваться в качестве природного эталона длины нанометрового диапазона.[1][2]

Объём элементарной ячейки[править | править код]

Объём элементарной ячейки можно вычислить, зная её параметры (длины и углы параллелепипеда). Если три смежных ребра ячейки представить в виде векторов, то объём ячейки V равен (с точностью до знака) тройному скалярному произведению этих векторов (т.е. скалярному произведению одного из векторов на векторное произведение двух других). В общем случае

{displaystyle V=abc{sqrt {1+2cos alpha cos beta cos gamma -cos ^{2}alpha -cos ^{2}beta -cos ^{2}gamma }}.}

Для моноклинных решёток α = γ = 90°, и формула упрощается до

{displaystyle V=abcsin beta .}

Для орторомбических, тетрагональных и кубических решёток угол β также равен 90°, поэтому[3]

{displaystyle V=abc.}

Для тригональных (ромбоэдрических) решёток α = β = γ ≠ 90°, а также a = b = c, поэтому

{displaystyle V=a^{3}{sqrt {1+2cos ^{3}alpha -3cos ^{2}alpha }}.}

Слоистые полупроводниковые гетероструктуры[править | править код]

Постоянство параметров решётки разнородных материалов позволяет получить слоистые, с толщиной слоёв в единицы нанометров сэндвичи разных полупроводников. Этот метод обеспечивает получение широкой запрещённой зоны во внутреннем слое полупроводника и используется при производстве высокоэффективных светодиодов и полупроводниковых лазеров.

Согласование параметров решётки[править | править код]

Параметры решётки важны при эпитаксиальном выращивании тонких монокристаллических слоёв другого материала на поверхности иного монокристалла — подложки. При значительной разнице параметров решётки материалов трудно получить монокристалличность и бездислокационность наращиваемого слоя. Например, в полупроводниковой технологии для выращивания эпитаксиальных слоёв монокристаллического кремния в качестве гетероподложки обычно используют сапфир (монокристалл оксида алюминия), так как оба имеют практически равные постоянные решётки, но с разным типом сингонии, у кремния — кубическая типа алмаза, у сапфира — тригональная.

Обыкновенно параметры решётки подложки и наращиваемого слоя выбирают так, чтобы обеспечить минимум напряжений в слое плёнки.

Другим способом согласования параметров решёток является метод формирования переходного слоя между плёнкой и подложкой, в котором параметр решётки изменяется плавно (например, через слой твёрдого раствора с постепенным замещением атомов вещества подложки атомами выращиваемой плёнки, так чтобы параметр решётки слоя твёрдого раствора у самой плёнки совпадал с этим параметром плёнки).

Например, слой фосфида индия-галлия с шириной запрещённой зоны 1,9 эВ может быть выращен на пластине арсенида галлия с помощью метода промежуточного слоя.

См. также[править | править код]

  • Триклинная сингония
  • Моноклинная сингония
  • Ромбическая сингония
  • Тетрагональная сингония
  • Кубическая сингония

Примечания[править | править код]

  1. ↑ R. V. Lapshin. Automatic lateral calibration of tunneling microscope scanners (англ.) // Review of Scientific Instruments  (англ.) (рус. : journal. — USA: AIP, 1998. — Vol. 69, no. 9. — P. 3268—3276. — ISSN 0034-6748. — doi:10.1063/1.1149091.
  2. ↑ R. V. Lapshin. Drift-insensitive distributed calibration of probe microscope scanner in nanometer range: Real mode (англ.) // Applied Surface Science : journal. — Netherlands: Elsevier B. V., 2019. — Vol. 470. — P. 1122—1129. — ISSN 0169-4332. — doi:10.1016/j.apsusc.2018.10.149.
  3. ↑ Dept. of Crystallography & Struc. Biol. CSIC. 4. Direct and reciprocal lattices (4 июня 2015). Дата обращения: 9 июня 2015. Архивировано 4 мая 2021 года.
Источник

Прямоугольный параллелепипед. Что это такое?

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Определение параллелепипеда

Начнем с того, что узнаем, что такое параллелепипед.

Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.

На рисунке два параллелограмма АВСD и A1B1C1D1. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA1, ВB1, CC1, DD1 параллельны друг другу. Образовавшаяся фигура — параллелепипед.

Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.

Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.

Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.

Параллелепипед — это:

Свойства параллелепипеда

Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.

Вот 4 свойства параллелепипеда, которые необходимо запомнить:

  1. Противолежащие грани параллелепипеда равны и параллельны друг другу.
  2. Все 4 диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
  3. Параллелепипед симметричен относительно середины его диагонали.
  4. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Подготовка к ЕГЭ по математике онлайн в школе Skysmart — отличный способ освежить знания и снять стресс перед экзаменом.

Прямой параллелепипед

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.

Свойства прямого параллелепипеда:

  1. Основания прямого параллелепипеда — одинаковые параллелограммы, лежащие в параллельных плоскостях.
  2. Боковые ребра прямого параллелепипеда равны, параллельны и перпендикулярны плоскостям оснований.
  3. Высота прямого параллелепипеда равна длине бокового ребра.
  4. Противолежащие боковые грани прямого параллелепипеда — равные прямоугольники.
  5. Диагонали прямого параллелепипеда точкой пересечения делятся пополам.

На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.

Формулы прямого параллелепипеда:

  • Площадь боковой поверхности прямого параллелепипеда
    Sб = Ро*h
    Ро — периметр основания
    h — высота
  • Площадь полной поверхности прямого параллелепипеда
    Sп = Sб+2Sо
    Sо — площадь основания
  • Объем прямого параллелепипеда
    V = Sо*h

Прямоугольный параллелепипед

Определение прямоугольного параллелепипеда:

Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.

Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.

Свойства прямоугольного параллелепипеда

Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.

  1. Прямоугольный параллелепипед содержит 6 граней. Все грани прямоугольного параллелепипеда — прямоугольники.
  2. Противолежащие грани параллелепипеда попарно параллельны и равны.
  3. Все углы прямоугольного параллелепипеда, состоящие из двух граней — 90°.
  4. Диагонали прямоугольного параллелепипеда равны.
  5. В прямоугольный параллелепипеде четыре диагонали, которые пересекаются в одной точке и делятся этой точкой пополам.
  6. Любая грань прямоугольного параллелепипеда может быть принята за основание.
  7. Если все ребра прямоугольного параллелепипеда равны, то такой параллелепипед является кубом.
  8. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

Формулы прямоугольного параллелепипеда:

  • Объем прямоугольного параллелепипеда
    V = a · b · h
    a — длина, b — ширина, h — высота
  • Площадь боковой поверхности
    Sбок = Pосн·c=2(a+b)·c
    Pосн — периметр основания, с — боковое ребро
  • Площадь поверхности
    Sп.п = 2(ab+bc+ac)

Диагонали прямоугольного параллелепипеда: теорема

Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.

Если есть теорема, нужно ее доказать. (с) Пифагор

Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.

Дан прямоугольный параллелепипед ABCDA1B1C1D1. Доказать теорему.

Доказательство теоремы:

Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.

Все грани прямоугольного параллелепипеда — прямоугольники.

ΔABD: ∠BAD = 90°, по теореме Пифагора

ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора

d² = d₁² + c² = a² + b² + c²

d² = a² + b² + c²

Доказанная теорема — пространственная теорема Пифагора.

Куб: определение, свойства и формулы

Кубом называется прямоугольный параллелепипед, все три измерения которого равны.

Каждая грань куба — это квадрат.

Свойства куба:

  1. В кубе 6 граней, каждая грань куба — квадрат.
  2. Противолежащие грани параллельны друг другу.
  3. Все углы куба, образованные двумя гранями, равны 90°.
  4. У куба четыре диагонали, которые пересекаются в центре куба и делятся пополам.
  5. Диагонали куба равны.
  6. Диагональ куба в √3 раз больше его ребра.
  7. Диагональ грани куба в √2 раза больше длины ребра.

Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.

Формулы куба:

  • Объем куба через длину ребра a
    V = a3
  • Площадь поверхности куба
    S = 6a2
  • Периметр куба
    P = 12a

Решение задач

Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.

Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.

Для наглядного решения обозначим измерения прямоугольного параллелепипеда: a – длина, b – ширина, c – высота. Тогда a = 10, b = 5, c = 8.

Так как в прямоугольном параллелепипеде всего по 4 — высота, ширина и длина, и все измерения равны между собой, то:
1) 4 * 10 = 40 (см) – сумма длин параллелепипеда;
2) 4 * 5 = 20 (см) – суммарное значение ширины параллелепипеда;
3) 4 * 8 = 32 (см) – сумма высот параллелепипеда;
4) 40 + 20 + 32 = 92 (см) – сумма длин всех ребер прямоугольного параллелепипеда.

Отсюда можно вывести формулу по нахождению суммы длин всех сторон ПП:
X = 4a + 4b + 4c (где X – сумма длин ребер).

Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.

Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.

Нужно найти длину ребра A1B1.

В фокусе внимания треугольник BDD1.
Угол D = 90°.

По теореме Пифагора:
BD1 2 = DD1 2 + BD 2
BD 2 = BD1 2 – DD1 2
BD 2 = 26 – 9 = 17
BD = √17
В треугольнике ADB угол А = 90°.
BD 2 = AD 2 + AB 2
AB 2 = BD 2 – AD 2 = (√17)2 — 4 2 = 1
A1B1 = AB = 1.

Задачка 3. Дан прямоугольный параллелепипед АВСDA1B1C1D1.

AB = 4
AD = 6
AA1= 5
Нужно найти отрезок BD1.

В треугольнике ADB угол A = 90°.

По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD1 угол D = 90°.
BD1 2 = 52 + 25 = 77
BD1 = √77.

Самопроверка

Теперь потренируйтесь самостоятельно — мы верим, что все получится!

Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.

Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.

Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.

Вычислите длину ребра AA1.

Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:

  • прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию;
  • параллелепипед называется прямоугольным, когда его боковые ребра перпендикулярны к основанию;
  • основание прямоугольного параллелепипеда — прямоугольник;
  • три измерения прямоугольного параллелепипеда: длина, ширина, высота;
  • диагональ параллелепипеда равна сумме квадратов его измерений.

Ребра параллелепипеда

Свойства

Прямоугольный параллелепипед строится на ребрах трех длин, расположенных под прямым углом друг к другу. Зная ребра параллелепипеда, можно найти все возможные параметры, характеризующие его. В первую очередь, каждая грань параллелепипеда представляет собой прямоугольник с двумя одинаковыми сторонами, периметр же всего объемного тела ищется как умноженная на четыре сумма всех сторон-ребер параллелепипеда. P=4(a+b+c)

Площадь прямоугольного параллелепипеда складывается из площадей всех его граней, то есть шести прямоугольников, попарно конгруэнтных. Площадь каждого прямоугольника равна произведению его сторон, поэтому чтобы найти площадь параллелепипеда, необходимо сложить эти произведения. S=2ab+2bc+2ac=2(ab+bc+ac)

Чтобы вычислить объем прямоугольного параллелепипеда, зная его ребро, нужно перемножить их между собой, так как объем любого прямого тела с двумя основаниями равен произведению площади основания на высоту тела, а в основании параллелепипеда находится прямоугольник, площадь которого также равна произведению – его сторон. V=abc

У прямоугольного параллелепипеда есть четыре диагонали – диагонали его боковых граней и основания, и диагональ самого параллелепипеда, проходящая через его внутреннее пространство. Все диагонали рассчитывается через прямоугольные треугольники по теореме Пифагора, где они являются гипотенузами. Для диагоналей боковых граней и основания катетами являются ребра параллелепипеда, а для четвертой диагонали, катеты представляют собой боковое ребро и диагональ основания. (рис. 22.1,22.2,22.3,22.4) d_1=√(a^2+c^2 ) d_2=√(a^2+b^2 ) d_3=√(b^2+c^2 ) d_4=√(a^2+〖d_3〗^2 )=√(a^2+b^2+c^2 )

Угол α, образованный внутренней диагональю прямоугольного параллелепипеда и диагональю основания, можно вычислить через отношение тангенса – бокового ребра а и диагонали основания d3.(рис.22.5) tan⁡α=a/d_3 =a/√(b^2+c^2 )

Прямоугольный параллелепипед

Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.

На рисунке изображен прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Его основаниями являются прямоугольники $ABCD$ и $A_1B_1C_1D_1$, а боковые ребра $AA_1, BB_1, CC_1$ и $DD_1$ перпендикулярны к основаниям.

Свойства прямоугольного параллелепипеда:

  1. В прямоугольном параллелепипеде $6$ граней и все они являются прямоугольниками.
  2. Противоположные грани попарно равны и параллельны.
  3. Все двугранные углы прямоугольного параллелепипеда – прямые.
  4. Диагонали прямоугольного параллелепипеда равны.
  5. Прямоугольный параллелепипед имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
  6. Любая грань прямоугольного параллелепипеда может быть принята за основание.
  7. Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
  8. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.

Чтобы были понятны формулы, введем обозначения:

$с$ – высота(она же боковое ребро);

$P_<осн>$ – периметр основания;

$S_<осн>$ – площадь основания;

$S_<бок>$ – площадь боковой поверхности;

$S_<п.п>$ – площадь полной поверхности;

$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.

$S_<бок>=P_<осн>·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.

Дополнительные сведения, которые пригодятся для решения задач:

$а$ – длина стороны.

$d=a√3$ – диагональ равна длине стороны, умноженной на $√3$.

Пирамида

Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) – треугольники, имеющие общую вершину.

Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.

Объем любой пирамиды равен трети произведения основания и высоты.

В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.

В основании лежит треугольник.

  • $S=/<2>$, где $h_a$ – высота, проведенная к стороне $а$.
  • $S=/<2>$, где $a,b$ – соседние стороны, $α$ – угол между этими соседними сторонами.
  • Формула Герона $S=√$, где $р$ – это полупериметр $p=/<2>$.
  • $S=p·r$, где $r$ – радиус вписанной окружности.
  • $S=/<4R>$, где $R$ – радиус описанной окружности.
  • Для прямоугольного треугольника $S=/<2>$, где $а$ и $b$ – катеты прямоугольного треугольника.
  • Для равностороннего треугольника $S=/<4>$, где $а$ – длина стороны.

В основании лежит четырехугольник.

  1. Прямоугольник.
    $S=a·b$, где $а$ и $b$ – смежные стороны.
  2. Ромб.
    $S=/<2>$, где $d_1$ и $d_2$ – диагонали ромба.
    $S=a^2·sin⁡α$, где $а$ – длина стороны ромба, а $α$ – угол между соседними сторонами.
  3. Трапеция.
    $S=<(a+b)·h>/<2>$, где $а$ и $b$ – основания трапеции, $h$ – высота трапеции.
  4. Квадрат.
    $S=a^2$, где $а$ – сторона квадрата.

Найдите объём многогранника, вершинами которого являются точки $C, A_1, B_1, C_1, D_1$ параллелепипеда $ABCDA_1B_1C_1D_1$, у которого $AB=8, AD=12, AA_1=4$.

Изобразим прямоугольный параллелепипед и на нем отметим вершины многогранника $C, A_1, B_1, C_1, D_1$, получим в итоге четырехугольную пирамиду. В основании пирамиды лежит прямоугольник, так основание пирамиды и прямоугольного параллелепипеда совпадают.

Объем пирамиды, в основании которой лежит прямоугольник

Для нашего рисунка стороны прямоугольника – это $А_1В_1$ и $A_1D_1$.

В прямоугольном параллелепипеде противоположные ребра равны и параллельны, следовательно, $AB=А_1В_1=8; AD=A_1D_1=12$.

Высотой в пирамиде $CA_1B_1C_1D_1$ будет являться ребро $СС_1$, так как оно перпендикулярно основанию (из прямоугольного параллелепипеда).

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

[spoiler title=”источники:”]

http://geleot.ru/education/math/geometry/calc/parallelepiped/edge

http://examer.ru/ege_po_matematike/teoriya/pryamiugolnyi_parallelepiped

[/spoiler]

Источник

Добавить комментарий