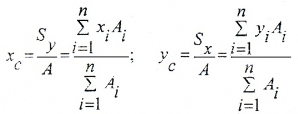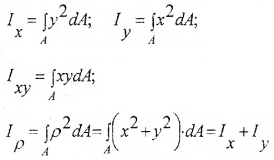Как найти параметр сечения

Как найти параметр сечения

Раздел 2

ВЫЧИСЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК СЕЧЕНИЙ

При выполнении расчётов на прочность и жёсткость необходимо знать положение главных центральных осей поперечного сечения и значения моментов инерции сечения относительно этих осей. Эти моменты инерции называются главными центральными моментами инерции и являются важнейшими геометрическими характеристиками сечения.

Сечения реальных конструкций часто состоят из нескольких отдельных элементов (или частей), в качестве которых могут быть как простые геометрические фигуры (чаще всего используются прямоугольник, круг, части круга, разные треугольники), так и прокатные профили (двутавр, швеллер, равнополочный и неравнополочный уголок и др.). Такие сечения называют сложными или составными. Составные сечения могут быть симметричными и несимметричными. Отсюда возникла потребность научиться вычислять геометрические характеристики для четырёх типов сечений: в этом разделе рассматривается вычисление геометрических характеристик симметричных и несимметричных сечений, составленных из прокатных профилей и простых фигур.

Задача 8. Вычисление геометрических характеристик симметричных сечений из прокатных профилей.

Задача 9. Вычисление геометрических характеристик симметричных сечений из простых фигур.

Задача 10. Вычисление геометрических характеристик несимметричных сечений из прокатных профилей.

Задача 11. Вычисление геометрических характеристик несимметричных сечений из простых фигур.

Цель этих задач − освоение методики вычисления главных моментов инерции для плоского сечения любой конфигурации и нахождения для него главных осей сечения.

При решении для сечения выбирают удобные оси координат, в которых выполняют необходимые расчёты. Координатные оси называют центральными, если они проходят через центр тяжести площади; и главными центральными, если центробежный момент инерции относительно этих осей равен нулю. По ходу решения необходимо иметь координаты центра

58

тяжести, площадь сечения, центральные моменты инерции как каждого элемента, так и всего составного сечения.

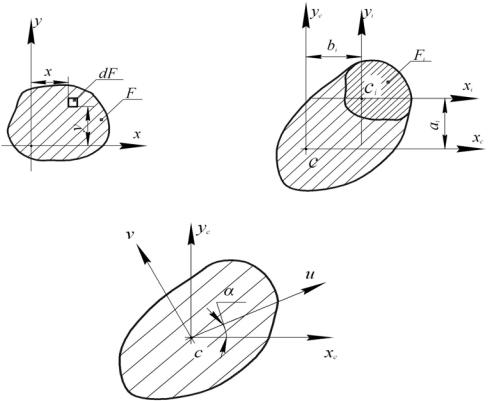
Осевые и центробежный моменты инерции как отдельного элемента так и всего сечения относительно любых осей х и у выражаются соответственно интегралами (рис. 2.1, а):

Ix y2 dF;

Iy x2 dF;

Ixy xy dF,

(2.1)

F

F

F

где х и у – текущие координаты элементарной площадки dF во взятой системе координат (х, у).

Интегрирование ведётся по площади F. Собственно по (2.1) и получены формулы геометрических характеристик сечений простой формы (прямоугольника, треугольника, круга и др.), которые можно найти в справочниках. Геометрические характеристики элементов в виде прокатных профилей (уголков, швеллеров, двутавров) вычислены также интегрированием согласно (2.1), и полученные значения даны в таблицах ГОСТа.

в

Рис. 2.1

59

Зная моменты инерции каждого i-го элемента I yi , Ixi , Ixi yi относи-

тельно его собственных осей (хi,

уi), можно вычислить центральные мо-

менты инерции всего сечения I yc ,

Ixc , Ixcyc относительно центральных осей

сечения (хс, ус), используя изменение моментов инерции элементов при па-

раллельном смещении осей:

Ixc (Ixi ai2 F);

Iyc (Ixi bi2 F);

Ixcyc (Ixiyi ai bi F) , (2.2)

n

n

n

где аi и bi – расстояния между соответствующими осями.

На рис. 2.1, б показаны центр тяжести Сi и центральные оси (хi, уi) для i-го элемента и также центр тяжести С и центральные (хс, ус) оси всего заданного сечения.

При вычислении моментов инерции сечения относительно любых осей (u, v), повернутых на некоторый угол α по отношению к первоначальным (хc, уc), используют соотношения (рис. 2.1, в):

Iv Ixc sin2

α Iyc cos2

α Ixcyc sin 2α,

Iu Ixc cos2

α Iyc sin2

α Ixcyc sin 2α,

(2.3)

Iuv

Ixc Iyc

sin 2α + Ixcyc cos2α.

2

Пользуясь последней формулой из (2.3), можно найти положение главных центральных осей сечения (u, v), т. е. тех осей, для которых цен-

тробежный момент инерции равен нулю: при Juv 0 получаем формулу для вычисления tg2α0 главных центральных осей:

tg2α0

2Ixcyc

.

(2.4)

Ixc Iyc

Главные центральные оси обозначают как (u, v), и главные центральные моменты инерции сечения называют Iu, Iv, их значения можно найти по (2.3), используя тригонометрические функции угла α0. Или для вычисления главных центральных моментов инерции сечения Iu, Iv можно использовать следующую формулу, полученную из (2.3) при подстановке

выражений cos2 α0 ,

sin2 α0 ,

sin 2α0 на основе тригонометрических соот-

ношений через tg2α0

по (2.4):

Iu

Imax

I

xc

I

yc

I

xc

I

yc

2

I 2 xcyc .

(2.5)

2

2

Iv

Imin

60

В формуле (2.5) знак плюс «+» перед радикалом относится к величине Imax, знак «–» к величине Imin.

Условие задач по разделу геометрических характеристик сечений

Плоское составное сечение задано схемой, на которой показаны элементы сечения и их расположение. В качестве элементов использованы простые геометрические фигуры (прямоугольник, круг, части круга, разные треугольники) и прокатные профили (двутавр, швеллер, равнополочный и неравнополочный уголок).

Необходимо вычислить главные моменты инерции заданного сечения и определить положение главных осей сечения.

Для вычисления главных моментов инерции Imax, Imin и для нахождения угла наклона главных осей (u, v) используют формулы (2.4) и (2.5), в которые входят неизвестные площадь и центральные моменты инерции сечения.

Чтобы вычисление было чётким, последовательным и обоснованным, требуется последовательно выполнить следующие пункты.

1.Вычертить сечение в масштабе, разбить его на отдельные элемен-

ты, для каждого из них провести собственные оси (xi, yi), записать значения площади Fi, осевых Ixi, Iyi и центробежного Ixiyi моментов инерции.

2.Определить положение центра тяжести (точки С) всего сечения, нанести его на сечение, провести центральные оси сечения (xс, yс).

3.Вычислить значения центральных моментов инерции всего сечения

Ixс, Iyс, Ixсyс.

4. Определить положение главных осей всего сечения (u, v), нанести оси на чертёж сечения и вычислить значения главных моментов инерции Imax, Imin, указать оси максимального и минимального моментов инерции в тексте и на чертеже сечения.

Задача 8

Вычисление геометрических характеристик симметричных сечений из прокатных профилей

Дана схема плоского симметричного сечения (рис. 2.2, а), составленного из прокатных профилей. Выполним расчёты для швеллера № 27 и двух уголков неравнополочных № 12,5/8 с толщиной полки t = 8 мм (рис. 2.2, б).

61

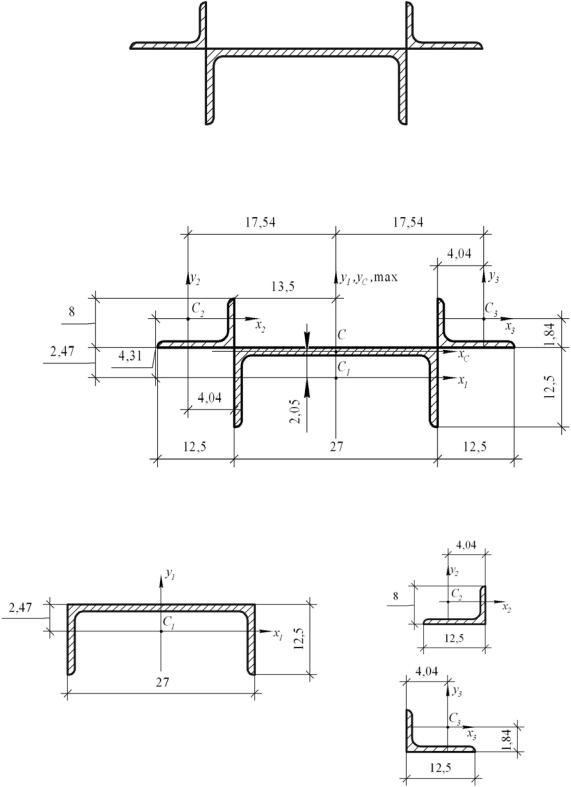
Заданная схема составного сечения

а

Чертёж всего составного сечения

б

1-й элемент сечения

2-й и 3-й элементы сечения

в

г

Рис. 2.2

62

Решение

В этой задаче определяем положение главных осей всего сечения (u, v) и вычисляем значения главных моментов инерции Imax, Imin для симметричного сечения, составленного из прокатных профилей. Эта особенность сечения учитывается в расчёте.

1. Выполнение чертежа сечения

Исходными данными для расчёта являются количество n профилей в сечении; вид каждого профиля, его расположение и геометрические размеры. Каждый профиль характеризуются площадью Fi, положением центра тяжести (точки Сi) и моментами инерции относительно собственных цен-

тральных осей: осевыми Ixi, Iyi и центробежным Ixiyi. Эти значения для прокатных профилей заданы в таблицах ГОСТa, для удобства решения задач

они приведены в табл. 4–7 прил. 1 данного пособия.

Сечение (рис. 2.2, а) состоит из 3 профилей: швеллера № 27 и двух неравнополочных уголков № 12,5/8 с толщиной полки t = 8 мм. Говорим, что сечение состоит из 3 элементов. Присвоим им индексы i = 1, 2, 3. Сначала выпишем необходимые значения для профилей. Следует заметить, что необходимо учитывать расположение профиля. Для наглядности изобразим элементы сечения отдельно (рис. 2.3, в, г), нанесём центры тяжести каждого и обозначим ихкакСi, через точкиСi проведём собственныеосикаждогоэлемента(xi, yi).

Для 1-го элемента (швеллера № 27): по ГОСТ 8240–93 (см. табл. 5 прил. 1 данного пособия) высота h = 270 мм; ширина полки b = 95 мм; толщина стенки s = 6 мм; толщина полки t = 9,8 мм; площадь F1 = 35,2 см2; осевые моменты Ix1 = 262 см4, Iy1 = 4160 см4; центробежный момент Ix1y1 = 0; расстояние до центра тяжести z0 = 2,47 см.

Для 2-го и 3-го элементов (уголков неравнополочных № 12,5/8 с толщиной полки t = 8 мм): по ГОСТ 8510–97 (см. табл. 7 прил. 1) ширина большей полки В = 125 мм; ширина меньшей полки b = 80 мм; толщина

полок s = 8 мм; площадь F2 = 16 см2; с учётом расположения профилей осевые моменты Ix2 = 81 см4, Iy2 = 255,6 см4 ; центробежный моменты

Ix2y2 = –84,1 см4; расстояния x0 = 1,84 cм, y0 = 4,04 cм.

Выполним в масштабе чертёж сечения, проставим габаритные размеры в сантиметрах (рис. 2.2, б) и проведём собственные оси элементов.

2. Определение положения центра тяжести

Центртяжести(точкаС) всего сеченияопределяют, используяформулы

x

Fi xi

; y

Fi yi

i

i

,

(2.6)

Fi

c

c

Fi

i

i

63

где xi и yi – координаты центра тяжести i-го элемента (точки Сi) во вспомогательных (исходных) осях, которые выбирают исходя из удобства вычислений. Такими осями (рис. 2.2, б) принимаем оси 1-го элемента (x1, y1).

Запишем во вспомогательных осях (x1, y1) координаты центра тяжести каждого элемента:

C1 0;0 , C2 17,54; , C3 17,54; .

Рассматриваемое сечение имеет ось симметрии – ось y1, центр тяжести такого составного симметричного сечения находится на оси симметрии, значит, xс = 0, и нужно найти только координату yс. Эту координату запишем по (2.6) при i = 3 и выполним вычисление:

y

c

F1 y1 F2 y2 F3 y3

0 2 4,31 16 2,05 см.

F1

F2

F3

35,2 2 16

В итоге получаем координаты центра тяжести всего сечения:

С(xc, yc) =C 0;2,05 .

Откладываем на чертеже сечения расстояние yc = 2,05 см от оси x1 вверх по оси y1, обозначаем точку С (рис. 2.2, б) и проводим центральные оси всего сечения (xc, yс).

3. Вычисление центральных моментов инерции

Для вычисления центральных моментов инерции всего сечения Ixс, Iyс, и Ixсyс используем формулы (2.2), в которые входят геометрические характеристики элементов, записанные выше:

2

2

,

Ixc Ixi ai

Fi ;

Iyc Iyi bi

Fi ; Ixcyc

Ixiyi aibi Fi

3

3

3

где ai и bi – расстояния между центральными осями i-го элемента и всего сечения, которые определим согласно чертежу сечения как разности соответствующих координат центра тяжести i-го элемента и центра тяжести всего сечения:

ai = yi – yc; bi = xi – xc.

(2.7)

Сначала вычислим эти расстояния:

a1 y1 yc 2,05 , b1 x1 xc 0 ;

a2 y2

yc 4,31 2,05 2,26 см,

b2 x2

xc 17,54 0 17,54 см;

a3 a2

2,26 см, b3 x2 xc 17,54 см.

64

Далее вычислим осевые центральные моменты инерции всего сечения по записанным выше формулам:

I

xc

I

x1

a

2

F I

x2

a2

F I

x3

a2 F

1

1

2

2

3

3

262 2,052

35,2 2 (83 2,262

16) 894,3см4;

I

yc

I

y1

b2

F I

y 2

b2 F I

y3

b2

F

1

1

2

2

3

3

4160 02 2(256 17,542 16) 14 528 см4.

Центробежный момент инерции Ixсyс рассматриваемого сечения вследствие симметрии равен нулю, в чём можно убедится при подстановке соответствующих величин, т. е. Ixсyс = 0.

4. Определение положения главных осей и значений главных моментов инерции

Так как центробежный момент инерции Ixсyс равен нулю, то это означает, что центральные оси всего сечения (xс, yс) есть главные оси (u, v), и центральные моменты инерции сечения есть главные моменты инерции. Укажем значения главных моментов инерции Imax, Imin:

Imax Iyc 14 528 см4; Imin Ixc 894,3 см4.

Следует заметить, что окончательно указывают в ответе и используют для дальнейших вычислениях в инженерных расчётах значения с 3 или 4 значащими цифрами, это соответствует достаточной точности (от 1 % до 0,1 %). Поэтому можно записать, учитывая 4-е значащие цифры:

Imax Iyc 14 530 см4; Imin Ixc 894,3 см4.

При нагружении данного сечения желательно, чтобы нагрузка шла по оси минимального момента инерции (по оси xс).

Задача 9

Вычисление геометрических характеристик симметричных сечений из простых фигур

Для заданного схемой симметричного плоского сечения из простых фигур вычислить главные моменты инерции и определить положение главных осей сечения.

65

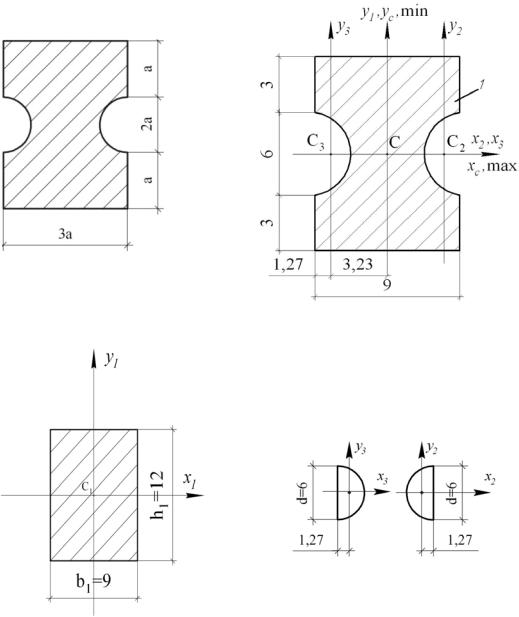
1-й вариант схемы сечения: сечение, имеющее две оси симметрии

Решение

Дано плоское симметричное сечение (рис. 2.3, а). Значение отрезка a = 3 мм.

Здесь требуется определить положение главных осей (u, v) и вычислить значения главных моментов инерции Imax, Imin для сечения, составленного из простых фигур и имеющего две оси симметрии, что будем использовать при решении.

Заданная схема сечения

Чертёж сечения

а

б

1-й элемент

2-й и 3-й элементы

в

г

Рис. 2.3

66

1. Выполнение чертежа сечения

Рассматриваемое сечение – составное. Используя заданное значение a =3 мм, вычертим сечение в масштабе и проставим числовые значения характерных размеров (рис. 2.3, б). Сечение можно представить состоящим из следующих простых фигур: прямоугольника высотой 4а =12 мм и шириной 3а = 9 мм и двух вырезов в виде полукругов диаметром 2а = 6 мм, т. е. составное сечение разложим на отдельные элементы (или фигуры). Присвоим им индексы i = 1, 2, 3 (рис. 2.3, б). Изобразим эти элементы отдельно, нанесём их центры тяжести Сi и через точки Сi проведём собственные оси каждого элемента (xi, yi) (рис. 2.3, в, г). Заметим, что центр тяжести полукруга удалён от диаметра (см. табл. 9 прил. 1) на расстояние

0,424r 0,424 3 1,272 1,27 мм.

Оси элементов перенесём на составное сечение (рис. 2.3, б).

2. Определение положения центра тяжести

Так как сечение имеет две оси симметрии, то центр тяжести всего сечения (точка С) находится на их пересечении − в точке С1, через эту точку и проходят центральные оси всего сечения, назовём их как xс и yс. Если за вспомогательные оси координат взять оси (x1, y1), то координаты центра тя-

жести всего сечения равны нулю: xс= 0, yс= 0, т. е. С(xc, yc) =C 0; 0 . Укажем во вспомогательных осях (x1, y1) координаты центра тяжести каждой фигуры:

C1 0;0 , C2 3,23; , C3 3,23; .

3. Вычисление центральных моментов инерции

Для вычисления центральных моментов инерции всего сечения Ixс, Iyс, Ixсyс используем формулы (2.2), в которые входят геометрические характеристики элементов: площадь Fi, осевые Ixi, Iyi и центробежный Ixiyi моменты инерции относительно собственных осей элементов (xi, yi). Эти значения получим по формулам, представленным в табл. 10 прил. 1. Необходимо сделать следующее примечание: для отверстий площадь и моменты инерции считаем отрицательными. В нашем примере отверстиями являются полукруги, для них площадь и моменты инерции принимаем со знаком «–».

Вычислим геометрические характеристики элементов (фигур). Для 1-й фигуры (прямоугольника):

2

b h 3

9 123

4

1

1

F 9 12 108 мм ; I

x1

1296 мм

;

1

12

12

b3 h

93 12

I y1

729 мм4; Ix1 y1 = 0.

12

12

67

Для 2-й и 3-й фигур (полукруга):

F F

πd 2

π 62

2

14,14 мм ;

2

3

8

8

Ix2

Ix3

π d 4

π 64

31,8

4

мм ;

64 2

64 2

I y 2 I y3 0,11 r4 0,11 34

8,9мм4; Ix2 y 2 = Ix3 y3 = 0.

Теперь используем (2.2), где расстояния между осями запишем по (2.7) как ai = yi – yc, bi = xi – xc; и вычислим осевые и центробежный моменты инерции всего сечения. Осевой момент инерции относительно оси xc

Ixc Ix1 y1 yC 2 F1 Ix2 y2 yC 2 F2 Ix3 y3 yC 2 F3

1296 0 2( 31,8 0) 1232 мм4.

Осевой момент инерции относительно оси yc

xi xС

2

Iyc Iyi

Fi

x x

2 F I

3

x x

2 F I

x x

2 F

I

y1

y2

y3

1

C

1

2

C

2

3

C

3

729 0 2 ( 8,9) 2 0 3,23 2 ( 14,4) 561мм4.

Центробежный момент инерции имеет выражение

Ixcyc Ixi yi

xi xC yi

yC Fi .

2

При подстановке значений

Ix1 y1 = 0, Ix2 y 2 = Ix3 y3 = 0, x2 = – x3 для рас-

сматриваемого симметричного составного сечения Ixсyс = 0.

4. Определение положения главных осей и значений главных моментов инерции

Так как центробежный момент инерции Ixсyс равен нулю, то это означает, что центральные оси всего сечения (xс, yс) есть главные оси (u, v), и центральные моменты инерции сечения есть главные моменты инерции. Укажем значения главных моментов инерции Imax, Imin:

Imax Ixc 1232 1230 мм4; Imin Iyc 561мм4.

При нагружении данного сечения желательно, чтобы нагрузка шла по оси yс как по оси минимального момента инерции.

68

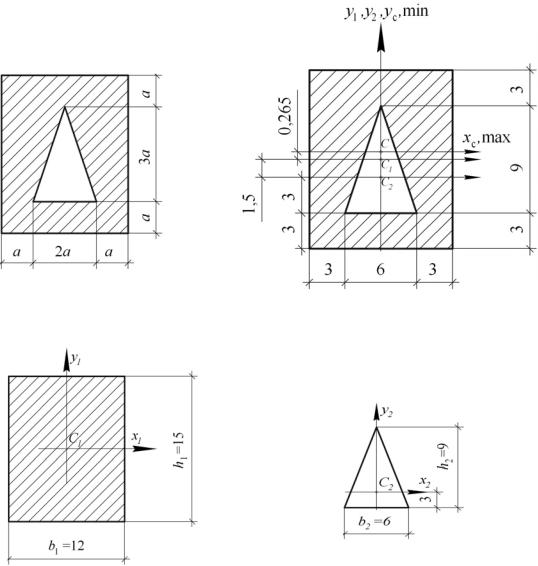
2-йвариантсхемысечения: сечение, имеющееоднуосьсимметрии

Дана схема плоского симметричного сечения (рис. 2.4, а). Значение отрезка a = 3 мм. При решении задачи требуется выполнить те же пункты, что и в 1-м варианте схемы сечения.

Заданная схема сечения

Чертёж сечения

а

б

1-йэлемент

2-йэлемент

в

г

Рис. 2.4

Решение

Как и в 1-м варианте задачи 9, требуется определить положение главных осей (u, v) и вычислить значения главных моментов инерции Imax, Imin для сечения, составленного из простых фигур, но в отличие от 1-го варианта сечение имеет только одну ось симметрии.

69

1. Выполнение чертежа сечения

Используя заданное значение a = 3 мм, вычертим сечение в масштабе и проставим числовые значения характерных размеров в миллиметрах (рис. 2.4, б). Рассматриваемое сечение – составное. Его можно представить состоящим из двух простых фигур: прямоугольника высотой h1 = 15 мм и шириной b1 = 12 мм и выреза в виде равнобедренного треугольника высотой h2 = 9 мм с длиной основания b2 = 6 мм. Присвоим им индексы i = 1, 2.

Изобразим эти элементы отдельно (рис. 2.4, в, г), нанесём центры тяжести каждого как С1 и С2 и через эти точки проведём собственные оси каждого элемента (x1, y1) и (x2, y2). Заметим, что центр тяжести треугольника удалён от основания на 3 мм (см. табл. 10 прил. 1).

Оси элементов перенесём на составное сечение (рис. 2.4, б).

2. Определение положения центра тяжести

Так как сечение имеет одну ось симметрии, то центр тяжести всего сечения находится на имеющейся оси симметрии – на оси yс. Если за вспомогательные оси координат взять оси (x1, y1), то абсцисса центра тяжести всего сечения xc = 0. Для определения положения центра тяжести С(xс; yс) всего сечения нужна вторая координата этой точки yс. Вычислим необходимое значение yс.

Сначала укажем во взятых вспомогательных осях (x1, y1) координаты центров тяжести элементов С1 и С2:

C1(x1, y1) = C1(0; 0), C2(x2, y2) = C2(0; –1,5).

Вычислим площади фигур:

F1 12 15 180 мм2; F2 926 27 мм2.

Теперь по (2.6) найдём значение yс:

yC

F1 y1

F2 y2

0 ( 1,5) ( 27)

0,265мм.

F

F

180 ( 27)

1

2

Получаем координаты центра тяжести всего сечения: С(xс; yс) =

С(0; 0,265).

Поставим эту точку на чертёж сечения и проведём центральные оси (xc, yc) всего сечения (рис. 2.4, б).

3. Вычисление центральных моментов инерции

Для вычисления центральных моментов инерции всего сечения Ixс, Iyс, Ixсyс используем формулы (2.2), в которые входят геометрические характеристики элементов: площадь Fi, осевые Ixi, Iyi и центробежный Ixiyi моменты

70

инерции относительно собственных осей элементов (xi, yi). Эти значения получим по формулам, представленным в табл. 10 прил. 1. Придерживаемся правила: для отверстий площадь и моменты инерции считать отрицательными. В нашем примере отверстием является треугольник, для него площадь и моменты инерции принимаем со знаком «–».

Вычислим геометрические характеристики элементов (фигур). Для 1-го элемента (прямоугольника) получим

2

I

b1 h13

12 153

4

F 12 15 180 мм ;

x

3375мм ;

1

12

12

1

I y

b3

h

123

15

2160мм4; Ix1 y1 = 0.

12

1

12

Для 2-го элемента (треугольника) получим

9 6

2

b h 3

6 93

4

2

2

F

27 мм ; I

x2

121,5 мм ;

2

2

36

36

b 3

h

63 9

I y 2

4

2

2

40,5мм ; Ix2 y 2 = 0.

48

48

Теперь, используя (2.2), в которые подставим расстояния между осями по (2.7) как ai = yi – yc, bi = xi – xc, запишем формулы осевых и центробежного моментов инерции всего сечения в следующем виде:

yi yC

2

;

xC

2

;

Ixc Ixi

Fi

I yc I yi xi

Fi

2

xi

2

Ixcyc Ixiyi

xC yi yC Fi .

2

Подсчитаем значения осевых моментов:

I

xc

I

x1

y y

2 F I

x2

y y

2 F

1 C

1

2 C

2

3375 ( 0,265)2180 ( 125,5) ( 1,5 0,265)2 ( 27) 3182 мм4;

Iyc Iy1 x1 xC 2 F1 Iy2 x2 xC 2 F2

2160 ( 40,5) 2120мм4.

Как видно по формуле центробежного момента инерции Ixсyс, для рассматриваемого симметричного составного сечения он равен нулю: Ixсyс= 0.

4. Определение положения главных осей и значений главных моментов инерции

Так как центробежный момент инерции Ixсyс равен нулю, то это означает, что центральные оси всего сечения (xс, yс) есть главные оси (u, v), а

71

центральные моменты инерции сечения есть главные моменты инерции. Укажем значения главных моментов инерции Imax, Imin:

Imax Ixc 3182 3180 мм4; Imin I yc 2120 мм4.

Здесь в окончательном ответе можно написать значения с 3-мя значащими цифрами: Imax Ixc 3180мм4; Imin I yc 2120мм4.

При нагружении данного сечения желательно, чтобы при изгибе нагрузка шла по оси yс как по оси минимального момента инерции.

Задача 10

Вычисление геометрических характеристик несимметричных сечений из прокатных профилей

Задана схема несимметричного сечения из прокатных профилей.

1-й вариант: сечение из 2 профилей

Решение

Рассмотрим несимметричное сечение, составленное из двутавра № 27 и неравнополочного уголка № 20/12,5 с толщиной полок t = 16 мм (чертёж сечения дан на рис. 2.5).

Вычислим главные моменты инерции и угол наклона главных осей, выполняя последовательно указанные выше пункты.

1. Выполнение чертежа сечения

Сечение состоит из 2 профилей (или из 2 элементов): присвоим двутавру индекс i = 1 и уголку i = 2. Пользуясь таблицами ГОСТа, выпишем в сантиметрах для каждого элемента габаритные размеры и расстояния до центров тяжести, площадь и моменты инерции: для двутавра из ГОСТ 8239–89, для уголка из ГОСТ 8510–97 (см. табл. 4 и 7 прил. 1). При этом нужно учесть расположение элементов и обозначение собственных осей согласно заданной схеме сечения. Для каждого из элементов проводим собственные оси (xi, yi) записываем значения площади Fi, осевых Ixi, Iyi и центробежного Ixiyi моментов инерции.

Для 1-го элемента (двутавра № 27) высота h = 27 см; ширина полки b = 12,5 см; площадь F1 = 40,2 см2; осевые и центробежный мо-

72

менты инерции Ix1 = 5010 см4, Iy1 = 260 см4 и, как результат симметрии двутавра, Ix1y1 = 0.

Для 2-го элемента (уголка № 20/12,5 с толщиной полок t = 16 мм) ширина полок B = 20 см, b = 12,5 см; расстояния до центральных осей x0 = 2,99 см, y0 = 6,71 см; площадь F2 = 49,8 см2; осевые и центробежный моменты инерции Ix2 = 617 см4, Iy2 = 2026 см4 и Ix2y2 = 2775 см4; в последнем используем знак «+» для изображённого расположения уголка (см. табл. 8 прил. 1).

Рис. 2.5

Теперь выполняем в масштабе чертёж всего сечения, на котором ставим габаритные размеры и проводим собственные оси элементов (рис. 2.5).

2. Определение положения центра тяжести

Для определения центра тяжести всего сечения используем формулы (2.6). За исходные оси возьмём центральные оси 2-го элемента (x2, y2) и

73

укажем в этих осях координаты центров тяжести профилей С1 и С2, x1 = 6,71 + 12,5/2 = 12,96 см, y1 = 27/2 + 12,5 – 2,99 = 23,01 см:

C1(x1, y1) = C1(12,96; 23,01), C2(x2, y2) = C2(0; 0).

Вычислим координаты xc, yc центра тяжести С всего сечения по (2.6):

xC

F1x1

F2x2

40,2 12,96 0

5,21см,

F

F

40,2 49,8

1

2

yC

F1 y1 F2 y2

40,2 23,01 0

9,25 см.

F F

40,2 49,8

1

2

Получаем координаты центра тяжести сечения: С(xс; yс) = С(5,21; 9,25). Поставим эту точку на чертёж сечения и проведём центральные оси (xc, yc) всего сечения (рис. 2.5).

3. Вычисление центральных моментов инерции

Центральные моменты инерции Ixс, Iyс, Ixсyс относительно центральных осей (xc, yc) запишем по (2.2):

2

Ix1

2

F1 Ix2

2

F2 ;

Ixc Ixi ai

Fi

a1

a2

2

2

I y1

2

F1 I y 2

2

F2 ;

I yc I yi bi

Fi

b1

b2

2

a1

b1 F1 Ix2 y2

a2 b2 F2 ,

Ixcyc Ixiyi

ai bi Fi Ix1y1

2

где ai и bi – расстояния между центральными осям i-го элемента и всего сечения, которые вычислим по (2.7) как ai = yi – yC, bi = xi – xC (рис. 2.5, б):

a1 y1 yc 23,01 9,25 13,76 см, b1 x1 xc 12,96 5,21 7,75см; a2 y2 yc 0 9,25 9,25см, b2 x2 xc 0 5,21 5,21см.

Тогда центральный момент инерции всего сечения Ixc относительно оси xс получает значение:

Ixc =5010 13, 762 40, 2 617 ( 9, 25)2 49,8 17500 см4.

Значение центрального момента инерции всего сечения Iyс относительно оси yс будет:

Iyс =260 7,752 40,2 2026 5,21 2 49,8 6052,3см4.

74

Значение центробежного момента инерции Ixсyс:

Ixсyс =0 7,75 2,62 40,2 2775 ( 9,25) ( 5,21) 49,8 9462 см4.

4. Определение положения главных осей и значений главных моментов инерции

Найдем положение главных осей, используя формулу (2.4):

tg2α0

2 Ixcyc

=

2 9462

1,65 .

Ixc I yc

17500 6052

Отсюда угол наклона главных осей α0 = –32,7º. Угол получен отрицательным, поэтому главные оси (u, v) покажем поворотом центральных осей (xс, yс) на угол 32,7º по часовой стрелке (причём ось u всегда наклонена к оси x под углом α0). Нанесём главные оси (u, v) на сечение (рис. 2.5).

Главные моменты инерции по (2.5)

Iu

Imax

I

xc

I

yc

I

xc

I

yc

2

=

I 2 xcyc

2

2

Iv

Imin

17500 6052

17500 6052 2

9462

2

22835

4

2

2

717

cм .

Моменты инерции Iu, Iv − это экстремальные моменты, т. е. один из них – Imax, другой – Imin. Сумма моментов инерции относительно всех взаимно перпендикулярных осей, проходящих через данную точку, есть величина постоянная:

Iu + Iv=Imax + Imin = 22 835+717= Ixc Iyс =17 500 + 6052 = 23 552 см4.

Итак, получаем Imax = 22 835см4, Imin =717см4. В ответе окончательно можно записать с точностью до 4 значащих цифр:

Imax = 22 840 см4; Imin = 717 см4.

Окончательным пунктом вычисления геометрических характеристик является назначение оси максимальных Imax и оси минимальных моментов Imin инерции, что очень важно для рационального расположения сечения по отношению к плоскости нагрузки. Установить назначение этих осей можно после получения значений Imax, Imin и угла α0. Существует правило: ось максимальных моментов инерции Imax наклонена под меньшим углом к той оси (xc или yc), относительно которой момент инерции имел наибольшее значение (Ixс или Iyс).

В нашем случае Ixс = 22 840 см4 > Iyс = 717 см4.

75

Тогда

Imax = Iu = 22 840 см4; Imin = Iv = 717 см4,

поэтому подписываем ось u как ось максимальных моментов инерции I max – ось max, а ось v как ось минимальных Imin – ось min.

2-й вариант схемы: сечение из 3 элементов

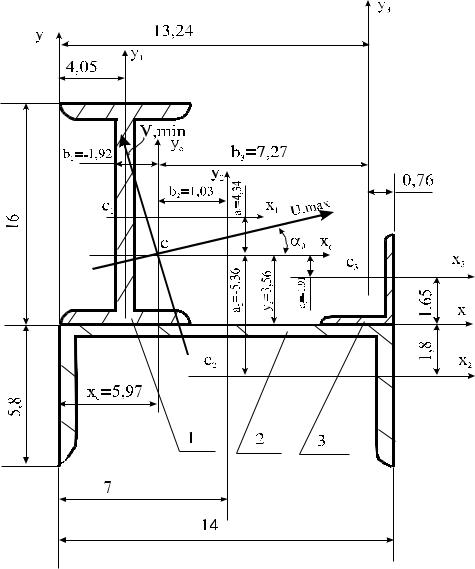
Рассмотрим вычисление главных моментов инерции и определение положения главных осей для несимметричного сечения, составленного из двутавра, швеллера и уголка (рис. 2.6). Сечение состоит из 3 профилей (элементов): двутавра № 16, швеллера № 14 и уголка № 5/3,2. При вычислении выполняем все пункты, указанные выше.

76

Решение

1. Выполнение чертежа сечения

Присвоим индексы элементам сечения: i = 1, 2, 3. Габаритные размеры, расстояния до центров тяжести, площадь и моменты инерции выбираем для двутавра из ГОСТ 8239–89, для швеллера – из ГОСТ 8240–93, для уголка – из ГОСТ 8510–97 (см. табл. 4, 5, 7 прил. 1). Пользуясь таблицами, запишем следующие значения в собственных осях элементов.

Для 1-го элемента (двутавра № 16) высота h = 16 см; ширина полки b = 8,1 см; площадь F1 = 20,2 см2; осевые и центробежный моменты инерции Ix1 = 873 см4, Iy1 = 58,6 см4 и запишем, учитывая симметрию двутавра,

Ix1y1 = 0.

Для 2-го элемента (швеллера № 14) высота h = 14 см; ширина полки b = 5,8 см; расстояние до центральной оси z0 = 1,67 см; площадь F2 = 15,6 см2; осевые и центробежный моменты инерции Ix2 = 51,5 см4, Iy2 = 493 см4 и, как результат симметрии швелллера, Ix2y2 = 0.

Для 3-го элемента (уголка № 5/3,2) ширина полок B = 5 см, b = 3,2 см; расстояния до центральных осей x0 = 0,76 см, y0 = 1,65 см; площадь F3 = 3,17 см2; осевые и центробежный моменты инерции Ix3 = 7,98 см4, Iy3 = 2,56 см4 и Ix3y3 = 2,59 см4. Необходимо помнить, что знак центробежного момента инерции Ixy уголка зависит от расположения его в сечении и направления собственных осей (знак может быть и положительным, и отрицательным). Для этого знака составлена табл. 8 прил. 1. В нашем случае будет знак «+».

Выполним чертёж сечения (рис. 2.6) и проставим на чертеже характерные размеры, нанесём центры тяжести Сi профилей, через которые проведём собственные оси элементов. На чертёже показаны собственные оси всех 3-х элементов сечения.

2. Определение положения центра тяжести

Выберем исходные оси (x, y) и укажем в этих осях координаты xi, yi центров тяжести (т. е. точек Сi) всех профилей:

C1(x1, y1) = C1(4,05; 8), C2(x2, y2) = C2(7; 1,8), C3(x3, y3) = C3(13,24; 1,65).

Определим координаты xc, yc центра тяжести (точки С) всего сечения по (2.6), используя здесь и далее для сокращения записи матричную форму, более удобную при i >2:

F1

20,2

(x , x , x ) F

(4,05; 7,0; 13,24 )

15,6

1

2 3

2

3,17

F

x

3

5,97 см;

c

F1 +F2

F

20,2 15,6 3,17

77

F1

20,2

(y , y

, y ) F

( 8,0; –1,8; 1,65)

15,6

1

2

3

2

3,17

F

y

3

3,56см.

c

F1

+F2 F

20,2+15,6 3,17

Получаем координаты точки С: С(xс; yс) = С(5,97; 3,56). Поставим эту точку на чертёж сечения и проведём центральные оси (xc, yc) всего сечения.

3. Вычисление центральных моментов инерции

Далее нужно вычислить в осях (xc, yc) центральные моменты инерции Ixс, Iyс, Ixсyс. Вычисление выполняем по (2.2), записывая в матричной форме:

I

x1

F

873

20,2

Ixс=

2

2

2

1

51,5

2

2

2

4

Ix2

+(а1

; a2 ; a3 )

F2

=

+(4,34 ;(–5,36) ; 1,91 )

15,6

= 1790,4 см ,

I

x3

F

7,98

3,17

3

где по (2.7)

8,0

4,34

1,8

5,36

см;

аi = (yi) – yc =

– 3,56 =

1,65

1,91

I

y1

F

58,6

20,2

Iyс=

2

2

2

1

2

2

2

4

I y 2

+(b1

; b2 ; b3 )

F2

=

493

+ (–1,92 ; 1,03 ; 7,27 )

15,6

= 812,7см ,

I

F

2,56

3,17

y3

3

где по (2.7)

4,05

–1,92

7,0

– 5,97 =

1,03

см;

(bi) = (xi) – xc =

7,27

13,24

Ix1y1

F1

Ixсyс= I

x2 y 2

+ (а1b1; a2b2; а3b3) F

=

2

I

x3 y3

F

3

0,0

20,2

=

0,0

+ (–1,92 4,34; 1,03 (–5,36); 7,27 (–1,91))

4

15,6

= –299,8 cм .

2,59

3,17

78

4. Определение положения главных осей и значений главных моментов инерции

Найдём угол α0 наклона главных осей, используя формулу (2.4):

tg(2α0 )=

2( 299,8)

0,63 .

1790,4 812,72

Отсюда угол α0 наклона главных осей α0 = 15,76º. Угол получен положительным, поэтому главные оси (u, v) покажем поворотом центральных осей (xс, yс) на угол 15,8º против часовой стрелки (причём ось u всегда наклонена к оси x под углом α0). Нанесём главные оси (u, v) на сечение.

Главные моменты инерции определяем по (2.5):

Iu

Imax

I

xc

I

yc

I

xc

I

yc

2

=

I 2 xcyc =

2

2

Iv

Imin

1790,4 812,7

1790,4 812,7 2

299,75

2

1875

4

2

2

cм .

728

Моменты инерции Iu, Iv − это экстремальные моменты, а сумма моментов инерции относительно всех взаимно перпендикулярных осей, проходящих через данную точку, есть величина постоянная:

Iu + Iv = Imax + Imin = 1875 + 728 = Ixc Iyс = 1790,4 + 812,7 = 2603 см4.

Получаем

Imax = 1875см4; Imin = 728см4.

Окончательным пунктом вычисления геометрических характеристик является назначение оси максимальных Imax и оси минимальных моментов Imin инерции, что очень важно для рационального расположения сечения по отношению к плоскости нагрузки. Установить назначение этих осей можно после получения значений Imax, Imin и угла α0. Используем правило: ось максимальных моментов инерции Imax наклонена под меньшим углом к той оси (xc или yc), относительно которой момент инерции имел наибольшее значение (Ixс или Iyс).

В нашем случае

Ixс = 1790,4 см4 > Iyс = 812,7 см4.

Тогда

Imax = Iu = 1875 см4; Imin = Iv =728см4,

поэтому подписываем ось u как ось максимальных моментов инерции Imax – ось max, а ось v как ось минимальных Imin – ось min.

79

Задача 11

Вычисление геометрических характеристик несимметричных сечений из простых фигур

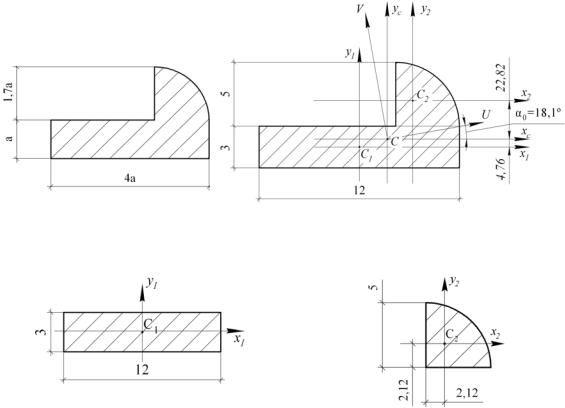
Дана схема сечения (рис. 2.7, а), составленного из 2 простых фигур: прямоугольника а 4а, т. е. высотой а и шириной 4а, и четверти круга радиуса r = 1,7а. Значение отрезка a = 3 мм.

Решение

1. Выполнение чертежа сечения

Используя заданное значение a = 3 см, найдём высоту прямоугольника h = 3 см; ширину прямоугольника b = 12 см; радиус четверти круга r = 5 см.

Выполним чертёж сечения и проставим числовые размеры фигур (рис. 2.7, б). Сечение состоит из 2 элементов: прямоугольника и четверти круга. Присвоим им индексы: i = 1, 2, укажем их на чертеже сечения.

Заданная схема сечения

Чертёж составного сечения

а

б

1-й элемент сечения

2-й элемент сечения

в

г

Рис. 2.7

80

2. Определение положения центра тяжести всего сечения

Найдем положение центра тяжести всего сечения, взяв вспомогательные координатные оси. Для удобства вычислений оси х и у проведены так, что они совпадают с основаниями четверти круга.

Укажем координаты хi и уi центров тяжести каждого элемента сечения относительно осей (х, у) (рис. 2.7, б):

C1( х1; у1) = C1 (–1; –1,5), C2 (х2; у2) = C2 (2,12; 2,12).

Определим координаты xc, yc центра тяжести (точки С) всего сечения по (2.6):

x

Fx

F x

36( 1) 19,6 2,12

0,1 см;

1 1

2

2

36 19,6

С

F1 F2

yС

F1 y1 F2 y2

36( 1,5) 19,6 2,12

0,22 см.

F F

36 19,6

1

2

Получаем координаты центра тяжести (точки С) всего сечения: С(xс; yс) = С(0,1; –0,22). Поставим эту точку на чертёж сечения и проведём центральные оси (xc, yc) всего сечения.

3. Вычисление центральных моментов инерции

В начале найдём геометрические характеристики элементов: центральные оси, площадь, осевые и центробежный моменты инерции. Для удобства изобразим отдельно элементы (рис. 2.7, в), нанесём центры тяжести каждого как Сi (см. табл. 10 прил. 1). Для прямоугольника центр тяжести С1 расположен на расстоянии h/2 =1,5 см и b/2 = 6 см от его сторон, а для четверти круга удалён от оснований на 0,424r = 0,424·5 = 2,12 см. Через точки Сi проведём собственные оси каждого элемента (xi, yi).

Площади и моменты инерции элементов (осевые Ixi, Iyi и центробежный Ixiyi) относительно собственных осей элементов (xi, yi), подсчитаем по известным формулам, которые можно найти в справочниках или взять из табл. 10 прил. 1.

Для 1-го элемента (прямоугольника) площадь F1 = 12 · 3 = 36 см2; осевые моменты инерции относительно своих центральных осей

Ix1 bh3

12 3 2

27 см4 ;

Iy1

b3h

123 3

432 см4;

12

12

12

12

центробежный момент инерции в силу симметрии Ix1y1 0 .

2

π 5

2

Для 2-го элемента (четверти круга): площадь F πr

19,6 см2;

2

4

4

моменты инерции относительно своих центральных осей

81

Ix1 Iy1 0,0549 r4 0,0549 54 34,3 см4;

центробежный момент инерции согласно табл. 8 прил. 1 запишем со зна-

ком «–»:

Ix1y1 –0,0165r4 –0,0165 54 10,29 см4.

Центральные моменты инерции Ixс, Iyс, Ixсyс

осях (xc, yc) по (2.2.):

2

;

2

; Ixcyc

Ixc Ixi ai

Fi

I yc I yi bi

Fi

2

2

всего сечения вычислим в

I

xiyi

a b F

,

i i i

2

где ai и bi – расстояния между центральными осям i-го элемента и всего се-

чения по (2.7), ai = yi – yс, bi = xi – xc :

a1 y1

yc 1,5 ( 0,22) 1,28 см, b1 x1 xc 1 0,1 1,1 см;

a2 y2

yc 2,12 ( 0,22) 2,34 см, b2 x2 xc 2,12 0,1 2,02 см.

Центральный момент инерции всего сечения относительно оси xс принимает следующее значение:

I

xc

I

x1

a2

F I

x2

a2

F

=

1

1

2

2

27 ( 1, 282 36 34, 4 2, 34 2 19,6 227,7 см4.

Вычислим центральный момент инерции всего сечения относительно оси yс:

I

yc

I

y1

b2

F I

y 2

b2

F =

1

1

2

2

432 ( 1,1)2 36 34,4 2,022 19,6 590см4.

Центробежный момент инерции

Ixcyc Ix1y1 a1 b1 F1 Ix2 y2 a2 b2 F2 =

0 ( 1,28) ( 1,1) 36 ( 10,2) 2,34 2,02 19,6 133,1см4.

4.Определение положения главных осей и значений главных моментов инерции

Найдем положение главных осей, используя формулу (2.4):

tg(2α0 )=

2 133,1

0,73.

127,7 590

Отсюда угол наклона главных осей α0 =18,1º. Угол получен положительным, поэтому главные оси (u, v) покажем поворотом центральных осей

82

(xс, yс) на угол 18,1º против часовой стрелки (причём ось u наклонена к оси x под углом α0). Нанесём главные оси (u, v) на сечение.

Главные моменты инерции по (2.5)

Iu

Imax

I

xc

I

yc

I

xc

I

yc

2

=

I 2 xc yc

2

2

Iv

Imin

127,7

590

127,7 590

2

133,1

2

634

4

2

2

cм .

184,7

Моменты инерции Iu, Iv − это экстремальные моменты. Сумма моментов инерции относительно всех взаимно перпендикулярных осей, проходящих через данную точку, есть величина постоянная:

Iu + Iv = Imax + Imin = 227,7 + 590 = Iхc Iус = 634 + 184,7 = 817,7 см4.

Получаем

Imax = 634 см4; Imin = 184,7 см4 ≈ 185 см4.

Окончательным пунктом вычисления геометрических характеристик является назначение оси максимальных Imax и оси минимальных моментов Imin инерции, что очень важно для рационального расположения сечения по отношению к плоскости нагрузки. Установить назначение этих осей можно после получения значений Imax, Imin и угла α0. Применяем правило: ось максимальных моментов инерции Imax наклонена под меньшим углом к той оси (xc оси yc), относительно которой момент инерции имел наибольшее значе-

ние (Ixс или Iyс).

В нашем случае

Ixс = 127,7 см4 < Iyс = 590 см4.

Тогда

Imax = Iv = 634 см4; Imin = Iu = 185 см4,

поэтому подписываем ось u как ось максимальных моментов инерции I max

– ось max, а ось v как ось минимальных Imin – ось min.

83

Источник

Расчёт геометрических характеристик сложного поперечного сечения

Добро пожаловать! Данный онлайн-калькулятор предназначен для расчёта всех характеристик
сложного поперечного сечения: центра тяжести, площади, моментов инерции, моментов
сопротивления, радиусов инерции. В итоге формируется отчёт с готовым решением и эскизом
сечения в масштабе. Удачи!

Начать новое сечение Объекты для расчёта отсутствуют

Операции

Двутавр

Номер двутавра:
Угол поворота, град.:

Швеллер

Номер швеллера:
Угол поворота, град.:

Равнополочный уголок

Ширина полки:
Толщина полки:
Угол поворота, град.:

Неравнопол. уголок

Высота × ширина:
Толщина полки:
Угол поворота, град.:

Неравнопол. уголок

Высота × ширина:
Толщина полки:
Угол поворота, град.:

Полоса (прямоугольник)

Ширина, мм:
Высота, мм:
Угол поворота, град.:

Круг

Радиус, мм:
Угол поворота, град.:

Полукруг

Радиус, мм:
Угол поворота, град.:

Четверть круга

Радиус, мм:
Угол поворота, град.:

Равнобедр. треугольник

Ширина, мм:
Высота, мм:
Угол поворота, град.:

Прямоуг. треугольник

Ширина, мм:
Высота, мм:
Угол поворота, град.:

Прямоуг. треугольник

Ширина, мм:
Высота, мм:
Угол поворота, град.:

Имена осей

Имена осей системы координат (для профилей в сечении и пр.)
абсцис:
ординат:
Имена главных осей
абсцис:
ординат:

Состав сечения

В данном расчёте не задано ни одного профиля. Для задания профилей перейдите в панель “Операции” и выберите необходимый профиль.
Источник

При расчёте элементов конструкций на прочность, жёсткость и устойчивость (классические расчёты в сопромате) используются следующие геометрические характеристики плоских сечений: площадь, моменты инерции, моменты сопротивления и другие.

Для простейших фигур, таких, как квадрат, прямоугольник, круг и т. д.– эти характеристики определяются по табличным формулам, для более сложных же поперечных сечений, как правило, состоящих из простых, характеристики нужно рассчитывать по специальным методикам.

Уроки по определению геометрических характеристик

В этом разделе ты сможешь найти уроки по расчёту различных геометрических характеристик, разного уровня сложности.

Нахождение центра тяжести сечения

В уроке рассмотрено сложное сечение, состоящее из простых фигур, для которого находятся координаты центра тяжести.

Фигура, состоящая из нескольких простых фигур

Нахождение осевых моментов инерции

В этом уроке рассмотрено симметричное сечение, состоящее из простых геометрических фигур, и для которого вычисляются осевые моменты инерции.

Симметричное сечение, состоящее из простых фигур

Справочные материалы для расчёта геометрических характеристик

В этом разделе ты найдёшь справочные материалы, которые могут понадобиться для расчёта геометрических характеристик.

Формулы для расчёта геометрических характеристик простейших сечений

  • Площади.
  • Моменты инерции.
  • Осевые моменты сопротивления.
  • Полярные моменты сопротивления.

Геометрические характеристики стандартных профилей

  • Двутавры.
  • Швеллеры.
  • Равнополочные уголки.
Источник

Рассмотрим формулы для определения геометрических характеристик плоских сечений: статического момента площади фигуры, осевых моментов инерции и радиуса инерции сечения.

При расчете элементов конструкций на прочность, жесткость и устойчивость приходится кроме общеизвестной характеристики – площади поперечного сечения A, оперировать такими геометрическими характеристиками сечений, как статический момент площади, момент инерции, момент сопротивления, радиус инерции.

Статический момент площади

Интегралы вида:

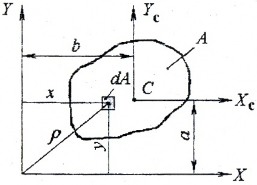
называются статическими моментами площади сечения A относительно осей X и Y соответственно.

В тех случаях, когда сечение может быть разделено на простейшие фигуры площади Ai и координаты центров тяжести xi и yi которых известны, статические моменты площади сложной фигуры определяются через суммирование

Статические моменты площади имеют размерность [м3] и могут принимать любые числовые значения. Для осей XC, YC, проходящих через центр тяжести сечения C (центральные оси), статические моменты равны нулю:

Координаты центров тяжести сечения определяются относительно так называемых вспомогательных осей по формулам:

Если сечение имеет ось симметрии, то центр тяжести находится на этой оси и его положение определяется одной координатой.

При наличии двух и более осей симметрии центр тяжести совпадает с точкой пересечения этих осей.

Моменты инерции

Моментами инерции площади сечения называют интегралы вида:

где:
Ix, Iy — осевые моменты инерции площади сечения относительно осей OX, OY соответственно;
Ixy — центробежный момент инерции;
Iρ — полярный момент инерции.

Размерность момента инерции [м4], Ix, Iy, I ρ всегда положительны, Ixy может принимать любые значения, при этом, если хотя бы одна из осей является осью симметрии, Ixy=0.

Зависимости между моментами инерции относительно параллельных осей выражаются формулами:

где a, b – расстояния между осями X, XC и Y, YC.

Оси, относительно которых Ixy=0, называют главными, а осевые моменты инерции относительно них – главными моментами инерции.

Главные оси, проходящие через центр тяжести сечения, называют главными центральными осями, а соответствующие им моменты инерции – главными центральными моментами инерции.

Главные оси характерны тем, что их моменты инерции принимают экстремальные значения (Imax, Imin).

Момент инерции сложного сечения относительно какой-либо оси находится суммированием моментов инерции составляющих его частей относительно той же оси:

Радиусы инерции

Величины

называют радиусами инерции сечения относительно осей OX и OY соответственно.

Эллипс, построенный в главных осях, с полуосями, равными главным радиусам инерции

называют эллипсом инерции.

Лекции по сопромату >
Примеры решения задач >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Источник

Зачем нужен момент инерции сечения

Несмотря на то, что наука о прочности давно уже шагнула вперёд, и давно уже развиваются многие её направления (строительная механика, механика разрушения, теория упругости и другие), а также несмотря на то, что всё чаще расчеты сложных конструкций выполняются при помощи метода конечного элемента посредством специализированных программных комплексов, прикидочные расчеты на основе методов сопромата не утратили своей актуальности. Ведь именно они, во-первых, позволяют дать оценку прочности конструкции «в полевых условиях» (без трудоёмкого построения конечно-элементной модели, без сложных математических выкладок), а во-вторых — позволяют это сделать достаточно быстро.

В основном, расчеты в сопротивлении материалов имеют целью проверить общую (а не местную) прочность балок. Поэтому расчетная схема принимается упрощенной, и многими конструктивными элементами, даже являющимися концентраторами напряжений, в ней пренебрегают. Тем не менее, несмотря на ряд упрощений в схеме и принятые допущения (гипотезы, принятые для построения теории сопротивления материалов), в этой науке разработаны методы, позволяющие с довольно большой точностью определить опасные сечения и напряжения, возникающие в них.

Вообще, поперечное сечение балки может представлять собой тавр, швеллер, двутавр, круг, прямоугольник, кольцо, полый прямоугольник и т.п. или может быть составным, т.е. составленным из нескольких однотипных или различных профилей. От его формы и размеров зависит прочность и жесткость балки. Площадь поперечного сечения является важной характеристикой, но знать только лишь её достаточно разве что для задач на центральное растяжение. Если же балка испытывает изгиб или кручение, то знать только лишь площадь поперечного сечения оказывается недостаточно. Балка может «проходить» (т.е. обладать достаточной прочностью и жесткостью) с одним типом сечения и «не проходить» с другим типом сечения такой же площади. В процессе решения задач по сопромату, касающихся определения напряжений в балке при её изгибе или кручении, проверке устойчивости сжатых стержней, а также при решении некоторых других задач требуется знать не только площадь, но и другие геометрические характеристики сечения (момент инерции площади сечения, момент сопротивления площади сечения, полярный момент инерции площади сечения). Во-первых, они требуются для решения конкретной задачи об определении напряжений в данной балке с заданными размерами поперечного сечения. Во-вторых, они нужны для выполнения сравнительного анализа разных типов сечений (например, выбора среди нескольких различных сечений с одинаковой площадью именно того сечения, которое будет лучше сопротивляться изгибу или кручению), для подбора оптимального сечения для балки, работающей в конкретно заданных условиях. Поскольку нахождение геометрических характеристик сечения требует определенных знаний и практических навыков, в любом учебнике или справочнике по сопромату выделен раздел, посвященный определению этих характеристик, а в любом задачнике по сопромату приведены задачи по нахождению момента инерции или момента сопротивления сечения.

Что такое момент инерции сечения

Обычно, когда речь идёт о геометрических характеристиках сечения, слово «площадь» опускают, чтобы не было нагромождения слов, и говорят не «момент инерции площади сечения», «момент сопротивления площади сечения», а просто «момент инерции сечения», «момент сопротивления сечения» или даже просто «момент инерции», «момент сопротивления». При этом различают осевой, полярный и центробежный момент инерции площади сечения.

Осевой момент инерции площади фигуры (сечения) — это интеграл произведений элементарных площадок данного сечения на квадраты их расстояний от рассматриваемой оси. Другое, менее распространенное его название – экваториальный момент инерции. Величина осевого момента инерции всегда положительна.

Полярный момент инерции площади фигуры (сечения) относительно данной точки (полюса) — это интеграл произведений элементарных площадок на квадраты их расстояний от полюса. Величина полярного момента инерции всегда положительна.

Центробежный момент инерции площади фигуры — это интеграл произведений элементарных площадок на их расстояния от координатных осей. В зависимости от положения осей центробежный момент инерции может быть положительным или отрицательным, а также равным нулю. При повороте осей вокруг начала координат на 90 градусов знак центробежного момента инерции меняется на обратный.

Задавая вопросы «в чем измеряется момент инерции», «какова единица измерения момента инерции», «как обозначается момент инерции» необходимо четко представлять, что именно имеется в виду: момент инерции сечения (о котором идёт речь в сопромате и, в частности, в настоящей статье) или же момент инерции тела (который упоминается в физике и в теории механизмов и машин). Размерность момента инерции сечения – это размерность длины в четвертой степени (например, см4, м4, мм4). Моменты инерции сечений стандартных профилей (швеллеров, уголков, тавров, двутавров) приведены в справочных таблицах в размерности «см4». При необходимости, данную в таблице величину можно представить в другой единице измерения. Обычно при решении задач возникает необходимость перевода этой величины в «мм4». Обозначается момент инерции сечения буквой I с нижним индексом, который указывает, относительно какой оси вычислена данная характеристика (например, Ix, Iy). Момент сопротивления сечения обозначается буквой W, также с нижним индексом, указывающим на ось, относительно которой дана эта величина (например, Wx, Wy). 

Что такое главные оси

Главные оси инерции – оси, относительно которых центробежный момент инерции равен нулю.

Главные центральные оси — главные оси, проходящие через центр тяжести сечения.

Как найти момент инерции сечения

При вычислении момента инерции сечения можно воспользоваться непосредственно определением момента инерции и вычислить эту характеристику сечения путём нахождения интеграла по площади. Так и поступают при нахождении момента инерции треугольника, круга, прямоугольника, кругового сектора и других простых фигур.

Обозначив характерные размеры сечения через параметры (т.е. буквами) и выполнив соответствующее интегрирование по площади, получают формулы для определения моментов инерции этих сечений. Ход решения показан, например, в учебнике по сопромату Г.С. Писаренко на примере вывода формул для определения момента инерции прямоугольника, треугольника, кругового сектора и эллипса. Такие формулы приведены во многих справочниках по сопромату (например, в книге Писаренко Г.С., Яковлев А.П. Матвеев В.В. Справочник по сопротивлению материалов. – К: Наукова думка, 1975, на страницах 24 — 77) для многих типов сечений (квадрат, полый квадрат, прямоугольник, полый прямоугольник, прямоугольник с круглым отверстием, прямоугольник с двумя отверстиями, прямоугольник с полукруглыми вырезами, повернутый прямоугольник, крестовина, корытное сечение, треугольник, трапеция, круг, кольцо, круговое незамкнутое тонкостенное кольцо, полукруг, четверть круга, круговой сектор, круговой сегмент, полукольцо, сектор кольца, круг с лыской, правильный шестиугольник, правильный многоугольник, круговое сечение с одной или с двумя шпоночными канавками, эллипс, полуэллипс, четверть эллипса, полый эллипс, параболический сегмент, параболический полусегмент, круговой треугольник, сечение железнодорожного рельса). Готовыми формулами из справочника пользоваться намного проще, чем выводить каждый раз нужную формулу самостоятельно путём интегрирования.

В этом же справочнике приведены и формулы для приближенного вычисления геометрических характеристик (F, I, W) сечений стандартных прокатных профилей: уголков (равнобокого и неравнобокого), швеллера, тавра, двутавра, однако на практике этими формулами пользуются весьма редко, т.к. все необходимые характеристики стандартных сечений уже вычислены и приведены в соответствующих нормативных документах (см. ГОСТ 8240-97 для швеллеров, ГОСТ 8509-93 для равнополочных уголков, ГОСТ 8510-86 для неравнополочных уголков, ГОСТ 26020-83 и ГОСТ 8239-89 для двутавров). Выдержки из перечисленных выше стандартов приведены во многих справочниках, учебниках и решебниках по сопромату.

Скачать примеры решения задач, касающиеся того, как найти момент инерции и момент сопротивления, можно здесь (бесплатно, без регистрации):

При вычислении моментов инерции сложных сечений их разбивают на отдельные простые части, моменты инерции которых известны.

Момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями.

Центробежный момент инерции относительно любой системы прямоугольных осей равен центробежному моменту инерции относительно системы центральных осей, параллельных данным, плюс произведение площади фигуры на координаты ее центра тяжести в новых осях.

При повороте прямоугольных осей сумма осевых моментов инерции не изменяется и равна полярному моменту инерции относительно начала координат.

Момент инерции фигуры относительно какой-либо оси можно представить в виде произведения площади фигуры на квадрат некоторой величины, называемой радиусом инерции.

Осевым моментом сопротивления называется отношение момента инерции относительно данной оси к расстоянию до наиболее удаленной точки поперечного сечения.

Размерность моментов сопротивления – единица длины в кубе (например, см3, м3, мм3).

Практическое значение имеют моменты сопротивления относительно главных центральных осей, которые обычно называются просто моментами сопротивления. Полярным моментом сопротивления называется отношение полярного момента инерции к расстоянию от полюса до наиболее удаленной точки сечения.

Источники:

  • Н.М. Беляев. Сопротивление материалов.
  •  Г.С. Писаренко, А.П. Яковлев, В.В. Матвеев. Справочник по сопротивлению материалов.
  • А.В. Александров, В.Д. Потапов, Б.П. Державин. Сопротивление материалов.
  • reshusam.ucoz.ru — Примеры определения моментов инерции сечений.

Дополнительно на Геноне:

  • Что такое сопромат
Источник

Добавить комментарий