Примеры решений: кривые второго порядка
В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости на тему Кривые второго порядка: приведение к каноническому виду, нахождение характеристик, построение графика т.п.
Кривые 2-го порядка: решения онлайн
Задача 1. Привести к каноническому виду уравнение кривой 2 порядка, найти все ее параметры, построить кривую.
Задача 2. Дана кривая. Привести к каноническому виду. Построить и определить вид кривой.
Задача 3. Выяснить вид кривой по общему уравнению, найти её параметры и положение в системе координат. Сделать рисунок.
Задача 4. Общее уравнение кривой второго порядка привести к каноническому. Найти координаты центра, координаты вершин и фокусов. Написать уравнения асимптот и директрис. Построить линии на графики, отметить точки.
Задача 5. Дана кривая $y^2+6x+6y+15=0$.
1. Докажите, что данная кривая – парабола.
2. Найдите координаты ее вершины.
3. Найдите значения ее параметра $р$.
4. Запишите уравнение ее оси симметрии.
5. Постройте данную параболу.
Задача 6. Дана кривая $5x^2+5y^2+6xy-16x-16y=16$.
1. Докажите, что эта кривая – эллипс.
2. Найдите координаты центра его симметрии.
3. Найдите его большую и малую полуоси.
4. Запишите уравнение фокальной оси.
5. Постройте данную кривую.
Задача 7. Найти уравнения параболы и её директрисы, если известно, что парабола имеет вершину в начале координат и симметрична относительно оси $Ox$ и что точка пересечения прямых $y=x$ и $x+y-2=0$ лежит на параболе.
Задача 8. Составить уравнение кривой, для каждой точки которой отношение расстояния до точки $F(0;10)$ к расстоянию до прямой $x=-4$ равно $sqrt<2/5>$. Привести это уравнение к каноническому виду и определить тип кривой.
Задача 9. Даны уравнения асимптот гиперболы $y=pm 5x/12$ и координаты точки $M(24,5)$, лежащей на гиперболе. Составить уравнение гиперболы.
Задача 10. Даны уравнение параболы $y=1/4 x^2+1$ и точка $C(0;2)$, которая является центром окружности. Радиус окружности $r=5$.
Требуется найти
1) точки пересечения параболы с окружностью
2) составить уравнение касательной и нормали к параболе в точках её пересечения с окружностью
3) найти острые углы, образуемые кривыми в точках пересечения. Чертёж.
Уравнения с параметрами.
Исследование и решение уравнений с параметрами считается не самым простым разделом школьной математики. Однако, параметр, как понятие, часто воспринимается школьниками гораздо более сложным, чем есть в действительности. Здесь в первом пункте представлены очень простые вводные примеры использования параметров в уравнениях. Те, для кого это понятие не составляет большой трудности, могут сразу перейти к решению задач, которые представлены ниже.
Что такое уравнение с параметром?
Допустим нам нужно решить уравнение 2х + 5 = 2 − x.
Решение: 2x + x = 2 − 5; 3x = −3; x = −3/3 = −1.
Теперь нужно решить уравнение 2x + 5 = 3 − x.
Решение: 2x + x = 3 − 5; 3x = −2; x = −2/3
Затем нужно решить уравнение 2x + 5 = 0,5 − x.
Решение: 2x + x = 0,5 − 5; 3x = −4,5; x = −4,5/3 = −1,5.
А потом может потребоваться решить уравнение 2x + 5 = 10,7 − x или уравнение 2x + 5 = −0,19 − x.
Понятно, что уравнения похожи, а потому их решение будет сопровождаться теми же действиями, что выше. Возникает естественный вопрос – сколько можно делать одно и то же?
Уменьшим себе трудозатраты. Заметим, что все эти уравнения отличаются только одним числом в правой части. Обозначим это число символом a .
Получим уравнение 2х + 5 = a − х,
где a – переменная величина, вместо которой можно подставить нужное числовое значение и получить нужное уравнение. Эта переменная и называется параметром.
Решим это уравнение так же, как и все предыдущие.
Решение: 2х + 5 = a − x; 2x + x = a − 5; 3x = a − 5; x = (a − 5)/3.
Теперь для того, чтобы найти ответы для двух последних примеров, мы можем не повторять полностью всё решение каждого уравнения, а просто подставить в полученную формулу для х числовое значение параметра а:
x = (10,7 − 5)/3 = 5,7/3 = 1,9;
x = (−0,19 − 5)/3 = −5,19/3 = −1,73.
Таким образом, под термином “уравнение с параметром”, фактически, скрывается целое семейство “почти одинаковых уравнений” , которые отличаются друг от друга только одним числом (одним слагаемым или одним коэффициентом) и одинаково решаются. Параметр – это число, которое меняется от уравнения к уравнению.
Полученную формулу для корня уравнения мы можем запрограммировать на компьютере. Достаточно будет только ввести значение параметра a, чтобы получить решение любого такого уравнения.
Рассмотрим еще один пример.
Замечаем, что они похожи друг на друга и отличаются только первым коэффициентом. Обозначим его, например, символом k.
Решим уравнение kх + 5 = 2 − x с параметром k.
С помощью этой формулы вычислим все ответы для приведенных уравнений.
x = −3/(2 + 1) = −1
x = −3/(3 + 1) = −0,75
x = −3/(−4 + 1) = 1
x = −3/(17 + 1) = −1/6
Можем ли мы теперь запрограммировать эту формулу и сказать, что с её помощью можно решить любое аналогичное уравнение?
Запрограммировать можем. Компьютер справится как с очень большими значениями коэффициента, так и с очень маленькими.
Например, если введём k = 945739721, то для уравнения заданного вида будет получен корень примерно равный −0,0000000031721201195353831188, если k = 0,0000004, то получим корень ≈ −2,9999988000004799998080000768.
Но, если мы введем в программу, казалось бы, более простое значение k = −1, то компьютер зависнет.
Почему?
Посмотрим внимательнее на формулу x = −3/(−1 + 1) = −3/0. Деление на ноль.
Посмотрим на соответствующее уравнение −1·х + 5 = 2 − x.
Преобразуем его −х + x = 2 − 5.
Оказывается, оно равносильно уравнению 0 = −3 (. ) и не может иметь корней.
Таким образом, из общего подхода к решению “почти одинаковых уравнений” могут существовать исключения, о которых нужно позаботиться отдельно. Т.е. провести предварительное исследование всего семейства уравнений. Именно этому и учатся на уроках математики с помощью так называемых задач с параметрами.
Графические способы решения уравнений
Сначала вспомним, что представляет собой графический способ решения обычного уравнения (без параметра).
Пусть дано уравнение вида f(x) = g(x) . Построим графики функций y = f(x) и y = g(x) и найдём точки пересечения этих графиков. Абсциссы точек пересечения и есть корни уравнения.
Для быстрого построения эскизов графиков повторите еще раз графики элементарных функций, которые изучаются в школьном курсе математики, и правила преобразования графиков функций.
Рассмотрим примеры.
1. Решить уравнение
2х + 5 = 2 − x

Ответ: x = −1.
2. Решить уравнение
2х 2 + 4х − 1 = 2х + 3

3. Решить уравнение
log2х = −0,5х + 4

Ответ: x = 2.
Первые два из приведенных уравнений вы можете решить и аналитически, так как это обычные линейное и квадратное уравнения. Второе уравнение содержит функции разных классов – степенную (здесь линейную) и трансцендентную (здесь логарифмическую). Для таких случаев выбор способов решения у школьников очень ограничен. Фактически, единственным доступным способом является именно графическое решение.
Внимание: Для корней, найденных графическим способом, обязательна проверка! Вы уверены, что на третьем рисунке пересечение именно в точке х = 4 , а не в точке 3,9 или 4,1? А если на реальном экзамене у вас нет возможности построить график достаточно точно? На чертеже “от руки” разброс может быть еще больше. Поэтому алгоритм действий должен быть следующим:
- Предварительный вывод: х ≈ 4.
- Проверка: log24 = −0,5·4 + 4; 2 = −2 + 4; 2 ≡ 2.
- Окончательный вывод х = 4.
Чтобы графически решать уравнения с параметрами надо строить не отдельные графики, а их семейства.
Решение уравнений с параметрами с помощью графиков.
Задача 1.
Найти все значения параметра q при которых уравнение |x + 1| − |x − 3| − x = q 2 − 8q + 13 имеет ровно 2 корня.
При каждом значении параметра q можно вычислить значение выражения q 2 − 8q + 13 . Результат обозначим переменной а.
Т.е. примем q 2 − 8q + 13 = a и решим уравнение с параметром |x + 1| − |x − 3| − x = a
Строим график функции y = |x + 1| − |x − 3| − x , расположенной в левой части уравнения.
Для этого разобьём числовую ось на отрезки точками, в которых каждый из встречающихся модулей принимает нулевое значение.

Для каждого из этих участков раскроем модули с учётом знаков.
Вспомним: по определению |x| = x, если х ≥ 0, и |x| = −x, если х Чтобы проверить знаки модулей на участке достаточно подставить любое промежуточное значение x из этого отрезка, например, −2, 0 и 4.
Таким образом на участке I, где −∞ имеем −(x + 1) + (x − 3) − x = − x − 4.
Следовательно, должны построить график функции y = − x − 4 .
Это линейная функция. Её график прямая линия, которую можно построить по двум точкам, например, x = 0, y = −4 и у = 0, x = −4. Cтроим всю прямую бледной линией, а затем выделяем часть графика, относящуюся только к рассматриваемому участку.
Аналогично, разбираемся с оставшимися двумя участками.
На участке II, где −1 имеем (x + 1) + (x − 3) − x = x − 2
и должны построить соответствующую часть графика функции y = x − 2 .
На участке III, где 3 , имеем (x + 1) − (x − 3) − x = − x + 4
и должны построить соответствующую часть графика функции y = − x + 4 .
Последовательное построение итогового графика показано ниже. (Чтобы увеличить рисунок, нужно щелкнуть по нему левой кнопкой мыши.)
Замечание: если вы освоили тему Преобразование графиков функций, то с этой частью задачи сможете справиться быстрее, чем показано в примере.
Итак, построение графика функции, расположенной в левой части уравнения, мы завершили. Посмотрим, что находится в правой части.
График функции y = a представляет собой прямую линию, параллельную оси абсцисс (Ox), и пересекающую ось ординат (Oy) в точке а. Так как а – параметр, который может принимать разные значения, то нужно построить целое семейство таких параллельных линий, пересекающих ось ординат на разной высоте. Очевидно, что все графики семейства построить мы не сможем, поскольку их бесконечное множество. Изобразим для примера несколько штук в районе уже построенного графика функции. Ниже прямые семейства y = a показаны красным цветом.
Из рисунка видно, что количество точек пересечения каждой из красных прямых с ранее построенным (зелёным) графиком зависит от высоты, на которой расположена эта прямая, т.е. от параметра а. Прямые, расположенные ниже y = −3 , пересекают график в одной точке, а значит эти уравнения имеют только одно решение. Прямые, проходящие на уровне −3 имеют по три точки пересечения, значит соответствующие уравнения будут иметь по три решения. Прямые, расположенные выше точки y = 1 , снова имеют только по одной точке пересечения.
Ровно две точки пересечения с зелёным графиком будут иметь только прямые y = 1 и y = −3 . Соответствующие уравнения будут иметь ровно два корня, что и требовалось определить в задании.
Однако мы нашли значения введённого нами параметра а, при котором заданное уравнение имеет 2 корня, а вопрос задачи состоял в том, чтобы найти все значения параметра q. Для этого придётся решить следующую совокупность уравнений: 
Это обычные квадратные уравнения, которые решаются через дискриминант или по теореме Виета. 
Таким образом, окончательный ответ: <2;4;6>.
Задача 2.
Найти все значения параметра a, при которых уравнение (2 − x)x(x − 4) = a имеет ровно 3 корня.
Рассмотрим функцию y = (2 − x)x(x − 4) . Видно, что если раскрыть скобки, то старший член будет −х 3 . Т.е. графиком функции должна быть кубическая парабола, причем на при x, стремящемcя к +∞, y → −∞, а при x, стремящемся к −∞, y → +∞.
Поскольку уравнение (2 − x)x(x − 4) = 0 имеет три корня 2, 0 и 4, то график функции будет пересекать ось абсцисс трижды.
Понятно, что при упомянутых условиях график непрерывной функции должен иметь участок с “волной”. Строим от руки эскиз графика.
Правая часть уравнения y = a такая же, как в предыдущей задаче. Поэтому дальнейшие построения не требуют комментариев. Смотрите рисунки. Чтобы увеличить, используйте щелчок мышью.






Из рисунков видно, что прямые, отделяющие линии с тремя точками пересечения от других случаев, проходят через экстремумы кубической функции. Поэтому определяем значения ymax и ymin через производную. (Исследовать функцию полностью не нужно, так как примерное положение точек экстремума мы видим на эскизе графика.) Обратите внимание на то, что при вычислении значений функции используются точные значения x и формулы сокращенного умножения. Приближенные значения в промежуточных вычислениях не используют.
Ответ: 
Задача для самостоятельного решения
Задача 3.
При каком наибольшем отрицательном значении параметра а уравнение  имеет один корень?
имеет один корень?
Ответ: -1,625
Задача реального экзамена ЗНО-2013 (http://www.osvita.ua/).
Переход на главную страницу сайта “Математичка”.

Есть вопросы? пожелания? замечания?
Обращайтесь – mathematichka@yandex.ru
Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено. Ставьте гиперссылку.
Кривые второго порядка – определение и построение с примерами решения
Содержание:
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру – значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде 
- Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения

- если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.
Это определение в более компактной записи выглядит следующим образом. Уравнение  называется уравнением фигуры, если
называется уравнением фигуры, если 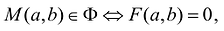 , то есть (а, b) – решение уравнения F(x,y) = 0.
, то есть (а, b) – решение уравнения F(x,y) = 0.
Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения  , т.е. уравнение фигуры задает эту фигуру.
, т.е. уравнение фигуры задает эту фигуру.
Возможны два вида задач:
- дано уравнение
 и надо построить фигуру Ф, уравнением которой является
и надо построить фигуру Ф, уравнением которой является  ;
; - дана фигура Ф и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения  и решается, чаще всего, методами математического анализа.
и решается, чаще всего, методами математического анализа.
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
Эллипс
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 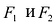 , есть величина постоянная (большая, чем расстояние между
, есть величина постоянная (большая, чем расстояние между 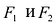 ).
).
Точки 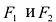 называются фокусами эллипса. Обозначив расстояние между фокусами через 2с, а сумму расстояний от точек эллипса до фокусов через 2а, имеем с b. В этом случае а называется большой полуосью, a b – малой.
называются фокусами эллипса. Обозначив расстояние между фокусами через 2с, а сумму расстояний от точек эллипса до фокусов через 2а, имеем с b. В этом случае а называется большой полуосью, a b – малой.
Если а =Ь, то уравнение (7.3) можно переписать в виде:
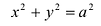 (7.5)
(7.5)
Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 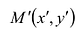 координаты которой задаются формулами
координаты которой задаются формулами 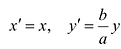 будет окружность (4) переводить в эллипс, заданный соотношением
будет окружность (4) переводить в эллипс, заданный соотношением 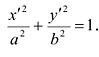
Число 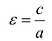 называется эксцентриситетом эллипса. Эксцентриситет
называется эксцентриситетом эллипса. Эксцентриситет 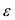 характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении
характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении 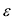 становится более вытянутым
становится более вытянутым
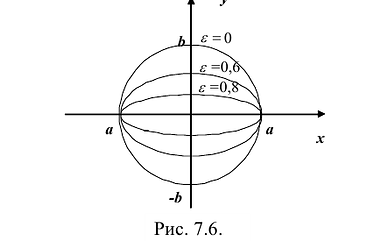
Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами 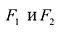 . Их длины
. Их длины 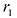 и
и 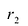 задаются формулами
задаются формулами 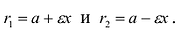 Прямые
Прямые 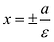 называются директрисами эллипса. Директриса
называются директрисами эллипса. Директриса 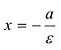 называется левой, а
называется левой, а 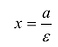 – правой. Так как для эллипса
– правой. Так как для эллипса 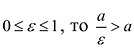 и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая – правее правой вершины.
и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая – правее правой вершины.
Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е. 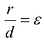
Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 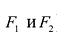 есть величина постоянная (не равная нулю и меньшая, чем расстояние между
есть величина постоянная (не равная нулю и меньшая, чем расстояние между 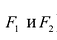 ).
).
Точки 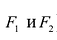 называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 2с. Модуль расстояний от точек гиперболы до фокусов
называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 2с. Модуль расстояний от точек гиперболы до фокусов 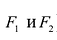 обозначим через а. По условию, а 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А – произвольная точка плоскости с координатами (х, у) и пусть
обозначим через а. По условию, а 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А – произвольная точка плоскости с координатами (х, у) и пусть 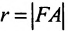 . Тогда точка А будет лежать на параболе, если r=d, где d- расстояние от точки А до директрисы. Фокус F имеет координаты
. Тогда точка А будет лежать на параболе, если r=d, где d- расстояние от точки А до директрисы. Фокус F имеет координаты 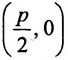 .
.
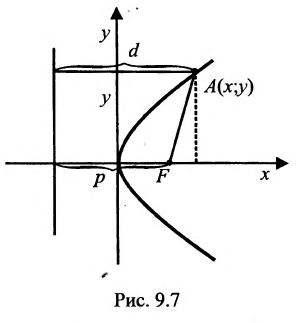
Тогда 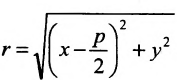 А расстояние
А расстояние 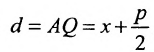 Подставив в формулу r=d, будем иметь
Подставив в формулу r=d, будем иметь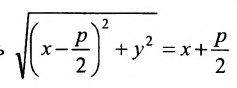 . Возведя обе части равенства в квадрат, получим
. Возведя обе части равенства в квадрат, получим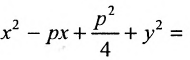
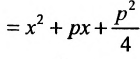 или
или
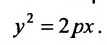 (9.4.1)
(9.4.1)
Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 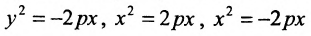 также определяют параболы.
также определяют параболы.
Легко показать, что уравнение 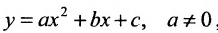 , определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а
, определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а 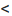 О. Для этого выделим полный квадрат:
О. Для этого выделим полный квадрат:
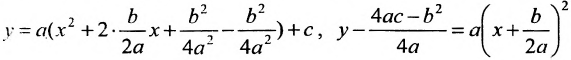
и сделаем параллельный перенос по формулам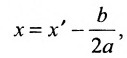
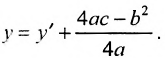
В новых координатах преобразуемое уравнение примет вид: 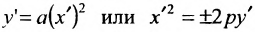 где р – положительное число, определяется равенством
где р – положительное число, определяется равенством 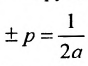 .
.
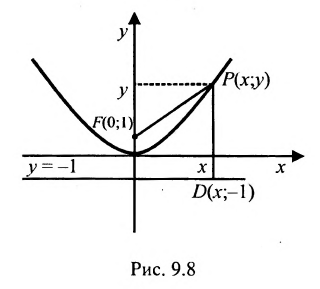
Пример:
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию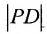 , называется параболой. Прямая у = -1 называется директрисой параболы, а точка F – фокусом параболы. Чтобы выяснить, как располагаются точки Р, удовлетворяющие условию
, называется параболой. Прямая у = -1 называется директрисой параболы, а точка F – фокусом параболы. Чтобы выяснить, как располагаются точки Р, удовлетворяющие условию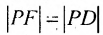 , запишем это равенство с помощью координат:
, запишем это равенство с помощью координат: 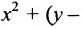
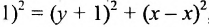 , или после упрощения
, или после упрощения 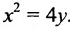 . Это уравнение геометрического места точек, образующих параболу (рис. 9.8).
. Это уравнение геометрического места точек, образующих параболу (рис. 9.8).
Кривые второго порядка на плоскости
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
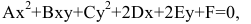
где коэффициенты А, В и С не равны одновременно нулю 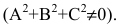
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению
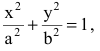 которое называют каноническим уравнением эллипса.
которое называют каноническим уравнением эллипса.
Число а называют большей полуосью эллипса, число 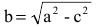 – мень-
– мень-
шей полуосью эллипса, 2а и 2b – соответственно большей и меньшей осями эллипса. Точки 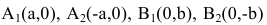 называют вершинами эллипса, а
называют вершинами эллипса, а 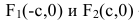 – его фокусами (рис. 12).
– его фокусами (рис. 12).
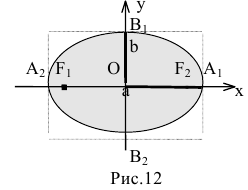
Координатные оси являются осями симметрии эллипса, а начало координат – его центром симметрии. Центр симметрии эллипса называется центром эллипса.
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид 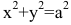 и определяет окружность радиуса а с центром в начале координат.
и определяет окружность радиуса а с центром в начале координат.
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
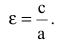
Эксцентриситет изменяется от нуля до единицы 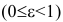 и характеризует форму эллипса. Для окружности
и характеризует форму эллипса. Для окружности 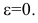 Чем больше эксцентриситет, тем более вытянут эллипс.
Чем больше эксцентриситет, тем более вытянут эллипс.
Пример:
Показать, что уравнение
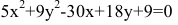
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:
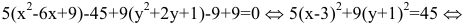
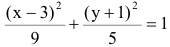 – каноническое уравнение эллипса с центром в точке
– каноническое уравнение эллипса с центром в точке 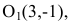 большей полуосью а=3 и меньшей полуосью
большей полуосью а=3 и меньшей полуосью 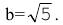
Найдем эксцентриситет эллипса:
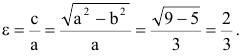
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 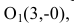 а оси
а оси 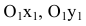 параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е.
параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е. 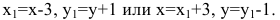
В новой системе координат координаты 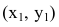 вершин и фокусов гиперболы будут следующими:
вершин и фокусов гиперболы будут следующими:
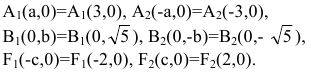
Переходя к старым координатам, получим:
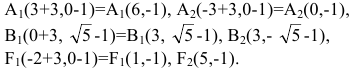
Построим график эллипса.
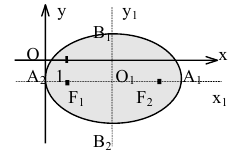 Задача решена.
Задача решена.
Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
[spoiler title=”источники:”]
http://mathematichka.ru/school/parametry/param_equation.html
http://www.evkova.org/krivyie-vtorogo-poryadka
[/spoiler]
Примеры решений: кривые второго порядка
В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости на тему Кривые второго порядка: приведение к каноническому виду, нахождение характеристик, построение графика т.п.
См. также: Решения по аналитической геометрии на плоскости,
Решения задач с квадратичными формами
Полезная страница? Сохрани или расскажи друзьям
Задача 1. Привести к каноническому виду уравнение кривой 2 порядка, найти все ее параметры, построить кривую.
$$9x^2-4y^2-90x-8y+185=0.$$
Задача 2. Дана кривая. Привести к каноническому виду. Построить и определить вид кривой.
$$6x^2+2sqrt{5}xy+2y^2=21.$$
Задача 3. Выяснить вид кривой по общему уравнению, найти её параметры и положение в системе координат. Сделать рисунок.
$$3x^2-6y^2-12x-108y-492=0.$$
Задача 4. Общее уравнение кривой второго порядка привести к каноническому. Найти координаты центра, координаты вершин и фокусов. Написать уравнения асимптот и директрис. Построить линии на графики, отметить точки.
$$9x^2+25y^2-18x-100y-116=0.$$
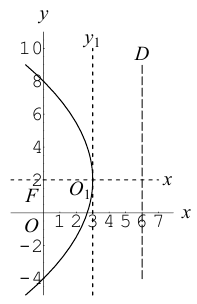
Задача 5. Дана кривая $y^2+6x+6y+15=0$.
1. Докажите, что данная кривая – парабола.
2. Найдите координаты ее вершины.
3. Найдите значения ее параметра $р$.
4. Запишите уравнение ее оси симметрии.
5. Постройте данную параболу.
Задача 6. Дана кривая $5x^2+5y^2+6xy-16x-16y=16$.
1. Докажите, что эта кривая – эллипс.
2. Найдите координаты центра его симметрии.
3. Найдите его большую и малую полуоси.
4. Запишите уравнение фокальной оси.
5. Постройте данную кривую.
Задача 7. Найти уравнения параболы и её директрисы, если известно, что парабола имеет вершину в начале координат и симметрична относительно оси $Ox$ и что точка пересечения прямых $y=x$ и $x+y-2=0$ лежит на параболе.
Задача 8. Составить уравнение кривой, для каждой точки которой отношение расстояния до точки $F(0;10)$ к расстоянию до прямой $x=-4$ равно $sqrt{2/5}$. Привести это уравнение к каноническому виду и определить тип кривой.
Задача 9. Даны уравнения асимптот гиперболы $y=pm 5x/12$ и координаты точки $M(24,5)$, лежащей на гиперболе. Составить уравнение гиперболы.
Задача 10. Даны уравнение параболы $y=1/4 x^2+1$ и точка $C(0;2)$, которая является центром окружности. Радиус окружности $r=5$.
Требуется найти
1) точки пересечения параболы с окружностью
2) составить уравнение касательной и нормали к параболе в точках её пересечения с окружностью
3) найти острые углы, образуемые кривыми в точках пересечения. Чертёж.
Не получаются задачи? Решим быстро и подробно!
Содержание:
Аналитическая геометрия
В этой главе все геометрические объекты мы будем определять и изучать с помощью соответствующих уравнений этих объектов и, следовательно, в принципе геометрия может быть изложена без единого чертежа. И, действительно, все чертежи, которые мы будем использовать, будут служить лишь для визуальной иллюстрации наших рассуждений.
Уравнение поверхности в выбранной декартовой системе координат 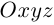
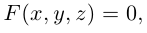
т. е. в виде связи или зависимости между координатами х, у, z произвольной точки поверхно-аналогично, уравнение
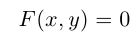
определяет некоторую линию (кривую) в системе координат 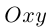 на плоскости.
на плоскости.
Кривая в пространстве может быть задана как пересечение двух поверхностей и, следовательно, она определяется системой из уравнений этих поверхностей:
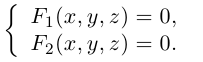
Кроме того, кривую на плоскости или в пространстве можно также задать с помощью зависимостей координат произвольной то’жи этой кривой от некоторого параметра, т. е. с помощью параметрических уравнений:

где t – действительный параметр.
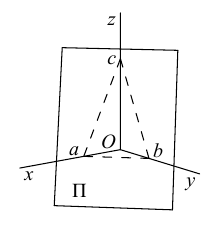
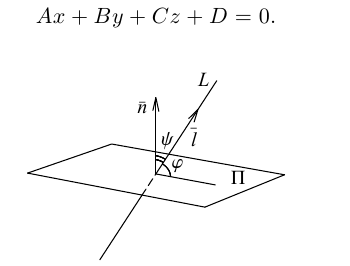
Плоскость в пространстве. Различные виды уравнения плоскости
Найдем уравнение плоскости в пространстве с выбранной в нем декартовой системой координат 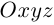 . Будем исходить из того, что положение этой плоскости полностью определяется точкой
. Будем исходить из того, что положение этой плоскости полностью определяется точкой 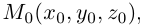 . через которую проходит плоскость и ненулевым вектором
. через которую проходит плоскость и ненулевым вектором 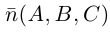 . ей перпендикулярным. Вектор
. ей перпендикулярным. Вектор  называется нормальным вектором плоскости.
называется нормальным вектором плоскости.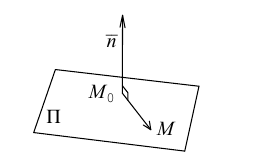
Пусть  — произвольная точка плоскости П. Тогда вектор
— произвольная точка плоскости П. Тогда вектор  ортогонален вектору
ортогонален вектору 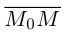 и, следовательно,
и, следовательно,
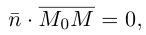
или, учитывая, что 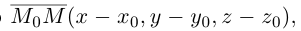 запишем в координатах уравнение плоскости П :
запишем в координатах уравнение плоскости П :
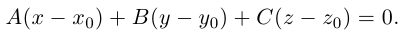
Преобразовав полученное уравнение к виду
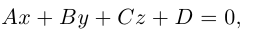
мы получим тем самым общее уравнение плоскости.
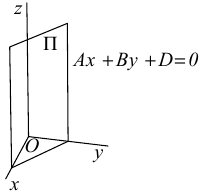
Рассмотрим теперь некоторые частные случаи общего уравнения плоскости. Если в общем уравнении плоскости отсутствует, одна из координат, то нормальный вектор  этой плоскости перпендикулярен соответствующей координатной оси и, следовательно, плоскость расположена параллельно этой координатной оси.
этой плоскости перпендикулярен соответствующей координатной оси и, следовательно, плоскость расположена параллельно этой координатной оси.
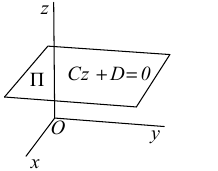
Аналогично, если в общем уравнении плоскости отсутствуют две координаты, то нормальный вектор данной плоскости перпендикулярен соответствующей координатной плоскости и, значит, плоскость расположена параллельно этой координатной плоскости.
Научимся теперь находить уравнение плоскости по трем элементам.
1) Плоскость, проходящая через точку, параллельно двум векторам.
Пусть плоскость  проходит через точку
проходит через точку  параллельно неколлинеарным векторам
параллельно неколлинеарным векторам 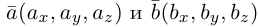 .
.
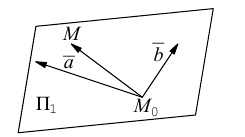
Обозначим через 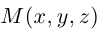 произвольную точку плоскости
произвольную точку плоскости  Для точек данной плоскости и только для них три вектора
Для точек данной плоскости и только для них три вектора 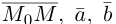 компланарны и, следовательно (глава II, §5, теорема), их смешанное произведение равно нулю, т. е.
компланарны и, следовательно (глава II, §5, теорема), их смешанное произведение равно нулю, т. е.
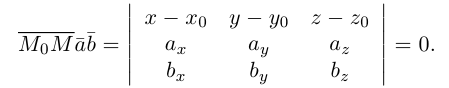
Раскрыв определитель (проще всего, разлагая его по первой строке), получим общее уравнение плоскости 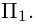
2)Плоскость, проходящая через две точки, параллельно вектору.
Найдем уравнение плоскости 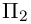 , проходящей через две точки
, проходящей через две точки 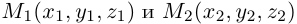 , параллельно ненулевому вектору
, параллельно ненулевому вектору 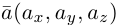 . Задача сводится к предыдущей, если положить, например,
. Задача сводится к предыдущей, если положить, например, 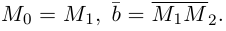 Тогда
Тогда
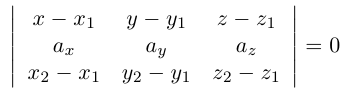
– искомое уравнение плоскости 
3)Плоскость, проходящая через три точки.
Если плоскость  проходит через три точки
проходит через три точки 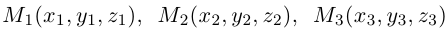 , не лежащие на одной прямой, то ее уравнение можно найти, как и в случае 1). положив например,
, не лежащие на одной прямой, то ее уравнение можно найти, как и в случае 1). положив например, 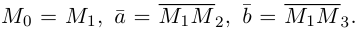 Следовательно, уравнение плоскости
Следовательно, уравнение плоскости  записать в виде:
записать в виде:
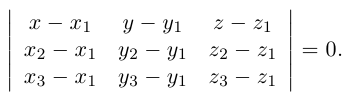
Замечание. Во всех трех случаях уравнение плоскости можно найти, вычислив предварительно ее нормальный вектор. Например, в первом случае в качестве нормального вектора можно взять векторное произведение 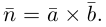 Тогда
Тогда 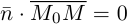 — уравнение плоскости.
— уравнение плоскости.
Пример №1
Найти уравнение плоскости 11 ^ – перпендикулярной плоскости
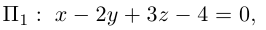
параллельной вектору 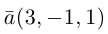 и проходящей через точку пересечения плоскости
и проходящей через точку пересечения плоскости 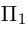 с координатного осью
с координатного осью 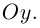
Решение. Из уравнения плоскости 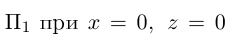 находим у = — 2. Следовательно, плоскость
находим у = — 2. Следовательно, плоскость  проходит через точку
проходит через точку 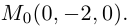 Кроме того,
Кроме того, 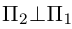 , поэтому нормальный вектор
, поэтому нормальный вектор 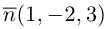 плоскости
плоскости 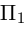 параллелен плоскости
параллелен плоскости  . Осталось записать искомое уравнение по трем элементам: точке
. Осталось записать искомое уравнение по трем элементам: точке  и векторам
и векторам  . Имеем:
. Имеем:
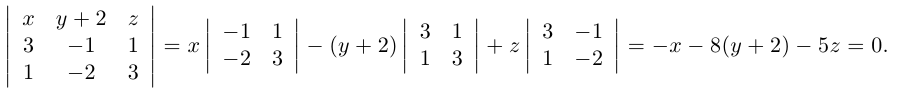
Таким образом, общее уравнение плоскости 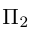 имеет вид:
имеет вид:
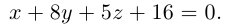
Пусть плоскость 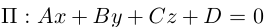 не проходит через начало координат и не параллельна ни одной из координатных осей. Тогда, очевидно, все числа A, В, С, D отличны от нуля.
не проходит через начало координат и не параллельна ни одной из координатных осей. Тогда, очевидно, все числа A, В, С, D отличны от нуля.
Разделив обе части уравнения плоскости на число D. мы можем записать его в виде:
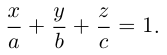
Числа а, b, с представляют собой величины отрезков, которые плоскость П отсекает на координатных осях. Полученное уравнение называется уравнением плоскости в отрезках.
Найдем теперь формулу для вычисления расстояния от точки 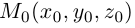 до плоскости
до плоскости 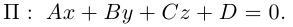
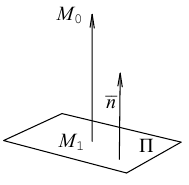
Обозначим искомое расстояние через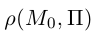 . Очевидно.
. Очевидно.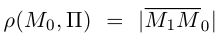 , где точка
, где точка 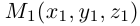 — основание перпендикуляра, опущенного из точки
— основание перпендикуляра, опущенного из точки 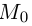 на плоскость П. Вычислим скалярное произведение коллинеарных векторов
на плоскость П. Вычислим скалярное произведение коллинеарных векторов 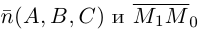 . С одной стороны,
. С одной стороны,
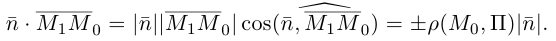
С другой,
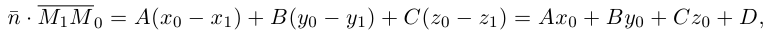
так как 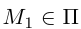 и поэтому
и поэтому 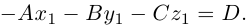 Следовательно, расстояние от точки
Следовательно, расстояние от точки 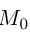 до плоскости П вычисляется по формуле:
до плоскости П вычисляется по формуле:
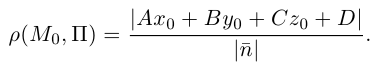
В заключение этого параграфа выясним характер взаимного расположения двух плоскостей. Пусть плоскости заданы своими общими уравнениями:
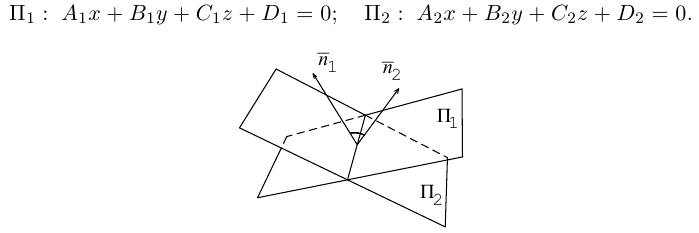
Очевидно, что угол 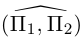 между этими плоскостями равен углу между их нормальными векторами
между этими плоскостями равен углу между их нормальными векторами 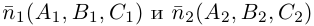 и, следовательно,
и, следовательно,
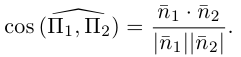
В частности,
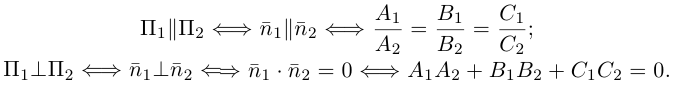
Пример №2
Убедиться в том, что плоскость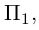 отсекающая на координатных осях
отсекающая на координатных осях 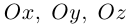 отрезки величиной 2, —1, 2 соответственно и плоскость
отрезки величиной 2, —1, 2 соответственно и плоскость
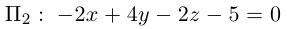
параллельны и найти расстояние между ними.
Решение. Запишем уравнение плоскости II| в отрезках:
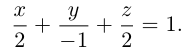
Преобразовав его к общему виду, получим:
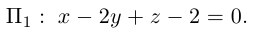
Так как нормальные векторы 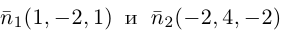 плоскостей
плоскостей 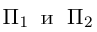 коллинеарны. то эти плоскости параллельны. Возьмем какую-нибудь точку в плоскости
коллинеарны. то эти плоскости параллельны. Возьмем какую-нибудь точку в плоскости 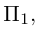 например,
например, 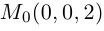 . Тогда
. Тогда
Уравнения прямой в пространстве
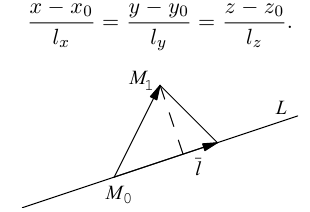
Пусть прямая L в пространстве с декартовой системой координат 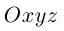 проходит через точку
проходит через точку 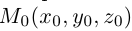 и параллельна ненулевому вектору
и параллельна ненулевому вектору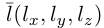 , который называется направляющим вектором прямой.
, который называется направляющим вектором прямой.
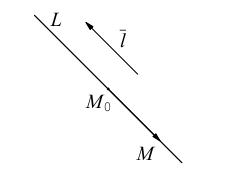
Обозначим через 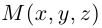 произвольную точку прямой L. Вектор
произвольную точку прямой L. Вектор 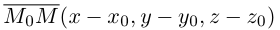 коллинеарен вектору
коллинеарен вектору 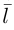 и, следовательно, их координаты пропорциональны, т. е.
и, следовательно, их координаты пропорциональны, т. е.
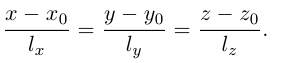
Эта двойная пропорция представляет собой канонические уравнения прямой в пространстве.
Заметим, что в канонических уравнениях прямой формально допускается запись нулей в знаменателях, это означает лишь то, что прямая перпендикулярна соответствующей координатной оси или координатной плоскости.
Если прямая проходит через две точки 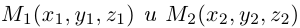 , то в качестве ее направляющего вектора можно взять вектор
, то в качестве ее направляющего вектора можно взять вектор 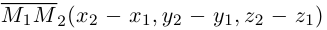 и, следовательно, канонические уравнения этой прямой имеют вид:
и, следовательно, канонические уравнения этой прямой имеют вид:
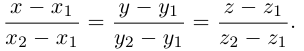
Коллинеарные векторы 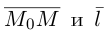 линейно связаны (глава II. §1), т.е. существует действительный параметр t такой, что
линейно связаны (глава II. §1), т.е. существует действительный параметр t такой, что
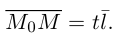
Если точка М перемещается вдоль прямой, параметр t изменяется в пределах от 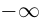 до
до 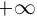 . Так как
. Так как 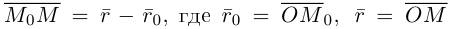 – радиусы-векторы точек
– радиусы-векторы точек 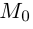 и М соответственно, то последнее уравнение мы можем переписать в виде
и М соответственно, то последнее уравнение мы можем переписать в виде
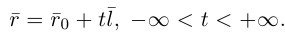
Это уравнение называется векторным уравнением прямой.
Переходя в полученном векторном уравнении к координатам, запишем параметрические уравнения прямой:
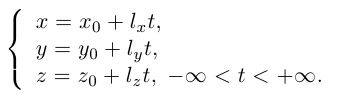
Прямую в пространстве можно задать также как пересечение двух плоскостей.
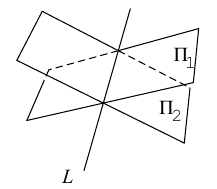
Система
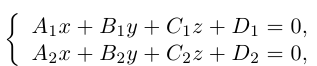
составленная из уравнений этих плоскостей, дает нам общие уравнения прямой в пространстве. Для перехода от общих к каноническим уравнениям прямой, достаточно найти какую-нибудь точку на ней, решив при фиксированном значении одной из координат систему уравнений плоскостей, а также определить направляющий вектор прямой, которым может служить векторное произведение нормальных векторов 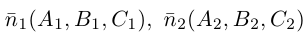 плоскостей. т. е. вектор
плоскостей. т. е. вектор 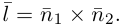
Пример №3
Найти канонические уравнения прямой
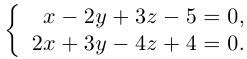
Решение. Полагая в данной системе z = 0, получим
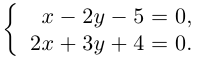
Решив эту систему, найдем х = 1, у = —2. Таким образом, мы получили точку 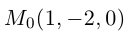 на прямой. Найдем ее направляющий вектор:
на прямой. Найдем ее направляющий вектор:
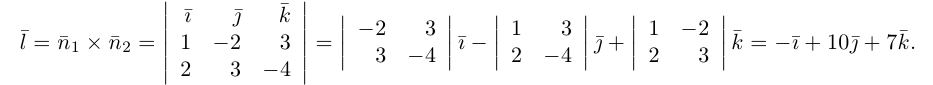
Осталось записать канонические уравнения данной прямой:
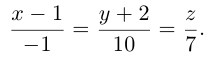
Научимся теперь вычислять расстояние от точки до прямой в пространстве. Пусть задана точка  и прямая L своими каноническими уравнениями
и прямая L своими каноническими уравнениями
Искомое расстояние 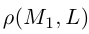 равно, очевидно, высоте треугольника, построенного, на векторах
равно, очевидно, высоте треугольника, построенного, на векторах 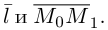 Воспользовавшись геометрическим смыслом длины векторного произведения (глава II. §4), найдем:
Воспользовавшись геометрическим смыслом длины векторного произведения (глава II. §4), найдем:
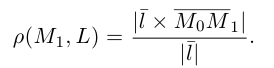
Пусть нам известны канонические уравнения двух прямых в пространстве:
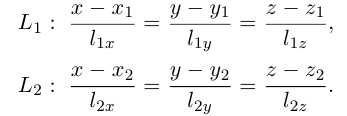
Очевидно, 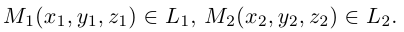
Один из углов между этими прямыми равен углу между их направляющими векторами 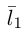 и
и 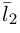 и, следовательно.
и, следовательно.
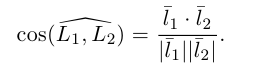
Изучим взаимное расположение прямых 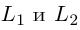 . Если направляющие векторы
. Если направляющие векторы 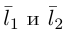 коллинеарны, то данные прямые параллельны или совпадают. Совпадать они будут в том случае, когда
коллинеарны, то данные прямые параллельны или совпадают. Совпадать они будут в том случае, когда 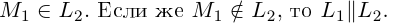
В случае, когда 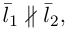 , прямые пересекаются или являются скрещивающимися.
, прямые пересекаются или являются скрещивающимися.
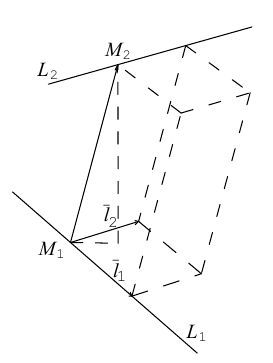
Прямые пересекаются, очевидно, тогда и только тогда, когда векторы  компланарны. В противном случае данные прямые являются скрещивающимися. Таким образом, для того, чтобы выяснить, являются ли две данные непараллельные прямые пересекающимися или скрещивающимися, достаточно вычислить смешанное произведение
компланарны. В противном случае данные прямые являются скрещивающимися. Таким образом, для того, чтобы выяснить, являются ли две данные непараллельные прямые пересекающимися или скрещивающимися, достаточно вычислить смешанное произведение  и, если оно окажется равным нулю, то прямые пересекаются, иначе – скрещиваются.
и, если оно окажется равным нулю, то прямые пересекаются, иначе – скрещиваются.
Расстояние  между двумя скрещивающимися прямыми равно, очевидно, расстоянию между параллельными плоскостями, в которых расположены эти прямые и, следовательно, равно высоте параллелепипеда, построенного на векторах
между двумя скрещивающимися прямыми равно, очевидно, расстоянию между параллельными плоскостями, в которых расположены эти прямые и, следовательно, равно высоте параллелепипеда, построенного на векторах 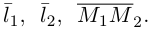 Отсюда, использовав геометрический смысл смешанного произведения (глава II. §5), мы и найдем искомое расстояние:
Отсюда, использовав геометрический смысл смешанного произведения (глава II. §5), мы и найдем искомое расстояние:
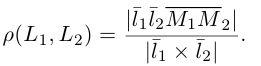
Пример №4
Убедиться в том, что прямые
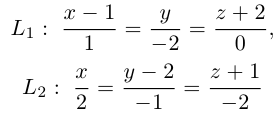
являются скрещивающимися. Найти расстояние между ними и уравнение общего перпендикуляра к ним.
Решение. Первая прямая проходит через точку 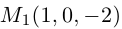 параллельно вектору
параллельно вектору 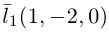 . а вторая – через точку
. а вторая – через точку 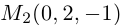 параллельно вектору
параллельно вектору 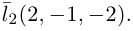 Вычислим смешанное произведение векторов
Вычислим смешанное произведение векторов 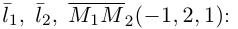
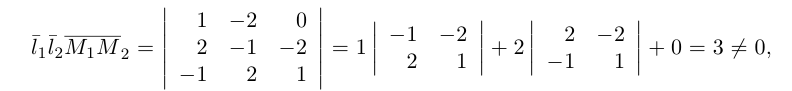
следовательно, прямые  являются скрещивающимися. Для вычисления расстояния между ними иенолтьзуем приведенную выше формулу. Так как
являются скрещивающимися. Для вычисления расстояния между ними иенолтьзуем приведенную выше формулу. Так как
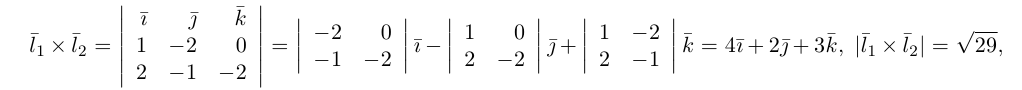
Осталось найти уравнение общего перпендикуляра к данным прямым. Заметим, прежде всего, что его направляющим вектором является уже вычисленный нами вектор  . Очевидно, указанный перпендикуляр расположен в пересечении двух плоскостей
. Очевидно, указанный перпендикуляр расположен в пересечении двух плоскостей 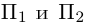 , проходящих через данные прямые параллельно вектору
, проходящих через данные прямые параллельно вектору 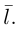 Найдем уравнения этих плоскостей по трем элементам. Первая из них проходит через точку
Найдем уравнения этих плоскостей по трем элементам. Первая из них проходит через точку 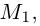 параллельно векторам
параллельно векторам 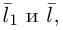 следовательно (§1),
следовательно (§1),
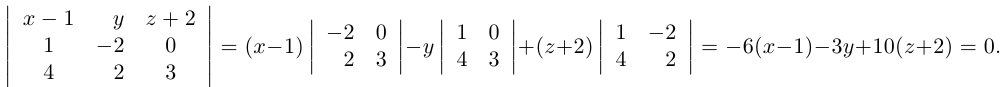
Таким образом, плоскость 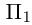 имеет уравнение
имеет уравнение 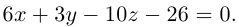 Аналогично, плоскость
Аналогично, плоскость 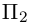 содержит точку
содержит точку 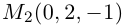 и расположена параллельно векторам
и расположена параллельно векторам 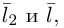 поэтому
поэтому
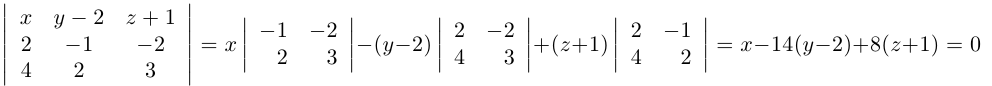
и, стало быть, 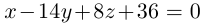 – уравнение плоскости
– уравнение плоскости 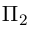 . Система из уравнений плоскостей
. Система из уравнений плоскостей 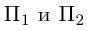 и даст нам общие уравнения перпендикуляра к прямым
и даст нам общие уравнения перпендикуляра к прямым 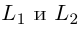 :
:
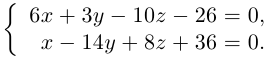
В заключение этого параграфа вычислим угол между прямой L, заданной каноническими уравнениями
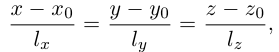
и плоскостью П, для которой известно ее общее уравнение
Очевидно, искомый угол 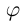 связан с углом
связан с углом 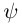 между направляющим вектором
между направляющим вектором 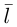 прямой и нормальным вектором
прямой и нормальным вектором 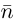 плоскости соотношением
плоскости соотношением 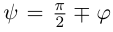 следовательно,
следовательно, 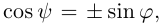 откуда,
откуда,
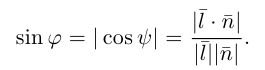
В частности, если 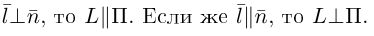
Прямая на плоскости
Для прямой на плоскости наблюдается большее разнообразие ее уравнений, так как на плоскости прямая фиксируется точкой, через которую она проходит и, либо вектором ей перпендикулярным (нормальным вектором), либо вектором ей параллельным (направляющим вектором) и, следовательно, для прямой на плоскости можно записывать как уравнения, характерные для плоскости в пространстве (§1), так и аналоги уравнений прямой в пространстве (§2). Перечислим, не повторяя деталей, изложенных в предыдущих двух параграфах, основные уравнения прямой на плоскости и связанные с ними формулы.
Пусть прямая L на плоскости с выбранной в ней системой координат 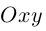 проходит через точку
проходит через точку 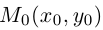 перпендикулярно ненулевому вектору
перпендикулярно ненулевому вектору 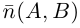 .
.
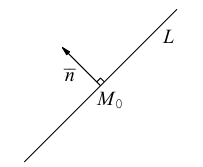
Уравнение такой прямой имеет вид:
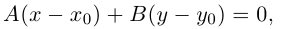
откуда после очевидных преобразований получим уравнение
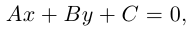
которое представляет собой общее уравнение прямой на плоскости.
Пусть прямая L отсекает на координатных осях  отрезки величиной а и Ь соответственно.
отрезки величиной а и Ь соответственно.
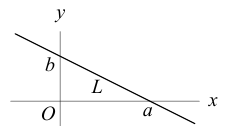
Тогда, как и для плоскости, мы можем записать уравнение прямой в отрезках:
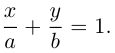
Если прямая L содержит точку 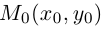 и расположена параллельно ненулевому вектору
и расположена параллельно ненулевому вектору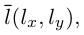
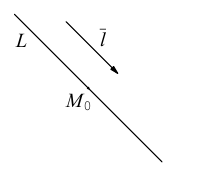
то ее каноническое уравнение имеет вид:
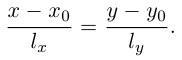
По аналогии с прямой в пространстве, прямая на плоскости может быть задана также векторным уравнением
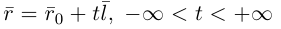
и параметрическими уравнениями
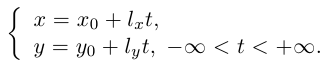
Расстояние от точки 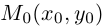 прямой L на плоскости, заданной общим уравнением
прямой L на плоскости, заданной общим уравнением 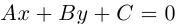 , может быть вычислено по формуле:
, может быть вычислено по формуле:
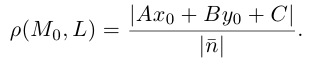
Найдем еще одно уравнение прямой на плоскости, характерное для этого геометрического объекта. Пусть прямая L, заданная своим каноническим уравнением 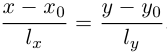 , непараллельна оси
, непараллельна оси 
Тогда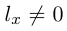 и мы можем записать уравнение прямой L с угловым коэффициентом:
и мы можем записать уравнение прямой L с угловым коэффициентом:
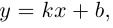
где 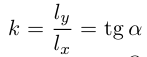 – угловой коэффициент прямой, b – величина отрезка, который отсекает эта прямая на оси
– угловой коэффициент прямой, b – величина отрезка, который отсекает эта прямая на оси 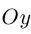 . В частности,
. В частности,
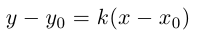
представляет собой уравнение прямой с угловым коэффициентом, которая проходит через точку 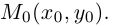
Если две прямые на плоскости заданы общими или каноническими уравнениями, то их взаимное расположение исследуется по аналогии с плоскостями или прямыми, заданными такими же уравнениями (§1 или §2). Изучим поэтому взаимное расположение двух прямых, которые заданы уравнениями с угловым коэффициентом. Итак, рассмотрим две прямые
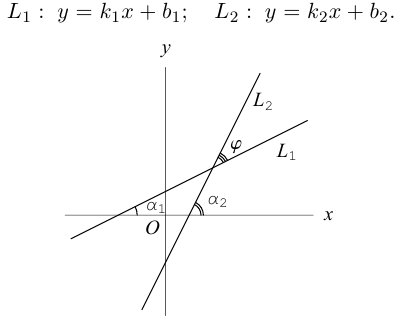
Предположим сначала, что прямые не являются перпендикулярными, обозначим через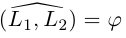 острый угол между ними. Тогда, очевидно,
острый угол между ними. Тогда, очевидно, 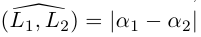 и, следовательно,
и, следовательно,
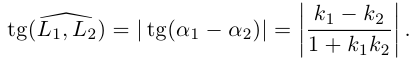
Если же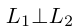 , то нормальные векторы
, то нормальные векторы 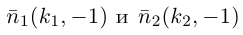 этих прямых ортогональны, следовательно,
этих прямых ортогональны, следовательно,
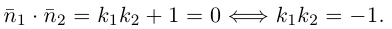
Таким образом, для перпендикулярности прямых 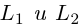 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы 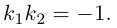
Очевидно. прямые 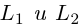 параллельны в том и только в том случае, когда равны углы, которые они образуют с осью Ох. Следовательно, для параллельности прямых
параллельны в том и только в том случае, когда равны углы, которые они образуют с осью Ох. Следовательно, для параллельности прямых 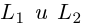 необходимо и достаточно, чтобы совпадали их угловые коэффициенты, т. е.
необходимо и достаточно, чтобы совпадали их угловые коэффициенты, т. е. 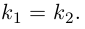
Пример №5
Даны прямая 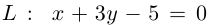 и точка А(—2, 1). Найти уравнения прямых
и точка А(—2, 1). Найти уравнения прямых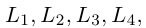 проходящих через точку А и таких, что
проходящих через точку А и таких, что 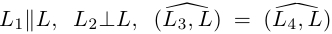
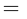
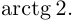
Решение. Прямые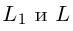 имеют общий нормальный вектор
имеют общий нормальный вектор 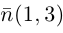 , поэтому,
, поэтому,
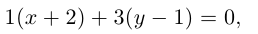
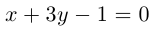 – общее уравнение прямой
– общее уравнение прямой 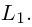
Так как 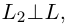 то направляющим вектором прямой
то направляющим вектором прямой 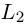 является нормальный вектор прямой L, следовательно,
является нормальный вектор прямой L, следовательно,
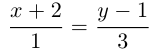 каноническое уравнение прямой
каноническое уравнение прямой 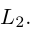
Из уравнения прямой L находим 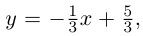 следовательно,
следовательно, 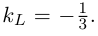 Тогда угловые коэффициенты прямых
Тогда угловые коэффициенты прямых 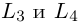 удовлетворяют уравнению
удовлетворяют уравнению
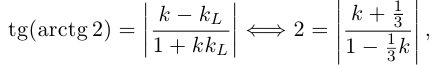
откуда, 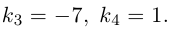 Осталось записать уравнения прямых
Осталось записать уравнения прямых 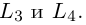
Кривые второго порядка на плоскости
В предыдущих трех параграфах нами были изучены линейные геометрические объекты -плоскость и прямая в пространстве и на плоскости. Мы показали, что в декартовой системе координат они определяются алгебраическими уравнениями первой степени, т. е. линейными уравнениями. Предметом нашего исследования в этом параграфе будут являться кривые второго порядка, т. е. линии на плоскости, уравнения которых в декартовой системе координат Оху имеют вид:
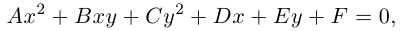
где А, В, С, D, Е, F – действительные числа. Мы убедимся в том, что, за исключением случаев вырождения данное уравнение определяет одну из трех замечательных линий — эллипс, гиперболу или параболу. Приведем сначала геометрическое определение каждой из этих линий и найдем их канонические уравнения.
Эллипс
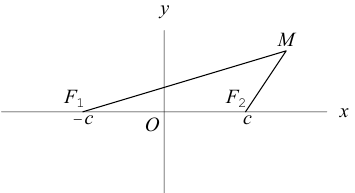
Определение: Эллипсом называется множество точек на плоскости, для каждой из которых сумма расстояний до двух фиксированных точек (фокусов эллипса) есть величина постоянная.
Найдем каноническое уравнение эллипса. Обозначим через 2с фокусное расстояние, т. е. расстояние между фокусами, а через 2а — постоянную сумму расстояний от точек эллипса до фокусов. Из неравенства треугольника следует, что 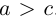 . Выберем декартову систему координат на плоскости следующим образом: ось Ох направим через фокусы, а начало координат выберем посередине между ними.
. Выберем декартову систему координат на плоскости следующим образом: ось Ох направим через фокусы, а начало координат выберем посередине между ними.
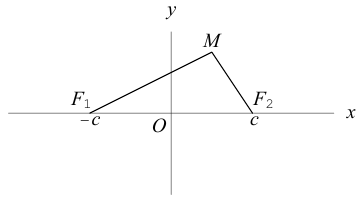
Пусть М(х, у) — произвольная точка эллипса. По определению этой линии,
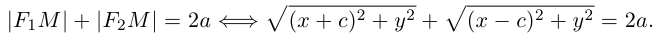
Упростим последнее уравнение:
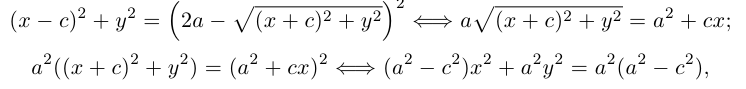
откуда, использовав обозначение 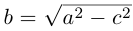 , мы и получим каноническое уравнение эллипса :
, мы и получим каноническое уравнение эллипса :
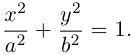
Построим эту линию. Для этого прежде всего заметим, что она симметрична относительно координатных осей и начала координат, так как переменные x и у входят в каноническое уравнение в квадратах. Отсюда следует, что эллипс достаточно построить в первой координатной четверти и затем отразить его относительно координатных осей. Из канонического уравнения эллипса находим:
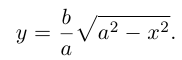
Очевидно, эта функция определена и убывает при 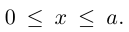 Кроме того, ее график располагается выше прямой
Кроме того, ее график располагается выше прямой 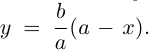 Из приведенных рассуждений следует, что эллипс представляет собой следующую замкнутую линию на плоскости:
Из приведенных рассуждений следует, что эллипс представляет собой следующую замкнутую линию на плоскости:
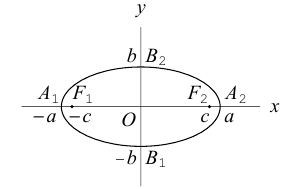
Числа а и b называются соответственно большой и малой полуосями эллипса. Точка O(0,0) -центр эллипса, точки 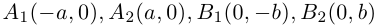 – вершины эллипса, отрезок
– вершины эллипса, отрезок 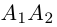 — большая,
— большая, 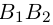 — малая оси эллипса.
— малая оси эллипса.
Форму эллипса характеризует величина 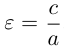 . равная отношению фокусного расстояния к длине большой оси. Это число называется эксцентриситетом эллипса. Очевидно,
. равная отношению фокусного расстояния к длине большой оси. Это число называется эксцентриситетом эллипса. Очевидно, 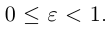 Так как
Так как
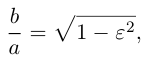
то при 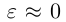 мы имеем
мы имеем 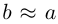 , и, следовательно, эллипс по форме мало отличается от окружности. В предельном случае, когда
, и, следовательно, эллипс по форме мало отличается от окружности. В предельном случае, когда 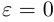 . полуоси совпадают и эллипс превращается в окружность. Если же
. полуоси совпадают и эллипс превращается в окружность. Если же 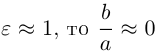 и эллипс является вытянутым вдоль оси Ох.
и эллипс является вытянутым вдоль оси Ох.
Замечание. В уравнении эллипса может оказаться, что 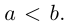 Тогда фокусы эллипса находятся на оси
Тогда фокусы эллипса находятся на оси 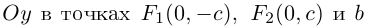 — большая,
— большая, 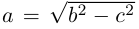 — малая полуоси эллипса.
— малая полуоси эллипса.
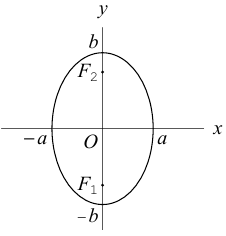
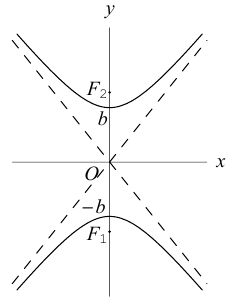
Гипербола
Определение: Гипербола представляет собой линию на плоскости, для каждой точки которой абсолютная величина разности расстояний до двух фиксированных точек (фокусов гиперболы) есть величина постоянная.
Обозначим и здесь фокусное расстояние через 2с. а через 2а — постоянную абсолютную величину разности расстояний от точек гиперболы до фокусов. Для гиперболы а < с, что следует из неравенства треугольника. Выберем декартову систему координат на плоскости точно также, как и при выводе канонического уравнения эллипса.
По определению гиперболы для произвольной точки М(х, у) этой линии
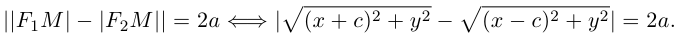
Избавляясь от корней в этом уравнении, получим:
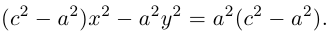
Обозначая здесь 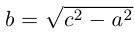 , получим каноническое уравнение гиперболы:
, получим каноническое уравнение гиперболы:
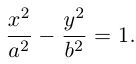
Как видно из ее уравнения, гипербола симметрична относительно координатных осей и начала координат. Из канонического уравнения гиперболы следует, что в первой четверти
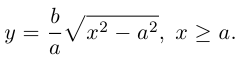
Эта функция возрастает, 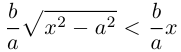 при всех
при всех 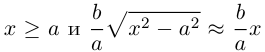 при больших х.
при больших х.
а а а а
Это означает, что в первой четверти гипербола, выходя из точки (а, 0) на оси Ох, приближается
затем при больших значениях х к прямой 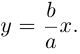 Следовательно, гипербола выглядит следующим образом:
Следовательно, гипербола выглядит следующим образом:
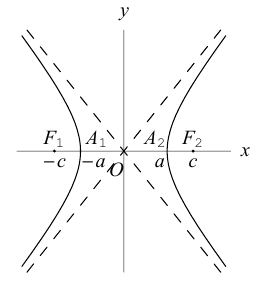
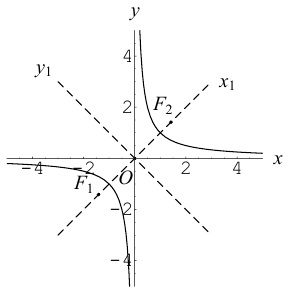
Прямые  называются асимптотами гиперболы. Точка O(0,0) – центр гиперболы. Точки
называются асимптотами гиперболы. Точка O(0,0) – центр гиперболы. Точки 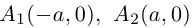 называются вершинами гиперболы. Ось симметрии гиперболы, пересекающая ее в вершинах, называется действительной осью. Вторая ось симметрии, не имеющая с гиперболой общих точек, называется мнимой осью гиперболы. Числа а и Ь называются соответственно действительной и мнимой полуосями гиперболы. Если полуоси равны, то гипербола называется равносторонней (равнобочной).
называются вершинами гиперболы. Ось симметрии гиперболы, пересекающая ее в вершинах, называется действительной осью. Вторая ось симметрии, не имеющая с гиперболой общих точек, называется мнимой осью гиперболы. Числа а и Ь называются соответственно действительной и мнимой полуосями гиперболы. Если полуоси равны, то гипербола называется равносторонней (равнобочной).
Как и для эллипса, определим эксцентриситет гиперболы как отношение половины фокусного расстояния к действительной полуоси:
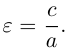
Так как
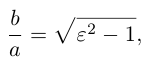
то эксцентриситет гиперболы характеризует величину угла, в котором она располагается. При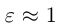 угол мал и, наоборот, если эксцентриситет велик, то и угол. в котором находится гипербола, близок к развернутому.
угол мал и, наоборот, если эксцентриситет велик, то и угол. в котором находится гипербола, близок к развернутому.
Замечание. В каноническом уравнении гиперболы знаки перед квадратами могут располагаться и в обратном порядке:
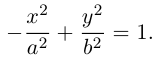
В этом случае фокусы и вершины находятся на оси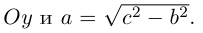
Парабола
Определение: Параболой называется множество точек плоскости, равноудаленных от. фиксированной точки (фокуса параболы) и фиксированной прямой (директрисы параболы).
Обозначим расстояние от фокуса до директрисы через р. Число р > 0 называется параметром параболы. Выберем удобную систему координат на плоскости: ось Ох направим через фокус F перпендикулярно директрисе D, а начало координат возьмем посередине между директрисой и фокусом.
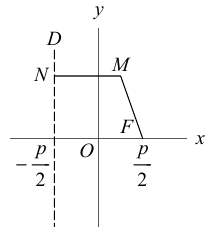
Если М(х,у) – произвольная точка параболы, то по определению этой кривой
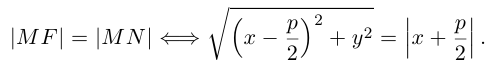
После возведения в квадрат и очевидных преобразований, получим каноническое уравнение параболы:
Очевидно, парабола проходит через начало координат и симметрична относительно оси Ох. Точка O(0,0) называется вершиной параболы, ось Ох – осью параболы.
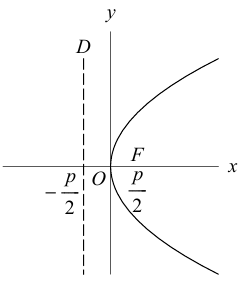
Замечание. Если бы при выборе системы координат мы направили ее оси в противоположные стороны, то каноническое уравнение параболы приняло бы вид:
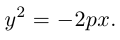
Аналогично, уравнения
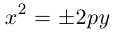
также определяют параболы, фокусы которых расположены на оси Оу. а директрисы параллельны оси Ох.
Приведение уравнения кривой второго порядка к каноническому виду
Покажем, что общее уравнение кривой второго порядка на плоскости, кроме случаев вырождения, определяет одну из линий — эллипс, гиперболу или параболу.
Выясним сначала, как преобразуются координаты точки на плоскости при параллельном переносе системы координат. Предположим, что осуществлен параллельный перенос системы координат Оху в точку 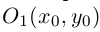 . Пусть
. Пусть 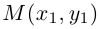 — координаты точки М в старой Оху, а
— координаты точки М в старой Оху, а 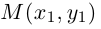 — координаты той же точки в новой
— координаты той же точки в новой 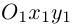 системе координат.
системе координат.
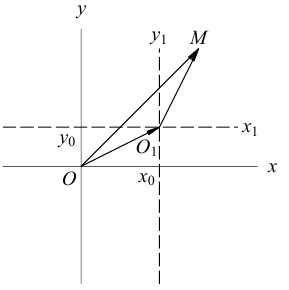
Так как 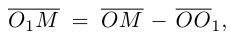 то новые и старые точки координаты на плоскости связаны линейными соотношениями:
то новые и старые точки координаты на плоскости связаны линейными соотношениями:
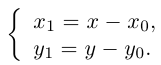
Рассмотрим теперь уравнение второго порядка на плоскости в частном случае, когда оно не содержит произведения координат ху :
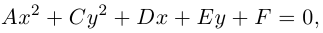
причем коэффициенты А и С не равны одновременно нулю. Здесь возможны три случая.
а) АС > 0. Очевидно, всегда можно считать, тгго А > 0, С > 0. Выделяя в уравнении второго порядка полные квадраты по переменным х и у, получим:
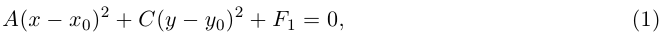
где 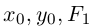 — некоторые действительные числа. Ясно, что при
— некоторые действительные числа. Ясно, что при 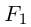 > 0 ни одна из точек плоскости не удовлетворяет этому уравнению. Если
> 0 ни одна из точек плоскости не удовлетворяет этому уравнению. Если 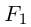 = 0, то единственным решением полученного уравнения является точка
= 0, то единственным решением полученного уравнения является точка 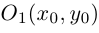 . Наконец, при
. Наконец, при 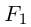 < 0 уравнение приводится к виду
< 0 уравнение приводится к виду
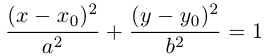
и, следовательно, в смещенной с помощью параллельного переноса в точку 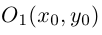 системе координат оно является каноническим уравнением эллипса:
системе координат оно является каноническим уравнением эллипса:
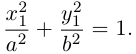
b) АС < 0. Будем считать для определенности, что А > 0. С < 0.
В этом случае исходное уравнение второго порядка также приводится к виду (1). При F = 0 оно определяет пару прямых, проходящих, через точку 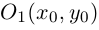 :
:
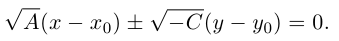
Если же 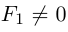 , то полученное уравнение мы можем преобразовать к виду
, то полученное уравнение мы можем преобразовать к виду
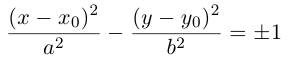
и, стало быть, после параллельного переноса системы координат в точку 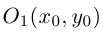 последнее уравнение является каноническим уравнением гиперболы:
последнее уравнение является каноническим уравнением гиперболы:
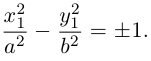
c) АС = 0. Предположим, например, что 
Выделяя в данном уравнении второго порядка полный квадрат по переменной у, получим:
С {у ~ Уо)2 + Dx + F1=0.
Если в этом уравнении D = 0, то при  > 0 множество решений этого уравнения пусто, а при
> 0 множество решений этого уравнения пусто, а при  < 0 полученное уравнение определяет пару прямых, параллельных оси Ох :
< 0 полученное уравнение определяет пару прямых, параллельных оси Ох :
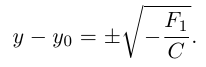
Если же 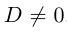 , то мы можем привести уравнение к виду:
, то мы можем привести уравнение к виду:
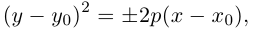
т.е. после параллельного переноса системы координат в точку 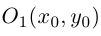 , мы получим тем самым каноническое уравнение параболы:
, мы получим тем самым каноническое уравнение параболы:
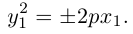
Аналогично. если в исходном уравнении второго порядка 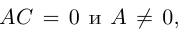 то, не принимая во внимание вырожденные случаи, это уравнение мы также можем привести к каноническому уравнению параболы:
то, не принимая во внимание вырожденные случаи, это уравнение мы также можем привести к каноническому уравнению параболы:
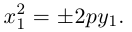
Пример №6
Привести уравнение второго порядка к каноническому виду, назвать и построить кривую:
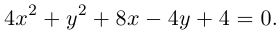
Решение. Выделяя полные квадраты по обеим переменным, получим:
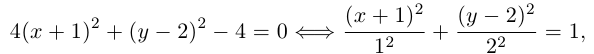
что представляет собой каноническое уравнение эллипса в смещенной в точку 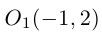 системе координат. Для этого эллипса
системе координат. Для этого эллипса 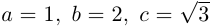 и, следовательно, фокусы находятся в точках
и, следовательно, фокусы находятся в точках 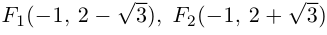 . Эксцентриситет эллипса равен
. Эксцентриситет эллипса равен 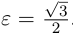
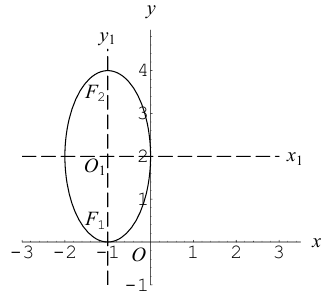
Пример №7
Найти каноническое уравнение параболы с вершиной в точке 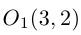 , осью симметрии, параллельной координатной оси Ох и фокусом на оси Оу. Построить параболу.
, осью симметрии, параллельной координатной оси Ох и фокусом на оси Оу. Построить параболу.
Решение. Фокус параболы находится в точке F(0 , 2), следовательно, уравнение параболы с учетом смещения имеет вид:
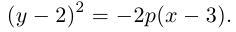
Здесь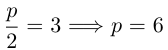 и, стало быть.
и, стало быть.
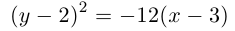
каноническое уравнение параболы.
Замечание. Для приведения к каноническому виду уравнения второго порядка, содержащего произведение координат ху, необходимо кроме параллельного переноса выполнить еще и поворот системы координат на определенный угол. Например, для равносторонней гиперболы ху = 1 следует повернуть систему координат Оху вокруг ее начала на угол 45° против часовой стрелки. Поскольку вершины гиперболы находятся на расстоянии 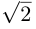 от начала координат. то в новой системе координат
от начала координат. то в новой системе координат 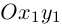 каноническое уравнение гиперболы имеет вид:
каноническое уравнение гиперболы имеет вид:
Поверхности второго порядка в пространстве
В заключение этой главы мы изучим поверхности в пространстве, которые в декартовой системе координат задаются алгебраическими уравнениями второй степени. Существуют пять видов таких поверхностей: эллипсоид, гиперболоиды, параболоиды, цилиндры второго порядка и конус второго порядка.
Поверхность вращения
Найдем уравнение поверхности, которая получается вращением некоторой линии вокруг одной из координатных осей. Пусть линия L, которая в координатной плоскости Oyz задается уравнением F(y, z) = 0. вращается вокруг оси Oz.
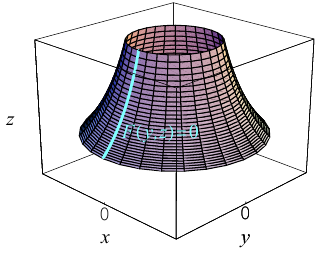
Пусть M(x,y,z) – произвольная точка на поверхности вращения. Перегоним ее по окружности, расположенной в сечении поверхности плоскостью, проходящей через данную точку перпендикулярно оси Oz, в точку N на линии L. Поскольку расстояние от точки М до оси Oz равно 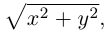 то точка N имеет координаты
то точка N имеет координаты 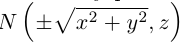 . Подставив координаты точки N в уравнение линии L. мы и получим тем самым уравнение поверхности вращения:
. Подставив координаты точки N в уравнение линии L. мы и получим тем самым уравнение поверхности вращения:
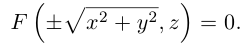
Найдем теперь уравнения поверхностей, которые получаются вращением кривых второго порядка с последующей линейной деформацией этих поверхностей.
Эллипсоид
Возьмем в плоскости Oyz эллипс
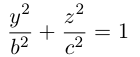
и будем вращать его вокруг оси Oz. В результате, как следует из предыдущего пункта, мы получим поверхность с уравнением
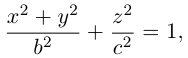
которая называется эллипсоидом вращения. Заменив в найденном уравнении координату х на —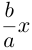 , т. е. линейно деформируя поверхность вдоль оси Ох с коэффициентом
, т. е. линейно деформируя поверхность вдоль оси Ох с коэффициентом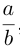 —, мы получим тем самым уравнение эллипсоида общего вида:
—, мы получим тем самым уравнение эллипсоида общего вида:
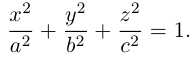
Положительные числа а, b, с называются полуосями эллипсоида.
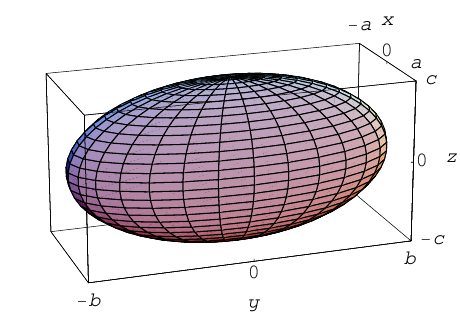
Очевидно, сечениями эллипсоида плоскостями параллельными координатным, являются эллипсы.
Замечание. В частном случае, когда а = b = с = R эллипсоид превращается в сферу
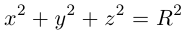
радиуса R с центром в начале координат.
Гиперболоиды
а) Однополостный гиперболоид.
Вращая гиперболу
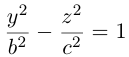
вокруг оси Oz, получим однополостный гиперболоид вращения с уравнением
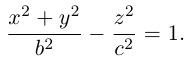
После линейной деформации вдоль оси Ох эта поверхность превращается в однополостный гиперболоид общего вида с осью Oz :
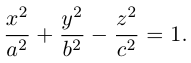
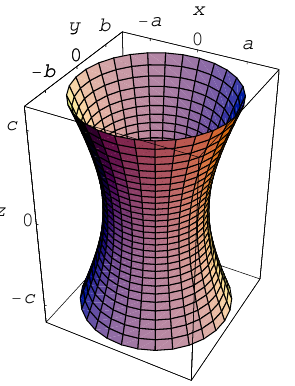
Аналогично, уравнения однополостных гиперболоидов с осями Ох и Оу имеют, соответственно, вид:
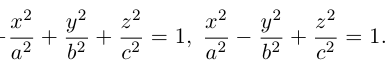
Сечениями однополостного гиперболоида плоскостями, перпендикулярными его оси, являются эллипсы, а в сечениях плоскостями, перпендикулярными другим координатным осям, располагаются гиперболы.
Двухполостный гиперболоид
Поверхность, полученная вращением вокруг оси Оz гиперболы
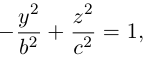
вершины которой расположены на оси вращения, называется двухполостным гиперболоидом вращения. Запишем уравнение двухполостного гиперболоида:
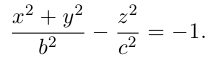
Линейная деформация двухполостного гиперболоида вращения вдоль оси Ох прообразует его в двухполостный гиперболоид общего вида с осью Oz. Уравнение этой поверхности имеет вид:
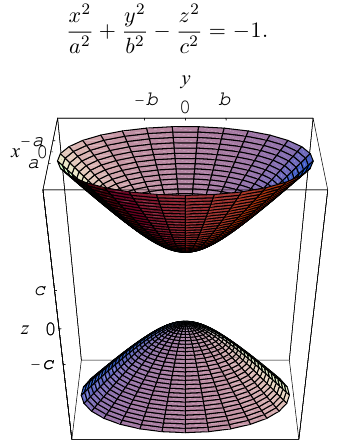
Двухполостные гиперболоиды с осями Ох и Оу имеют, соответственно, уравнения:
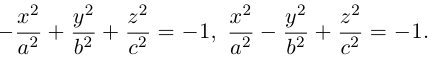
Как и в случае однополостного гиперболоида, сечениями двухполостного гиперболоида плоскостями, параллельными координатным, являются эллипсы и гиперболы.
Параболоиды
а) Эллиптический параболоид
Вращение параболы вокруг ее оси приводит к поверхности, которая называется параболоидом вращения. В частности, если параболу с каноническим уравнением 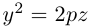 вращать вокруг оси Oz, то, как следует из пункта 0, уравнение полученного параболоида вращения имеет вид:
вращать вокруг оси Oz, то, как следует из пункта 0, уравнение полученного параболоида вращения имеет вид:
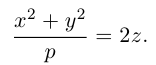
Линейная деформация параболоида вращения вдоль оси Оу превращает его в эллиптический параболоид с уравнением:
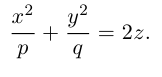
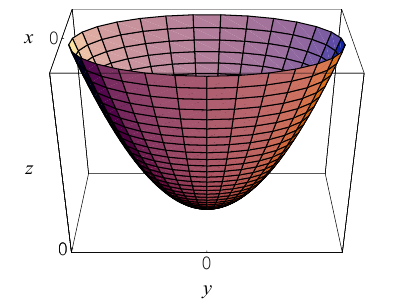
Положительные числа p, q называются параметрами параболоида, точка O(0,0) – вершина, ось Oz – ось эллиптического параболоида.
Уравнения эллиптических параболоидов с осями Ох и Оу имеют, соответственно, вид:
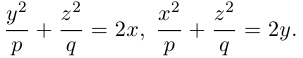
Как следует из уравнения эллиптического параболоида, плоскости, перпендикулярные его оси, пересекают эту поверхность по эллипсам, а в сечениях плоскостями, параллельными другим координатным, находятся параболы.
Замечание. Изменение знака в правой части уравнения эллиптического параболоида приводит к отражению этой поверхности относительно координатной плоскости, перпендикулярной оси параболоида.
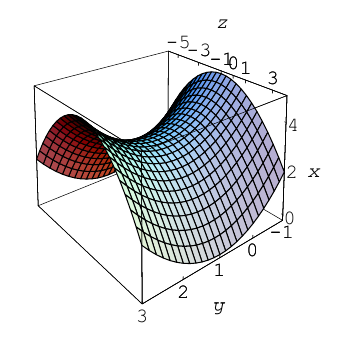
b) Гиперболический параболоид.
Будем поступательно перемещать образующую параболу
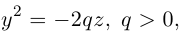
расположенную в плоскости Oyz, параллельно самой себе вдоль направляющей параболы
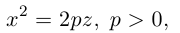
находящейся в плоскости Oxz. Полученная таким образом поверхность называется гиперболическим параболоидом или седловидной поверхностью.
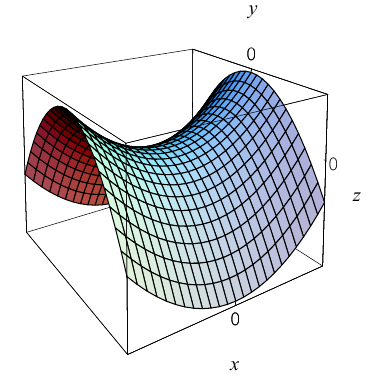
Найдем уравнение этой поверхности. Пусть М(х. у, z) – произвольная точка гиперболического параболоида. По его построению точка М принадлежит параболе с вершиной в точке 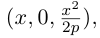 , параллельной параболе
, параллельной параболе 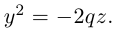 Так как координаты произвольной точки
Так как координаты произвольной точки 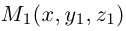 этой параболы удовлетворяют уравнению
этой параболы удовлетворяют уравнению
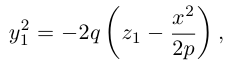
то, подставив в него координаты точки М, мы и получим после несложных преобразований уравнение гиперболического параболоида:
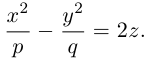
Здесь, как и для эллиптического параболоида, числа р, q – параметры гиперболического параболоида, точка O(0,0) и ось Oz – соответственно вершина и ось гиперболического параболоида.
Замечание 1. Седловидная поверхность может быть также получена перемещением параболы 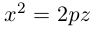 параллельно самой себе вдоль параболы
параллельно самой себе вдоль параболы 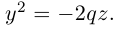
Судя по уравнению гиперболического параболоида, в сечениях этой поверхности плоскостями z = h > 0 находятся гиперболы, действительные оси которых параллельны координатной оси Ох. Аналогично, плоскости z = h < 0 пересекают данную поверхность по гиперболам с действительными осями, параллельными оси Оу. Наконец, плоскость Оху пересекает гиперболический параболоид по двум прямым 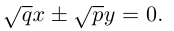
Гиперболические параболоиды, осями которых служат координатные оси Ох и Оу, имеют, соответственно, уравнения:
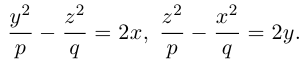
Замечание 2. Отразив седловидную поверхность относительно координатной плоскости, перпендикулярной ее оси, получим гиперболический параболоид, уравнение которого отличается знаком правой части от уравнения исходной поверхности.
Цилиндры второго порядка
Цилиндром второго порядка называется поверхность, полученная перемещением некоторой прямой (образующей) вдоль кривой второго порядка (направляющей), расположенной в плоскости, не содержащей образующую, параллельно фиксированному ненулевому вектору в пространстве.
Ограничимся случаем, когда направляющая расположена в одной из координатных плоскостей, а образующая перпендикулярна этой плоскости. Возьмем для определенности в плоскости Оху кривую второго порядка и будем перемещать прямую, параллельную оси Oz, вдоль этой кривой. Так как проекцией любой точки M(x,y,z) полученного таким образом цилиндра на плоскость Оху является точка N(x,y), принадлежащая кривой второго порядка, то координаты точки М удовлетворяют уравнению этой кривой. Следовательно, уравнением построенного цилиндра является уравнение его направляющей.
Перечислим теперь цилиндры второго порядка.
1) 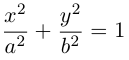 – эллиптический цилиндр.
– эллиптический цилиндр.
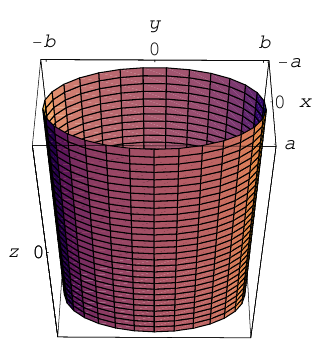
В частности, при а = b мы получим круговой цилиндр.
2 2 X у
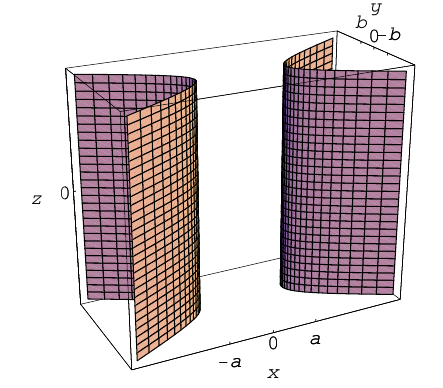
2) 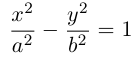 – гиперболический цилиндр.
– гиперболический цилиндр.
3) 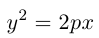 – параболический цилиндр.
– параболический цилиндр.
Аналогичные уравнения имеют цилиндры второго порядка, образующие которых параллельны осям Ох и Оу, а направляющие расположены в координатных плоскостях Oyz и Oxz, соответственно.
Конус второго порядка
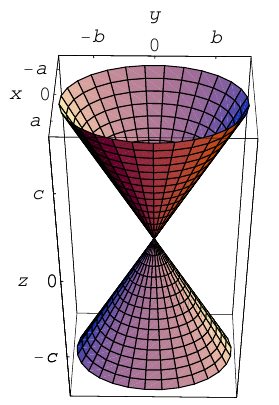
Конус второго порядка представляет собой поверхность, которая может быть получена перемещением прямой (образующей), имеющей неподвижную точку, которая называется вершиной конуса, вдоль кривой второго порядка (направляющей), расположенной в плоскости, не содержащей вершину.
Найдем уравнение конуса, вершина которого совпадает с началом координат, а направляющей служит эллипс с уравнением
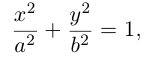
расположенный в плоскости z = с, с > 0.
Пусть M(x,y,z) – произвольная точка конуса. Обозначим через 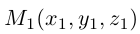 точку перс-сечения образующей, проходящей через точку М, с направляющей. Координаты точки
точку перс-сечения образующей, проходящей через точку М, с направляющей. Координаты точки 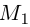 удовлетворяют уравнениям
удовлетворяют уравнениям
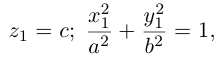
а точки M – уравнениям
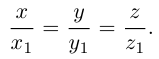
Из последних уравнений мы находим:
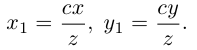
Подставив найденные выражения для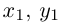 в уравнение эллипса, получим после несложных преобразований уравнение конуса второго порядка:
в уравнение эллипса, получим после несложных преобразований уравнение конуса второго порядка:
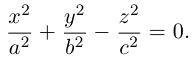
Координатная ось Oz называется осью конуса. Если а = b, то конус является круговым.
Конусы второго порядка с осями Ох и Оу имеют, соответственно, уравнения:
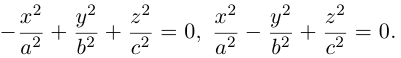
Покажем, что вид конуса второго порядка не зависит от выбора направляющей. Действительно, если в качестве направляющей взять гиперболу
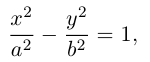
находящегося в плоскости 2 = с, то после рассуждений, аналогичных предыдущим, получим поверхность с уравнением
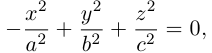
т. е. конус с осью Ох. Если же за направляющую мы выберем в плоскости z = с параболу с уравнением
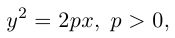
то построенный таким образом конус имеет уравнение
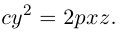
Наблюдая со стороны положительной полуоси Оу, повернем систему координат Oxz вокруг оси Оу на угол 45° против часовой стрелки. Тогда произведение xz в системе координат 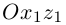
запишется как 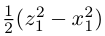 (§4, пункт 4, замечание). Следовательно, в новой системе координат Oxyz найденное уравнение поверхности приобретает вид
(§4, пункт 4, замечание). Следовательно, в новой системе координат Oxyz найденное уравнение поверхности приобретает вид
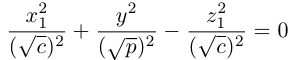
и, стало быть, эта поверхность является конусом с осью 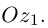
Как следует из уравнения конуса и его построения, плоскости, перпендикулярные его оси, пересекают эту поверхность по эллипсам, сечениями конуса плоскостями, параллельными его оси, являются гиперболы, и, наконец, в сечениях конуса плоскостями, параллельными образующей, располагаются параболы.
Приведение уравнения поверхности второго порядка к каноническому виду
По аналогии с уравнением кривой второго порядка (§4, пункт 4), уравнение поверхности второго порядка, не содержащее произведений координат, мы можем за счет выделения полных квадратов привести к уравнению одной из рассмотренных в пунктах 1—5 поверхностей. Следовательно, мы получим одну из поверхностей второго порядка в смещенной с помощью параллельного переноса системе координат. Исключение, правда, составляет случай, когда уравнение поверхности содержит полный квадрат и два линейных слагаемых относительно других координат. Такая поверхность представляет собой параболический цилиндр в смещенной с помощью параллельного переноса и повернутой затем вокруг одной из координатных осей системе координат.
Пример №8
Привести уравнение второго порядка
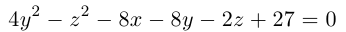
к каноническому виду, назвать и построить поверхность.
Решение. После выделения полных квадратов по переменным у, z получим:
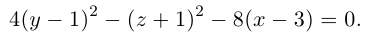
Переписав это уравнение в виде
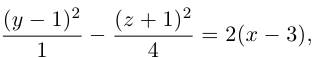
мы замечаем, что в смещенной с помощью параллельного переноса в точку 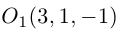 системе координат, эта поверхность представляет собой гиперболический параболоид с параметрами р = 1, q = 4.
системе координат, эта поверхность представляет собой гиперболический параболоид с параметрами р = 1, q = 4.
Прямая на плоскости. Общее уравнение прямой на плоскости
Докажем, что всякая прямая на плоскости задается в любой пдск уравнением первой степени относительно двух переменных.
Если A – некоторая точка на прямой  – вектор, перпендикулярный ей, то, во-первых, через A перпендикулярно
– вектор, перпендикулярный ей, то, во-первых, через A перпендикулярно  проходит единственная прямая на плоскости, а, во-вторых, для любой точки
проходит единственная прямая на плоскости, а, во-вторых, для любой точки  вектор
вектор 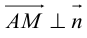 . Таким свойством обладают только точки, лежащие на
. Таким свойством обладают только точки, лежащие на .
.
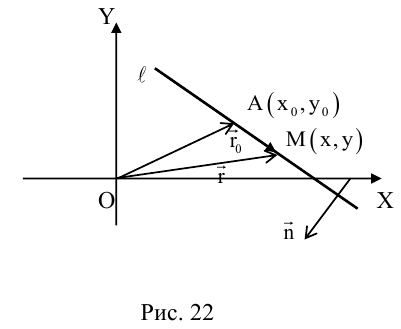
Чтобы вывести уравнение прямой, зададим на плоскости пдск XOY .
В этой системе координат 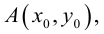
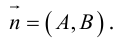
Пусть M (x, y) – произвольная точка
на  . Тогда (рис. 22 )
. Тогда (рис. 22 ) 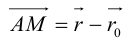 . Так как
. Так как 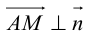 , то по свойству 5 скалярного произведения
, то по свойству 5 скалярного произведения 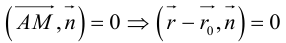 – векторное уравнение прямой
– векторное уравнение прямой  .
.
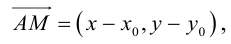 поэтому по формуле (2.5) получим
поэтому по формуле (2.5) получим

Координаты точек, лежащих на прямой , связаны соотношением (3.1). Если же
, связаны соотношением (3.1). Если же 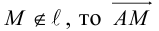 не перпендикулярен
не перпендикулярен 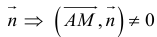 значит, координаты M не будут удовлетворять полученному уравнению. Поэтому (3.1) – уравнение прямой, проходящей через заданную точку, перпендикулярно заданному вектору. Заметим, что это уравнение линейно относительно переменных x и y .
значит, координаты M не будут удовлетворять полученному уравнению. Поэтому (3.1) – уравнение прямой, проходящей через заданную точку, перпендикулярно заданному вектору. Заметим, что это уравнение линейно относительно переменных x и y .
Определение: Любой ненулевой вектор 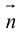 , перпендикулярный прямой
, перпендикулярный прямой  , называется ее нормальным вектором, или нормалью.
, называется ее нормальным вектором, или нормалью.
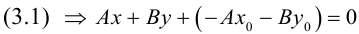 . Обозначая
. Обозначая 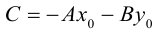 , получим
, получим

(3.2) – общее уравнение прямой на плоскости, 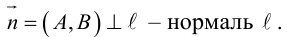
Уравнение прямой с направляющим вектором
Определение: Любой ненулевой вектор 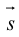 , параллельный прямой, называется ее направляющим вектором.
, параллельный прямой, называется ее направляющим вектором.
Если A – некоторая точка на прямой 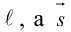 – вектор, параллельный ей, то, во-первых, через A параллельно
– вектор, параллельный ей, то, во-первых, через A параллельно 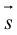 проходит единственная прямая, а, во-вторых, для любой точки
проходит единственная прямая, а, во-вторых, для любой точки 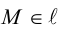 вектор
вектор 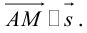 Таким свойством обладают только точки, лежащие на
Таким свойством обладают только точки, лежащие на  .
.
Чтобы вывести уравнение прямой, зададим на плоскости пдск XOY . В этой системе координат 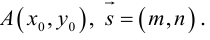
Пусть M (x, y) – произвольная точка на . Тогда  и
и 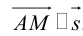 . Запишем условие коллинеарности векторов:
. Запишем условие коллинеарности векторов:

(3.3) – уравнение прямой на плоскости с направляющим вектором.
Если 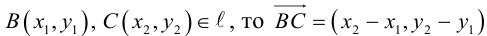 – направляющий вектор прямой , поэтому уравнение прямой, проходящей через две точки имеет вид:
– направляющий вектор прямой , поэтому уравнение прямой, проходящей через две точки имеет вид:

Уравнение прямой с угловым коэффициентом
Пусть 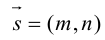 – направляющий вектор прямой
– направляющий вектор прямой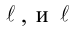 не параллельна оси OY , тогда
не параллельна оси OY , тогда 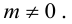
Определение: Угловым коэффициентом прямой 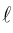 называется число
называется число
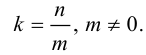
Очевидно, что если 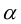 – угол между прямой
– угол между прямой 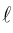 и положительным направлением оси ОХ, то
и положительным направлением оси ОХ, то 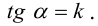
Рассмотрим уравнение (3.3) прямой с направляющим вектором 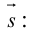
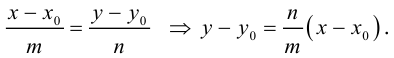
Отсюда следует (3.5) – уравнение прямой с заданным угловым коэффициентом, проходящей через заданную точку 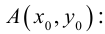

Из (3.5) получим 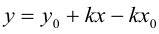 . Обозначим
. Обозначим 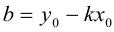 , тогда
, тогда

(3.6) – уравнение прямой с угловым коэффициентом.
Угол между прямыми на плоскости
Определение: Углом между двумя прямыми на плоскости называется любой из двух смежных углов, образованных ими при пересечении. Если прямые параллельны, то угол между ними равен 0 или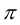 радиан.
радиан.
Пусть прямые заданы общими уравнениями.
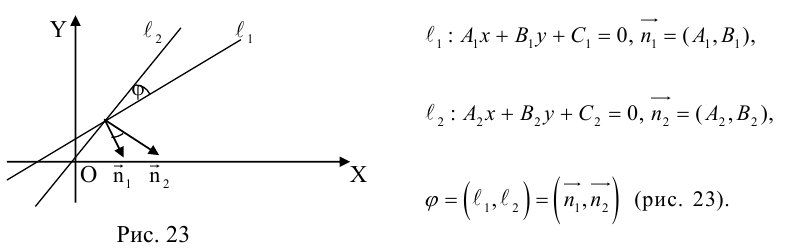
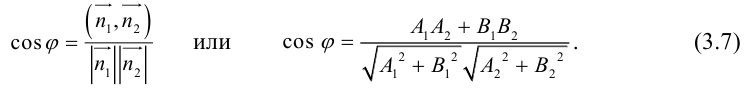
Условие параллельности прямых:
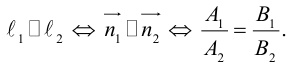
Условие перпендикулярности прямых:
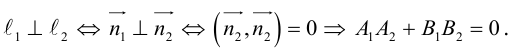
Рассмотрим случай, когда прямые заданы уравнениями с угловым коэффициентом.
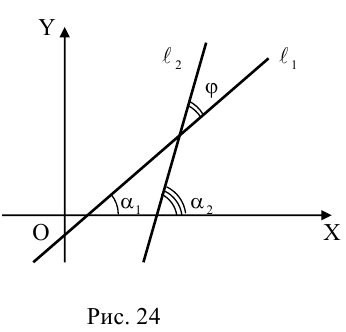
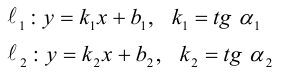
Так как 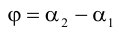 (рис. 24 ), то
(рис. 24 ), то
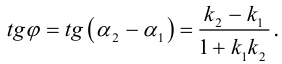
Условие параллельности прямых:
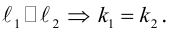
Условие перпендикулярности:
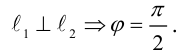 Так как
Так как 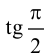
не существует, то 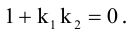
Пример №9
Даны вершины треугольника: 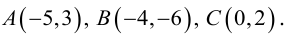
Написать:
а) уравнение медианы AM , б) высоты AH , в) найти угол между AM и AH
(рис. 25).

Перепишем уравнение медианы в общем виде:
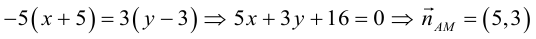 – нормаль АМ.
– нормаль АМ.
б)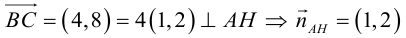 – нормаль AH . Уравнение прямой (3.1), проходящей через точку A перпендикулярно вектору
– нормаль AH . Уравнение прямой (3.1), проходящей через точку A перпендикулярно вектору 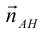 :
:
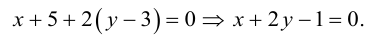
в)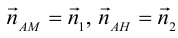 . По формуле (3.7)
. По формуле (3.7) 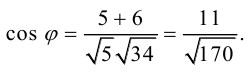
Расстояние от точки до прямой на плоскости
Пусть в некоторой пдск XOY задана прямая 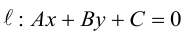 и точка
и точка 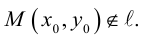 Найдем расстояние от точки M до прямой .
Найдем расстояние от точки M до прямой .
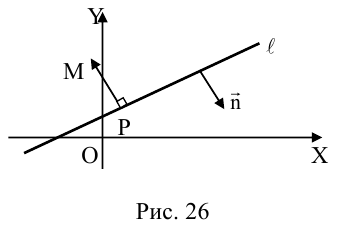
Пусть 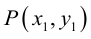 – проекция точки M на
– проекция точки M на 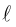 (рис. 26), тогда
(рис. 26), тогда 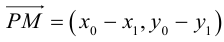 .
.
Нормаль
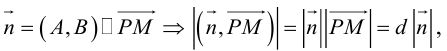
где d – искомое расстояние, 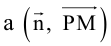 – скалярное произведение.
– скалярное произведение.
Следовательно,
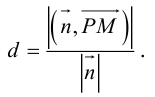
Так как 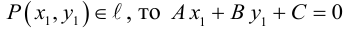 . Поэтому
. Поэтому
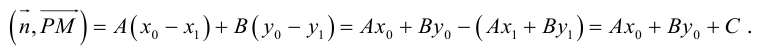
Отсюда 
(3.8) – формула для вычисления расстояния от точки до прямой на плоскости.
Пример №10
Найти длину высоты 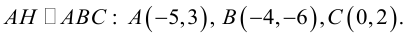
Уравнение 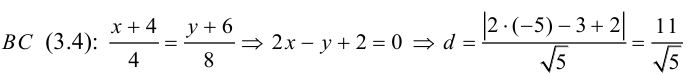 –
–
искомая длина высоты АН.
Кривые второго порядка
Окружность
Определение: Кривые второго порядка – плоские линии, которые в пдск XOY задаются уравнениями второй степени относительно двух переменных x,y.
Определение: Окружностью называется совокупность точек плоскости, равноудаленных от фиксированной точки, называемой ее центром.
Выведем уравнение окружности. Зададим пдск XOY . Пусть 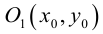 – фиксированная точка (центр окружности), а R – расстояние от точек окружности до ее центра (радиус окружности). Если
– фиксированная точка (центр окружности), а R – расстояние от точек окружности до ее центра (радиус окружности). Если  – произвольная точка окружности, то длина
– произвольная точка окружности, то длина 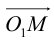 равна R .
равна R . 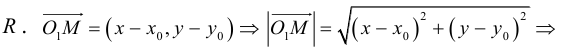

Если точка M (x, y) не лежит на окружности, то 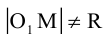 и ее координаты уравнению (3.9) не удовлетворяют, поэтому, (3.9) – уравнение окружности с центром
и ее координаты уравнению (3.9) не удовлетворяют, поэтому, (3.9) – уравнение окружности с центром 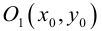 радиуса R .
радиуса R .
Если 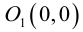 , то уравнение окружности примет вид:
, то уравнение окружности примет вид:

(3.10) – каноническое уравнение окружности.
Пример №11
Показать, что уравнение 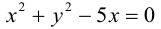 задает окружность (то есть найти ее центр и радиус).
задает окружность (то есть найти ее центр и радиус).
Приведем данное уравнение к виду (3.9), выделив полный квадрат по переменной x :
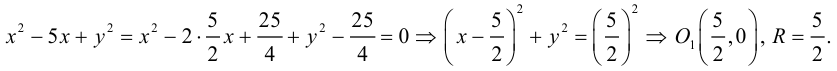
Пример №12
Написать уравнение линии центров окружностей
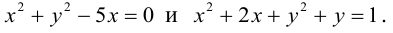
Найдем центр второй окружности:
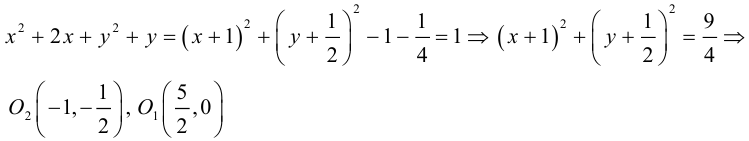
Уравнение прямой (3.4), проходящей через две точки:
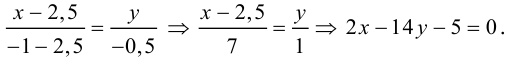
Эллипс
Определение: Эллипс – совокупность точек плоскости, сумма расстояний от которых до двух фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная и большая, чем расстояние между фокусами.
Чтобы вывести уравнение эллипса, выберем пдск следующим образом: ось абсцисс проведем через фокусы  , а ось ординат – посередине отрезка
, а ось ординат – посередине отрезка  перпендикулярно оси абсцисс. Обозначим расстояние между фокусами
перпендикулярно оси абсцисс. Обозначим расстояние между фокусами  тогда
тогда  . Пусть M(x, y) – произвольная точка, лежащая на эллипсе, а 2a – сумма расстояний от точек на эллипсе до
. Пусть M(x, y) – произвольная точка, лежащая на эллипсе, а 2a – сумма расстояний от точек на эллипсе до  ,
,
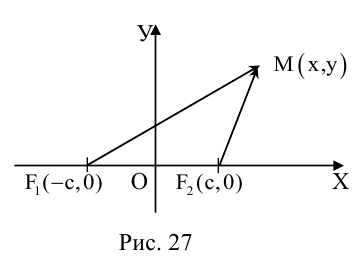
2a>2c определению эллипса.
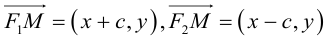 (рис. 27).
(рис. 27).
Запишем в виде уравнения свойство точек, принадлежащих эллипсу, сформулированное в определении:
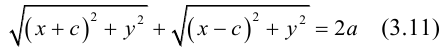
(3.11) – уравнение эллипса в выбранной системе координат. Преобразуем его к
более простому (каноническому) виду. Для этого умножим (3.11) на сопряженное выражение:
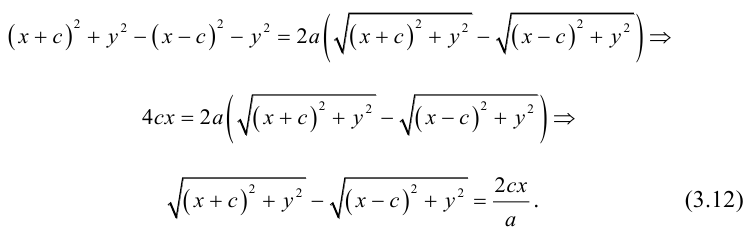
Сложим (3.11) и (3.12) и результат возведем в квадрат:
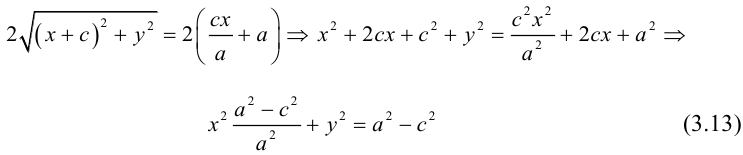
Так как по определению a>c, то есть 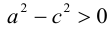 , то обозначим
, то обозначим 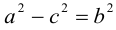 .
.
Тогда из (3.13) получим:

(3.14) – каноническое уравнение эллипса.
Исследуем форму эллипса по его каноническому уравнению. Найдем точки пересечения с осями координат:
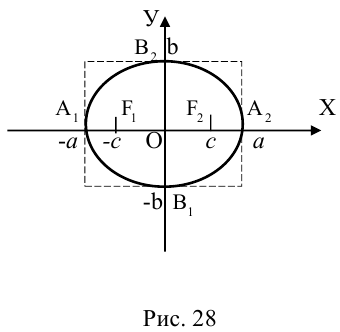
Из (3.14) следует, что
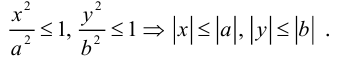
Значит, эллипс расположен в прямоугольнике со сторонами 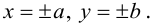 .
.
Кроме того, из уравнения следует, что он симметричен относительно OX и OY . O(0,0) – точка пересечения осей симметрии – центр симметрии эллипса.
Ось, на которой лежат фокусы, называется фокальной осью эллипса. Точки пересечения эллипса с осями симметрии называются его вершинами.
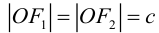 – полуфокусное расстояние,
– полуфокусное расстояние, 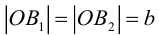 – малая полуось,
– малая полуось,
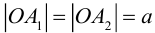 – большая полуось эллипса и
– большая полуось эллипса и 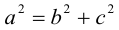 (рис. 28).
(рис. 28).
Отношение полуфокусного расстояния к длине большой полуоси 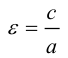 называется эсцентриситетом эллипса. Он характеризует форму эллипса.
называется эсцентриситетом эллипса. Он характеризует форму эллипса.
Так как 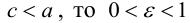 , и чем меньше
, и чем меньше 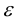 , тем больше эллипс похож на окружность. Для окружности
, тем больше эллипс похож на окружность. Для окружности 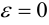 .
.
ЗАМЕЧАНИЕ 1. Уравнение эллипса, центр которого 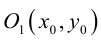 , а оси симметрии параллельны координатным осям, имеет вид:
, а оси симметрии параллельны координатным осям, имеет вид:

ЗАМЕЧАНИЕ 2. К кривым второго порядка эллиптического типа относятся также мнимый эллипс
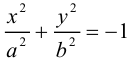 и точка
и точка 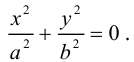
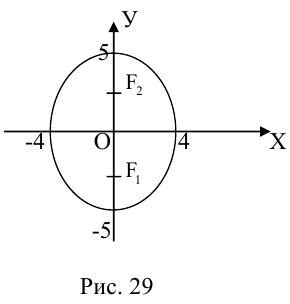
Пример №13
Найти эксцентриситет эллипса 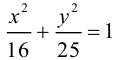 (рис. 29).
(рис. 29).
Так как 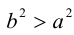 , то фокусы лежат на оси OY и поэтому
, то фокусы лежат на оси OY и поэтому 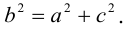
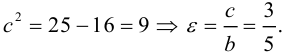
Гипербола
Определение: Гипербола – совокупность точек плоскости, модуль разности расстояний от которых до двух фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная, не равная нулю и меньшая, чем расстояние между фокусами.
Чтобы вывести уравнение гиперболы, выберем пдск следующим образом:
ось абсцисс проведем через фокусы  , а ось ординат – посередине отрез-
, а ось ординат – посередине отрез-
ка  перпендикулярно оси абсцисс. Тогда
перпендикулярно оси абсцисс. Тогда 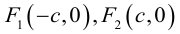 – фокусы гиперболы (рис. 30). Пусть M(x, y) – произвольная точка, лежащая на гиперболе.
– фокусы гиперболы (рис. 30). Пусть M(x, y) – произвольная точка, лежащая на гиперболе.
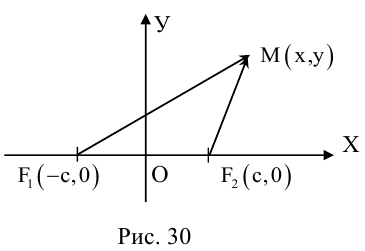
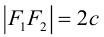 – расстояние между фокусами, 2a – модуль разности расстояний от точек на гиперболе до
– расстояние между фокусами, 2a – модуль разности расстояний от точек на гиперболе до 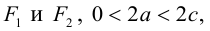
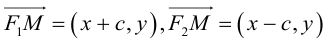 (рис. 30).
(рис. 30).
Запишем свойство точек, принадлежащих гиперболе, сформулированное в определении:
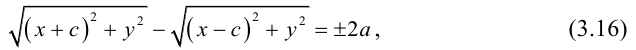
(3.16) – уравнение гиперболы в выбранной системе координат ( «+» – если разность расстояний положительна, и «–» – если отрицательна). Чтобы привести это уравнение к более простому виду, умножим (3.16) на сопряженное выражение и выполним такие же действия, как при упрощении уравнения эллипса, после чего получим:

По определению 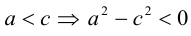 . Обозначим
. Обозначим 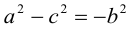 , тогда (3.17) перепишется в виде:
, тогда (3.17) перепишется в виде:

(3.18) – каноническое уравнение гиперболы.
Исследуем форму гиперболы по ее каноническому уравнению.
Из (3.18) следует, что гипербола симметрична относительно осей координат. Если x=0, 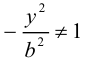 , значит, точек пересечения с OY нет; если y = 0 , то
, значит, точек пересечения с OY нет; если y = 0 , то 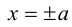 . Точки пересечения с осями симметрии называются вершинами гиперболы. Кроме того, из (3.18) следует, что
. Точки пересечения с осями симметрии называются вершинами гиперболы. Кроме того, из (3.18) следует, что 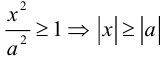 . Точка пересечения осей симметрии называется центром гиперболы. Ось симметрии, на которой расположены фокусы, называется фокальной осью. При этом фокальная ось также называется действительной (с ней гипербола пересекается), а ось симметрии, с которой гипербола не пересекается, называется ее мнимой осью.
. Точка пересечения осей симметрии называется центром гиперболы. Ось симметрии, на которой расположены фокусы, называется фокальной осью. При этом фокальная ось также называется действительной (с ней гипербола пересекается), а ось симметрии, с которой гипербола не пересекается, называется ее мнимой осью.
c – полуфокусное расстояние, a – действительная полуось, b – мнимая полуось. Отношение полуфокусного расстояния к длине действительной полуоси называется эксцентриситетом гиперболы: 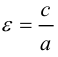 . Так как по определению
. Так как по определению 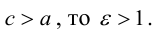
Считая, что 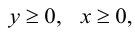 из (3.18) получим, что
из (3.18) получим, что 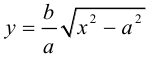 – уравнение части гиперболы, расположенной в первой четверти. Заметим, что при неограниченном возрастании
– уравнение части гиперболы, расположенной в первой четверти. Заметим, что при неограниченном возрастании 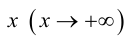 разность
разность 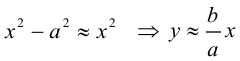 , то есть при достаточно больших x гипербола приближается к прямой
, то есть при достаточно больших x гипербола приближается к прямой 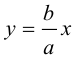 ,
,
причем ординаты точек на ней меньше соответствующих ординат точек на этой
прямой: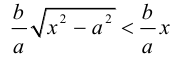 . Прямая
. Прямая 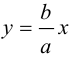 называется асимптотой гиперболы.
называется асимптотой гиперболы.
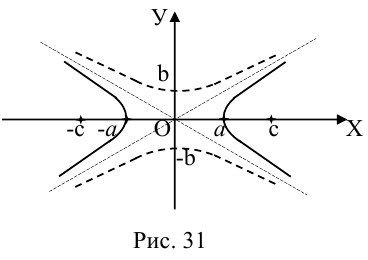
Из симметрии гиперболы следует, что то же самое происходит во второй, третьей и четвертой четвертях. Поэтому 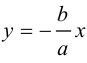 – также асимптота.
– также асимптота.
Итак, прямые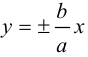 – асимптоты гиперболы (3.18), а гипербола – кривая, состоящая из двух ветвей (рис. 31).
– асимптоты гиперболы (3.18), а гипербола – кривая, состоящая из двух ветвей (рис. 31).
Если фокусы гиперболы лежат на OY , то ее уравнение имеет вид:

Гиперболы (3.18) и (3.19) называются сопряженными (рис. 31). Уравнения асимптот (3.19) такие же, как и для (3.18), но действительной является ось OY .
Если a = b, то гипербола называется равносторонней: 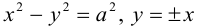 – уравнения ее асимптот (рис. 32 ).
– уравнения ее асимптот (рис. 32 ).
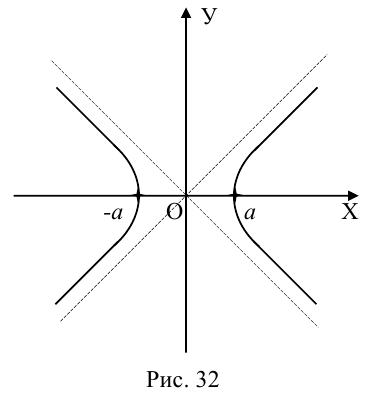
Очевидно, в этом случае асимптоты перпендикулярны. После поворота осей координат на  против часовой стрелки, получим гиперболу, задаваемую уравнением
против часовой стрелки, получим гиперболу, задаваемую уравнением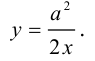
ЗАМЕЧАНИЕ 1. Если центр гиперболы в точке  , а оси симметрии параллельны координатным осям, то уравнение гиперболы имеет вид
, а оси симметрии параллельны координатным осям, то уравнение гиперболы имеет вид
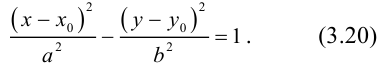
ЗАМЕЧАНИЕ 2. К кривым второго порядка гиперболического типа относится также пара пересекающихся прямых: 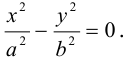
Пример №14
Найти координаты центра и написать уравнения асимптот гиперболы 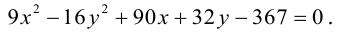
Приведем данное уравнение к виду (3.20):
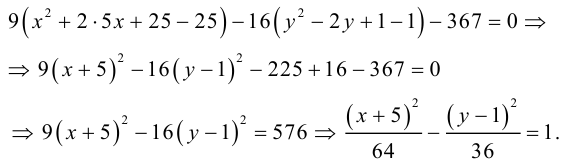
Таким образом, 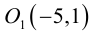 – центр,
– центр, 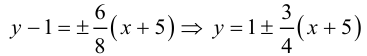 – уравнения асимптот данной гиперболы.
– уравнения асимптот данной гиперболы.
Парабола
Определение: Парабола – совокупность точек плоскости, равноудаленных от фиксированной точки этой плоскости, называемой фокусом, и фиксированной прямой, не проходящей через эту точку, называемой директрисой. Чтобы вывести уравнение параболы, выберем пдск следующим образом: ось абсцисс проведем через фокус перпендикулярно директрисе, а ось ординат посередине между фокусом и директрисой (рис. 33).
Пусть расстояние между фокусом F и директрисой DK равно p . Тогда 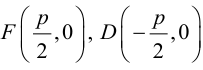 . Если M(x, y) – произвольная точка на параболе, то по определению
. Если M(x, y) – произвольная точка на параболе, то по определению
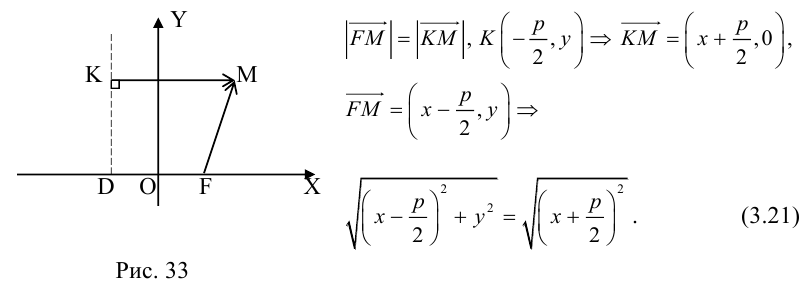
(3.21) – уравнение параболы в выбранной системе координат.
Упростим его:
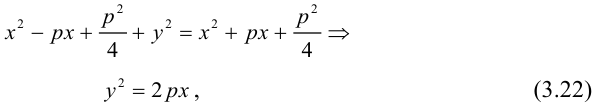
(3.22) – каноническое уравнение параболы; p называется ее параметром.
Из уравнения следует, что парабола симметрична относительно OX и проходит через начало координат. Кроме того, если  , поэтому кривая лежит в правой полуплоскости и с ростом величины
, поэтому кривая лежит в правой полуплоскости и с ростом величины  также растет. Точка пересечения параболы с осью симметрии называется ее вершиной (рис. 34).
также растет. Точка пересечения параболы с осью симметрии называется ее вершиной (рис. 34).
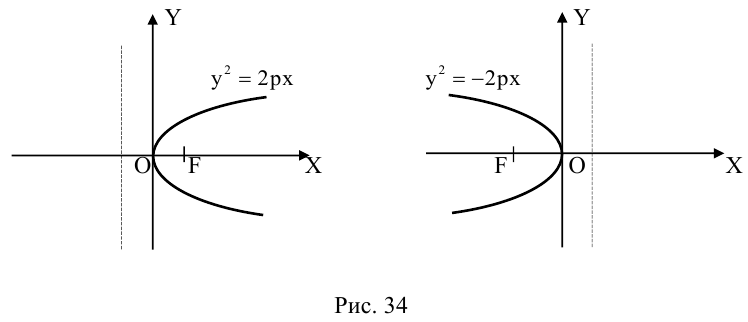
Если фокус параболы на оси ОУ (рис. 35), то ее каноническое уравнение имеет вид 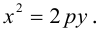
ЗАМЕЧАНИЕ 1. Если вершина параболы в точке 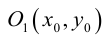 и ось симметрии параллельна OX , то ее уравнение имеет вид
и ось симметрии параллельна OX , то ее уравнение имеет вид 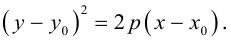
ЗАМЕЧАНИЕ 2. К кривым второго порядка параболического типа относятся также 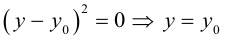 – пара совпадающих прямых;
– пара совпадающих прямых;
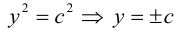 – пара параллельных прямых;
– пара параллельных прямых; 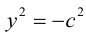 пара мнимых параллельных прямых.
пара мнимых параллельных прямых.
Пример №15
Написать уравнение геометрического места точек, равноудаленных от прямой x + y – 1 = 0 и точки F(-3,2).
По определению множество точек, равноудаленных от данных точки и прямой, является параболой. Пусть M (x, y) – произвольная точка искомой параболы, тогда 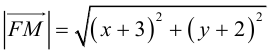 . Расстояние от точки M до прямой x + y – 1 = 0 вычисляется по формуле (3.8):
. Расстояние от точки M до прямой x + y – 1 = 0 вычисляется по формуле (3.8): 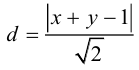 . Из условия следует, что
. Из условия следует, что
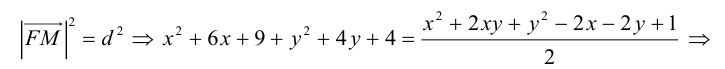 – уравнение искомого геометрического места точек.
– уравнение искомого геометрического места точек.
Если оси координат системы XOY повернуть на угол 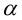 так, чтобы одна из них стала параллельна директрисе, а затем перенести начало координат в точку
так, чтобы одна из них стала параллельна директрисе, а затем перенести начало координат в точку  – вершину параболы, то в новой системе
– вершину параболы, то в новой системе  уравнение параболы будет каноническим
уравнение параболы будет каноническим  (рис. 36).
(рис. 36).
ЗАМЕЧАНИЕ. Можно показать, что, кроме окружности, эллипса, гиперболы, параболы и вырожденных случаев, указанных в замечаниях, других кривых второго порядка не существует.
Преобразования координат на плоскости
Преобразование координат — замена системы координат на плоскости, в пространстве или, в самом общем случае, на заданном n-мерном многообразии.
Параллельный перенос координатных осей
Пусть на плоскости задана пдск ХОУ. Будем называть ее “старой”. “Новая” система координат 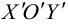 получена из “старой” параллельным переносом осей в точку
получена из “старой” параллельным переносом осей в точку  . Выясним, как связаны координаты
. Выясним, как связаны координаты  одной и той же точки М в этих системах координат.
одной и той же точки М в этих системах координат.
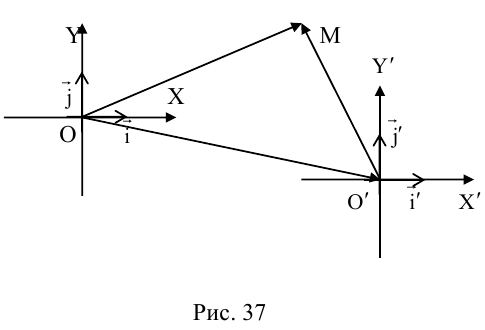
Пусть  – орты координатных осей системы ХОУ, а
– орты координатных осей системы ХОУ, а 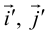 – системы
– системы 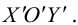
Тогда 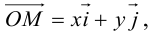
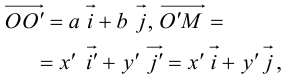
так как 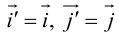 по определению равенства векторов (рис. 37).
по определению равенства векторов (рис. 37).
Так как 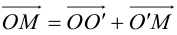 , то
, то
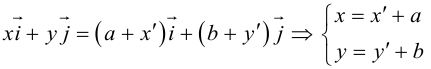
или

(3.23) – формулы параллельного переноса осей пдск.
Поворот координатных осей на угол α
Поворот координатных осей на угол 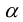 .
.
Пусть “новая” пдск 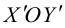 получена из “старой” системы координат XOY поворотом осей ОХ и ОУ на угол
получена из “старой” системы координат XOY поворотом осей ОХ и ОУ на угол 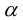 (рис. 38) и М(х, у) – произвольная точка в системе XOY . Выясним, какими станут ее координаты в “новой” пдск.
(рис. 38) и М(х, у) – произвольная точка в системе XOY . Выясним, какими станут ее координаты в “новой” пдск.
Из рис. 38 очевидно, что

Так как 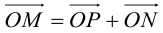 , то
, то
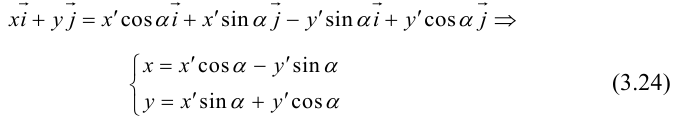
(3.24) – формулы поворота координатных осей на угол , выражающие старые координаты точки через новые.
Если обозначить 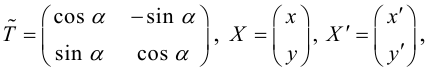 , то (3.24) можно переписать:
, то (3.24) можно переписать: 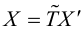 . Так как
. Так как 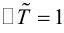 , то существует
, то существует 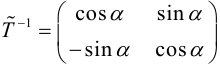 и
и
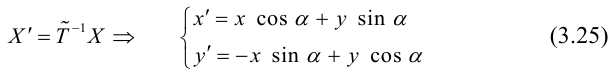
(3.25) – формулы поворота координатных осей на угол 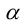 , выражающие новые координаты точки через старые.
, выражающие новые координаты точки через старые.
Пример №16
Каким будет уравнение прямой x + y – 1 = 0 после поворота координатных осей на угол 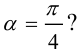
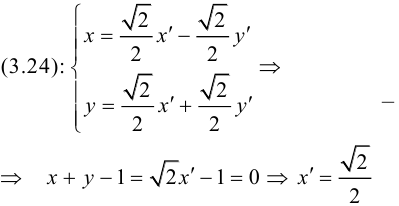
новое уравнение прямой (рис. 39).
Линейные преобразования на плоскости
Рассмотрим систему линейных уравнений:

Каждой точке плоскости M(x, y) по формулам (3.26) можно поставить в соответствие единственную точку 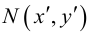 той же плоскости. При этом точка N называется образом точки M , а точка M – прообразом точки N . Кроме того,уравнения (3.26) линейны относительно x и y , поэтому будем говорить, что (3.26) определяют линейное преобразование плоскости в себя.
той же плоскости. При этом точка N называется образом точки M , а точка M – прообразом точки N . Кроме того,уравнения (3.26) линейны относительно x и y , поэтому будем говорить, что (3.26) определяют линейное преобразование плоскости в себя.
Преобразование (3.26) определяется матрицей  , которая называется матрицей линейного преобразования. Обозначая ,
, которая называется матрицей линейного преобразования. Обозначая ,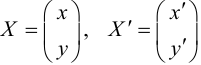
(3.26) можно переписать в виде 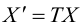 . Можно показать, что определитель
. Можно показать, что определитель 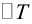 равен коэффициенту изменения площадей при линейном преобразовании (3.26). При этом
равен коэффициенту изменения площадей при линейном преобразовании (3.26). При этом  , если в результате преобразования направление обхода некоторого контура не меняется, и
, если в результате преобразования направление обхода некоторого контура не меняется, и 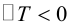 , если оно меняется на противоположное. Поясним это на примерах.
, если оно меняется на противоположное. Поясним это на примерах.
Пример №17
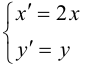 – растяжение вдоль
– растяжение вдоль
оси OX в 2 раза. 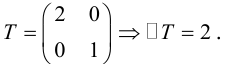
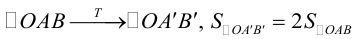 (рис. 40).
(рис. 40).
Пример №18
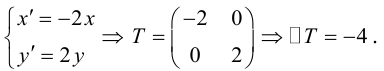
при этом направление обхода 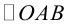 от O к A , затем к B – по часовой стрелке, а соответствующее направление обхода
от O к A , затем к B – по часовой стрелке, а соответствующее направление обхода 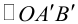 – против часовой стрелки. Геометрически данное преобразование – растяжение вдоль OX и OY в 2 раза и отражение симметрично относительно оси OY (рис. 41).
– против часовой стрелки. Геометрически данное преобразование – растяжение вдоль OX и OY в 2 раза и отражение симметрично относительно оси OY (рис. 41).
Определение: Линейное преобразование (3.26) называется невырожденным, если 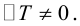
В этом случае существует обратная матрица 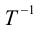 и можно найти
и можно найти 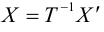 . То есть, если
. То есть, если 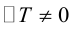 , то не только у каждого прообраза существует единственный образ, но и наоборот: для каждого образа существует единственный прообраз. В этом случае говорят, что (3.26) устанавливает взаимно однозначное соответствие между точками плоскости, или линейное преобразование плоскости на себя.
, то не только у каждого прообраза существует единственный образ, но и наоборот: для каждого образа существует единственный прообраз. В этом случае говорят, что (3.26) устанавливает взаимно однозначное соответствие между точками плоскости, или линейное преобразование плоскости на себя.
Можно показать, что невырожденное линейное преобразование переводит прямую в прямую, а кривую второго порядка – в кривую второго порядка.
Пример №19
Пусть 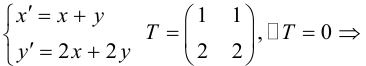 преобразование вырожденное.
преобразование вырожденное.
Какими будут образы точек, лежащих, например, на прямой x + y – 1 = 0
(рис. 42)?
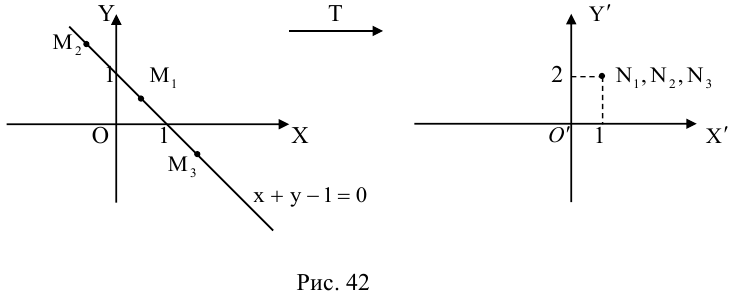
Очевидно, что если 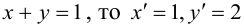 , то есть у точки N(1,2) существует бесконечное множество прообразов: все они лежат на прямой x + y – 1 = 0. Потому данное вырожденное линейное преобразование не устанавливает взаимно-однозначного соответствия между точками плоскости.
, то есть у точки N(1,2) существует бесконечное множество прообразов: все они лежат на прямой x + y – 1 = 0. Потому данное вырожденное линейное преобразование не устанавливает взаимно-однозначного соответствия между точками плоскости.
Пример №20
Рассмотрим формулы (3.25):
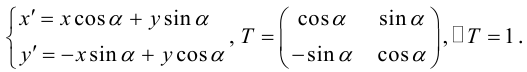
Очевидно, что поворот осей пдск на угол 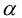 – линейное преобразование.
– линейное преобразование.
Так как это линейное преобразование невырожденное, то существует
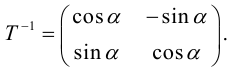
Заметим, что в этом случае 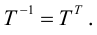
Определение: Матрица A называется ортогональной, если 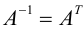 .
.
Линейное преобразование, матрица которого ортогональна, называется ортогональным.
Таким образом, поворот координатных осей – ортогональное линейное преобразование.
Можно показать, что если A – ортогональная матрица, то 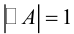 (доказать самостоятельно). Таким образом, в результате ортогональных линейных преобразований на плоскости площади фигур остаются неизменными.
(доказать самостоятельно). Таким образом, в результате ортогональных линейных преобразований на плоскости площади фигур остаются неизменными.
Произведение линейных преобразований
Рассмотрим матрицы 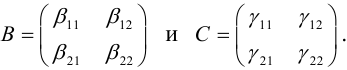 Каждая из них определяет линейное преобразование плоскости. Если M(x, y) – некоторая точка плоскости, то под действием линейного преобразования
Каждая из них определяет линейное преобразование плоскости. Если M(x, y) – некоторая точка плоскости, то под действием линейного преобразования 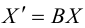 с матрицей B она перейдет в точку
с матрицей B она перейдет в точку 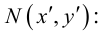

В свою очередь точка N под действием линейного преобразования 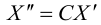 с матрицей C перейдет в точку
с матрицей C перейдет в точку 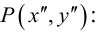

Такое последовательное выполнение линейных преобразований называется их произведением: 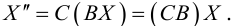
Покажем, что произведение линейных преобразований также линейное преобразование, и найдем его матрицу. Подставим (3.27) в (3.28):
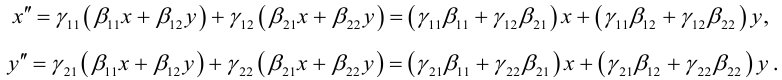
То есть
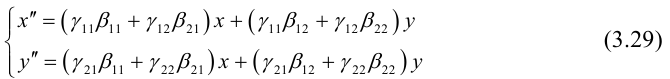
(3.29) – система линейных уравнений, а потому произведение линейных преобразований линейно. Матрица (3.29) имеет вид:
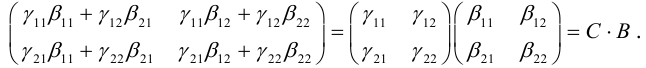
Таким образом, матрица произведения линейных преобразований равна произведению их матриц. Само же правило умножения матриц, сформулированное в гл.1, находит объяснение в этом выводе.
Приведение квадратичной формы к каноническому виду
Определение: Квадратичной формой относительно двух переменных x и y называется однородный многочлен второй степени:
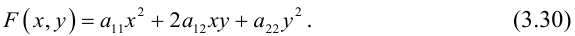
Уравнение 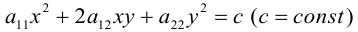 задает на плоскости кривую второго порядка, причем, так как вместе с точкой M(x, y) , лежащей на этой кривой, ей принадлежит и точка
задает на плоскости кривую второго порядка, причем, так как вместе с точкой M(x, y) , лежащей на этой кривой, ей принадлежит и точка 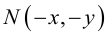 , кривая симметрична относительно
, кривая симметрична относительно
начала координат, то есть является центральной кривой (эллиптического или гиперболического типа).
Предположим, что уравнение 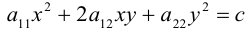 задает в пдск ХОУ эллипс. Если
задает в пдск ХОУ эллипс. Если 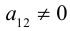 , то это уравнение не является каноническим уравнением эллипса, а потому, хотя О(0, 0) – его центр, оси симметрии не совпадают с ОХ и ОУ (рис. 43). Тем не менее, заметим, что если оси системы XOY повернуть на
, то это уравнение не является каноническим уравнением эллипса, а потому, хотя О(0, 0) – его центр, оси симметрии не совпадают с ОХ и ОУ (рис. 43). Тем не менее, заметим, что если оси системы XOY повернуть на
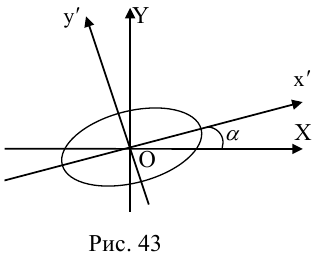
угол 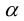 , то в системе
, то в системе 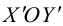 эллипс будет задаваться каноническим уравнением: кривая симметрична относительно
эллипс будет задаваться каноническим уравнением: кривая симметрична относительно  . Найдем линейное преобразование, соответствующее этому повороту.
. Найдем линейное преобразование, соответствующее этому повороту.
Матрица 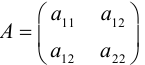 называется матрицей квадратичной формы (3.30).
называется матрицей квадратичной формы (3.30).
Пусть 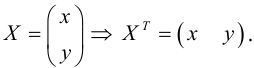
Вычислим 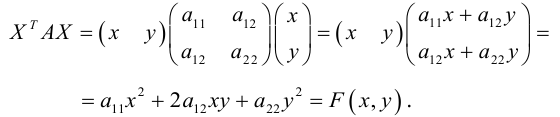
Таким образом, квадратичная форма может быть записана в матричном виде:

Пусть x, y – координаты точек плоскости в системе XOY , а 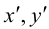 – координаты точек плоскости в новой системе
– координаты точек плоскости в новой системе 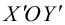 , где кривая задается каноническим уравнением. Переход от “старых” координат к “новым” будем искать в виде
, где кривая задается каноническим уравнением. Переход от “старых” координат к “новым” будем искать в виде
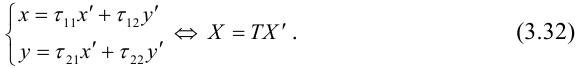
(3.32) – ортогональное линейное преобразование с матрицей
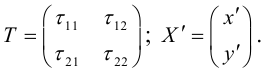
По определению ортогональной матрицы

(В результате ортогонального преобразования не происходит изменение площадей фигур, то есть фигуры не деформируются.)
Чтобы узнать, как изменится матрица квадратичной формы в результате линейного преобразования (3.32), подставим (3.32) в (3.31): 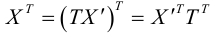 (свойство 5 умножения матриц)
(свойство 5 умножения матриц)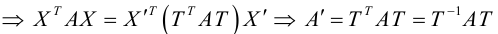
(свойство 2 умножения матриц и равенство (3.33)) – матрица новой квадратичной формы.
Так как в “новой” системе координат кривая должна задаваться каноническим уравнением, то есть в нем должно отсутствовать произведение координат xy, то 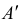 имеет вид:
имеет вид: 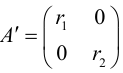
, где 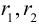 – неизвестные числа. Умножим равенство
– неизвестные числа. Умножим равенство 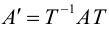 на матрицу T слева. Так как
на матрицу T слева. Так как 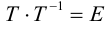 , то получим:
, то получим:
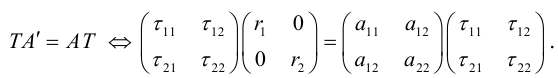
По определению равных матриц имеем:
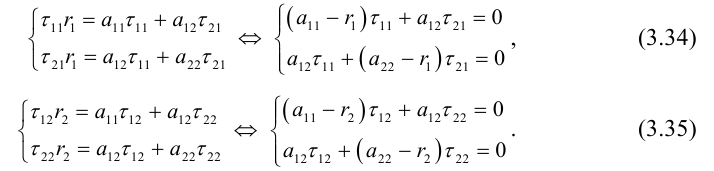
Системы уравнений (3.34), (3.35) – линейные и однородные. Они имеют нетривиальное решение, если их определители равны 0.
Это означает, что  являются решениями уравнения
являются решениями уравнения
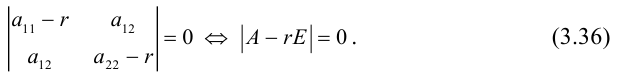
Уравнение (3.36) называется характеристическим уравнением матрицы A (характеристическим уравнением квадратичной формы). Его решения 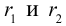 называются собственными значениями матрицы A (квадратичной формы).
называются собственными значениями матрицы A (квадратичной формы).
Покажем, что дискриминант квадратного уравнения (3.36) положителен, то есть любая квадратичная форма двух переменных имеет 2 различных собственных значения.
Вычислим определитель (3.36):
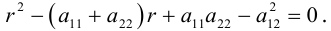
Дискриминант 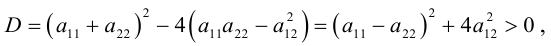
так как 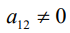 (иначе квадратичная форма будет канонической).
(иначе квадратичная форма будет канонической).
Таким образом, коэффициентами при 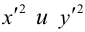 в каноническом виде квадратичной формы являются ее собственные значения, то есть решения уравнения (3.36).
в каноническом виде квадратичной формы являются ее собственные значения, то есть решения уравнения (3.36).
Решим (3.36) и подставим  в (3.34). Система имеет бесконечное множество решений и пусть
в (3.34). Система имеет бесконечное множество решений и пусть  – одно их них. Так как система (3.34) однородная, то
– одно их них. Так как система (3.34) однородная, то  – тоже решение. Подберем k так, чтобы вектор
– тоже решение. Подберем k так, чтобы вектор
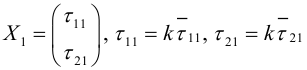 был единичным:
был единичным: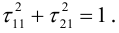
Векторы  называется собственными векторами квадратичной формы, соответствующими собственному значению
называется собственными векторами квадратичной формы, соответствующими собственному значению  , или первыми собственными векторами. Их направление называется первым главным направлением квадратичной формы. Таким образом, первым собственным вектором квадратичной формы называется любое ненулевое решение системы (3.34).
, или первыми собственными векторами. Их направление называется первым главным направлением квадратичной формы. Таким образом, первым собственным вектором квадратичной формы называется любое ненулевое решение системы (3.34).
Аналогично подставим 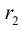 в (3.35) и найдем
в (3.35) и найдем 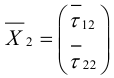 – второй собственный вектор, соответствующий собственному значению r2 . Его направление называется вторым главным направлением квадратичной формы.
– второй собственный вектор, соответствующий собственному значению r2 . Его направление называется вторым главным направлением квадратичной формы. 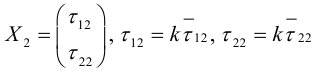 – второй единичный собственный вектор, то есть
– второй единичный собственный вектор, то есть 
Можно показать, что  . Кроме того,
. Кроме того, 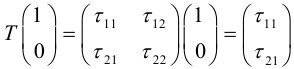 – первый собственный вектор, а
– первый собственный вектор, а 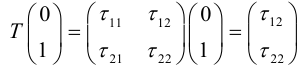 – второй собственный
– второй собственный
вектор, поэтому ортами “новой” системы координат  , к которой мы перейдем в результате линейного преобразования с матрицей T , являются единичные собственные векторы квадратичной формы, найденные как решения систем (3.34), (3.35). Направив оси “новой” системы координат вдоль собственных векторов
, к которой мы перейдем в результате линейного преобразования с матрицей T , являются единичные собственные векторы квадратичной формы, найденные как решения систем (3.34), (3.35). Направив оси “новой” системы координат вдоль собственных векторов 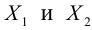 , получим систему координат, в которой квадратичная форма будет иметь канонический вид
, получим систему координат, в которой квадратичная форма будет иметь канонический вид 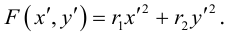
ВЫВОД.
Чтобы привести квадратичную форму к каноническому виду, надо:
- Составить и решить характеристическое уравнение (3.36); его решения – собственные значения – являются коэффициентами при
 в каноническом виде квадратичной формы.
в каноническом виде квадратичной формы. - Найти единичные собственные векторы, решив (3.34) и (3.35); они будут ортами новой системы координат
 .При этом если ось
.При этом если ось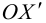 сонаправлена с
сонаправлена с 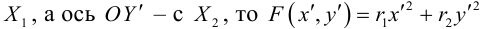 – канонический вид, который квадратичная форма имеет в системе
– канонический вид, который квадратичная форма имеет в системе 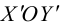 .
.
Приведение общего уравнения кривой второго порядка к каноническому виду
Общее уравнение кривой второго порядка имеет вид:
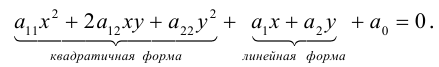
В результате невырожденного линейного преобразования с матрицей T квадратичная форма перейдет в квадратичную форму, линейная – в линейную, а свободный член 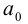 не изменится. Каждую группу слагаемых будем преобразовывать отдельно, а именно: найдем ортогональное преобразование, приводящее квадратичную форму к каноническому виду, затем посмотрим, как в результате этого преобразования изменится линейная форма (ортогональное преобразование в нашем случае – это поворот осей).
не изменится. Каждую группу слагаемых будем преобразовывать отдельно, а именно: найдем ортогональное преобразование, приводящее квадратичную форму к каноническому виду, затем посмотрим, как в результате этого преобразования изменится линейная форма (ортогональное преобразование в нашем случае – это поворот осей).
После поворота осей подберем параллельный перенос новой системы 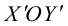 так, чтобы после него уравнение кривой стало каноническим.
так, чтобы после него уравнение кривой стало каноническим.
Пример №21
Привести к каноническому виду ранее полученное уравнение параболы (стр. 58) и построить ее:
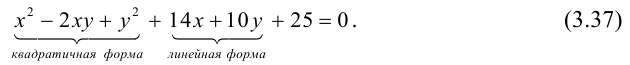
1) Составим матрицу квадратичной формы: 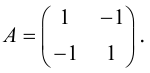
2) Составим и решим характеристическое уравнение (3.36):
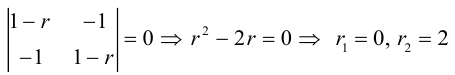 – собственные значения.
– собственные значения.
3) Найдем первый единичный собственный вектор, то есть решим систему (3.34):
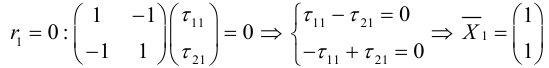 – первый собственный вектор.
– первый собственный вектор.
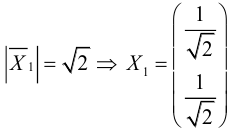 – первый единичный собственный вектор (орт оси
– первый единичный собственный вектор (орт оси  ).
).
4) Найдем второй единичный собственный вектор, то есть решим (3.35):
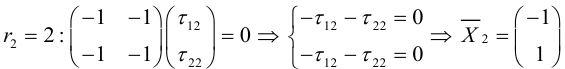 – второй собственный вектор.
– второй собственный вектор.
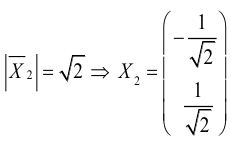 – второй единичный собственный вектор (орт оси
– второй единичный собственный вектор (орт оси  ) .
) .
Заметим, что 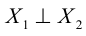 ,так как скалярное произведение
,так как скалярное произведение 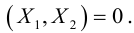
В полученной таким образом системе координат  , взяв несколько контрольных точек, нарисуем параболу
, взяв несколько контрольных точек, нарисуем параболу 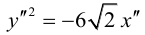 (рxис. 44).
(рxис. 44).
Сравните эскиз (рис. 36) и данный рисунок, являющийся результатом точных расчетов.
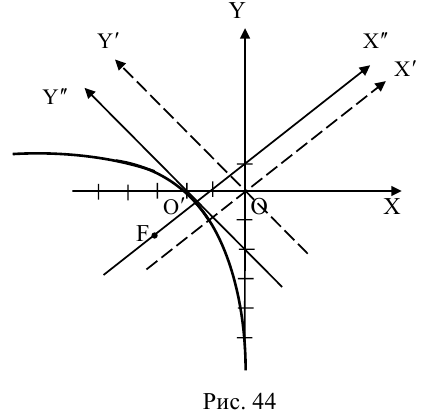
Плоскость
Покажем, что плоскость в пространстве задается в любой пдск линейным уравнением относительно трех переменных x, y, z.
Если A – некоторая точка на плоскости 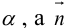 – вектор, перпендикулярный ей, то, во-первых, через A перпендикулярно
– вектор, перпендикулярный ей, то, во-первых, через A перпендикулярно 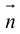 проходит единственная плоскость, а, во-вторых, для любой точки
проходит единственная плоскость, а, во-вторых, для любой точки 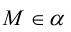 вектор
вектор 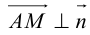 . Таким свойством обладают только точки, лежащие на
. Таким свойством обладают только точки, лежащие на 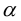 .
.
Чтобы вывести уравнение плоскости, зададим в пространстве пдск OXYZ . В этой системе координат 
Пусть M(x,y,z) – произвольная точка на плоскости  .
.
Тогда 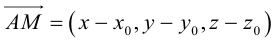 и
и 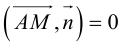 (рис. 45).
(рис. 45).
Вычислив скалярное произведение, получим:
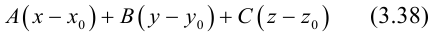
Координаты точек, лежащих в плоскости  , связаны соотношением (3.38). Если же
, связаны соотношением (3.38). Если же 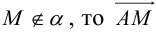 не перпендикулярен
не перпендикулярен 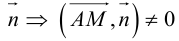 ,значит, координаты такой точки не удовлетворяют полученному уравнению. Поэтому (3.38) – уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору. Заметим, что это уравнение линейно относительно x, y, z.
,значит, координаты такой точки не удовлетворяют полученному уравнению. Поэтому (3.38) – уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору. Заметим, что это уравнение линейно относительно x, y, z.
Раскрыв скобки в (3.38), получим 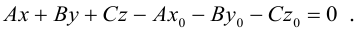
Обозначим 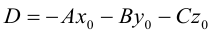 , тогда уравнение (3.38) примет вид:
, тогда уравнение (3.38) примет вид:

(3.39) – общее уравнение плоскости в пространстве,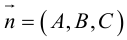 – ее нормаль.
– ее нормаль.
Определение: Любой ненулевой вектор 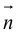 , перпендикулярный плоскости
, перпендикулярный плоскости  , называется ее нормальным вектором, или нормалью.
, называется ее нормальным вектором, или нормалью.
Особые случаи расположения плоскости
Выясним, какие особенности в расположении плоскости влечет за собой равенство нулю одного или нескольких коэффициентов в уравнении (3.39).
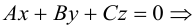 координаты точки O(0,0,0) удовлетворяют уравнению, значит, плоскость проходит через начало координат.
координаты точки O(0,0,0) удовлетворяют уравнению, значит, плоскость проходит через начало координат. 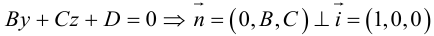 , так как
, так как 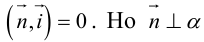 , значит, плоскость
, значит, плоскость  .
. 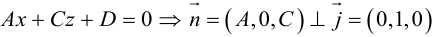 , так как
, так как 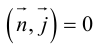 .Значит, плоскость
.Значит, плоскость  .
.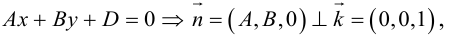 так как
так как  . Значит, плоскость
. Значит, плоскость  .
. 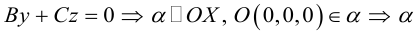 проходит через OX .
проходит через OX . 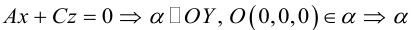 проходит через OY .
проходит через OY . 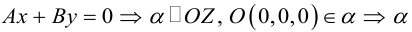 проходит через OZ .
проходит через OZ . -
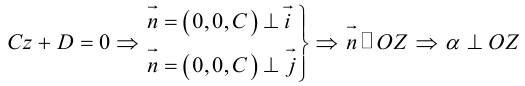 или
или  .
. 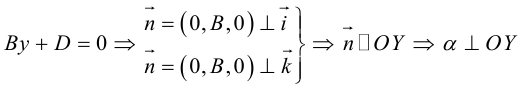 или
или 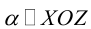 .
. -
 или
или  .
. 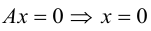 – плоскость YOZ .
– плоскость YOZ . 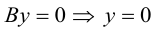 – плоскость XOZ .
– плоскость XOZ . 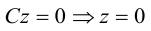 – плоскость XOY .
– плоскость XOY .
Уравнение плоскости в отрезках
Пусть плоскость  не параллельна ни одной из координатных осей и не проходит через начало координат. Тогда она отсекает на координатных осях отрезки a,b,c (рис. 46). Выведем уравнение такой плоскости.
не параллельна ни одной из координатных осей и не проходит через начало координат. Тогда она отсекает на координатных осях отрезки a,b,c (рис. 46). Выведем уравнение такой плоскости.
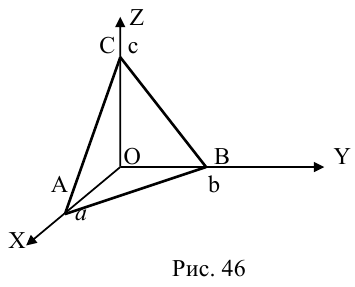
Рассмотрим 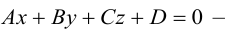 общее уравнение плоскости. Так как
общее уравнение плоскости. Так как 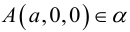 , то
, то 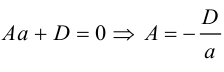 .
.
Аналогично 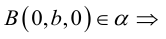
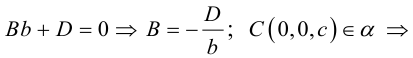
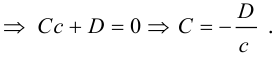
Подставив А, В, С в общее уравнение, получим
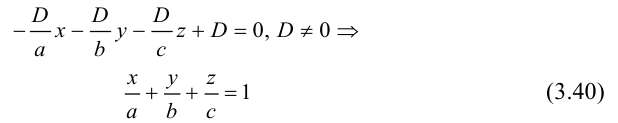
(3.40) – уравнение плоскости в отрезках.
Пример №22
Вычислить объем тетраэдра, образованного плоскостями
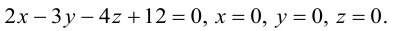
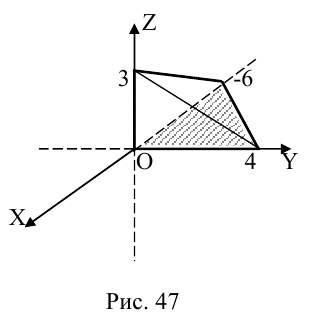
Перепишем уравнение плоскости в виде (3.40):
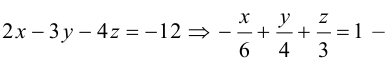
уравнение данной плоскости в отрезках. Поэтому (рис. 47)
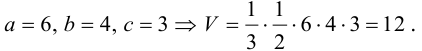
Уравнение плоскости, проходящей через три точки
Пусть в некоторой пдск заданы три точки, не лежащие на одной прямой:
 . Известно, что через них проходит единственная плоскость
. Известно, что через них проходит единственная плоскость 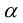 .
.
Чтобы вывести ее уравнение, рассмотрим произвольную точку этой плоскости M(x,y,z) . Тогда 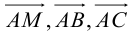 – компланарные векторы, и их смешанное произведение равно нулю:
– компланарные векторы, и их смешанное произведение равно нулю: 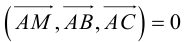 . Тогда по формуле (2.9) получим
. Тогда по формуле (2.9) получим
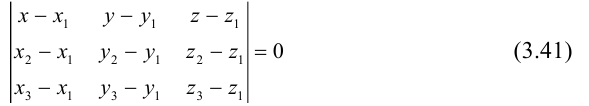
(3.41) – уравнение плоскости, проходящей через три точки.
ЗАМЕЧАНИЕ. Если точки лежат на одной прямой, то векторы 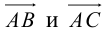 коллинеарны и их соответствующие координаты пропорциональны. Поэтому в определителе (3.41) две строки пропорциональны и по свойству 6 определителей он тождественно равен нулю, что означает, что координаты любой точки M(x,y,z) удовлетворяют уравнению (3.41). Это иллюстрация того факта, что через прямую и любую точку можно провести плоскость.
коллинеарны и их соответствующие координаты пропорциональны. Поэтому в определителе (3.41) две строки пропорциональны и по свойству 6 определителей он тождественно равен нулю, что означает, что координаты любой точки M(x,y,z) удовлетворяют уравнению (3.41). Это иллюстрация того факта, что через прямую и любую точку можно провести плоскость.
Пример №23
Написать уравнение плоскости, проходящей через точки
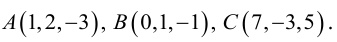
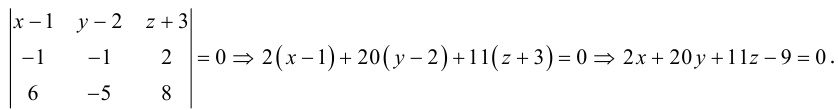
Угол между плоскостями
Определение: Углом между плоскостями называется любой из двух смежных двугранных углов, образованных плоскостями при их пересечении.
Если плоскости параллельны, то угол между ними равен 0 или  радиан.
радиан.
Рассмотрим плоскости 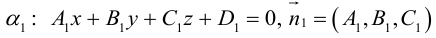 и
и
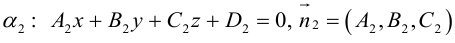 .
.
Очевидно, 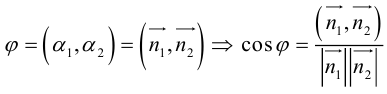
или 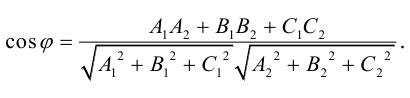
Если 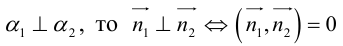 –0 условие перпендикулярности плоскостей.
–0 условие перпендикулярности плоскостей.
Если 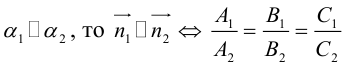 – условие параллельности плоскостей.
– условие параллельности плоскостей.
Пример №24
Найти угол между плоскостями
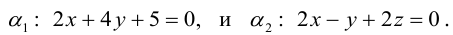
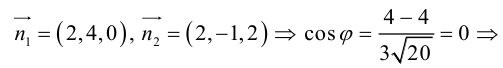 плоскости перпендикулярны.
плоскости перпендикулярны.
Прямая линия в пространстве
Всякая линия в пространстве есть результат пересечения двух поверхностей. В частности прямую линию можно рассматривать как результат пересечения двух плоскостей
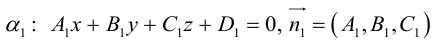
и
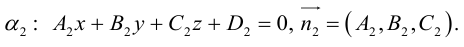
Если  не параллельна
не параллельна  , то есть
, то есть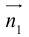 не коллинеарен
не коллинеарен 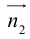 , то система уравнений
, то система уравнений
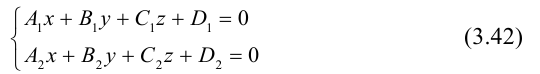
определяет прямую линию в пространстве.
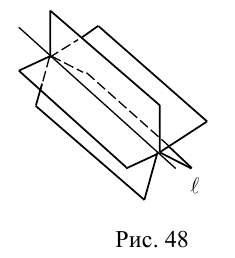
Уравнения (3.42) называются общими уравнениями прямой в пространстве.
Очевидно, одна и та же прямая может быть результатом пересечения разных пар плоскостей (рис. 48), поэтому прямую в пространстве можно задать различными способами.
Уравнения (3.42) неудобны в использовании, так как не дают представления о расположении прямой относительно выбранной системы координат.
Поэтому выведем более удобные уравнения, эквивалентные (3.42), то есть из бесконечного множества плоскостей, проходящих через данную прямую, выберем в некотором смысле более заметную пару.
Канонические уравнения прямой в пространстве
Пусть в некоторой пдск задана прямая  , проходящая через точку
, проходящая через точку  параллельно ненулевому вектору
параллельно ненулевому вектору  . Такой вектор называется направляющим вектором этой прямой.
. Такой вектор называется направляющим вектором этой прямой.
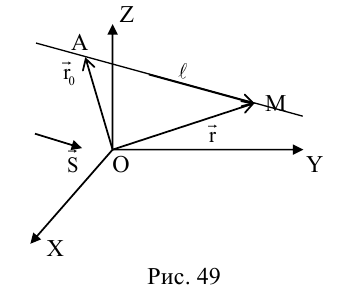
Для произвольной точки 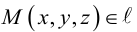 вектор
вектор 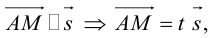 где t – не-который числовой множитель. Кроме того,
где t – не-который числовой множитель. Кроме того, 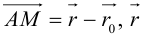 – радиус-вектор точки M ,
– радиус-вектор точки M , 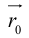 – радиус вектор точки A
– радиус вектор точки A
(рис. 49).
Отсюда 
(3.43) – векторное уравнение прямой в пространстве. Из (3.43) получаем:

(3.44) – параметрические уравнения прямой в пространстве, 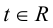 – параметр.
– параметр.
Выразим из каждого уравнения (3.44) параметр:
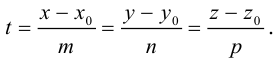
Тогда 
(3.45) – канонические уравнения прямой в пространстве, то есть уравнения прямой, проходящей через точку 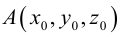 параллельно вектору
параллельно вектору 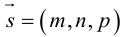 .
.
Заметим, что уравнения (3.45) задают прямую как результат пересечения плоскостей
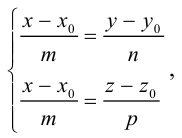
одна из которых параллельна OZ , а вторая – OY или как
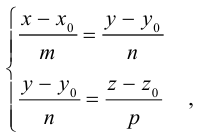
где первая плоскость параллельна OZ , а вторая – OX .
Если прямая  проходит через две заданные точки
проходит через две заданные точки 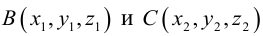 , то
, то 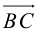 направляющий вектор этой прямой, поэтому из (3.45) получим:
направляющий вектор этой прямой, поэтому из (3.45) получим:

(3.46) – уравнения пространственной прямой, проходящей через две заданные точки.
Угол между прямыми в пространстве
Рассмотрим прямые, заданные в некоторой пдск каноническими уравнениями:
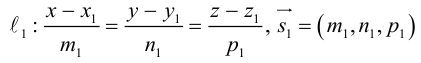
и
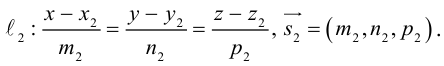
Определение: Углом между прямыми в пространстве называется угол между двумя пересекающимися прямыми, проходящими через произвольную точку пространства параллельно данным.
Из определения следует, что 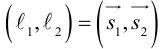 . Если
. Если 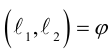 , то
, то
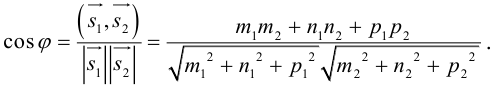
1)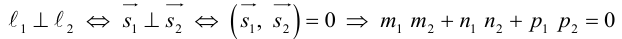 – условие перпендикулярности прямых.
– условие перпендикулярности прямых.
2)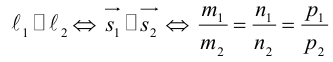 – условие параллельности прямых в пространстве.
– условие параллельности прямых в пространстве.
Пример №25
Найти угол между прямой 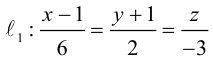 и прямой
и прямой  , проходящей через точки
, проходящей через точки 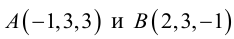 .
.
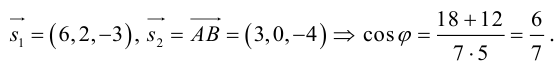
Заметим, что уравнение прямой 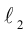 имеет вид:
имеет вид: 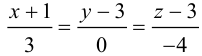 . В данном случае ноль в знаменателе писать принято: он означает, что направляющий вектор прямой (и сама прямая) параллелен плоскости XOZ . Эта прямая является результатом пересечения плоскостей
. В данном случае ноль в знаменателе писать принято: он означает, что направляющий вектор прямой (и сама прямая) параллелен плоскости XOZ . Эта прямая является результатом пересечения плоскостей 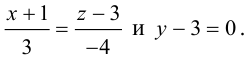
Приведение общих уравнений прямой в пространстве к каноническому виду
Рассмотрим прямую  , заданную общими уравнениями (3.42) в пространстве:
, заданную общими уравнениями (3.42) в пространстве:
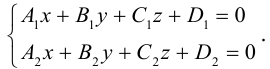
Привести эти уравнения к каноническому виду можно двумя способами:
- найти координаты какой-либо точки
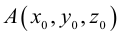 , лежащей на
, лежащей на  , ее направляющий вектор s и написать уравнения (3.45);
, ее направляющий вектор s и написать уравнения (3.45); - найти координаты двух точек, лежащих на
 , и воспользоваться уравнениями (3.46).
, и воспользоваться уравнениями (3.46).
1 способ.
Координаты точки A – любое частное решение системы линейных уравнений (3.42). Эта система имеет бесконечное множество решений, так как ранги основной и расширенной матриц 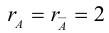 , а число неизвестных
, а число неизвестных 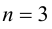 .
.
 – направляющий вектор прямой
– направляющий вектор прямой  , поэтому
, поэтому 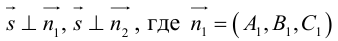 – нормаль плоскости
– нормаль плоскости 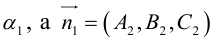 – нормаль плоскости
– нормаль плоскости  . Из определения векторного произведения векторов следует, что тогда
. Из определения векторного произведения векторов следует, что тогда 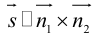 . Так как
. Так как 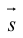 – произвольный вектор, параллельный
– произвольный вектор, параллельный 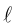 , то будем считать, что
, то будем считать, что 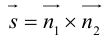 .
.
Пример №26
Привести уравнения прямой 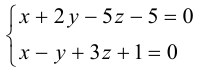 к каноническому виду.
к каноническому виду.
Найдем какое-нибудь частное решение этой системы: пусть, например,
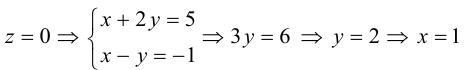 , то есть точка A(1,2,0) лежит на прямой.
, то есть точка A(1,2,0) лежит на прямой.
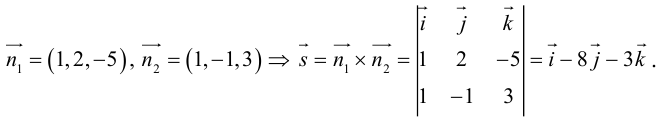
Таким образом, 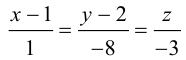 – канонические уравнения данной прямой.
– канонические уравнения данной прямой.
2 способ.
Найдем два произвольных частных решения системы уравнений, задающей прямую.
В рассмотренном примере 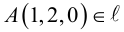 . Пусть теперь
. Пусть теперь
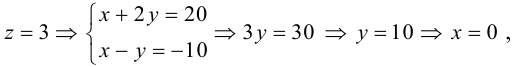
тогда 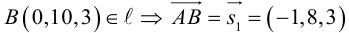 – направляющий вектор прямой, который отличается от найденного ранее только знаком. Поэтому уравнения
– направляющий вектор прямой, который отличается от найденного ранее только знаком. Поэтому уравнения 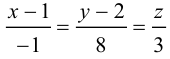 совпадают (с точностью до знака) с уже найденными.
совпадают (с точностью до знака) с уже найденными.
Угол между прямой и плоскостью
Определение: Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость.
Пусть в некоторой пдск заданы плоскость
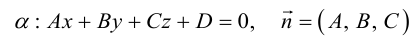
и прямая
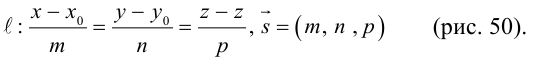
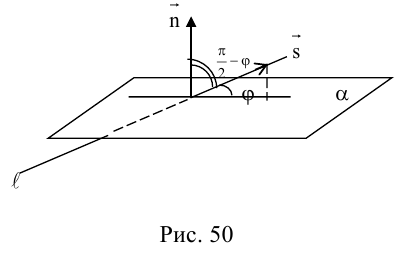
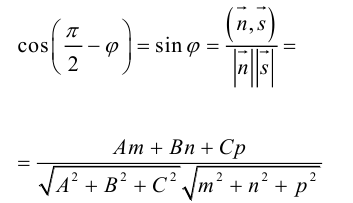


Определение общих точек прямой и плоскости
Чтобы найти общие точки прямой : 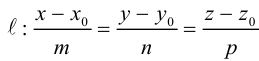 и плоскости
и плоскости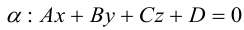 , надо решить систему линейных уравнений:
, надо решить систему линейных уравнений:
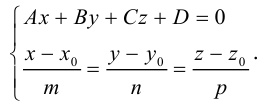
Решение этой системы будет наименее трудоемким, если перейти к параметрическим уравнениям прямой (3.44):
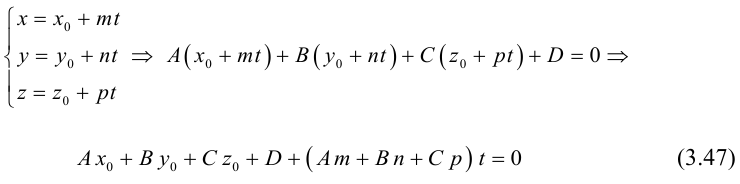
1) Пусть 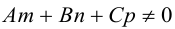 . Это значит, что прямая не параллельна плоскости, а потому они имеют одну общую точку. Из (3.47) найдем
. Это значит, что прямая не параллельна плоскости, а потому они имеют одну общую точку. Из (3.47) найдем
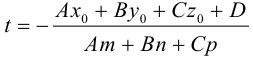
и по формулам (3.44) M(x,y,z) – их точку пересечения.
2) Пусть 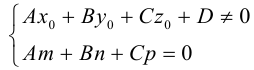 . Это означает, что в (3.47) решений нет: выполнено условие параллельности прямой и плоскости, при этом точка
. Это означает, что в (3.47) решений нет: выполнено условие параллельности прямой и плоскости, при этом точка 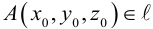 , но не лежит в плоскости
, но не лежит в плоскости  , значит, прямая и плоскость общих точек не имеют.
, значит, прямая и плоскость общих точек не имеют.
3) Пусть 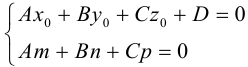 . Тогда любое
. Тогда любое 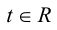 – решение (3.47) и система имеет бесконечно много решений: выполнено условие параллельности прямой и плоскости и точка
– решение (3.47) и система имеет бесконечно много решений: выполнено условие параллельности прямой и плоскости и точка 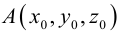 , лежащая на прямой, лежит в плоскости. Это значит, что прямая лежит в плоскости, то есть имеет с ней бесконечное множество общих точек.
, лежащая на прямой, лежит в плоскости. Это значит, что прямая лежит в плоскости, то есть имеет с ней бесконечное множество общих точек.
Пример №27
Найти проекцию точки 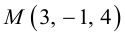 на плоскость
на плоскость 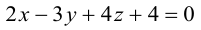 (рис. 53).
(рис. 53).
Пусть прямая  проходит через точку М перпендикулярно плоскости
проходит через точку М перпендикулярно плоскости  . Точка ее пересечения с плоскостью и будет искомой проекцией. В качестве направляющего вектора
. Точка ее пересечения с плоскостью и будет искомой проекцией. В качестве направляющего вектора 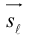 можно взять нормаль к плоскости
можно взять нормаль к плоскости 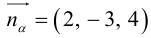 .
.
Напишем канонические уравнения прямой (3.45):

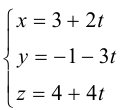 Подставим x,y,z в уравнение плоскости:
Подставим x,y,z в уравнение плоскости:
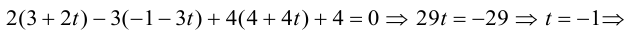
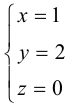 , то есть P 1,2,0 – искомая проекция.
, то есть P 1,2,0 – искомая проекция.
Цилиндрические поверхности
Уравнение F(x, y, z)=0 задает в пространстве некоторую поверхность.
Пусть уравнение содержит только две переменные, например, F(x,y)=0.Рассмотренное в плоскости XOY , оно задает некоторую кривую. Но ему будут удовлетворять и все точки пространства, которые проецируются в точки этой кривой, так как в уравнении отсутствует z , то есть все точки M(x,y,z) у которых х и у связаны соотношением  – произвольно.
– произвольно.
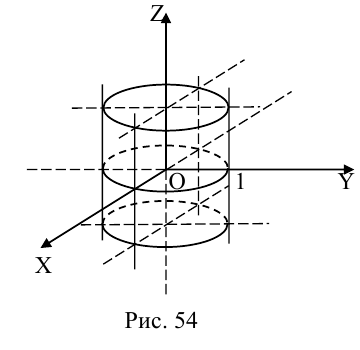
Пример №28
Построить поверхность 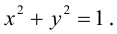
На плоскости это уравнение задает окружность с центром О(0, 0) и R=1.
В пространстве ему удовлетворяют координаты всех точек, проекция которых на плоскость ХОУ лежит на этой окружности. Очевидно, что эта поверхность – круговой цилиндр
(рис. 54).
Цилиндрические поверхности бывают не только круговыми.
Определение: Цилиндрической называется поверхность, полученная движением прямой, параллельной некоторому вектору, и пересекающей при движении некоторую кривую. При этом движущаяся прямая называется образующей, а кривая, которую она пересекает, называется направляющей цилиндрической поверхности.
Для поверхности 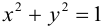 образующая параллельна оси OZ (так как в уравнении z отсутствует), а направляющей является окружность в плоскости XOY .
образующая параллельна оси OZ (так как в уравнении z отсутствует), а направляющей является окружность в плоскости XOY .
ВЫВОД. Если уравнение поверхности содержит только две переменные, то оно задает цилиндрическую поверхность. У поверхности F(y,z) ,образующая параллельна OX , а направляющая лежит в плоскости YOZ . Для поверхности F(x,z) ,образующая параллельна OY , направляющая в плоскости XOZ .
Пример №29
Построить и назвать поверхности 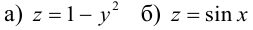 Эти уравнения задают цилиндрические поверхности. В первом случае направляющей является парабола в плоскости YOZ , а образующая параллельна OX (рис. 55). Во втором – образующая синусоида в плоскости XOZ , образующая параллельна OY (рис. 56).
Эти уравнения задают цилиндрические поверхности. В первом случае направляющей является парабола в плоскости YOZ , а образующая параллельна OX (рис. 55). Во втором – образующая синусоида в плоскости XOZ , образующая параллельна OY (рис. 56).
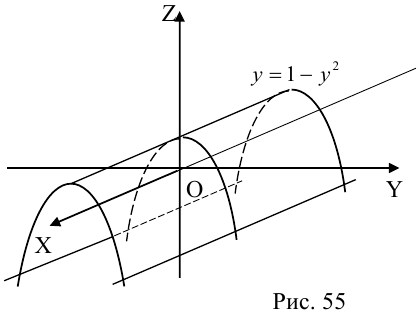
Поверхности вращения
Определение: Поверхностью вращения называется поверхность, полученная в результате вращения плоской кривой вокруг оси, лежащей в ее
плоскости.
Из определения следует, что сечением такой поверхности любой плоскостью, перпендикулярной оси вращения, является окружность.
Пусть в плоскости YOZ задана кривая  – координаты точки в плоской системе координат YOZ . Эта кривая вращается вокруг оси OZ . Выведем уравнение поверхности вращения.
– координаты точки в плоской системе координат YOZ . Эта кривая вращается вокруг оси OZ . Выведем уравнение поверхности вращения.
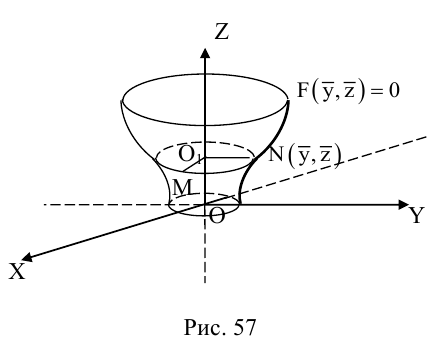
Пусть M(x,y,z) – произвольная точка на поверхности, 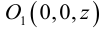 , z– центр окружности сечения, проходящего через точку M , а
, z– центр окружности сечения, проходящего через точку M , а 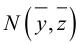 – точка, лежащая на кривой и одновременно в рассматриваемом сечении (рис. 57).
– точка, лежащая на кривой и одновременно в рассматриваемом сечении (рис. 57).
Тогда 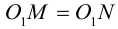 – радиусы сечения.
– радиусы сечения.
Но 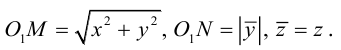
Таким образом, уравнение поверхности вращения получим, если в уравнении кривой 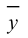 заменим на
заменим на 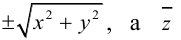 – на z. Тогда получим:
– на z. Тогда получим:
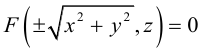 – уравнение поверхности вращения (OZ – ось вращения).
– уравнение поверхности вращения (OZ – ось вращения).
Очевидно, что если кривая F(y,z)=0 вращается вокруг OY , то уравнение
поверхности вращения имеет вид: 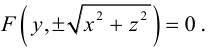
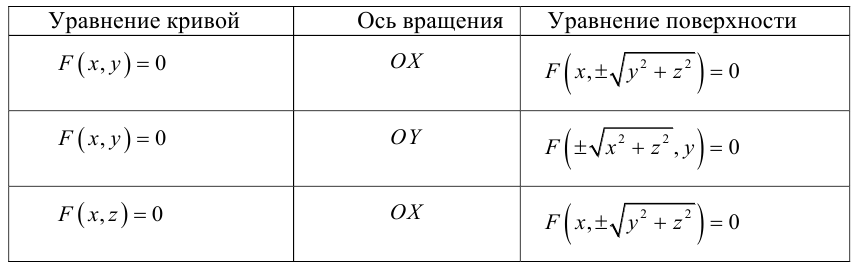
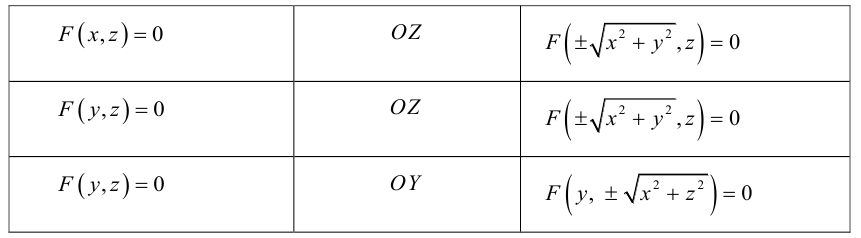
Некоторые поверхности второго порядка
1. Пусть эллипс 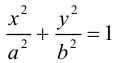 вращается вокруг оси OY .
вращается вокруг оси OY .
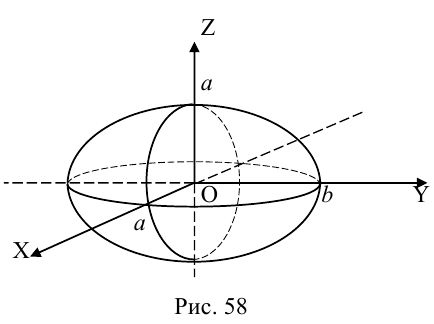
Полученная поверхность является поверхностью второго порядка, так ее уравнение 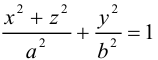 – второй степени относительно переменных x,y,z . Она называется эллипсоидом вращения (рис. 58).
– второй степени относительно переменных x,y,z . Она называется эллипсоидом вращения (рис. 58).
Поверхность, задаваемая уравнением 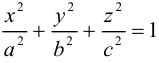 , называется трехосным эллипсоидом.
, называется трехосным эллипсоидом.
2. Если гипербола 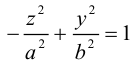 вращается вокруг оси OZ , то уравнение
вращается вокруг оси OZ , то уравнение
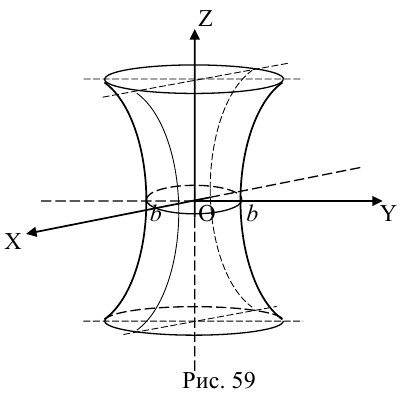
поверхности вращения имеет вид
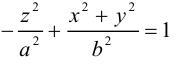
или
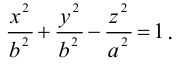
Такая поверхность называется однополостным гиперболоидом вращения (рис. 59).
3. Если гипербола 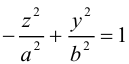 вращается вокруг оси OY , то уравнение поверхности имеет вид
вращается вокруг оси OY , то уравнение поверхности имеет вид 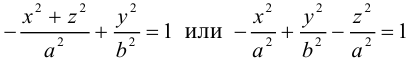 . Такая поверхность называется двуполостным гиперболоидом вращения (рис. 60).
. Такая поверхность называется двуполостным гиперболоидом вращения (рис. 60).
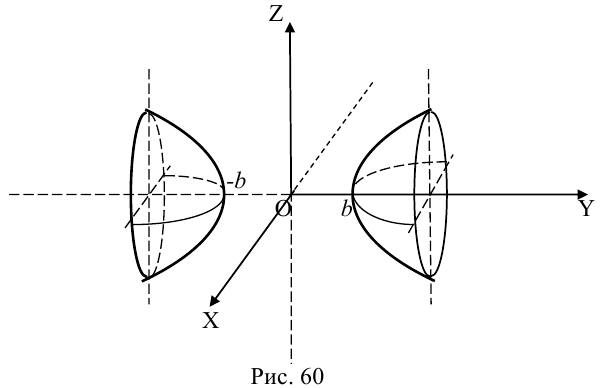
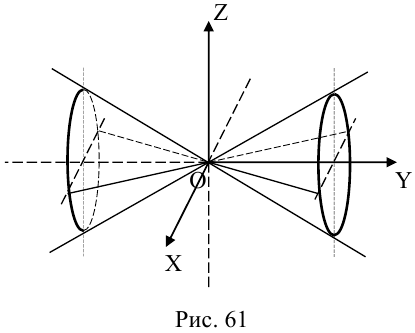
4. Если пара пересекающихся прямых 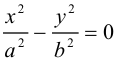 вращается вокруг оси OY , то получается конус вращения с уравнением
вращается вокруг оси OY , то получается конус вращения с уравнением 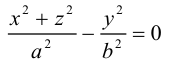 или
или 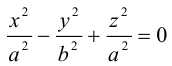 (рис. 61).
(рис. 61).
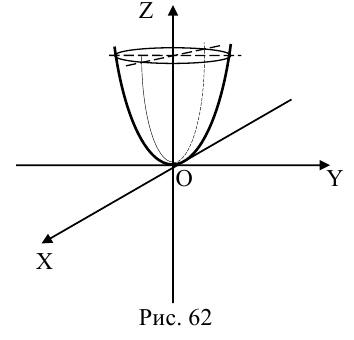
5. При вращении параболы 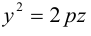 вокруг оси OZ получается поверхность
вокруг оси OZ получается поверхность 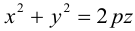 , которая называется эллиптическим параболоидом вращения (рис. 62).
, которая называется эллиптическим параболоидом вращения (рис. 62).
Лекции по предметам:
- Математика
- Алгебра
- Линейная алгебра
- Векторная алгебра
- Геометрия
- Высшая математика
- Дискретная математика
- Математический анализ
- Теория вероятностей
- Математическая статистика
- Математическая логика
Установим на
плоскости прямоугольную систему
координат и рассмотрим общее уравнение
второй степени
![]() ,
,
(8.4.1)
в
котором
![]() .
.
Множество
всех точек плоскости, координаты которых
удовлетворяют уравнению (8.4.1), называется
кривой
(линией)
второго
порядка.
Для
всякой кривой второго порядка существует
прямоугольная система координат,
называемая канонической, в которой
уравнение этой кривой имеет один из
следующих видов:
1)
![]() (эллипс);
(эллипс);
2)
![]()
(мнимый эллипс);
3)
![]() (пара мнимых пересекающихся прямых);
(пара мнимых пересекающихся прямых);
4)
![]() (гипербола);
(гипербола);
5)
![]() (пара пересекающихся прямых);
(пара пересекающихся прямых);
6)
![]() (парабола);
(парабола);
7)
![]() (пара
(пара
параллельных прямых);
8)
![]()
(пара мнимых параллельных прямых);
9)
![]() (пара совпадающих прямых).
(пара совпадающих прямых).
Уравнения
1)–9) называются каноническими
уравнениями кривых второго порядка.
Решение
задачи приведения уравнения кривой
второго порядка к каноническому виду
включает нахождение канонического
уравнения кривой и канонической системы
координат. Приведение к каноническому
виду позволяет вычислить параметры
кривой и определить ее расположение
относительно исходной системы координат.
Переход от исходной прямоугольной
системы координат
![]() к канонической
к канонической![]() осуществляется путем поворота осей
осуществляется путем поворота осей
исходной системы координат вокруг точкиО
на некоторый угол
и последующего параллельного переноса
системы координат.
Инвариантами
кривой второго порядка
(8.4.1) называются такие функции от
коэффициентов ее уравнения, значения
которых не меняются при переходе от
одной прямоугольной системы координат
к другой такой же системе.
Для кривой второго
порядка (8.4.1) сумма коэффициентов при
квадратах координат
![]() ,
,
определитель,
составленный из коэффициентов при
старших членах
![]()
и определитель
третьего порядка

являются
инвариантами.
Значение
инвариантов s,
,
можно использовать для определения
типа и составления канонического
уравнения кривой второго порядка (табл.
8.1).
Таблица
8.1
Классификация кривых второго порядка, основанная на инвариантах
|
> Кривая эллиптического типа |
0 |
s |
|
s |
||
|
= |
Пара |
|
|
< Кривая гиперболического типа |
0 |
Гипербола |
|
= |
Пара |
|
|
= Кривая параболического типа |
0 |
Парабола |
|
= |
Пара (различных, или |
Рассмотрим подробнее
эллипс, гиперболу и параболу.
Эллипсом
(рис. 8.1) называется геометрическое место
точек плоскости, для которых сумма
расстояний до двух фиксированных точек
![]() этой плоскости, называемыхфокусами
этой плоскости, называемыхфокусами
эллипса,
есть величина постоянная (большая, чем
расстояние между фокусами). При этом не
исключается совпадение фокусов эллипса.
Если фокусы совпадают, то эллипс
представляет собой окружность.
Полусумму
расстояний от точки эллипса до его
фокусов обозначают через а,
половину расстояний между фокусами –
с.
Если прямоугольная система координат
на плоскости выбрана так, что фокусы
эллипса располагаются на оси Оx
симметрично относительно начала
координат, то в этой системе координат
эллипс задается уравнением
![]() ,
,
(8.4.2)
называемым
каноническим
уравнением эллипса,
где
![]() .
.

Рис. 8.1
При
указанном выборе прямоугольной системы
координат эллипс симметричен относительно
осей координат и начала координат. Оси
симметрии эллипса называют его осями,
а центр его
симметрии – центром
эллипса.
Вместе с тем часто осями эллипса называют
числа 2a
и 2b,
а числа a
и b
– большой
и малой
полуосью
соответственно.
Точки
пересечения эллипса с его осями называются
вершинами
эллипса.
Вершины эллипса имеют координаты (а,
0),
(–а,
0), (0, b),
(0, –b).
Эксцентриситетом
эллипса
называется число
![]() . (8.4.3)
. (8.4.3)
Поскольку
0
c
< a,
эксцентриситет эллипса 0
< 1, причем у окружности
= 0. Перепишем равенство (8.4.3) в виде
 .
.
Отсюда
видно, что эксцентриситет характеризует
форму эллипса: чем ближе
к нулю, тем больше эллипс похож на
окружность; при увеличении
эллипс становится более вытянутым.
Пусть
![]() – произвольная точка эллипса,
– произвольная точка эллипса,
![]() и
и![]() – расстояния от точкиМ
– расстояния от точкиМ
до фокусов F1
и F2
соответственно. Числа r1
и r2
называются фокальными
радиусами точки
М
эллипса
и вычисляются по формулам
![]() .
.
Директрисами
отличного от окружности эллипса
с каноническим уравнением (8.4.2) называются
две прямые
![]() .
.
Директрисы эллипса
расположены вне эллипса (рис. 8.1).
Отношение
фокального радиуса
![]() точкиM
точкиM
эллипса к расстоянию
![]() от этой точки до отвечающей фокусу
от этой точки до отвечающей фокусу![]() директрисы равно эксцентриситету
директрисы равно эксцентриситету
этого эллипса (фокус и директриса
считаются соответствующими, если они
расположены по одну сторону от центра
эллипса).
Гиперболой
(рис. 8.2) называется геометрическое место
точек плоскости, для которых модуль
разности расстояний до двух фиксированных
точек
![]() и
и![]() этой плоскости, называемыхфокусами
этой плоскости, называемыхфокусами
гиперболы,
есть величина постоянная (не равная
нулю и меньшая, чем расстояние между
фокусами).
Пусть
расстояние между фокусами равно 2с,
а указанный модуль разности расстояний
равен 2а.
Выберем прямоугольную систему координат
так же, как и для эллипса. В этой системе
координат гипербола задается уравнением
![]() ,
,
(8.4.4)
называемым
каноническим
уравнением гиперболы,
где
![]() .
.
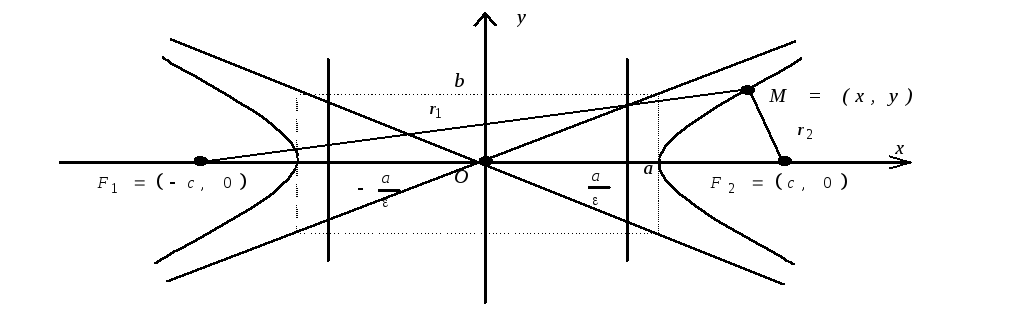
Рис. 8.2
При данном выборе
прямоугольной системы координат оси
координат являются осями симметрии
гиперболы, а начало координат – ее
центром симметрии. Оси симметрии
гиперболы называют ее осями,
а центр симметрии – центром
гиперболы.
Прямоугольник со сторонами 2a
и 2b,
расположенный, как показано на рис. 8.2,
называется основным
прямоугольником гиперболы.
Числа 2a
и 2b
– оси гиперболы, а числа a
и b
– ее полуоси.
Прямые, являющиеся продолжением
диагоналей основного прямоугольника,
образуют асимптоты
гиперболы
![]() .
.
Точки пересечения
гиперболы с осью Ox
называются вершинами
гиперболы.
Вершины гиперболы имеют координаты (а,
0), (–а,
0).
Эксцентриситетом
гиперболы
называется число
![]() . (8.4.5)
. (8.4.5)
Поскольку
с
> a,
эксцентриситет гиперболы
> 1. Перепишем равенство (8.4.5) в виде
 .
.
Отсюда
видно, что эксцентриситет характеризует
форму основного прямоугольника и,
следовательно, форму самой гиперболы:
чем меньше ,
больше вытягивается основной прямоугольник,
а вслед за ним и сама гипербола вдоль
оси Ox.
Пусть
![]() – произвольная точка гиперболы,
– произвольная точка гиперболы,![]() и
и![]() – расстояния от точкиМ
– расстояния от точкиМ
до фокусов F1
и F2
соответственно. Числа r1
и r2
называются фокальными
радиусами точки
М
гиперболы
и вычисляются по формулам

Директрисами
гиперболы
с каноническим уравнением (8.4.4) называются
две прямые
![]() .
.
Директрисы
гиперболы пересекают основной
прямоугольник и проходят между центром
и соответствующей вершиной гиперболы
(рис. 8.2).
О тношение
тношение
фокального радиуса![]() точкиM
точкиM
гиперболы к расстоянию
![]() от этой точки до отвечающей фокусу
от этой точки до отвечающей фокусу![]() директрисы равно эксцентриситету
директрисы равно эксцентриситету
этой гиперболы (фокус и директриса
считаются соответствующими, если они
расположены по одну сторону от центра
гиперболы).
Параболой
(рис. 8.3) называется геометрическое место
точек плоскости, для которых расстояние
до некоторой фиксированной точки F
(фокуса
параболы)
этой плоскости равно расстоянию до
некоторой фиксированной прямой
(директрисы
параболы),
также расположенной в рассматриваемой
плоскости.
Выберем
начало О
прямоугольной системы координат в
середине отрезка [FD],
представляющего собой перпендикуляр,
опущенный из фокуса F
на директрису (предполагается, что фокус
не принадлежит директрисе), а оси Ox
и Oy
направим так, как показано на рис. 8.3.
Пусть длина отрезка [FD]
равна p.
Тогда в выбранной системе координат
![]() иканоническое
иканоническое
уравнение параболы
имеет вид
![]() . (8.4.6)
. (8.4.6)
Величина
p
называется параметром
параболы.
Парабола имеет
ось симметрии, которая называется осью
параболы.
Точка пересечения параболы с ее осью
называется вершиной
параболы.
Если парабола задана своим каноническим
уравнением (8.4.6), то осью параболы является
ось Ox.
Очевидно, вершиной параболы является
начало координат.
Пример 1.
Точка А
= (2, –1) принадлежит эллипсу, точка
F
= (1, 0) является его фокусом, соответствующая
F
директриса задана уравнением
![]() .
.
Составьте уравнение этого эллипса.
Решение.
Будем считать систему координат
прямоугольной. Тогда расстояние
![]() от точкиА
от точкиА
до директрисы
![]() в соответствии с соотношением (8.1.8), в
в соответствии с соотношением (8.1.8), в
котором![]()
![]()
![]() ,
,
равно
 .
.
Расстояние
![]() от точкиА
от точкиА
до фокуса F
равно
![]() ,
,
что
позволяет определить эксцентриситет
эллипса
![]() .
.
Пусть M
= (x,
y)
– произвольная точка эллипса. Тогда
расстояние
![]() от точкиМ
от точкиМ
до директрисы
![]() по формуле (8.1.8) равно
по формуле (8.1.8) равно

а
расстояние
![]() от точкиМ
от точкиМ
до фокуса F
равно
![]() .
.
Поскольку для
любой точки эллипса отношение
![]() есть величина постоянная, равная
есть величина постоянная, равная
эксцентриситету эллипса, отсюда имеем
 ,
,
или
![]() ,
,
или
![]() .
.
Пример
2. Кривая
задана уравнением
![]()
в
прямоугольной системе координат. Найдите
каноническую систему координат и
каноническое уравнение этой кривой.
Определите тип кривой.
Решение.
Квадратичная форма
![]() имеет матрицу
имеет матрицу
![]() .
.
Ее
характеристический многочлен
![]()
имеет
корни 1
= 4 и 2
= 9. Следовательно, в ортонормированном
базисе из собственных векторов матрицы
А
рассматриваемая квадратичная форма
имеет канонический вид
![]() .
.
Перейдем к построению
матрицы ортогонального преобразования
переменных, приводящего рассматриваемую
квадратичную форму к указанному
каноническому виду. Для этого будем
строить фундаментальные системы решений
однородных систем уравнений
![]() и ортонормировать их.
и ортонормировать их.
При
![]() эта система имеет вид
эта система имеет вид
![]()
Ее
общим решением является
![]() .
.
Здесь одна свободная переменная. Поэтому
фундаментальная система решений состоит
из одного вектора, например, из вектора![]() .
.
Нормируя его, получим вектор
![]() .
.
При
![]() также построим вектор
также построим вектор
![]() .
.
Векторы
![]() и
и![]() уже ортогональны, так как относятся к
уже ортогональны, так как относятся к
различным собственным значениям
симметричной матрицыА.
Они составляют канонический
ортонормированный базис данной
квадратичной формы. Из столбцов их
координат строится искомая ортогональная
матрица (матрица поворота)
![]() .
.
Проверим правильность
нахождения матрицы Р
по формуле
![]() ,
,
где![]() – матрица квадратичной формы в базисе
– матрица квадратичной формы в базисе![]() :
:
Матрица
Р
найдена верно.
Выполним
преобразование переменных
![]()
и
запишем уравнение данной кривой в новой
прямоугольной системе координат со
старым центром и направляющими векторами
![]() :
:

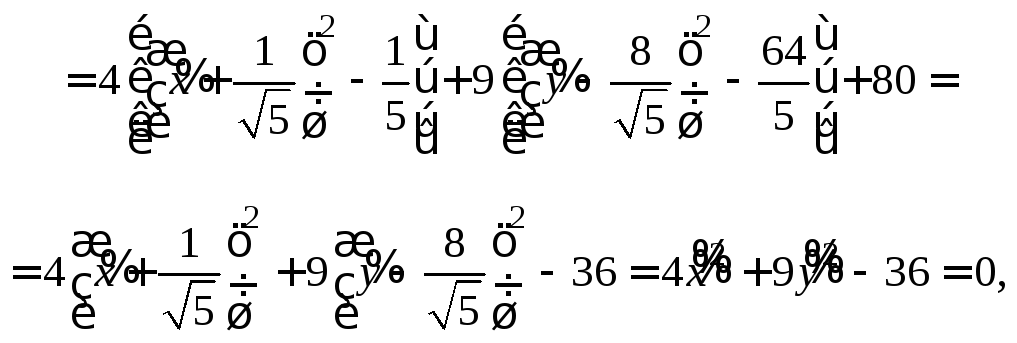
где
![]() .
.
Получили каноническое
уравнение эллипса
![]() .
.
В силу того, что
результирующее преобразование
прямоугольных координат определяется
формулами
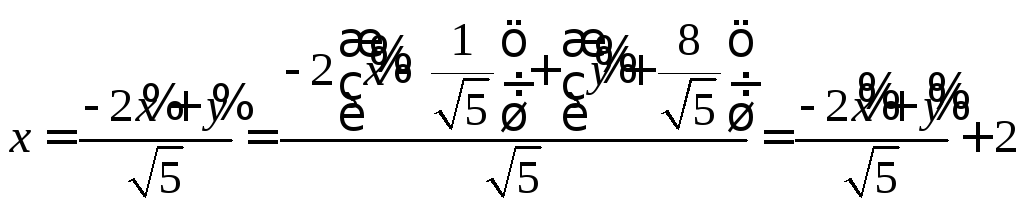 ,
,
 ,
,
каноническая
система координат
![]() имеет начало
имеет начало![]() и направляющие векторы
и направляющие векторы![]() .
.
Пример 3.
Применяя теорию инвариантов, определите
тип и составьте каноническое уравнение
кривой
![]() .
.
Решение.
Поскольку
![]()
и
 ,
,
в
соответствии с табл. 8.1 заключаем, что
это – гипербола.
Так как s
= 0, характеристический многочлен матрицы
квадратичной формы
![]()
![]() .
.
Его
корни
![]() и
и![]() позволяют записать каноническое
позволяют записать каноническое
уравнение кривой
![]() ,
,
где
С
находится из условия
 ,
,
или
![]() .
.
Искомое каноническое
уравнение кривой
![]() .
.
В задачах этого
параграфа координаты x,
y
предполагаются прямоугольными.
8.4.1.
Для эллипсов
![]() и
и![]() найдите:
найдите:
а) полуоси;
б) фокусы;
в) эксцентриситет;
г) уравнения
директрис.
8.4.2.
Составьте уравнения эллипса, зная его
фокус
![]() ,
,
соответствующую директрисуx
= 8 и эксцентриситет
![]() .
.
Найдите второй фокус и вторую директрису
эллипса.
8.4.3.
Составьте
уравнение эллипса, фокусы которого
имеют координаты (1, 0) и (0, 1), а большая
ось равна двум.
8.4.4.
Дана гипербола
![]() .
.
Найдите:
а)
полуоси a
и b;
б) фокусы;
в) эксцентриситет;
г) уравнения
асимптот;
д) уравнения
директрис.
8.4.5.
Дана гипербола
![]() .
.
Найдите:
а)
полуоси а
и b;
б) фокусы;
в) эксцентриситет;
г) уравнения
асимптот;
д) уравнения
директрис.
8.4.6.
Точка
![]() принадлежит гиперболе, фокус которой
принадлежит гиперболе, фокус которой![]() ,
,
а соответствующая директриса задана
уравнением![]() .
.
Составьте уравнение этой гиперболы.
8.4.7.
Составьте уравнение параболы, если даны
ее фокус
![]() и директриса
и директриса![]() .
.
8.4.8.
Даны вершина параболы
![]() и уравнение директрисы
и уравнение директрисы![]() .
.
Составьте уравнение этой параболы.
8.4.9.
Составьте уравнение параболы, фокус
которой находится в точке
![]()
и
директриса задана уравнением
![]() .
.
8.4.10.
Составьте уравнение кривой второго
порядка, зная ее эксцентриситет
![]() ,
,
фокус![]() и соответствующую директрису
и соответствующую директрису![]() .
.
8.4.11.
Определите тип кривой второго порядка,
составьте ее каноническое уравнение и
найдите каноническую систему координат:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
ж)
![]() ;
;
з)
![]() ;
;
и)
![]() ;
;
к)
![]() ;
;
л)
![]() .
.
8.4.12.
Докажите, что кривая второго порядка,
заданная уравнением
![]() ,
,
является
эллипсом. Найдите длины полуосей и
эксцентриситет этого эллипса, координаты
центра и фокусов, составьте уравнения
осей и директрис.
8.4.13.
Докажите, что кривая второго порядка,
заданная уравнением
![]() ,
,
является
гиперболой. Найдите длины полуосей и
эксцентриситет этой гиперболы, координаты
центра и фокусов, составьте уравнения
осей, директрис и асимптот.
8.4.14.
Докажите, что кривая второго порядка,
заданная уравнением
![]() ,
,
является
параболой. Найдите параметр этой
параболы, координаты вершин и фокуса,
составьте уравнения оси и директрисы.
8.4.15.
Каждое из следующих уравнений приведите
к каноническому виду. Изобразите на
чертеже соответствующую кривую второго
порядка относительно исходной
прямоугольной системы координат:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
ж)
![]() ;
;
з)
![]() ;
;
и)
![]() .
.
8.4.16.
Применяя теорию инвариантов, определите
тип и составьте каноническое уравнение
кривой:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() .
.
Соседние файлы в папке сборник
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Кривые второго порядка и их нахождение и решение
- Окружность
- Эллипс
- Гипербола
- Парабола
- Общее уравнение второго порядка с двумя переменными
- Кривые второго порядка
- Окружность и его уравнения
- Эллипс и его уравнения
- Гипербола и ее уравнение
- Асимптоты гиперболы
- Парабола и ее уравнение
- Линии второго порядка. Общее уравнение линии второго порядка
- Окружность и ее уравнение
- Каноническое уравнение эллипса. Эксцентриситет
- Каноническое уравнение гиперболы. Асимптоты. Эксцентриситет
- Каноническое уравнение параболы
- Кривые линии второго порядка
- Круг
- Эллипс
- Гипербола
- Парабола
- Общее уравнение кривой второго порядка: типы кривых
- Канонические уравнения окружности и эллипса
- Каноническое уравнение гиперболы. Асимптоты гиперболы
- Парабола. Каноническое уравнение
- Возведение общего уравнения кривой второго порядка к каноническому виду
- Квадратичные формы. Применение к превращению уравнений кривой 2-го порядка
Кривые второго порядка и их нахождение и решение
Кривые, которые получаются при пересечении круговой конической поверхности плоскостью называются конечными поверхностями или кониками. К ним относятся такие кривые как окружность, эллипс, гипербола, парабола.
Действительно:
– Если плоскость пересекает коническую поверхность перпендикулярно оси вращения, то в пересечении образуется окружность, если плоскость проходит через вершину конуса, то в пересечении образуется точка, то есть вырожденная окружность (рис. 1).

– Если плоскость пересекает только одну часть конической поверхности и не параллельна ни одной образующей, тогда в пересечении будет эллипс (рис. 2).
– Если плоскость пересекает одну часть конической поверхности и параллельна одной образующей, тогда в пересечении будет парабола (рис. 3а), если плоскость проходит через вершину и одну из образующих, тогда в пересечении будет прямая, то есть вырожденная парабола (рис. 3б).

– Если плоскость пересекает две части конической поверхности и параллельна оси конической поверхности, то в пересечении будет гипербола (рис. 4а), если секущая плоскость проходит через вершину конуса и пересекает две его части, то в пересечении будет пара прямых, которые пересекаются, то есть вырожденная гипербола (рис. 4б).
Рассмотрим каждую из этих кривых.
Окружность
Окружностью называется множество точек плоскости, равноудалённых от данной точки, которая называется центром. Если точка С — цент окружности, R — её радиус, М — произвольная точка окружности, то по определению окружности


Данное равенство является уравнением окружности радиуса R с центром в точке С.
Пусть на плоскости задана прямоугольная декартовая система координат (рис. 5) и точка  центр окружности радиуса R. Пусть М(х, у) — произвольная точка этой окружности. Поскольку
центр окружности радиуса R. Пусть М(х, у) — произвольная точка этой окружности. Поскольку  , то уравнение окружности можно записать
, то уравнение окружности можно записать

Данное уравнение называют общим уравнением окружности или уравнением окружности радиуса R с центром в точке 
Например, уравнение

является уравнением окружности радиуса R=5, с центром в точке (1; -3).
Если центр окружности совпадает с началом координат, то уравнение окружности принимает вид:

Данное уравнение называют каноническим уравнением окружности.
Пример 1. Составить уравнение окружности радиуса R=9 с центром в точке C(3; -6).
Решение:
Подставив значения координат точки С и значение радиуса в уравнение окружности, получаем  , или
, или

Пример 2. Доказать, что уравнение  является уравнением окружности. Найти её центр и радиус.
является уравнением окружности. Найти её центр и радиус.
Решение:
Преобразуем левую часть заданного уравнения

Это уравнение является уравнением окружности с центром в точке (-2; 1), радиус окружности равен 3.
Эллипс
Эллипсом называется множество точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же самой плоскости постоянна и больше чем расстояние между этими точками.
Такие точки называются фокусами эллипса, а расстояние между ними фокальным расстоянием. Покажем, как, исходя из определения эллипса, можно разбить эллиптическую клумбу. Забьём в землю два колышка (рис. 6) потом нитку свяжем в кольцо и натянем это кольцо на оба колышка. Натянув нитку третьим колышком, чертим эллипс. Изменив расстояние между колышками и длину нитки, получаем эллипсы разных размеров и форм.

Обозначим фокусы эллипса буквами  Путь фокальное расстояние
Путь фокальное расстояние  . Если М — произвольная точка эллипса (рис. 7), то по определению эллипса сумма
. Если М — произвольная точка эллипса (рис. 7), то по определению эллипса сумма  является величиной постоянной. Обозначив её через
является величиной постоянной. Обозначив её через  , получаем
, получаем

Заметим, что по определению эллипса  то есть
то есть  Предыдущее равенство является уравнением эллипса. Если точка
Предыдущее равенство является уравнением эллипса. Если точка  совпадает с точкой
совпадает с точкой  то уравнение эллипса приобретает вид
то уравнение эллипса приобретает вид

Это уравнение является уравнением окружности радиуса  с центром в точке
с центром в точке  . Таким образом, окружность является отдельным случаем эллипса.
. Таким образом, окружность является отдельным случаем эллипса.

Выберем систему координат так, чтобы ось абсцисс проходила через фокусы эллипса, ось ординат через середину отрезка 
 и перпендикулярна ему.
и перпендикулярна ему.
Тогда фокусами будут точки  любая точка эллипса, тогда
любая точка эллипса, тогда

подставляя найденные значения  в уравнении эллипса, получаем
в уравнении эллипса, получаем

Сведём данное уравнение до простейшего вида. Для этого перенесём второе слагаемое в правую часть и возведём обе части в квадрат

после упрощений получаем

Возведя обе части в квадрат получаем

по определению эллипса  поэтому
поэтому  положительное число. Обозначим его через
положительное число. Обозначим его через  , то есть
, то есть  . Тогда уравнение приобретает вид
. Тогда уравнение приобретает вид

Разделив обе части равенства на  получим
получим

Это уравнение называется каноническим уравнением эллипса.
Если  то есть
то есть  то уравнение эллипса приобретает вид
то уравнение эллипса приобретает вид

что вычисляет уравнение окружности.
Пример 1. Составить каноническое уравнение эллипса, который проходит через точку М(5;0), если фокальное расстояние равно 6.
Решение:
Поскольку фокальное расстояние равняется 6, то с=3. Запишем уравнение эллипса

По условию задачи точка М(5; 0) принадлежит эллипсу, следовательно

отсюда  Найдём
Найдём 
Следовательно, искомым уравнением эллипса является уравнение

Пример 2. Доказать, что уравнение  является уравнением эллипса, найти координаты фокусов и фокальное расстояние.
является уравнением эллипса, найти координаты фокусов и фокальное расстояние.
Решение:
Разделив обе части уравнений на 3600, получаем

это является уравнением эллипса.
Из уравнение  следует, что
следует, что  Поскольку
Поскольку  отсюда с=8. Фокусы эллипса находятся в точках
отсюда с=8. Фокусы эллипса находятся в точках  и
и  . Фокальное расстояние
. Фокальное расстояние

Исследуем эллипс по его уравнению.
1. Эллипс не проходит через начало системы координат, так как координаты точки О(0; 0) не удовлетворяют уравнение.
2. Эллипс пересекает каждую из осе координат в двух точках.
Чтобы вычислить координаты точек пересечения эллипса с осью Ох, необходимо решить уравнение  , и у=0, получим
, и у=0, получим 
Следовательно, точками пересечения эллипса с осью Ох будут 
Аналогично находим точки пересечения с осью Оу: 
Точки А, В, С, D называют вершинами эллипса.
Отрезок АВ называется большой осью эллипса, отрезок ВD — малой осью. Фокусы эллипса  и
и  лежат на большой оси. Длина большой оси равняется
лежат на большой оси. Длина большой оси равняется  , малой оси
, малой оси  . Числа
. Числа  и
и  называются полуосями эллипса.
называются полуосями эллипса.
3. Эллипс имеет две взаимно перпендикулярные оси симметрии, а также центр симметрии.
Это легко показать, так как неизвестные в уравнение входят только во второй степени. Центр симметрии эллипса называется центром эллипса.
4. Эллипс можно получить равномерным сжиманием окружности.
Рассмотрим окружность радиуса  с центром в начале координат. Пусть
с центром в начале координат. Пусть  произвольная точка окружности (рис. 9).
произвольная точка окружности (рис. 9).

Тогда  . Точки
. Точки  на окружности поставим поставим в соответствие точку
на окружности поставим поставим в соответствие точку  такую, чтобы
такую, чтобы  и
и  . Точки
. Точки  найдём благодаря сдвигу точки
найдём благодаря сдвигу точки  , при котором абсцисса не меняется, а ордината уменьшается в отношении
, при котором абсцисса не меняется, а ордината уменьшается в отношении . Координаты точки
. Координаты точки  удовлетворяют уравнение эллипса
удовлетворяют уравнение эллипса

Следовательно,  находится на эллипсе.
находится на эллипсе.
Таким образом, эллипс можно достать с окружности равномерным сжатием до оси Ох, при котором, ордината точек уменьшается в том самом соотношении  . Отсюда вытекает, что форма эллипса зависит от значения
. Отсюда вытекает, что форма эллипса зависит от значения  . Чем меньше это соотношение, тем более сжатым будет эллипс, и, наоборот, чем больше соотношение
. Чем меньше это соотношение, тем более сжатым будет эллипс, и, наоборот, чем больше соотношение  , тем эллипс будет более округлым. Если значение
, тем эллипс будет более округлым. Если значение  наибольшее, то есть
наибольшее, то есть  =1, то эллипс превращается в окружность. Для характеристики формы эллипса целесообразно пользоваться не соотношением
=1, то эллипс превращается в окружность. Для характеристики формы эллипса целесообразно пользоваться не соотношением  , а соотношением
, а соотношением  . Соотношение полу-фокусного расстояния с к большой полуоси
. Соотношение полу-фокусного расстояния с к большой полуоси  называется эксцентриситетом эллипса. Его обозначают буквой е.
называется эксцентриситетом эллипса. Его обозначают буквой е.

Поскольку  , то эксцентриситет эллипса удовлетворяет неравенство
, то эксцентриситет эллипса удовлетворяет неравенство  . Отсюда
. Отсюда 
Пример. Дано два эллипса  . Сравнить их форму.
. Сравнить их форму.
Решение:
Перепишем уравнение эллипсов в виде  . Для первого эллипса
. Для первого эллипса  соответственно
соответственно  Для второго эллипса
Для второго эллипса  , соответственно
, соответственно  . В данном случаи
. В данном случаи  , соответственно второй эллипс сжатый до большой оси больше чем первый.
, соответственно второй эллипс сжатый до большой оси больше чем первый.
Гипербола
Гиперболой называется множество точек плоскости, для каждой из которых модуль разности расстояний к двум данным точкам плоскости постоянный и меньший чем расстояние между этими точками.
Такие точки называются фокусами гиперболы, а расстояние между ними – фокальным расстоянием.
Обозначим фокусы гиперболы буквами  Пусть фокальное расстояние
Пусть фокальное расстояние 

Если М – произвольная точка гиперболы (рис. 10), то по определению гиперболы модуль разности  постоянный. Обозначив его как
постоянный. Обозначив его как  , получаем
, получаем

Отметим, что по определениям гиперболы  , то есть
, то есть 
Данное равенство является уравнением гиперболы. Выберем систему координат так, чтобы ось абсцисс проходила через фокус гиперболы; ось ординат проходила через середину отрезка  перпендикулярно ему. Тогда фокусами гиперболы будут точки
перпендикулярно ему. Тогда фокусами гиперболы будут точки  и
и 
Пусть  любая точка гиперболы, тогда
любая точка гиперболы, тогда
 и
и 
Подставляя значения  и
и  в уравнение получим
в уравнение получим

Это уравнение является гиперболой в выбранной системе координат. Его можно привести к более простому виду.
Пусть  , тогда уравнение можно записать без знака модуля:
, тогда уравнение можно записать без знака модуля:

Возведём обе части уравнения в квадрат

По определению гиперболы  поэтому
поэтому  положительное число. Обозначим его
положительное число. Обозначим его  , то есть положим
, то есть положим  , тогда уравнение приобретает вид
, тогда уравнение приобретает вид

Разделив почленно на  , получим уравнение
, получим уравнение

Если  , тогда уравнение записывают без знака модуля
, тогда уравнение записывают без знака модуля

и также, как при  , сводится к конечному виду.
, сводится к конечному виду.
Уравнение  называется каноническим уравнением гиперболы.
называется каноническим уравнением гиперболы.
Пример 1. Записать каноническое уравнение гиперболы, которая проходит через точку  , если фокальное расстояние гиперболы равняется 10.
, если фокальное расстояние гиперболы равняется 10.
Решение. Поскольку  то с=5. Запишем каноническое решение уравнения гиперболы
то с=5. Запишем каноническое решение уравнения гиперболы

По условию точка принадлежит гиперболе, следовательно:

Из второго уравнения получим соотношение для вычисления

Решим систему:

найдём  Искомым уравнением является уравнение
Искомым уравнением является уравнение 
Пример 2. Доказать, что уравнение

является уравнением гиперболы. Найти координаты фокусов.
Решение: Разделив обе части уравнения на 580, получим

Это является уравнением гиперболы, для которой  . Из соотношения
. Из соотношения  находим
находим  Следовательно, фокусы гиперболы находятся в точках
Следовательно, фокусы гиперболы находятся в точках 
Исследуем гиперболу по её уравнениям.
Рассмотрим гиперболу, заданную в некоторой прямоугольной декартовой системе координат своим каноническим уравнением

Приведём такие свойства гиперболы:
1. Гипербола не имеет общих точек с осью Оу, а ось Ох пересекает в двух точках.
Чтобы вычислить координаты точек пересечения гиперболы с осью Оу, необходимо решить совместно их уравнения

Подставляя х=0 в уравнение гиперболы, получим  , а это означает, что система не имеет решения. Следовательно, гипербола не пересекает ось ординат.
, а это означает, что система не имеет решения. Следовательно, гипербола не пересекает ось ординат.
Чтобы вычислить координаты точек пересечения с осью Ох, необходимо решить совместно их уравнения

Точка пересечения гиперболы с осью Ох должна иметь ординату у=0 и, кроме того, должна принадлежать гиперболе. Подставив у=0 в уравнение гиперболы, получим

Следовательно, точками пересечения гиперболы с осью Ох будут точки  и
и  ; они называются вершинами гиперболы.
; они называются вершинами гиперболы.
Отрезок АВ называется действительной осью гиперболы. Длина отрезка АВ, очевидно, равна  . Число
. Число  называют действительной полуосью гиперболы, число b – мнимой полуосью.
называют действительной полуосью гиперболы, число b – мнимой полуосью.
2. Гипербола имеет две взаимно перпендикулярные оси симметрии.
В уравнение переменные х и у входят только во второй степени. Таким образом, если координаты точки N(x; y) удовлетворяют уравнение, то это же уравнение будут удовлетворять и координаты точек  и
и 
Легко увидеть, что точка  симметрична точке N относительно оси ординат, точка N2 симметрична точке N относительно оси абсцисс. Таким образом, гипербола имеет две оси симметрии, они взаимно перпендикулярны.
симметрична точке N относительно оси ординат, точка N2 симметрична точке N относительно оси абсцисс. Таким образом, гипербола имеет две оси симметрии, они взаимно перпендикулярны.
3. Гипербола имеет центр симметрии.
Если координаты точки N(x; y) удовлетворяют уравнение гиперболы, то это же уравнение удовлетворяют и координаты  Точка К, очевидно, симметрична точке N относительно начала координат. Таким образом, гипербола имеет центр симметрии.
Точка К, очевидно, симметрична точке N относительно начала координат. Таким образом, гипербола имеет центр симметрии.
Центр симметрии гиперболы называется центром гиперболы.
4. Гипербола пересекается с прямой  в двух точках. Если
в двух точках. Если  то общих точек у гиперболы и прямой нет.
то общих точек у гиперболы и прямой нет.
Чтобы вычислить координаты точек пересечения гиперболы и прямой у=kх, необходимо решить систему уравнений

При  , то есть при
, то есть при  полученное уравнение, а потому и система решений не имеют. Следовательно, прямые, которые проходят через начало координат с угловым коэффициентом, модуль которого больше или равен
полученное уравнение, а потому и система решений не имеют. Следовательно, прямые, которые проходят через начало координат с угловым коэффициентом, модуль которого больше или равен  не пересекают гиперболу. Прямые, уравнения которых имеют вид
не пересекают гиперболу. Прямые, уравнения которых имеют вид  , называются асимптотами гиперболы.
, называются асимптотами гиперболы.
При  то есть при
то есть при  система имеет два решения:
система имеет два решения:

Таким образом, каждая прямая, которая проходит через начало координат с угловым коэффициентом, модуль которой меньше чем  пересекает гиперболу в двух точках. При k=0 из формул получаем
пересекает гиперболу в двух точках. При k=0 из формул получаем  то есть прямая у=0 пересекает гиперболу в её вершинах.
то есть прямая у=0 пересекает гиперболу в её вершинах.
Поскольку гипербола симметрична относительно осей координат, то достаточно выучить её формулу в первом квадранте координатной плоскости. По формулам

имеем, что из возрастания k от  (при этом прямая у=kх поворачивается против часовой стрелки) и абсциссы, и ординаты точек пересечения прямой с гиперболой возрастают. Прямая у=kх пересекает гиперболу в более отдалённых от начала координат точках. Следовательно, гипербола имеет вид, изображённый на рис. 11. Она составляется из двух не связанных между собой частей, которые называются её ветками.
(при этом прямая у=kх поворачивается против часовой стрелки) и абсциссы, и ординаты точек пересечения прямой с гиперболой возрастают. Прямая у=kх пересекает гиперболу в более отдалённых от начала координат точках. Следовательно, гипербола имеет вид, изображённый на рис. 11. Она составляется из двух не связанных между собой частей, которые называются её ветками.

Как уже видели (рис. 11), ветка гиперболы размещена выше от асимптоты  и ниже от асимптоты
и ниже от асимптоты  . Поэтому соотношения
. Поэтому соотношения  полуосей гиперболы определяют её формулу. Чем меньше это соотношение, тем сильнее гипербола сжата до оси Ох.
полуосей гиперболы определяют её формулу. Чем меньше это соотношение, тем сильнее гипербола сжата до оси Ох.
Как и в случаи эллипса, для характеристики формулы гиперболы целесообразно пользоваться не соотношением  , а соотношением
, а соотношением  .
.
Соотношение полуфокусного расстояния с к действительной полуоси  называется эксцентриситетом гиперболы. Эксцентриситет обозначают буквой е. Следовательно,
называется эксцентриситетом гиперболы. Эксцентриситет обозначают буквой е. Следовательно,

Поскольку для гиперболы  , то эксцентриситет гиперболы удовлетворяет неравенству
, то эксцентриситет гиперболы удовлетворяет неравенству  .
.
Выразим эксцентриситет гиперболы через соотношение  её полуосей:
её полуосей:

то есть: 
Согласно формуле, меньшим значением соотношения  соответствуют меньшие значения эксцентриситету. Таким образом, чем меньше эксцентриситет гиперболы, тем сильнее сжата она к оси абсцисс.
соответствуют меньшие значения эксцентриситету. Таким образом, чем меньше эксцентриситет гиперболы, тем сильнее сжата она к оси абсцисс.
Гипербола называется равносторонней (или равнобокой), если длины её полуосей равны между собой. Поскольку для равносторонней гиперболы  то её уравнение имеет вид:
то её уравнение имеет вид:

Асимптотами равносторонней гиперболы являются прямые у=х и у= -х. Следовательно, асимптоты равносторонней гиперболы взаимно перпендикулярны.
Эксцентриситет равносторонней гиперболы:

Пример 3. Даны фокусы гиперболы  и
и  и её асимптоту 4х+3у=0. Найти уравнение гиперболы.
и её асимптоту 4х+3у=0. Найти уравнение гиперболы.
Решение.
Записав уравнение асимптоты в виде  , найдём соотношение полуосей гиперболы
, найдём соотношение полуосей гиперболы 
Из условия задачи вытекает, что с=10. Поэтому  Задача сводится к решению уравнений
Задача сводится к решению уравнений

Подставив  во второе уравнение системы, получим
во второе уравнение системы, получим

откуда  Теперь находим
Теперь находим  Следовательно, гипербола имеет уравнение
Следовательно, гипербола имеет уравнение 
Парабола
Параболой называется множество точек на плоскости, для каждой из которых расстояние до данной точки равно расстоянию до данной прямой, которая не проходит через данную точку.
Такая точка называется фокусом параболы, а прямая — директрисой (направляющей). Расстояние от фокуса до директрисы называется фокальным параметром параболы и обозначается как р.
Выберем систему координат таким образом, чтобы ось Ох была проведена через фокус F перпендикулярно к директрисе. Точка пересечения оси абсцисс с директрисой обозначим D (рис. 12), за начало координат О возьмём середину отрезка DF, за положительное направление оси Ох — направление луча OF/
В этой системе координат фокус F имеет координаты  , а уравнением директрисы является уравнение
, а уравнением директрисы является уравнение

Пусть М(х; у) — любая искомая точка искомого множества. Опустим из точки М перпендикуляр на директрису, и пусть N — основа этого перпендикуляра. Тогда |MN| является расстоянием от точки М до директрисы и, следовательно,


Это уравнение является уравнением параболы в выбранной системе координат. Его можно упростить. В следствии того, что обе части уравнения неотъемлемые, то уравнение

равносильно предыдущему уравнению. В результате преобразований получим уравнение

Оно называется каноническим уравнением параболы.
Приведём такие свойства параболы:
1. Парабола имеет ось симметрии.
Переменная у входит в уравнение только во второй степени. Поэтому, если координаты точки М1(х; у) удовлетворяют уравнение параболы, то и его координаты N2 (х; -у) будут удовлетворять его. Точка N1 симметрична точке N2 относительно оси Ох. Следовательно, ось Ох является симметрией параболы. Ось симметрии параболы называется осью параболы. Точка пересечения параболы с осью называется вершиной параболы. Вершина параболы находится в начале координат.

2. Парабола расположена в полуплоскости 
Правда, поскольку параметр р положительный, то уравнения могут удовлетворять только точки с неотрицательными абсциссами, то есть точки полуплоскости 
3. Парабола является объединением графиков функций

Чтобы убедиться в этом, достаточно решить уравнение относительно переменной у.
Пример 1. Световой луч у=-2 падает на зеркало, осевым сечением которого является парабола у2=24х (рис. 14). Найти уравнение прямой, которой принадлежит отражённый луч.

Решение.
Если падающий луч параллельный главной оптической оси параболического зеркала, то отражённый луч проходит через его фокус. В этом случаи ось параболического зеркала совпадает с осью Ох. Прямая у=-2 параллельна оси абсцисс, и поэтому отражённый луч пройдёт через фокус параболы у2=24х. Поскольку 2р=24, то есть  , то фокусом параболы является точка F(6; 0).
, то фокусом параболы является точка F(6; 0).
Чтобы найти точки падения светового луча, необходимо решить систему уравнений

Решив эту систему, найдём точку падения луча  .
.
Отражённый луч принадлежит прямой, которая проходит через точки  и
и  .
.
Запишем уравнение этой прямой

Отсюда получим 
Если фокус параболы расположенный левее оси Оу (рис. 15), то есть имеет координаты  , то уравнение параболы будет:
, то уравнение параболы будет:

Если фокус параболы лежит на оси Оу (рис. 16), то есть имеет координаты  , то уравнение параболы будет:
, то уравнение параболы будет:

Если фокус параболы лежит правее оси Оу (рис. 17), то есть имеет координаты  , то уравнение параболы будет:
, то уравнение параболы будет:


Общее уравнение второго порядка с двумя переменными
Общее уравнение второго порядка с двумя переменными имеет вид

Рассмотренные ранее канонические уравнения прямых являются частными случаями данного уравнения.
1.  уравнение будет иметь вид
уравнение будет иметь вид

и, соответственно, будет уравнением окружности.
2.  уравнение будет иметь вид
уравнение будет иметь вид

и, соответственно, будет уравнением эллипса.
3.  уравнение будет иметь вид
уравнение будет иметь вид

и, соответственно, будет уравнением гиперболы.
4.  уравнение будет иметь вид
уравнение будет иметь вид

и, соответственно, будет уравнением параболы.
Кривые второго порядка
Кривыми второго порядка называются линии, уравнения которых являются уравнениями второй степени относительно бегущих координат. Общий вид уравнения кривой второго порядка
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0. (2.109)
К кривым второго порядка относятся круг, эллипс, гипербола и парабола.
Окружность и его уравнения
Определение 1. Окружностью называется множество точек плоскости, равноудаленных от заданной точки, называется центром окружности.

Рис. 50.
Пусть центр окружности находится в произвольной точке С (a, b) (рис. 50). Выходя из определения 1, расстояние произвольной точки M (x, y) плоскости к центру C (a, b) — величина постоянная и равна r. По формуле (2.3) имеем  . Возведя обе части этого равенства в квадрат, получим уравнение, которое называется нормальным уравнением окружности:
. Возведя обе части этого равенства в квадрат, получим уравнение, которое называется нормальным уравнением окружности:
(x – a) 2 + (y – b) 2 = r 2. (2.110)
Выясним условия, при которых общее уравнение второй степени с двумя переменными (2.109) является уравнением окружности. В этом уравнении А, В и С не равны нулю одновременно, т .е. A2 + B2 + C2 ≠ 0. Когда в уравнении (2.110) раскрываем скобки, то получим
x2 + y2 – 2ax – 2by + (a2 + b2 – r2) = 0. (2.111)
Чтобы уравнения (2.109) и (2.111) представляли одну и ту же линию, нужно, чтобы коэффициент B = 0, а все остальные пропорциональны, в частности
 , отсюда A = C ≠ 0. Теперь уравнение (2.109) имеет вид:
, отсюда A = C ≠ 0. Теперь уравнение (2.109) имеет вид:
Ax2 + Ay2 + Dx + Ey + F = 0. (2.112)
Уравнение (2.112) называется общим уравнением окружности.
Обе части уравнения (2.112) поделим на A ≠ 0 и дополним члены, содержащие x и y, до полных квадратов. Получим
 (2.113)
(2.113)
Сравнивая (2.113) с уравнением окружности (2.110), можно сделать вывод, что уравнение (2.109) является уравнением окружности при следующих трех условиях:
1) A = C, 2) B = 0, 3) D2 + E2 – 4AE > 0.
При выполнении этих условий для окружности (2.113) центр находится в точке  а радиус
а радиус 
Пример 1. Привести общее уравнение окружности x2 + y2 – 6x + 4y – 3 = 0 к нормальному виду.
Решение. Сгруппируем члены с x и y и дополним их до полного квадрата, тогда получим
(x2 – 6 x + 9) – 9 + (y2 + 4 y + 4) – 4 – 3 = 0, или (x – 3) 2 + (y + 2) 2 = 16. Координаты центра окружности a = 3, b = 2, а радиус окружности r = 4.
Пример 2 (экономического характера). Два предприятия, расстояние между которыми 80 км, производят некоторую продукцию, причем фабрично-заводская цена продукции на обоих предприятиях одинакова и равна p. Пусть транспортные расходы на перевозку единицы продукции от компании A до потребителя составляет 10 руб./км, а от компании B составляет 6 руб./км. Как будет размещен рынок сбыта, если расходы потребителей должны быть одинаковыми?

Рис. 51.
Решение. Оси координат проведем через середину отрезка AB. Предположим, что потребитель находится в точке M (x, y); введем обозначения AM = s1, BM = s2 (рис. 51). Расходы потребителя на покупку единицы изделия у компании A составляют
p + s1⋅ 10, а у предприятия B — p + s2⋅ 6. Расходы потребителей одинаковые, если p + s1⋅ 10 = p + s2⋅ 6, или 10 s1 = 6 s2, 5 s1 = 3 s2.
Из рис. 51 видно, что  или
или 
Аналогично  или
или  .
.
Для потребителя расходы на покупку продукции одинаковые, если  . Возведем обе части в квадрат и сгруппируем. Получим x2 + y2 + 170 x + 1600 = 0 и, выделив полный квадрат относительно x, имеем
. Возведем обе части в квадрат и сгруппируем. Получим x2 + y2 + 170 x + 1600 = 0 и, выделив полный квадрат относительно x, имеем
(x + 85)2 + y2 = 5625. Это нормальное уравнение окружности, центр которой находится на оси абсцисс с абсциссой “–85”, а радиус окружности r = 75.
Для потребителей, которые находятся на этой окружности, расходы на покупку изделия одинаковы. Для потребителей, которые находятся за окружностью, расходы на покупку продукции меньше на предприятии B, а для потребителей, которые находятся внутри окружности — на предприятии A. Значит, рынок будет распределен следующим образом:
а) потребители, которые находятся внутри окружности, будут приобретать данные изделия на предприятии А;
б) для потребителей, находящихся на окружности, все равно, на каком предприятии будут производиться закупки;
в) потребители, которые находятся снаружи окружности, будут закупать изделия на предприятии В.
Эллипс и его уравнения
Определение 2. Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух заданных точек, называемых фокусами, есть величина постоянная.
Исходя из определения 2, выведем уравнение эллипса. Пусть заданы две точки, которые называются фокусами, F1 и F2, расстояние между которыми обозначим через 2с (фокальное расстояние) (рис.52). Через фокусы проведем прямую, которую возьмем за ось абсцисс, а за ось ординат возьмем прямую, перпендикулярную оси OX, проходящую через середину отрезка F1F2 (точка О).
Поскольку расстояние между фокусами приняли за 2с, то координаты фокусов будут соответственно F1 (c, 0) и F2 (–c, 0).

Рис. 52.
Пусть M (x, y) произвольная точка эллипса. Отрезки F1M и F2M, соединяющие точку эллипса с его фокусами, называют локальными радиус-векторами этой точки и обозначают r1 и r2 . Тогда r1 + r2 является величиной постоянной по определению, обозначим ее через 2а:
r1 + r2 = 2а (2.114)
(2а > 2с, потому что в треугольнике F1MF2 сумма двух сторон больше третьей). Покажем, какому уравнению удовлетворяют координаты точки M (x, y).
Найдем r1 и r2:
 , (2.115)
, (2.115)
 . (2.116)
. (2.116)
Возведя обе части (2.115) и (2.116) в квадрат и отнимая, получим
 . (2.117)
. (2.117)
Расписав разность квадратов в (2.117) и учитывая (2.114), получим
 . (2.118)
. (2.118)
Рассмотрим систему из уравнений (2.114) и (2.118):
 (2.119)
(2.119)
Из этой системы находим
 (2.120)
(2.120)
 . (2.121)
. (2.121)
Подставим (2.121) в (2.116), получим
 , или
, или
 . (2.122)
. (2.122)
Обозначим a2 – c2 = b2 (2.123)
и тогда (2.122) перепишем после простых преобразований в виде
 . (2.124)
. (2.124)
Уравнение (2.124) является каноническим уравнением эллипса. Это уравнение второй степени, значит, эллипс — кривая второго порядка. Уравнение (2.124) содержит x и y в четных степенях, значит, кривая, определяемая этим уравнением, симметрична относительно осей Оx и Оy. Оси симметрии эллипса называют его осями. Точку О называют центром эллипса. Из уравнения (2.124) найдем y:
 (2.125)
(2.125)
Так как у, который находится в первом квадранте, является положительным, то
 . (2.126)
. (2.126)
Из равенства (2.126) видно, если x = 0, то y = b и при возрастании x от нуля до a, y убывает от b к нулю.
В первом квадранте часть эллипса — это дуга A1B1. Если провести зеркальное отражение этой дуги относительно осей координат, то мы получим весь эллипс (рис. 52).
Если в уравнении (2.124) y = 0, то x = ± a, a если x = 0, то y = ± b. Значит вершинами эллипса есть точки A1 (a, 0), A2 (–a, 0), B1 (0, b), B2 (0, –b). Отрезок A2 A1 = 2a, а отрезок B2 B1 = 2b. Эти
отрезки соответственно называются большой и малой осями эллипса. Соответственно, a и b — большая и малая полуоси эллипса.
Определение 3. Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большой оси.
Обозначим эксцентриситет через ε, то тогда
 . (2.127)
. (2.127)
Если a = b (ε = 0), то эллипс превращается в окружность. Подставим (2.127) в (2.120) и (2.121), тогда получим
r1 = a – εx, (2.128)
r2 = a + εx. (2.129)
Эти формулы используются при решении задач.
Пример 3. Составить каноническое уравнение эллипса, зная, что большая ось 2a = 10, а эксцентриситет ε = 0,8.
Решение. Из уравнения (2.127) найдем c. Зная, что a = 5, c = a ⋅ ε = 5 ⋅ 0,8 = 4. А теперь найдем b из равенства (2.123):
b2 = a2 – c2 = 52 – 42 = 25 – 16 = 9, b = 3.
Подставляя a = 5, b = 3 в уравнение (2.124), получим  .
.
Гипербола и ее уравнение
Определение 4. Гиперболой называется множество точек плоскости, абсолютное значение разницы расстояний которых от двух заданных точек, называемых фокусами, есть величина постоянная.
Основываясь на определении 4, выведем каноническое уравнение гиперболы. Пусть заданы две точки F1 и F2 , являющиеся фокусами гиперболы. Обозначим расстояние между ними через 2c, а абсолютную величину разности расстояний точки гиперболы от точек F1 и F2 обозначим через 2a (a > 0). За ось абсцисс возьмем прямую, проходящую через фокусы, а за ось ординат возьмем прямую, перпендикулярную оси абсцисс и проходящую через середину отрезка F2F1 (рис. 58), то есть через точку О. Поскольку F2F1 = 2с, то координатами фокусов будут соответственно F1 (c; 0) и F2(–c; 0), а фокальные радиусы соответственно r1 = F1M, r2 = F2M,  , где M (x, y) — произвольная точка гиперболы.
, где M (x, y) — произвольная точка гиперболы.

Рис. 58.
Пользуясь формулой расстояния между двумя точками и определением 4, имеем уравнение гиперболы:
 (2.130)
(2.130)
Запишем это уравнение в таком виде:
 или
или
 . (2.131)
. (2.131)
Возведя в квадрат обе части этого уравнения, получим:

или после упрощения  . Опять возведя обе части полученного уравнения в квадрат, получим после упрощений
. Опять возведя обе части полученного уравнения в квадрат, получим после упрощений
x2 (c2 – a2) – a2 y2 = a2 (c2 – a2). (2.132)
Разделив обе части уравнения (2.132) на a2 (c2 – a2), получим:
 . (2.133)
. (2.133)
Покажем, что c2 – a2 > 0 (c > a). Поскольку в любом треугольнике разность двух сторон меньше трех, то
 или 2a < 2c, или a < c . Тогда c2 – a2 величина положительная, и ее обозначим через b2. То есть
или 2a < 2c, или a < c . Тогда c2 – a2 величина положительная, и ее обозначим через b2. То есть
c2 – a2 = b2. (2.134)
Подставляя (2.134) в (2.133), получим каноническое уравнение гиперболы
 . (2.135)
. (2.135)
Уравнение (2.135) является уравнением второй степени, значит гипербола является кривой второго порядка. Исследуем форму гиперболы по ее уравнению (2.135). Поскольку уравнение содержит x и y только в четных степенях, то гипербола симметрична относительно обеих осей координат.
Найдя y и x из уравнения (2.135), получим
 (2.136)
(2.136)
 (2.137)
(2.137)
Из уравнения (2.136) можно сделать следующие выводы:
а) значения у мнимые, если | х | < a , значит гипербола не пересекает оси Оу и не имеет точек, находящихся в полосе, ограниченной прямыми х = ± a;
б) когда x = ± a, y = 0, значит гипербола пересекает ось абсцисс в двух точках A1 (a, 0) и A2 (–a, 0), которые называются вершинами гиперболы;
в) для каждого | x | > a, ордината y имеет два значения, которые отличаются только знаком, отсюда следует, что гипербола симметрична относительно оси Оx.
Уравнение (2.137) показывает, что гипербола симметрична и относительно оси Оy.
При неограниченном росте абсциссы x ордината также неограниченно растет. Поскольку гипербола находится вне полосы, ограниченной прямыми x = ± a, то гипербола состоит из двух отдельных веток (рис. 59).
Отрезок A2 A1 называется действительной осью гиперболы, а точки A1 (a, 0) и A2 (–a, 0) —вершинами гиперболы. Отрезок B1B2, соединяющий точки В1 (0, b) и В2 (0, –b), называется мнимой осью гиперболы. Точки F1 (c, 0) и F2 (–c, 0) называются фокусами гиперболы.

Рис. 59.
Гипербола, которая определяется уравнением  , имеет действительную ось B2B1 = 2b, а воображаемая ось A2A1 = 2a (показана на рис. 59 пунктиром) называется сопряженной по отношению к гиперболе
, имеет действительную ось B2B1 = 2b, а воображаемая ось A2A1 = 2a (показана на рис. 59 пунктиром) называется сопряженной по отношению к гиперболе
 .
.
Если действительная и мнимая оси равны, то гипербола называется равносторонней, а ее уравнение будет x2 – y2 = a2.
Степень сжатия гиперболы характеризуется ее эксцентриситетом.
Определение 5. Эксцентриситетом гиперболы называется отношение расстояния между фокусами 2с к длине ее действительной оси 2a, то есть
 . (2.138)
. (2.138)
Так как для гиперболы с > a, то ε > 1.
Примечание. Для гиперболы легко показать как связаны r1 и r2 с ε, а именно
 (х > 0),
(х > 0),
 (х > 0), (2.139)
(х > 0), (2.139)
 (х < 0),
(х < 0),
 (x <0). (2.140)
(x <0). (2.140)
Формулы (2.139) и (2.140) получаются аналогично как и для эллипса.
Предоставим читателю самостоятельно убедиться в справедливости формул (2.139) и (2.140).
Асимптоты гиперболы
Определение 6. Прямая l называется асимптотой кривой (k), если расстояние d = MN от точки M кривой до точки N прямой l стремится к нулю при неограниченном удаленные точки M от начала координат вдоль кривой (k) в том или ином направлении (рис. 60).

Рис. 60.
Покажем, что прямая  (2.141) является асимптотой гиперболы (2.135). Для этого рассмотрим прямую MN, параллельной оси Oy (рис. 59). Абсцисса точки M и точки N одна и та же, то есть x, а ордината точки M является y, а точки N ∈ Y.
(2.141) является асимптотой гиперболы (2.135). Для этого рассмотрим прямую MN, параллельной оси Oy (рис. 59). Абсцисса точки M и точки N одна и та же, то есть x, а ордината точки M является y, а точки N ∈ Y.
Найдем разницу между ординатами (Y-y) точек N и M, которые имеют одну и ту же абсциссу  .
.
Теперь умножим и разделим правую часть этого равенства на  и после упрощений получим
и после упрощений получим  .
.
Отсюда видно, что при неограниченном увеличении абсциссы x разница (Y-y) неограниченно уменьшается. Таким образом, точка гиперболы ограниченно удаляясь по ветке гиперболы, неограниченно приближается к асимптоте  , но никогда ее не достигает. Значит, гипербола (2.135) имеет две асимптоты
, но никогда ее не достигает. Значит, гипербола (2.135) имеет две асимптоты  и
и  , которые совпадают с диагональю прямоугольника и проходят через начало координат.
, которые совпадают с диагональю прямоугольника и проходят через начало координат.
Пример 4. Составить уравнение гиперболы, если известно, что она проходит через точку M1 (10; 5) и имеет асимптоты  и
и  .
.
Решение. Из условия задачи получаем, что  и координатs точки M1 удовлетворяют уравнению гиперболы, то есть
и координатs точки M1 удовлетворяют уравнению гиперболы, то есть  Таким образом, получили систему двух уравнений с двумя неизвестными:
Таким образом, получили систему двух уравнений с двумя неизвестными:

Из первого уравнения находим  и подставляем во второе уравнение
и подставляем во второе уравнение  или
или 
Отсюда  Далее находим
Далее находим 
Итак, искомое уравнение гиперболы будет 
Парабола и ее уравнение
Определение 7. Параболой называется множество точек плоскости, одинаково удаленных от заданной точки, называемой фокусом, и от заданной прямой, называемой директрисой.
Исходя из определения 7, выведем уравнение параболы. Пусть прямая AB является директрисой параболы, а точка F является ее фокусом (рис. 61).

Рис. 61.
Проведем через точку F прямую, перпендикулярную директрисе AB, и возьмем эту прямую за ось абсцисс, а за ось ординат возьмем прямую, перпендикулярную оси абсцисс и проходящую через точку O, середину отрезка CF. Длину отрезка CF обозначим через p (p > 0). Координаты фокуса будут  , а уравнение директрисы AB есть
, а уравнение директрисы AB есть  .
.
Пусть точка M (x, y) является произвольной точкой параболы. Опустим из точки M перпендикуляр на директрису AB в точке D и соединим точку M с фокусом F. Тогда
по определению 7 имеем, что DM = MF. Точка D имеет координаты  По формуле расстояния между двумя точками находим
По формуле расстояния между двумя точками находим
 .
.
Это и будет уравнение параболы относительно выбранной системы координат. Возведя обе части данного уравнения в квадрат и упростив, получим
y2 = 2 px. (2.142)
Уравнение (2.142) и является каноническим уравнением параболы. Как видно из уравнения (2.142), парабола является линией второго порядка, и все ее точки размещены справа от оси Оy. Парабола проходит через начало координат. Решив уравнение (2.142) относительно y, получим
 . (2.143)
. (2.143)
Так как p > 0, то y будет действительной величиной только тогда, когда x положительные, а когда p < 0, то парабола определена для x ≤ 0.
Из (2.143) видно, что каждому значению x соответствует два знания y, которые равны по абсолютной величине, но противоположны по знаку.
Значит ось Оx является осью симметрии для параболы. Точку O (0,0) называют вершиной параболы.
Если x неограниченно растет, то и y неограниченно растет. Величина р называется параметром параболы и при увеличении р парабола расширяется, то есть ее точки будут удаляться от оси Ох.
Если уравнение параболы имеет вид y2 = –2px, то вершина параболы находится в начале координат, осью симметрии является ось абсцисс, но парабола размещена слева от оси Oy (рис. 62), а директриса такой параболы будет размещена справа от оси ординат, а фокус  будет слева от начала координат.
будет слева от начала координат.
Если директриса параболы параллельна оси абсцисс, а фокус находится на оси ординат, то уравнение параболы имеет вид: x2 = ± 2py. (2.144)


Рис. 62. Рис. 63.
Парабола (2.144) изображена на рис. 63. Эта парабола симметрична относительно оси Oy и размещена над осью абсцисс, если в уравнении взять знак (+), и под осью абсцисс, если взять знак (-).
Если в уравнении (2.144) обозначить  , то получим уравнение параболы y = ax2, которую изучают в средней школе.
, то получим уравнение параболы y = ax2, которую изучают в средней школе.
Пример 5. Фермы, поддерживающие железнодорожный мост длиной 112 м, имеют вид параболы, которая задается уравнением y = ax2. Найти уравнение соответствующей параболы, если наибольшая высота мостовой арки составляет 44 м.
Решение. Возьмем за начало координат вершину фермы. Тогда симметричные точки в основании фермы будут иметь координаты (-56; -44) и (56; -44). Подставляя любую пару координат в уравнение y = ax2, получим – 44 = a ⋅ 3136. Отсюда
 .
.
Таким образом, мостовая ферма имеет вид параболы  .
.
Линии второго порядка. Общее уравнение линии второго порядка
Напомним, что линия второго порядка – это множество точек, координаты которых удовлетворяют уравнениям вида
 , (1)
, (1)
где коэффициенты a,b,c,d,e,f– действительные числа, причем хотя бы одно из чисел a,b,c отлично от нуля, то есть  . В частности, к линиям второго порядка относятся окружность, эллипс, гипербола и парабола. Заметим, что множеством точек (
. В частности, к линиям второго порядка относятся окружность, эллипс, гипербола и парабола. Заметим, что множеством точек ( ;
; ) с действительными координатами, удовлетворяющими уравнению (1), может быть не только одна из названых линий. Уравнение (1) может определять на плоскости
) с действительными координатами, удовлетворяющими уравнению (1), может быть не только одна из названых линий. Уравнение (1) может определять на плоскости  также две прямые (
также две прямые ( ), одну прямую (
), одну прямую ( -2 =0), точку (
-2 =0), точку ( =0) или не определять ни одной точки (
=0) или не определять ни одной точки ( + 1 = 0).
+ 1 = 0).
Линии второго порядка называют также коническими сечениями, так как их можно получить пересечением кругового конуса с плоскостью. Окружность образуется как линия пересечения плоскости, перпендикулярной к оси конуса и не проходящей через его вершину (рис. 1, а); эллипс – линия пересечения плоскости, пересекающей все образующие конуса, не перпендикулярная к оси конуса и не проходящая через его вершину (рис. 1, б); если пересечь двуполостной конус плоскостью, параллельной двум образующим, то получим гиперболу (рис. 1, в), а одной образующей – параболу (рис. 1, г).

Кривые второго порядка – важная составляющая окружающего мира.
1. Планеты Солнечной системы движутся по эллипсам, имеющим общий фокус, в котором расположено Солнце.
2. Если в фокусе параболы разместить источник света, то лучи, отразившись от параболы, пойдут параллельно ее оси. На этом свойстве основывается конструкция прожектора.
3. Движение материальной точки под действием центрального поля силы тяготения осуществляется по одной из линий второго порядка.
Окружность и ее уравнение
Окружностью называют множество точек плоскости (рис. 2), находящихся на одинаковом расстоянии  (радиус окружности) от заданной точки плоскости
(радиус окружности) от заданной точки плоскости  (центра окружности). Уравнение окружности имеет вид
(центра окружности). Уравнение окружности имеет вид
 . (2)
. (2)
Если в уравнении (2) раскрыть скобки, то получим общее уравнение окружности
 , (3)
, (3)
где А = -2а , В = -2b, С =  . Поэтому окружность – линия второго порядка.
. Поэтому окружность – линия второго порядка.
 Рис. 2. Окружность
Рис. 2. Окружность
Уравнение окружности имеет следующие свойства.
1°. Коэффициенты  и
и  равны между собой.
равны между собой.
2°. В уравнении отсутствует член с произведением  .
.
Если центр окружности расположен в начале координат, то а =b = 0 и уравнение (2) имеет вид
 . (4)
. (4)
Уравнение (4) называется каноническим уравнением окружности.
Пример №7
Найти центр и радиус окружности  .
.
Решение:
Сгруппируем произведения с переменной  и переменной
и переменной  и дополним полученные выражения до полных квадратов:
и дополним полученные выражения до полных квадратов:

Поэтому, точка (-2; 3) – центр окружности, a  = 6 – его радиус.
= 6 – его радиус.
Каноническое уравнение эллипса. Эксцентриситет
Возьмем на плоскости две точки  и
и  , и разместим прямоугольную систему координат так, чтобы ось
, и разместим прямоугольную систему координат так, чтобы ось  проходила через них, а начало координат делило отрезок
проходила через них, а начало координат делило отрезок  пополам. Эллипсом называют множество всех точек плоскости, сумма расстояний которых от данных точек
пополам. Эллипсом называют множество всех точек плоскости, сумма расстояний которых от данных точек  и
и  этой плоскости, называемых фокусами, есть величина постоянная и больше расстояния между фокусами (рис. 3, а). Расстояние между фокусами называют фокальным и обозначают через
этой плоскости, называемых фокусами, есть величина постоянная и больше расстояния между фокусами (рис. 3, а). Расстояние между фокусами называют фокальным и обозначают через  . Сумму расстояний от произвольной точки эллипса
. Сумму расстояний от произвольной точки эллипса  до фокусов обозначим через
до фокусов обозначим через 
 . Тогда фокусы имеют координаты
. Тогда фокусы имеют координаты  (-с; 0 и
(-с; 0 и  (c; 0), и по определению эллипса
(c; 0), и по определению эллипса  , то есть а > с.
, то есть а > с.

Каноническим уравнением эллипса называется равенство
 (5)
(5)
где
 . (6)
. (6)
Отметим некоторые свойства эллипса.
1°. Эллипс симметричен относительно осей  и
и  , а также относительно точки
, а также относительно точки  (0; 0), которую называют центром эллипса.
(0; 0), которую называют центром эллипса.
2°. Эллипс пересекает оси координат в точках  (а; 0),
(а; 0),  (-а; 0),
(-а; 0),  (0; b),
(0; b),  (0; –b). Эти точки называются вершинами эллипса (рис. 3, б). Величины
(0; –b). Эти точки называются вершинами эллипса (рис. 3, б). Величины  и
и  называются, соответственно, большой и малой осями эллипса, а числа а и b – большой и малой полуосями эллипса.
называются, соответственно, большой и малой осями эллипса, а числа а и b – большой и малой полуосями эллипса.
3°. Если а = b , то уравнение (5) принимает вид  , то есть получается уравнение окружности. Поэтому окружность является частным случаем эллипса. При а = b имеем с = 0, то есть окружность – это эллипс, у которого фокусы совпадают с его центром.
, то есть получается уравнение окружности. Поэтому окружность является частным случаем эллипса. При а = b имеем с = 0, то есть окружность – это эллипс, у которого фокусы совпадают с его центром.
Мера отклонения эллипса от окружности характеризуется величиной  , которая называется эксцентриситетом эллипса и равняется отношению половины его фокального расстояния к длине большой полуоси:
, которая называется эксцентриситетом эллипса и равняется отношению половины его фокального расстояния к длине большой полуоси:
 (7)
(7)
причем  , поскольку
, поскольку  . Из формул (6) и (7) получим
. Из формул (6) и (7) получим
 .
.
Итак, если  = 0 , то b = а , то есть эллипс превращается в окружность; если
= 0 , то b = а , то есть эллипс превращается в окружность; если  приближается к единице, то отношение осей b/а уменьшается, то есть эллипс все больше растягивается вдоль оси
приближается к единице, то отношение осей b/а уменьшается, то есть эллипс все больше растягивается вдоль оси  .
.
4°. Пусть  – произвольная точка эллипса с фокусами
– произвольная точка эллипса с фокусами  и
и  (рис. 3, б). Расстояния
(рис. 3, б). Расстояния  и
и  , называются фокальными радиусами точки
, называются фокальными радиусами точки  . Очевидно, что
. Очевидно, что  . Прямые
. Прямые  называются директрисами эллипса. Отношение фокальных радиусов произвольной точки эллипса к расстояниям от этой точки до соответствующих директрис есть величина постоянная и равна эксцентриситету эллипса, то есть
называются директрисами эллипса. Отношение фокальных радиусов произвольной точки эллипса к расстояниям от этой точки до соответствующих директрис есть величина постоянная и равна эксцентриситету эллипса, то есть
 . (8)
. (8)
Пример №8
Составить каноническое уравнение эллипса, фокусы которого расположены на оси  симметрично начала координат, если расстояние между фокусами равно 14, а эксцентриситет равен 7/9 .
симметрично начала координат, если расстояние между фокусами равно 14, а эксцентриситет равен 7/9 .
Решение:
Поскольку 2с = 14, то с = 7. Из формул (7) и (6) получим а = 9 и  = 32. Поэтому искомое уравнение имеет вид
= 32. Поэтому искомое уравнение имеет вид

Каноническое уравнение гиперболы. Асимптоты. Эксцентриситет
Гиперболой называется множество всех точек плоскости, модуль разности расстояний от которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.
Обозначим через  и
и  фокусы гиперболы, расстояние между ними – через 2с, а модуль разности расстояний от произвольной точки гиперболы до фокусов – через 2а. По определению а<с. Возьмем на плоскости прямоугольную систему координат
фокусы гиперболы, расстояние между ними – через 2с, а модуль разности расстояний от произвольной точки гиперболы до фокусов – через 2а. По определению а<с. Возьмем на плоскости прямоугольную систему координат  так, чтобы ось
так, чтобы ось  проходила через фокусы, а начало координат делило бы отрезок
проходила через фокусы, а начало координат делило бы отрезок  пополам (рис. 4). Точка
пополам (рис. 4). Точка  плоскости принадлежит гиперболе тогда и только тогда, когда
плоскости принадлежит гиперболе тогда и только тогда, когда  . Каноническое уравнение гиперболы имеет вид
. Каноническое уравнение гиперболы имеет вид
 (9) где
(9) где
 (10)
(10)
 . Рис. 4. Гипербола и ее свойства Рассмотрим некоторые свойства гиперболы.
. Рис. 4. Гипербола и ее свойства Рассмотрим некоторые свойства гиперболы.
1°. Гипербола симметрична относительно осей  ,
,  и начала координат.
и начала координат.
2°. Удаляясь в бесконечность, переменная точка  гиперболы неограниченно приближается к одной из прямых
гиперболы неограниченно приближается к одной из прямых
 -. (11)
-. (11)
Такие прямые называются асимптотами гиперболы.
Оси симметрии называются осями гиперболы, а точка пересечения осей – ее центром. Ось  пересекает гиперболу в двух точках
пересекает гиперболу в двух точках  (а; 0) и
(а; 0) и  (-а; 0), которые называются вершинами гиперболы. Действительной осью называют отрезок
(-а; 0), которые называются вершинами гиперболы. Действительной осью называют отрезок  , соединяющий вершины гиперболы, и его длину
, соединяющий вершины гиперболы, и его длину  . Отрезок
. Отрезок  , который соединяет точки
, который соединяет точки  (0; b) и
(0; b) и  (0; –b), и его длина, называется мнимой осью. Величины а и b, соответственно, называются действительной и мнимой полуосями гиперболы. Прямоугольник со сторонами 2а и 2b называется основным прямоугольником гиперболы.
(0; –b), и его длина, называется мнимой осью. Величины а и b, соответственно, называются действительной и мнимой полуосями гиперболы. Прямоугольник со сторонами 2а и 2b называется основным прямоугольником гиперболы.
При построении гиперболы (9) удобно сначала построить ее основной прямоугольник (рис. 4), провести прямые, проходящие через противоположные вершины этого прямоугольника, – асимптоты гиперболы и определить вершины  и
и  гиперболы. Уравнение
гиперболы. Уравнение
 12)
12)
также определяет гиперболу, которая называется сопряженной гиперболе (9). Гипербола (12) показана на рис. 4 штриховой линией. Вершины этой гиперболы находятся в точках  (0; b) и
(0; b) и  (0; –b), а ее асимптоты совпадают с асимптотами гиперболы (9).
(0; –b), а ее асимптоты совпадают с асимптотами гиперболы (9).
3°. Эксцентриситет гиперболы определяется как отношение половины фокального расстояния к длине ее действительной полуоси:
 . (13)
. (13)
Поскольку с > а, то  > 1. Кроме того, из формул (10) и (13) следует, что
> 1. Кроме того, из формул (10) и (13) следует, что 
Поэтому эксцентриситет гиперболы характеризует ее форму: чем больше эксцентриситет, тем больше отношение  , то есть тем больше основной прямоугольник растягивается в направлении оси
, то есть тем больше основной прямоугольник растягивается в направлении оси  , а гипербола отклоняется oт оси
, а гипербола отклоняется oт оси  ; чем ближе эксцентриситет к единице, тем больше основной прямоугольник растягивается в направлении оси
; чем ближе эксцентриситет к единице, тем больше основной прямоугольник растягивается в направлении оси  и гипербола приближается к этой оси.
и гипербола приближается к этой оси.
4°. Прямые . , где а – действительная полуось гиперболы, а
, где а – действительная полуось гиперболы, а  — ее эксцентриситет, называют директрисами гиперболы. Директрисы гиперболы имеют такое же свойство (8), как и директрисы эллипса.
— ее эксцентриситет, называют директрисами гиперболы. Директрисы гиперболы имеют такое же свойство (8), как и директрисы эллипса.
Пример №9
Составить каноническое уравнение гиперболы, фокусы которой расположены на оси  симметрично начала координат, действительная ось равна 6, а эксцентриситет
симметрично начала координат, действительная ось равна 6, а эксцентриситет  .
.
Решение:
Поскольку 2а = 6, то а= 3. Из формул (10) и (13) находим, что b = 4. Искомое уравнение имеет вид

Каноническое уравнение параболы
Параболой называется множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой, и не проходит через фокус.
Пусть заданы фокус  и директриса, причем расстояние между ними равно р. Возьмем прямоугольную систему координат
и директриса, причем расстояние между ними равно р. Возьмем прямоугольную систему координат  так, чтобы ось
так, чтобы ось  проходила через фокус, перпендикулярно к директрисе, а ось
проходила через фокус, перпендикулярно к директрисе, а ось  делила расстояние между фокусом
делила расстояние между фокусом  и директрисой пополам. Тогда фокус имеет координаты
и директрисой пополам. Тогда фокус имеет координаты  , а
, а  – уравнение директрисы. Пусть
– уравнение директрисы. Пусть  – произвольная точка плоскости, а отрезки МВ и MF расстояния от нее до директрисы и фокуса. Точка М тогда принадлежит параболе, когда MВ = MF (рис. 5).
– произвольная точка плоскости, а отрезки МВ и MF расстояния от нее до директрисы и фокуса. Точка М тогда принадлежит параболе, когда MВ = MF (рис. 5).
 Рис. 5. Парабола и ее свойства
Рис. 5. Парабола и ее свойства
Каноническое уравнение параболы имеет вид
 . (14)
. (14)
Ось симметрии параболы называется ее осью; точка пересечения оси с параболой – вершиной параболы; число, равное расстоянию от фокуса до директрисы, – параметром параболы. Осью параболы, заданной уравнением (14), является ось  , вершиной – точка
, вершиной – точка  (0; 0) и параметром – число р .
(0; 0) и параметром – число р .
Замечание. Используя свойство 4° эллипса и гиперболы и определение параболы, можно дать такое общее определение кривой второго порядка (кроме окружности): множество точек, для которых отношение  расстояния до фокуса и до соответствующей директрисы есть величина постоянная. Это эллипс при 0 <
расстояния до фокуса и до соответствующей директрисы есть величина постоянная. Это эллипс при 0 <  < 1, парабола при
< 1, парабола при  = 1 или гипербола при
= 1 или гипербола при  > 1.
> 1.
Пример №10
В параболу  вписан равносторонний треугольник так, что одна из вершин совпадает с вершиной параболы. Найти сторону треугольника и сделать рисунок.
вписан равносторонний треугольник так, что одна из вершин совпадает с вершиной параболы. Найти сторону треугольника и сделать рисунок.
Решение:
Пусть точка А( ) – одна из вершин треугольника. Тогда другими его вершинами будут точки
) – одна из вершин треугольника. Тогда другими его вершинами будут точки  и
и  (0; 0). Поскольку треугольник равносторонний, то АВ = АО= ВО, откуда
(0; 0). Поскольку треугольник равносторонний, то АВ = АО= ВО, откуда  . Решая это уравнение вместе с уравнением
. Решая это уравнение вместе с уравнением  , находим
, находим  . Поэтому сторона треугольника равна
. Поэтому сторона треугольника равна  .
.

Рис. 6 Иллюстрация к примеру 4.
Эта лекция взята из раздела о предмете высшая математика, там вы найдёте другие лекци по всем темам высшей математики:
Другие темы которые вам помогут понять высшую математику:
Кривые линии второго порядка
Кривая второго порядка — геометрическое место точек плоскости, прямоугольные координаты которых удовлетворяют уравнению вида.
Круг
Кругом называется геометрическое место точек плоскости, которые равноудалены от одной и той же точки этой плоскости (рис. 2.13).
Уравнение круга с центром  и радиусом
и радиусом  имеет вид:
имеет вид:  (2.16). В случае, когда центр круга находится в начале координат, уравнение имеет вид:
(2.16). В случае, когда центр круга находится в начале координат, уравнение имеет вид: 

Круг – уравнение второго порядка. Общее уравнение кривой второго порядка:  являет собой круг, если коэффициенты при квадратах координат равны между собой
являет собой круг, если коэффициенты при квадратах координат равны между собой  и если отделенный член с произведением координат
и если отделенный член с произведением координат  то есть
то есть 
Эллипс
Эллипсом называется геометрическое место точек, сумма расстояний которых к двум фиксированным точкам, что называются фокусами, является постоянными и равны  (рис. 2.14). Каноническое уравнение эллипса имеет вид:
(рис. 2.14). Каноническое уравнение эллипса имеет вид:

Координаты фокусов эллипса  и
и  Расстояние между фокусами равно
Расстояние между фокусами равно  Точки пересечения эллипса с осями координат
Точки пересечения эллипса с осями координат 
 и
и  – называются вершинами эллипса.
– называются вершинами эллипса.
Отрезки  – называются осями эллипса.
– называются осями эллипса.
Эксцентриситет эллипса 

Расстояние  и
и  точки
точки  эллипса к эго фокусам называются фокальными радиусами этой точки и обозначаются по формулам:
эллипса к эго фокусам называются фокальными радиусами этой точки и обозначаются по формулам:

Две прямые, которые параллельны к малой оси эллипса и находятся от нее на расстоянии  называются директрисами эллипса. Их уравнение:
называются директрисами эллипса. Их уравнение:
 или
или 
Уравнение эллипса с осями, что параллельные координатными осям, имеет вид:

где  – координаты центра эллипса.
– координаты центра эллипса.
Гипербола
Гиперболой называют геометрическое место точек, для каждой их которых абсолютное значение разницы расстояний от двух заданный точек, что называется фокусами, является величина постоянная и равна  (рис. 2.15). Каноничное уравнение гиперболы имеет вид:
(рис. 2.15). Каноничное уравнение гиперболы имеет вид:


Координаты фокусов гиперболы  и
и  Расстояние между фокусами равно
Расстояние между фокусами равно 
Точки пересечения гиперболы с осью абсцисс  называются действительными вершинами. Расстояние
называются действительными вершинами. Расстояние  называется действительной осью гиперболы.
называется действительной осью гиперболы.
Точки  называются мнимыми вершинами, а отрезок
называются мнимыми вершинами, а отрезок  – мнимой осью гиперболы.
– мнимой осью гиперболы.
Эксцентриситет гиперболы 
Расстояние  и
и  точки
точки  гиперболы к его фокусам называются фокальными радиусами этой точки и обозначаются формулами:
гиперболы к его фокусам называются фокальными радиусами этой точки и обозначаются формулами:

по условию, что точка  лежит на правой ветке гиперболы.
лежит на правой ветке гиперболы.
Две прямые, которые параллельны мнимой оси гиперболы и находятся от нее на расстоянии  называются директрисами гиперболы. Их уравнение:
называются директрисами гиперболы. Их уравнение:

Прямые, которые обозначаются уравнением:

называются асимптотами гиперболы.
Две гиперболы, что заданы уравнениями:

называются спряженными. Они имеют общие асимптоты.
Если оси гиперболы равны, то есть  то гипербола называется равнобедренной или равносторонней. Ее уравнение имеет вид:
то гипербола называется равнобедренной или равносторонней. Ее уравнение имеет вид:

Ее асимптотами служат биссектрисы координатных углов.
Если за оси координат принять асимптоты равносторонней гиперболы, то ее уравнение получит вид:  где
где 
Парабола
Параболой называется геометрическое место точек равноудаленных от заданной точки – фокуса и заданной прямой – директрисы (рис. 2.16).
Каноничное уравнение параболы имеет вид:

где  – расстояние от фокуса к директрисе. Вершина параболы находится в начале координат, осью симметрии является ось абсцисс.
– расстояние от фокуса к директрисе. Вершина параболы находится в начале координат, осью симметрии является ось абсцисс.

Координаты фокуса  Уравнение директрисы
Уравнение директрисы  имеет вид:
имеет вид:

Фокальный радиус  параболы равен
параболы равен 
Эксцентриситет параболы считается равным единице, то есть 
Если осью симметрии параболы служит ось ординат (рис. 2.17), то уравнение параболы имеет вид:

Уравнение директрисы в этом случае: 

Уравнение параболы с осью симметрии =, которая параллельна одной из координатных осей, имеет вид: 
или

где  – координаты вершин параболы.
– координаты вершин параболы.
Примеры решения задач:
Задача 2.51.
Сложить уравнение круга с центром в точке  и радиусам, что равны 6.
и радиусам, что равны 6.
Решение. В уравнении (2.16)  получим
получим 
 Сразу получим:
Сразу получим:

Задача 2.52
Обозначить центр и радиус угла, которое задано уравнением:
Решение. Как в заданном уравнении коэффициент при  и
и  равны между собой и отделенный член с произведением координат, то заданное уравнение является уравнением круга. Его необходимо привести к виду (2.16). Выпишем члены, которые содержат только
равны между собой и отделенный член с произведением координат, то заданное уравнение является уравнением круга. Его необходимо привести к виду (2.16). Выпишем члены, которые содержат только  и член, которые содержат только
и член, которые содержат только 
Выделим полный квадрат:

Левая часть заданного уравнения запишем так:

откуда: 
Уравнивая полученное уравнение с уравнением (2.16) приходим к выводу, что это уравнение обозначает круг, центр которого имеет координаты 
Задача 2.53
Сложить уравнение круга, что проходит через точки  и
и  если центр его лежит на прямой
если центр его лежит на прямой 
Решение. Каноническое уравнение круга:

Так как круг проходит через точки  и
и  то координаты этих точек должны удовлетворять уравнению круга. Отсюда имеет два уравнения:
то координаты этих точек должны удовлетворять уравнению круга. Отсюда имеет два уравнения:

если центр круга находится на прямой  то координаты центра должны удовлетворять уравнению прямой. Получим третье уравнение:
то координаты центра должны удовлетворять уравнению прямой. Получим третье уравнение: 
решим систему уравнений:

отнимем от первого уравнения второе.
Получим систему:

Получим:

подставим полученное значение  в уравнении
в уравнении  получим значение параметра
получим значение параметра 

Таким образом, координаты центра круга: 
Чтобы обозначить  воспользуется уравнением:
воспользуется уравнением:

Следует, уравнение круга:

Задача 2.54
Сложим уравнение круга, что проходит через три заданные точки:  и
и 
Решение. Искомое уравнение имеет вид  Так как круг проходит через заданные точки, то координаты каждой из этих точек удовлетворяют уравнению круга.
Так как круг проходит через заданные точки, то координаты каждой из этих точек удовлетворяют уравнению круга.
Подставим по очереди в искомое уравнение координаты заданных точек, получим три уравнения для определения  и
и 

От первого уравнения отнимем второе, а потом от первого уравнения отнимем третье. Получим систему двух уравнений с двумя неизвестными:

Откуда. 
Для нахождения  воспользуемся точкой
воспользуемся точкой  и уравнением:
и уравнением:

искомое уравнение круга имеет вид: 
Задача 2.55
Найти длину осей, координаты фокусов и эксцентриситет эллипса 
Решение. Приведем эти уравнения к каноничному виду (2.17):

Разделив обе части заданного уравнения на 144, получим:

отсюда получим, что  Следует,
Следует, 
 Зная
Зная  и
и  из соотношения
из соотношения  находим
находим 

Координаты фокусов будут:  и
и 
эксцентриситет эллипса 
Задача 2.56
Большая ось эллипса равно 8, а расстояние между директрисами равно 16. Найти уравнение эллипса. Чему равен его эксцентриситет?
Решение. Для нахождения уравнения эллипса необходимо найти его полуоси  и
и  По условию
По условию 
Полуось  находим из соотношения
находим из соотношения  а
а  можно найти, используя расстояние между директрисами
можно найти, используя расстояние между директрисами

Таким образом, 
Получим уравнение эллипса: 
Эксцентриситет эллипса будет 
Задача 2.57
Сложить уравнение гиперболы, фокусы которого находятся на оси абсцисс, симметрично началу координат, если задана точка  гиперболы и уравнения асимптот
гиперболы и уравнения асимптот 
Решение. Для нахождения уравнения гиперболы  необходимо найти ее полуось
необходимо найти ее полуось  и
и  Воспользуется условием: точка
Воспользуется условием: точка  находятся на гиперболе, а это означает, что координаты точки
находятся на гиперболе, а это означает, что координаты точки  должны удовлетворять уравнению гиперболы:
должны удовлетворять уравнению гиперболы:

Уравнение асимптот  а у нас получится
а у нас получится  следует,
следует, 
Получили систему уравнений:

Подставим полученные значения параметров в каноничное уравнение гиперболы:

Таким образом, получим искомое уравнение гиперболы:

Задача 2.58
Найти каноническое уравнение гиперболы, если угол между ее асимптотами равно  и расстояние между фокусами равны
и расстояние между фокусами равны 
Решение. Каноничное уравнение гиперболы имеет вид:

Уравнение асимптот  где
где  а
а  – угол наклона асимптоты к оси
– угол наклона асимптоты к оси 
Так как угол между асимптотами равен  , то
, то 
Отсюда, 
По условию задачи  то
то  Из соотношения
Из соотношения  получим второе уравнение:
получим второе уравнение: 
Решим систему уравнений:

Получим уравнение: 
Задача 2.59
Вычислить длину стороны правильного треугольника, который вписан в параболу 
Решение. Треугольник  размещенный симметрично относительно оси параболы. Одна из его вершин совпадает с вершиной параболы, а противоположная сторона – перпендикуляр к оси параболы (рис. 2.18).
размещенный симметрично относительно оси параболы. Одна из его вершин совпадает с вершиной параболы, а противоположная сторона – перпендикуляр к оси параболы (рис. 2.18).
По условию задачи  равносторонний. Угол
равносторонний. Угол  то
то  Пусть координаты точки
Пусть координаты точки  Из
Из  получим
получим  то есть
то есть 
Следует, точка  имеет координаты
имеет координаты 

Эта точка лежит на параболе, ее координаты удовлетворяют уравнению параболы. Отсюда:

тогда,

Длина сторон треугольника 
Общее уравнение кривой второго порядка: типы кривых
Кривой второго порядка называется линия, которая описывается уравнением

где  переменные – текущие координаты точек линии;
переменные – текущие координаты точек линии;
 заданные действительные числа – коэффициенты при переменных и свободный член
заданные действительные числа – коэффициенты при переменных и свободный член  ; при этом числа
; при этом числа  одновременно не могут равняться нулю:
одновременно не могут равняться нулю: 
Уравнение (8.1) называют общим уравнением линии 2-го порядка. При определенных условиях относительно значений коэффициентов при переменных и свободного члена оно описывает одну из четырех, знакомых со школы, кривых: круг, эллипс, гиперболу, параболу.
Однако может случиться, что не существует точек  с действительными координатами, которые бы удовлетворяли уравнения (8.1). В этом случае кривую 2-го порядка называют мнимой кривой. Например, уравнение
с действительными координатами, которые бы удовлетворяли уравнения (8.1). В этом случае кривую 2-го порядка называют мнимой кривой. Например, уравнение  , определяет воображаемое круг.
, определяет воображаемое круг.
Кроме того, имеют место случаи вырождения кривых 2-го порядка в прямые или точку. К примеру:
 уравнению удовлетворяют лишь координаты точки
уравнению удовлетворяют лишь координаты точки 
 уравнения параллельных или совпадающих прямых;
уравнения параллельных или совпадающих прямых;
 уравнения прямых, пересекающихся
уравнения прямых, пересекающихся 
Известно, что в зависимости от знака величины  уравнения (8.1) описывает один из трех типов линий второго порядка:
уравнения (8.1) описывает один из трех типов линий второго порядка:
1) эллиптический, если  уравнение (8.1) описывает эллипс (окружность при
уравнение (8.1) описывает эллипс (окружность при  и
и  ), кажущуюся кривую или кривую, вырождается в точку;
), кажущуюся кривую или кривую, вырождается в точку;
2) гиперболический, если  уравнение (8.1) описывает гиперболу или пару прямых, пересекающихся;
уравнение (8.1) описывает гиперболу или пару прямых, пересекающихся;
3) параболический, если  уравнение (8.1) описывает параболу, пару параллельных прямых или воображаемую кривую.
уравнение (8.1) описывает параболу, пару параллельных прямых или воображаемую кривую.
Канонические уравнения окружности и эллипса
Круг – это множество точек плоскости, расстояние от которых до одной фиксированной точки, называется центром, является величиной постоянной. Расстояние от центра круга до любой точки называют радиусом круга.
Каноническое уравнение окружности (7.2) было получено в примере к главе 7:

Если в уравнении (8.2) раскрыть скобки, получим общее уравнение кривой 2-го порядка при  и
и  , то есть уравнение
, то есть уравнение

которое называется общим уравнением круга.
Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух фиксированных точек (фокусов) является величиной постоянной. Пусть точка  является произвольной точкой эллипса (рис. 8.1), фокусы эллипса расположены на оси
является произвольной точкой эллипса (рис. 8.1), фокусы эллипса расположены на оси  и находятся в точках
и находятся в точках  , а сумма расстояний точек эллипса к фокусам
, а сумма расстояний точек эллипса к фокусам
равна  .
.

Рис. 8.1
Тогда согласно определению эллипса имеет место соотношение:  . Используя формулу расстояния между двумя точками, имеем:
. Используя формулу расстояния между двумя точками, имеем:

или

Далее избавляемся от иррациональности поднесением к квадрату обеих частей (8.4) и упрощаем:

или

Уравнение (8.5) называют каноническим уравнением эллипса.
Поскольку  (сумма двух сторон треугольника больше третьей стороны), поэтому обозначение
(сумма двух сторон треугольника больше третьей стороны), поэтому обозначение  – через
– через  является корректным.
является корректным.
Анализируя уравнение (8.5), делаем выводы:
1) точки эллипса не выходят за пределы прямоугольника, который описывается неровностями:  (рис. 8.2), что вытекает из развязанного относительно переменной
(рис. 8.2), что вытекает из развязанного относительно переменной  уравнения (8.5):
уравнения (8.5):


Рис. 8.2
2) эллипс является симметричным относительно осей координат, поскольку уравнение содержит только квадраты текущих координат  и
и  , поэтому координатные оси являются осями симметрии эллипса; ось симметрии, на которой лежат фокусы, называется фокальной осью; точку пересечения осей симметрии называют центром симметрии, или центром эллипса;
, поэтому координатные оси являются осями симметрии эллипса; ось симметрии, на которой лежат фокусы, называется фокальной осью; точку пересечения осей симметрии называют центром симметрии, или центром эллипса;
3) кривая пересекает координатные оси в точках – вершинах эллипса – с абсциссами  и с ординатами
и с ординатами  (рис. 8.2):
(рис. 8.2):  ,
,  отрезки
отрезки  и
и  , соединяющих противоположные вершины эллипса, а также их длины
, соединяющих противоположные вершины эллипса, а также их длины  и
и  , называют соответственно большой и малой осями эллипса; длины
, называют соответственно большой и малой осями эллипса; длины  и
и  – большой и малой полуосями.
– большой и малой полуосями.
Форма эллипса относительно оси  определяется отношением расстояния между фокусами
определяется отношением расстояния между фокусами  к большой оси
к большой оси  , которое называется эксцентриситетом эллипса
, которое называется эксцентриситетом эллипса  :
:

С помощью соотношения  эксцентриситет
эксцентриситет  легко подать через полуоси
легко подать через полуоси  и
и  :
:

Каноническое уравнение окружности  (см. (7.3)) является частным случаем канонического уравнения эллипса (8.5) при условии, что
(см. (7.3)) является частным случаем канонического уравнения эллипса (8.5) при условии, что  . Но если
. Но если  , то
, то  . То есть, эксцентриситет окружности равен нулю.
. То есть, эксцентриситет окружности равен нулю.
Если эксцентриситет эллипса  стремится к нулю (
стремится к нулю ( ), то по своей форме эллипс приближается к кругу; если же
), то по своей форме эллипс приближается к кругу; если же  приближается к единице (
приближается к единице ( ), то полуось эллипса
), то полуось эллипса  стремится к нулю, а эллипс – к вырождению в отрезок.
стремится к нулю, а эллипс – к вырождению в отрезок.
Известно, что планеты и кометы движутся по орбитам, имеющих форму эллипса. Орбиты планет близки к кругам, а орбиты комет – до вытянутых эллипсов (эксцентриситет орбиты Земли и кометы Галлея равны соответственно 0,02 и 0,97).
Прямые  , параллельные малой оси эллипса, называются директрисами эллипса.
, параллельные малой оси эллипса, называются директрисами эллипса.
Расстояния от произвольной точки эллипса до его фокусов называют локальными радиусами эллипса (рис. 8.1):

Фокальные радиусы связаны соотношением  (по определению эллипса), а их связь с эксцентриситетом описывается равенствами
(по определению эллипса), а их связь с эксцентриситетом описывается равенствами 
Замечания. Каноническое уравнение эллипса можно получить, выбирая фокусы на оси  , тогда будет большой полуось
, тогда будет большой полуось  .
.
Найдем уравнение эллипса  , который проходит через точку
, который проходит через точку  , а его эксцентриситет равен 0,8. Для этого необходимо определить параметры его уравнения.
, а его эксцентриситет равен 0,8. Для этого необходимо определить параметры его уравнения.
Поскольку точка  , то ее координаты удовлетворяют уравнениюе эллипса. Согласно условию зада
, то ее координаты удовлетворяют уравнениюе эллипса. Согласно условию зада
чи  , откуда
, откуда  . Таким образом, для нахождения параметров эллипса имеем систему уравнений:
. Таким образом, для нахождения параметров эллипса имеем систему уравнений:

Следовательно, уравнение эллипса имеет вид:

Каноническое уравнение гиперболы. Асимптоты гиперболы
Гиперболой называется множество точек плоскости, модуль разности расстояний которых до двух фиксированных точек, называемых фокусами, есть величиной постоянной, отличной от нуля.
Выберем оси координат таким образом, чтобы фокусы гиперболы  и
и  были расположены на оси
были расположены на оси  , а модуль разности расстояний от точек гиперболы до фокусов обозначим
, а модуль разности расстояний от точек гиперболы до фокусов обозначим 
Воспользуемся рисунком 8.1, на котором теперь  – произвольная точка гиперболы. Согласно определению
– произвольная точка гиперболы. Согласно определению  . Отсюда, применив формулу расстояния между двумя точками, получаем:
. Отсюда, применив формулу расстояния между двумя точками, получаем:

или

Выполняем преобразования, аналогичные тем, которые осуществлялись при выводе уравнения эллипса:

или

Уравнение (8.9) называется каноническим уравнением гиперболы.
Поскольку  (разница двух сторон треугольника всегда меньше третьей стороны), поэтому разница
(разница двух сторон треугольника всегда меньше третьей стороны), поэтому разница  – есть положительным числом, которое обозначили через
– есть положительным числом, которое обозначили через  .
.
Анализ полученного уравнения позволяет прийти к выводам:
1) точки гиперболы выходят (кроме двух) за пределы вертикальной полосы, которая описывается неравенством:  (рис. 8.3). Это следует из развязанного относительно переменной
(рис. 8.3). Это следует из развязанного относительно переменной  уравнения (8.9):
уравнения (8.9):

2) гипербола симметрична относительно осей координат, поскольку ее уравнение содержит только квадраты переменных  и
и  , поэтому координатные оси являются осями симметрии гиперболы; ось симметрии, на которой лежат фокусы, называется фокальной, или действительной осью; вторая – мнимой осью симметрии; точка пересечения осей симметрии является центром симметрии гиперболы, или центром гиперболы;
, поэтому координатные оси являются осями симметрии гиперболы; ось симметрии, на которой лежат фокусы, называется фокальной, или действительной осью; вторая – мнимой осью симметрии; точка пересечения осей симметрии является центром симметрии гиперболы, или центром гиперболы;
3) кривая пересекает ось  в точках – вершинах гиперболы – с абсциссами
в точках – вершинах гиперболы – с абсциссами 

 (рис. 8.3); с осью
(рис. 8.3); с осью  кривая общих точек не имеет; ось
кривая общих точек не имеет; ось  называется действительной, а вот
называется действительной, а вот  – мнимой осями гиперболы. Отрезок
– мнимой осями гиперболы. Отрезок  , соединяющий вершины гиперболы, принадлежит действительной оси
, соединяющий вершины гиперболы, принадлежит действительной оси  ; отрезок
; отрезок  принадлежит воображаемой оси гиперболы
принадлежит воображаемой оси гиперболы  .
.

Рис. 8.3
Прямоугольник со сторонами  и
и  и центром симметрии в начале координат называют основным прямоугольником гиперболы.
и центром симметрии в начале координат называют основным прямоугольником гиперболы.
Асимптотой гиперболы называется прямая, расстояние до которой от точек гиперболы стремится к нулю при неограниченном росте абсциссы  .
.
Асимптоты гиперболы описываются уравнениями прямых:

на которых лежат диагонали основного прямоугольника гиперболы.
Пусть  точка гиперболы, где
точка гиперболы, где  . Найдем расстояние от этой точки до асимптоты с уравнением
. Найдем расстояние от этой точки до асимптоты с уравнением  по формуле (7.26):
по формуле (7.26):

Поделим и умножим правую часть (8.11) на выражение, сопряженный к выражению под знаком модуля, то есть на выражение  , тогда получим:
, тогда получим:

При неограниченном росте  знаменатель дроби неограниченно увеличивается, а самый дробь уменьшается и приближается к нулю.
знаменатель дроби неограниченно увеличивается, а самый дробь уменьшается и приближается к нулю.
Аналогично можно показать, что прямая  также является асимптотой гиперболы.
также является асимптотой гиперболы.
Согласно определению асимптот гиперболы ее геометрическое изображение начинают с построения основного прямоугольника и его диагоналей.
Части графика кривой при  и
и  называют ветвями гиперболы.
называют ветвями гиперболы.
Как и для эллипса, форму гиперболы характеризует отношение фокусного расстояния  к действительной оси
к действительной оси  , как и для эллипса, такое отношение называется эксцентриситетом:
, как и для эллипса, такое отношение называется эксцентриситетом:

Прямые  , параллельные мнимой оси гиперболы, называются директрисами гиперболы.
, параллельные мнимой оси гиперболы, называются директрисами гиперболы.
Расстояния от произвольной точки гиперболы до ее фокусов называют фокальными радиусами гиперболы:

Фокальные радиусы связаны соотношением  (по определению гиперболы), а их связь с эксцентриситетом описывается равенствами
(по определению гиперболы), а их связь с эксцентриситетом описывается равенствами  ,
,  , где знак
, где знак  соответствует правой (левой) ветви гиперболы.
соответствует правой (левой) ветви гиперболы.
Примечание:
1) каноническое уравнение гиперболы в случае расположения ее фокусов на оси  имеет вид:
имеет вид:

тогда действительной осью гиперболы является  , а мнимой –
, а мнимой –  .
.
Кривые, описываемые уравнениями (8.9) и (8.14), называются взаимно сопряженными гиперболами;
2) если в уравнениях (8.9) и (8.14)  , то получим:
, то получим:
 или
или 
Кривые, описываемые уравнениями (8.15), называются равносторонними гиперболами.
Пусть задано общее уравнение гиперболы:  .
.
Найдем ее параметры и определим координаты вершин.
Запишем уравнение гиперболы в канонической форме: 
Отсюда имеем: и
и  , тогда
, тогда  полуоси гиперболы, а вершины гиперболы имеют координаты:
полуоси гиперболы, а вершины гиперболы имеют координаты: 
Парабола. Каноническое уравнение
Параболой называется множество точек плоскости, равноудаленных от фиксированной точки (фокуса) и фиксированной прямой (директрисы).
Выберем на плоскости систему координат  (рис. 8.4). Обозначим расстояние от фокуса параболы
(рис. 8.4). Обозначим расстояние от фокуса параболы  до директрисы
до директрисы  через
через 
 . Найдем уравнение параболы с фокусом в точке
. Найдем уравнение параболы с фокусом в точке  , и директрисой, параллельной оси
, и директрисой, параллельной оси  , с уравнением
, с уравнением 

Рис. 8.4
Пусть  произвольная точка параболы. Тогда согласно определению параболы
произвольная точка параболы. Тогда согласно определению параболы  . По формуле расстояния между двумя точками имеем:
. По формуле расстояния между двумя точками имеем:

или

Уравнение (8.16) называется каноническим уравнением параболы.
Число  – расстояние от фокуса до директрисы – называют параметром параболы.
– расстояние от фокуса до директрисы – называют параметром параболы.
Анализ уравнения (8.16) позволяет прийти к выводам:
1) парабола симметрична относительно оси  , потому переменная
, потому переменная  входит в
входит в
уравнения в второй степени; ось симметрии ( ) называют осью параболы (рис. 8.5 а) переменная
) называют осью параболы (рис. 8.5 а) переменная  не может быть отрицательной
не может быть отрицательной  ; точка
; точка  , принадлежащей кривой и является точкой пересечения параболы с ее осью, называется вершиной параболы;
, принадлежащей кривой и является точкой пересечения параболы с ее осью, называется вершиной параболы;
2) при росте  по модулю от
по модулю от  до
до  переменная y неограниченно растет по закону
переменная y неограниченно растет по закону  . Если
. Если  , то получаем уравнение параболы
, то получаем уравнение параболы  , которое известно еще из школьного курса математики.
, которое известно еще из школьного курса математики.
Парабола с фокусом в точке  и директрисой
и директрисой  (Рис. 8.5 в) описывается уравнением:
(Рис. 8.5 в) описывается уравнением:


Рис. 8.5
Задачи на составление канонических уравнений параболы сводятся к отысканию только одной величины – параметра 
Составим каноническое уравнение параболы, проходящей через точку  , а ее осью является ось
, а ее осью является ось  .
.
Поскольку точка  лежит в четвертом квадранте и осью симметрии параболы является ось
лежит в четвертом квадранте и осью симметрии параболы является ось  , то соответствующее уравнение имеет вид:
, то соответствующее уравнение имеет вид:  . Подставляем координаты заданной точки в уравнение и находим значение p, при котором оно удовлетворяется:
. Подставляем координаты заданной точки в уравнение и находим значение p, при котором оно удовлетворяется:
 или
или 
Уравнение  и
и  определяют ветви параболы. Кривые круга, эллипс и гипербола называются центральными кривыми второго порядка, а парабола – нецентральной; ее эксцентриситетом считается отношение фокального радиуса
определяют ветви параболы. Кривые круга, эллипс и гипербола называются центральными кривыми второго порядка, а парабола – нецентральной; ее эксцентриситетом считается отношение фокального радиуса  произвольной точки
произвольной точки  параболы до расстояния
параболы до расстояния  (рис. 8.4) от этой точки до директрисы, то есть
(рис. 8.4) от этой точки до директрисы, то есть  .
.
Задача вывода уравнений кривых 2-го порядка усложняется, если центр центральных кривых лежит не в начале координат и (или) оси симметрии не является координатными осями; а для нецентральных кривых – если фокус не лежит на координатной оси и (или) директриса не ортогональная одной из осей координат.
Для установления положение на плоскости кривых 2-го порядка, которые описываются общим уравнением, путем параллельного переноса и (или) поворота исходной системы координат переходят к такой системе координат, в которой общее уравнение приобретает каноническому виду.
Возведение общего уравнения кривой второго порядка к каноническому виду
Выберем на плоскости две системы координат, тогда координаты той же точки в этих системах будут разными.
Задача преобразования координат заключается в том, чтобы найти связь между координатами точек в двух системах координат, одну из которых назовем выходной, вторую – новой. Любую новую систему координат  (рис. 8.6) можно получить из исходной системы
(рис. 8.6) можно получить из исходной системы  параллельным переносом, то есть перемещением начала координат в точку
параллельным переносом, то есть перемещением начала координат в точку  с сохранением направления осей (что дает систему координат
с сохранением направления осей (что дает систему координат  ), а затем поворотом системы
), а затем поворотом системы  на определенный угол
на определенный угол  вокруг точки
вокруг точки  .
.

Рис. 8.6
Параллельный перенос. Выберем на плоскости произвольную точку  . Пусть
. Пусть  – исходная,
– исходная,  – новая система координат (рис. 8.7) с началом в точке
– новая система координат (рис. 8.7) с началом в точке  . Тогда пара
. Тогда пара  определяет координаты точки
определяет координаты точки  в исходной системе координат, а
в исходной системе координат, а  – координаты этой же точки
– координаты этой же точки  в новой системе координат.
в новой системе координат.

Рис. 8.7
Введем в рассмотрение радиусы-векторы 

Вектор  является разницей векторов
является разницей векторов  и
и  что позволяет определить связь между координатами точки в системах координат:
что позволяет определить связь между координатами точки в системах координат:

Соотношения (8.17) называются формулами параллельного переноса.
Поворот осей координат. Установим связь между координатами произвольной точки  плоскости в системах с общим началом и различным направлением осей координат. Пусть
плоскости в системах с общим началом и различным направлением осей координат. Пусть  – исходная, а
– исходная, а  – новая системы координат (рис. 8.8), тогда пара (
– новая системы координат (рис. 8.8), тогда пара ( определяет координаты точки
определяет координаты точки  в исходной системе координат, а
в исходной системе координат, а  – координаты этой же точки в новой системе координат.
– координаты этой же точки в новой системе координат.

Рис. 8.8
Обозначим через  угол поворота исходной системы вокруг точки
угол поворота исходной системы вокруг точки  . Найдем направляющие косинусы новых осей
. Найдем направляющие косинусы новых осей  и
и  в исходной системе, или, что то же самое, координаты единичных векторов
в исходной системе, или, что то же самое, координаты единичных векторов  и
и  новой системы координат в системе
новой системы координат в системе  :
:

Найдем проекции вектора  на новые оси координат как скалярные произведения этого вектора на направляющие векторы
на новые оси координат как скалярные произведения этого вектора на направляющие векторы  и
и  соответственно:
соответственно:

Соотношение (8.18) называют формулами поворота осей координат.
Если осуществляется параллельный перенос и поворот осей координат, то исходные координаты  , можно определить через новые
, можно определить через новые  следующим образом:
следующим образом:

Найдем уравнение равносторонней гиперболы  в системе координат, которая полученная из исходной системы поворотом вокруг начала координат на угол
в системе координат, которая полученная из исходной системы поворотом вокруг начала координат на угол  .
.
По формуле (8.18) выражаем текущие координаты точек исходной системы через текущие координаты новой системы:

Подставляем выражения для  и
и  в исходное уравнение и получаем уравнение гиперболы в новых координатах, асимптотами которой является оси новой системы
в исходное уравнение и получаем уравнение гиперболы в новых координатах, асимптотами которой является оси новой системы  :
:

Рассмотрим применение формул параллельного переноса и поворота осей координат до сведения общего уравнения кривой 2-го порядка к каноническому виду.
1. Сведение к каноническому виду общего уравнения, не содержит произведения переменных 

Преобразование уравнения (8.20) в уравнение каноническому виду осуществляется с помощью параллельного переноса системы координат, которому предшествует выделение полных квадратов по обоим переменным.
Пусть задано общее уравнение кривой: 
 Определим тип этой кривой и ее параметры. Решение задачи предполагает следующие этапы:
Определим тип этой кривой и ее параметры. Решение задачи предполагает следующие этапы:
а) устанавливаем тип заданной кривой 

 уравнение описывает кривую гиперболического типа;
уравнение описывает кривую гиперболического типа;
б) группируем в левой части уравнения члены с переменными  ,
,  и выделяем полные квадраты двучлена с этими переменными:
и выделяем полные квадраты двучлена с этими переменными:

в) вводим новые координаты:  и записываем каноническое уравнение в новой системе с началом в точке
и записываем каноническое уравнение в новой системе с началом в точке 

Итак, заданная кривая 2-го порядка является гиперболой с полуосями:  и центром в точке
и центром в точке 
2. Возведение общего уравнения кривой к каноническому виду.

Преобразование этого уравнения в уравнение каноническому виду осуществляется в два этапа:
1-й этап. С помощью поворота осей координат сводим общее уравнение к уравнению (8.20), которое не содержит произведения переменных. Соответствующий угол поворота осей  определяется соотношением (выводить его не будем):
определяется соотношением (выводить его не будем):

откуда по формулам тригонометрии имеем:

где знак выбирается в зависимости от того, в какой четверти находится угол  .
.
По формуле (8.18) выражаем текущие координаты точек исходной системы через текущие координаты новой системы:

что дает возможность получить уравнения относительно переменных  и
и  , которое не содержит их произведения.
, которое не содержит их произведения.
2-й этап. С помощью параллельного переноса осей координат превращаем уравнение, которое было получено на первом этапе, на уравнение канонического виду.
Замечания. Преобразование общего уравнения кривой 2-го порядка можно начинать с параллельного переноса осей с целью избавиться членов, содержащих переменные в первой степени. В этом случае получают квадратичную форму, которую приводят к каноническому виду известными методами, например, методами Лагранжа, Якоби, Сильвестра. Кроме того применяют аппарат приведения матрицы коэффициентов квадратичной формы к диагональному виду с помощью собственных чисел и собственных векторов этой матрицы. Данные методы являются достаточно громоздкими и выходят за рамки данного учебника.
Приведем еще один пример применения параллельного переноса осей.
Проведем исследование кривой 2-го порядка, заданной общим уравнением:

Это уравнение можно представить в виде дробно линейной функции:

Поделим числитель на знаменатель дроби (8.24), то есть выделяем целую часть дроби, а именно:

Обозначим:

Уравнение (8.25) в новой системе координат приобретает следующий вид:

Следовательно, графиком дробно-линейной функции является гипербола с асимптотами, параллельными осям координат, и центром симметрии в точке 
Квадратичные формы. Применение к превращению уравнений кривой 2-го порядка
Пусть  переменные величины. Квадратичной формой
переменные величины. Квадратичной формой  называется однородный многочлен второй степени относительно переменных
называется однородный многочлен второй степени относительно переменных 

где  коэффициенты при переменных (числовые параметры).
коэффициенты при переменных (числовые параметры).
Квадратичная форма  , в которой a
, в которой a  , называется симметричной:
, называется симметричной:

Квадратичная форма  , которая содержит только квадраты переменных, называется канонической (или говорят: имеет канонический вид):
, которая содержит только квадраты переменных, называется канонической (или говорят: имеет канонический вид):

Матрица  составленная из числовых параметров
составленная из числовых параметров  называется матрицей квадратичной формы, a матрица-столбец
называется матрицей квадратичной формы, a матрица-столбец  вектором переменных.
вектором переменных.
Теорема 8.1 (о матричной записи квадратичной формы). Любую квадратичную форму можно представить в матричном виде как произведение двух линейных преобразований, первое из которых тождественно  , а матрицей второго есть матрица
, а матрицей второго есть матрица  квадратичной формы:
квадратичной формы: 
Доказательство. С помощью тождественных алгебраических преобразований получаем:

Теорема обобщается на квадратичные формы относительно любого конечного числа переменных:

При  переменные обозначают буквами без индексов:
переменные обозначают буквами без индексов:  .
.
Теорема 8.2 (о сведении симметричной квадратичной формы к каноническому виду). Если вектор переменных  является линейной комбинацией векторов ортонормированного базиса
является линейной комбинацией векторов ортонормированного базиса  , составленного из собственных векторов матрицы
, составленного из собственных векторов матрицы  , то симметричная квадратичная форма приобретает каноническому виду:
, то симметричная квадратичная форма приобретает каноническому виду:

где  – коэффициенты разложения вектора
– коэффициенты разложения вектора  по базису
по базису 
 собственные числа матрицы симметричной квадратичной формы.
собственные числа матрицы симметричной квадратичной формы.
Доказательство. Подставим в матричный запись квадратичной формы вместо  его выражение через базис из собственных векторов
его выражение через базис из собственных векторов  и
и  матрицы
матрицы  , и раскроем скобки в соответствии со свойствами линейного оператора:
, и раскроем скобки в соответствии со свойствами линейного оператора:

После перехода к ортонормированному базису с учетом свойств: 
 , получаем (8.29).
, получаем (8.29).
Если по теореме 8.2 сводить к каноническому виду уравнение кривых второго порядка, то в зависимости от того, каким будет определитель матрицы квадратичной формы  сравнению с нулем, возможны следующие случаи:
сравнению с нулем, возможны следующие случаи:
 кривая эллиптического типа;
кривая эллиптического типа;
 кривая гиперболического типа;
кривая гиперболического типа; 
 кривая параболического типа.
кривая параболического типа.
Покажем справедливость третьего соотношения:
Пусть,  тогда
тогда 
Найдем собственные числа:

В новом (ортонормированном) базисе уравнением кривой будет квадрат только одной переменной, а значит соответствующая линия является кривой параболического типа.
Аналогично доводятся другие случаи, когда каноническая форма (8.29) содержит слагаемые соответствии с одинаковыми или разными знаками.
Для использования квадратичных форм с целью упрощения уравнений кривых второго порядка коэффициенты при переменных обозначают строчными буквами с индексами:

Сведем к канонической форме общее уравнение кривой

где 
В данном уравнении  для свободного члена
для свободного члена  предлагается рассмотреть три значения.
предлагается рассмотреть три значения.
а)  . Осуществим параллельный перенос так, чтобы в новой системе координат уравнение не имело переменных в первой степени. Для этого переходим к новым координатам:
. Осуществим параллельный перенос так, чтобы в новой системе координат уравнение не имело переменных в первой степени. Для этого переходим к новым координатам:

решаем систему двух линейных уравнений:

определяя таким образом начало новой координатной системы  :
:

В системе  кривая описывается уравнением
кривая описывается уравнением

которое в левой части содержит квадратичную форму относительно переменных 
Находим собственные числа матрицы этой квадратичной формы:

Поскольку  , то кривая эллиптического типа.
, то кривая эллиптического типа.
Определяем собственные векторы, принадлежащие каждому собственному числу:

Векторы  и
и  составляют ортогональный базис новой системы координат
составляют ортогональный базис новой системы координат  .
.
Переходим от полученного базиса к ортонормированному:

в котором каноническая форма заданного уравнения имеет вид:
 и описывает воображаемый эллипс.
и описывает воображаемый эллипс.
 В системе
В системе  исходное уравнение принимает вид:
исходное уравнение принимает вид:

Следовательно, имеем случай вырождения кривой в точку.
 Каноническая форма заданного уравнения в новой системе такова:
Каноническая форма заданного уравнения в новой системе такова:

то есть кривой является эллипс с параметрами 
Замечания. Для кривых параболического типа упрощения уравнения начинают, как правило, с поворота осей координат.
В заключение отметим, что существуют величины, составленные из коэффициентов уравнения (и свободного члена), которые не изменяются при переходе от одной прямоугольной декартовой системы координат к другой такой же системы. Эти величины называются инвариантами кривой второго порядка. К ним относятся:
1) сумма коэффициентов при квадратах координат: 
2) определитель, образованный из коэффициентов при старших членах:

3) определитель, составленный из параметров уравнения:

По значениям инвариантов, возведенными в табл. 8.1, устанавливают не только тип кривой, но и возможные случаи ее вырождения.
Инварианты кривой второго порядка и распознавания за ними типа кривой Таблица 8.1

Установим, вырожденная ли линия второго порядка, заданная уравнением:

Вычисляем инварианты кривой и анализируем результаты:

Согласно табл. 8.1 кривая гиперболического типа, распадается на две прямые, пересекающиеся: 
Лекции:
- Линейные дифференциальные уравнения
- Теорема Муавра Лапласа
- Вычислить двойной интеграл
- Формула Ньютона-Лейбница
- Найти первую и вторую производные функции
- Признаки сходимости рядов
- Цилиндр
- Условный экстремум
- Коэффициент вариации
- Функция плотности распределения
