Примечание: дробные числа записывайте
через точку, а не запятую.
Округлять до -го знака после запятой.
Образцы выполнения некоторых заданий
Рассмотрим решения некоторых практических упражнений.
Задание 2(е)
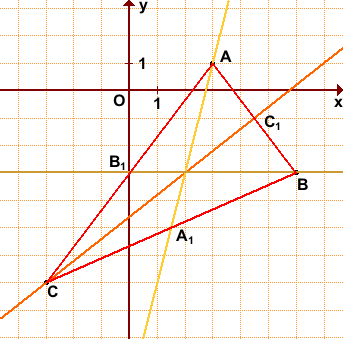
На плоскости даны точки А(11; -5), В(6;7), С(-10; -5). Найти уравнение биссектрисы угла А.
Решение задания 2(е)
Найдем направляющий вектор биссектрисы как сумму ортов векторов и
,
или (умножая на )
.
; ;
; .
.
Таким образом, в качестве направляющего вектора биссектрисы угла А можно взять вектор и уравнение биссектрисы будет иметь вид
.
Задание 3
Дана точка (0;2) пересечения медиан треугольника и уравнения двух его сторон 5х – 4у + 15 = 0 и 4х + у – 9 = 0. Найти координаты вершин треугольника и уравнение третьей стороны.
Решение Координаты одной вершины найдем как координаты точки пересечения данных сторон, для чего решим систему уравнений
Получаем или
Точка Оц пересечения медиан треугольника называется его центром. Отметим одно свойство центра треугольника, которое используем для нахождения координат остальных вершин:
; ,
где хц, уц – координаты центра треугольника;
хi, yi – координаты i-ой вершины треугольника,
Для доказательства этих формул рассмотрим треугольник А1А2А3, где Аi(xi;yi), i = 1-3 (см.рис.2.1).
Рис.2.1. Вспомогательный чертеж к заданию 3
Пусть В середина стороны А1А2. Тогда А3В – медиана треугольника А1А2А3. По известному из элементарной геометрии свойству медиан треугольника .
Тогда координаты точки В найдем по формулам
и ,
а координаты центра Оц из векторного соотношения , которое в координатной форме записывается так
, .
Отсюда, выражая хц и уц через xi, yi, получим требуемые формулы.
Вернемся к решению задания 3. Используя доказанные формулы, полагая в них х1 = 1 и у1 = 5, хц = 0 и уц = 2, получим два уравнения, которым должны удовлетворять координаты остальных двух вершин
; ,
Еще два уравнения получим, если потребуем, чтобы искомые точки, вершины треугольника, принадлежали заданным сторонам, т.е. их координаты удовлетворяли уравнениям этих сторон
Итак, для определения четырех неизвестных х2, у2, х3, у3, мы имеем четыре независимых (!) условия (уравнения)
Решив эту систему, получим х2 = -3, у2 = 0, х2= 2, у3 = 1.
Наконец, уравнение третьей стороны запишем как уравнение прямой, проходящей через две заданные точки (-3;0) и (2;1)
или .
Итак, уравнение третьей стороны x – 5у + 3 = 0, а вершины треугольника имеют координаты (1;5), (-3;0), (2;1).
Задание 7
Составить уравнение линии, для каждой точки М которой, отношение расстояний до точки F( ) и до прямой
равно .
Привести уравнение линии к каноническому виду, определить тип линии и построить линию на чертеже. Показать на чертеже фокусы, директрисы, асимптоты (если они имеются у построенной линии).
Замечание. Отметим, что в заданиях этого модуля ; ; .
Пусть n = 101. Тогда:
, т.к. ;
, т.к. ;
, т.к. .
Итак, для n = 101 первая часть задания 7 принимает вид:
Составить уравнение линии, для каждой точки М которой, отношение расстояния до точки F(-4;1) и до прямой x = 1
равно .
Решение задания 7 (для n = 101).
Пусть М(х;у) произвольная точка искомой линии, r – расстояние от М до F и d – расстояние от точки М до прямой x = 1. Тогда
и .
По условию , т.е. d = 2r.
– уравнение искомой линии.
Упростим уравнение линии и приведем его к каноническому виду. Для этого возведем обе части уравнения в квадрат и выполним следующие преобразования уравнения
х 2 – 2х +1 = 4х 2 + 32х + 64 + 4(у – 1) 2 ,
3х 2 + 34х + 4(у – 1) 2 + 63 = 0,
,
.
Последнее уравнение – это каноническое уравнение эллипса с полуосями и ( ), центр которого находится в точке с координатами . Координаты вершин эллипса
и , т.е. (-9;1), , ,
. Построим эллипс на чертеже (см.рис.2.2).
Рис.2.2. Эллипс с уравнением
Фокусы эллипса имеют координаты , где .
.
Итак, координаты фокусов F1(-4;1), F2( ;1).
Директрисы эллипса имеют уравнения , где е – эксцентриситет эллипса
.
Уравнения директрис , т.е.
D2: .
Отметим фокусы и директрисы эллипса на рис.2.2.
Обратите внимание на совпадение фокуса F1 с точкой, данной в условии задания 7, на совпадение директрисы D1 с прямой х = 1 из условия этого задания, и совпадение эксцентриситета е с параметром е в условии. По этому поводу см. теоретическое упражнение 18.
В пространстве даны точки А(-2; -4;1), В(3;1; -1), С(5;1;1),
S(1;-4;0). Найти координаты центра и радиус вписанной в пирамиду SABC сферы (условие сформулировано для n = 101).
Решение задания 4(м)
Пусть точка О(x0;y0;z0) – центр сферы, вписанной в пирамиду SABC. Найдем точку О как точку, равноудаленную от граней пирамиды. Для этого найдем уравнения всех граней и расстояния от точки О до этих граней (уравнения некоторых граней находятся в предшествующих пункту М пунктах задания 4).
Грань АВС. Уравнение грани
или 5х – 7у – 5z – 13 = 0.
Точки О и S лежат по одну сторону от грани АВС, поэтому отклонения этих точек от грани АВС имеют одинаковые знаки. Отклонение (S) точки S от грани АВС равно
> 0.
.
Аналогично все делается для граней ABS, BCS, CAS.
Грань ABS имеет уравнение 5х + у + 15z – 1 = 0 и
.
Грань BCS имеет уравнение 5х – 3у – 5z – 17 = 0 и
.
Наконец, грань CAS имеет уравнение 5х – 7у + 15z + 33 = 0 и
.
Так как О – центр сферы, вписанной в пирамиду SABC, то
d(O; ABC) = d(O; ABS) = d(O; BCS) = d(O; CAS) = r,
где r – радиус вписанной сферы.
Тогда координаты точки О должны удовлетворять системе
В отличие от других заданий этого модуля, коэффициенты и решение этой системы найдем приближенно, с помощью микрокалькулятора или ЭВМ. Получим систему
и уравнение вписанной сферы
.
1. Общее уравнение прямой на плоскости. Нормальный вектор прямой. Угол между прямыми. Условия параллельности и перпендикулярности.
2. Уравнение прямой с угловым коэффициентом. Угол между прямыми. Условия параллельности и перпендикулярности.
3. Каноническое и параметрическое уравнения прямой на плоскости. Направляющий вектор прямой. Угол между прямыми. Условия параллельности и перпендикулярности.
4. Уравнение прямой, проходящей через две заданные точки.
5. Уравнения прямых, проходящих через данную точку параллельно и перпендикулярно данной прямой (3 случая задания данной прямой: общим уравнением, каноническим уравнением, уравнением с угловым коэффициентом).
6. Общее уравнение плоскости в пространстве, нормальный вектор плоскости. Угол между плоскостями. Условие параллельности и перпендикулярности.
7. Уравнение плоскости, проходящей через три данные точки, не лежащие на одной прямой.
8. Общее, каноническое и параметрическое уравнения прямой в пространстве. Угол между прямыми. Условия параллельности и перпендикулярности.
9. Угол между прямой и плоскостью в пространстве. Условие параллельности и перпендикулярности прямой и плоскости.
10. Уравнение плоскости, проходящей через данную точку, перпендикулярно данной прямой. Уравнение прямой, проходящей через данную точку, перпендикулярно данной плоскости.
11. Расстояние от точки до: прямой на плоскости; прямой в пространстве; плоскости в пространстве.
12. Уравнение линии на плоскости. Общее уравнение кривой второго порядка.
13. Каноническое и параметрическое уравнения окружности.
14. Эллипс (фокусы и директрисы, фокальные радиусы точки, эксцентриситет). Каноническое и параметрическое уравнения эллипса.
15. Гипербола (фокусы, директрисы и асимптоты, фокальные радиусы точки, эксцентриситет). Каноническое и параметрическое уравнения гиперболы.
16. Парабола (фокус и директриса, фокальный радиус точки, эксцентриситет). Каноническое уравнение параболы.
17. Приведение общего уравнения кривой второго порядка к каноническому виду.
18. Полярные координаты на плоскости. Уравнение линии в полярных координатах.
19. Уравнение поверхности в пространстве. Общее уравнение поверхностей второго порядка.
20. Основные типы поверхностей второго порядка и их канонические уравнения.
1. Бугров Н.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. – М.: Наука, 1980. 176 с.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.1: Учебное пособие для студентов втузов. – 3-е изд., перераб. и доп. – М.: Высшая школа, 1980. 320 с.
3. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. – М.: Наука, 1981. 232 с.
4. Клетеник Д.В. Сборник задач по аналитической геометрии. – М.: Наука, 1980. 240 с.
5. Сборник задач по математике для втузов. Линейная алгебра и основы математического анализа/Под ред. А.В. Ефимова, Б.П. Демидович. – М.: Наука, 1981, 464 с.
6. Высшая математика. Методические указания и контрольные задания/Под ред. Ю.С. Арутюнова. – М.: Высшая школа, 1985.
7. Гусак А.А. Пособие к решению задач по высшей математике. – Изд. 3-е. – Минск: Изд-во БГУ, 1973. 532 с.
8. Кузнецов А.А. Сборник заданий по высшей математике (типовые расчеты): Учеб. пособие для втузов. – М.: Высшая школа, 1983. 175 с.
9. Погорелов А.В.Аналитическая геометрия.– М.:Наука, 1968. 176с
[spoiler title=”источники:”]
http://mathhelpplanet.com/static.php?p=onlain-reshit-treugolnik
http://poisk-ru.ru/s5347t9.html
[/spoiler]
Как составить уравнение медианы треугольника по координатам его вершин?
Медиана соединяет вершину треугольника с серединой противолежащей стороны. Следовательно, при решении задачи составления уравнения медианы нужно:
- Найти координаты середины отрезка по координатам его концов.
- Составить уравнение прямой, проходящей через две точки: найденную середину отрезка и противолежащую вершину.
Пример.
Дано: ΔABC, A(3;1), B(6;-3), C(-3;-7).
Найти уравнения медиан треугольника.
Решение:
Обозначим середины сторон BC, AC, AB через A1, B1, C1.
1) По формулам координат середины отрезка
Уравнение медианы AA1 будем искать в виде y=kx+b.
Найдём уравнение прямой, проходящей через точки A(3;1) и A1(1,5;-5). Составляем и решаем систему уравнений:
Отсюда k= 4; b= -11.
Уравнение медианы AA1: y=4x-11.
2) Аналогично, координаты точки B1 — середины отрезка AC
Можно в уравнение y=kx+b подставить координаты точек B(6;-3) и B1(0;-3) и найти k и b. Но так как ординаты обеих точек равны, уравнение медианы BB1 можно найти ещё быстрее: y= -3.
3) Координаты точки C1 — середины отрезка BC:
C(-3;-7), C(4,5;-1), y=kx+b:
Отсюда уравнение медианы CC1 : y=0,8x-4,6.
уравнения прямой, проходящей через точку М1(2; 0; -3) параллельно:
5};
канонические уравнения прямой, проходящей через
данные точки:
параметрические уравнения прямой, проходящей
через точку М1(1; -1; -3) параллельно:
4};
параметрические уравнения прямой, проходящей
через данные точки:
-6; 1) проведена прямая. Определить
точки пересечения этой прямой с координатными
плоскостями.
1012
треугольника А(3; 6; -7), В(-5; 2; 3), С(4; -7; -2). Составить
параметрические уравнения его медианы,
проведенной из вершины С.
треугольника А(3; -1; -1), В(1; 2; -7), С(-5; 14; -3). Составить
канонические уравнения биссектрисы его
внутреннего угла при вершине С.
треугольника А(2; -1; -3), В(5; 2; -7), С(-7; 11; 6). Составить
канонические уравнения биссектрисы его внешнего
угла при вершине А.
треугольника А(1; -2; -4), В(3; 1; -3), С(5; 1; -7). Составить
параметрические уравнения его высоты,
опущенного из вершины В на противоположную
сторону.
проекции какого-нибудь ее направляющего вектора
а на координатные оси. Найти общее выражение
проекций произвольного направляющего вектора
этой прямой на координатные оси.
разложение какого-нибудь ее направляющего
вектора а по базису i, j, k. Выразить в общем виде
разложение произвольного направляющего вектора
этой прямой по базису i, j, k.
канонические уравнения прямой, проходящей через
точку М1(2; 3; -5) параллельно
прямой
канонические уравнения следующих прямых:
параметрические уравнения следующих прямых:
параллельность прямых:
перпендикулярность прямых:
угол между прямыми
угол между прямыми
косинус угла между прямыми
прямые, заданные параметрическими уравнениями
каком значении l они пересекаются?
Доказать,
что условие, при котором две прямые и
лежат в одной плоскости, может быть
представлено в следующем виде:
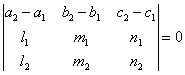
уравнения прямой, которая проходит через точку М1(-1;
2; -3) перпендикулярно к вектору a={6;
-2; -3} и пересекает прямую
уравнения прямой, которая проходит через точку
М(-4; -5; 3) и пересекает две прямые
1031
параметрические уравнения общего
перпендикуляра двух прямых, заданных
уравнениями
уравнения движения точки М(x; y; z):
уравнения движения точки М(x; y; z):
пройдет эта точка за промежуток времени от t1=0
до t2=7.
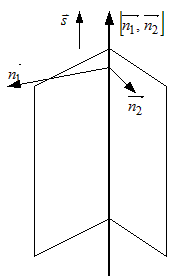
уравнения движения точки М(x; y; z), которая, имея
начальное положение М0(3; -1; -5), движется прямолинейно и равномерно
в направлении вектора s={-2; 6; 3} со скоростью v=21.
уравнения движения точки М(x; y; z), которая,
двигаясь прямолинейно и равномерно, прошла
расстояние от точки М1(-7; 12; 5) до точки М2(9; -4; -3) за промежуток времени от t1=0
до t2=4.
движется прямолинейно и равномерно из
начального положения М0(20; -18; -32)
в направлении, противоположном
вектору s={3; -4; -12}, со скоростью v=26. Составить
уравнения движения точки М и определить точку, с
которой она совпадает в момент времени t=3.
и N(x, y, z) движутся прямолинейно и равномерно:
первая из начального положения М0(-5;
4; -5) со скоростью vM=14 в направлении вектора s={3; -6; 2}, вторая
из начального положения N0(-5; 16; -6) со скоростью vN=13 в направлении, противоположном
вектору r={-4; 12; -3}. Составить уравнения движения
каждой из точек и, убедившись, что их траектории
пересекаются, найти:
пересечения их траекторий;
затраченное на движение точки М от М0
до Р;
затраченное на движение точки N от N0
до Р;
отрезков M0P и N0P.
Ника
Высший разум
(181432)
13 лет назад
Решение:
1) Найдем уравнение медианы АМ, для этого найдем координаты точки М (4;3;5)
(х-1)/(4-1)=(у-2)/(3-2)=(z-3)/(5-3)
(x-1)/3=(y-2)/1=(z-3)/2 – искомое уравнение медианы.
2) Найдем каноническое уравнение высоты АН, для этого найдем уравнение стороны ВС:
(x-3)/2=(y-4)/(-2)=(z-4)/2
Направляющий вектор этой прямой n(2;-2;2) является нормальным вектором для плоскости проходящей через точку А и перпендикулярно прямой ВС
2(x-1)-2(y-2)+2(z-3)=0
x-y+z-2=0 – уравнение плоскости, найдем основание перпендикуляра, точку Н:
(x-3)/2=t
(y-4)/(-2)=t
(z-4)/2=t
Получили:
x=2t+3
y=2t+4
z=2t+4
2t+3-2t-4+2t+4-2=0
2t=-1
t=-0.5
Тогда H(2;3;3)
Уравнение высоты:
(x-1)/1=(y-2)/1=(z-3)/0
Елена Гужвенко
Гений
(53581)
13 лет назад
Помогу про высоту.
1) Найти вектор ВС=(2,-2,3), он будет перпендикулярен высоте АН.
2) Найдем координаты любого вектора (х, у, z), параллельного АН, то есть перпендикулярного ВС.
Возьмем х=0, у=1, найдем z с помощью скалярного произведения ВС на (0,1,z):
2*0+(-2)*1+3*z=0
-2=-3z
z=2/3
Нашли вектор, параллельный АН, тогда уравнение высоты АН:
(x-1)/0=(y-2)/1=(z-3)/(2/3) каноническое уравнение высоты АН
 Параметрические уравнения Параметрические уравненияпрямой |
|---|
| Прямая линия однозначно определена, если на ней задана точка 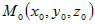 и ненулевой вектор, параллельный этой прямой. В и ненулевой вектор, параллельный этой прямой. Вдальнейшем такой вектор будем называть направляющим вектором. Если 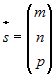 – направляющий вектор, то для любой точки – направляющий вектор, то для любой точки 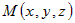 , принадлежащей прямой справедливо: , принадлежащей прямой справедливо: 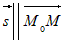 . Из определения коллинеарных векторов следует соотношение . Из определения коллинеарных векторов следует соотношение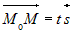 . Так как вектор . Так как вектор 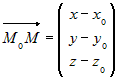 , то последнее равенство равносильно , то последнее равенство равносильносистеме |
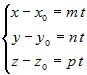 , или , или 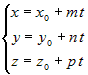 . . |
Полученные три уравнения называются параметрическими уравнениями прямой, а 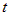 – –параметром. |
 Канонические уравнения Канонические уравненияпрямой |
|---|
| Если использовать условие коллинеарности векторов, выраженное через их координаты, то получим уравнения, которые называются каноническими уравнениями прямой: |
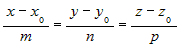 . . |
 Задача 1 Задача 1 |
|---|
|
Напишите канонические уравнения прямой, проходящей через точки |
 Решение Решение |
|
Вектор
|
Следует заметить, что канонические и параметрические
уравнения прямой выглядят различно, в зависимости от того, координаты какой
точки в них подставлены вместо чисел 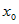
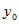
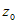
вектора равна нулю, а это означает, что один из знаменателей в канонических
уравнениях равен нулю. Такая запись для канонических уравнений прямой считается
вполне допустимой. Чтобы понять, как в данном случае расположена в пространстве
прямая, перейдем к параметрическим уравнениям. Для этого каждое из трех равных
отношений обозначим через 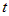
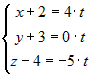
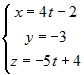
плоскости 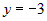
 Задача 2 Задача 2 |
|---|
|
Составьте параметрические уравнения медианы, проведенной из вершины |
 Решение Решение |
|
На медиане |
 Ответ: Ответ: |
|
|
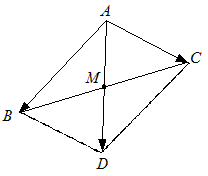 |
| Рис. 8 |
 Угол между прямыми Угол между прямыми |
|---|
Пусть 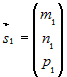 и и 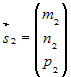 – направляющие векторы двух прямых. Угол – направляющие векторы двух прямых. Угол 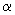 между прямыми определяется как между прямыми определяется какугол между их направляющими векторами. Для косинуса этого угла справедлива формула: |
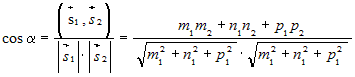 . . |
 Условие Условиеперпендикулярности прямых |
|---|
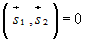 или или 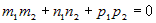 . . |
 Условие параллельности Условие параллельностипрямых |
|---|
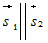 или или 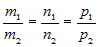 . . |
 Условия пересечения Условия пересеченияпрямых в пространстве |
|||||||
|---|---|---|---|---|---|---|---|
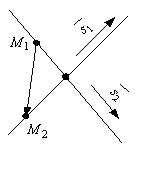
Если 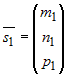 и и 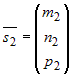 – направляющие векторы двух прямых, а – направляющие векторы двух прямых, а 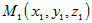 и и 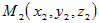 – точки на этих прямых, то прямые пересекаются или – точки на этих прямых, то прямые пересекаются илискрещиваются в зависимости от того, компланарны или нет векторы 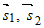 и и 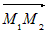 (рис.9). (рис.9). |
|||||||
Прямые скрещиваются, если смешанное произведение 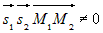 (рис.9 a). (рис.9 a). |
|||||||
Прямые пересекаются, если смешанное произведение 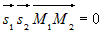 (рис.9 b). (рис.9 b). |
|||||||
|
 Задача 3 Задача 3 |
|---|
|
При каком значении |
 Решение Решение |
|
Для первой прямой: направляющий вектор
Поскольку |
 Ответ: Ответ: |
|
|
 Приведение общих уравнений прямой к Приведение общих уравнений прямой кканоническому виду |
||
|---|---|---|
Пусть прямая задана общими уравнениями 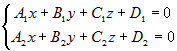 . . |
||
|
||
| Если нужно привести ее уравнения к каноническим или параметрическим, то следует выбрать на этой прямой какую-то точку и найти вектор, параллельный ей. Координатами точки, принадлежащей прямой, является любое из решений заданной линейной системы. Направляющим вектором прямой является вектор 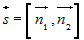 , где , где 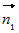 и и 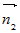 – нормальные векторы плоскостей, задающих прямую – нормальные векторы плоскостей, задающих прямую(рис. 10). |
 Задача 4 Задача 4 |
|---|
|
Приведите уравнения прямой |
 Решение Решение |
|
Выберем на прямой точку с аппликатой
Следовательно, канонические уравнения прямой имеют вид |
 Ответ: Ответ: |
|
|
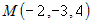 и
и 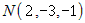 .
.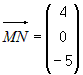 параллелен прямой, следовательно, мы можем выбрать
параллелен прямой, следовательно, мы можем выбрать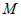 , получим систему канонических
, получим систему канонических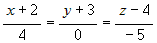 .
.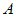 в треугольнике
в треугольнике 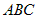 , если заданы координаты его вершин
, если заданы координаты его вершин 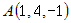 ,
, 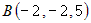 и
и 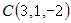 .
.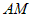 задана точка
задана точка 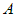 (рис.8). Направляющим вектором для нее может
(рис.8). Направляющим вектором для нее может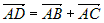 (рис. 8). Вычислим координаты векторов
(рис. 8). Вычислим координаты векторов 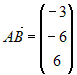 и
и 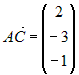 , а также вектора
, а также вектора 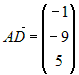 . Подставим в параметрические уравнения прямой
. Подставим в параметрические уравнения прямой 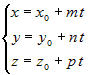 вместо
вместо 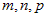 координаты вектора
координаты вектора 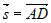 , а вместо
, а вместо 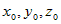 – координаты точки
– координаты точки 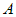 . Получим
. Получим 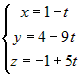 .
.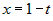 ,
, 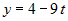 ,
, 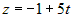 .
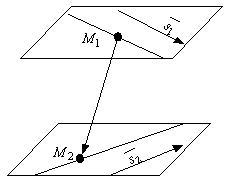
.
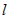 прямые
прямые 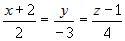 и
и 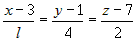 пересекаются?
пересекаются?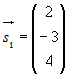 и точка
и точка 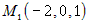 . Для второй прямой: направляющий вектор
. Для второй прямой: направляющий вектор 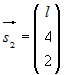 и точка
и точка 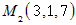 . Вычислим координаты вектора
. Вычислим координаты вектора 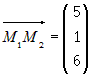 и учтем, что прямые пересекаются, если смешанное
и учтем, что прямые пересекаются, если смешанное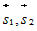 и
и 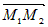 равно нулю.
равно нулю.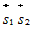
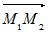 =
=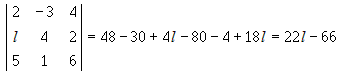 .
.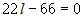 , то
, то 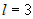 .
.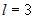 .
.
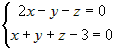 к каноническому виду.
к каноническому виду.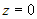 . Подставим
. Подставим 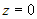 в общие уравнения прямой и найдем остальные
в общие уравнения прямой и найдем остальные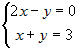 . Складывая уравнения системы, получим
. Складывая уравнения системы, получим 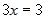 , или
, или 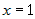 . Подставляя это в любое уравнение, найдем
. Подставляя это в любое уравнение, найдем 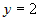 , Итак, точка
, Итак, точка 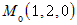 принадлежит прямой. Нормальные векторы плоскостей,
принадлежит прямой. Нормальные векторы плоскостей,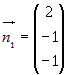 и
и 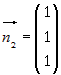 . Тогда направляющий вектор прямой равен их векторному
. Тогда направляющий вектор прямой равен их векторному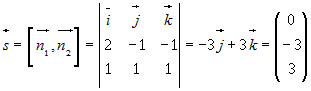 .
.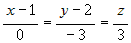 .
.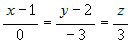 .
.