
















Параметрическое задание кривой
- Кривая параметрическая Н°1.Подход к делу problem. So до сих пор мы рассматривали только 2 вида назначений кривых: уравнение v = f (x) (явная задача) или уравнение F (x, y)= O (неявная задача)).Однако теоретическая механика очень естественно приводит к различным видам линий assignments. In дело в том, что
установка движения точки-это средство нахождения положения (то есть координат) любого момента времени t. Чтобы полностью определить движение точки, определите линию, на которой будет находиться точка move. So, в этом примере линии даны с использованием
So например, эквационный х = 2Т г = 3Т-2(1)
Людмила Фирмаль
2 равенств (I).Конечно, очень легко получить более знакомые задачи в той же линии. Именно так. Для любого момента x 3x /будет t = — q, t y =-2. Это соединение X и y обеспечивает явное определение линии*).Видно, что эта задача получается путем исключения времени t из Формулы (1). В рассматриваемом
примере, тот факт, что переменная T показывает время не играет никакой роли. Например, предположим, что следующие X и y зависят от вспомогательных переменных: х = Т-ФЛ, г = т Изменение его даст вам различные точки(.x, комбинация которых состоит из нескольких линий. значение t обозначается равенством t = x-1 с соответствующим значением x, поэтому y =(x-I) 1 для
- любой точки линии, и я получил явную задачу линии. Из этого видно, что вы обрабатываете 1 пару болтов. Чтобы суммировать вышесказанное, пара уравнений Где t-вспомогательная переменная, определяющая lnnnu. Способ определения этой линии называется параметрическим, а переменная t называется
параметром. за исключением t, вы получаете нормальное (явное или неявное) уравнение для той же строки. Замечание. Если функция < p (/) уравнения ( * ) задана и непрерывна с определенным интервалом p, q, то линия, определяемая этими уравнениями, называется непрерывной curve. In в частности, линия, определяемая уравнением y = sf (x) (заданным f (x)
быть определена уравнением. х = т, у = F(т) (а ^ т ^ б). н°2.
Людмила Фирмаль
и последовательным в интервале[i, b]), является непрерывной кривой, поскольку она также может Параметрические уравнения для окружностей и эллипсов. Рассмотрим окружность с радиусом R, центрированную вокруг начала координат
(рис.181).Положение любой точки M в этой окружности полностью определяется установкой угла f, который образуется осью Ox и радиусом OM. It естественно выразить координаты x и y точки M под этим углом. Из рисунков это сразу понятно (2) х = р COS в ТТ г = РС НТ. Эти уравнения (*) являются параметрическими
уравнениями окружности. Параметр T может быть изменен с-oo на — | — oo, но если вы хотите получить каждую точку круга по 1 разу, достаточно пройти t через зазор. Однако, это более удобно для обработки закрытых пробелов. Так, т, как правило,
изменяется в пределах 0 ^ / ^ 2ir, но точка с получает в 2 раза. T= 0 и в = 2ir. Чтобы получить нормальное уравнение окружности, необходимо исключить параметр T из (2).Это проще всего, если вы возьмете уравнение (2) на 2 квадрата и добавите результат. Очевидно, это приводит к известному уравнению Найти
параметрическое уравнение эллипса (3) Полезно помнить, что он получается из круга * * + > ■ = A (4)рисунок 181. Имеют диаметр с большой осью эллипса, иногда используют сжатие、 То есть любая точка M в эллипсе(3) берется из точки N в окружности (4). Б Ордината точки Н В соответствии с вышеизложенным
параметрическое уравнение окружности(4) имеет вид x = acos/, ^ = asin/.Но тогда понятно, что параметрическое уравнение (3) эллипса получается умножением. форма ординаты y имеет вид) (5) * = acosf, г = БС НТ. Чтобы получить все точки овала, достаточно
изменить Т выпускного вечера. Жуткий 0 ^ t ^кроме того, каждая точка эллипса, кроме точки (a, 0), получается только 1 раз, а точки(a, 0) — 2 раза (t = 0 и t = 2k).Если мы разделим первое уравнение (5) на a, а затем разделим 2-е уравнение на b, то полученное уравнение будет добавлено на 2 и станет каноническим уравнением эллипса(3).
Сравнение параметрических уравнений окружности и эллипса дает удобный метод построения любого числа точек в эллипсе. То есть, пара уравнений х-acoet, у = грех Т(6) U определяет окружность с радиусом A вокруг начала координат и пару уравнений х = б сое т, у = B грех Т(7) — Окружность b с тем же центром и радиусом; чтобы получить точку (l, y), как показывает уравнение (5), p / 82.Если
вы лежите на овале, вам нужно найти x Используйте первое выражение(6) и 2-е выражение (7) с y. но эти xn-y легко найти графически, так как в формулах (6) и (7) параметром T является угол наклона радиус-вектора точки относительно оси Ox. So, чтобы составить точку M (q, y) эллипса (5), нарисуйте окружность (6) и (7)
и нарисуйте луч на оси Ox под углом t от начала координат. Найдите точки A и B пересечения этого луча и ранее упомянутой окружности и проведите через них прямую линию, параллельную оси, вы получите точку M (см. Рисунок 182).П°3.Циклоида * важные
кривые-давайте познакомимся с циклоидой. Это также хороший пример параметрического определения линии. Определение циклоида представляет собой линию, которая представлена точкой окружности, которая катится без скольжения или вращения Из этого определения сразу видно, что циклоида состоит из ряда дуг, как
показано на рисунке 1. 183, высота этих арок равна 2R. R-радиус окружности. Ниже расстояние между соседними точками разворотаAB, BC,…равно 2π/?Это значение по умолчанию. Найдите параметрические уравнения циклоиды. В качестве оси Ox возьмите прямую линию, по которой катится круг, и для начала координат
возьмите положение точки M, которая представляет собой циклоиду острия в этой точке. Эта точка находится на оси Ox. Нарисуйте этот момент как первый момент, вращающийся круг в первый момент, а затем второй. t представляет собой угол, образованный в момент t радиусом вращающейся окружности, направленной
к точке A окружности, которая касается точки I и оси Ox, представляющей циклоиду. (Рисунок 184) радиус CXM и u ° С / а возьмем этот угол т. 184. Попробуйте параметр 8a Через него отрегулируйте точки x и y м-циклоиды. Что касается координат Y, то это довольно просто. г => ВМ = объявление = ОБК-CjZ)= /? — R cos t.
(8) Чтобы найти абсциссу X, нужно рассмотреть эквивалентность отрезка OA и дуги AM. OA = AM. (9 )) При таком равенстве окружность не будет скользить или вращаться. Следующий метод проверки эквивалентности очень очевиден(9): представьте себе катящийся круг, выполненный в виде деревянного кольца. Накройте этот обруч лентой, которая не растягивается, прибив ее правый край гвоздем
к точке O оси Ox, а левый край-к обручу. При вращении обруча лента начинает растекаться по оси Ox, и в момент t отсечение оси OA закрывается той частью ленты, которая упала вниз. С дугой AM обруч. Это*) доказывает(9). еще проще: t-значение угла AC% M, так как это Радиан、 AM = Rt Так… x = OB = OA-BA = AM-MD = Rt-Rsint (10) Если
сравнить (8)и(10), то получим параметрическое уравнение циклоиды х = р(т-Син т), г = р (- стоимость). Параметр Т может изменяться от-ОО до-Е-ОО. Пересечение начала координат и ближайших к нему справа циклоид соответствует значению Ox = t * 2.Это происходит потому, что круг качения приобретается после 1 rotation. In в этом случае
t будет n; = 2nR. In кроме того, из (11) видно, что координаты (π/,, 2/) находятся в высшей точке соответствующего cycloid. To будьте осторожны невозможно представить Y в качестве одной из основных функций Икс. И от x до y возможно| f = Arccos ^ l, но результат Формула очень трудоемкая. Параметрическое уравнение
проще. в N°4.Эвольвента circle. In в теории зацепления используется кривая, называемая эвольвентой окружности. Эвольвента окружности определения-это линия, которая описывается точкой нити и расстегивается от этой окружности, пока она прочно растянута. Предполагается, что нить неэластична и предварительно обмотана вокруг вышеуказанных кругов. Найти параметрическое
уравнение для эвольвенты circle. To сделайте это, поместите начало координат в центр круга и нарисуйте ось Ox Ноль ноль В тот момент, когда нить еще полностью обмотана вокруг окружности, точка окружности, в которой расположена точка, описывающая эвольвенту. Рисунок 185 эта точка обозначается A. 185 показывает положение потока виртуальной машины в некоторой точке в time. So, здесь B-
точка, в которой нить исчезает из окружности, а M-точка, в которой она описывает эвольвенту. Радиус окружности? Угол наклона оси Ox и Луча OB представлен через t. поскольку нить не является растяжимой、 Отрезок VM равен дуге AB окружности. То есть, BM = RT. обратите внимание, что нить остается прочно натянутой, поэтому она спускается по касательной от окружности. Таким образом,
нить VM перпендикулярна радиусу органического вещества. Поэтому углы AOB и MBD равны углам, где каждая сторона перпендикулярна друг другу. Следовательно,£МБД = T, и из треугольника МВС См = РТ грех ЦБ = стоимость РТ. Теперь вы можете легко найти X и y координаты точки м. Другими словами、 х = ое = ОД + де = ОД-ТСМ = стоимости Р + РТ грех г = ВС = ДК = ДБ-КБ = Р грех Т-РТ стоимость. Рисунок 185.Наконец. х = /?(потому что * — Ф — * грех/),; г = р (т Син-/ Кос Т), (’ Где: 0 f < — f-co. Легко видеть, что Эвольвента круга
представляет собой spiral. It показано на рисунке. 185 баллов N соответствует значению t шп п Итак, его координаты g= -, y-Rt, но это очевидно и сразу очевидно. Интересно отметить, что определение эвольвенты в круге является в некотором смысле определением циклоиды и»двойника».То есть, если вы рисуете касательную к точке а в точке А и начинаете вращаться вокруг окружности, то в момент, когда точка касательной перемещается в точку в, точка А (которая
считается точкой касательной) становится позицией м. Таким образом, эвольвентный круг представляет собой линию, которая представлена тонкой линией, когда последняя катит круг (без скольжения). П°5.Параметрический дифференциал. Предположим, вы хотите нарисовать касательную к кривой, определяемой параметрическим уравнением * = T(0,>> = » K0(13) В точке M (x, y), соответствующей значению параметра T. To сделайте это, дайте
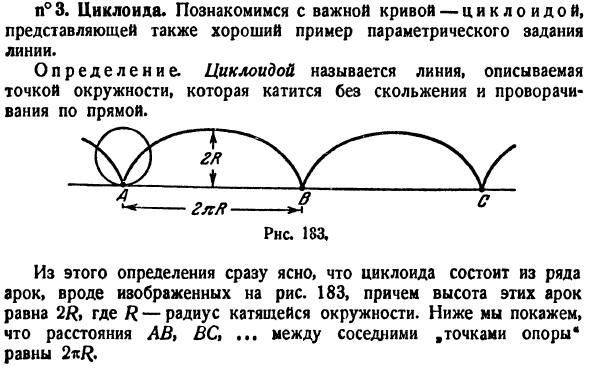
t приращение At и в результате получите ту же самую точку кривой AfCtf-J-A * » Y + AC) (13).Угловой коэффициент Т * Секущий MN равен или равен Важно отметить, что производная, фигурирующая в (15) , должна быть рассчитана для величины t, определяющей контакт M. Угловой коэффициент m интересующего тангенса является
пределом формулы (14) для N — + M, то есть, но так как D * — > 0 Вы будете Работать ДД: (15 )) Так… Образцы. Нарисуйте касательную к кривой + г = Тл-7т(16) Очки*)А!(2). Решение. Координаты точки M определяются из(16). xi = 17, y%=2.In сложение, x = bP—4/, y = 4P-7.So, t = 2 — Это X / = 20, yt = 25, угловой коэффициент Желаемый тангенс. Форма искомого уравнения имеет вид y-2 = 4 (l-17> Замечание.
Приведенная выше строка g:=?( * ), Y =φ (f), функция равна (t), φ (/).Если эти функции не только непрерывны, но и имеют непрерывные производные от y’0, то, как показывает уравнение (15), кривая имеет определенную касательную в каждой точке, и ее положение непрерывно изменяется с изменением контакта.
Кроме того, указанные касательные никогда не будут параллельны оси Oy. Учитывая, что координаты x и y полностью равны, линии x =
.Где f (/j u f ( / ) имеет непрерывную производную、 <Р ’»<0 + р»)> а В частности, под это определение подпадает линия y = f ( * ), где f (x) имеет непрерывную производную. Где роль параметра T-абсцисса ш=■»+*?> ми- Теперь зададим следующие общие вопросы: пусть
x и y зависят от вспомогательных переменных t, как показано в (13). в первом выражении (13) обозначим t из x, а затем присвоим его 2-му выражению, вы увидите, что y является функцией x, то есть y = f(x).Попробуйте найти производную этой функции. Для этого достаточно вспомнить, что интересующей нас производной является только угловой коэффициент касательной прямой y = / ( * ),
а ее параметрическим уравнением является уравнение (13).Таким образом, она задается формулой(15). Чтобы правильно понять это важное выражение, следует помнить, что точка дифференцирования t справа от (17) является значением параметра, и согласно формуле x = y (t) она соответствует точке дифференцирования x, где Y’x находится. Соотношения(17) легко получить с помощью чисто формальных
вычислений. dypy / ДТ Вау, х]’ Затем попробуйте найти 2-ю производную yx той же функции y = f (x).Это легко сделать, используя формулу (17).То есть он временно представляет y’X с Z. А затем… ** ух-з» (17) Значение (18) Однако, поскольку Z = yx = — m、 / ГМ-ГМ Узнайте, наконец, из (18)и (19) Образцы. Установите вогнутое направление
кривой х =(* + 3Т + л> г = 2Т * — (21) В точке Af (l). Решение. Из (21), x’f = 2t + 3, x? = 2,г = г г! = 12 /.Итак, если t = 1, то это выглядит так:= jc / = 2, y ’ < = 6, yi =12.By формула (20) M 、_ 12.5-6-2 _ 48 А-Б ’ 125 ′ поскольку yk> 0, кривая точки M (21) направлена вогнутой поверхностью вверх.
Смотрите также:
Предмет высшая математика

Параметрическое задание кривой



















Параметрическое задание кривой
- Кривая параметрическая Н°1.Подход к делу problem. So до сих пор мы рассматривали только 2 вида назначений кривых: уравнение v = f (x) (явная задача) или уравнение F (x, y)= O (неявная задача)).Однако теоретическая механика очень естественно приводит к различным видам линий assignments. In дело в том, что
установка движения точки-это средство нахождения положения (то есть координат) любого момента времени t. Чтобы полностью определить движение точки, определите линию, на которой будет находиться точка move. So, в этом примере линии даны с использованием
So например, эквационный х = 2Т г = 3Т-2(1) Людмила Фирмаль
2 равенств (I).Конечно, очень легко получить более знакомые задачи в той же линии. Именно так. Для любого момента x 3x /будет t = — q, t y =-2. Это соединение X и y обеспечивает явное определение линии*).Видно, что эта задача получается путем исключения времени t из Формулы (1). В рассматриваемом
примере, тот факт, что переменная T показывает время не играет никакой роли. Например, предположим, что следующие X и y зависят от вспомогательных переменных: х = Т-ФЛ, г = т Изменение его даст вам различные точки(.x, комбинация которых состоит из нескольких линий. значение t обозначается равенством t = x-1 с соответствующим значением x, поэтому y =(x-I) 1 для
- любой точки линии, и я получил явную задачу линии. Из этого видно, что вы обрабатываете 1 пару болтов. Чтобы суммировать вышесказанное, пара уравнений Где t-вспомогательная переменная, определяющая lnnnu. Способ определения этой линии называется параметрическим, а переменная t называется
параметром. за исключением t, вы получаете нормальное (явное или неявное) уравнение для той же строки. Замечание. Если функция Людмила Фирмаль
и последовательным в интервале[i, b]), является непрерывной кривой, поскольку она также может Параметрические уравнения для окружностей и эллипсов. Рассмотрим окружность с радиусом R, центрированную вокруг начала координат
(рис.181).Положение любой точки M в этой окружности полностью определяется установкой угла f, который образуется осью Ox и радиусом OM. It естественно выразить координаты x и y точки M под этим углом. Из рисунков это сразу понятно (2) х = р COS в ТТ г = РС НТ. Эти уравнения (*) являются параметрическими
уравнениями окружности. Параметр T может быть изменен с-oo на — | — oo, но если вы хотите получить каждую точку круга по 1 разу, достаточно пройти t через зазор. Однако, это более удобно для обработки закрытых пробелов. Так, т, как правило,
изменяется в пределах 0 ^ / ^ 2ir, но точка с получает в 2 раза. T= 0 и в = 2ir. Чтобы получить нормальное уравнение окружности, необходимо исключить параметр T из (2).Это проще всего, если вы возьмете уравнение (2) на 2 квадрата и добавите результат. Очевидно, это приводит к известному уравнению Найти
параметрическое уравнение эллипса (3) Полезно помнить, что он получается из круга * * + > ■ = A (4)рисунок 181. Имеют диаметр с большой осью эллипса, иногда используют сжатие、 То есть любая точка M в эллипсе(3) берется из точки N в окружности (4). Б Ордината точки Н В соответствии с вышеизложенным
параметрическое уравнение окружности(4) имеет вид x = acos/, ^ = asin/.Но тогда понятно, что параметрическое уравнение (3) эллипса получается умножением. форма ординаты y имеет вид) (5) * = acosf, г = БС НТ. Чтобы получить все точки овала, достаточно
изменить Т выпускного вечера. Жуткий 0 ^ t ^кроме того, каждая точка эллипса, кроме точки (a, 0), получается только 1 раз, а точки(a, 0) — 2 раза (t = 0 и t = 2k).Если мы разделим первое уравнение (5) на a, а затем разделим 2-е уравнение на b, то полученное уравнение будет добавлено на 2 и станет каноническим уравнением эллипса(3).
Сравнение параметрических уравнений окружности и эллипса дает удобный метод построения любого числа точек в эллипсе. То есть, пара уравнений х-acoet, у = грех Т(6) U определяет окружность с радиусом A вокруг начала координат и пару уравнений х = б сое т, у = B грех Т(7) — Окружность b с тем же центром и радиусом; чтобы получить точку (l, y), как показывает уравнение (5), p / 82.Если
вы лежите на овале, вам нужно найти x Используйте первое выражение(6) и 2-е выражение (7) с y. но эти xn-y легко найти графически, так как в формулах (6) и (7) параметром T является угол наклона радиус-вектора точки относительно оси Ox. So, чтобы составить точку M (q, y) эллипса (5), нарисуйте окружность (6) и (7)
и нарисуйте луч на оси Ox под углом t от начала координат. Найдите точки A и B пересечения этого луча и ранее упомянутой окружности и проведите через них прямую линию, параллельную оси, вы получите точку M (см. Рисунок 182).П°3.Циклоида * важные
кривые-давайте познакомимся с циклоидой. Это также хороший пример параметрического определения линии. Определение циклоида представляет собой линию, которая представлена точкой окружности, которая катится без скольжения или вращения Из этого определения сразу видно, что циклоида состоит из ряда дуг, как
показано на рисунке 1. 183, высота этих арок равна 2R. R-радиус окружности. Ниже расстояние между соседними точками разворотаAB, BC,…равно 2π/?Это значение по умолчанию. Найдите параметрические уравнения циклоиды. В качестве оси Ox возьмите прямую линию, по которой катится круг, и для начала координат
возьмите положение точки M, которая представляет собой циклоиду острия в этой точке. Эта точка находится на оси Ox. Нарисуйте этот момент как первый момент, вращающийся круг в первый момент, а затем второй. t представляет собой угол, образованный в момент t радиусом вращающейся окружности, направленной
к точке A окружности, которая касается точки I и оси Ox, представляющей циклоиду. (Рисунок 184) радиус CXM и u ° С / а возьмем этот угол т. 184. Попробуйте параметр 8a Через него отрегулируйте точки x и y м-циклоиды. Что касается координат Y, то это довольно просто. г => ВМ = объявление = ОБК-CjZ)= /? — R cos t.
(8) Чтобы найти абсциссу X, нужно рассмотреть эквивалентность отрезка OA и дуги AM. OA = AM. (9 )) При таком равенстве окружность не будет скользить или вращаться. Следующий метод проверки эквивалентности очень очевиден(9): представьте себе катящийся круг, выполненный в виде деревянного кольца. Накройте этот обруч лентой, которая не растягивается, прибив ее правый край гвоздем
к точке O оси Ox, а левый край-к обручу. При вращении обруча лента начинает растекаться по оси Ox, и в момент t отсечение оси OA закрывается той частью ленты, которая упала вниз. С дугой AM обруч. Это*) доказывает(9). еще проще: t-значение угла AC% M, так как это Радиан、 AM = Rt Так… x = OB = OA-BA = AM-MD = Rt-Rsint (10) Если
сравнить (8)и(10), то получим параметрическое уравнение циклоиды х = р(т-Син т), г = р (- стоимость). Параметр Т может изменяться от-ОО до-Е-ОО. Пересечение начала координат и ближайших к нему справа циклоид соответствует значению Ox = t * 2.Это происходит потому, что круг качения приобретается после 1 rotation. In в этом случае
t будет n; = 2nR. In кроме того, из (11) видно, что координаты (π/,, 2/) находятся в высшей точке соответствующего cycloid. To будьте осторожны невозможно представить Y в качестве одной из основных функций Икс. И от x до y возможно| f = Arccos ^ l, но результат Формула очень трудоемкая. Параметрическое уравнение
проще. в N°4.Эвольвента circle. In в теории зацепления используется кривая, называемая эвольвентой окружности. Эвольвента окружности определения-это линия, которая описывается точкой нити и расстегивается от этой окружности, пока она прочно растянута. Предполагается, что нить неэластична и предварительно обмотана вокруг вышеуказанных кругов. Найти параметрическое
уравнение для эвольвенты circle. To сделайте это, поместите начало координат в центр круга и нарисуйте ось Ox Ноль ноль В тот момент, когда нить еще полностью обмотана вокруг окружности, точка окружности, в которой расположена точка, описывающая эвольвенту. Рисунок 185 эта точка обозначается A. 185 показывает положение потока виртуальной машины в некоторой точке в time. So, здесь B-
точка, в которой нить исчезает из окружности, а M-точка, в которой она описывает эвольвенту. Радиус окружности? Угол наклона оси Ox и Луча OB представлен через t. поскольку нить не является растяжимой、 Отрезок VM равен дуге AB окружности. То есть, BM = RT. обратите внимание, что нить остается прочно натянутой, поэтому она спускается по касательной от окружности. Таким образом,
нить VM перпендикулярна радиусу органического вещества. Поэтому углы AOB и MBD равны углам, где каждая сторона перпендикулярна друг другу. Следовательно,£МБД = T, и из треугольника МВС См = РТ грех ЦБ = стоимость РТ. Теперь вы можете легко найти X и y координаты точки м. Другими словами、 х = ое = ОД + де = ОД-ТСМ = стоимости Р + РТ грех г = ВС = ДК = ДБ-КБ = Р грех Т-РТ стоимость. Рисунок 185.Наконец. х = /?(потому что * — Ф — * грех/),; г = р (т Син-/ Кос Т), (’ Где: 0 f > = » K0(13) В точке M (x, y), соответствующей значению параметра T. To сделайте это, дайте
t приращение At и в результате получите ту же самую точку кривой AfCtf-J-A * » Y + AC) (13).Угловой коэффициент Т * Секущий MN равен или равен Важно отметить, что производная, фигурирующая в (15) , должна быть рассчитана для величины t, определяющей контакт M. Угловой коэффициент m интересующего тангенса является
пределом формулы (14) для N — + M, то есть, но так как D * — > 0 Вы будете Работать ДД: (15 )) Так… Образцы. Нарисуйте касательную к кривой + г = Тл-7т(16) Очки*)А!(2). Решение. Координаты точки M определяются из(16). xi = 17, y%=2.In сложение, x = bP—4/, y = 4P-7.So, t = 2 — Это X / = 20, yt = 25, угловой коэффициент Желаемый тангенс. Форма искомого уравнения имеет вид y-2 = 4 (l-17> Замечание.
Приведенная выше строка g:=?( * ), Y =φ (f), функция равна (t), φ (/).Если эти функции не только непрерывны, но и имеют непрерывные производные от y’0, то, как показывает уравнение (15), кривая имеет определенную касательную в каждой точке, и ее положение непрерывно изменяется с изменением контакта.
Кроме того, указанные касательные никогда не будут параллельны оси Oy. Учитывая, что координаты x и y полностью равны, линии x =
.Где f (/j u f ( / ) имеет непрерывную производную、 а В частности, под это определение подпадает линия y = f ( * ), где f (x) имеет непрерывную производную. Где роль параметра T-абсцисса ш=■»+*?> ми- Теперь зададим следующие общие вопросы: пусть
x и y зависят от вспомогательных переменных t, как показано в (13). в первом выражении (13) обозначим t из x, а затем присвоим его 2-му выражению, вы увидите, что y является функцией x, то есть y = f(x).Попробуйте найти производную этой функции. Для этого достаточно вспомнить, что интересующей нас производной является только угловой коэффициент касательной прямой y = / ( * ),
а ее параметрическим уравнением является уравнение (13).Таким образом, она задается формулой(15). Чтобы правильно понять это важное выражение, следует помнить, что точка дифференцирования t справа от (17) является значением параметра, и согласно формуле x = y (t) она соответствует точке дифференцирования x, где Y’x находится. Соотношения(17) легко получить с помощью чисто формальных
вычислений. dypy / ДТ Вау, х]’ Затем попробуйте найти 2-ю производную yx той же функции y = f (x).Это легко сделать, используя формулу (17).То есть он временно представляет y’X с Z. А затем… ** ух-з» (17) Значение (18) Однако, поскольку Z = yx = — m、 / ГМ-ГМ Узнайте, наконец, из (18)и (19) Образцы. Установите вогнутое направление
кривой х =(* + 3Т + л> г = 2Т * — (21) В точке Af (l). Решение. Из (21), x’f = 2t + 3, x? = 2,г = г г! = 12 /.Итак, если t = 1, то это выглядит так:= jc / = 2, y ’ 0, кривая точки M (21) направлена вогнутой поверхностью вверх.






















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Параметрические уравнения прямой на плоскости: описание, примеры, решение задач
Одним из подпунктов темы «Уравнение прямой на плоскости» является вопрос составления параметрических уравнений прямой на плоскости в прямоугольной системе координат. В статье ниже рассматривается принцип составления подобных уравнений при определенных известных данных. Покажем, как от параметрических уравнений переходить к уравнениям иного вида; разберем решение типовых задач.
Вывод параметрических уравнений прямой на плоскости
Конкретная прямая может быть определена, если задать точку, которая принадлежит этой прямой, и направляющий вектор прямой.
Допустим, нам задана прямоугольная система координат O x y . А также заданы прямая а с указанием лежащей на ней точки М 1 ( x 1 , y 1 ) и направляющий вектор заданной прямой a → = ( a x , a y ) . Дадим описание заданной прямой a , используя уравнения.
Используем произвольную точку М ( x , y ) и получим вектор М 1 М → ; вычислим его координаты по координатам точек начала и конца: M 1 M → = ( x – x 1 , y – y 1 ) . Опишем полученное: прямая задана множеством точек М ( x , y ) , проходит через точку М 1 ( x 1 , y 1 ) и имеет направляющий вектор a → = ( a x , a y ) . Указанное множество задает прямую только тогда, когда векторы M 1 M → = ( x – x 1 , y – y 1 ) и a → = ( a x , a y ) являются коллинеарными.
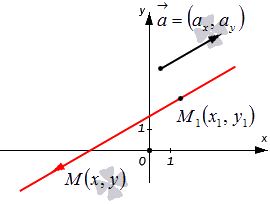
Существует необходимое и достаточное условие коллинеарности векторов, которое в данном случае для векторов M 1 M → = ( x – x 1 , y – y 1 ) и a → = ( a x , a y ) возможно записать в виде уравнения:
M 1 M → = λ · a → , где λ – некоторое действительное число.
Уравнение M 1 M → = λ · a → называют векторно-параметрическим уравнением прямой.
В координатной форме оно имеет вид:
M 1 M → = λ · a → ⇔ x – x 1 = λ · a x y – y 1 = λ · a y ⇔ x = x 1 + a x · λ y = y 1 + a y · λ
Уравнения полученной системы x = x 1 + a x · λ y = y 1 + a y · λ носят название параметрических уравнений прямой на плоскости в прямоугольной системе координат. Суть названия в следующем: координаты всех точек прямой возможно определить по параметрическим уравнениям на плоскости вида x = x 1 + a x · λ y = y 1 + a y · λ при переборе всех действительных значений параметра λ
Составление параметрических уравнений прямой на плоскости
Согласно вышесказанному, параметрические уравнения прямой на плоскости x = x 1 + a x · λ y = y 1 + a y · λ определяют прямую линию, которая задана в прямоугольной системе координат, проходит через точку М 1 ( x 1 , y 1 ) и имеет направляющий вектор a → = ( a x , a y ) . Следовательно, если заданы координаты некоторой точки прямой и координаты ее направляющего вектора, то возможно сразу записать параметрические уравнения заданной прямой.
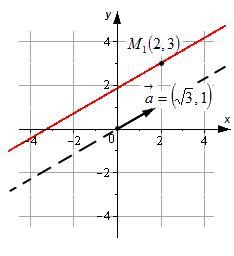
Необходимо составить параметрические уравнения прямой на плоскости в прямоугольной системе координат, если заданы принадлежащая ей точка М 1 ( 2 , 3 ) и ее направляющий вектор a → = ( 3 , 1 ) .
Решение
На основе исходных данных получим: x 1 = 2 , y 1 = 3 , a x = 3 , a y = 1 . Параметрические уравнения будут иметь вид:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 2 + 3 · λ y = 3 + 1 · λ ⇔ x = 2 + 3 · λ y = 3 + λ
Ответ: x = 2 + 3 · λ y = 3 + λ
Необходимо отметить: если вектор a → = ( a x , a y ) служит направляющим вектором прямой а, а точки М 1 ( x 1 , y 1 ) и М 2 ( x 2 , y 2 ) принадлежат этой прямой, то ее возможно определить, задав параметрическими уравнениями вида: x = x 1 + a x · λ y = y 1 + a y · λ , а также и таким вариантом: x = x 2 + a x · λ y = y 2 + a y · λ .
К примеру, нам заданы направляющий вектор прямой a → = ( 2 , – 1 ) , а также точки М 1 ( 1 , – 2 ) и М 2 ( 3 , – 3 ) , принадлежащие этой прямой. Тогда прямую определяют параметрические уравнения: x = 1 + 2 · λ y = – 2 – λ или x = 3 + 2 · λ y = – 3 – λ .
Следует обратить внимание и на такой факт: если a → = ( a x , a y ) – направляющий вектор прямой a , то ее направляющим вектором будет и любой из векторов μ · a → = ( μ · a x , μ · a y ) , где μ ϵ R , μ ≠ 0 .
Таким образом, прямая а на плоскости в прямоугольной системе координат может быть определена параметрическими уравнениями: x = x 1 + μ · a x · λ y = y 1 + μ · a y · λ при любом значении μ , отличном от нуля.
Допустим, прямая а задана параметрическими уравнениями x = 3 + 2 · λ y = – 2 – 5 · λ . Тогда a → = ( 2 , – 5 ) – направляющий вектор этой прямой. А также любой из векторов μ · a → = ( μ · 2 , μ · – 5 ) = 2 μ , – 5 μ , μ ∈ R , μ ≠ 0 станет направляющим вектором для заданной прямой. Для наглядности рассмотрим конкретный вектор – 2 · a → = ( – 4 , 10 ) , ему соответствует значение μ = – 2 . В таком случае заданную прямую можно также определить параметрическими уравнениями x = 3 – 4 · λ y = – 2 + 10 · λ .
Переход от параметрических уравнений прямой на плоскости к прочим уравнениям заданной прямой и обратно
В решении некоторых задач применение параметрических уравнений является не самым оптимальным вариантом, тогда возникает необходимость перевода параметрических уравнений прямой в уравнения прямой другого вида. Рассмотрим, как же это сделать.
Параметрическим уравнениям прямой вида x = x 1 + a x · λ y = y 1 + a y · λ будет соответствовать каноническое уравнение прямой на плоскости x – x 1 a x = y – y 1 a y .
Разрешим каждое из параметрических уравнений относительно параметра λ , приравняем правые части полученных равенств и получим каноническое уравнение заданной прямой:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x – x 1 a x λ = y – y 1 a y ⇔ x – x 1 a x = y – y 1 a y
При этом не должно смущать, если a x или a y будут равны нулю.
Необходимо осуществить переход от параметрических уравнений прямой x = 3 y = – 2 – 4 · λ к каноническому уравнению.
Решение
Запишем заданные параметрические уравнения в следующем виде: x = 3 + 0 · λ y = – 2 – 4 · λ
Выразим параметр λ в каждом из уравнений: x = 3 + 0 · λ y = – 2 – 4 · λ ⇔ λ = x – 3 0 λ = y + 2 – 4
Приравняем правые части системы уравнений и получим требуемое каноническое уравнение прямой на плоскости:
x – 3 0 = y + 2 – 4
Ответ: x – 3 0 = y + 2 – 4
В случае, когда необходимо записать уравнение прямой вида A x + B y + C = 0 , при этом заданы параметрические уравнения прямой на плоскости, необходимо сначала осуществить переход к каноническому уравнению, а затем к общему уравнению прямой. Запишем всю последовательность действий:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x – x 1 a x λ = y – y 1 a y ⇔ x – x 1 a x = y – y 1 a y ⇔ ⇔ a y · ( x – x 1 ) = a x · ( y – y 1 ) ⇔ A x + B y + C = 0
Необходимо записать общее уравнение прямой, если заданы определяющие ее параметрические уравнения: x = – 1 + 2 · λ y = – 3 · λ
Решение
Для начала осуществим переход к каноническому уравнению:
x = – 1 + 2 · λ y = – 3 · λ ⇔ λ = x + 1 2 λ = y – 3 ⇔ x + 1 2 = y – 3
Полученная пропорция идентична равенству – 3 · ( x + 1 ) = 2 · y . Раскроем скобки и получим общее уравнение прямой: – 3 · x + 1 = 2 · y ⇔ 3 x + 2 y + 3 = 0 .
Ответ: 3 x + 2 y + 3 = 0
Следуя вышеуказанной логике действий, для получения уравнения прямой с угловым коэффициентом, уравнения прямой в отрезках или нормального уравнения прямой необходимо получить общее уравнение прямой, а от него осуществлять дальнейший переход.
Теперь рассмотрим обратное действие: запись параметрических уравнений прямой при другом заданном виде уравнений этой прямой.
Самый простой переход: от канонического уравнения к параметрическим. Пусть задано каноническое уравнение вида: x – x 1 a x = y – y 1 a y . Каждое из отношений этого равенства примем равным параметру λ :
x – x 1 a x = y – y 1 a y = λ ⇔ λ = x – x 1 a x λ = y – y 1 a y
Разрешим полученные уравнения относительно переменных x и y :
x = x 1 + a x · λ y = y 1 + a y · λ
Необходимо записать параметрические уравнения прямой, если известно каноническое уравнение прямой на плоскости: x – 2 5 = y – 2 2
Решение
Приравняем части известного уравнения к параметру λ : x – 2 5 = y – 2 2 = λ . Из полученного равенства получим параметрические уравнения прямой: x – 2 5 = y – 2 2 = λ ⇔ λ = x – 2 5 λ = y – 2 5 ⇔ x = 2 + 5 · λ y = 2 + 2 · λ
Ответ: x = 2 + 5 · λ y = 2 + 2 · λ
Когда необходимо осуществить переход к параметрическим уравнениям от заданного общего уравнения прямой, уравнения прямой с угловым коэффициентом или уравнения прямой в отрезках, необходимо исходное уравнение привести к каноническому, а после осуществлять переход к параметрическим уравнениям.
Необходимо записать параметрические уравнения прямой при известном общем уравнении этой прямой: 4 x – 3 y – 3 = 0 .
Решение
Заданное общее уравнение преобразуем в уравнение канонического вида:
4 x – 3 y – 3 = 0 ⇔ 4 x = 3 y + 3 ⇔ ⇔ 4 x = 3 y + 1 3 ⇔ x 3 = y + 1 3 4
Приравняем обе части равенства к параметру λ и получим требуемые параметрические уравнения прямой:
x 3 = y + 1 3 4 = λ ⇔ x 3 = λ y + 1 3 4 = λ ⇔ x = 3 · λ y = – 1 3 + 4 · λ
Ответ: x = 3 · λ y = – 1 3 + 4 · λ
Примеры и задачи с параметрическими уравнениями прямой на плоскости
Рассмотрим чаще всего встречаемые типы задач с использованием параметрических уравнений прямой на плоскости в прямоугольной системе координат.
- В задачах первого типа заданы координаты точек, принадлежащих или нет прямой, описанной параметрическими уравнениями.
Решение таких задач опирается на следующий факт: числа ( x , y ) , определяемые из параметрических уравнений x = x 1 + a x · λ y = y 1 + a y · λ при некотором действительном значении λ , являются координатами точки, принадлежащей прямой, которая описывается этими параметрическими уравнениями.
Необходимо определить координаты точки, которая лежит на прямой, заданной параметрическими уравнениями x = 2 – 1 6 · λ y = – 1 + 2 · λ при λ = 3 .
Решение
Подставим в заданные параметрические уравнения известное значение λ = 3 и осуществим вычисление искомых координат: x = 2 – 1 6 · 3 y = – 1 + 2 · 3 ⇔ x = 1 1 2 y = 5
Ответ: 1 1 2 , 5
Также возможна следующая задача: пусть задана некоторая точка M 0 ( x 0 , y 0 ) на плоскости в прямоугольной системе координат и нужно определить, принадлежит ли эта точка прямой, описываемой параметрическими уравнениями x = x 1 + a x · λ y = y 1 + a y · λ .
Чтобы решить подобную задачу, необходимо подставить координаты заданной точки в известные параметрические уравнения прямой. Если будет определено, что возможно такое значение параметра λ = λ 0 , при котором будут верными оба параметрических уравнения, тогда заданная точка является принадлежащей заданной прямой.
Заданы точки М 0 ( 4 , – 2 ) и N 0 ( – 2 , 1 ) . Необходимо определить, являются ли они принадлежащими прямой, определенной параметрическими уравнениями x = 2 · λ y = – 1 – 1 2 · λ .
Решение
Подставим координаты точки М 0 ( 4 , – 2 ) в заданные параметрические уравнения:
4 = 2 · λ – 2 = – 1 – 1 2 · λ ⇔ λ = 2 λ = 2 ⇔ λ = 2
Делаем вывод, что точка М 0 принадлежит заданной прямой, т.к. соответствует значению λ = 2 .
Далее по аналогии проверим заданную точку N 0 ( – 2 , 1 ) , подставив ее координаты в заданные параметрические уравнения:
– 2 = 2 · λ 1 = – 1 – 1 2 · λ ⇔ λ = – 1 λ = – 4
Очевидно, что не существует такого параметра λ , которому будет соответствовать точка N 0 . Другими словами, заданная прямая не проходит через точку N 0 ( – 2 , 1 ) .
Ответ: точка М 0 принадлежит заданной прямой; точка N 0 не принадлежит заданной прямой.
- В задачах второго типа требуется составить параметрические уравнения прямой на плоскости в прямоугольной системе координат. Самый простой пример такой задачи (при известных координатах точки прямой и направляющего вектора) был рассмотрен выше. Теперь разберем примеры, в которых сначала нужно найти координаты направляющего вектора, а потом записать параметрические уравнения.
Пример 8
Задана точка M 1 1 2 , 2 3 . Необходимо составить параметрические уравнения прямой, проходящей через эту точку и параллельной прямой x 2 = y – 3 – 1 .
Решение
По условию задачи прямая, уравнение которой нам предстоит опередить, параллельна прямой x 2 = y – 3 – 1 . Тогда в качестве направляющего вектора прямой, проходящей через заданную точку, возможно использовать направляющий вектор прямой x 2 = y – 3 – 1 , который запишем в виде: a → = ( 2 , – 1 ) . Теперь известны все необходимые данные для того, чтобы составить искомые параметрические уравнения:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 1 2 + 2 · λ y = 2 3 + ( – 1 ) · λ ⇔ x = 1 2 + x · λ y = 2 3 – λ
Ответ: x = 1 2 + x · λ y = 2 3 – λ .
Задана точка М 1 ( 0 , – 7 ) . Необходимо записать параметрические уравнения прямой, проходящей через эту точку перпендикулярно прямой 3 x – 2 y – 5 = 0 .
Решение
В качестве направляющего вектора прямой, уравнение которой надо составить, возможно взять нормальный вектор прямой 3 x – 2 y – 5 = 0 . Его координаты ( 3 , – 2 ) . Запишем требуемые параметрические уравнения прямой:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 0 + 3 · λ y = – 7 + ( – 2 ) · λ ⇔ x = 3 · λ y = – 7 – 2 · λ
Ответ: x = 3 · λ y = – 7 – 2 · λ
- В задачах третьего типа требуется осуществить переход от параметрических уравнений заданной прямой к прочим видам уравнений, которые ее определяют. Решение подобных примеров мы рассматривали выше, приведем еще один.
Пример 10
Дана прямая на плоскости в прямоугольной системе координат, определяемая параметрическими уравнениями x = 1 – 3 4 · λ y = – 1 + λ . Необходимо найти координаты какого-либо нормального вектора этой прямой.
Решение
Чтобы определить искомые координаты нормального вектора, осуществим переход от параметрических уравнений к общему уравнению:
x = 1 – 3 4 · λ y = – 1 + λ ⇔ λ = x – 1 – 3 4 λ = y + 1 1 ⇔ x – 1 – 3 4 = y + 1 1 ⇔ ⇔ 1 · x – 1 = – 3 4 · y + 1 ⇔ x + 3 4 y – 1 4 = 0
Коэффициенты переменных x и y дают нам требуемые координаты нормального вектора. Таким образом, нормальный вектор прямой x = 1 – 3 4 · λ y = – 1 + λ имеет координаты 1 , 3 4 .
Элементы дифференциальной геометрии. Естественная параметризация
Содержание:






По этой ссылке вы найдёте полный курс лекций по математике:
Наглядный геометрический объест — плоская кривая — приточных определениях приводит к нескольким различным, хотя и близким понятиям. Плоскую кривую можно понимать и как некоторое множество точек на плоскости и как множество точек плоскости вместе с очередностью их прохождения — ориентацией. Приведем два наиболее распространенных подхода к определению того, что представля ет собой плоская кривая. Пусть на плоскости введена прямоугольная декартова система координат Оху.
Определение 1 (неявный способ задания):
Плоской кривой называется множество 7 точек М плоскости, координаты х и у которых при подстановке в уравнение ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ Плоские кривые. Способы задания. Естественная параметризация обращают его в тождество. Пример 1 Уравнение , задает окружность радиуса а с центром в точке 0(0,0) <рис. 1).
Другим распространенным способом задания плоской кривой является параметрический способ задания. Определение 2. Параметризованной плоской кривой называется множество 7 точек М плоскости, координаты г и у которых определяются соотношениями непрерывные на отрезке [а, 6] функции. Пример 2. — параметрические уравнения окружности радиуса а с центром в точке 0(0,0). При изменении параметра t от 0 до 2т соответствующая точка обегает окружность против часовой стрелки.
Данное определение допускает естественную физическую интерпретацию. Если воспринимать параметр t как время, то параметрически заданную кривую можно рассматривать как след движущейся точки М(х, у), координаты которой изменяются со временем по правилу (2). При этом вовсе не исключается случай, когда при своем движении переменная точка М в некоторый момент t* может вновь оказаться там, где ранее (в момент i, она уже находилась: (рис.2). Геометрически этоодна и та же точка.
Однако вследствие того, что в рассматриваемом процессе мы попадаем в нее дважды в разные моменты времени, это две разные точки кривой, задаваемой параметрическими уравнениями (2). Замечание. Строго говоря, определении I и 2 вводят в рассмотрение разные объекты. Поэтому для того, чтобы не впасть в заблуждение, нужно ясно представлять, в каком именно смысле рассматривается задаваемая кривая. Пусть кривая 7 задана параметрическими уравнениями называется начальной тонкой этой кривой, а точка ) — конечной тонкой кривой 7.
Кривая 7 называется замкнутой, если ее начальная и конечная точки совпадают (рис. 4).
– Рис. 4 Одно и то же м ножество точекн а плоскости можно задавать при помощи различных параметрических уравнений. Пример 3. Уравнения задают окружность радиуса а, обходимую в положительном направлении. Легко видеть, что, положив в формулах (3) 2хг3, мы приходим к соотношениям (4). Определение. Функция подчиненная условиям: а) Н<т) непрерывна на отрезке [а, /3]; h(r) строго возрастает на отрезке [се, >3]; в) область значения функции h(r) — отрезок [а, Ь], называется непрерывной заменой параметра кривой 7 (рис. 5). ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ Плоские кривые.
Способы задания
Естественная параметризация Заменяя в формулах (2) параметр t на функцию Л(т), получаем уравнения — другую параметризацию кривой 7. Любую кривую можно параметризовать многими различными способами. Определение 3. Плоская кривая 7 называется п-гладкой относительно параметризации если функции ) принадлежит классу .
Если порядок п гладкости функций несуществен, то говорят просто о гладкой кривой. Пример 4. Кривая заданная уравнениями является 3-гладкой (рис. в а). Пример S. Кривая 7, заданная уравнениями является 2-гладкой. Однако множеств о точек на плоскости, описываемое этими уравнениями, имеет • точке О (при t ) особенность — излом (рис.вб). Это означает, что гладкость функций . задающих кривую, не обеспечивает плавного ее изменения.
Отметим, что производные этих функций при tодновременно обращаются а нуль. ТЪчка Мо гладкой кривой у, отвечающая значению t0 параметра, М0 в которой называется особой точкой этой кривой (относительно заданной параметризации). Точка Мо(*о) гладкой кривой 7, в которой называется обыкновенной, ншрегулярной, точкой этой кривой. Пример в. Все точки окружности (3) являются регулярными.
Пример 7. У кривой, задаваемой уравнениями (астроида) четыре особых точки (при t ж 0, | Последнее неравенство означает, что скорость кривой 7 относительно заданной параметризации не обращается в нуль ни в одной точке кривой. При изменении параметра t текущая точка M(t) перемещается порегулярной кривой 7, нигде не оста- навливаясь и не поворачивая вспять, поскольку скорость регулярной кривой ни при каких значениях параметра не обращается в нуль.
Возможно вам будут полезны данные страницы:
Пусть 7 — регулярная кривая, заданная параметрически. Обозначим через Мо точку кривой 7, отвечающую значению £о параметра, а через М — точку кривой 7, отвечающую значению t параметра из некоторой окрестности точки to (рис. 8, 9). Прямая М0Т называется касательной регулярной кривой 7 вточке Мо, если при (или, что то же, ) наименьший Д0 из углов между этой прямой и переменной прямой MqM стремится к нулю (рис. 9). Регулярная кривая имеет касательную в каждой своей точке.
Вектор скорости кривой в точке Мо коллинеарен ее ка- сательной в этой точке. Прямая, проходящая через точку Мо перпендикулярно касательной кривой 7 в этой точке, называется нормалью кривой вточке Мо. Замена параметра называется регулярной у если Л'(т во всех точках отрезка [а, /3]. В случае неявного задания (1) кривая 7 будет регулярной, если в каждой ее точке М(х, у) выполняется неравенство Точка Мо(жо> Уо) неявно заданной кривой 7 называется особой, если в этой точке Пример 8.
Кривая, заданная уравнением
(леммисюга Бернулт), имеет одну особую точку 0(0,0) — узел (рис.10). Различают несколько типов особых точек. Пусть М0(хо, уо) — особая точка кривой 7, Введем следующие обозначения возврата первого рода. Пример 12. (рис. 14). — точка возврата второго рода. Гладкая (тем более регулярная) кривая спрямляема. Длина кривой 7, заданной уравнениями (2), вычисляется по формуле Значение функции равно длине переменной дуги кривой7, заключенной между точками (рис. 15).
Функция на отрезке [а, 6) строго возрастает, Пример 11. ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ Плоские кривые. Способы задания. Естественная параметризация и является гладкой на отрезке [а, 6]. Кроме того, область значений функции s(t) совпадает с отрезком [0, 5]. Тем самым, длину дуги можно взять за новый, естественный (натуральный) параметр кривой.
Параметризация кривой, где в качестве параметра взята длина дуги з, называется естественной параметризацией. Если естественная параметризация кривой, то Поэтому естественно параметризованную кривую часто называют кривой с единичной скоростью. Пример 13. Параметризация окружности радиусе а является естественной:
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/parametricheskie-uravnenija-prjamoj-na-ploskosti/
http://natalibrilenova.ru/elementyi-differentsialnoj-geometrii-estestvennaya-parametrizatsiya-/
[/spoiler]

Пример параметрической кривой.
Параметрическое представление — используемая в математическом анализе разновидность представления переменных, когда их зависимость выражается через дополнительную величину — параметр.
Параметрическое представление функции[править | править код]
Предположим, что функциональная зависимость 



Тогда формулы:
задают параметрическое представление функции одной переменной.
Если предположить, что обе эти функции 



и производная функции 
Параметрическое представление даёт такое важное преимущество, что позволяет изучать неявные функции в тех случаях, когда их приведение к явному виду иначе как через параметры затруднительно или невозможно через элементарные функции.
Параметрическое представление уравнения[править | править код]
Параметрическое представление для более общего случая: когда переменные связаны уравнением (или системы уравнений, если переменных больше двух).
Параметрическое уравнение[править | править код]
Близкое понятие — параметрическое уравнение[2] множества точек, когда координаты точек задаются как функции от некоторого набора свободных параметров.
Если параметр один, мы получим параметрическое уравнение кривой.
(кривая на плоскости),
(кривая в 3-мерном пространстве),
Выражая координаты точек поверхности через два свободных параметра, мы получим параметрическое задание поверхности.
Примеры[править | править код]
Уравнение окружности имеет вид:
Параметрическое уравнение окружности:
Гипербола описывается следующим уравнением:
Параметрическое уравнение правой ветви гиперболы :
См. также[править | править код]
- Параметрическое задание поверхности
Примечания[править | править код]
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. Том I. Москва 1969 г. Стр 218.
- ↑ Математическая энциклопедия. — М.: Советская энциклопедия, 1984. — Т. 5. — С. 221—222.
Ссылки[править | править код]
- Параметрическое задание кривой. Лекции по математическому анализу
- Лекции по математическому анализу. доцент кафедры математического анализа Иркутского госуниверситета Романова О. А.
Макеты страниц
При отыскании уравнения геометрического места по данному его свойству не всегда бывает удобно или возможно выразить это свойство непосредственно в виде уравнения, связывающего текущие координаты х, у. В таком случае бывает полезно ввести третью, вспомогательную переменную величину, через которую можно выразить отдельно абсциссу х и ординату у любой точки геометрического места.
Совокупность двух полученных таким путем уравнений

также может служить для построения и исследования кривой, так как при каждом значении t она определяет положение соответствующей точки кривой.
Такой способ задания кривой называется параметрическим, вспомогательная же переменная t — параметром. Для получения Уравнения кривой в обычном (явном или неявном) виде как зависимости, связывающей х и у, нужно из двух уравнений (9) исключить параметр t, что можно сделать, хотя бы решив одно из этих Уравнений относительно t и подставив полученный результат в другое.
С параметрическим заданием кривых особенно часто приходится иметь дело в механике, при исследовании траектории движущейся точки, положение которой зависит от времени  , а потому и координаты суть функции от t. Определив эти функции, мы и получим параметрическое задание траектории.
, а потому и координаты суть функции от t. Определив эти функции, мы и получим параметрическое задание траектории.
Так, например, параметрическое уравнение окружности с центром в точке  и радиусом
и радиусом  будет
будет

Перепишем эти уравнения:

Возводя обе части в квадрат и складывая, исключим парамегр t и получим обычное уравнение окружности

Точно так же непосредственно ясно, что

есть параметрическое уравнение эллипса

Положим, что у, как функция от  , определена параметрически формулами (9).
, определена параметрически формулами (9).
Приращение параметра  вызовет соответствующие приращения
вызовет соответствующие приращения  и мы получим, деля числитель и знаменатель дроби на
и мы получим, деля числитель и знаменатель дроби на  следующее выражение для производной от у до
следующее выражение для производной от у до 

или

Составим вторую производную от у по х:

Применяя правило нахождения дифференциала частного, получим [50]

Но, в силу (9),

Подставляя это в (13) и сокращая на  получим окончательно
получим окончательно

Заметим, что выражение  по формуле (13) отличается от выражения той же производной по формуле (3) из
по формуле (13) отличается от выражения той же производной по формуле (3) из 

потому что это последняя формула выведена лишь в том предположении, что  есть независимая переменная, а при параметрическом представлении (9) независимой переменной является t. Если х есть независимая переменная, то dx считается уже постоянным [50], т. е. не зависящим от
есть независимая переменная, а при параметрическом представлении (9) независимой переменной является t. Если х есть независимая переменная, то dx считается уже постоянным [50], т. е. не зависящим от  как дифференциал постоянной. При этом формула (13) переходит в (15).
как дифференциал постоянной. При этом формула (13) переходит в (15).
Имея возможность определить у и  мы тем самым можем решить вопрос о направлении касательной к кривой, о выпуклости и вогнутости кривой и т. д.
мы тем самым можем решить вопрос о направлении касательной к кривой, о выпуклости и вогнутости кривой и т. д.
В качестве примера рассмотрим кривую, заданную уравнением

и называемую «листом Декарта».
Введем переменный параметр t, полагая

и рассмотрим точки пересечения прямой (17) с переменным угловым коэффициентом t и кривой (16). Подставляя в уравнение (16) выражение у из уравнения (17) и сокращая на  , получим
, получим

а уравнение (17) даст нам тогда

Эти уравнения дают параметрическую форму представления листа Декарта. Определим производные от х и у по 

Для исследования изменения х и у разобьем весь промежуток  изменения t на такие отдельные части, внутри которых производные
изменения t на такие отдельные части, внутри которых производные  сохраняют неизменный знак и не обращаются в бесконечность. Для этого нам придется отметить значения:
сохраняют неизменный знак и не обращаются в бесконечность. Для этого нам придется отметить значения:

при которых эти производные обращаются в нуль или бесконечность. Знаки  внутри этих промежутков определятся без труда по формулам (18); вычислив значения х и у на концах промежутков, мы получим, таким образом, приведенную ниже таблицу.
внутри этих промежутков определятся без труда по формулам (18); вычислив значения х и у на концах промежутков, мы получим, таким образом, приведенную ниже таблицу.
В соответствии с этой схемой мы получим кривую, изображенную на рис. 85.

Рис. 85.

Для вычисления углового коэффициента касательной имеем формулу

Обратим внимание на то, что  обращаются в нуль при
обращаются в нуль при  и кривая, как это видно из чертежа, пересекает сама себя в начале координат.
и кривая, как это видно из чертежа, пересекает сама себя в начале координат.
Формула (19) дает нам

т. е. две ветви кривой, взаимно пересекающиеся в начале координат, касаются — одна оси ОХ и другая оси 
При стремлении t к  и у стремятся к бесконечности, и кривая имеет бесконечную ветвь. Определим асимптоту:
и у стремятся к бесконечности, и кривая имеет бесконечную ветвь. Определим асимптоту:
угловой коэффициент асимптоты равен  ,
,

т. e. уравнение асимптоты будет

Предположим, что функция x (t) имеет обратную t Ф(x) , тогда
является функцией от х. Уравнения (3.9) определяют у как функцию от х, и говорят, что функция задана параметрически. Для того чтобы получить из (3.9) (3.10) надо из (3.9) исключить t.
Например, координаты любой точки окружности выра-
|
x r cos t |
||
|
зятся через параметр t следующим образом: |
. |
|
|
y r sin t |
||
|
Это параметрическое уравнение окружности. |
Если ис- |
ключить из этих уравнений параметр t, то получим уравнение окружности, содержащее только х и у. Возведем уравнения в квадрат и сложим: x2 r 2 cos2 t , y 2 r 2 sin 2 t , x2 y 2 r 2 .
Найдем производную от функции y(x) заданной параметрически уравнениями y (t), x (t) , t0 t T .
|
Предположим, что эти функции имеют производные и |
|||||||||||||
|
функция x (t) имеет обратную t Ф(x) , тогда |
y Ф(x) |
||||||||||||
|
и по правилу дифференцирования сложной функции: |
|||||||||||||
|
y‘ |
‘ |
Ф‘(x) , |
Ф‘ |
1 |
. Тогда |
||||||||
|
x |
x |
||||||||||||
|
t |
‘t |
||||||||||||
|
y‘ |
‘t |
y‘t |
. |
(3.11) |
|||||||||
|
x |
|||||||||||||
|
‘t |
x‘t |
||||||||||||
Примеры 3.8. Найти производные заданных функций.
x a cos t, 1) y b sin t. .
43

Решение. Функция задана параметрическими уравне-
|
ниями. Найдем производные |
x‘t |
a sin t |
, |
|||||||||||||||||
|
y‘t |
b cos t |
|||||||||||||||||||
|
тогда y‘ |
b cos t |
. |
||||||||||||||||||
|
x |
||||||||||||||||||||
|
a sin t |
||||||||||||||||||||
|
2) |
x a(t sin t), . |
|||||||||||||||||||
|
y a(1 cos t). |
||||||||||||||||||||
|
a(1 |
cos t), |
|||||||||||||||||||
|
Решение. xt |
||||||||||||||||||||
|
y |
a sin t. |
|||||||||||||||||||
|
t |
||||||||||||||||||||
|
t |
t |
|||||||||||||||||||
|
sin t |
2sin |
cos |
t |
|||||||||||||||||
|
y‘ |
2 |
2 |
ctg |
. |
||||||||||||||||
|
x |
cos t |
|||||||||||||||||||
|
1 |
t |
2 |
||||||||||||||||||
|
2 sin |
2 |
|||||||||||||||||||
|
2 |
||||||||||||||||||||
3.9. Неявная функция и ее дифференцирование
Пусть значения двух переменных х и у связаны между собой некоторым уравнением, которое обозначим
F(x, y) = 0. (3.12)
Если функция у = f(x), определенная на некотором интервале (a,b) такова, что уравнение (3.12) при подстановке в него вместо у выражения f(x) обращается в тождество относительно х, то функция у = f(x) есть неявная функция, определенная уравнением (3.12).
Так, например, уравнение
|
x 2 y 2 |
a 2 |
0 |
(3.13) |
||||
|
неявно определяет следующие элементарные функции |
|||||||
|
y |
a 2 x 2 , |
y |
a 2 x 2 . |
(3.14) |
Действительно, после подстановки в уравнение (3.13) этих значений получаем тождество
44
x2 (a 2 x2 ) a 2 0 .
Выражения (3.14) получились путем решения уравнения (3.13) относительно у. Но не всякую неявно заданную функцию можно представить явно, т.е. можно представить в виде у = f(x), где f(x) есть элементарная функция. Так, например,
функции, заданные уравнениями y 6 y x 2 0, y x sin y 0, не выражаются через элементарные функции,
т.е. эти уравнения нельзя разрешить относительно у.
Пусть функция задана уравнением (3.13). Для того, чтобы найти производную неявной функции, не преобразовывая ее в явную, продифференцируем обе части (3.13 ) по х, считая, что у есть функция от х. Пользуясь правилом дифференцирования сложной функции, получим 2x 2 yy 0 ,откуда y x / y.
|
Пример 3.9. Найти производную функции |
|||
|
y3 3y 2ax 0. |
|||
|
Решение. 3y 2 y 3y 2a 0, 3y ( y 2 1) 2a, |
|||
|
y |
2a |
||
|
. |
|||
|
3(1 y 2 ) |
|||
|
3.10. Дифференциал |
|||
|
Пусть функция y=f(x) дифференцируема на [a,b]. |
|||
|
Следовательно, существует предел y f (x) lim |
y . |
||
|
x 0 |
x |
||
|
Но тогда по свойству бесконечно малых, функцию |
|||
|
имеющую предел можно представить в виде |
|||
|
y y , |
(3.15) |
||
|
x |
где α – бесконечно малая, т.е. 0 при х 0. Умножим
(3.15) на х
45

|
y y x x . |
(3.16) |
|
Так как в общем случае y 0 , произведение |
y x есть |
бесконечно малая величина первого порядка относительно x . Произведение x есть бесконечно малая высшего порядка относительно x
lim x lim 0 .x 0 x x 0
Приращение y состоит из двух слагаемых, первое из
которых называется главной частью приращения, линейной относительно x . Произведение y x называется дифферен-
|
циалом и обозначается dy. |
|
|
dy= y x . |
(3.17) |
Найдем дифференциал функции y=x. dy y x x , dx x .
Дифференциал независимой переменной совпадает с ее приращением.. Формулу (3.17) можно переписать в виде
dy f (x)dx .
Из этого соотношения следует, что f (x) dydx , то есть
производная есть отношение дифференциала функции к дифференциалу независимой переменной.
Из (3.16) следует, что приращение функции отличается от дифференциала на величину бесконечно малую высшего порядка относительно x .
Если f `(x) 0 , x является бесконечно малой высшего порядка относительно dy .
Поэтому можно положить y dy .
f (x x) f (x) f (x) x .
Это приближенное равенство можно использовать в приближенных вычислениях.
46
Пример 3. 10. Найти dy и y функции y=x³.
Решение. y (x x)3 x3 3x2 x 3x(x)2 (x)3 , dy f (x)dx 3x2 x.
Задача нахождения дифференциала равносильна нахождению производной. Следовательно большинство теорем и формул, относящихся к производным, имеют место и для дифференциала.
3.11. Производные различных порядков
Пусть функция y=f(x) дифференцируема на [a,b]. Значение производной y также является функцией x.
Дифференцируя эту функцию, мы получим так называе-
мую производную второго порядка. Обозначают y или f (x) . Например, y x4 , y 4x3 , y 12x 2 .
Производная от второй производной называется производной третьего порядка y . Аналогично y IV , yV , yVI .
Производной n-го порядка от функции f(x) называется производная от производной (n-1)-го порядка и обозначается
символом y (n) ; y (n) ( y (n 1) ) – порядок производной указывается скобках.
Примеры 3.11. Найти выражения производных любого порядка n.
1. y ekx , y kekx , y k 2 ekx , …, y(n) k nekx . 2. y sin x ,
y cos x sin( 2 x) ,
y sin x sin(x 2 2 ) ,
47

y cos x sin(x 3 2 ) ,
. . . . . . . . . . . . . . . . . . .
y(n) sin(x n 2 ) .
3.12. Уравнения касательной и нормали
Рассмотрим кривую, уравнение которой y=f(x). На кривой выберем точку M(x1,y1), и напишем уравнение касательной к данной кривой в точке M.
Уравнение прямой с угловым коэффициентом k, проходящей через данную точку, имеет вид (y-y1)=k(x-x1). Для каса-
тельной k = tg α = f (х1), поэтому уравнение касательной: (y y1)= f ( x1) (x x1).
Рис. 16 Нормалью к кривой в данной точке называется прямая,
проходящая через точку, перпендикулярно касательной. Угловой коэффициент нормали связан с угловым коэффициентом
|
касательной формулой kn |
1 |
. |
|
kt |
Следовательно, уравнение нормали к кривой в т. М имеет вид
|
y y1 |
1 |
(x x1 ) . |
|
|
f (x1 ) |
|||
|
48 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #


![{displaystyle y=psi [theta (x)]=f(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a6655d55a827496eda07b74aa951808c63e912a)







