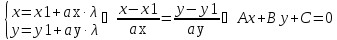Как найти параметрическое уравнение прямой через общее - Сайт, где вы сможете решить свои вопросы

Получить уравнение прямой, проходящей через две точки помогут созданные нами калькуляторы. Предлагаем найти каноническое и параметрическое уравнение прямой, а также уравнение прямой с угловым коэффициентом как на плоскости, так и в пространстве.

Прямая – это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.

Уравнения прямой, проходящей через две точки могут быть следующих видов:

каноническое уравнение,
параметрическое уравнение,
общее уравнение прямой,
уравнение прямой с угловым коэффициентом,
уравнение прямой в полярных координатах и другие.

Для получения уравнений введите координаты двух точек прямой. Онлайн-калькулятор найдет уравнения и выдаст результат с подробным решением.

Каноническое уравнение прямой на плоскости

{dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a}}

x_a и y_a – координаты первой точки A,

x_b и y_b – координаты второй точки B

Параметрическое уравнение прямой на плоскости

{begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a end{cases}}

x_a, y_a – координаты точки, лежащей на прямой,

{l;m} – координаты направляющего вектора прямой,

t – произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.

Каноническое уравнение прямой в пространстве

{dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a} = dfrac{z-z_a}{z_b-z_a}}

x_a, y_a и z_a – координаты первой точки A,

x_b, y_b и z_b – координаты второй точки B

Параметрическое уравнение прямой в пространстве

{ begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a \ z=n cdot t + z_a end{cases} }

x_a, y_a и z_a – координаты точки, лежащей на прямой,

{l;m;n} – координаты направляющего вектора прямой,

t – произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.

Пример нахождения уравнения прямой, проходящей через две точки

Найдем уравнения прямой, проходящей через точки A(1,2) и B(3,8).

Каноническое уравнение прямой

Каноническое уравнение прямой, проходящей через две точки имеет вид {dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a}}

Подставим в формулу координаты точек A и B: {dfrac{x-1}{3-1} = dfrac{y-2}{8-2}}

Получаем каноническое уравнение прямой: {dfrac{x-1}{2} = dfrac{y-2}{4}}

Уравнение прямой с угловым коэффициентом

Из канонического уравнения получаем уравнение прямой с угловым коэффициентом: {y=3x-1}

Параметрическое уравнение прямой

Параметрическое уравнение прямой имеет вид:

{ begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a end{cases} }

где {x_a, y_b} – координаты точки, лежащей на прямой, {{l;m}} – координаты направляющего вектора прямой, t – произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении. В качестве координат используем координаты точки {A(x_a, y_b)}.

Найдем координаты направляющего вектора:

overline{AB} = {x_b – x_a; y_b – y_a} = {3-1; 8-2} = {2; 6}

Получаем параметрическое уравнение:

begin{cases} x=2 t + 1 \ y=6 t + 2 end{cases}

Используем калькулятор для проверки полученного ответа.

Источник

Параметрическое уравнение прямой на плоскости

В данной статье мы рассмотрим параметрическое уравнение прямой на плоскости. Приведем примеры построения параметрического уравнения прямой, если известны две точки этой прямой или если известна одна точка и направляющий вектор этой прямой. Представим методы преобразования уравнения в параметрическом виде в канонический и общий виды.

Параметрическое уравнение прямой L на плоскости представляется следующей формулой:

где x₁, y₁ координаты некоторой точки M₁ на прямой L. Вектор q={m, p} является направляющим вектором прямой L, t − некоторый параметр.

Отметим что при записи уравнения прямой в параметрическом виде, направляющий вектор прямой не должен быть нулевым вектором, т.е хотя бы один координат направляющего вектора q должен быть отличным от нуля.

Для построения прямой на плоскости в декартовой прямоугольной системе координат, заданной параметрическим уравнением (1), достаточно задать параметру t две разные значения, вычислить x и y и провести через эти точки прямую линию. При t=0 имеем точку M₁(x₁, y₁) при t=1, получим точку M₂(x₁+m, y₁+p).

Для составления параметрического уравнения прямой на плоскости L достаточно иметь точку на прямой L и направляющий вектор прямой или две точки, принадлежащие прямой L. В первом случае, для построения параметрического уравнения прямой нужно координаты точки и направляющего вектора вставить в уравнение (1). Во втором случае сначала нужно найти направляющий вектор прямой q={m, p}, вычисляя разности соответствующих координатов точек M₁ и M₂: m=x₂−x₁, p=y₂−y₁(Рис.1). Далее, аналогично первому случаю, подставить координаты одной из точек (не имеет значение какой именно) и направляющего вектора q прямой в (1).

Можно также вывести формулу параметрического уравнения прямой, проходящей через две точки. Для этого подставим значения m=x₂−x₁, p=y₂−y₁ в (1), получим параметрическое уравнение прямой на плоскости, проходящей через точки M₁(x₁, y₁) и M₂(x₂, y₂):

Пример 1. Прямая проходит через точку M=(3,−1) и имеет направляющий вектор q={−3, 5}. Построить параметрическое уравнение прямой.

Решение. Для построения параметрического уравнения прямой, подставим координаты точки и направляющего вектора в уравнение (1):

Ответ:

Пример 2. Прямая проходит через точки M₁=(−5, 2) и M₂=(−2, 3). Построить параметрическое уравнение прямой.

Решение. Воспользуемся формулой (2). Подставим координаты точек M₁ и M₂ в уравнение (2):

Упростим полученное уравнение:

Ответ:

Приведение параметрического уравнения на плоскости к каноническому виду

Выразим параметр t в (1) через переменные x и y:

Из выражений (3), можем записать каноническое уравнение прямой на плоскости:

Обратное преобразование смотрите здесь.

Пример 3. Прямая на плоскости представлена следующим параметрческим уравнением:

Привести данное уравнение прямой к каноническому виду.

Решение: Выразим параметр t через переменные x и y:

Из выражений (5), можем записать:

Ответ.

Приведение параметрического уравнения на плоскости к общему виду

Для приведения параметрического уравнения прямой на плоскости к общему виду, в формулах (1) выразим из второго уравнения параметр t через переменную y и подставим в первое уравнение:

Умножим обе части уравнения (6) на p и группируем элементы уравнения:

Сделаем обозначения: A=p, B=−m, C=−px₁+my₁. Тогда получим общее уравнение прямой:

Обратное преобразование смотрите здесь.

Пример 4. Прямая на плоскости представлена следующим параметрческим уравнением:

Привести данное уравнение прямой к общему виду.

Решение: В уравнении (9) имеем: x₁=−5, y₁=0, m=4, p=−2. Подставим эти значения в формулу (7):

Упростив выражение (10) получим общее уравнение прямой (9):

Ответ.

Источник

Простейшая
линия на плоскости – прямая.

Уравнение
линии на плоскости:

Уравнение
с угловым коэффициентом–

Под углом
наклона
прямой понимается наименьший угол, на
который нужно повернуть вокруг точки
пересечения прямой и оси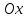против часовой стрелки осьдо ее совпадения с прямой.

Число
=tgназываетсяугловым коэффициентомпрямой, а уравнение–уравнением прямой с угловым
коэффициентом.

Если прямая проходит через начало
координат, то
и, следовательно, уравнение прямой будет
иметь вид.

Если прямая параллельна оси
,
то,
следовательно,=tg=0
и уравнение имеет вид.

Если прямая параллельна оси
,
тои уравнение теряет смысл, так как для
нее угловой коэффициент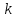=tg=tgне существует. В этом случае уравнение
прямой будет иметь вид,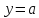
где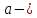абсцисса
точки пересечения прямой с осью.

Общее
уравнение–,
где,
так как нормальный векторпрямойL:не равен нулю и перпендикулярен прямойL.

Возможны два случая.

Если
,
то уравнение имеет вид,
причем,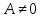
т. е..
Это есть уравнение прямой, параллельной
осии проходящей через точку.

Если
,
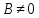
то получаем уравнение.
Это есть уравнение прямой с угловым
коэффициентом=tg=.

Есть частные случаи общего уравнение
прямой:

Если
,
то уравнение приводится к виду.
Это есть уравнение прямой, параллельной
оси;
Если
,
то прямая параллельна оси;
Если
,
то получаем.
Уравнению удовлетворяют координаты
точки,
прямая проходит через начало координат.

Уравнение
прямой, проходящей через две заданные
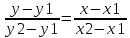
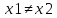
точки–(при,).

Пусть прямая проходит через точки
М₁(x₁;y₁)иM₂(x₂;y₂).
Уравнение прямой, проходящей через
точкуМ₁, имеет видy–y₁=k(x–x₁),
гдеk– пока
неизвестный коэффициент.

Так как прямая проходит через точку
M₂(x₂;y₂),
то координаты этой точки должны
удовлетворять уравнениюy₂–y₁=k(x₂–x₁).
Отсюда находим.
Подставляя найденное значение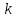в уравнениеy–y₁=k(x–x₁),
получим уравнение прямой, проходящей
через точкиМ₁иM₂:.

Параметрическое
уравнение –

Пусть на плоскости зафиксирована
прямоугольная
декартова система координатOxy.
Зададим прямуюa, указав лежащую на
ней точкуM₁(x₁;y₁)
и направляющий вектор этой прямой.

Возьмем произвольную точку плоскости
M(x;y).
Мы можемвычислить
координаты вектора.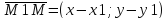
Очевидно, что множество всех точек
M(x;y)
задают прямую, проходящую через точкуM₁(x₁;y₁)
и имеющую направляющий вектор,
тогда и только тогда, когда векторы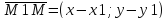иколлинеарны.

Необходимое
и достаточное условие коллинеарности
векторов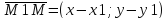изаписывается в виде уравнения,
где– некоторое действительное число.
Полученное уравнение называется
векторно-параметрическим уравнением
прямой. Векторно-параметрическое
уравнение прямой в координатной форме
имеет вид.
Уравнения полученной системыназываютсяпараметрическими
уравнениями прямойна плоскости.

Каноническое
уравнение –

Пусть на плоскости зафиксирована
прямоугольная
декартова система координатOxy.
Нужно получить уравнение прямойa,
еслиM₁(x₁;y₁)
– некоторая точка прямойaи-направляющий
вектор прямойa.

Пусть M(x;y)-
плавающая точка прямойa. Тогда
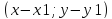
векторявляется направляющим вектором прямойaи имеет координаты.
Очевидно, что множество всех точекM(x;y)на
плоскости определяют прямую, проходящую
через точкуM₁(x₁;y₁)
и имеющую направляющий вектортогда
и только тогда, когда векторыи– коллинеарны.

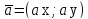
Равенство
в координатной форме имеет вид.

Если
и,
то мы можем записать.

Полученное уравнение вида
называютканоническим уравнениемпрямойна плоскости. Это уравнение также
называют уравнением прямой в каноническом
виде.

* Уравнение
прямой в отрезках –

Пусть прямая пересекает ось в точке
М₁(),
а ось– в точкеМ₂().
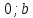
В этом случае уравнение имеет вид,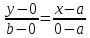
т. е..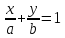
Это уравнение называетсяуравнением
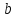
прямой в отрезках, так как числаиуказывают, какие отрезки отсекает прямая
на осях координат.

Полярное
уравнение –
.

Положение прямой можно определить,
указав расстояние
от полюса О до данной прямой и уголмежду полярной осью ОР и осью,
проходящей через полюс О перпендикулярно
данной прямой.

Для любой точки М()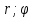
на данной прямой имеем:

пр_l=.

С другой стороны,

пр_l=||.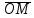

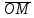
Следовательно,

Полученное уравнение и есть уравнение
прямой в полярных координатахилиполярное уравнение прямой.

Нормальное
уравнение прямой –

Пусть прямая определяется заданием
и.
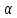
Рассмотрим прямоугольную систему
координатOxy. Введем
полярную систему, взявОза полюс иOx за полярную ось.
Уравнение прямой можно записать в виде,
т. е..

Но, в силу формул, связывающих прямоугольные
и полярные координаты, имеем:
,.
Следовательно уравнениепрямой в прямоугольной системе координат
имеет вид.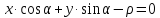

Это уравнение называется нормальным
уравнением прямой.

Геометрический
смысл коэффициентов в уравнениях прямой.

Коэффициент kв уравнении прямой с
точностью до знака равен тангенсу
острого угла, который образует прямая
с осью.

Переход из
одного вида уравнения в другой.

Приведение общего уравнения прямойк каноническому уравнению прямой: если,
то переносим слагаемое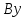в правую часть равенствас
противоположным знаком.
В левой части равенства выносимАза скобки.
Полученное равенство можно записать
как пропорцию вида.

Если
,
то оставляем в левой части общего
уравнения прямойтолько слагаемое,
а остальные переносим в правую часть с
противоположным знаком:.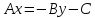
Теперь выносим в правой части равенства–Bза скобки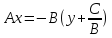и записываем полученное равенство в
виде пропорции.

Переход от общего уравнения прямой к
параметрическим уравнениям прямой
проводится в два этапа: сначала общее
уравнение приводится к каноническому
виду, а затем осуществляется переход
от канонического уравнения прямой к
параметрическим уравнениям прямой.

Разберем этот алгоритм при решении
примера.

Нужно написать параметрические уравнения
прямой, которая задана общим уравнением
прямой
.

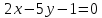
Сначала приведем исходное общее уравнение
прямой к каноническому уравнению
прямой:.

Теперь принимаем левую и правую части
полученного уравнения равными параметру
Теперь принимаем левую и правую части
полученного уравнения равными параметру
:.

Из общего уравнения прямой вида
получить
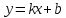
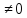
уравнение прямой с угловым коэффициентомвозможно лишь тогда, когда.

Для этого в левой части общего уравнения
прямой оставить только слагаемое:.
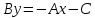
Затем разделить обе части полученного
равенства на число B, которое отлично
от нуля,.

Чтобы получить уравнение прямой в
отрезках вида
из общего уравнения прямой переносим
числоСв правую часть равенствас противоположным знаком, делим обе
части полученного равенства на–С,
и в заключении переносим в знаменатели
коэффициенты при переменных x иy:

Чтобы привести общее уравнение прямой
к нормальному виду нужно обе части
равенства
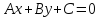
умножить на так называемый нормирующий
множитель, который равен.
Знак нормирующего множителя берется
противоположным знаку слагаемогоС.
Если,
то знак нормирующего множителя не имеет
значения и может быть выбран произвольно.

Для перехода к общему уравнению от
уравнения прямой в отрезках и уравнения
прямой с угловым коэффициентом достаточно
просто собрать все слагаемые в левой
части равенства:

Каноническое уравнение прямой приводится
к общему уравнению прямой с помощью
следующих преобразований:

От параметрических уравнений прямой
следует сначала перейти к каноническому
уравнению прямой, а уже потом к общему
уравнению прямо:

Соседние файлы в папке 1семестр_ответы

Источник

Прямая в пространстве – это линия, которая проходит от одной точки к другой, а также за пределы этих точек в бесконечность. Есть несколько видов уравнения прямой в пространстве: каноническое, параметрическое, угол между двумя прямыми в пространстве и т. д. Про это расскажем в данной статье и для наглядности предоставим несколько примеров.

Параметрическое и каноническое уравнение прямой в пространстве
Уравнение прямой в пространстве, которая проходит через две заданные точки
Общее уравнение прямой – переход к каноническому уравнению
Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых
Примеры решения задач

Параметрическое и каноническое уравнение прямой в пространстве

Параметрическое и каноническое уравнение прямой рассматривается практически так, как и для прямой на плоскости. Значит, нужно составить уравнение прямой , которая проходит через данную точку $M_{1} (x_{1}, y_{1}, z_{1})$ параллельно направляющему вектору .

Пусть, – произвольная точка прямой, тогда векторы $overline{M_{1}M} = (x - x_{1}, y - y_{1}, z - z_{1})$ и коллинеарные, а это значит, что координаты их пропорциональны, поэтому получаем:

${x - x_{1}over{l}} = {y - y_{1}over{m}} = {z - z_{1}over{p}}$

(1)

это и есть канонические уравнения прямой.

Приравнивая каждую из дробей (1) к параметру , запишем параметрические уравнения прямой:

$left{ begin{aligned} x = lt + x_{0}\ y = mt + y_{0}\ z = pt + z_{0} end{aligned}$

(2)

Уравнение прямой в пространстве, которая проходит через две заданные точки

Уравнение прямой в пространстве – тема очень лёгкая, так как здесь самое важное – знать нужную формулу. Тогда легко можно решить любую задачу.

Итак, через две точки $M_{1}(x_{1}, y_{1}z_{1}$ и $M_{2}(x_{2}, y_{2}, z_{2})$ можно не только геометрично провести линию, но и сложить её уравнения.

За направляющий вектор возьмём $overline{S} = overline{M_{1}M} = (x_{2} - x_{1}, y_{2} - y_{1}, z_{2} - z_{1})$ , тогда по формуле (1) у нас получается:

${x - x_{1}over{x_{2} - x_{1}}} = {y - y_{1}over{y_{2} - y_{1}}} = {z - z_{1}over{z_{2} - z_{1}}}$

(3)

уравнение прямой в пространстве, которые проходят через две заданные точки.

Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.

Подробнее

Общее уравнение прямой – переход к каноническому уравнению

Объяснение про общее уравнение прямой начнём с прямой, которая задана двумя плоскостями, что пересекаются по этой прямой.

Пусть известны их уравнения:

$left{begin{aligned}A_{1}x + B_{1}y + C_{1}z + D_{1} = 0\A_{2}x + B_{2}y + C{2}z + D_{2} = 0 end{aligned}$

(4)

Тогда система (4) называется общим уравнением прямой.

Чтобы перейти к каноническим уравнениям вида (1), необходимо найти вектор и точку $M_{0}$ этой прямой.

Точку $M_{0}$ находим, как один из решений системы (4). Например, положив в (4) находим $x_{0}, y_{0}$ , тогда и точку $M_{0} (x_{0}, y_{0}, 0)$ . Направляющий вектор , который параллелен к каждой из плоскостей $P_{1}$ и $P_{2}$ и перпендикулярен к их нормальным векторам $overline{n_{1}} = (A_{1}, B_{1}, C_{1})$ и $overline{n_{2}} = (A_{2}, B_{2}, C_{2})$ , то есть $overline{S}perp{overline{n_{1}}}$ , $overline{S}perp{overline{n_{2}}}$ . (см. рис. 1). Поэтому вектор можно найти при помощи векторного произведения $overline{n_{1}}$ и $overline{n_{2}}$

= $overline{n}_{1}$ x $overline{n}_{2}$ = $begin{vmatrix} overline{i}&overline{j}&overline{k}\ A_{1}&B_{1}&C_{1}\ A_{2}&B_{2}&C_{2} end{vmatrix}$

Найдены координаты $M_{0}$ и подставим в каноническое уравнение (1).

Например, от общих уравнений прямой:

$left{begin{aligned} 2x + 7y - z - 4 = 0\ 4x - 9y - 2z - 8 = 0 end{aligned}$

Перейдём к каноническим, положив в системе (при нём относительно больше коэффициенты). найдём $x = 2, z = 0, M_{0} (2, 0, 0)$ . Нормальные векторы $overline{n_{1}} = (2, 7, -1)$ и $overline{n_{2}} = (4, -9, -2)$ . Тогда направляющий вектор

Рис. 1

$overline{S} = overline{n}_{1}$ x $overline{n}_{2}$ = $begin{vmatrix} overline{i}&overline{j}&overline{k}\ 2&7&-1\ 4&-9&-2 end{vmatrix} = -23overline{i} - 0overline{j} - 46overline{k}$ ,

и канонические уравнения станут:

Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых

Угол между двумя прямыми :

${x - x_{1}over{l_{1}}} = {y - y_{1}over{m_{1}}} = {z - z_{1}over{p_{1}}}$ и ${x - x_{2}over{l_{2}}} = {y - y_{2}over{m_{2}}} = {z - z_{2}over{p_{2}}}$

равен углу между их направляющими векторами $overline{S_{1}} = (l_{1}, m_{1}, p_{1})$ и $overline{S_{2}} = (l_{2}, m_{2}, p_{2})$ , поэтому

${cosvarphi = cos(overline{S}_{1}}, overline{S}_{2}})$ = ${l_{1}l_{2} + m_{1}m_{2} + p_{1}p_{2}}over{sqrt{l_{1}^2 + m_{1}^2 + p_{1}^2}} * {sqrt{l_{2}^2 + m_{2}^2 + p_{2}^2}}$

(5)

Условия параллельности и перпендикулярности прямых соответственно запишутся:

${l_{1}over{l_{2}}} = {m_{1}over{m_{2}}} = {p_{1}over{p_{2}}}$ и $l_{1}l_{2} + m_{1}m_{2} + p_{1}p_{2} = 0$ .

(6)

Примеры решения задач

Давайте рассмотрим первый пример, где можно двумя способами построить прямую:

Задача

При точке и направляющем векторе необходимо:

составить каноническое уравнение прямой;
построить эту прямую.

Решение

1) По формуле (1) запишем каноническое уравнение прямой :

= .

2) Рассмотрим два способа построения прямой .

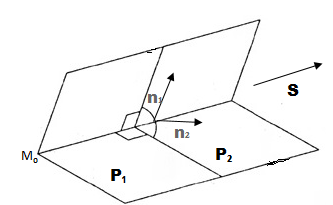
Первый способ

В системе координат строим вектор и точку и проводим через точку прямую параллельную вектору .

Второй способ

По формуле (2) запишем каноническое уравнение прямой в параметрическом виде:

$left{begin{aligned} x = 3t + 1\ y = 0 * t + 5\ z = 4t + 2 end{aligned} right$

На рисунке видно, что при произвольных значениях из системы находим координаты соответствующих точек, которые принадлежат прямой . Так при находим координаты $M_{1}(4, 5, 6)$ . Через две точки и $M_{1}$ проводим прямую .

Очевидно, что найти острый угол между прямыми совершенно не сложно при знании темы и определённых формул. Давайте разберём такой пример:

Задача

Найти острый угол между прямыми:

(7)

Решение

По формуле (7) получаем:

= ${6 * (-2) + (-2)(-1) + 3 * (-2)}over{sqrt{6^2 + (-2)^2 + 3^2} * sqrt{(-2)^2 + (-1)^2 + (-2)^2}$ = =

Так как , тогда угол тупой, , а острый угол .

Ответ

Рассмотрим последний пример, где нужно составить уравнение. Здесь, как и в каждой задаче, важно знать и понимать, какой формулой нужно воспользоваться.

Задача

Составить уравнение прямой , которая проходит через точку и параллельна прямой .

Решение

От параметрического уравнения переходим к каноническому При условии параллельности прямых $overline{S}||overline{S_{1}}$ то есть направляющим вектором новой прямой может служить известный вектор и по формуле (1) у нас получается:

Ответ

Источник

Прямая (прямая линия) – это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.

Уравнение прямой на плоскости

Любую прямую на плоскости можно задать уравнением прямой первой степени вида

A x + B y + C = 0

где A и B не могут быть одновременно равны нулю.

Уравнение прямой с угловым коэффициентом

Общее уравнение прямой при B≠0 можно привести к виду

y = k x + b

где k – угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.

k = tg φ

Уравнение прямой в отрезках на осях

Если прямая пересекает оси OX и OY в точках с координатами (a, 0) и (0, b), то она может быть найдена используя формулу уравнения прямой в отрезках

Уравнение прямой, проходящей через две различные точки на плоскости

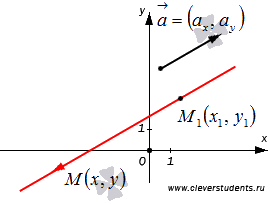
Если прямая проходит через две точки M(x₁, y₁) и N(x₂, y₂), такие что x₁ ≠ x₂ и y₁ ≠ y₂, то уравнение прямой можно найти, используя следующую формулу

x – x₁	=	y – y₁
x₂ – x₁	y₂ – y₁

Параметрическое уравнение прямой на плоскости

Параметрические уравнения прямой могут быть записаны следующим образом

x = l t + x₀y = m t + y₀

где N(x₀, y₀) – координаты точки лежащей на прямой, a = {l, m} – координаты направляющего вектора прямой.

Каноническое уравнение прямой на плоскости

Если известны координаты точки N(x₀, y₀) лежащей на прямой и направляющего вектора a = {l; m} (l и m не равны нулю), то уравнение прямой можно записать в каноническом виде, используя следующую формулу

Пример 1. Найти уравнение прямой проходящей через две точки M(1, 7) и N(2, 3).

Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки

x – 12 – 1 = y – 73 – 7

Упростив это уравнение получим каноническое уравнение прямой

x – 11 = y – 7-4

Выразим y через x и получим уравнение прямой с угловым коэффициентом

y – 7 = -4(x – 1)

y = -4x + 11

Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN.

MN = {2 – 1; 3 – 7} = {1; -4}

Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой

x = t + 1y = -4t + 7

Пример 2. Найти уравнение прямой проходящей через две точки M(1, 3) и N(2, 3).

Решение. Так как M_y – N_y = 0, то невозможно записать уравнение прямой проходящей через две точки.

Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN.

MN = {2 – 1; 3 – 3} = {1; 0}

Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой

x = t + 1y = 3

Уравнение прямой в пространстве

Уравнение прямой, проходящей через две различные точки в пространстве

Если прямая проходит через две точки M(x₁, y₁, z₁) и N(x₂, y₂, z₂), такие что x₁ ≠ x₂, y₁ ≠ y₂ и z₁ ≠ z₂, то уравнение прямой можно найти используя следующую формулу

x – x₁	=	y – y₁	=	z – z₁
x₂ – x₁	y₂ – y₁	z₂ – z₁

Параметрическое уравнение прямой в пространстве

Параметрические уравнения прямой могут быть записаны следующим образом

	x = l t + x₀
y = m t + y₀
z = n t + z₀

где (x₀, y₀, z₀) – координаты точки лежащей на прямой, {l; m; n} – координаты направляющего вектора прямой.

Каноническое уравнение прямой в пространстве

Если известны координаты точки M(x₀, y₀, z₀) лежащей на прямой и направляющего вектора n = {l; m; n}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу

x – x₀	=	y – y₀	=	z – z₀
l	m	n

Прямая как линия пересечения двух плоскостей

Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений

	A₁x + B₁y + C₁z + D₁ = 0
A₂x + B₂y + C₂z + D₂ = 0

при условии, что не имеет место равенство

A₁	=	B₁	=	C₁	.
A₂	B₂	C₂

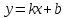
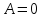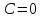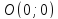Источник

Каноническое уравнение прямой на плоскости

Параметрическое уравнение прямой на плоскости

Каноническое уравнение прямой в пространстве

Параметрическое уравнение прямой в пространстве

Пример нахождения уравнения прямой, проходящей через две точки

Каноническое уравнение прямой

Уравнение прямой с угловым коэффициентом

Параметрическое уравнение прямой

Параметрическое уравнение прямой на плоскости

Приведение параметрического уравнения на плоскости к каноническому виду

Приведение параметрического уравнения на плоскости к общему виду

Параметрическое и каноническое уравнение прямой в пространстве

Уравнение прямой в пространстве, которая проходит через две заданные точки

Общее уравнение прямой – переход к каноническому уравнению

Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых

Примеры решения задач

Уравнение прямой на плоскости

Уравнение прямой с угловым коэффициентом

Уравнение прямой в отрезках на осях

Уравнение прямой, проходящей через две различные точки на плоскости

Параметрическое уравнение прямой на плоскости

Каноническое уравнение прямой на плоскости

Уравнение прямой в пространстве

Уравнение прямой, проходящей через две различные точки в пространстве

Параметрическое уравнение прямой в пространстве

Каноническое уравнение прямой в пространстве

Прямая как линия пересечения двух плоскостей

Вам также может понравиться

Как найти папку приложения на маке

Как найти могилу человека по номеру

Как найти данные на воевавшего родственника

Добавить комментарий Отменить ответ