Экспоненциально распределенная случайная величина
На странице Непрерывная случайная величина мы разобрали примеры решений для произвольно заданных законов распределения (многочлены, логарифмы и т.п.). Здесь же мы разберем примеры только для одного типа СВ – распределенных по показательному (или экспоненциальному) закону.
Плотность распределения величины $X$ с экспоненциальным законом распределения задается формулой:
$$
f(x)=
left{
begin{array}{l}
0, x lt 0\
lambda e^{-lambda x}, xge 0 \
end{array}
right.
$$
Функция распределения величины $X$:
$$
F(x)=
left{
begin{array}{l}
0, x lt 0\
1- e^{-lambda x}, xge 0 \
end{array}
right.
$$
Здесь $lambda$ – единственный параметр данного распределения, полностью определяющий его свойства. В частности, числовые характеристики выражаются через этот параметр: $M(X)=1/lambda$, $D(X)=1/lambda^2$.
Экспоненциальное распределение моделирует время между двумя последовательными свершениями события, а параметр $lambda$ описываетс среднее число наступлений события в единицу времени. Обычно с помощью этого закона описывают: продолжительность обслуживания покупателя, время жизни оборудования до отказа, промежуток времени между поломками и т.п.
В этом разделе мы приведем разные примеры задач с полным решением, где используются показательно распределенные случайные величины.
Спасибо за ваши закладки и рекомендации
Примеры решений
Задача 1. Среднее время безотказной работы прибора равно 80 часов. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти:
а) выражение его плотности вероятности и функции распределения;
б) вероятность того, что в течение 100 часов прибор не выйдет из строя.
Задача 2. Известно, что время работы прибора до первого отказа подчиняется показательному распределению со средним значением 1 год. Какова вероятность, что до первого отказа пройдет не менее 2 лет?
Задача 3. Установлено, что время ремонта телевизоров есть случайная величина $X$, распределенная по показательному закону с параметром $lambda=1/3$ (1/день). Определить вероятность того, что на ремонт телевизора потребуется не менее 5 дней.
Задача 4. Время в годах безотказной работы прибора подчинено показательному закону, т.е. плотность распределения этой случайной величины такова: $f(t)=2e^{-2t}$ при $tge 0$ и $f(t)=0$ при $tlt 0$.
1) Найти формулу функции распределения этой случайной величины.
2) Определить вероятность того, что прибор проработает не более года.
3) Определить вероятность того, что прибор безотказно проработает 3 года.
4) Определить среднее ожидаемое время безотказной работы прибора.
Задача 5. Предполагая, что случайное время обслуживания абонента службой «09» распределено по показательному закону и средняя продолжительность обслуживания составляет 1,5 минуты, найдите вероятность того, что абонент будет обслужен более, чем за 2 минуты.
Задача 6. Длительность телефонного разговора подчиняется показательному закону. Найти среднюю длительность разговора, если вероятность того, что разговор продлится более 5 минут, равна 0,4.
Задача 7. Случайная величина задана плотностью распределения $p(x)=ce^{-3x}$ при $x gt 0$, и ноль в остальных случаях. Найти постоянную $c$, математическое ожидание, дисперсию и среднее квадратическое отклонение.
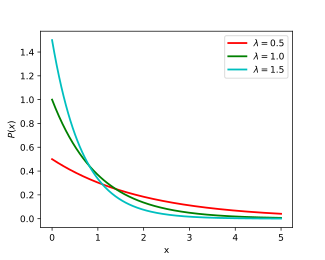
Задача 8. Непрерывная случайная величина $xi$ распределена по показательному закону с параметром $lambda$, равному номеру варианта 9. Найти плотность распределения случайной величины $xi$, функцию распределения, построить графики этих функций. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины $xi$ и вероятность того, что $xi$ принимает значения, меньшие своего математического ожидания.
Задача 9. Случайная величина $xi$ распределена по показательному закону с параметром 2. Найти $M_{xi}$, $D_{xi}$ вероятность попадания $xi$ в интервал $(-1;2)$. Нарисовать графики плотности распределения и функции распределения $xi$.
Задача 10. Известно, что $Х$ распределено по экспоненциальному закону $Exp(lambda)$. Найдите вероятность события $|Х – МХ | lt 3sigma$ (“правило $3sigma$” для показательного распределения).
Мы отлично умеем решать задачи по теории вероятностей
Решебник по теории вероятности онлайн
Больше 11000 решенных и оформленных задач по теории вероятности:
| Показательное распределение | |
|---|---|
 Плотность вероятности Плотность вероятности |
|
 Функция распределения Функция распределения |
|
| Обозначение |
 |
| Параметры |
 — интенсивность или обратный коэффициент масштаба — интенсивность или обратный коэффициент масштаба |
| Носитель |
 |
| Плотность вероятности |
 |
| Функция распределения |
 |
| Математическое ожидание |
 |
| Медиана |
 |
| Мода |
 |
| Дисперсия |
 |
| Коэффициент асимметрии |
 |
| Коэффициент эксцесса |
 |
| Дифференциальная энтропия |
 |
| Производящая функция моментов |
 |
| Характеристическая функция |
 |
Экспоненциа́льное (или показа́тельное[1]) распределе́ние — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.
Определение[править | править код]
Случайная величина 

.
Пример. Пусть есть магазин, в который время от времени заходят покупатели. При определённых допущениях время между появлениями двух последовательных покупателей будет случайной величиной с экспоненциальным распределением. Среднее время ожидания нового покупателя (см. ниже) равно 

В этой статье для определённости будем предполагать, что плотность экспоненциальной случайной величины 

Функция распределения[править | править код]
Интегрируя плотность, получаем функцию экспоненциального распределения:
Моменты[править | править код]
Несложным интегрированием находим, что производящая функция моментов для экспоненциального распределения имеет вид:
,
откуда получаем все моменты:
.
В частности,
,
,
.
Независимость событий[править | править код]
Пусть 

Пример. Пусть автобусы приходят на остановку случайно, но с некоторой фиксированной средней интенсивностью. Тогда количество времени, уже затраченное пассажиром на ожидание автобуса, не влияет на время, которое ему ещё придётся прождать.
Связь с другими распределениями[править | править код]
- Экспоненциальное распределение является частным случаем гамма-распределения:
- Экспоненциальное распределение может быть получено из непрерывного равномерного распределения методом обратного преобразования. Пусть
. Тогда:
- Экспоненциальное распределение с параметром
— это частный случай распределения хи-квадрат:
Примечания[править | править код]
- ↑ Андрей Рукосуев, Виктор Башлыков, Константин Балдин. Основы теории вероятностей и математической статистики. Учебник. — Litres, 2016-03-26. — С. 80. — 489 с. — ISBN 9785457365889.
- ↑ Королюк, 1985, с. 135.
- ↑ Виктор Каштанов, Алексей Медведев. Теория надежности сложных систем. — 2018. — С. 498. — 608 с.
Литература[править | править код]
- Королюк В. С., Портенко Н. И.,Скороход А. В., Турбин А. Ф. Справочник по теории вероятностей и математической статистике. — М.: Наука, 1985. — 640 с.
Показательное распределение
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины
, которое описывается плотностью:
где
–
постоянная положительная величина.
Показательное
распределение определяется одним параметром
. Эта особенность распределения указывает на
его преимущество по сравнению с распределениями, зависящими от большего числа
параметров. Обычно параметры неизвестны и приходится находить их оценки
(приближенные значения); разумеется, проще оценить один параметр, чем два или три.
Примером непрерывной случайной величины, распределенной по показательному
закону, может служить время между появлениями двух последовательных событий
простейшего потока.
Функция распределения
показательного закона:
Графики плотности и
функции распределения показательного закона изображены на рисунке.
Вероятность попадания в
интервал
непрерывной
случайной величины
, распределенной по показательному закону:
Числовые характеристики показательного (экспоненциального) распределения
Математическое ожидание случайной величины, распределенной по показательному закону:
Дисперсия случайной величины, распределенной по показательному закону:
Среднее квадратическое отклонение случайной величины,
распределенной по показательному закону:
Коэффициенты асимметрии и эксцесса
для показательного распределения:
Таким
образом, математическое ожидание и среднее квадратическое
отклонение экспоненциального распределения равны между собой.
Показательный закон
распределения играет большую роль в теории массового обслуживания и теории
надежности. Так, например, интервал времени
между
двумя соседними событиями в простейшем потоке имеет показательное распределение
с параметром
–
интенсивностью потока.
При решении задач, которые выдвигает практика, приходится
сталкиваться с различными распределениями непрерывных случайных величин.
Смежные темы решебника:
- Непрерывная случайная величина
- Нормальный закон распределения случайной величины
- Равномерный закон распределения случайной величины
Примеры решения задач
Пример 1
Случайная величина
задана функцией распределения
Найдите математическое
ожидание и среднее квадратическое отклонение этого
распределения.
Найдите вероятность того,
что случайная величина примет значение от 0,2 до 1.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Математическое
ожидание случайной величины, распределенной по показательному закону:
Среднее
квадратическое отлонение:
Вероятность того, что
случайная величина примет значение от 0,2 до 1
Ответ
.
Пример 2
На шоссе установлен контрольный пункт для
проверки технического состояния автомобилей. Найти математическое ожидание и
среднее квадратическое отклонение случайной величины T – время ожидания
очередной машины контролером, если поток машин простейший и время (в часах)
между прохождениями машин через контрольный пункт распределено по
показательному закону f(t)=5e-5t.
Указание: Время ожидания машины
контролером и время прохождения машин через контрольный пункт распределены
одинаково.
Решение
В нашем случае
параметр показательного распределения
Математическое
ожидание:
Дисперсия:
Среднее
квадратическое отклонение:
Ответ:
Пример 3
Постройте
интегральную и дифференциальную функции распределения случайной величины X.
Найдите математическое ожидание M(X), дисперсию D(X),
среднее квадратическое отклонение σ(X), моду xmod, медиану xmed , если известно, что
случайная величина X имеет показательное распределение с параметром λ=1.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Плотность
распределения случайной величины
, распределенной по
показательному закону:
Функция
распределения:
Построим
графики дифференциальной и интегральной функций распределения:
График дифференциальной функции распределения
График интегральной функции распределения
Математическое
ожидание показательно распределенной случайной величины
:
Дисперсия:
Среднее
квадратическое отклонение:
найдем, исходя из условия:
Пример 4
Случайная
величина
распределена показательно с дисперсией 0,25.
Найти математическое ожидание и вероятность попадания
в интервал (0,5;1).
Решение
Дисперсия
случайной величины, распределенной по показательному закону:
Математическое
ожидание случайной величины, распределенной по показательному закону:
Вероятность
попадания в интервал
непрерывной случайной величины
, распределенной по
показательному закону:
В нашем
случае:
Ответ:
Задачи контрольных и самостоятельных работ
Задача 1
Время
безотказной работы двигателя автомобиля распределено по показательному закону.
Известно, что среднее время наработки двигателя на отказ между техническим
обслуживанием 100 ч. Определить вероятность безотказной работы двигателя за 80
ч.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
Среднее
время работы элемента, входящего в пожарно-техническое устройство, равно 1000
часов. Определить вероятность того, что элемент будет работать от 950 до 1150
часов, если время работы элемента распределено по показательному закону.
Задача 3
Вероятность
безотказной работы элемента распределена по экспоненциальному закону
f(t)=e-0.05t
Найти
вероятность того, что в результате испытания случайная величина попадет в
интервал (11;35). Найти характеристики данного распределения случайной
величины.
Задача 4
Непрерывная
случайная величина X задана интегральной функцией распределения
Найти
постоянную C, математическое ожидание случайной величины X,
вероятность попадания случайной величины в интервал [2;4].
Задача 5
Время
между отказами прибора распределено по показательному закону со средним
значением 25 часов. Определить математическое ожидание и дисперсию времени
безотказной работы автомобиля. Найти вероятность того, что очередной отказ
произойдет не позднее 15 часов.
Задача 6
Время
безотказной работы телевизора определенной модели описывается показательным (экспоненциальным)
законом распределения с постоянной λ. Что вероятнее, его безотказная работа в
промежутке времени [x1,x2]
или [x3,x4]? Записать
функции f(x),F(x) и построить их графики.
λ=1/10, x1=3, x2=5, x3=4, x4=8
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 7
Испытывают
два независимо работающих элемента. Длительность времени t безотказной
работы первого элемента имеет показательное распределение с параметром 0,02,
второго -показательное распределение с параметром 0,06. Найдите вероятность
того, что за время длительностью t=6 ч откажет только один
элемент.
Задача 8
Среднее
время работы каждого из трех элементов, входящих в техническое устройство,
равно T=850 часов. Для безотказной работы устройства необходима безотказная
работа хотя бы одного из трех этих элементов. Определить вероятность, что
устройство будет работать от t1=750 до t2=820 часов, если время
работы каждого из трех элементов независимо и распределено по показательному
закону.
Задача 9
Время
устранения повреждения на канале связи T -случайная величина,
распределенная по закону f(t)=λe-λt (t≥0). Среднее время
восстановления канала – 10 минут. Определить вероятность того, что на
восстановление канала потребуется от 5 до 10 минут.
Задача 10
Дана плотность
распределения случайной величины X.
По какому
закону распределения случайная величина? Найти математическое ожидание,
дисперсию, функцию распределения?
Задача 11
Время
безотказной работы механизма подчинено показательному закону с плотностью
распределения вероятностей f(t)=0.04e-0.04t при t > 0 (t –
время в часах). Найти вероятность того, что механизм проработает безотказно не
менее 100 часов.
Задача 12
Длительность телефонного разговора
является случайной величиной, распределенной по показательному закону.
Известно, что средняя длительность телефонного разговора равна 9 минутам. Найти
вероятность того, что разговор будет длиться:
а) не более 5 минут.
б) более 5 минут.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 13
Случайная величина ξ подчинена
показательному закону с параметром λ=5:
Найдите вероятность того, что
случайная величина ξ примет значение меньшее, чем ее математическое ожидание.
Задача 14
Случайная
величина ξ имеет плотность вероятностей (показательное распределение)
Найдите
вероятность P{ξ>Mξ}
Задача 15
Время T
(минут), затрачиваемое клиентами парикмахерской в ожидании своей очереди,
удовлетворяет показательному распределению с параметром λ=0,05. Какова
вероятность того, что время ожидания превысит 25 минут и каково среднее время
ожидания.
Задача 16
Время T (час),
необходимое на ремонт легкового автомобиля удовлетворяет показательному
распределению с параметром λ=0,2. Какова вероятность того, что время ремонта
одного автомобиля не превысит 6 часов, и сколько часов в среднем затрачивается
на ремонт одного автомобиля.
Задача 17
Время
ожидания у бензоколонки автозаправочной станции является случайной величиной X,
распределенной по показательному закону, со средним временем ожидания, равным t0. Найти вероятности
следующих событий:
Задача 18
Случайная
величина X задана показательным законом распределения и
числовыми значениями параметров M(X)=3 и σx=3.
Требуется:
1) найти
функцию плотности f(x).
2) найти
вероятность попадания СВ X в указанный интервал [a,b]=[2,4].
Задача 19
Случайная
величина ξ задана функцией распределения
Найдите
математическое ожидание и среднее квадратическое отклонение этого
распределения.
Задача 20
Случайная величина ξ распределена по
показательному закону с параметром λ=0,3. Найдите математическое ожидание и
среднее квадратическое отклонение этой случайной величины.
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Определение.
Непрерывная
случайная величина
,
плотность распределения которой задается
формулой
называется
показательной
или
экспоненциальной
с параметром
.
График плотности
вероятности
равномерно
распределенной случайной величины
изображен на рисунке 1
Рис.
1.
В большом числе
случаев показательное распределение
описывает время безотказной работы
прибора, при этом число
интерпретируется как интенсивность
отказа. Это распределение находит также
широкое применение в демографии.
Свойства показательного распределения
Свойство 1.
Интегральная
функция распределения показательной
случайной величины записывается в виде

Доказательство.
Для того, что бы найти интегральную
функцию распределения показательной
случайной величины, воспользуемся
свойством 3 дифференциальной функции
распределения
.
Рассмотрим следующие
два случая:
-
Если
,
топри
.
Поэтому
.
-
Если
,
то из свойства аддитивности определенного
интеграла получаем
.
Из рассмотренных
случаев следует, что интегральная
функция
показательно распределенной случайной
величины записывается в виде
График интегральной
функции
показательно распределенной случайной
величины изображен на рисунке 2
|
1 |
Рис.
2.
Свойство 2.
Математическое
ожидание случайной показательной
случайной величины определяется по
формуле
.
Доказательство.
.
Свойство 3.
Дисперсия
случайной величины показательной
случайной величины определяется по
формуле
.
Доказательство.
Воспользовавшись формулой для вычисления
дисперсии непрерывной случайной величины
,
находим
Свойство 4.
Среднее квадратическое отклонение
случайной величины показательной
случайной величины вычисляется по
формуле
.
Доказательство.
Так как среднее квадратическое отклонение
,
то среднее
квадратическое отклонение для равномерно
распределенной случайной величины
находим
Пример.
5. Нормальный закон распределения.
Нормальный закон
распределения наиболее часто встречается
на практике, Главная особенность,
выделяющая его среди других законов,
состоит в том, что он является предельным
законом, к
которому приближаются другие законы
распределения при весьма часто
встречающихся типичных условиях.
Определение.
Непрерывная
случайная величина
имеет
нормальный
закон распределения или
закон
распределения Гаусса
с параметрами
и
,
если ее плотность распределения
вероятности имеет вид

Кривую нормального
закона распределения называют нормальной
или
гауссовой
кривой.
Выясним прежде
всего теоретико-вероятностный смысл
параметров нормального закона
распределения.
Теорема.
Если случайная величина
распределена по нормальному закону, то
1) математическое
ожидание случайной величины
равно параметру
этого закона, т.е.
,
2) средне
квадратическое отклонение случайной
величины
равно параметру
этого закона, т.е.
.
Доказательство.
Для того чтобы
определить вид нормальной кривой,
проведем исследование дифференциальной
функции распределения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Not to be confused with the exponential family of probability distributions.
|
Probability density function |
|
|
Cumulative distribution function |
|
| Parameters |
 rate, or inverse scale rate, or inverse scale |
|---|---|
| Support |
 |
 |
|
| CDF |
 |
| Quantile |
 |
| Mean |
 |
| Median |
 |
| Mode |
 |
| Variance |
 |
| Skewness |
 |
| Ex. kurtosis |
 |
| Entropy |
 |
| MGF |
 |
| CF |
 |
| Fisher information |
 |
| Kullback-Leibler divergence |
 |
| CVaR (ES) |
 |
| bPOE |
 |
In probability theory and statistics, the exponential distribution or negative exponential distribution is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts.
The exponential distribution is not the same as the class of exponential families of distributions. This is a large class of probability distributions that includes the exponential distribution as one of its members, but also includes many other distributions, like the normal, binomial, gamma, and Poisson distributions.
Definitions[edit]
Probability density function[edit]
The probability density function (pdf) of an exponential distribution is
Here λ > 0 is the parameter of the distribution, often called the rate parameter. The distribution is supported on the interval [0, ∞). If a random variable X has this distribution, we write X ~ Exp(λ).
The exponential distribution exhibits infinite divisibility.
Cumulative distribution function[edit]
The cumulative distribution function is given by
Alternative parametrization[edit]
The exponential distribution is sometimes parametrized in terms of the scale parameter β = 1/λ, which is also the mean:
Properties[edit]
Mean, variance, moments, and median[edit]
The mean is the probability mass centre, that is, the first moment.
The mean or expected value of an exponentially distributed random variable X with rate parameter λ is given by
In light of the examples given below, this makes sense: if you receive phone calls at an average rate of 2 per hour, then you can expect to wait half an hour for every call.
The variance of X is given by
so the standard deviation is equal to the mean.
The moments of X, for 
The central moments of X, for 
where !n is the subfactorial of n
The median of X is given by
where ln refers to the natural logarithm. Thus the absolute difference between the mean and median is
in accordance with the median-mean inequality.
Memorylessness property of exponential random variable[edit]
An exponentially distributed random variable T obeys the relation
This can be seen by considering the complementary cumulative distribution function:
When T is interpreted as the waiting time for an event to occur relative to some initial time, this relation implies that, if T is conditioned on a failure to observe the event over some initial period of time s, the distribution of the remaining waiting time is the same as the original unconditional distribution. For example, if an event has not occurred after 30 seconds, the conditional probability that occurrence will take at least 10 more seconds is equal to the unconditional probability of observing the event more than 10 seconds after the initial time.
The exponential distribution and the geometric distribution are the only memoryless probability distributions.
The exponential distribution is consequently also necessarily the only continuous probability distribution that has a constant failure rate.
Quantiles[edit]
The quantile function (inverse cumulative distribution function) for Exp(λ) is
The quartiles are therefore:
- first quartile: ln(4/3)/λ
- median: ln(2)/λ
- third quartile: ln(4)/λ
And as a consequence the interquartile range is ln(3)/λ.
Conditional Value at Risk (Expected Shortfall)[edit]
The conditional value at risk (CVaR) also known as the expected shortfall or superquantile for Exp(λ) is derived as follows:[1]
Buffered Probability of Exceedance (bPOE)[edit]
The buffered probability of exceedance is one minus the probability level at which the CVaR equals the threshold 
Kullback–Leibler divergence[edit]
The directed Kullback–Leibler divergence in nats of 

Maximum entropy distribution[edit]
Among all continuous probability distributions with support [0, ∞) and mean μ, the exponential distribution with λ = 1/μ has the largest differential entropy. In other words, it is the maximum entropy probability distribution for a random variate X which is greater than or equal to zero and for which E[X] is fixed.[2]
Distribution of the minimum of exponential random variables[edit]
Let X1, …, Xn be independent exponentially distributed random variables with rate parameters λ1, …, λn. Then
is also exponentially distributed, with parameter
This can be seen by considering the complementary cumulative distribution function:
The index of the variable which achieves the minimum is distributed according to the categorical distribution
A proof can be seen by letting 
Note that
is not exponentially distributed, if X1, …, Xn do not all have parameter 0.[3]
Joint moments of i.i.d. exponential order statistics[edit]
Let 

Let 
For 
![{displaystyle operatorname {E} left[X_{(i)}X_{(j)}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d350557a602c2566c092558fff0aefb0049c7c9)


This can be seen by invoking the law of total expectation and the memoryless property:
The first equation follows from the law of total expectation.
The second equation exploits the fact that once we condition on 

![{displaystyle operatorname {E} left[X_{(j)}mid X_{(j)}geq xright]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00169b33907d379235fd4561c63c13d4c51a619a)
![{displaystyle operatorname {E} left[X_{(j)}right]+x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/775aa6cfd6c5d2b1e4b70ce3108a17f93f7b0224)
Sum of two independent exponential random variables[edit]
The probability distribution function (PDF) of a sum of two independent random variables is the convolution of their individual PDFs. If 




The entropy of this distribution is available in closed form: assuming 
where 

In the case of equal rate parameters, the result is an Erlang distribution with shape 2 and parameter 
[edit]
- If X ~ Laplace(μ, β−1), then |X − μ| ~ Exp(β).
- If X ~ Pareto(1, λ), then log(X) ~ Exp(λ).
- If X ~ SkewLogistic(θ), then
.
- If Xi ~ U(0, 1) then
- The exponential distribution is a limit of a scaled beta distribution:
- Exponential distribution is a special case of type 3 Pearson distribution.
- If X ~ Exp(λ) and Xi ~ Exp(λi) then:
, closure under scaling by a positive factor.
- 1 + X ~ BenktanderWeibull(λ, 1), which reduces to a truncated exponential distribution.
- keX ~ Pareto(k, λ).
- e−X ~ Beta(λ, 1).
- 1/keX ~ PowerLaw(k, λ)
, the Rayleigh distribution
, the Weibull distribution
- μ − β log(λX) ∼ Gumbel(μ, β).
, a geometric distribution on 0,1,2,3,…
, a geometric distribution on 1,2,3,4,…
- If also Y ~ Erlang(n, λ) or
then
- If also λ ~ Gamma(k, θ) (shape, scale parametrisation) then the marginal distribution of X is Lomax(k, 1/θ), the gamma mixture
- λ1X1 − λ2Y2 ~ Laplace(0, 1).
- min{X1, …, Xn} ~ Exp(λ1 + … + λn).
- If also λi = λ then:
- If also Xi are independent, then:
- If also λ = 1:
- If also λ = 1/2 then X ∼ χ2
2; i.e., X has a chi-squared distribution with 2 degrees of freedom. Hence:
- If
and
~ Poisson(X) then
(geometric distribution)
- The Hoyt distribution can be obtained from exponential distribution and arcsine distribution
- The exponential distribution is a limit of the κ-exponential distribution in the
case.
- Exponential distribution is a limit of the κ-Generalized Gamma distribution in the
and
cases:
Other related distributions:
- Hyper-exponential distribution – the distribution whose density is a weighted sum of exponential densities.
- Hypoexponential distribution – the distribution of a general sum of exponential random variables.
- exGaussian distribution – the sum of an exponential distribution and a normal distribution.
Statistical inference[edit]
Below, suppose random variable X is exponentially distributed with rate parameter λ, and 

Parameter estimation[edit]
The maximum likelihood estimator for λ is constructed as follows.
The likelihood function for λ, given an independent and identically distributed sample x = (x1, …, xn) drawn from the variable, is:
where:
is the sample mean.
The derivative of the likelihood function’s logarithm is:
Consequently, the maximum likelihood estimate for the rate parameter is:
This is not an unbiased estimator of 


The bias of 
which yields the bias-corrected maximum likelihood estimator
An approximate minimizer of mean squared error (see also: bias–variance tradeoff) can be found, assuming a sample size greater than two, with a correction factor to the MLE:
This is derived from the mean and variance of the inverse-gamma distribution, 
Fisher information[edit]
The Fisher information, denoted 

Plugging in the distribution and solving gives:
This determines the amount of information each independent sample of an exponential distribution carries about the unknown rate parameter 
Confidence intervals[edit]
The 100(1 − α)% confidence interval for the rate parameter of an exponential distribution is given by:[9]
which is also equal to:
where χ2
p,v is the 100(p) percentile of the chi squared distribution with v degrees of freedom, n is the number of observations of inter-arrival times in the sample, and x-bar is the sample average. A simple approximation to the exact interval endpoints can be derived using a normal approximation to the χ2
p,v distribution. This approximation gives the following values for a 95% confidence interval:
This approximation may be acceptable for samples containing at least 15 to 20 elements.[10]
Bayesian inference[edit]
The conjugate prior for the exponential distribution is the gamma distribution (of which the exponential distribution is a special case). The following parameterization of the gamma probability density function is useful:
The posterior distribution p can then be expressed in terms of the likelihood function defined above and a gamma prior:
Now the posterior density p has been specified up to a missing normalizing constant. Since it has the form of a gamma pdf, this can easily be filled in, and one obtains:
Here the hyperparameter α can be interpreted as the number of prior observations, and β as the sum of the prior observations.
The posterior mean here is:
Occurrence and applications[edit]
Occurrence of events[edit]
The exponential distribution occurs naturally when describing the lengths of the inter-arrival times in a homogeneous Poisson process.
The exponential distribution may be viewed as a continuous counterpart of the geometric distribution, which describes the number of Bernoulli trials necessary for a discrete process to change state. In contrast, the exponential distribution describes the time for a continuous process to change state.
In real-world scenarios, the assumption of a constant rate (or probability per unit time) is rarely satisfied. For example, the rate of incoming phone calls differs according to the time of day. But if we focus on a time interval during which the rate is roughly constant, such as from 2 to 4 p.m. during work days, the exponential distribution can be used as a good approximate model for the time until the next phone call arrives. Similar caveats apply to the following examples which yield approximately exponentially distributed variables:
- The time until a radioactive particle decays, or the time between clicks of a Geiger counter
- The time it takes before your next telephone call
- The time until default (on payment to company debt holders) in reduced-form credit risk modeling
Exponential variables can also be used to model situations where certain events occur with a constant probability per unit length, such as the distance between mutations on a DNA strand, or between roadkills on a given road.
In queuing theory, the service times of agents in a system (e.g. how long it takes for a bank teller etc. to serve a customer) are often modeled as exponentially distributed variables. (The arrival of customers for instance is also modeled by the Poisson distribution if the arrivals are independent and distributed identically.) The length of a process that can be thought of as a sequence of several independent tasks follows the Erlang distribution (which is the distribution of the sum of several independent exponentially distributed variables).
Reliability theory and reliability engineering also make extensive use of the exponential distribution. Because of the memoryless property of this distribution, it is well-suited to model the constant hazard rate portion of the bathtub curve used in reliability theory. It is also very convenient because it is so easy to add failure rates in a reliability model. The exponential distribution is however not appropriate to model the overall lifetime of organisms or technical devices, because the “failure rates” here are not constant: more failures occur for very young and for very old systems.
Fitted cumulative exponential distribution to annually maximum 1-day rainfalls using CumFreq[11]
In physics, if you observe a gas at a fixed temperature and pressure in a uniform gravitational field, the heights of the various molecules also follow an approximate exponential distribution, known as the Barometric formula. This is a consequence of the entropy property mentioned below.
In hydrology, the exponential distribution is used to analyze extreme values of such variables as monthly and annual maximum values of daily rainfall and river discharge volumes.[12]
- The blue picture illustrates an example of fitting the exponential distribution to ranked annually maximum one-day rainfalls showing also the 90% confidence belt based on the binomial distribution. The rainfall data are represented by plotting positions as part of the cumulative frequency analysis.
In operating-rooms management, the distribution of surgery duration for a category of surgeries with no typical work-content (like in an emergency room, encompassing all types of surgeries).
Prediction[edit]
Having observed a sample of n data points from an unknown exponential distribution a common task is to use these samples to make predictions about future data from the same source. A common predictive distribution over future samples is the so-called plug-in distribution, formed by plugging a suitable estimate for the rate parameter λ into the exponential density function. A common choice of estimate is the one provided by the principle of maximum likelihood, and using this yields the predictive density over a future sample xn+1, conditioned on the observed samples x = (x1, …, xn) given by
The Bayesian approach provides a predictive distribution which takes into account the uncertainty of the estimated parameter, although this may depend crucially on the choice of prior.
A predictive distribution free of the issues of choosing priors that arise under the subjective Bayesian approach is
which can be considered as
- a frequentist confidence distribution, obtained from the distribution of the pivotal quantity
;[13]
- a profile predictive likelihood, obtained by eliminating the parameter λ from the joint likelihood of xn+1 and λ by maximization;[14]
- an objective Bayesian predictive posterior distribution, obtained using the non-informative Jeffreys prior 1/λ;
- the Conditional Normalized Maximum Likelihood (CNML) predictive distribution, from information theoretic considerations.[15]
The accuracy of a predictive distribution may be measured using the distance or divergence between the true exponential distribution with rate parameter, λ0, and the predictive distribution based on the sample x. The Kullback–Leibler divergence is a commonly used, parameterisation free measure of the difference between two distributions. Letting Δ(λ0||p) denote the Kullback–Leibler divergence between an exponential with rate parameter λ0 and a predictive distribution p it can be shown that
where the expectation is taken with respect to the exponential distribution with rate parameter λ0 ∈ (0, ∞), and ψ( · ) is the digamma function. It is clear that the CNML predictive distribution is strictly superior to the maximum likelihood plug-in distribution in terms of average Kullback–Leibler divergence for all sample sizes n > 0.
Random variate generation[edit]
A conceptually very simple method for generating exponential variates is based on inverse transform sampling: Given a random variate U drawn from the uniform distribution on the unit interval (0, 1), the variate
has an exponential distribution, where F−1 is the quantile function, defined by
Moreover, if U is uniform on (0, 1), then so is 1 − U. This means one can generate exponential variates as follows:
Other methods for generating exponential variates are discussed by Knuth[16] and Devroye.[17]
A fast method for generating a set of ready-ordered exponential variates without using a sorting routine is also available.[17]
See also[edit]
- Dead time – an application of exponential distribution to particle detector analysis.
- Laplace distribution, or the “double exponential distribution”.
- Relationships among probability distributions
- Marshall–Olkin exponential distribution
References[edit]
- ^ a b Norton, Matthew; Khokhlov, Valentyn; Uryasev, Stan (2019). “Calculating CVaR and bPOE for common probability distributions with application to portfolio optimization and density estimation” (PDF). Annals of Operations Research. Springer. 299 (1–2): 1281–1315. doi:10.1007/s10479-019-03373-1. Retrieved 2023-02-27.
- ^ Park, Sung Y.; Bera, Anil K. (2009). “Maximum entropy autoregressive conditional heteroskedasticity model” (PDF). Journal of Econometrics. Elsevier. 150 (2): 219–230. doi:10.1016/j.jeconom.2008.12.014. Archived from the original (PDF) on 2016-03-07. Retrieved 2011-06-02.
- ^ Michael, Lugo. “The expectation of the maximum of exponentials” (PDF). Archived from the original (PDF) on 20 December 2016. Retrieved 13 December 2016.
- ^ Eckford, Andrew W.; Thomas, Peter J. (2016). “Entropy of the sum of two independent, non-identically-distributed exponential random variables”. arXiv:1609.02911 [cs.IT].
- ^ Ibe, Oliver C. (2014). Fundamentals of Applied Probability and Random Processes (2nd ed.). Academic Press. p. 128. ISBN 9780128010358.
- ^ Richard Arnold Johnson; Dean W. Wichern (2007). Applied Multivariate Statistical Analysis. Pearson Prentice Hall. ISBN 978-0-13-187715-3. Retrieved 10 August 2012.
- ^ NIST/SEMATECH e-Handbook of Statistical Methods
- ^ Elfessi, Abdulaziz; Reineke, David M. (2001). “A Bayesian Look at Classical Estimation: The Exponential Distribution”. Journal of Statistics Education. 9 (1). doi:10.1080/10691898.2001.11910648.
- ^ Ross, Sheldon M. (2009). Introduction to probability and statistics for engineers and scientists (4th ed.). Associated Press. p. 267. ISBN 978-0-12-370483-2.
- ^ Guerriero, V. (2012). “Power Law Distribution: Method of Multi-scale Inferential Statistics”. Journal of Modern Mathematics Frontier. 1: 21–28.
- ^ “Cumfreq, a free computer program for cumulative frequency analysis”.
- ^ Ritzema, H.P., ed. (1994). Frequency and Regression Analysis. Chapter 6 in: Drainage Principles and Applications, Publication 16, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. pp. 175–224. ISBN 90-70754-33-9.
- ^ Lawless, J. F.; Fredette, M. (2005). “Frequentist predictions intervals and predictive distributions”. Biometrika. 92 (3): 529–542. doi:10.1093/biomet/92.3.529.
- ^ Bjornstad, J.F. (1990). “Predictive Likelihood: A Review”. Statist. Sci. 5 (2): 242–254. doi:10.1214/ss/1177012175.
- ^ D. F. Schmidt and E. Makalic, “Universal Models for the Exponential Distribution”, IEEE Transactions on Information Theory, Volume 55, Number 7, pp. 3087–3090, 2009 doi:10.1109/TIT.2009.2018331
- ^ Donald E. Knuth (1998). The Art of Computer Programming, volume 2: Seminumerical Algorithms, 3rd edn. Boston: Addison–Wesley. ISBN 0-201-89684-2. See section 3.4.1, p. 133.
- ^ a b Luc Devroye (1986). Non-Uniform Random Variate Generation. New York: Springer-Verlag. ISBN 0-387-96305-7. See chapter IX, section 2, pp. 392–401.
External links[edit]
- “Exponential distribution”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Online calculator of Exponential Distribution



![{mathbb {E}}left[X^{n}right]={frac {n!}{lambda ^{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5d4cb253ad5dd1370612f4f86a0547888f14d41)
![{mathbb {E}}[X]={frac {1}{lambda }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/765e7def8230bfcf3b34a728a31be449a21a1950)
![{mathbb {E}}left[X^{2}right]={frac {2}{lambda ^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3356cc884b4c02cb12e1f67f8e17f5bd3bb1f6d6)
![operatorname {D}[X]={frac {1}{lambda ^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75e237db2aae16603e24b99110d67f9d4aa25cc2)



![Usim U[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff6e45472430f8b45e7bbb99bef71249034d30eb)







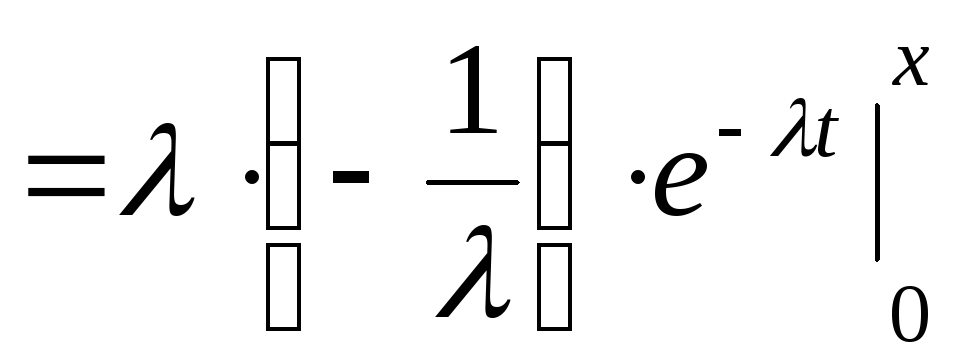
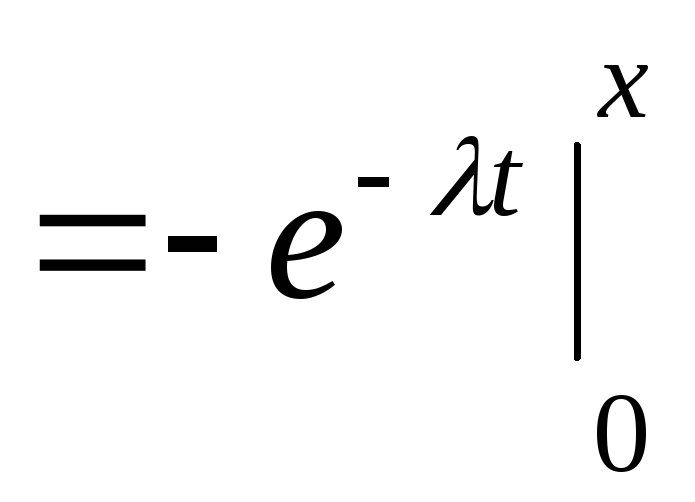












![{displaystyle operatorname {E} [X]={frac {1}{lambda }}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9efa3ce3c964c59532609b3d6b8f01ce88f6221)
![{displaystyle operatorname {Var} [X]={frac {1}{lambda ^{2}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c450db5013b1cfdaf5ea71106c9d13834e02d61)
![{displaystyle operatorname {E} left[X^{n}right]={frac {n!}{lambda ^{n}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f5d3a82fbcff5a294e5360fb05b1e5f2166ec09)

![{displaystyle operatorname {m} [X]={frac {ln(2)}{lambda }}<operatorname {E} [X],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f19becbfbc702d8c33a9698c779384fe3f4dca1)
![{displaystyle left|operatorname {E} left[Xright]-operatorname {m} left[Xright]right|={frac {1-ln(2)}{lambda }}<{frac {1}{lambda }}=operatorname {sigma } [X],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e48a50d7c835e2c16f59682fe49712aa41a54d8a)

![{displaystyle {begin{aligned}Pr left(T>s+tmid T>sright)&={frac {Pr left(T>s+tcap T>sright)}{Pr left(T>sright)}}\[4pt]&={frac {Pr left(T>s+tright)}{Pr left(T>sright)}}\[4pt]&={frac {e^{-lambda (s+t)}}{e^{-lambda s}}}\[4pt]&=e^{-lambda t}\[4pt]&=Pr(T>t).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/126da1213459cde98ae372eae857a18183675f5a)


![{displaystyle {begin{aligned}{bar {q}}_{alpha }(X)&={frac {1}{1-alpha }}int _{alpha }^{1}q_{p}(X)dp\&={frac {1}{(1-alpha )}}int _{alpha }^{1}{frac {-ln(1-p)}{lambda }}dp\&={frac {-1}{lambda (1-alpha )}}int _{1-alpha }^{0}-ln(y)dy\&={frac {-1}{lambda (1-alpha )}}int _{0}^{1-alpha }ln(y)dy\&={frac {-1}{lambda (1-alpha )}}[(1-alpha )ln(1-alpha )-(1-alpha )]\&={frac {-ln(1-alpha )+1}{lambda }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8cb6c9508565c42978ca1153dc0f6bfd0199a45c)








![{displaystyle {begin{aligned}operatorname {E} left[X_{(i)}X_{(j)}right]&=sum _{k=0}^{j-1}{frac {1}{(n-k)lambda }}operatorname {E} left[X_{(i)}right]+operatorname {E} left[X_{(i)}^{2}right]\&=sum _{k=0}^{j-1}{frac {1}{(n-k)lambda }}sum _{k=0}^{i-1}{frac {1}{(n-k)lambda }}+sum _{k=0}^{i-1}{frac {1}{((n-k)lambda )^{2}}}+left(sum _{k=0}^{i-1}{frac {1}{(n-k)lambda }}right)^{2}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0135f144a56c4b7565f7faa61cc3abb42afe9c0d)
![{displaystyle {begin{aligned}operatorname {E} left[X_{(i)}X_{(j)}right]&=int _{0}^{infty }operatorname {E} left[X_{(i)}X_{(j)}mid X_{(i)}=xright]f_{X_{(i)}}(x),dx\&=int _{x=0}^{infty }xoperatorname {E} left[X_{(j)}mid X_{(j)}geq xright]f_{X_{(i)}}(x),dx&&left({textrm {since}}~X_{(i)}=ximplies X_{(j)}geq xright)\&=int _{x=0}^{infty }xleft[operatorname {E} left[X_{(j)}right]+xright]f_{X_{(i)}}(x),dx&&left({text{by the memoryless property}}right)\&=sum _{k=0}^{j-1}{frac {1}{(n-k)lambda }}operatorname {E} left[X_{(i)}right]+operatorname {E} left[X_{(i)}^{2}right].end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be5949313f3639a86ac81484ac8ca7f4f9edb4d4)
![{displaystyle {begin{aligned}f_{Z}(z)&=int _{-infty }^{infty }f_{X_{1}}(x_{1})f_{X_{2}}(z-x_{1}),dx_{1}\&=int _{0}^{z}lambda _{1}e^{-lambda _{1}x_{1}}lambda _{2}e^{-lambda _{2}(z-x_{1})},dx_{1}\&=lambda _{1}lambda _{2}e^{-lambda _{2}z}int _{0}^{z}e^{(lambda _{2}-lambda _{1})x_{1}},dx_{1}\&={begin{cases}{dfrac {lambda _{1}lambda _{2}}{lambda _{2}-lambda _{1}}}left(e^{-lambda _{1}z}-e^{-lambda _{2}z}right)&{text{ if }}lambda _{1}neq lambda _{2}\[4pt]lambda ^{2}ze^{-lambda z}&{text{ if }}lambda _{1}=lambda _{2}=lambda .end{cases}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2db15dda49fe8482485a68c9d7c9b1c1d46ee95)






















![{displaystyle {frac {d}{dlambda }}ln L(lambda )={frac {d}{dlambda }}left(nln lambda -lambda n{overline {x}}right)={frac {n}{lambda }}-n{overline {x}} {begin{cases}>0,&0<lambda <{frac {1}{overline {x}}},\[8pt]=0,&lambda ={frac {1}{overline {x}}},\[8pt]<0,&lambda >{frac {1}{overline {x}}}.end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65ec59bc9ccff1952291621e3eccc741ee1341a2)

![{displaystyle Bequiv operatorname {E} left[left({widehat {lambda }}_{text{mle}}-lambda right)right]={frac {lambda }{n-1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6df9c9d7b6d1a8ffc31748e7cdf0cc750b442e4)


![{displaystyle {mathcal {I}}(lambda )=operatorname {E} left[left.left({frac {partial }{partial lambda }}log f(x;lambda )right)^{2}right|lambda right]=int left({frac {partial }{partial lambda }}log f(x;lambda )right)^{2}f(x;lambda ),dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c70bd835b54bb1b7f344dbf1f04d170bd1d4852)












![{displaystyle {begin{aligned}operatorname {E} _{lambda _{0}}left[Delta (lambda _{0}parallel p_{rm {ML}})right]&=psi (n)+{frac {1}{n-1}}-log(n)\operatorname {E} _{lambda _{0}}left[Delta (lambda _{0}parallel p_{rm {CNML}})right]&=psi (n)+{frac {1}{n}}-log(n)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02702bfd262096d01f27b67eab961ff7ccb512a9)



