Для чего
Обычно при изучении нейронных сетей встречается много теории и новых терминов. Это усваивается сильно лучше, если некоторое время “поиграть с параметрами”. Мы взяли простой широкоизвестный датасет (MNIST, изображения рукописных цифр), простую однослойную FNN (Нейронная сеть прямого распространения) и подвигали параметры в разные стороны, отмечая и сравнивая, что происходит.
Конечно, непосредственно для распознавания и классификации изображений лучше применять не FNN (Нейронные сети прямого распространения), а CNN (Сверточные нейронные сети), в том числе многослойные и предобученные. С этим согласны, и целью данной статьи не является попытка превысить на FNN точность распознавания на CNN. В данной статье мы просто подвигаем гиперпараметры и сделаем соответствующих выводы.
Полученные выводы могут быть действительно полезны и применимы впоследствии, когда для решения соответствующих задач будет необходимо “тюнить” предобученные сверточные сети – менять штатный классификатор (последние слои) на свой – в этом случае как раз и пригодится понимание применения гиперпараметров.
Общий подход
Общий подход такой: выбираем гиперпараметр и обучаем сеть, подставляя поочередно несколько значений. Тестируем несколько значений количества признаков, размера батча и так далее.
Подготовка данных
Подготовка данных происходит абсолютно стандартно, как и в большинстве роликов и статей по MNIST, поэтому особо не комментируем, просто прикладываем.
Библиотеки
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import keras
from keras.models import Sequential
from keras.layers import Dense, Flatten, Dropout
from keras.datasets import mnist
from keras.callbacks import ReduceLROnPlateau
from keras.callbacks import ModelCheckpoint Скачивание и преобразование данных
# Скачиваем данные и сразу распределяем на обучающую и тестовую выборки
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# Преобразуем данные в интервал [0,1]
x_train = x_train / 255
x_test = x_test / 255
y_train_cat = keras.utils.to_categorical(y_train, 10)
y_test_cat = keras.utils.to_categorical(y_test, 10)Проверка корректности данных
# проверяем формы
print(x_train.shape, y_train.shape, x_test.shape, y_test.shape)
# выводим выбранный вектор данных из обучающей выборки
print(x_train[7777])
выводим метку класса
print(y_train[7777])
# выводим метку класса в one-hot-codding
print(y_train_cat[7777])
# Выводим выбранное изображение
plt.imshow(x_train[7777], cmap='binary')
plt.axis('off') # без осей
plt.show()
# Выводим первых 25 изображений из обучающей выборки
plt.figure(figsize=(20,10))
for i in range(25):
plt.subplot(5,5,i+1)
plt.xticks([])
plt.yticks([])
plt.imshow(x_train[i], cmap=plt.cm.binary)
plt.show()Базовая комплектация сети
Берем самый простой стандартный вариант:
FNN: входной слой, один скрытый слой, выходной слой;
на выходе 10 нейронов (потому что 10 цифр = 10 классов);
функции активации – “relu” и “softmax” (стандарт);
функция потерь – “categorical_crossentropy” (стандарт, когда несколько классов);
метрика качества – “accuracy” (стандарт);
оптимизатор – “adam” (стандарт);
размер батча – 32 (надо с чего-то начинать);
размер валидационной выборки – 20% (стандарт).
Запускаем первый раз на 20 эпох и смотрим, что к чему.
model = keras.Sequential([
Flatten(input_shape=(28, 28, 1)),
Dense(128, activation='relu'),
Dense(10, activation='softmax')
])
model.compile(
optimizer='adam',
loss='categorical_crossentropy',
metrics=['accuracy']
)
history = model.fit(
x_train, y_train_cat,
batch_size=32,
epochs=20,
validation_split=0.2
)Выводим цифры …
print('train:', model.evaluate(x_train, y_train_cat, verbose = 0))
print('test:', model.evaluate(x_test, y_test_cat, verbose = 0))
print( 'val_loss:', np.argmin(history.history['val_loss']), history.history['val_loss'][np.argmin(history.history['val_loss'])] )
print( 'val_accuracy:', np.argmax(history.history['val_accuracy']), history.history['val_accuracy'][np.argmax(history.history['val_accuracy'])] )train: [0.023798486217856407, 0.9946833252906799]
test: [0.09774788469076157, 0.9769999980926514]
val_loss: 7 0.08434651792049408
val_accuracy: 18 0.9779166579246521
… и графики.
plt.plot(list(range(1,len(history.history['loss'])+1)),history.history['loss'])
plt.plot(list(range(1,len(history.history['val_loss'])+1)),history.history['val_loss'])
plt.title("loss and val_loss")
plt.grid(True)
plt.show()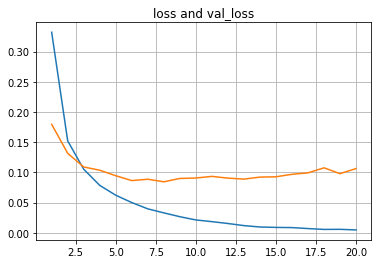
plt.plot(list(range(1,len(history.history['accuracy'])+1)),history.history['accuracy'])
plt.plot(list(range(1,len(history.history['val_accuracy'])+1)),history.history['val_accuracy'])
plt.title("accuracy and val_accuracy")
plt.grid(True)
plt.show()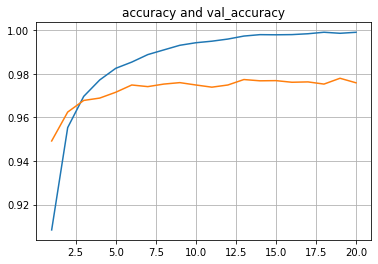
В первом приближении видим, что все “как по учебнику”:
ошибка на обучающей выборке уменьшается;
ошибка на валидационной выборке сначала уменьшается, потом увеличивается – переобучение;
точность на обучающей выборке подходит вплотную к 1.0;
точность на валидационной выборке доходит до 0.978;
точность на тестовой выборке 0.977.
Отсюда начинаем перебирать параметры.
128 нейронов в скрытом слое, батчи 16-32-64-128

Видно, что чем больше размер батча, тем плавнее линии валидационной выборки.
Также видно, что при увеличении размера батча ошибка на валидацинной выборке задирается вверх меньше, прогиб смещается правее, то есть переобучение уменьшается.
Объединим графики для наглядности:
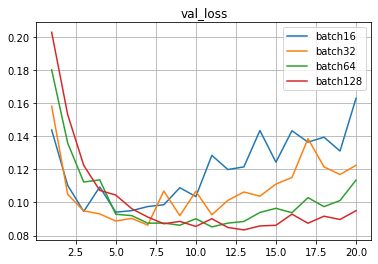

Видно, что точность валидационной выборки идет очень походе и практически одинаково.
Точность на тестовой выборке у всеx очень близкая,
находится в интервале 0.9769-0.9789, разница в десятые и сотые доли процента.
batch16: 0.9771999716758728
batch32: 0.978600025177002
batch64: 0.9789000153541565
batch128: 0.9768999814987183
С учетом изначально заложенной вариативности, вызванной случайными наборами инициации весов, а также случайным формированием состава каждого батча, можно сказать, что при 128 нейронах в скрытом слое точность в данном случае абсолютно идентична и практически не зависит от размера батча в данном диапазоне.
256 нейронов в скрытом слое, батчи 16-32-64-128
Принципиально, ситуация та же, что и при 128 нейронах.
Существенных изменений при переходе от 128 нейронов к 256 не наблюдается.



Точность на тестовой выборке также очень близко,
находится в интервале 0.9795-0.9810,
и это интервально чуть лучше, чем 0.9769-0.9789 (на 128) .
batch16: 0.9794999957084656
batch32: 0.9801999926567078
batch64: 0.9785000085830688
batch128: 0.9810000061988831
Видно, что при 256 нейронах в скрытом слое точность в данном случае также абсолютно идентична и практически не зависит от размера батча в данном диапазоне.
512 нейронов в скрытом слое, батчи 16-32-64-128
Ситуация с переобученностью стала более заметна.
Ошибка на валидационной выборке задирается вверх порезче.и прогиб смещается левее.
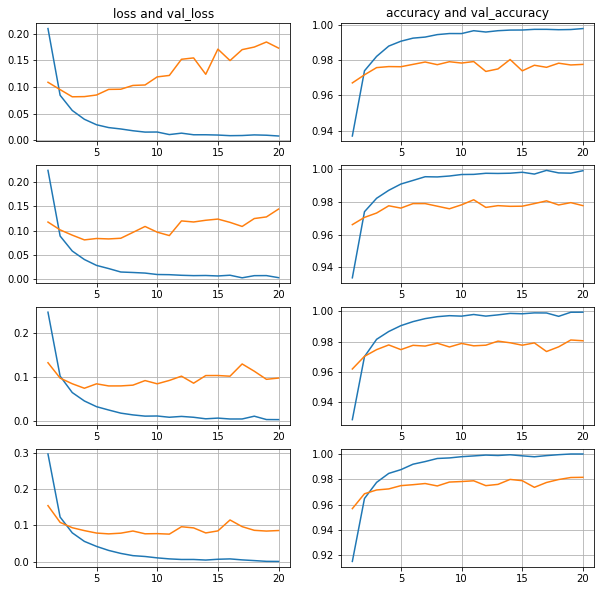

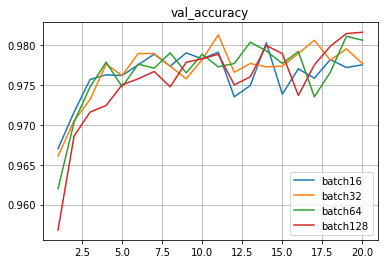
Точность на тестовой выборке также очень близко,
находится в интервале 0.9783-0.9824
и это интервально чуть лучше, чем 0.9795-0.9810 (256) и 0.9769-0.9789 (128).
batch16: 0.9789000153541565
batch32: 0.9782999753952026
batch64: 0.9815000295639038
batch128: 0.9824000000953674
Видно, что и при 256 нейронах в скрытом слое точность в данном случае также абсолютно идентична и практически не зависит от размера батча в данном диапазоне.
1024 нейрона в скрытом слое, батчи 16-32-64-128
Ну и совсем для ясности сделаем замер на 1024 нейрона, и видим все то же самое.
Прогиб ошибки смещается левее из-за увеличившегося количества нейронов, и смещается правее по мере увеличения размера батча.
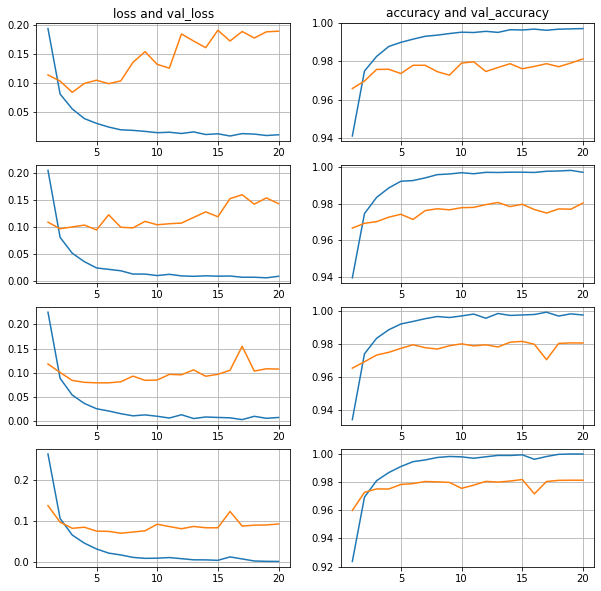


Точность на тестовой выборке также очень близко,
находится в интервале 0.9806-0.9841, и это интервально чуть лучше, чем при 128, 256 и 512 нейронах.
batch16: 0.9805999994277954
batch32: 0.9811999797821045
batch64: 0.982200026512146
batch128: 0.9840999841690063
В данном случае точность подозрительно повышается с увеличением размера батча в заданном диапазоне. Необходимо в дальнейшем проверить, является ли это случайностью или закономерностью.
Необходимо отметить некоторое интервальное улучшение точности в целом при увеличении количества нейронов :
128: 0.9769-0.9789
256: 0.9795-0.9810
512: 0.9783-0.9824
1024: 0.9806-0.9841.
Объединяем полученные данные
Ошибка (‘loss’) на тестовой выборке:
|
ПризнакиБатчи |
16 |
32 |
64 |
128 |
|
128 |
0.1382 |
0.1004 |
0.0930 |
0.0860 |
|
256 |
0.1268 |
0.1047 |
0.0843 |
0.0742 |
|
512 |
0.1393 |
0.1253 |
0.0860 |
0.0717 |
|
1024 |
0.1615 |
0.1267 |
0.0957 |
0.0704 |


Точность (‘accuracy’) на тестовой выборке:
|
ПризнакиБатчи |
16 |
32 |
64 |
128 |
|
128 |
0.9772 |
0.9786 |
0.9789 |
0.9769 |
|
256 |
0.9795 |
0.9802 |
0.9785 |
0.9810 |
|
512 |
0.9789 |
0.9783 |
0.9815 |
0.9824 |
|
1024 |
0.9806 |
0.9812 |
0.9822 |
0.9841 |


Предварительные выводы по количествам нейронов скрытого слоя и размерам батчей
Предварительные выводы следующие:
-
С увеличением размера батча линии валидационной выборки становятся плавнее.
-
С увеличением размера батча ошибка валидационной выборки задирается вверх меньше, прогиб смещается правее, то есть переобучение уменьшается.
-
С увеличением количества нейронов скрытого слоя ошибка валидационной выборки задирается вверх резче, прогиб смещается левее, то есть переобучение увеличивается.
-
С увеличением размера батча ошибка тестовой выборки в целом уменьшается.
-
В отношении точности тестовой выборки с увеличением размера батча неочевидно, в конечном итоге зависит от переобученности и количества нейронов. Предположительно, возможно подобрать такое соотношение количества нейронов и размера батча, что точность будет выше.
-
С увеличением количества нейронов скрытого слоя ошибка тестовой выборки сначала падает, а потом или продолжает падать или начинает расти – переобучение. При этом чем меньше размер батча, тем выше уходит ошибка, и чем больше размер батча, тем меньше ошибка и может продолжать снижаться. То есть при увеличении количества нейронов ошибка может уменьшаться при соответствующем подборе размере батча.
-
С увеличением количества нейронов скрытого слоя точность тестовой выборки в целом увеличивается, и это зависит от переобученности и размера батча.
-
Самые лучшие результаты в данном примере наблюдаются при максимальном количестве признаков (1024) по мере увеличения размера батча.
Берем сразу большой батч (batch1024)
На примерах выше видно, как линии сглаживаются при увеличении размера батча, а на размере 128 ошибка как бы зависает. Так и хочется взять батч еще побольше, чтобы ошибка двигалась вниз. Делаем скачок и берем размер батча 1024.



Можно сказать, что все ожидаемо:
1. линии гладкие;
2. ошибка валидационной выборки постепенно снижается;
3. линии ошибки идут ровненько одна за другой – чем больше батч, тем ниже линия:
4. линии точности также идут ровненько одна за другой – чем больше батч, тем выше линия
Дополнительно стало заметно, что пересечения линий обучающей и валидационной выборок происходят левее, то есть раньше, по мере увеличения количества нейронов скрытого слоя.
Также видно, что здесь уже не хватает эпох и оптимум может быть где-то правее.
И действительно, примерно за 40 эпох точность стабилизируется.


Таким образом становится понятен общий подход к подбору гиперпараметров:
1. увеличивать количество нейронов скрытого слоя;
2. под новое количество нейронов скрытого слоя подстраивать размер батча, чтобы сдвигать переобучение на более поздний срок;
3. увеличивать количество эпох
4. отслеживать, когда происходит переобучение.
Альтернативный вариант – представить нейросеть, осуществляющую распознавание и классификацию, как функцию от соответствующих гиперпараметров, и надстроить отдельную “управляющую” нейронную сеть, определяющую оптимум данной функции стандартным для нейросети способом. Подбор гиперпарметров с помощью “управляющей” нейросети – тема для отдельной статьи.
Добавляем уменьшение шага
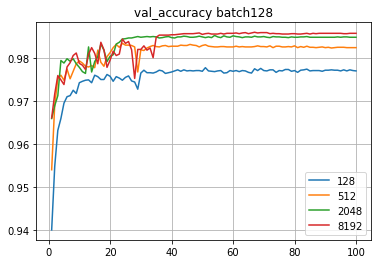
Запустим обучение с batch128 сразу на 100 эпох,
количество нейронов в скрытом слое: 128-512-2048-8192.
Конечно, будет переобучение.
Существует функция, сохраняющая лучшие результаты (ModelCheckpoint). Однако наша задача – академическая, поэтому сохранять лучший результат не будем, просто смотрим графики 100 эпох, функцию прикладываем на случай, если понадобится.
сheckpoint = ModelCheckpoint('mnist-fnn.h5',
monitor='val_acc',
save_best_only=True,
verbose=1)Понимая, что будет переобучение, добавим сразу уменьшение шага обучения.
Уменьшаем шаг обучения в два раза, если заданное количество эпох точность не повышается. При этом возможно задать и минимальное пороговое значение шага обучения.
reduce_on_plateau = ReduceLROnPlateau(monitor='val_accuracy',
patience=3,
verbose=1,
factor=0.5,
min_lr=0.0000001
)Из нескольких тестируемых комбинаций лучшая точность была 0.9869 (8192 признака, уменьшение шага в два разе, если в течение 3 эпох точность не увеличивается, ограничение на минимальный шаг обучение e-07).

Добавляем Dropout
Для сравнения:
20 эпох 1024 нейрона давали следующие значения точности :
batch16: 0.9806
batch32: 0.9812
batch64: 0.9822
batch128: 0.9841
100 эпох batch128 с уменьшением шага обучения давали следующие значения точности :
128 нейронов: 0.9787
512 нейронов: 0.9822
2048 нейронов: 0.9849
8192 нейронов: 0.9869
С применением Dropout (0.1-0.2-0.3-0.4-0.5) 100 эпох, 1024 признака, batch128, без уменьшения шага – точность 0.9854 на Dropout 0.5.
За несколько итераций точность повысилась до 0.9860
(4096 нейронов, batch512, Dropout 0.8, уменьшение шага в 2 раза, если 3 эпохи точность не поднимается).

Изначально допускаем, что во всех представленных случаях параметры не оптимальные, но вполне могут применяться для совместного сравнения.
Таким образом в ряде случаев (но не во всех) применение Dropout дает точность выше, чем без Dropout в случае переобучения, и сравнимую с уменьшением шага обучения при схожих количествах признаков и размерах батчей. Представляется, что наиболее вероятный ориентир для применения Dropout – уменьшение вычислений и соответствующее сокращение времени при достижении приемлемых и не самых высоких показателей точности.
Выводы
Выводы получились интересные.
1. Сеть мгновенно доходит до точности 97,7-97.8%, и такая точность достигается “легко и сразу”.
2. Следующий 1% точности (до 98.7%) достигается уже с трудом, нужно подбирать.
3. Забегая вперед, можно сказать, что CNN дают точность выше 99.5%, но этот “крайний” процент (выше 99%) достигается уже с очень большим трудом.
Таким образом видно, что определенная “пороговая” точность (в данном примере порядка 97.7%) достигается достаточно уверенно и стабильно, и за этот показатель можно смело подписываться и заключать контракт, а вот после этого значения каждая десятая и даже сотая доля процента может потребовать существенных усилий.
Касательно общего алгоритма подбора краткий вывод получился такой:
Для лучшего результата точности целесообразно брать количество нейронов “побольше” (насколько позволяют вычислительные мощности и время) и следить, чтобы сеть не переобучалась. Для контроля переобучения подбирать размер батча и dropout, а для окончательного “шлифования” подбирать схему уменьшения шага обучения.
Что дальше
Вариантом развития представляется тестирование FNN в несколько слоев, а также тестирование CNN в несколько слоев с разными размерами ядер.
Вероятно, следует проводить отдельные серии по наборам гиперпараметрам, чтобы усреднить вариативность, связанную со случайными наборами инициации весов, а также случайным формированием состава каждого батча, то есть запускать обучение несколько раз при одних и тех же параметрах.
Отдельным вариантом развития является представляется создание “управляющей” нейронной сети, которая “самостоятельно” будет подбирать архитектуру и гиперпараметры “контролируемых” нейронных сетей.
I’m using Lasagne to create a CNN for the MNIST dataset. I’m following closely to this example: Convolutional Neural Networks and Feature Extraction with Python.
The CNN architecture I have at the moment, which doesn’t include any dropout layers, is:
NeuralNet(
layers=[('input', layers.InputLayer), # Input Layer
('conv2d1', layers.Conv2DLayer), # Convolutional Layer
('maxpool1', layers.MaxPool2DLayer), # 2D Max Pooling Layer
('conv2d2', layers.Conv2DLayer), # Convolutional Layer
('maxpool2', layers.MaxPool2DLayer), # 2D Max Pooling Layer
('dense', layers.DenseLayer), # Fully connected layer
('output', layers.DenseLayer), # Output Layer
],
# input layer
input_shape=(None, 1, 28, 28),
# layer conv2d1
conv2d1_num_filters=32,
conv2d1_filter_size=(5, 5),
conv2d1_nonlinearity=lasagne.nonlinearities.rectify,
# layer maxpool1
maxpool1_pool_size=(2, 2),
# layer conv2d2
conv2d2_num_filters=32,
conv2d2_filter_size=(3, 3),
conv2d2_nonlinearity=lasagne.nonlinearities.rectify,
# layer maxpool2
maxpool2_pool_size=(2, 2),
# Fully Connected Layer
dense_num_units=256,
dense_nonlinearity=lasagne.nonlinearities.rectify,
# output Layer
output_nonlinearity=lasagne.nonlinearities.softmax,
output_num_units=10,
# optimization method params
update= momentum,
update_learning_rate=0.01,
update_momentum=0.9,
max_epochs=10,
verbose=1,
)
This outputs the following Layer Information:
# name size
--- -------- --------
0 input 1x28x28
1 conv2d1 32x24x24
2 maxpool1 32x12x12
3 conv2d2 32x10x10
4 maxpool2 32x5x5
5 dense 256
6 output 10
and outputs the number of learnable parameters as 217,706
I’m wondering how this number is calculated? I’ve read a number of resources, including this StackOverflow’s question, but none clearly generalizes the calculation.
If possible, can the calculation of the learnable parameters per layer be generalised?
For example, convolutional layer: number of filters x filter width x filter height.
Все курсы > Вводный курс > Занятие 21
В завершающей лекции вводного курса ML мы изучим основы нейронных сетей (neural network), более сложных алгоритмов машинного обучения.
Алгоритмы нейронных сетей принято относить к области глубокого обучения (deep learning). Все изученные нами ранее алгоритмы относятся к так называемому традиционному машинному обучению (traditional machine learning).
Прежде чем перейти к этому занятию, настоятельно рекомендую пройти предыдущие уроки вводного курса.
Смысл, структура и принцип работы
Смысл алгоритма нейронной сети такой же, как и у классических алгоритмов. Мы также имеем набор данных и цель, которой хотим добиться, обучив наш алгоритм (например, предсказать число или отнести объект к определенному классу).
Отличие нейросети от других алгоритмов заключается в ее структуре.

Как мы видим, нейронная сеть состоит из нейронов, сгруппированных в слои (layers), у нее есть входной слой (input layer), один или несколько скрытых слоев (hidden layers) и выходной слой (output layer). Каждый нейрон связан с нейронами предыдущего слоя через определенные веса.
Количество слоев и нейронов не ограничено. Эта особенность позволяет нейронной сети моделировать очень сложные закономерности, с которыми бы не справились, например, линейные модели.
Функционирует нейросеть следующим образом.
На первом этапе данные подаются в нейроны входного слоя (x и y) и умножаются на соответствующие веса (w1, w2, w3, w4). Полученные произведения складываются. К результату прибавляется смещение (bias, в данном случае b1 и b2).
$$ w_{1}cdot x + w_{3}cdot y + b_{1} $$
$$ w_{2}cdot x + w_{4}cdot y + b_{2} $$
Получившаяся сумма подаётся в функцию активации (activation function) для ограничения диапазона и стабилизации результата. Этот результат записывается в нейроны скрытого слоя (h1 и h2).
$$ h_{1} = actfun(w_{1}cdot x + w_{3}cdot y + b_{1}) $$
$$ h_{2} = actfun(w_{2}cdot x + w_{4}cdot y + b_{2}) $$
На втором этапе процесс повторяется для нейронов скрытого слоя (h1 и h2), весов (w5 и w6) и смещения (b3) до получения конечного результата (r).
$$ r = actfun(w_{5}cdot h_{1} + w_{6}cdot h_{2} + b_{3}) $$
Описанная выше нейронная сеть называется персептроном (perceptron). Эта модель стремится повторить восприятие информации человеческим мозгом и учитывает три этапа такого процесса:
- Восприятие информации через сенсоры (входной слой)
- Создание ассоциаций (скрытый слой)
- Реакцию (выходной слой)
Основы нейронных сетей на простом примере
Приведем пример очень простой нейронной сети, которая на входе получает рост и вес человека, а на выходе предсказывает пол. Скрытый слой в данном случае мы использовать не будем.

В качестве функции активации мы возьмём сигмоиду. Ее часто используют в задачах бинарной (состоящей из двух классов) классификации. Приведем формулу.
$$ f(x) = frac{mathrm{1} }{mathrm{1} + e^{-x}} $$
График сигмоиды выглядит следующим образом.
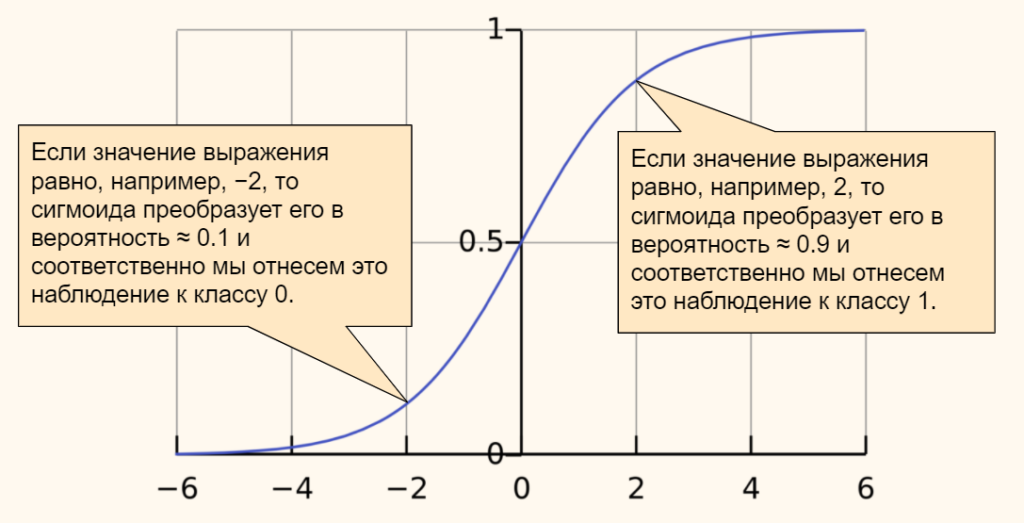
Эта функция преобразует любые значения в диапазон (или вероятность) от 0 до 1. В случае задачи классификации, если результат (вероятность) близок к нулю, мы отнесем наблюдение к одному классу, если к единице, то к другому. Граница двух классов пройдет на уровне 0,5.
Общее уравнение нейросети выглядит следующим образом.
$$ r = sigmoid(w_{1}cdot weight + w_{2}cdot height + bias) $$
Теперь предположим, что у нас есть следующие данные и параметры нейросети.
Откроем ноутбук к этому занятию⧉
|
# даны вес и рост трех человек # единицей мы обозначим мужской пол, а нулем – женский. data = { ‘Иван’: [84, 180, 1], ‘Мария’: [57, 165, 0], ‘Анна’: [62, 170, 0] } |
|
# и даны следующие веса и смещение w1, w2, b = 0.3, 0.1, –39 |
Пропустим первое наблюдение через нашу нейросеть. Следуя описанному выше процессу, вначале умножим данные на соответствующие веса и прибавим смещение.
|
r = w1 * data[‘Иван’][0] + w2 * data[‘Иван’][1] + b |
Теперь к полученному результату (r) применим сигмоиду.
|
np.round(1 / (1 + np.exp(–r)), 3) |
Результат близок к единице, значит пол мужской. Модель сделала верный прогноз. Повторим эти вычисления для каждого из наблюдений.
|
# пройдемся по ключам и значениям нашего словаря с помощью метода .items() for k, v in data.items(): # вначале умножим каждую строчку данных на веса и прибавим смещение r1 = w1 * v[0] + w2 * v[1] + b # затем применим сигмоиду r2 = 1 / (1 + np.exp(–r1)) # если результат больше 0,5, модель предскажет мужской пол if r2 > 0.5: print(k, np.round(r2, 3), ‘male’) # в противном случае, женский else: print(k, np.round(r2, 3), ‘female’) |
|
Иван 0.985 male Мария 0.004 female Анна 0.032 female |
Как мы видим, модель отработала верно.
Обучение нейронной сети
В примере выше был описан первый этап работы нейронной сети, называемый прямым распространением (forward propagation).
И кажется, что этого достаточно. Модель справилась с поставленной задачей. Однако, обратите внимание, веса были подобраны заранее и никаких дополнительных действий от нас не потребовалось.
В реальности начальные веса выбираются случайно и отклонение истинного результата от расчетного (т.е. ошибка) довольно велико.
Как и с обычными алгоритмами ML, для построения модели, нам нужно подобрать идеальные веса или заняться оптимизацией. Применительно к нейронным сетям этот процесс называется обратным распространением (back propagation).

В данном случае мы как бы двигаемся в обратную сторону и, уже зная результат (и уровень ошибки), с учётом имеющихся данных рассчитываем, как нам нужно изменить веса и смещения, чтобы уровень ошибки снизился.
Для того чтобы математически описать процесс оптимизации, нам не хватает знаний математического анализа (calculus) и, если говорить более точно, понятия производной (derivative).
Затем, уже с новыми весами, мы снова повторяем весь процесс forward propagation слева направо и снова рассчитываем ошибку. После этого мы вновь меняем веса в ходе back propagation.
Эти итерации повторяются до тех пор, пока ошибка не станет минимальной, а веса не будут подобраны идеально.
Создание нейросети в библиотеке Keras
Теперь давайте попрактикуемся в создании и обучении нейронной сети с помощью библиотеки Keras. В первую очередь установим необходимые модули и библиотеки.
|
# установим библиотеку tensorflow (через нее мы будем пользоваться keras) и модуль mnist !pip install tensorflow mnist |
И импортируем их.
|
# импортируем рукописные цифры import mnist # и библиотеку keras from tensorflow import keras |
1. Подготовка данных
Как вы вероятно уже поняли, сегодня мы снова будем использовать уже знакомый нам набор написанных от руки цифр MNIST (только на этот раз воспользуемся не библиотекой sklearn, а возьмем отдельный модуль).
В модуле MNIST содержатся чёрно-белые изображения цифр от 0 до 9 размером 28 х 28 пикселей. Каждый пиксель может принимать значения от 0 (черный) до 255 (белый).
Данные в этом модуле уже разбиты на тестовую и обучающую выборки. Посмотрим на обучающий набор данных.
|
# сохраним обучающую выборку и соответсвующую целевую переменную X_train = mnist.train_images() y_train = mnist.train_labels() # посмотрим на размерность print(X_train.shape) print(y_train.shape) |
Как мы видим, обучающая выборка содержит 60000 изображений и столько же значений целевой переменной. Теперь посмотрим на тестовые данные.
|
# сделаем то же самое с тестовыми данными X_test = mnist.test_images() y_test = mnist.test_labels() # и также посмотрим на размерность print(X_test.shape) print(y_test.shape) |
Таких изображений и целевых значений 10000.
Посмотрим на сами изображения.
|
# создадим пространство для четырех картинок в один ряд fig, axes = plt.subplots(1, 4, figsize = (10, 3)) # в цикле for создадим кортеж из трех объектов: id изображения (всего их будет 4), самого изображения и # того, что на нем представлено (целевой переменной) for ax, image, label in zip(axes, X_train, y_train): # на каждой итерации заполним соответствующее пространство картинкой ax.imshow(image, cmap = ‘gray’) # и укажем какой цифре соответствует изображение с помощью f форматирования ax.set_title(f‘Target: {label}’) |

Нейросети любят, когда диапазон входных значений ограничен (нормализован). В частности, мы можем преобразовать диапазон [0, 255] в диапазон от [–1, 1]. Сделать это можно по следующей формуле.
$$ x’ = 2 frac {x-min(x)}{max(x)-min(x)}-1 $$
Применим эту формулу к нашим данным.
|
# функция np.min() возвращает минимальное значение, # np.ptp() – разницу между максимальным и минимальным значениями (от англ. peak to peak) X_train = 2. * (X_train – np.min(X_train)) / np.ptp(X_train) – 1 X_test = 2. * (X_test – np.min(X_test)) / np.ptp(X_test) – 1 |
Посмотрим на новый диапазон.
|
# снова воспользуемся функцией np.ptp() np.ptp(X_train) |
Теперь нам необходимо «вытянуть» изображения и превратить массивы, содержащие три измерения, в двумерные матрицы. Мы уже делали это на занятии по компьютерному зрению.
Применим этот метод к нашим данным.
|
# “вытянем” (flatten) наши изображения, с помощью метода reshape # у нас будет 784 столбца (28 х 28), количество строк Питон посчитает сам (-1) X_train = X_train.reshape((–1, 784)) X_test = X_test.reshape((–1, 784)) # посмотрим на результат print(X_train.shape) print(X_test.shape) |
Посмотрим на получившиеся значения пикселей.
|
# выведем первое изображение [0], пиксели с 200 по 209 X_train[0][200:210] |
|
array([–1. , –1. , –1. , –0.61568627, 0.86666667, 0.98431373, 0.98431373, 0.98431373, 0.98431373, 0.98431373]) |
Наши данные готовы. Теперь нужно задать конфигурацию модели.
2. Конфигурация нейронной сети
Существует множество различных архитектур нейронных сетей. Пока что мы познакомились с персептроном или в более общем смысле нейросетями прямого распространения (Feed Forward Neural Network, FFNN), в которых данные (сигнал) поступают строго от входного слоя к выходному.
Такую же сеть мы и будем использовать для решения поставленной задачи. В частности, на входе мы будем одновременно подавать 784 значения, которые затем будут проходить через два скрытых слоя по 64 нейрона каждый и поступать в выходной слой из 10 нейронов (по одному для каждой из цифр или классов).

В первую очередь воспользуемся классом Sequential библиотеки Keras, который укажет, что мы задаём последовательно связанные между собой слои.
|
# импортируем класс Sequential from tensorflow.keras.models import Sequential # и создадим объект этого класса model = Sequential() |
Далее нам нужно прописать сами слои и связи между нейронами.
Тип слоя Dense, который мы будем использовать, получает данные со всех нейронов предыдущего слоя. Функцией активации для скрытых слоев будет уже известная нам сигмоида.
|
# импортируем класс Dense from tensorflow.keras.layers import Dense # и создадим первый скрытый слой (с указанием функции активации и размера входного слоя) model.add(Dense(64, activation = ‘sigmoid’, input_shape = (784,))) # затем второй скрытый слой model.add(Dense(64, activation = ‘sigmoid’)) # и наконец выходной слой model.add(Dense(10, activation = ‘softmax’)) |
Выходной слой будет состоять из 10 нейронов, по одному для каждого из классов (цифры от 0 до 9). В качестве функции активации будет использована новая для нас функция softmax (softmax function).
Если сигмоида подходит для бинарной классификации, то softmax применяется для задач многоклассовой классификации. Приведем формулу.
$$ text{softmax}(vec{z})_{i} = frac{e^{z_i}}{sum_{j=1}^K e^{z_i}} $$
Функция softmax на входе принимает вектор действительных чисел (z), применяет к каждому из элементов zi экспоненциальную функцию и нормализует результат через деление на сумму экспоненциальных значений каждого из элементов.
На выходе получается вероятностное распределение любого количества классов (K), причем каждое значение находится в диапазоне от 0 до 1, а сумма всех значений равна единице. Приведем пример для трех классов.

Очевидно, вероятность того, что это кошка, выше. Теперь, когда мы задали архитектуру сети, необходимо заняться ее настройками.
Работа над ошибками. Внимательный читатель безусловно обратил внимание, что вероятности на картинке не соответствуют приведенным в векторе значениям. Если подставить эти числа в формулу softmax вероятности будут иными.
|
z = ([1, 2, 0.5]) np.exp(z) / sum(np.exp(z)) |
|
array([0.2312239 , 0.62853172, 0.14024438]) |
Впрочем, алгоритм по-прежнему уверен, что речь идет о кошке.
3. Настройки
Настроек будет три:
- тип функции потерь (loss function) определяет, как мы будем считать отклонение прогнозного значения от истинного
- способ или алгоритм оптимизации этой функции (optimizer) поможет снизить потерю или ошибку и подобрать правильные веса в процессе back propagation
- метрика (metric) покажет, насколько точна наша модель
Функция потерь
В первую очередь, определимся с функцией потерь. Раньше, например, в задаче регрессии, мы использовали среднеквадратическую ошибку (MSE). Для задач классификации мы будем использовать функцию потерь, называемую перекрестной или кросс-энтропией (cross-entropy). Продолжим пример с собакой, кошкой и попугаем.
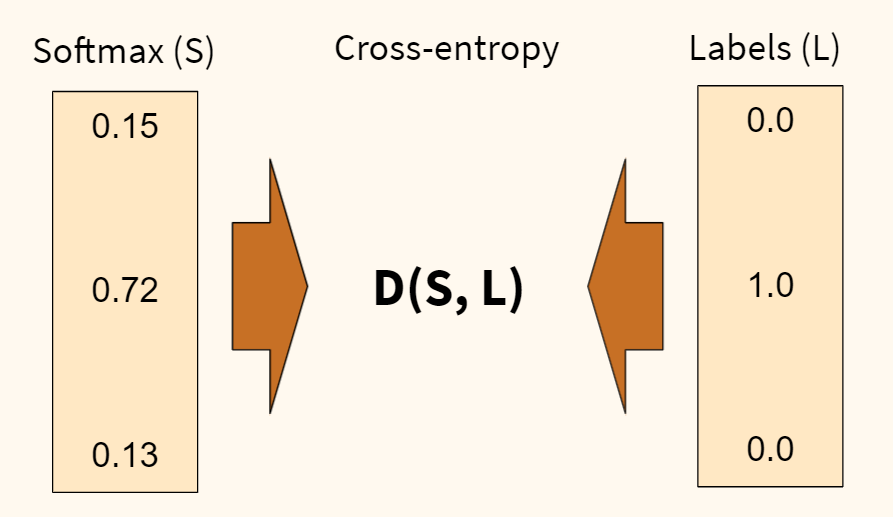
Функция перекрестной энтропии (D) показывает степень отличия прогнозного вероятностного распределения (которое мы получили на выходе функции softmax (S)) от истинного (наша целевая переменная (L)). Чем больше отличие, тем выше ошибка.
Также обратите внимание, наша целевая переменная закодирована, вместо слова «кошка» напротив соответсвующего класса стоит единица, а напротив остальных классов — нули. Такая запись называется унитарным кодом, хотя чаще используется анлийский термин one-hot encoding.
Когда мы будем обучать наш алгоритм, мы также применим эту кодировку к нашим данным. Например, если в целевой переменной содержится цифра пять, то ее запись в one-hot encoding будет следующей.

В дополнение замечу, что функция кросс-энтропии, в которой применяется one-hot encoding, называется категориальной кросс-энтропией (categorical cross-entropy).
Отлично! С тем как мы будем измерять уровень ошибки (качество обучения) нашей модели, мы определились. Теперь нужно понять, как мы эту ошибку будем минимизировать. Для этого существует несколько алгоритмов оптимизации.
Алгоритм оптимизации
Классическим алгоритмом является, так называемый, метод стохастического градиентного спуска (Stochastic Gradient Descent или SGD).
Если предположить для простоты, что наша функция потерь оптимизирует один вес исходной модели, и мы находимся изначально в точке А (с неидеальным случайным весом), то наша задача — оказаться в точке B, где ошибка (L) минимальна, а вес (w) оптимален.

Спускаться мы будем вдоль градиента, то есть по кратчайшему пути. Идею градиента проще увидеть на функции с двумя весами. Такая функция имеет уже три измерения (две независимых переменных, w1 и w2, и одну зависимую, L) и графически похожа на «холмистую местность», по которой мы будем спускаться по наиболее оптимальному маршруту.
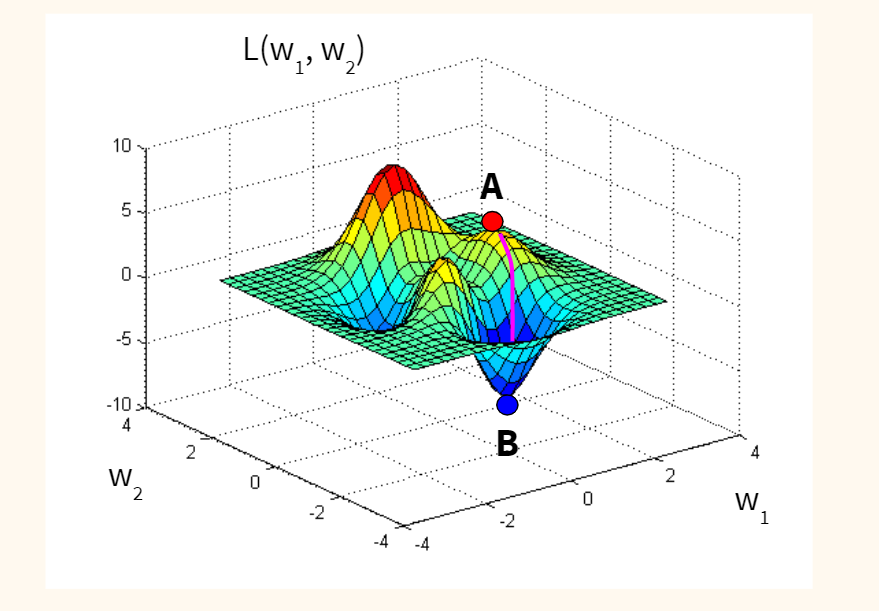
Стохастичность (или случайность) этого алгоритма заключается в том, что мы берем не всю выборку для обновления весов модели, а лишь одно или несколько случайных наблюдений. Такой подход сильно сокращает время оптимизации.
Метрика
Остается определиться с метрикой качества. Здесь мы просто возьмём знакомую нам метрику accuracy, которая посчитает долю правильно сделанных прогнозов.
Посмотрим на используемый код.
|
model.compile( loss = ‘categorical_crossentropy’, optimizer = ‘sgd’, metrics = [‘accuracy’] ) |
4. Обучение модели
Теперь давайте соберём все описанные выше элементы и посмотрим на работу модели в динамике. Повторим ещё раз изученные выше шаги.
- Значения пикселей каждого изображения поступают в 784 нейрона входного слоя
- Далее они проходят через скрытые слои, где они умножаются на веса, складываются, смещаются и поступают в соответствующую функцию активации
- На выходе из функции softmax мы получаем вероятности для каждой из цифр
- После этого результат сравнивается с целевой переменной с помощью функции перекрестной энтропии (функции потерь); делается расчет ошибки
- На следующем шаге алгоритм оптимизации стремится уменьшить ошибку и соответствующим образом изменяет веса
- После этого процесс повторяется, но уже с новыми весами.
Давайте выполним все эти операции в библиотеке Keras.
|
# вначале импортируем функцию to_categorical, чтобы сделать one-hot encoding from tensorflow.keras.utils import to_categorical |
|
# обучаем модель model.fit( X_train, # указываем обучающую выборку to_categorical(y_train), # делаем one-hot encoding целевой переменной epochs = 10 # по сути, эпоха показывает сколько раз алгоритм пройдется по всем данным ) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
Epoch 1/10 1875/1875 [==============================] – 4s 2ms/step – loss: 2.0324 – accuracy: 0.4785 Epoch 2/10 1875/1875 [==============================] – 3s 2ms/step – loss: 1.2322 – accuracy: 0.7494 Epoch 3/10 1875/1875 [==============================] – 3s 2ms/step – loss: 0.7617 – accuracy: 0.8326 Epoch 4/10 1875/1875 [==============================] – 3s 2ms/step – loss: 0.5651 – accuracy: 0.8663 Epoch 5/10 1875/1875 [==============================] – 3s 2ms/step – loss: 0.4681 – accuracy: 0.8827 Epoch 6/10 1875/1875 [==============================] – 3s 2ms/step – loss: 0.4121 – accuracy: 0.8923 Epoch 7/10 1875/1875 [==============================] – 3s 2ms/step – loss: 0.3751 – accuracy: 0.8995 Epoch 8/10 1875/1875 [==============================] – 3s 2ms/step – loss: 0.3487 – accuracy: 0.9045 Epoch 9/10 1875/1875 [==============================] – 3s 2ms/step – loss: 0.3285 – accuracy: 0.9090 Epoch 10/10 1875/1875 [==============================] – 3s 2ms/step – loss: 0.3118 – accuracy: 0.9129 <keras.callbacks.History at 0x7f36c3f09490> |
На обучающей выборке мы добились неплохого результата, 91.29%.
5. Оценка качества модели
На этом шаге нам нужно оценить качество модели на тестовых данных.
|
# для оценки модели воспользуемся методом .evaluate() model.evaluate( X_test, # который применим к тестовым данным to_categorical(y_test) # не забыв закодировать целевую переменную через one-hot encoding ) |
|
313/313 [==============================] – 1s 1ms/step – loss: 0.2972 – accuracy: 0.9173 [0.29716429114341736, 0.9172999858856201] |
Результат «на тесте» оказался даже чуть выше, 91,73%.
6. Прогноз
Теперь давайте в качестве упражнения сделаем прогноз.
|
# передадим модели последние 10 изображений тестовой выборки pred = model.predict(X_test[–10:]) # посмотрим на результат для первого изображения из десяти pred[0] |
|
array([1.0952151e-04, 2.4856537e-04, 1.5749732e-03, 7.4032680e-03, 6.2553445e-05, 8.7646207e-05, 9.4199123e-07, 9.7065586e-01, 5.3100550e-04, 1.9325638e-02], dtype=float32) |
Работа над ошибками. На видео я говорю про первые десять изображений. Разумеется, это неверно. Срез [-10:] выводит последние десять изображений.
В переменной pred содержится массив numpy с десятью вероятностями для каждого из десяти наблюдений. Нам нужно выбрать максимальную вероятность для каждого изображения и определить ее индекс (индекс и будет искомой цифрой). Все это можно сделать с помощью функции np.argmax(). Посмотрим на примере.
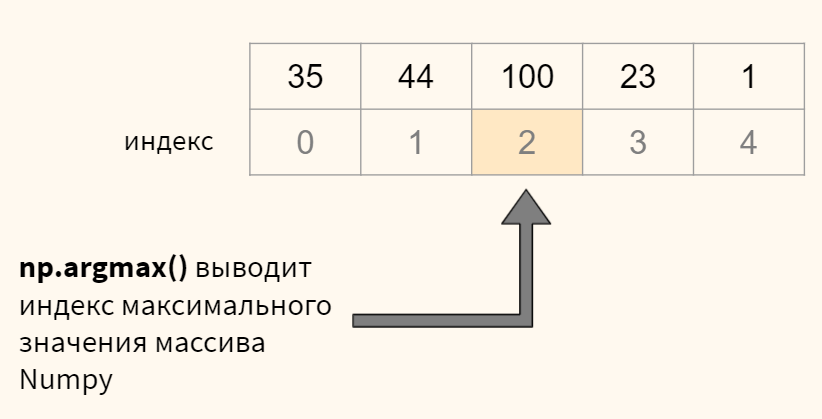
Теперь применим к нашим данным.
|
# для кажого изображения (то есть строки, axis = 1) # выведем индекс (максимальное значение), это и будет той цифрой, которую мы прогнозируем print(np.argmax(pred, axis = 1)) # остается сравнить с целевой переменной print(y_test[–10:]) |
|
[7 8 9 0 1 2 3 4 5 6] [7 8 9 0 1 2 3 4 5 6] |
Для первых десяти цифр модель сделала верный прогноз.
7. Пример улучшения алгоритма
Существует множество параметров модели, которые можно настроить. В качестве примера попробуем заменить алгоритм стохастического градиентного спуска на считающийся более эффективным алгоритм adam (суть этого алгоритма выходит за рамки сегодняшней лекции).
Посмотрим на результат на обучающей и тестовой выборке.
|
# снова укажем настройки модели model.compile( loss = ‘categorical_crossentropy’, optimizer = ‘adam’, # однако заменим алгоритм оптимизации metrics = [‘accuracy’] ) # обучаем модель методом .fit() model.fit( X_train, # указываем обучающую выборку to_categorical(y_train), # делаем one-hot encoding целевой переменной epochs = 10 # прописываем количество эпох ) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
Epoch 1/10 1875/1875 [==============================] – 4s 2ms/step – loss: 0.2572 – accuracy: 0.9252 Epoch 2/10 1875/1875 [==============================] – 4s 2ms/step – loss: 0.1738 – accuracy: 0.9497 Epoch 3/10 1875/1875 [==============================] – 4s 2ms/step – loss: 0.1392 – accuracy: 0.9588 Epoch 4/10 1875/1875 [==============================] – 4s 2ms/step – loss: 0.1196 – accuracy: 0.9647 Epoch 5/10 1875/1875 [==============================] – 4s 2ms/step – loss: 0.1062 – accuracy: 0.9685 Epoch 6/10 1875/1875 [==============================] – 4s 2ms/step – loss: 0.0960 – accuracy: 0.9708 Epoch 7/10 1875/1875 [==============================] – 4s 2ms/step – loss: 0.0883 – accuracy: 0.9732 Epoch 8/10 1875/1875 [==============================] – 4s 2ms/step – loss: 0.0826 – accuracy: 0.9747 Epoch 9/10 1875/1875 [==============================] – 4s 2ms/step – loss: 0.0766 – accuracy: 0.9766 Epoch 10/10 1875/1875 [==============================] – 4s 2ms/step – loss: 0.0699 – accuracy: 0.9780 <keras.callbacks.History at 0x7f36c3d74590> |
|
# и оцениваем результат “на тесте” model.evaluate( X_test, to_categorical(y_test) ) |
|
313/313 [==============================] – 1s 1ms/step – loss: 0.1160 – accuracy: 0.9647 [0.11602973937988281, 0.9646999835968018] |
Как вы видите, с помощью одного изменения мы повысили долю правильных прогнозов до 96,47%.
Более подходящие для работы с изображениями сверточные нейронные сети (convolutional neural network, CNN) достигают свыше 99% точности на этом наборе данных, как это видно в примере⧉ на официальном сайте библиотеки Keras.
Подведем итог
На сегодняшнем занятии изучили основы нейронных сетей. В частности, мы узнали, что такое нейронная сеть, какова ее структура и алгоритм функционирования. Многие шаги, например, оценка уровня ошибки через функцию кросс-энтропии или оптимизация методом стохастического градиентного спуска, разумеется, требуют отдельного занятия. Эти уроки еще впереди.
При этом, я надеюсь, у вас сложилось целостное представление о том, что значит создать и обучить нейросеть, и какие шаги для этого требуются.
Вопросы для закрепления
Перечислите типы слоев нейронной сети
Посмотреть правильный ответ
Ответ: обычно используется входной слой, один или несколько скрытых слоев и выходной слой.
Из каких двух этапов состоит обучение нейронной сети?
Посмотреть правильный ответ
Ответ: вначале (1) при forward propagation мы пропускаем данные от входного слоя к выходному, затем, рассчитав уровень ошибки, (2) начинается обратный процесс back propagation, при котором, мы улучшаем веса исходной модели.
Для чего используются сигмоида и функция softmax в выходном слое нейронной сети в задачах классификации?
Посмотреть правильный ответ
Ответ: сигмоида используется, когда нужно предсказать один из двух классов, если классов больше двух, применяется softmax.
Ответы на вопросы
Вопрос. Что означает число 1875 в результате работы модели?
Ответ. Я планировал рассказать об этом на курсе по оптимизации, но попробую дать общие определения уже сейчас. Как я уже сказал, при оптимизации методом градиентного спуска мы можем использовать (1) все данные, (2) часть данных или (3) одно наблюдение для каждого обновления весов. Это регулируется параметром batch_size (размер партии).
- в первом случае, количество наблюдений (batch, партия) равно размеру датасета, веса не обновляются пока мы не пройдемся по всем наблюдениям, это простой градиентный спуск
- во втором случае, мы берем часть наблюдений (mini-batch, мини-партия), и когда обработаем их, то обновляем веса; после этого мы обрабатываем следующую партию
- и наконец мы можем взять только одно наблюдение и сразу после его анализа обновить веса, это классический стохастический градиентный спуск (stochastic gradient descent), параметр batch_size = 1
В чем преимущество каждого из методов? Если мы берем всю партию и по результатам ее обработки обновляем веса, то двигаемся к минимуму функции потерь наиболее плавно. Минус в том, что на расчет требуется время и вычислительные мощности.
Если берем только одно наблюдение, то считаем все быстро, но расчет минимума функции потерь менее точен.
В библиотеке Keras (и нашей нейросети) по умолчанию используется второй подход и размер партии равный 32 наблюдениям (
batch_size = 32). С учетом того, что в обучающей выборке 60000 наблюдений, разделив 60000 на 32 мы получим 1875 итераций или обновлений весов в рамках одной эпохи. Отсюда и число 1875.
Повторим, алгоритм обрабатывает 32 наблюдения, обновляет веса и после этого переходит к следующей партии (batch) из 32-х наблюдений. Обработав таким образом 60000 изображений, алгоритм заканчивает первую эпоху и начинает вторую. Размер партии и количество эпох регулируется параметрами batch_size и epochs соответственно.
Прохожу курс по машинному обучению.
В разделе на нейронные сети (в тесте) просят посчитать количество параметров у нейронной сети, если нам известно:
- количество входных признаков
- количество нейронов в скрытом слое
- количество нейронов в выходном слое.
Не могли бы вы мне подсказать, где можно взять необходимую литературу, где описан процесс расчета данных параметров или формулу для расчета?
Jack_oS
12.5k7 золотых знаков18 серебряных знаков48 бронзовых знаков
задан 8 фев 2021 в 14:49
![]()
4
Формула для расчета количества обучаемых параметров модели:
sum([p.numel() for p in model.parameters() if p.requires_grad])
ответ дан 24 мар 2021 в 13:27
AlexAlex
111 бронзовый знак
Нейронная сеть — попытка с помощью математических моделей воспроизвести работу человеческого мозга для создания машин, обладающих искусственным интеллектом.
Искусственная нейронная сеть обычно обучается с учителем. Это означает наличие обучающего набора (датасета), который содержит примеры с истинными значениями: тегами, классами, показателями.
Неразмеченные наборы также используют для обучения нейронных сетей, но мы не будем здесь это рассматривать.
Например, если вы хотите создать нейросеть для оценки тональности текста, датасетом будет список предложений с соответствующими каждому эмоциональными оценками. Тональность текста определяют признаки (слова, фразы, структура предложения), которые придают негативную или позитивную окраску. Веса признаков в итоговой оценке тональности текста (позитивный, негативный, нейтральный) зависят от математической функции, которая вычисляется во время обучения нейронной сети.
Раньше люди генерировали признаки вручную. Чем больше признаков и точнее подобраны веса, тем точнее ответ. Нейронная сеть автоматизировала этот процесс.
Искусственная нейронная сеть состоит из трех компонентов:
- Входной слой;
- Скрытые (вычислительные) слои;
- Выходной слой.
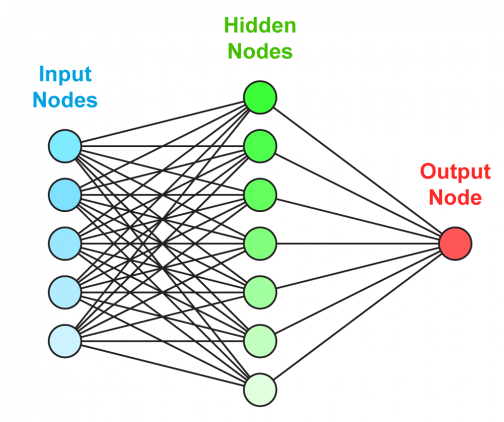
Обучение нейросетей происходит в два этапа:
- Прямое распространение ошибки;
- Обратное распространение ошибки.
Во время прямого распространения ошибки делается предсказание ответа. При обратном распространении ошибка между фактическим ответом и предсказанным минимизируется.
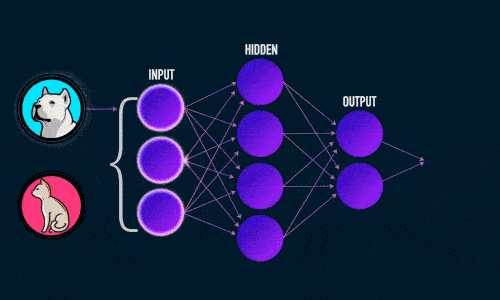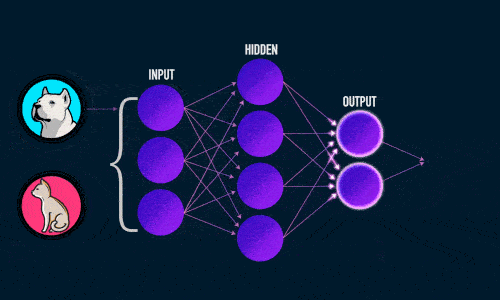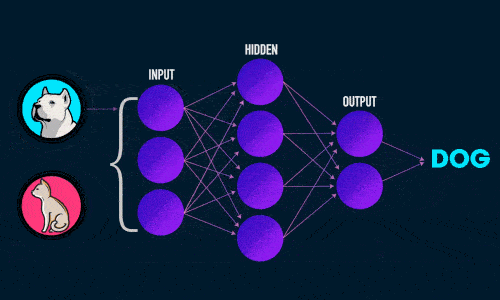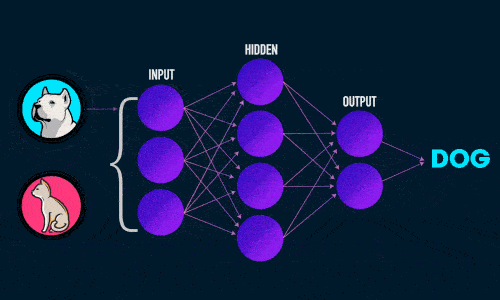
Прямое распространение ошибки
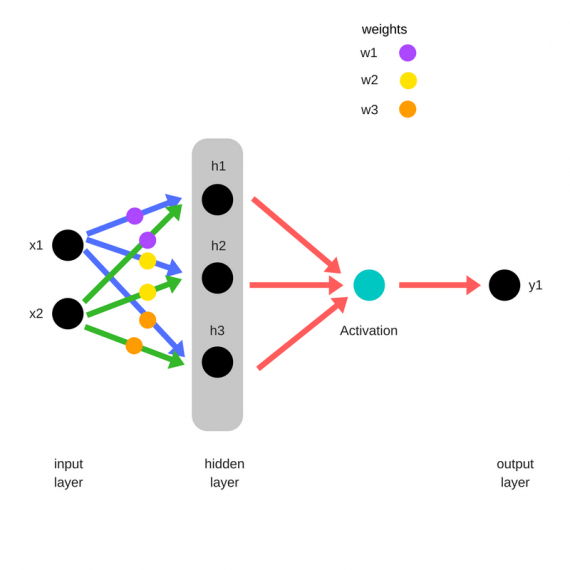
Зададим начальные веса случайным образом:
- w1
- w2
- w3
Умножим входные данные на веса для формирования скрытого слоя:
- h1 = (x1 * w1) + (x2 * w1)
- h2 = (x1 * w2) + (x2 * w2)
- h3 = (x1 * w3) + (x2 * w3)
Выходные данные из скрытого слоя передается через нелинейную функцию (функцию активации), для получения выхода сети:
- y_ = fn(h1 , h2, h3)
Обратное распространение
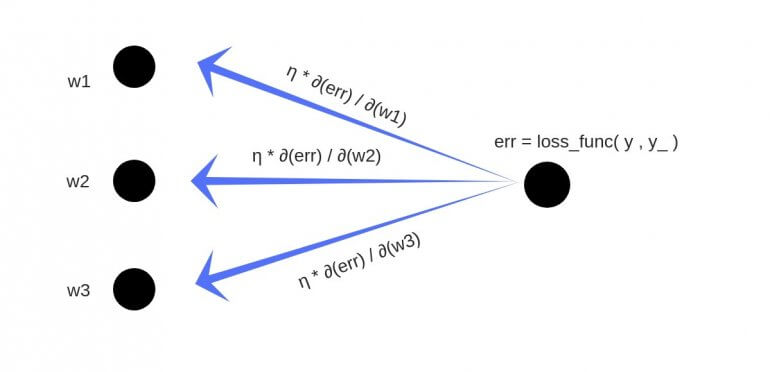
- Суммарная ошибка (total_error) вычисляется как разность между ожидаемым значением «y» (из обучающего набора) и полученным значением «y_» (посчитанное на этапе прямого распространения ошибки), проходящих через функцию потерь (cost function).
- Частная производная ошибки вычисляется по каждому весу (эти частные дифференциалы отражают вклад каждого веса в общую ошибку (total_loss)).
- Затем эти дифференциалы умножаются на число, называемое скорость обучения или learning rate (η).
Полученный результат затем вычитается из соответствующих весов.
В результате получатся следующие обновленные веса:
- w1 = w1 — (η * ∂(err) / ∂(w1))
- w2 = w2 — (η * ∂(err) / ∂(w2))
- w3 = w3 — (η * ∂(err) / ∂(w3))
То, что мы предполагаем и инициализируем веса случайным образом, и они будут давать точные ответы, звучит не вполне обоснованно, тем не менее, работает хорошо.

 Если вы знакомы с рядами Тейлора, обратное распространение ошибки имеет такой же конечный результат. Только вместо бесконечного ряда мы пытаемся оптимизировать только его первый член.
Если вы знакомы с рядами Тейлора, обратное распространение ошибки имеет такой же конечный результат. Только вместо бесконечного ряда мы пытаемся оптимизировать только его первый член.
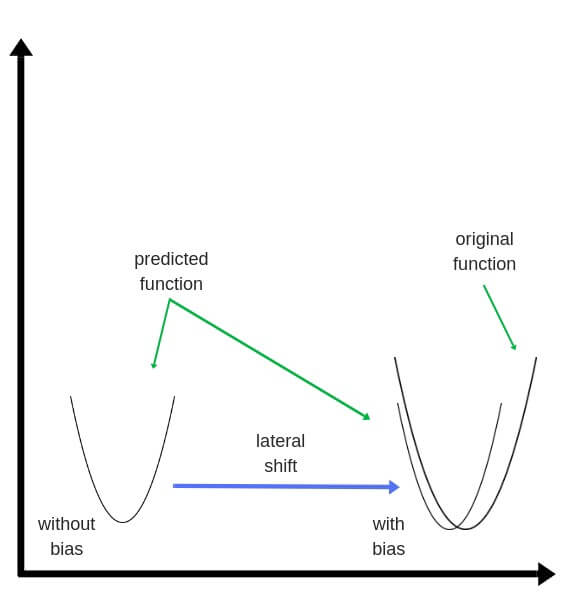
Смещения – это веса, добавленные к скрытым слоям. Они тоже случайным образом инициализируются и обновляются так же, как скрытый слой. Роль скрытого слоя заключается в том, чтобы определить форму базовой функции в данных, в то время как роль смещения – сдвинуть найденную функцию в сторону так, чтобы она частично совпала с исходной функцией.
Частные производные
Частные производные можно вычислить, поэтому известно, какой был вклад в ошибку по каждому весу. Необходимость производных очевидна. Представьте нейронную сеть, пытающуюся найти оптимальную скорость беспилотного автомобиля. Eсли машина обнаружит, что она едет быстрее или медленнее требуемой скорости, нейронная сеть будет менять скорость, ускоряя или замедляя автомобиль. Что при этом ускоряется/замедляется? Производные скорости.
Разберем необходимость частных производных на примере.
Предположим, детей попросили бросить дротик в мишень, целясь в центр. Вот результаты:
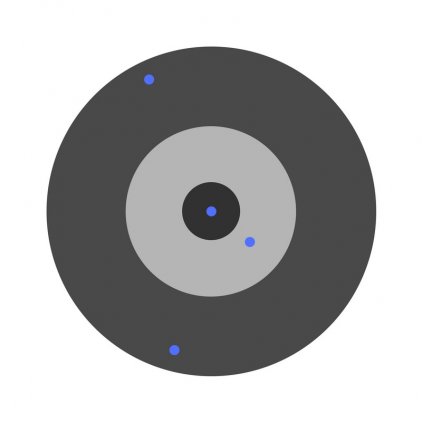
Теперь, если мы найдем общую ошибку и просто вычтем ее из всех весов, мы обобщим ошибки, допущенные каждым. Итак, скажем, ребенок попал слишком низко, но мы просим всех детей стремиться попадать в цель, тогда это приведет к следующей картине:
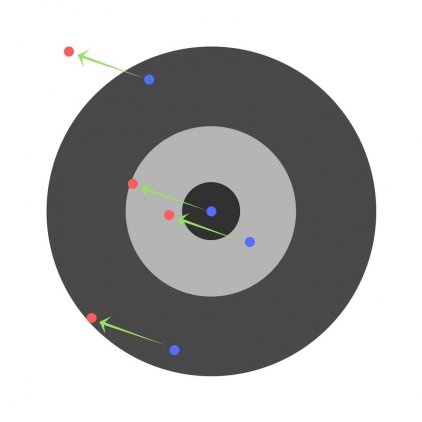
Ошибка нескольких детей может уменьшиться, но общая ошибка все еще увеличивается.
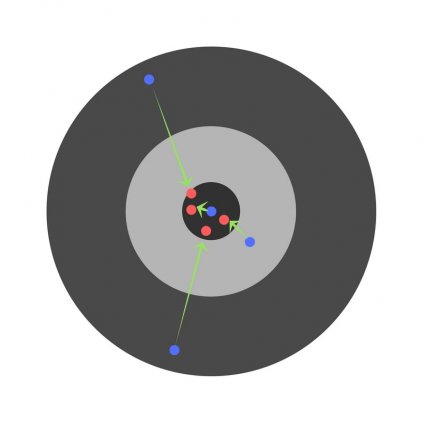
Найдя частные производные, мы узнаем ошибки, соответствующие каждому весу в отдельности. Если выборочно исправить веса, можно получить следующее:
Гиперпараметры
Нейронная сеть используется для автоматизации отбора признаков, но некоторые параметры настраиваются вручную.
Скорость обучения (learning rate)
Скорость обучения является очень важным гиперпараметром. Если скорость обучения слишком мала, то даже после обучения нейронной сети в течение длительного времени она будет далека от оптимальных результатов. Результаты будут выглядеть примерно так:
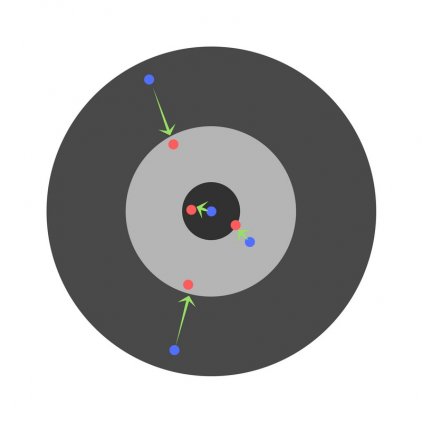
С другой стороны, если скорость обучения слишком высока, то сеть очень быстро выдаст ответы. Получится следующее:
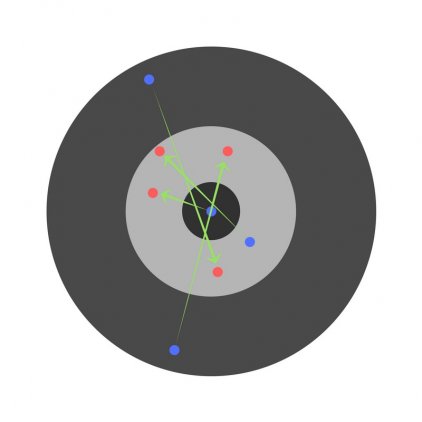
Функция активации (activation function)
Функция активации — это один из самых мощных инструментов, который влияет на силу, приписываемую нейронным сетям. Отчасти, она определяет, какие нейроны будут активированы, другими словами и какая информация будет передаваться последующим слоям.
Без функций активации глубокие сети теряют значительную часть своей способности к обучению. Нелинейность этих функций отвечает за повышение степени свободы, что позволяет обобщать проблемы высокой размерности в более низких измерениях. Ниже приведены примеры распространенных функций активации:
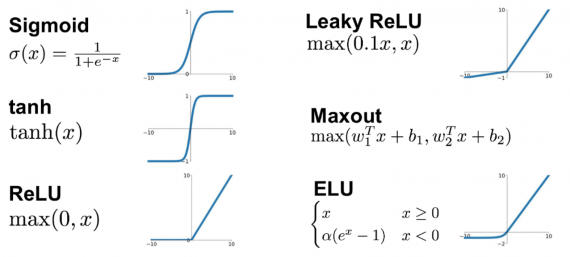
Функция потери (loss function)
Функция потерь находится в центре нейронной сети. Она используется для расчета ошибки между реальными и полученными ответами. Наша глобальная цель — минимизировать эту ошибку. Таким образом, функция потерь эффективно приближает обучение нейронной сети к этой цели.
Функция потерь измеряет «насколько хороша» нейронная сеть в отношении данной обучающей выборки и ожидаемых ответов. Она также может зависеть от таких переменных, как веса и смещения.
Функция потерь одномерна и не является вектором, поскольку она оценивает, насколько хорошо нейронная сеть работает в целом.
Некоторые известные функции потерь:
- Квадратичная (среднеквадратичное отклонение);
- Кросс-энтропия;
- Экспоненциальная (AdaBoost);
- Расстояние Кульбака — Лейблера или прирост информации.
Cреднеквадратичное отклонение – самая простая фукция потерь и наиболее часто используемая. Она задается следующим образом:
Функция потерь в нейронной сети должна удовлетворять двум условиям:
- Функция потерь должна быть записана как среднее;
- Функция потерь не должна зависеть от каких-либо активационных значений нейронной сети, кроме значений, выдаваемых на выходе.
Глубокие нейронные сети
Глубокое обучение (deep learning) – это класс алгоритмов машинного обучения, которые учатся глубже (более абстрактно) понимать данные. Популярные алгоритмы нейронных сетей глубокого обучения представлены на схеме ниже.
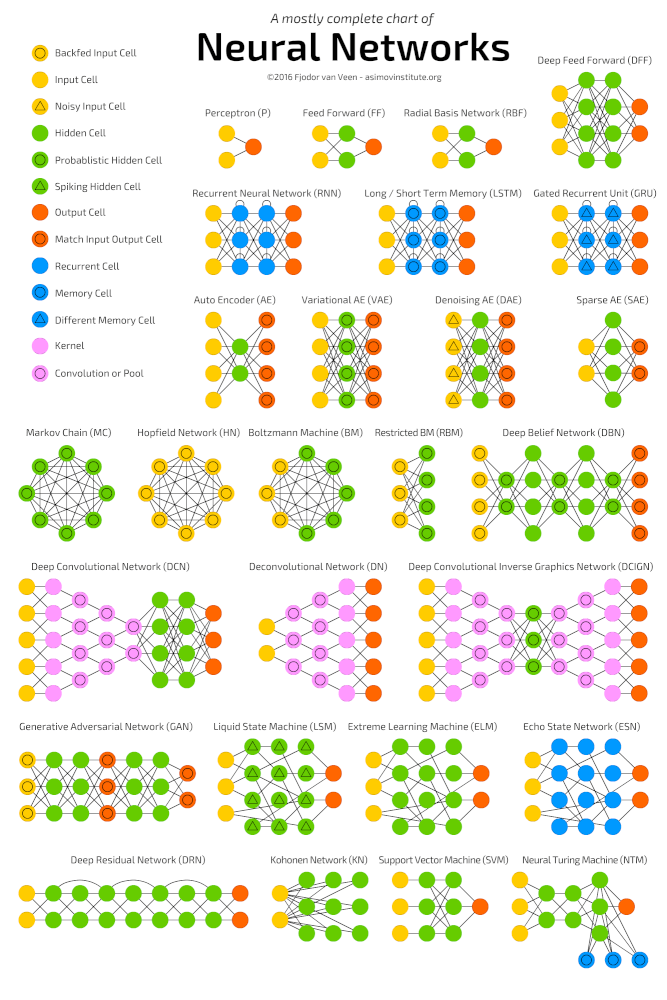
Более формально в deep learning:
- Используется каскад (пайплайн, как последовательно передаваемый поток) из множества обрабатывающих слоев (нелинейных) для извлечения и преобразования признаков;
- Основывается на изучении признаков (представлении информации) в данных без обучения с учителем. Функции более высокого уровня (которые находятся в последних слоях) получаются из функций нижнего уровня (которые находятся в слоях начальных слоях);
- Изучает многоуровневые представления, которые соответствуют разным уровням абстракции; уровни образуют иерархию представления.
Пример
Рассмотрим однослойную нейронную сеть:
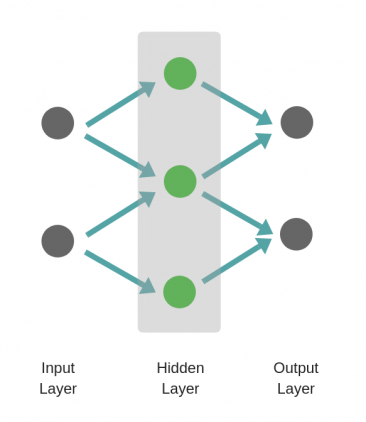
Здесь, обучается первый слой (зеленые нейроны), он просто передается на выход.
В то время как в случае двухслойной нейронной сети, независимо от того, как обучается зеленый скрытый слой, он затем передается на синий скрытый слой, где продолжает обучаться:
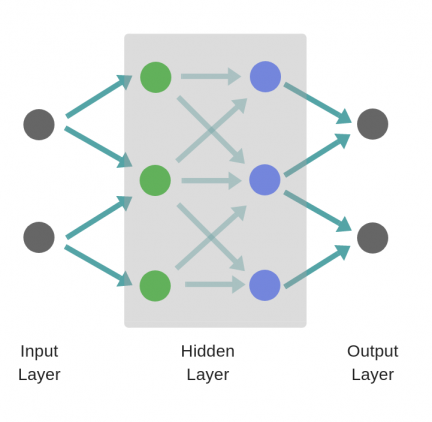
Следовательно, чем больше число скрытых слоев, тем больше возможности обучения сети.
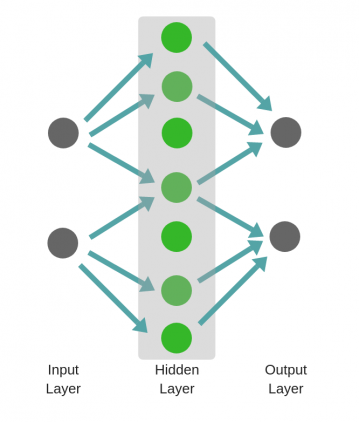
Не следует путать с широкой нейронной сетью.
В этом случае большое число нейронов в одном слое не приводит к глубокому пониманию данных. Но это приводит к изучению большего числа признаков.
Пример:
Изучая английскую грамматику, требуется знать огромное число понятий. В этом случае однослойная широкая нейронная сеть работает намного лучше, чем глубокая нейронная сеть, которая значительно меньше.
Но
В случае изучения преобразования Фурье, ученик (нейронная сеть) должен быть глубоким, потому что не так много понятий, которые нужно знать, но каждое из них достаточно сложное и требует глубокого понимания.
Главное — баланс
Очень заманчиво использовать глубокие и широкие нейронные сети для каждой задачи. Но это может быть плохой идеей, потому что:
- Обе требуют значительно большего количества данных для обучения, чтобы достичь минимальной желаемой точности;
- Обе имеют экспоненциальную сложность;
- Слишком глубокая нейронная сеть попытается сломать фундаментальные представления, но при этом она будет делать ошибочные предположения и пытаться найти псевдо-зависимости, которые не существуют;
- Слишком широкая нейронная сеть будет пытаться найти больше признаков, чем есть. Таким образом, подобно предыдущей, она начнет делать неправильные предположения о данных.
Проклятье размерности
Проклятие размерности относится к различным явлениям, возникающим при анализе и организации данных в многомерных пространствах (часто с сотнями или тысячами измерений), и не встречается в ситуациях с низкой размерностью.
Грамматика английского языка имеет огромное количество аттрибутов, влияющих на нее. В машинном обучении мы должны представить их признаками в виде массива/матрицы конечной и существенно меньшей длины (чем количество существующих признаков). Для этого сети обобщают эти признаки. Это порождает две проблемы:
- Из-за неправильных предположений появляется смещение. Высокое смещение может привести к тому, что алгоритм пропустит существенную взаимосвязь между признаками и целевыми переменными. Это явление называют недообучение.
- От небольших отклонений в обучающем множестве из-за недостаточного изучения признаков увеличивается дисперсия. Высокая дисперсия ведет к переобучению, ошибки воспринимаются в качестве надежной информации.
Компромисс
На ранней стадии обучения смещение велико, потому что выход из сети далек от желаемого. А дисперсия очень мала, поскольку данные имеет пока малое влияние.
В конце обучения смещение невелико, потому что сеть выявила основную функцию в данных. Однако, если обучение слишком продолжительное, сеть также изучит шум, характерный для этого набора данных. Это приводит к большому разбросу результатов при тестировании на разных множествах, поскольку шум меняется от одного набора данных к другому.
Действительно,
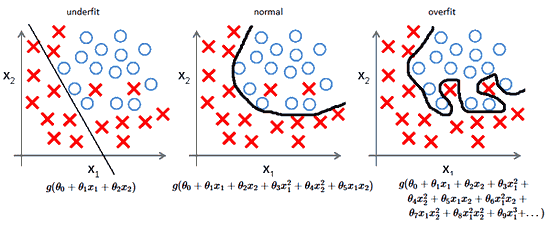
алгоритмы с большим смещением обычно в основе более простых моделей, которые не склонны к переобучению, но могут недообучиться и не выявить важные закономерности или свойства признаков. Модели с маленьким смещением и большой дисперсией обычно более сложны с точки зрения их структуры, что позволяет им более точно представлять обучающий набор. Однако они могут отображать много шума из обучающего набора, что делает их прогнозы менее точными, несмотря на их дополнительную сложность.
Следовательно, как правило, невозможно иметь маленькое смещение и маленькую дисперсию одновременно.
Сейчас есть множество инструментов, с помощью которых можно легко создать сложные модели машинного обучения, переобучение занимает центральное место. Поскольку смещение появляется, когда сеть не получает достаточно информации. Но чем больше примеров, тем больше появляется вариантов зависимостей и изменчивостей в этих корреляциях.
