Как найти параметры прямоугольника 2 класс

Сначала измерим стороны треугольника.

Длины сторон треугольника равны (4) см, (3) см, (6) см.

(Р)  (=)  (3) см (+)  (4) см (+)  (6) см (=)  (13) см.

Дан квадрат, длина стороны которого равна (4) см.

У квадрата все стороны равны.

(Р)  (=)  (4) см (+)  (4) см (+)  (4) см (+)  (4) см (=)  (16) см.

Математика, 2 класс. Урок № 49

Периметр прямоугольника

Перечень вопросов, рассматриваемых в теме:

Изучение правила вычисления периметра прямоугольника.

Глоссарий по теме:

Прямоугольник – четырёхугольник, у которого все углы прямые.

Периметр – сумма длины всех сторон плоской фигуры.

Основная и дополнительная литература по теме урока:

1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –

8-е изд. – М.: Просвещение, 2017. – с.16.

2. Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М.А.Бантова –

7-е изд., дораб. – М.: Просвещение, 2016. – с.22.

Открытые электронные ресурсы по теме урока:

Интересные факты о математике. Познай мир. URL:

https://knowworld.ru/fakty/interesnyie-faktyi-o-matematike/ (дата обращения: 18.08.2018)

Теоретический материал для самостоятельного изучения

Прямоугольные предметы окружают нас повсюду.

Рамки, телефоны, тетради и многое другое.

Данная фигура – прямоугольник. Вспомним, какие отличительные особенности прямоугольника мы знаем.

Прямоугольник – это четырёхугольник, у которого четыре прямых угла и стороны попарно равны.

Рассмотрим следующую задачу: «Вокруг дачного участка необходимо поставить забор. Ширина этого участка – 5 метров, длина – 10 метров. Забор какой длины получится?»

Забор ставят по границам участка, поэтому, чтобы узнать длину забора, нужно знать длину каждой из сторон.

длина

ширина

длина

У данного прямоугольника стороны равны: 5 метров, 10 метров, 5 метров, 10 метров.

Составим выражение для подсчета длины забора. Это первый способ вычислений: 5 + 10 + 5 + 10

Воспользуемся переместительным законом сложения:

5 + 10 + 5 + 10 = 5 + 5 + 10 + 10

В данном выражении есть суммы одинаковых слагаемых

5 + 5 и 10 + 10

В этой записи рядом стоят две пары одинаковых чисел. А ведь сумму одинаковых слагаемых можно заменить умножением. Это второй способ вычислений:

5 + 5 + 10 + 10 = 5 · 2 + 10 · 2

Теперь воспользуемся распределительным законом умножения относительно сложения. Это третий способ вычислений: 5 · 2 + 10 · 2 = (5 + 10) · 2

Этот способ можно назвать рациональным, то есть, наиболее удобным и коротким, потому что в нём меньше действий, чем в предыдущих способах.

Найдём значение выражения (5 + 10) · 2

Сначала выполняем действие в скобках: 5 + 10 = 15

А затем повторяем число 15 два раза: 15 · 2 = 30.

Ответ: 30 метров забор вокруг участка.

Забор вокруг участка – это периметр этого участка. Периметр прямоугольника – сумма длин всех его сторон.

Делаем вывод: периметр прямоугольника – сумма длин всех его сторон. Чтобы найти периметр, надо измерить каждую сторону, а результаты сложить, или заменить сложение умножением как в способах номер 2 и 3.

Тренировочные задания.

1. Решите задачу: Длина листа картона 4 см. Ширина 3 см. Вычислите периметр данного листа. Запишите решение тремя способами.

Правильный ответ:

1 способ. 4+3+4+3=14 (см)

2 способ. 4 · 2+ 3·2=14 (см)

3 способ. (4+3) ·2=14 (см)

Ответ: 14 сантиметров периметр листа картона.

2. Выберите верное решение:

Длина прямоугольника 5 см, ширина 3 см. Чему равен периметр прямоугольника?

А) 8 см Б) 13 см В) 16 см

Правильный ответ В) 16 см

В данной публикации мы рассмотрим определение, свойства и признаки одной из основных геометрических фигур – прямоугольника. Также приведем формулы, с помощью которых можно найти его площадь и периметр.

Определение прямоугольника

Прямоугольник – это четырехугольник, у которого все углы равны 90° (т.е. являются прямыми).

∠ABC = ∠BCD = ∠BAD = ADC = 90°

Прямоугольник состоит из:

• длины – более длинная пара сторон. Обычно обозначаются латинской буквой, например, a;
• ширины – более короткая пара сторон. Чаще всего обозначаются как b.

Сам прямоугольник обычно записывается путем перечисления его вершин, например, ABCD в нашем случае.

Примечание: Прямоугольник является разновидностью параллелограмма.

Свойства прямоугольника

Свойство 1

Противоположные стороны прямоугольника попарно параллельны и равны.

• AD = BC = a, AD || BC
• AB = CD = b, AB || CD

Свойство 2

Длина и ширина прямоугольника одновременно являются его высотами, т.к. они взаимно перпендикулярны.

• a – это высота h₁, проведенная к стороне b
• b – это высота h₂, проведенная к стороне a

Свойство 3

Если соединить середины сторон прямоугольника, то получится ромб.

Свойство 4

Квадрат диагонали (d) прямоугольника равняется сумме квадратов его смежных сторон.

d² = a² + b²

Это следует из теоремы Пифагора, которую можно применить к любому из прямоугольных треугольников, которые образуются в результате деления диагональю прямоугольника.

Свойство 5

Диагонали прямоугольника равны, и в точке пересечения делятся пополам.

• AC = BD = d
• AE = EC = BE = ED

Свойство 6

Около любого прямоугольника можно описать окружность, радиус (R) которой равен половине диагонали этого прямоугольника.

Следовательно, диаметр окружности равен полной длине диагонали прямоугольника.

Признаки прямоугольника

Параллелограмм является прямоугольником, если верно одно из следующих утверждений:

• Его диагонали равны.
• Все его углы равны.
• Если квадрат диагонали равен сумме квадратов его смежных сторон.

Формулы

1. Площадь прямоугольника (S):

S = a ⋅ b

2. Периметр прямоугольника (P):

P = a + a + b + b = 2a + 2b

–
Здравствуйте, мои дорогие ребята! Сегодня мои друзья и помощники Плюс и Минус
заняты очень важным делом. Они принимают участие в турнире по скоростному решению
примеров. А нам необходимо познакомиться с новой темой. И я решила сама вам её
объяснить. Но прежде, чем приступить, я прошу вас отгадать загадку:

1. Обведи кирпич мелком

На асфальте целиком,

И получится фигура –

Ты, конечно, с ней знаком.

2.Она похожа на окно,

на дверь, на стол, на книжку,

на шоколадку, на тетрадь

пенал, планшет, коврижку.

Ну что, ребята, вы догадались, о какой фигуре сегодня пойдёт речь?
Я думаю, что вы уже поняли, что говорить мы будем о прямоугольнике.

А сейчас внимательно посмотрите на монитор. Что вы видите на
экране?

Конечно, эти фигуры можно назвать одним словом – многоугольники.
Среди них есть фигуры с тремя углами, с четырьмя, пятью и так далее.

Вы уже знакомы с темой «Углы». И помните, что углы бывают разными –
прямыми, тупыми, острыми.

А фигура, о которой мы сегодня будем говорить, называется прямоугольник.
Вы слышите? Прямо угольник. Я думаю, вы догадались, если мы говорим, что это прямоугольник,
значит у этой фигуры прямые углы.

Посмотрите на наш рисунок. Сейчас мы при помощи линейки-угольника
проверим, в каких фигурах есть прямые углы. Рассмотрим первую фигуру.

Это семиугольник. Давайте проверим его углы:

Как видите, у этой фигуры есть один прямой угол, а остальные –
непрямые.

Вторая фигура – пятиугольник:

У неё два прямых угла, но три остальных – непрямые.

Третья фигура тоже пятиугольник. У неё уже три прямых угла. Четвёртая
фигура – треугольник. Пятая фигура, её название – трапеция.

Шестая фигура – ромб:

У этих фигур нет ни одного прямого угла.

А вот седьмая фигура и восьмая:

У этих фигур все углы – прямые.

Вот такие фигуры, у которых все углы прямые, можно назвать – прямоугольники.
Обратите внимание, что обе фигуры с прямыми углами – четырёхугольники,
то есть фигуры, у которых 4 угла и 4 стороны. Конечно, разнообразных
четырёхугольников – великое множество. Но прямоугольниками можно назвать
только те четырёхугольники, у которых все углы прямые.

А сейчас я предлагаю вам познакомиться с интересным свойством
прямоугольников. Для этого нам понадобятся линейка и циркуль.

Вот перед нами прямоугольник. Измеряем его верхнюю сторону:

Она равна 6 сантиметрам. А теперь измерим ту сторону, которая
находится внизу, то есть напротив верхней. Её поэтому называют противоположной
стороной, она тоже равна шести сантиметрам.

Измеряем боковую сторону:

Она равна 2 сантиметра. Измеряем противоположную ей сторону. Она
тоже равна 2 сантиметра. Получается, что противоположные стороны прямоугольника
равны? А, может быть, только в этом прямоугольнике так получилось. Давайте проверим
на другом прямоугольнике.

Так, получаем:

Стороны равны и противоположные стороны тоже равны.

Теперь мы уже с полной уверенностью можем сказать, что у
прямоугольников противоположные стороны равны. И поэтому,
когда мы обозначаем длину сторон прямоугольника, совсем не обязательно
подписывать каждую сторону. Можно подписать только одну длинную сторону и одну сторону,
которая короче. Ведь мы знаем, что противоположные стороны прямоугольника равны.
Поэтому, подписав одну из сторон, мы знаем, что и противоположная сторона этого
прямоугольника будет иметь такую же длину.

Кстати, стороны прямоугольников имеют свои названия. Обычно у прямоугольников
есть 2 более длинные стороны, и 2 стороны покороче. Длинную сторону так и
называют – длина, а вот та сторона, которая короче, называется ширина.

Обратите внимание вот на эту фигуру:

Это тоже прямоугольник. Но это не совсем обычный прямоугольник.
Сейчас мне на помощь придёт циркуль. Он измерит все стороны этого
прямоугольника. Получаем, все стороны этого прямоугольника равны. Такой
прямоугольник, у которого все стороны равны, называется квадрат. А, так
как все стороны квадрата равны, то мы можем подписывать только одну из них,
зная, что и все остальные стороны квадрата имеют ту же длину.

Итак:

·                  
четырёхугольник, у которого все углы прямые называется прямоугольником;

·                  
противоположные стороны прямоугольника равны между собой;

·                  
прямоугольник, у которого все стороны равны, называется квадратом.

А
сейчас я хочу вам открыть ещё одну маленькую тайну прямоугольников.

Давайте
проведём линию из вершины одного из углов прямоугольника к вершине
противоположного угла:

Посмотрите,
наш прямоугольник как бы разделился на два треугольника. Такая линия, которая
соединяет вершины противоположных углов прямоугольника, называется диагональ.
Теперь так же соединим линией и оставшиеся два угла:

Получили
длины диагоналей равные 6 сантиметров.

Ну,
что вы заметили?

Диагонали
прямоугольника тоже равны между собой.

Ну
вот и подходит к концу наш урок. Давайте ещё раз повторим всё то, о чём мы
сегодня говорили:

·       
четырёхугольник, у которого все углы прямые называется
прямоугольником;

·       
прямоугольник, у которого все стороны равны, называется квадратом;

·       
противоположные стороны прямоугольника равны между собой;

·       
диагонали прямоугольника равны между собой;

А
теперь нам пора прощаться. До свидания! До новых встреч!

Цели:

1. Образовательные:
   
   1. Создать условия для ознакомления со свойством сторон прямоугольника (противоположные стороны прямоугольника равны);
   2. Содействовать закреплению умений выполнять письменные приёмы сложения и вычитания вида 36+28, 32-24, делать проверку; решению задач изученных видов, закреплению вычислительных умений и навыков.
2. Развивающие: Способствовать развитию мышления, речи, памяти, внимания, умений анализировать, обобщать, делать выводы.
3. Воспитательные: Способствовать воспитанию культуры речи, настойчивости в учебе, формированию умений осуществлять взаимоконтроль, взаимосотрудничество.

Оборудование: геометрические фигуры, краткие записи к задачам, материалы для игры “Геометрия вокруг нас”, опорные схемы сложения и вычитания 36+28, 32-24, раздаточный материал (геометрические фигуры, полоски бумаги).

Ход урока

1. Самоопределение к учебной деятельности.

Цель: Создание условий для положительного самоопределения к деятельности на уроке.

Прозвенел звонок,
Начинается урок (дети – хором)

Учитель:

В кругу друзей
Лучше считать,
Легче решать
И побеждать!

– Пусть эти слова будут девизом нашего урока.

1) Математическая разминка

– 17 увеличить на 8

– 22 уменьшить на 6

– Первое слагаемое 19, второе – 6. Вычислить сумму.

– Найдите сумму 7 и 5.

– Уменьшаемое 15, вычитаемое 9. Чему равна разность?

– Найдите разность 24 и 16, 12 и 7.

– На сколько 18 больше 9?

– На сколько 8 меньше 16?

2) Прочитайте записи и выполните действия:

(50+20)+2		13-(6+4)
(80+7)+10		13-6+4

– Сравните записи во втором столбике. Почему получились разные результаты?

3) Игра: “Найдите лишнее выражение”.

37-7		70-40		62-32		76-36
20+10		100-70		48-18

– Докажите.

4) Задачи.

• Мальчик за 1 четверть исписал 6 тетрадей, а за вторую – 4 тетради. Сколько всего тетрадей он исписал за 2 четверть?
• У Игоря и Жени 11 голубей. У Жени 7 голубей. Сколько голубей у Игоря?

5) На смекалку.

• На ветке сидели 5 синиц и 7 воробьев. 6 птиц улетели. Улетел ли хоть один воробей?

2. Актуализация знаний.

Цель: способствовать повторению знаний о геометрических фигурах и их свойствах.

1) Игра: “Геометрия вокруг нас”.

– По координатам букв прочитайте слово и скажите, что оно означает.

4		Е		Я
3	Г		О
2		Т		И
1	М		Р
	1	2	3	4

(1;3),	(2;4),	(3;3),	(1;1),	(2;4),	(2;2),	(3;1),	(4;2),	(4;4).
Г	Е	О	М	Е	Т	Р	И	Я

– Что означает слово “Геометрия”?

Геометрия – раздел математики, изучающий пространственные отношения и формы (из “Толкового словаря” С. И. Ожегова).

– Назовите геометрические фигуры.

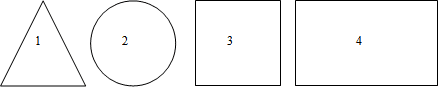
– Какие свойства этих геометрических фигур вы знаете?

– Назовите предметы или части предметов, которые имеют такую геометрическую форму.

– Для чего нам нужно знать свойства геометрических фигур?

Вывод (делают дети): Чтобы сделать мебель или другие предметы мы должны знать свойства геометрических фигур.

– Какие две геометрические фигуры можно назвать одним словом? (фигуры 3 и 4 – прямоугольники)

– Докажите, что эти фигуры прямоугольники (У этих фигур все углы прямые).

2) Работа в парах

– Найдите среди геометрических фигур прямоугольники.

(Чертеж на доске и у детей).

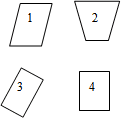
– Как проверили? (Использовали угольник, модель прямого угла).

3. Постановка проблемы.

Цель: способствовать выявлению у детей необходимости получения новых знаний о свойствах прямоугольника.

1. Практическая работа.
   – Вырежьте из бумаги в клетку любой прямоугольник.
   – Как удобней вырезать? (По сторонам клеточек, т.к. у клеток углы прямые).
2. Какое свойство прямоугольника мы использовали для того, чтобы вырезать прямоугольник? (Все углы прямоугольника прямые)
3. А какие свойства есть еще у прямоугольника?
4. Какую же мы поставим перед собой цель? (Выяснить, какими свойствами обладает прямоугольник).
5. Итак, тема урока “Свойства сторон прямоугольника”.

4. Проектирование и фиксация нового знания.

Цель: вывести правило, что противоположные стороны прямоугольника равны.

1. Посмотрите внимательно на прямоугольник, вглядитесь, может, вы еще что-то интересное заметите у прямоугольника?
   Дополнительно: Обратите внимание на стороны прямоугольника.
   (Стороны, находящиеся друг напротив друга – одинаковые).
2. А как можно назвать эти стороны, которые находятся напротив друг друга. (Эти стороны, находящиеся напротив друг друга, называются противоположными).
   – Почему они так называются? (положены друг против друга)
3. А что это значит: стороны, находящиеся друг напротив друга одинаковые? (Они равны по длине)
4. Практическая работа.
   Найдем их и покажем синим и красным цветом противоположные стороны.
   – А как проверить наше наблюдение, что противоположные стороны прямоугольника равны?
   • Измерить длину противоположных сторон и сравнить.
   • Можно проверить перегибанием (практическая работа).
5. Проанализируйте нашу работу и сделайте вывод. (Противоположные стороны прямоугольника равны)
6. Сравните наш вывод с выводом учебника на странице 28.

5. Физминутка.

6. Первичное закрепление.

Цель: применить свойства сторон прямоугольника при измерении длин сторон.

1. (В тетрадях на печатной основе) Измерить стороны прямоугольников, подписать длины сторон.
2. Начертить прямоугольник со сторонами 2 см и 4 см.
   – Почему даны только 2 измерения, ведь у прямоугольника 4 стороны?
3. Работа с заданиями№1,2 в учебнике на странице 28.

7. Самостоятельная работа с самопроверкой.

Цели:

1. тренировать способность к самоконтролю и самооценке.
2. проверить умение проверять правила на практике.

– А теперь представим, что мы строители, нам надо сделать раму для окна. Она имеет прямоугольную форму. У вас на партах 4 полоски бумаги разной длины. Как это сделать удобнее, быстрее?

Самостоятельная работа.

Изготовление прямоугольной рамки (клей, ножницы, полоски бумаги).

– Какие 2 правила вы соблюдали при построении прямоугольной рамки? (Все углы должны быть прямые и противоположные стороны равны).

– Проверьте себя и свою работу.

8. Повторение пройденного материала.

Цели:

1. закрепление решения примеров вида 36+28, 32-24.
2. анализ и решение текстовых задач.

• Повторение алгоритма решения примеров вида 36+28, 32-24 (стр. 11, 25, учебник)
• Решение примеров №4, страница 28 (у доски 3 ученика).
• Решение выражений №2 страница 28 с комментированием.
  Для “сильных” №27 страница 34 в тетради на печатной основе.
• Самостоятельное составление и решение задач №3 (1,2) страница 28.

Взаимопроверка.

9. Домашнее задание:

страница 28 правило, решить примеры №8 страница 29.

10. Рефлексия учебной деятельности на уроке.

Цели:

1. зафиксировать новое содержание, изученное на уроке.
2. оценить собственную деятельность.
3. зафиксировать неразрешенные затруднения.

– Что нового узнали о свойствах прямоугольника?

– Где можно использовать новые знания?

– Кто доволен работой на уроке?

– Над чем стоит поработать?

– Потренируйтесь дома.

– Спасибо за урок!

Литература: М.И. Моро, М.А. Бантова, Г.В. Бельтюкова, С.И. Волкова, С.В. Степенова. Математика. Учебник для 2 класса начальной школы. Москва. «Просвещение», 2006.