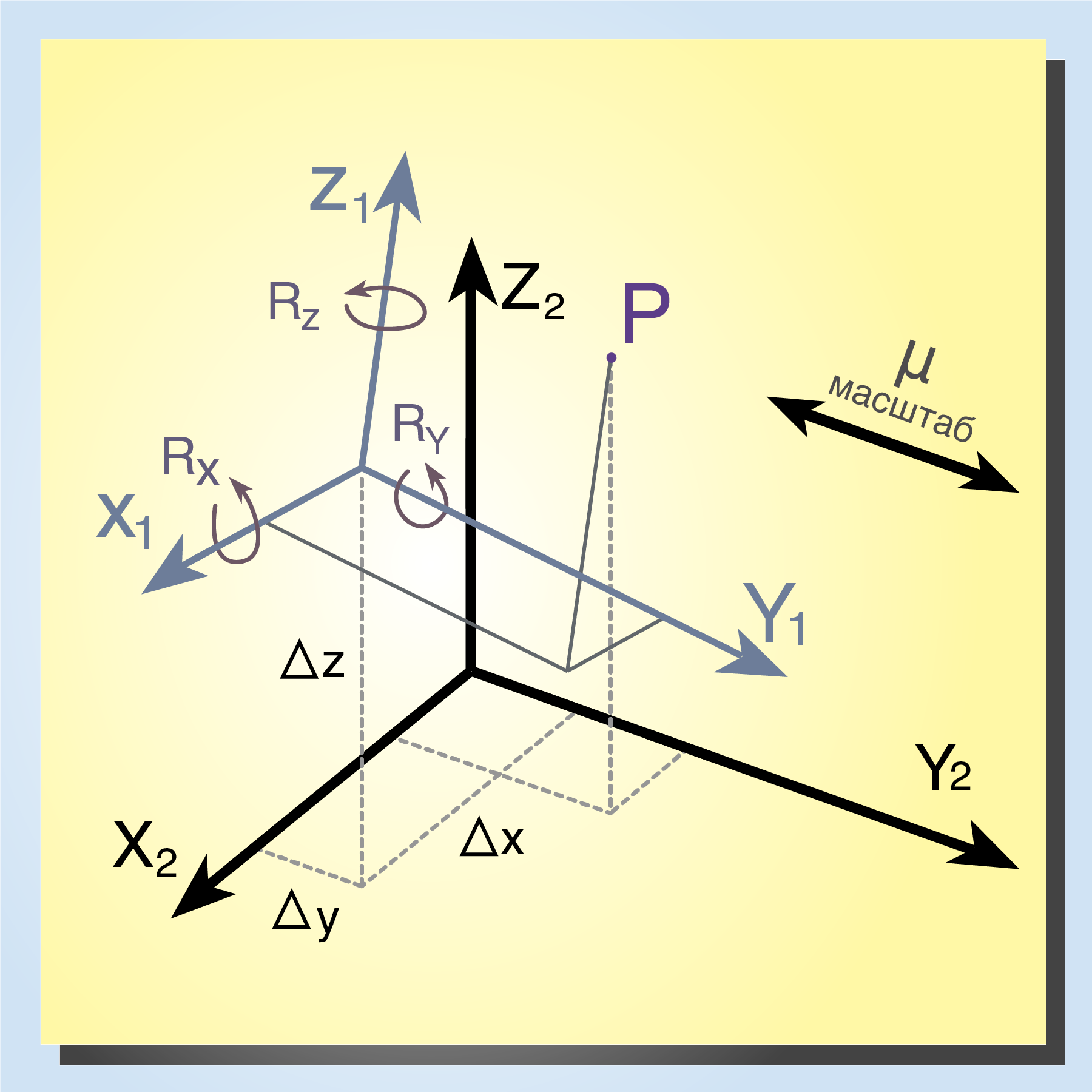
Как решается задача перехода из одной системы координат в другую? Разберемся с одним из стандартных вариантов – семипараметрическим преобразованием Гельмерта (или Хельмерта).
Преобразование из системы отсчета 1 в систему отсчета 2 можно описать через семь возможных параметров — три угла поворота вокруг каждой из осей (Rx, Ry, Rz), три компонента вектора сдвига (Δx, Δy, Δz) и масштабный коэффициент μ. Так и получается наиболее распространенное в геодезии семипараметрическое преобразование Гельмерта.
При преобразовании Гельмерта параллельные линии остаются параллельными, средняя точка отрезка прямой остается средней точкой, а все точки на прямой остаются на прямой.
Xt = C + μRX;
● X – изначальный вектор;
● Xt – конечный вектор;
● C – вектор трансляции со сдвигами осей;
● μ – масштабный коэффициент;
● R – матрица вращения, состоит из матриц Rx, Ry, Rz.
Это преобразование обычно выполняется в три этапа. Сначала исходная точка с геодезическими координатами преобразуется в трехмерные геоцентрические координаты (XYZ). Затем выполняется преобразование, после чего геоцентрические координаты преобразуются обратно в геодезические.
Пример применения – описание преобразования Гельмерта в программном обеспечении для перехода между системами координат PROJ.
Если параметры преобразования неизвестны, их можно вычислить с помощью точек, координаты которых известны до и после преобразования. Поскольку всего нужно определить семь параметров, необходимо знать как минимум координаты двух точек и одну координату третьей точки (например, Z-координату). Это дает систему с семью уравнениями и семью неизвестными, которую можно решить.
В некоторых задачах достаточно использовать преобразование с пятью параметрами, состоящее из трех сдвигов, только одного поворота вокруг оси Z и одного изменения масштаба. А если преобразование происходит в двумерном пространстве, потребуется всего четыре параметра (два сдвига, масштабирование, одно вращение). Их можно определить по двум известным точкам, а если имеется больше точек, то можно провести проверку.
У метода есть модификации – например, трансформация, учитывающая скорости изменения семи параметров во времени. Для их вычисления необходимо знать изменения координат опорных пунктов. Этот метод используется в высокоточных сетях, где производятся регулярные наблюдения, и для него нужно уже четырнадцать параметров — семь параметров метода Гельмерта и семь значений скоростей изменения каждого параметра.
Преобразование Гельмерта использует только один масштабный коэффициент, поэтому оно не подходит, например, для сравнения деформаций бумаги при сканировании старых планов и карт. В этих случаях предпочтительнее использовать более общее аффинное преобразование.
О точности преобразования
Хотя этот метод является математически точным, результат зависит от точности используемых параметров. На практике эти параметры вычисляются на основе как минимум трех известных точек. Однако их точность влияет на последующие параметры преобразования, поскольку эти точки будут содержать свои ошибки, к которым добавятся ошибки формул на разных этапах перехода. Итоговое преобразование будет лишь наилучшей оценкой из возможных.
Источники:
● Методы трансформации геодезических и пространственных прямоугольных координат, их алгоритмы, параметры, точность – Г. Д. Курошев, А. А. Харунжий, Вестник СПбГУ, 2012.
● Helmert transformation.
● Helmert Datum Shift Methods.
Наборы параметров и источники
Переход с одной системы координат на другую может осуществляться разными способами и использовать разные наборы параметров перехода.
В нашей стране наиболее распространенной является система координат СК-42 (так же известная как Pulkovo 1942), набирают оборот ПЗ-90 и СК-95 и наконец приходится иметь дело с массой данных в WGS 84. Цель этой статьи собрать в одном месте распространенные наборы параметров пересчета из одной системы координат в другую, применяющиеся для территории России. Для осуществления обратного преобразования необходимо использовать инвертированные значения параметров.
Содержание
- 1 3-х параметрическое преобразование
- 1.1 СК-42 -> WGS84
- 1.2 СК95 -> ПЗ-90
- 2 7-ми параметрическое преобразование
- 2.1 СК42 -> WGS84
- 2.2 СК-42 -> ПЗ-90
- 2.3 СК-42 -> ПЗ-90.02
- 2.4 СК-95 -> ПЗ-90.02
- 2.5 СК-95-> WGS84
- 2.6 ПЗ-90 -> WGS84
- 2.7 ПЗ-90.02 -> WGS84
- 2.8 ПЗ-90.02 ->ПЗ-90
- 3 Источники информации
- 4 Ссылки по теме
3-х параметрическое преобразование
Так же известно как преобразование Молоденского.
Три параметра используемые в этом преобразовании: dX, dY, dZ (т.н. линейные элементы трансформирования, единицы измерения – метры) определяют смещение центра эллипсоида по осям X, Y, Z.
Набор параметров включает: dX, dY, dZ
СК-42 -> WGS84
| # | dX | dY | dZ | Источник |
|---|---|---|---|---|
|
1 |
28 |
-130 |
-95 |
World Geodetic System 1984. NIMA, 2000 >>> То же: EPSG::1254 |
|
2 |
23.92 |
-141.27 |
-80.91 |
ГОСТ 51794-2001 >>> |
Группа параметров #1 используется так же в наборе “Pulkovo 1942-1 (Russia)” в ERDAS IMAGINE и ArcGIS Pulkovo_1942_To_WGS_1984.
СК95 -> ПЗ-90
| # | dX | dY | dZ | Источник |
|---|---|---|---|---|
|
1 |
25.90 |
-130.94 |
-81.76 |
ГОСТ 51794-2001 То же: EPSG::1257, ГОСТ 51794-2008 (Приложение Б) >>> |
7-ми параметрическое преобразование
Так же известно как преобразование Bursa-Wolf (Position Vector/Coordinate frame rotation). Отличается от 3-х параметрического добавлением угловых элементы трансформирования ωx, ωy, ωz (единицы измерения – секунды) и дифференциального различия масштабов систем координат m.
Набор параметров включает: dX, dY, dZ, ωx, ωy, ωz, m
СК42 -> WGS84
| # | dX | dY | dZ | ωx | ωy | ωz | m | Источник |
|---|---|---|---|---|---|---|---|---|
|
1 |
23.92 |
-141.27 |
-80.9 |
0 |
0.35 |
0.82 |
-0.12*10-6 |
ГОСТ 51794-2001 То же: EPSG::1267 |
| 2 |
23.92 |
-141.27 |
-80.9 |
0 |
-0.35 |
-0.82 |
-0.12*10-6 |
Mapinfo 1013 |
|
3 |
27 |
-135 |
-84.5 |
0 |
0 |
-2.686*10-6 |
2.263*10-7 |
ERDAS IMAGINE |
|
4 |
24 |
-123 |
-94 |
-9.69e-07 |
1.212e-06 |
6.3*10-7 |
1.1*10-6 |
ERDAS IMAGINE |
| 5 | 25 | -141 | -78.5 | 0 | -0.35 | -0.736 | 0 | EPSG::15865 |
| 6 | 24 | -123 | -94 | -0.02 | 0.25 | 0.13 | 1.1*10-6 |
Mapinfo 1001 |
СК-42 -> ПЗ-90
| # | dX | dY | dZ | ωx | ωy | ωz | m | Источник |
|---|---|---|---|---|---|---|---|---|
|
1 |
25±2 |
-141±2 |
-80±3 |
0±0.1 |
-0.35±0.1 |
-0.66±0.1 |
(0±0.25)10-6 |
ГОСТ 51794-2001 >>> То же: EPSG::15844 |
| 2 | 25 | -141 | -80 | 0 | -0.35 | -0.66 | 0 |
ГОСТ 51794-2008 (Приложение Б) >>> |
СК-42 -> ПЗ-90.02
| # | dX | dY | dZ | ωx | ωy | ωz | m | Источник |
|---|---|---|---|---|---|---|---|---|
| 1 | 23.93 | -141.03 | -79.98 | 0 | -0.35 | -0.79 | -0.22*10-6 |
ГОСТ 51794-2008 (Приложение А) >>> |
СК-95 -> ПЗ-90.02
| # | dX | dY | dZ | ωx | ωy | ωz | m | Источник |
|---|---|---|---|---|---|---|---|---|
| 1 | 24.83 | -130.97 | -81.74 | 0 | 0 | -0.13 | -0.22*10-6 |
ГОСТ 51794-2008 (Приложение А) >>> |
СК-95-> WGS84
| # | dX | dY | dZ | ωx | ωy | ωz | m | Источник |
|---|---|---|---|---|---|---|---|---|
| 1 |
24.82 |
-131.21 |
-82.66 |
0 |
0 |
-0.16 |
-0.12*10-6 |
Mapinfo 1014 |
ПЗ-90 -> WGS84
| # | dX | dY | dZ | ωx | ωy | ωz | m | Источник |
|---|---|---|---|---|---|---|---|---|
|
1 |
0 |
0 |
1.5 |
0 |
0 |
-0.076 |
0 |
EPSG::15843 |
| 2 |
-1.08±0.2 |
-0.27±0.2 |
-0.9±0.3 |
0 |
0 |
-0.16±0.1 |
(-0.12±0.06)10-6 |
ГОСТ 51794-2001 >>> Тоже: EPSG::1244 Тоже: Mapinfo 1012 |
| 3 | -1.10 | -0.30 | -0.90 | 0 | 0 | -0.20±0.01 | -0.12*10-6 |
ГОСТ 51794-2008 (Приложение Г) >>> |
ПЗ-90.02 -> WGS84
| # | dX | dY | dZ | ωx | ωy | ωz | m | Источник |
|---|---|---|---|---|---|---|---|---|
|
1 |
-0.36 |
0.08 |
0.18 |
0 |
0 |
0 |
0 |
ГОСТ 51794-2008 (Приложение В) >>> |
ПЗ-90.02 ->ПЗ-90
| # | dX | dY | dZ | ωx | ωy | ωz | m | Источник |
|---|---|---|---|---|---|---|---|---|
|
1 |
1.07 |
0.03 |
-0.02 |
0 |
0 |
0.13 |
0.22*10-6 |
ГОСТ 51794-2008 (Приложение Г) >>> |
Источники информации
ERDAS IMAGINE: Файл spheroid.tab, например: C:GisIMAGINE9.0etcspheroid.tab
ArcGIS Desktop: Файл geographic_transformations.pdf, например: C:GisArcGISDocumentationgeographic_transformations.pdf
Mapinfo: Internal datum parameters used in MapInfo Professional >>> или в XLS
EPSG: Отдельная база в виде базы MS Access, либо онлайн репозиторий
ГОСТ 51794-2001, ГОСТ 51794-2008 >>>
Ссылки по теме
- Загрузка данных с GPS в нужной системе координат (DNRGarmin)
- Разница в определении координат в WGS84 и СК42
- Использование Arcview Projection Utility для перевода данных из одной системы координат в другую
В соответствии с постановлением Российской Федерации «Об установлении государственных систем координат, государственной системы высот и государственной гравиметрической системы» №1240 от 24 ноября 2016 г. устанавливаются государственные системы координат:
- ГСК-2011 – для использования при осуществлении геодезических и картографических работ;
- ПЗ-90.11 – для геодезического обеспечения орбитальных полётов, решения навигационных задач и выполнения геодезических и картографических работ в интересах обороны.
Применяемые ранее государственные системы координат СК-42 и СК-95 могут использоваться до 1 января 2021 года.
Параметры трансформации между системами координат определены в ГОСТ 32453-2017.
Начиная с 32-битной версии MapInfo Pro 15.0.1 и 64-битной версии MapInfo Pro 16.0.1 появилсь возможность использовать современные эллипсоиды применяемые в Российской федерации.
Для задания системы координат требуется указать датум, тип проекции и её параметры, а также, при необходимости: параметры сдвига, поворота и растяжения/сжатия для аффинного преобразования и, для достижения необходимой точности при хранении координат охват (bounds).
Для определения датума в MapInfo Pro используется следующая информация:
- Модель эллипсоида. Эллипсоид описывается: длиной в метрах главной полуоси a и геометрическим (полярным) сжатием f. Из-за малых величин f, на практике используют обратную величину 1/f. MapInfo Pro поддерживает более 50 заранее заданных эллипсоидов.
- Параметры преобразования эллипсоида к WGS 84:
- Три параметра сдвига центра эллипсоида ΔX, ΔY, ΔZ. Эти параметры задают смещение в метрах вдоль каждой из осей.
- Три параметра поворота эллипсоида на заданный угол в секундах ωx, ωy, ωz.
- Масштабный параметр трансформирования m.
- Долгота нулевого меридиана в градусах к востоку от Гринвича.
Параметры эллипсоидов для России, используемые в ГИС MapInfo Pro:
№ |
Название |
a |
1/f |
|
3 |
Красовского |
6378245.0 |
298.3 |
|
56* |
ГСК-2011 |
6378136.5 |
298.2564151 |
|
52 |
ПЗ-90 |
6378136.0 |
298.257839303 |
|
57* |
ПЗ-90.11 |
6378136.0 |
298.25784 |
* Эллипсоиды добавлены начиная с 32-битной версии MapInfo Pro 15.0.1 и 64-битной версии MapInfo Pro 16.0.1.
Поддержка для младших версий не предусмотрена.
Датумы для России, используемые в ГИС MapInfo Pro:
№ |
Название |
№ эллипсоида |
ΔX |
ΔY |
ΔZ |
ωx |
ωy |
ωz |
m |
Нулевой меридиан |
|
1012 |
Российская ПЗ-90 |
52 |
-1.08 |
-0.27 |
-0.9 |
0 |
0 |
-0.16 |
-0.12 |
0 |
|
1013 |
Российская СК-42 |
52 |
23.92 |
-141.27 |
-80.9 |
0 |
-0.35 |
-0.82 |
-0.12 |
0 |
|
1014 |
Российская СК-95 |
52 |
24.82 |
-131.21 |
-82.66 |
0 |
0 |
-0.16 |
-0.12 |
0 |
Внимание: приведённые выше датумы устарели и не соответствуют ГОСТ 32453-2017.
Параметры трансформации
Для использования систем координат соответствующим ГОСТ 32453-2017 в MapInfo Pro требуется самостоятельно задать требуемые параметры.
При трансформации координат из одного датума в другой используется формула принимающая семь параметров: 3 параметра сдвига, 3 параметра поворота, масштабный параметр трансформирования. Известно два варианта этой формулы: “Поворот координатной системы” (Coordinate Frame rotation) EPSG:1032 и “Преобразование радиуса-вектора” (Position Vector transformation) EPSG:1033. Формулы могут быть приведены одна к другой заменой знаков трёх значений параметров поворота на противоположные. Это создаёт большую путаницу, тем более что в литературе оба метода иногда называют преобразованием Бурша-Вольфа и преобразованием Гельмерта.
В ГОСТ 32453-2017 и MapInfo Pro используется формула “Поворот координатной системы”. А в ISO 19111 и например в известной библиотеке Proj (ранее Proj.4) используется “Преобразование радиуса-вектора”. Таким образом, чтобы использовать приведённый здесь параметры датумов в Proj требуется изменить знаки у параметров поворота ωx, ωy, ωz.
В ГОСТ 32453-2017 указаны параметры пересчёта координат в ПЗ-90.11, а в MapInfo Pro (как и во многих других ГИС) преобразование координат осуществляется через WGS-84. Ниже приведены параметры пересчёта СК-42, СК-95, ГСК-2011 и ПЗ-90 в WGS-84, полученные путём сложения параметров трансформации этих систем координат в ПЗ-90.11 и параметров трансформации ПЗ-90.11 в WGS-84.
Датумы, согласно ГОСТ 32453-2017:
Название |
№ эллипсоида |
ΔX |
ΔY |
ΔZ |
ωx |
ωy |
ωz |
m |
Нулевой меридиан |
|
ПЗ-90 |
57 |
-1.43 |
0.05 |
0.2 |
0 |
0 |
-0.13 |
-0.22 |
0 |
|
ПЗ-90.02 |
57 |
-0.36 |
0.08 |
0.18 |
0 |
0 |
0 |
0 |
0 |
|
ПЗ-90.11 |
57 |
0.013 |
-0.106 |
-0.022 |
0.0023 |
-0.00354 |
0.00421 |
0.008 |
0 |
|
СК-42 |
3 |
23.57 |
-140.95 |
-79.8 |
0 |
-0.35 |
-0.79 |
-0.22 |
0 |
|
СК-95 |
3 |
24.47 |
-130.89 |
-81.56 |
0 |
0 |
-0.13 |
-0.22 |
0 |
|
ГСК-2011 |
56 |
0.013 |
-0.092 |
-0.03 |
0.001738 |
-0.003559 |
0.004263 |
0.0074 |
0 |
Настройка MapInfo Pro
В MapInfo Pro параметры систем координат задаются в файле MapInfow.prj. Файл проекций MapInfow.prj, находится в той же папке, где установлена MapInfo Pro, а начиная с 17 версии в подпапке с языком программы (ru – для русского). Следует отметить, что чаще всего, программа MapInfo Pro установлена в папке «Program Files», что требует прав Администратора для редактирования этого файла. Для редактирования этого файла можно использовать любой текстовый редактор, например, Блокнот.
Каждая строка файла MapInfow.prj определяет координатную систему или категорию.
Координатная система задаётся строкой:
“Название КС”, Тип_проекции, Датум, , … параметры проекции
Название КС: название, которое будет появляться в списке проекций.
Тип_проекции: номер, определяющий уравнения, которыми задаются координатная система.
Датум: номер, определяющий параметры датума.
Чтобы создать координатную систему с собственным датумом, следует вместо номера датума использовать номер 9999, после которого должны быть перечислены значения в следующем порядке:
9999, Номер_Эллипсоида, ΔX, ΔY, ΔZ, ωx, ωy, ωz, m, Нулевой_Меридиан
Например, для проекции Долгота/Широта СК-95:
“Долгота/Широта (СК-95)”, 1, 9999, 3, 24.47, -130.89, -81.56, 0, 0, -0.13, -0.22, 0
Цифра «1» после названия системы координат означает, что используется проекция Долгота/Широта.
Для проекции Гаусса-Крюгера в СК-42:
“ГК Зона 7 (СК-42)”, 8, 9999, 3, 23.57, -140.95, -79.8, 0, -0.35, -0.79, -0.22, 0, 7, 39, 0, 1, 7500000, 0
Цифра «8» после названия системы координат означает, что используется поперечная проекция Меркатора (Гаусса-Крюгера), значения – «7, 39, 0, 1, 7500000, 0» являются параметрами проекции Гаусса-Крюгера для 7 зоны. Значения для других зон можно взять из файла MapInfow.prj для “— Гаусса-Крюгера (Пулково 1942) —“
Категории проекций используются для группировки систем координат. Чтобы задать свою категорию проекций требуется указать в отдельной строке:
— Название категории —
Координатные системы, определённые после этой строки будут помещены в эту категорию.
Подробнее о задании собственных систем координат можно узнать в руководстве пользователя (MapInfoProUserGuide.pdf), включённом в поставку MapInfo Pro.
Параметры систем координат проекции Долгота/Широта
Ниже приводятся строки, которые можно использовать в файле MapInfow.prj:
— Долгота / Широта (ГОСТ 32453-2017) —
“Долгота/Широта (ПЗ-90)”, 1, 9999, 57, -1.43, 0.05, 0.2, 0, 0, -0.13, -0.22, 0
“Долгота/Широта (ПЗ-90.02)”, 1, 9999, 57, -0.36, 0.08, 0.18, 0, 0, 0, 0, 0
“Долгота/Широта (ПЗ-90.11)”, 1, 9999, 57, 0.013, -0.106, -0.022, 0.0023, -0.00354, 0.00421, 0.008, 0
“Долгота/Широта (СК-42)”, 1, 9999, 3, 23.57, -140.95, -79.8, 0, -0.35, -0.79, -0.22, 0
“Долгота/Широта (СК-95)”, 1, 9999, 3, 24.47, -130.89, -81.56, 0, 0, -0.13, -0.22, 0
“Долгота/Широта (ГСК-2011)”, 1, 9999, 56, 0.013, -0.092, -0.03, 0.001738, -0.003559, 0.004263, 0.0074, 0
Смена системы координат без перепроецирования в MapInfo Pro
Часто пользователи MapInfo Pro создают таблицы на территорию России, используя проекцию Гаусса-Крюгера (Пулково 1942). Однако, датум (номер 1001), используемый в данной системе координат, входящий в стандартную поставку MapInfo, предназначен для использования на территории Германии. В связи с этим, при передаче данных в другие ГИС или при переходе в другую координатную систему (например, ГСК-2011) происходит искажение координат объектов.
В этом случаем требуется сменить систему координат таблицы, при этом не трансформируя координаты.
Для того, чтобы изменить систему координат без перепроецирования необходимо сделать следующее:
- экспортировать таблицу в mif/mid;
- сменить строку системы координат в mif-файле используя любой текстовый редактор, например, Блокнот;
- импортировать mif/mid в tab-файл.
Можно также воспользоваться инструментами, позволяющими автоматизировать процесс. Например «Репроекция таблиц» (автор Дмитрий Мазуров) доступно на сайте http://glab2007.narod.ru/d/mu.html. Для 64-битных версий MapInfo Pro можно использовать CoordsysChanger (автор Peter Horsbøll Møller) доступный на торговой площадке MapInfo MarketPlace или по ссылке http://mapinfomarketplace.pitneybowes.com/product/4d68d42c-7d5a-40c8-ab37-56c005176049
Материал для статьи предоставлен Варущенко С.С. (ИПНГ РАН) и Макаровым С.Б. (МИИГАиК)
Вопросы и предложения по статье: support@mapinfo.ru
УДК 528.236
ПОЛУЧЕНИЕ ПАРАМЕТРОВ СВЯЗИ МЕЖДУ СИСТЕМАМИ КООРДИНАТ
КОСВЕННЫМ МЕТОДОМ
RECEIVING CONNECTION PARAMETERS BETWEEN THE COORDINATE SYSTEMS WITH THE HELP OF THE INDIRECT METHOD
Суханов Сергей Иванович1,
кандидат техн. наук, e-mail: sukhanov-s@mail.ru Sukhanov Segey I., С. Sc.
Прокопенко Евгения Викторовна2,
кандидат физ-мат. наук, доцент, e-mail: pev-05@mail.ru Prokopenko Evgenia V., С. Sc., Associate Professor
‘Алтайский государственный университет, 656000, Россия, г. Барнаул, пр. Ленина, 61 Altai State University, 656049, Russia, Barnaul, pr. Lenina 61
2Кузбасский государственный технический университет имени Т.Ф. Горбачева, 650000, Россия, г. Кемерово, ул. Весенняя, 28
T.F. Gorbachev Kuzbass State Technical University, 28 streetVesennyaya, Kemerovo, 650000, Russian Federation
Аннотация. При выполнении геодезических работ возникает задача перевода координат из одной системы координат в другую. Преобразования координат в зависимости от задач бывают как двумерные так и трехмерные. Двухмерный метод применяется для преобразования координат из одной декартовой системы в другую. Трехмерный метод применяется для преобразования пространственных прямоугольных координат. Оба преобразования изначально не являются взаимно однозначными преобразованиями. В статье описываются способы получение формул взаимно согласованных преобразований как двухмерных, так и трехмерных координат.
Abstract. Carrying out geodesic tasks faces a problem of appropriate conversion of map data from one coordinate system into another. Depending on the tasks conversion of coordinates can be both two-dimensional and three-dimensional. The two-dimensional technique is used to convert coordinates from one Cartesian system to another. The three-dimensional method is used to convert Cartesian three-dimensional coordinates. Both conversion techniques are initially not one-to-one transformations. The article focuses on the methods of obtaining one-to-one transformation formulas for both two-dimensional and three-dimensional coordinates.
Ключевые слова: система координат, коэффициенты преобразований, балансировка, погрешность координат, пространственные прямоугольные координаты
Keywords: coordinate system, conversion coefficients, balancing adjustment, coordinate error, Cartesian three-dimensional coordinates
При выполнении геодезических работ с использованием спутниковых технологий, возникает задача преобразования координат пунктов государственной геодезической сети из одной местной системы в систему координат того административного округа, где выполняются данные работы. При этом могут возникать серьезные затруднения, так как зачастую существующие «ключи» перехода к этим системам из государственной системы координат не дают нужной точности.
Проводя данный вид работ на территории городов и сельских территорий, возникает необходимость совместного использования карт выполненных в разных системах координат, что приводит к необходимости преобразования координат из одной системы координат в другую.[1].
Методы преобразования координат бывают как двумерные, так и трехмерные. Двухмерный метод применяется для преобразования одной плоской координатной системы в другую подобную систему. В каждом регионе нашей страны для ведения кадастра применяется своя система координат. В Алтайском крае принята СК-22, полученная из СК-63 линейным сдвигом. Архитектура же, в свою очередь, работает с планшетами, выпущенными еще в советское время, когда на территориях городов и сельских поселений Алтая существовали свои местные системах координат.
Алгоритм перехода из одной местной системы координат в другую близок к аффиннову преобразованию, которое представляется в виде поворота осей и сдвига начала координат, при которых ис-
пользуются четыре параметра [2]:
/ X ‘ сова вта^ / X }
= т +
ь ^-Бта со а
(1)
где а — угол разворота осей координат, т— масштабирующий множитель, а и Ъ — системы координат.
Построение данных преобразований традиционно производится с использованием таблицы опорных точек. Для определения этих параметров необходимо иметь два совмещенных пункта, координаты которых известны в обеих системах координат.
Применение ОРЭ-приемников при геодезических измерениях повысило точность геодезических измерений, что привело к необходимости более точного пересчета координат из СК-22 в мировую систему VGS-84.f3]. Корректный переход между системами достигается при использовании математически строгих преобразований, например, решением уравнения Крюгера. На практике часто применяется способ, описанный Гельбертом.
Данный метод относится к трехмерным способам преобразования координат, неотъемлемой частью которого является задача пересчета координат из одной прямоугольной пространственной системы в другую.
Преобразование пространственных прямоугольных координат выполняется по формуле:
-й>г
где Ах, Ау, Аг – линейные элементы, сох, СО СО 2 – угловые элементы, т— масштабирующий множитель, а и Ъ — системы координат.
В данном способе используются семь параметров: три параметра взаимно-однозначного ориентирования, три углового взаимного ориентирования и один масштабирующий множитель.
Порядок вычислений таков: по геодезическим координатам системы а рассчитываются прямоугольные пространственные координаты Ха, уа , 2а . Используя параметры преобразования (2) координаты х , уа , га преобразуются в прямоугольные координаты: хь, уь, 2Ь. Затем координаты хь, уь, преобразуются в геодезические координаты системы Ъ .
Применяя описанные методики для двумерно трехмерного случаев, можно самостоятельно решить проблему поиска параметров перехода от одной системы координат к другой, но данные преобразования будут несогласованными. Несогласованность в данном случае означает, что, про-
/ X
= т
2
уь
со2 / X ГДх]
1 У + (2)
1 У а
изводя преобразование из системы а в Ь , а затем из Ъ в а, начальные и конечные значения не совпадут.
Для получения согласованных данных в двумерном случае запишем преобразование координат из системы а в Ъ в следующем виде:
^Ах^
с X
= т
У;
а обратное :
г. Л
О, Ух
ч-Уу
Ч-У У а
= т,
а2 Ъ2 К-Ь2 а2,
/ х
и
+
(АхЛ
ь 1ау,
(3)
(4)
где
а1 = соБаа; Ьх = ът.аа; а2 = со$аь; Ь2 = этс^.
Правую часть формулы (3) подставим в формулу (4):
X
У)а
= тьта
~Ь2 аи
а
-Ь
/ х
+ т,
Ь Ь2
у-Ь2 а2;
1 и
У а
+
+
чАУу
а
Ах
Правую часть формулы (4) подставим в формулу (3):
/— X
ЦУ
= тать
а2 Ъ2 у-Ь2 а2,
У.
+
^Ах^
+
к~Ь а> ъ .АУ,
Для того, чтобы преобразования (3) и (4) были согласованны, то есть
/ х
X
/ X
У)а
кУ;ь
х
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
У У 6
необходимо выполнение следующих условий:
тьта
а2 Ъ2 К-Ь2 а2,
тать
т.
~Ьг я, у
/ а n
Ах
К-Ь2 а2;
т,
ьу.
Ах
Ау.
аи а2 Ъ2 -Ъ2 а2;
/а N
Ах
‘1 О
0 1
ч
1 (Г
0 1,
+
Ау.
V -7 У МСК VУ VGS-M
АхЛ
+
Ах
мск ч^у
уОу
‘Ч У
Аналогично плоскому случаю,общий вид трехмерного преобразования из системы координата в Ъ можно записать в следующем виде:
/ X
У = тх
, 2 ,
1
— а кЬ,
а обратное:
/ х
У
2У
=
-а2
ах 1
а2 1
-с,
-ы
-Ъ.,
1
/ X ( /Ах
У + Ау
а Ы
V / х 1 ‘ДдЛ
+ АУ
К?) Ь м
(5)
(6)
Запишем преобразование из а в Ъ и обратно:
/ л
У
/ X
У
/
У
—>
/ X
У
К2 У
с—^
X
-> У
Ч
/-
2
V Уг,
Несогласованность в трехмерном случае означает, что:
/ N /—
г X X
У – У
а
/оЛ
/ X
У
Ч*/
/— X
У
Выведем условия согласованности для трехмерного случая. Правую часть формулы (5) подставим в формулу (6):
/-л X ( 1 а2
У ~ тЬта -а2 1
2 [ь2 ~С2
У а
-М
+ т.
-а.
-я,
V ь
-с,
«1 1
-С,
-Ь2УЛх)
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
1
Ау
Аг
Ах) Ау
Подставим правую часть формулы (6) в формулу (5), получим выражение:
X
У
1
V л
= тать
1
-а
V*.
+ т,
-ах
-а2
а! 1
-с,
1 1
а2 1
-с2
-Л
у
/ А
+
1
м ( Ах^|
4У + 4У
Аг .
/6
/а
Отсюда следует, что условиями согласованности являются следующие выражения:
т.т
тт.
а о
т,
т,
-а2
-ах Ч*>
-а2 Ъ2
«2 1
-¿2
ау 1
-с,
С2 1
-V 1
-а,
Ч*.
‘ 1
-в2
4^2
а, 1
-¿1 1
-с,
а2 1
а1 1
-с
-ъ2
С2 1
1
Ах
АУ Аг
‘Ах
АУ Аг
/а Ч
+
/й
1
С2 1
Ау А^
Ах Ау Аг
(1 0 °1
= 0 1 0
/ 0 к
( 0 0)
= 0 1 0
/ 0 к
о
А ^
о о
При пересчете из одной системы в другую накапливаются ошибки не только из-за неточных формул преобразований координат, но и из-за ошибок округления при вычислениях. В результате использования при расчетах согласованных преобразований, как двумерном, так и в трехмерном случаях можно нивелировать суммарные погрешности вычислений. Согласованные преобразования пространственных координат из одной системы в другую помогает получать параметры связи точнее, чем в «ключах».
СПИСОК ЛИТЕРАТУРЫ
1. Руководство пользователя по выполнению работ в системе координат 1995 года (СК-95). ГКИНП (ГНТА)-06-278-04. – М.: ЦНИИГАиК, 2004. – 89 с.
2. Поклад, Г.Г., Гриднев С.П. Геодезия. Учебное пособие для вузов.- М.: Академический Проект, 2007.-592 с.
3. Руководство по обновлению цифровых топографических карт и планов на ЦФС по материалам аэрокосмических съемок. Проект. – М.: ЦНИИГАиК, 2007.
4. Оскорбин Н.М., Суханов С.И. Оценка параметров формул прямого и обратного преобразования
пространственных координат // Геодезия и картография. – 2011. №6. – С. 26-29
5. Подшивалов В.П. Оценка параметров преобразования координат на плоскости методом наименьших квадратов // Автоматизированные технологии изысканий и проектирования. – М., 2010. – № 4(39). – С. 69-72.
REFERENCES
1. Rukovodstvo polzovatelya ро vypolneniyu rabot v sisteme koordinat 1995 goda (SK-95). GKINP (GNTA) -06-278-04. – M.: TSNIIGA AiK, 2004. – 89 s.
2. Poklad G.G., Gridnev S.P. Goedezia. Uchebnoe posobie dlya vuzov [Geodesy. Textbook for high schools]- M.: Akademicheskiy Proekt, 2007. – 592 s.
3. Rukovodstvo po obnovleniyu tsifrovykh topograficheskikh kart i planov ha TSFS po materialam aero-kosmicheskikh syemok. Proekt. – M.: TSNIIGA AiK, 2007.
4. Oskorbin N.M., Sukhanov S. I. Otsenka parametrov formul pryamogo i obratnogo preobrazovaniya prostranstvennykh koordinat [Parameter Estimation of Reciprocal Conversion Formulas of Spatial Coordi-nates]//Geodesy and Cartography. – 2011 №6. – S. 26-29
5. Podshivalov V.P. Otsenka parametrov preobrazovaniya koordinat na ploskosti metodom naimenshikh kvadratov [Evaluation of Coordinate Transformation Parameters on the Plane Using the Method of Least-squares]// Avtomatizirovannye tekhnologii izyskaniy i proektirovaniya – M., 2010. – № 4(39). – S. 69-72.
Поступило в редакцию 30.01.2017 Received 30.01.2017