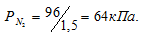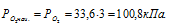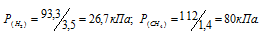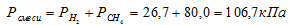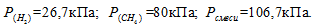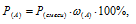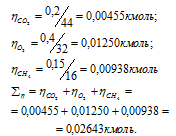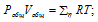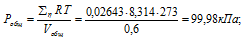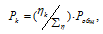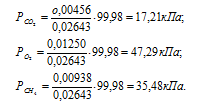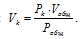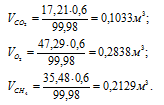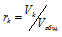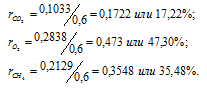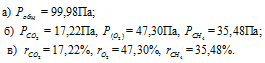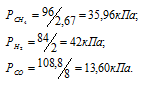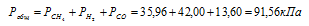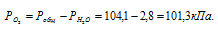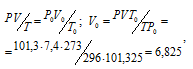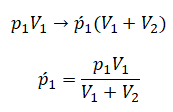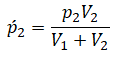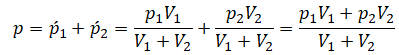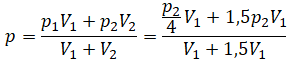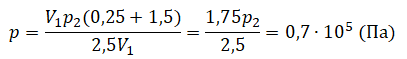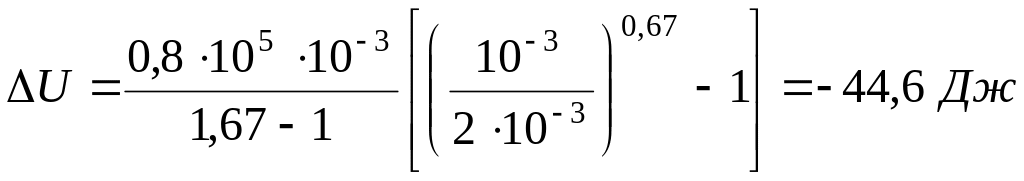Как найти парциальное давление задача

Задачи на нахождение парциального давления газов и общего давления смеси

Задача 41. 
Смешивают 0,04м³ азота, находящегося под давлением 96кПа (720мм. рт. ст.), с 0,02м³ кислорода. Общий объем смеси 0,06м³, а общее давление 97,6кПа (732мм. рт. ст.). Каким было давление взятого кислорода?
Решение:
По условию задачи объём азота увеличился в 1,5 раза (0,06/0,04 = 1,5), а объём кислорода – в 3 раза (0,06/0,02 = 3). Во столько же раз уменьшились парциальные давления газов. 

Следовательно,

Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь). Отсюда   Исходя из того, что объём кислорода до смешения был в три раза больше, чем после смешения, рассчитаем давление кислорода до смешения: 

Ответ: Р_общ.  = 100,8кПа.

---

Задача 42. 
Газовая смесь приготовлена из 2л Н₂ (Р = 93,3 кПа) и 5л CH₄ (Р = 112 кПа). Объем смеси равен 7л. Найти парциальные давления газов и общее давление смеси.
Решение:
По условию задачи объём водорода увеличился в 3,5 раза (7/2 = 3,5), а объём метана – в 1,4 раза (7/5 = 1,4). Во столько же раз уменьшились парциальные давления газов. 

Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь). 

Отсюда:

Ответ:

---

Задача 43. 
Газовая смесь состоит из NO и СО₂. Вычислить объемное содержание газов в смеси (в %), если их парциальные давления равны соответственно 36,3 и 70,4 кПа (272 и 528мм. рт. ст.).
Решение:
Согласно закону Дальтона парциальное давление данного газа прямо пропорционально его мольной доли на общее давление смеси газов:

где Р(смеси) – общее давление смеси; Р(А) – парциальное давление данного газа; _(A) – мольная доля данного газа.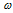 

Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь). 

Отсюда:                   

Ответ: 34,02%NO; 65,98%CO.

---

Задача 44. 
В закрытом сосуде вместимостью 0,6м³ находится при 0 °С смесь, состоящая из 0,2кг СО₂, 0,4кг 02 и 0,15кг СН₄. Вычислить: а) общее давление смеси; б) парциальное давление каждого из газов; в) процентный состав смеси по объему.
Решение:
Вычислим общее количество газов в смеси по уравнению: 

,  где

– количество газа, кмоль; m – масса газа, кг; М – молекулярная масса газа, кг/моль. Тогда: 

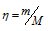
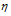
а) Общее давление смеси газов определяем по уравнению:

Тогда:

б) Парциальные давления газов рассчитываем по уравнению: 

где R_k и 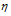_k , соответственно, парциальное давление, и количество газа в смеси. 

Тогда

 в) Парциальные объёмы газов рассчитаем по уравнению:

Тогда 

Отношение парциальных (приведённых) объёмов отдельных газов к общему объёму смеси называется объёмной долей и определяется по формуле: 

Тогда

Ответ:

---

Задача 45. 
Газовая смесь приготовлена из 0,03м³ СН₄, 0,04м³ Н₂ и 0,01м³ СО. Исходные давления СН₄, Н₂ и СО составляли ответственно 96, 84 и 108,8 кПа (720, 630 и 816мм рт. ст.). Объем смеси равен 0,08м³. Определить парциальные давления газов и общее давление смеси.
Решение:
По условию задачи объём метана увеличился после смешения в 2,67 раза (0,08/0,03 = 2,67), объём водорода – в 2 раза (0,08/0,04 = 2), а объём угарного газа – в 8 раз (0,08/0,01 = 8). Во столько же раз уменьшились парциальные давления газов. Следовательно,

Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь). 

Отсюда:

Ответ: 

---

Задача 46. 
В газометре над водой находятся 7,4л кислорода при 23 °С и давлении 104,1 кПа (781 мм. рт. ст.). Давление насыщенного водяного пара при 23 °С равно 2,8 кПа (21мм. рт. ст.). Какой объем займет находящийся в газометре кислород при нормальных условиях?
Решение:
Парциальное давление кислорода равно разности общего давления и парциального давления паров воды:

Обозначив искомый объём через  и, используя объединённое уравнение закона Бойля- Мариотта и Гей-Люссака, находим:

 где Р и V – давление и объём газа при температуре Т = 296К (273 +23 = 296); Р₀ = 101,325кПа; Т₀ = 273К; Р = 104,1кПа;  – объём газа при н.у.

Ответ: V₀ =6,825л.

---

Смесям идеальных газов характерно свойство аддитивности двух показателей: парциального давления и объёма. Другими словами, любому включённому в смесь инертному газу характерно такое поведение, какое было бы, если б он в единственном числе заполнял предлагаемый объём. Для лучшего понимания разумно разобраться, что выражают указанные величины.

Говоря об идеальных газах и их смеси, следует понимать, что изменение условий, например температуры или давления, всё же может спровоцировать химическую реакцию. Важным параметром такой смеси является молярная (весовая) концентрация газового компонента. Данная величина измеряется в мг/м³ и показывает количество конкретного компонента в единице объёма газовой смеси.

Парциальное давление

Описывая характеристику состояния компонентов идеальной смеси газообразных веществ, парциальное давление, создаваемое i-ым газом в случае удаления других компонентов из сохраняемых условий, является показателем p_i.

Следует отметить, что равность средней кинетической энергии находящихся в смеси молекул определяет равенство температур всех компонентов термодинамически уравновешенной газовой смеси. Найти общее давление смеси идеальных газов представляется возможным через закон Дальтона, отражаемый аддитивность парциальных давлений, а именно [p=sum p_{i}].

Пользуясь данным законом, найдём давление смеси идеальных газов через следующую формулировку: [p=sum_{i}^{N}=1 rightarrow p_{i}=frac{R T}{V} sum_{i}^{N}=1^{v_{i}}], где N – количество вошедших в смесь газов, v_i– количественный показатель молей i-го газа. Отсюда парциальное давление можно выразить формулой [p_{i}=x_{i} p], где x_i – молярная концентрация i-го газа.

Понятие парциального объёма

Описывая характеристику состояния компонентов идеальной смеси газообразных веществ, парциальный объём, занимаемый i-ым газом в случае удаления других компонентов из сохраняемых условий, является показателем V_i. Аддитивность парциального объёма определяет закон Амага, выраженный формулой [V=sum_{i}^{N}=1 V_{i}].

Зная, что характеризующие состояние смеси инертных газов показатели подчиняются уравнению Менделеева-Клапейрона, выведем формулу:

[p V=frac{m}{mu_{s m}} R T] данное уравнение свои параметры относит ко всей газовой смеси.

[pV=mR_{s m} T] такой вариант уравнения содержит показатель R_sm, обозначающий удельную газовую составляющую смеси.

Уравнение Менделеева-Клапейрона показывает возможность изменения трёх характеризующих состояние идеального газа параметров.

Примеры вычисления парциального давления и объёма

Задача №1

Условие: в сосуде объёмом 2 м³, при постоянной температуре 290 К находится 0,20*10^-3 кг гелия и 1*10^-3 кг водорода. Необходимо вычислить давление смеси и парциальное давление гелия.

Решение.

Сначала вычислим количество молей каждого компонента, используя следующую формулу:

[mathrm{v}{mathrm{i}}=frac{mathrm{m}{mathrm{i}}}{mu_{mathrm{i}}}]

Для расчёта количество молей водорода в смеси нам понадобится его молярная масса, которую возьмём из таблицы Менделеева:

[mu_{mathrm{H}_{2}}=2 * 10^{-3} frac{mathrm{кг}}{text { моль }}]

Теперь можно найти количество молей водорода в смеси:

[mathrm{v}_{mathrm{H}_{2}}=frac{mathrm{m}_{mathrm{H}_{2}}}{mu_{mathrm{H}_{2}}}=frac{1 * 10^{-3}}{2 * 10^{-3}}=0,5 text { (моль) }]

Зная молярную массу гелия из таблицы Менделеева, рассчитаем количество молей гелия в смеси:

[mathrm{v}_{mathrm{He}}=frac{mathrm{m}_{mathrm{He}}}{mu_{mathrm{He}}}=frac{4 * 10^{-3}}{20 * 10^{-3}}=0,2 text { (моль) }]

Теперь можно найти парциальное давление каждого из компонентов с помощью уравнения Менделеева-Клапейрона:

[mathrm{p}_{mathrm{i}} mathrm{V}=mathrm{v}_{mathrm{i}} mathrm{RT}]

Сначала нужно рассчитать давление водорода:

[mathrm{p}_{mathrm{H}_{2}} mathrm{~V}=mathrm{v}_{mathrm{H}_{2}} mathrm{RT} rightarrow mathrm{p}_{mathrm{H}_{2}}=frac{mathrm{v}_{mathrm{H}_{2}} mathrm{RT}}{mathrm{V}}=frac{0,5 * 8,31 * 290}{1}=1205 text { (Па) }]

Рассчитаем парциальное давление гелия:

[mathrm{p}_{mathrm{He}}=frac{mathrm{v}_{mathrm{He}} mathrm{RT}}{mathrm{V}}=frac{0,2 * 8,31 * 290}{1}=482 text { (Па) }]

Теперь найдём полное давление газовой смеси, сложив значения компонентов:

[mathrm{p}=mathrm{p}_{mathrm{H}_{2+}} mathrm{p}_{mathrm{H}}=1205+482=1687 text { Па }]

Ответ: парциальное давление гелия равно 482 Па, а общее давление 1205 Па.

---

Задача №2

Условие: идеальная газовая смесь состоит из 0,5 кг углекислого газа и 0,25 кг кислорода, какой объём они займут, если давление равно 1 атм, а температура смеси равна 300 К?

Решение.

Найдём суммарную массу газовой смеси:

[mathrm{m}=mathrm{m}_{mathrm{O}_{2}}+mathrm{m}_{mathrm{CO}_{2}}=0,5+0,25=0,75 text { (кг) }]

Вычислим массовые компоненты смеси:

[g_{mathrm{O}_{2}}=frac{0,25}{0,75}=0,33] [mathrm{g}_{mathrm{CO}_{2}}=frac{0,5}{0,75}=0,67]

Тогда газовая постоянная смеси равняется:

[mathrm{R}_{mathrm{sm}}=mathrm{R} sum_{mathrm{i}=1}^{mathrm{N}} frac{mathrm{g}_{mathrm{i}}}{mu_{mathrm{i}}}=8,31left(frac{0,33}{32 * 10^{-3}}+frac{0,67}{46 * 10^{-3}}right)=200left(frac{text { Дж }}{text { кгК }}right)]

Пользуясь уравнением Менделеева-Клапейрона, и, зная, что 1 атм равна 10⁵ Па,вычислим объём смеси:

[mathrm{V}_{mathrm{sm}}=frac{mathrm{m}_{mathrm{sm}} mathrm{R}_{mathrm{sm}} mathrm{T}_{mathrm{sm}}}{mathrm{P}_{mathrm{sm}}}=frac{0,75 * 200 * 300}{10^{5}}=0,45left(mathrm{м}^{3}right)]

Ответ: при заданных условиях смесь займёт 0,45 м^3.

Навык определения парциальных давлений и объёма актуален в машиностроении, энергетике и других промышленностях, связанных с использованием тепловых двигателей, приводимых в действие парами высокой температуры.

Закон Дальтона

Давление смеси газов равно сумме их парциальных давлений.

p = p₁’ + p₂’ + … .

К примеру, давление воздуха складывается из давления азота, кислорода, углекислого газа, водяного пара и т. д.

Определение

Парциальное давление — давление, которое производил бы данный газ, если бы другие газы отсутствовали.

Применение закона Дальтона при решении задач

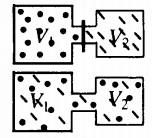
Самая популярная задача на закон Дальтона, это случай, когда газы находятся в сосудах, соединенных трубкой с краном. По условию этой задачи нужно найти давление, которое установится после того, как этот кран будет открыт.

После открытия крана первый и второй газы заполнят оба сосуда. Используем закон Бойля — Мариотта для первого газа (так как температура остается постоянной):

Этот же закон можем применить для второго газа. Тогда мы получим:

Применим закон Дальтона и получим:

Пример №1. Два сосуда соединены трубкой с краном. Определить давление, которое установится после того, как кран будет открыт. Считать, что объем второго сосуда в 1,5 раза больше первого. Давление во втором сосуде составляет половину от атмосферного давления. В первом сосуде оно меньше в 4 раза.

Проанализируем условия задачи и запишем:

V₂ = 1,5V₁

p₂ = 4p₁

p₂ = 10⁵ Па

Теперь можем применить выведенную ранее формулу:

Преобразуем выражение и найдем установившееся давление:

Задание EF17512

Три одинаковых сосуда, содержащих разреженный газ, соединены друг с другом трубками малого диаметра: первый сосуд – со вторым, второй – с третьим. Первоначально давление газа в сосудах было равно соответственно р, 3р и р. В ходе опыта сначала открыли и закрыли кран, соединяющий второй и третий сосуды, а затем открыли и закрыли кран, соединяющий первый сосуд со вторым. Как изменилось в итоге (уменьшилось, увеличилось или осталось неизменным) количество газа в первом сосуде? (Температура газа оставалась в течение всего опыта неизменной.)

---

Алгоритм решения

1.Записать исходные данные.

2.Применить закон Дальтона для определения давления в первом сосуде.

3.Применить закон Менделеева — Клапейрона для установления характера изменения количества газа в первом сосуде в ходе эксперимента.

Решение

Запишем исходные данные:

• Объемы сосудов равны: V₁ = V₂ = V₃ = V.

• Температуры равны: T₁ = T₂ = T₃ = T.

• Давления распределены следующим образом: p₁ = p, p₂ = 3p, p₃ = p.

После того, как открыли кран между 2 и 3 сосудом, объем возрос вдвое, и давление распределилось по нему равномерно. Согласно закону Дальтона, оно стало равным сумме давлений, оказываемых газами в количестве вещества ν₂ и ν₃. Так как объем после открытия крана увеличивается вдвое, то парциальное давление каждого из количества вещества равно половине исходного давления:

p23=p2+3p2=2p

Потом кран 2–3 закрыли, но открыли кран 1–2. Применим закон Дальтона, получим:

p12=2p2+p2=3p2

Теперь применим закон Менделеева — Клапейрона:

pV=νRT

Для начального состояния газа в 1 сосуде:

pV=ν1RT

Для конечного состояния газа в 1 сосуде:

3p2V=ν2RT

Так как температура и объем неизменны, но давление увеличилось в 1,5 раза, то и количество газа в первом сосуде увеличилось в 1,5 раза.

Ответ: Увеличилось

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18873

В сосуде неизменного объёма при комнатной температуре находилась смесь неона и аргона, по 1 моль каждого. Половину содержимого сосуда выпустили, а затем добавили в сосуд 1 моль аргона. Как изменились в результате парциальное давление неона и давление смеси газов, если температура газов в сосуде поддерживалась неизменной?

Для каждой величины определите соответствующий характер изменения:

1. увеличилась
2. уменьшилась
3. не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

---

Алгоритм решения

1.Записать исходные данные.

2.Установить характер изменения парциального давления неона.

3.Применить закон Менделеева — Клапейрона, чтобы установить характер изменения общего давления смеси газов.

Решение

Исходные данные:

• Количество неона: ν₁ = 1 моль.

• Количество аргона: ν₂ = 1 моль.

• Количество впущенного аргона: ν₄ = 1 моль.

Сначала парциальное давление неона и аргона равно. Это объясняется тем, что давление газов при неизменном количестве вещества зависит только от объема и температуры. Эти величины постоянны.

Когда из сосуда выпустили половину газовой смеси, в нем оказалось по половине моля каждого из газов. Затем в сосуд впустили 1 моль аргона. Следовательно, в сосуде стало содержаться 0,5 моль неона и 1,5 моль аргона. Запишем уравнение Менделеева — Клапейрона:

pV=νRT

Из уравнения видно, что давление и количество вещества — прямо пропорциональные величины. Следовательно, если количество неона уменьшилось, то его парциальное давление тоже уменьшилось.

Общая сумма количества вещества равна сумме количеств вещества 1 (неона) и 2 (аргона): 0,5 + 1,5 = 2 (моль). Изначально в сосуде тоже содержалось 2 моль газа. Так как количество вещества, температура и объем сохранились, давление тоже осталось неизменным.

Ответ: 23

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 3.4k

Когда мы имеем дело со смесями газов, важно знать, что они имеют такие характеристики, как парциальный объем и парциальное давление. Для начала определим, что такое смесь идеальных газов.

Смесь идеальных газов – это смесь нескольких газообразных веществ, которые при заданных условиях не будут вступать в определенные химические реакции.

При смене условий (например, повышении температуры, понижении давления) газовая смесь все же может вступать во взаимодействие. Важный параметр любой такой смеси – так называемая весовая концентрация gi i-ного газа-компонента.

Здесь:

• N – количество газов, из которых состоит смесь;
• xi i-го газа  – молярная концентрация указанного газа в составе смеси;
• νi – количество молей i-го газа, присутствующего в смеси.

Понятие парциального давления

Парциальное давление – это особая характеристика, описывающая состояние компонентов смеси идеальных газов. Сформулируем основное определение:

Парциальным называется давление pi, которое могло бы создаваться i-ым газом в смеси при условии отсутствия остальных газов и сохранения исходного объема и температуры.

Формула парциального давления будет выглядеть так:

pi=miμiRTV=μiRTV

Объем смеси здесь обозначен буквой V, ее температура – T.

Следует подчеркнуть, что поскольку средние кинетические энергии молекул смеси равны, то существует и равенство температур всех компонентов газовой смеси, находящейся в состоянии термодинамического равновесия.

Для нахождения давления смеси идеальных газов нужно воспользоваться законом Дальтона в следующей формулировке:

p=∑i=1Npi=RTV∑i=1Nνi

Исходя из него, мы можем выразить парциальное давление так:

pi=xip.

Понятие парциального объема

У газовой смеси также есть такая характеристика, как парциальный объем.

Парциальный объем Vi i-газа в газовой смеси – это такой объем, который мог бы иметь газ при условии отсутствия всех остальных газов и сохранении исходной температуры и объема.

Если речь идет о смеси идеальных газов, то к ней применим закон Амага:

V=∑i=1NVi

В самом деле, при выражении νi из формулы выше у нас получится следующее:

νi=pViRT; p=RTVpRT∑i=1NVi→V=∑i=1NVi

Для расчета парциального объема газа используется следующая формула:

Vi=xiV.

Нам известно, что параметры, определяющие состояние смеси идеальных газов, будут подчиняться уравнению Менделеева-Клайперона. Формула будет выглядеть так:

pV=mμsmRT.

Все параметры данного уравнения будут относиться ко всей смеси. Это же уравнение удобнее записать так:

pV=mRsmT.

Здесь параметры Rsm=Rμsm=R∑i=1Nqiμi означают удельную газовую постоянную смеси.

Пример
1. В сосуде
объемом 2 см³
находится смесь 4 кг гелия и 2 кг водорода
при температуре 27 ⁰С.
Определить давление и молярную массу
смеси газов.

Дано:
V
= 2
м³;
m₁
= 4
кг; m₂
= 2
кг; ₁
= 410^-3
кг/моль; ₂
= 2х

х10^-3
кг/моль; Т =
300 К.

Найти:
P,
.

Решение.
По закону Дальтона давление смеси газов
равно сумме парциальных давлений газов,
входящих в эту смесь: Р=Р₁+Р₂.

Парциальное давление р1 и р2 выразим из уравнения состояния

;

;

;
;

Давление смеси

.

Молярная масса смеси

,

где
₁
и ₂
– число молей
гелия и водорода.

Так
как

и

,
для молярной массы смеси

.

Подставляя численные значения, получим

.

Ответ:
Р = 2493
кПа; 
= 310^-3
кг/моль.

Пример
2. Объем
аргона, находящегося при давлении 80
кПа, увеличился от 1 до 2 л. На сколько
изменится внутренняя энергия газа, если
расширение производилось а) изобарно;
б) адиабатно?

Дано:
V₁=1
л; V₂=2
л; Р=0,810⁵
Па; =4010^-3
кг/моль; i=3.

Найти:
U.

Решение.
а) Изобарный процесс. Изменение внутренней
энергии при любом процессе определяется
выражением

.

Запишем уравнение
Менделеева-Клапейрона для начального
и конечного состояний газа:

;

.

Вычитая
из второго выражения первое, получим:

.

Подставляя
это выражение в формулу для U,
получим

.

Произведем
вычисления:

.

б)
Адиабатный процесс. При адиабатном
процессе теплообмен отсутствует, т.е.
Q
= 0 и
работа совершается за счет внутренней
энергии

А=-U
.

Формула
работы при адиабатном процессе имеет
вид:

,

где

.
При i
= 3

= 1,67.

Так
как

,
изменение внутренней энергии

.

Подставляя
численные значения, получим:

.

Знак
минус означает что внутренняя энергия
газа убывает.

Ответ:
U_из
= 121 Дж,
U_ад
= -44,6 Дж.

Пример
3. Тепловая
машина работает по обратимому циклу
Карно. Температура нагревателя Т₁
= 500 К.
Получая от нагревателя за цикл Q₁
= = 1 кДж
тепла, машина совершает работу А
= 350 Дж. Найти
КПД цикла, температуру охладителя и
количество тепла, отдаваемое охладителю.

Дано:
Т₁
= 500 К, А
= 350 Дж, Q₁
= 1 кДж.

Найти:
,
Т₂,
Q₂.

Решение.
КПД цикла

.
Температуру охладителя Т₂
найдем из выражения КПД цикла Карно

,

отсюда

.

Количество
тепла, отданное охладителю, Q₂=Q₁
–
A
.

Подставляя
численные значения, найдем искомые
величины:

.

Т₂
= 500(1 – 0,35) =
325 К;

Q₂
= (10³
– 350) Дж = 650 Дж.

Ответ:

=35 %, Т₂
= 325 К, Q₂
= 650 Дж.

Пример
4. Найти
изменение энтропии при переходе 6 г
водорода от объема 20 л под давлением
150 кПа к объему 60 л под давлением 100 кПа.

Дано:

= 210^-3
кг/моль, m
= 60 г, Р₁
= 150 кПа, V₁
= 20 л, Р₂
= 100 кПа, V₂
= 60 л, i
= 5.

Найти:
S.

Решение.
Запишем выражение для изменения энтропии
S:

. (1)

Выразим


Q
из первого начала термодинамики:

.
(2)

Температуру
Т
выразим из уравнения Менделеева-Клапейрона.

,
. (3)

Отсюда

. (4)

Подставим
выражения (2), (3), (4) в выражение (1):

. (5)

Поскольку

,
изменение энтропии

. (6)

Подставляя
численные значения, получим:

.

Ответ:
S
= 71 Дж/К.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #