Как найти парето оптимальные оценки

Эффекти́вность по Паре́то — такое состояние системы, при котором ни один показатель системы не может быть улучшен без ухудшения какого-либо другого показателя.

Таким образом, по словам самого Парето: «Всякое изменение, которое никому не приносит убытков, а некоторым людям приносит пользу (по их собственной оценке), является улучшением»^{[источник не указан 2568 дней]}. Значит, признаётся право на все изменения, которые не приносят никому дополнительного вреда.

Множество состояний, оптимальных по Парето, называют «множеством Парето», «множеством альтернатив, оптимальных в смысле Парето» либо «множеством парето-оптимальных альтернатив». Используются также термины «компромиссные», «не улучшаемые» альтернативы.

В экономике ситуация, когда достигнута оптимальность по Парето, — это ситуация, когда все выгоды от обмена сторон исчерпаны.

Эффективность по Парето является одним из центральных понятий для современной экономической науки. На основе этого понятия строятся Первая и Вторая теоремы благосостояния.

Одним из приложений парето-оптимальности является т. н. парето-распределение ресурсов (трудовых ресурсов и капитала) при международной экономической интеграции, то есть экономическом объединении двух и более государств. Интересно, что парето-распределение до и после международной экономической интеграции было адекватно математически описано.

Экономический анализ показывает, что добавленная стоимость секторов экономики и доходы трудовых масс находятся в противоречии, что в физике аналогично хорошо известным уравнением теплопроводности, движением частиц газа или жидкости в пространстве. Эта аналогия даёт возможность применить физические методы анализа в отношении экономических задач по дрейфу экономических параметров.

Оптимум по Парето подразумевает, что суммарное благосостояние общества достигает максимума, а распределение благ и ресурсов становится оптимальным, если любое изменение этого распределения ухудшает благосостояние хотя бы одного субъекта экономической системы.

Парето-оптимальное состояние рынка — ситуация, когда нельзя улучшить положение любого участника экономического процесса, одновременно не снижая благосостояния как минимум одного из остальных.

Согласно критерию Парето (критерию роста общественного благосостояния), движение в сторону оптимума возможно лишь при таком распределении ресурсов, которое увеличивает благосостояние по крайней мере одного человека, не нанося ущерба никому другому.

См. также[править | править код]

• Равновесие Нэша
• Дилемма заключённого
• Закон Парето
• Кривая Филлипса

Литература[править | править код]

• Блауг М. Экономическая теория благосостояния Парето // Экономическая мысль в ретроспективе = Economic Theory in Retrospect. — М.: Дело, 1994. — С. 540—561. — XVII, 627 с. — ISBN 5-86461-151-4.
• Ногин В. Д. Множество и принцип Парето. — СПб: Издательско-полиграфическая ассоциация высших учебных заведений, 2022, 2-е издание, исправленное и дополненное, 111 с.
• Ногин В. Д. Принятие решений в многокритериальной среде: количественный подход. — М.: ФИЗМАТЛИТ, 2002, 2005, 176 с.
• Ногин В. Д. Сужение множества Парето: аксиоматический подход. — М.: ФИЗМАТЛИТ, 2016, 272 с.
• Петросян Л. А., Зенкевич Н. А., Шевкопляс Е. В. Теория игр. СПб: БХВ-Петербург, 2012, 432 с.
• Подиновский В. В., Ногин В. Д. Парето-оптимальные решения многокритериальных задач. — М.: Наука, 1982, 2007.
• Посицельская Л. Н. Равновесие и Парето-оптимальность в шумной дуэли дискретного типа с ненулевой суммой // Фундамент. и прикл. матем., 8:4 (2002), 1111—1128
• Посицельская Л. Н. Равновесие и оптимальность по Парето в шумных дискретных дуэлях с произвольным количеством действий // Фундамент. и прикл. матем., 13:2 (2007), 147—155

Ссылки[править | править код]

• Агапова И. И. Взгляд на экономическую теорию благосостояния В. Парето. «Оптимум по Парето»

Множество Парето

Множество Парето содержит точки третьего класса, каждую из которых можно переместить во множестве М лишь при условии уменьшения хотя бы одной из координат.

• Ввод данных
• Решение

С помощью калькулятора среди исходных точек выделяются точки третьего класса, из которых формируется множество Парето.

Операция называется оптимальной по Парето, если не существует операций, которые бы ее доминировали. Соответственно, решение x ∈ Q называется оптимальным по Парето, если не существует решений, которые бы его доминировали.

В случае, если количество Парето-оптимальных решений больше одного, то для определения лучшего решения можно применить:

• взвешивающую формулу f(x,y)=2x-y, если x→max, y→min.
• метод идеальной точки

Применение множества Парето в задачах оптимизации

Считается, что наилучшие решения многокритериальной задачи следует искать именно среди множества Парето. Поэтому построение множества Парето нередко считают первым необходимым шагом в решении любой многокритериальной задачи.

1. Биматричные игры.
2. Метод последовательных уступок.
3. Метод идеальной точки.
4. Анализ доходности и риска финансовых операций.

Примеры

Пример №1

Пример. Необходимо отобрать в множество Парето микросхемы ПЗУ из 10 штук. ПЗУ характеризуются емкостью и быстродействием. На графике наши объекты расположатся следующим образом:

Быстродействие
Емкость

5
7
1
8
2
6
10
9
3
4

Решение. Характеристики ПЗУ Быстродействие и Емкость максимизируются, т.е. чем выше их значение, тем лучше ПЗУ. Рассмотрим ПЗУ5 и ПЗУ1. ПЗУ1 лучше ПЗУ5 по емкости, поэтому ПЗУ5 можно отбросить. Также ПЗУ6 хуже ПЗУ2 по быстродействию и, поэтому в дальнейшем рассматриваться не будет. Наиболее плохими характеристиками обладают ПЗУ7,8,9,10. Из ПЗУ1,2,3,4 нельзя выбрать наилучшее, потому что у каждого из них одна из характеристик (быстродействие или емкость) лучше чем у других, а другая хуже. Эти ПЗУ1,2,3,4 и составляют множество Парето.

Пример №2

Пусть имеется задача с двумя целевыми функциями.

	X1	X2	X3	X4	X5	X6	X7	X8
F1	13	32	17	-3	11	12	2	14
F2	1	5	2	15	9	43	5	11

Требуется найти оптимальные по Парето решения, если целевые функции требуется максимизировать.

Решение. Критерии оптимизации:

x → max, y → max

Операция №2 доминирует над №1,3,7.

Операция №5 доминирует над №7.

Операция №6 доминирует над №4,5,7.

Операция №8 доминирует над №1,5,7.
Загрузка…
Следовательно, операции №2,6,8, оптимальны по Парето.

Операции, оптимальные по Парето, не обязательно являются «самыми лучшими» и даже просто «хорошими» – эти операции не являются худшими.

Пример №3

Инвестор рассматривает четыре инвестиционные операции со случайными эффективностями, описываемыми случайными величинами E1, E2, E3, E4 с рядами распределения:

E1	2	5	8	4
p	1/6	1/2	1/6	1/6

E2	2	3	4	12
p	1/2	1/6	1/6	1/6

E3	3	5	8	10
p	1/6	1/6	1/2	1/6

E4	1	2	4	8
p	1/2	1/6	1/6	1/6

Требуется определить, какие из этих операций оптимальны по Парето.

Решение. Ожидаемые эффективности и риски равны соответственно MЕ₁ = 4.81, σ₁ = 1.77, MЕ₂ = 4.16, σ₂ = 3.57, MЕ₃ = 7.00, σ₃ = 2.30, MЕ₄ = 2.81, σ₄ = 2.54. Нанесем точки (ME_i; σ_i) на единый график (рис.). i-я операция доминирует j-ю, если точка, соответствующая i-й операции, находится на графике правее и ниже точки, соответствующей j-й операции.

Критерии оптимизации:

MЕ → max, σ → min
Загрузка…

Рисунок – График «риск – доходность»

Видно, что первая операция доминирует вторую и четвертую, третья операция также доминирует вторую и четвертую. При этом первая операция не доминирует третью, а третья не доминирует первую. Первая и третья операции, таким образом, оптимальны по Парето.

Оптимальность по Парето Введение

В
науке и технике достаточно актуальны
задачи многокритериальной
оптимизации [1,2,3], требующие одновременной
оптимизации сразу по нескольким функциям
(критериям). Краеугольным понятием в
многокритериальной оптимизации является
– Парето-оптимальная
(недоминируемая) альтернатива,
т.к. поиск приемлемой (“оптимальной”)
альтернативы, являющейся решением
многокритериальной задачи, следует
выполнять на множестве недоминируемых
альтернатив. Именно поэтому так актуальны
методы, позволяющие выделять подмножества
Парето-оптимальных альтернатив из
множества возможных альтернатив.

Для
облегчения результатов полезно всё
время проводить аналогию с однокритериальным
(классическим) случаем. Пусть имеется
область D
и задана функция f(X)
– целевая функция (критерий). Задача
оптимизации имеет вид

min
f(X)

XD

Точка
X₁D
называется оптимальной (недоминируемой,
неулучшаемой), если не существует точки
X₂D,
для которой f(X₁)>f(X₂)
(целевая функция минимизируется).
Аналогично в МЗО можно исключить из
области D точки, которые заведомо не
могут оказаться наилучшими.

Очевидно,
что в обобщённом смысле определение
оптимальности можно трактовать как
описание (выделение) в подмножестве D
некоторого нового подмножества D₀,
т.е. некоторое сужение D до D₀
D.
В зависимости от характера описания,
подмножество D₀
может оказаться пустым, состоять из
одного элемента, содержать более одного
элемента. Описание D₀
можно проводить либо только с помощью
критериев Fi,
либо использовать дополнительные
условия. Здесь мы рассмотрим направление,
которое связано с определением
оптимальности по Парето².

Отношение доминирования по Парето. Парето-оптимальность

Как
было сказано раньше для всякого решения
XD
набор его оценок по всем критериям, т.е.
набор (F₁(X),
F₂(X),
. . .,Fm(X)),
есть векторная оценка решения X.
Векторная оценка X
содержит полную информацию о ценности
(полезности) этого решения для ЛПР и
сравнение любых двух решений заменяется
сравнение их векторных оценок. Пусть в
МЗО требуется получить меньшие значения
каждого частного критерия (минимизировать
частные критерии) Fi(X).

Опр.
Пусть
имеются два решения X₁
и X₂.
Говорят, что решение X₁
лучше (предпочтительнее, эффективнее,
доминирует) решения X₂,
если F_i(X₁)<=F_i(X₂)
для всех i=1,m, и хотя бы для одного j – го
критерия выполняется строгое неравенство
F_i(X₁)<F_i(X₂)
или

Опр.
Решение
X₂
называется доминируемым, если существует
решение X₁,
не хуже чем X₂,
т.е. для любой оптимизируемой функции
Fi,
I=1,
2, …, m,

Fi(X₂)Fi(X₁)
при максимизации функции Fi,

Fi(X₂)Fi(X₁)
при минимизации Fi.

В
случае доминирования при переходе от
X₂
к X₁
ничего не будет проиграно ни по одному
из частных критериев, но в отношении j
– го частного критерия точно будет
получен выигрыш. Говорят, что решение
X₁
лучше (предпочтительнее) решения X₂.

Опр.
Стратегия X₁D
называется эффективной (оптимальной
по Парето), если не существует стратегии
X₂D
такой, что Fi(X₂)Fi(X₁),
i=1,
. . ., m,
F(X₂)F(X₁),
или

Опр.
Если решение не доминируемо никаким
другим решением, то оно называется
недоминируемым или оптимальным в смысле
Парето.

Очевидно,
тогда в составе множества D нет смысла
сохранять решение X₂,
оно вытесняется (или, как говорят,
“доминируется”) решением X₁.
Ладно, выбросим, решение X₂
как
неконкурентоспособное и перейдём к
сравнению других решений по всем
критериям. В результате такой процедуры
отбрасывания заведомо непригодных,
невыгодных решений множество D обычно
сильно уменьшается: в нём сохраняются
только так называемые эффективные
(иначе “паретовские”) решения, характерные
тем, что ни для одного из них не существует
доминирующего решения. Множество
таких точек и называется множеством
точек оптимальных по Парето. Множество
точек оптимальных по Парето лежат между
точками оптимумов, полученных при
решении задачи математического
программирования для каждого частного
критерия. В литературе множество точек
оптимальных по Парето, как правило,
обозначают буквой P (PD).

Опр.
Множество векторных оценок, соответствующих
множеству эффективных точек, называют
областью компромиссов
(переговорным
множеством)
или множеством Парето в области критериев.
Будем обозначать Y_P
(Y_P
Y_D).

Опр.
Множество векторных оценок, соответствующих
множеству неэффективных точек
(доминируемых решений), называют областью
согласия Y_c.

В
области Y_c
нет
противоречия между частными критериями
оптимальности, т.к. каждая точка XD
может быть изменена таким образом, что
будет одновременно улучшены все частные
критерии.

Если
область критериев Y_D
состоит только из области согласия Y_c,
то существует единственная точка X_optD,
в которой все частные критерии согласованны
между собой в том смысле, что при движении
к точке X_opt
все F_i(X)
i=1,
2, . . ., m,
одновременно улучшаются. Все частные
критерии достигают минимума в т. X_opt

(см.
рис. 1). Такую точку называют оптимальным
решение и при
этом значения

всех
частных критериев достигают в ней
минимума.

Рис.
1. Критерии F₁
и F₂
непротиворечивы

Однако
такая ситуация встречается крайне
редко. Наиболее типичным является
случай, когда частные критерии являются
противоречивыми и минимум по каждому
из них достигается в различных точках.
В этом случае уменьшение одного частного
критерия приводит к увеличению других
частных критериев (рис. 2).

Рис.
2. Критерии F₁
и F₂
противоречивы
на отрезке [1; 2]

Оптимальность
по Парето означает, что нельзя дальше
улучшать значение одного критерия, не
ухудшая при этом хотя бы одного из
остальных.

Проиллюстрируем
приём выделения паретовских решений
на примере задачи с двумя критериями
F₁
и F₂
(оба требуется максимизировать). Множество
D состоит из 11 возможных решений. Каждому
решению соответствуют определённые
значения показателей F₁
и F₂.
Пусть имеются следующие векторные
оценки: F(X₁)=(2;4),
F(X₂)=(3;5),
F(X₃)=(3;3),
F(X₄)=(5;2),
F(X₅)=(4;3),
F(X₆)=(1;3),
F(X₇)=(2;3),
F(X₈)=(3;2),
F(X₉)=(2;2),
F(X₁₀)=(3;1),
F(X₁₁)=(2;1).
Векторные оценки исходов представим
точками координатной плоскости (по оси
абсцисс откладываем значения критерия
F₁,
а по оси ординат – значения критерия
F₂).
Используем принцип оптимальности по
Парето для выделения эффективных
решений. Решение X₁
вытесняется решением X₂,
решение X₂
лучше решений X₃,
X₇,
X₈,
X₉,
X₁₀
и X₁₁.
Решение X₄
по первому критерию лучше решения X₅,
а по второму наоборот, т.е. имеем
неулучшаемые решения, и т.д. После
проведённого анализа у нас остались
три решения X₂,X₄,
X₅
оптимальных по Парето.

Построим
критериальное пространство для нашей
задачи. Как известно паре чисел
соответствует точка на плоскости.
Занумеруем точки соответственно номеру
решения (рис.
3).
Из рисунка видно, что эффективные точки
лежат на правой верхней границе области
возможных решений (Ауд. решить данную
задачу, когда оба критерия нужно
минимизировать).

Рис.
3. Множество Y_k

Когда
из множества возможных решений выделены
эффективные, “переговоры” могут вестись
уже в пределах этого “эффективного”
множества. На рис 3. образуют три решения
X₂,
X₄,
X₅;
из них X₄
лучше по критерию F₁,
а решение X₂
по критерию F₂.
Дело ЛПР, выбрать тот вариант, который
для него предпочтителен и “приемлем”
по обоим критериям.

Замечание.
Точка Y₁
выбирается в Y_D
в том и только в том случае, когда любая
другая точка Y₂
из Y_D
имеет хотя бы по одной координате
значение больше чем Y₁
(критерии минимизируются).

Замечание.
Для определения эффективных точек
используют правило “уголка”. Уголок
вида ∟ используется для определения
компромиссных точек в критериальном
пространстве, когда критерии
максимизируются, а уголок ┐когда
критерии минимизируются.

В
случае, когда множество допустимых
исходов является непрерывным, их
векторные оценки “заполняют”
некоторую область Y_D
на плоскости и получается “картинка”
вроде изображённой на рис.4. В этом случае
множество Парето-оптимальных оценок
(красная линия) представляет собой часть
границы Y_D,
образно говоря, её “юго-западную”
границу”. Если критерии максимизируются
то – “северо-восточную” границу
области Y_D.

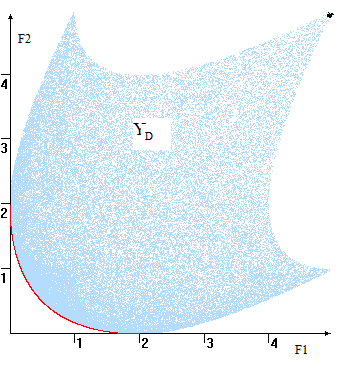
Рис.
4. Пространство оценок Y_D

и компромиссная кривая (красный цвет)

Замечание.
В случае невыпуклой области её
Парето-оптимальная граница может иметь
более “экзотический” вид, например,
состоять из отдельных линий и/или точек.
Для данного примера (критерии
максимизируются) —
это правый пик.

Замечание.
Экономисты так определяют оптимальность
по Парето. Состояние называется
оптимальным по Парето, если выполняется
следующее условие: ничьё
благосостояние не может быть улучшено
без ухудшения благосостояния кого-либо
другого (см.
История экономических учений. /Под ред.
В. Автономова: Учеб. Пособие. – М.: ИНФА
– М, 2000. – 784 с. (стр. 242)).

Таким
образом, под оптимально-компромиссным
решением
будем понимать одну из эффективных
точек, являющуюся предпочтительней с
точки зрения ЛПР. Задача векторной
оптимизации не позволяет однозначно
ответить на вопрос, получено ли оптимальное
решение. Положительный ответ на этот
вопрос зависит от качественной информации
о важности частных критериев, которая
имеется у ЛПР.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Привет, Вы узнаете про Парето-оптимальные (эффективные) векторные оценки и варианты, их свойства, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
Парето-оптимальные (эффективные) векторные оценки и варианты, их свойства , настоятельно рекомендую прочитать все из категории Теория принятия решений.

Отношение (9.1) остается и при т > 2 отношением строгого частичного порядка , т.е. обладает свойствами антирефлексивности (у > у — не выполнено), антисимметричности ((у > у*) А (у* >у)=* (у = У*)) и транзитивности ((у > у*) А А (у* > у**) => (у > у**)).

Обратите внимание!

В отличие от Л , в пространстве Л”‘ существуют пары векторных критериев у, у*, как удовлетворяющие отношениям у > у* или у* > у, так и не удовлетворяющие ни одному из этих отношений. Таким образом, критериальное пространство Л™ — частично упорядоченная группа .

Проиллюстрируем смысл критериального пространства как частично упорядоченной группы геометрически для случая т = 2, т.е. для двух критериев /,(х) и/2(х). При т = 3, т.е. в критериальном пространстве Л , геометрическая интерпретация становится менее наглядной. Приведем два примера, отвечающие двум часто встречающимся (и в теории, и на практике) вариантам множества альтернатив X: дискретному случаю и области возможных вариантов.

Пример: дискретное множество альтернатив. Если множество решений X с Л дискретно , т.е. все его точки изолированы , то оно может быть либо конечным (X = {хр х2,хп}), либо счетным множеством (X = {х,, х2,…, хп,…}). На практике ситуация конечного множества может возникнуть, если имеется несколько (например, п = 10) вариантов приобретаемого товара, представленных проектов и т.н. Критериями г/, и у0 в этом случае могут быть, в частности, цена и качество (товара, проекта).

Каждой альтернативе хк с номером к сопоставим точку Ук плоскости 9?2 с координатами г/, = /{(хк) и у2 = /2(хк). Тогда графическое представление при п = 10 множества возможных оценок У = {ух, у2,…, г/10} в критериальном пространстве 9?2 представляет собой набор изолированных точек {Ур У2,…, У10} (рис. 9.1). Отметим, что согласно введенному вначале предположению критерий, отвечающий цене (скажем, ух), подвергнут преобразованию М – /{(х) так, что минимальной цене соответствует максимальное значение г/,. В данной ситуации отношение строгого порядка, введенное формулами (9.1), можно интерпретировать в терминах предпочтений ЛГ1Р следующим образом. Если две оценки ух и ук удовлетворяют отношению у. > ук, то точка У- лежит правее и выше точки Ук, и тогда ЛПР может исключить вариант ук как явно менее предпочтительный по сравнению с у..

Рис. 9.1. Дискретное множество возможных оценок У в двумерном критериальном пространстве 9?2 и образ соответствующего множества Парето — Эджворта

Из рис. 9.1 очевидно, что, хотя множество возможных оценок У и не является линейно упорядоченным множеством, т.е . Об этом говорит сайт https://intellect.icu . все 10 альтернатив нельзя выстроить в определенном порядке, но частичная упорядоченность группы позволяет выделить из множества Уточки У1? У2, У^ и У8, расположенные на рис. 9.1 правее и выше всех остальных вариантов. Иными словами, при выборе наилучшего решения ЛПР может убрать из рассмотрения все остальные альтернативы и выбирать только из четырех: х,, х2, х4 и х8. Между собой эти варианты несравнимы согласно формуле (9.1). Величины критериев у] и у2 достигают максимума в различных точках: критерий г/, достигает максимума в точке У8, тогда как величинау2 — в точке Ух, т.е. одновременный максимум на множестве X не реализуется. Промежуточные варианты У2 и У4 представляют собой компромиссные решения, которые вполне могут соответствовать предпочтениям ЛПР.

Такое сужение множества альтернатив X с исходных 10 до четырех, само собой разумеющееся при взгляде на иллюстрацию, перестает быть наглядным в случае критериальных пространств более высоких размерностей т или же для более сложных множеств альтернатив X. Именно изучение в самом общем случае этого сужения, именуемого множеством Парето — Эджворта, и составляет предмет данной главы.

Следующий пример более сложного множества альтернатив X естественно было бы назвать непрерывным множеством (так как непрерывность – общепринятое противопоставление дискретности ), но формально в математике непрерывными считают исключительно линейно упорядоченные множества . Как мы убедились, линейная упорядоченность уже при т = 2 отсутствует. Поэтому назовем множество X областью, представляющей собой с точки зрения топологии связное подмножество топологического пространства. Нередко областью считают только открытое множество, но для теории принятия удобнее рассматривать замкнутую область, т.е. замыкание области, включающее также границу.

Пример: область как множество альтернатив. Если множество решений X связно, то между любыми «соседними» по величинам критериев альтернативами всегда могут быть промежуточные варианты. Тогда X обязано быть несчетным множеством. Подобная ситуация возникает, в частности, при выборе оптимальных значений двух управляющих параметров (финансовых регуляторов, технических показателей и т.п.) некоторой системы при условии, что регулировка этих параметров может осуществляться непрерывно в некоторых пределах. Графическое представление множества возможных оценок У в критериальном пространстве может иметь вид наподобие фигуры У, заштрихованной на рис. 9.2.

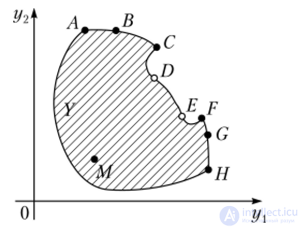
Рис. 9.2. Область возможных оценок У в двумерном критериальном

пространстве и образ соответствующего множества Парето — Эджворта

Как и на рис. 9.1, координаты каждой точки на рис. 9.2 (например, координаты точек А, В, С, I), Е, В, С, Я, М) представляют собой величины критериев ух и у2 для некоторой альтернативы из множества X. Но здесь, если ЛПР стремится достичь наибольшего значения обоих критериев у{ и у2, т.е. требуется их максимизация, то частичная упорядоченность группы позволяет ЛПР выделить из множества X альтернативы с образами из отрезков ВС, ОЕ и ВС границы заштрихованной области У, расположенными, как и на рис. 9.1, правее и выше всех остальных вариантов. Иными словами, при выборе наилучшего решения ЛПР может убрать из рассмотрения все остальные альтернативы с векторными оценками из заштрихованной области У и выбирать только точки трех указанных отрезков.

3

Обратите внимание!

Концы отрезков ВС и ГС остаются в числе представляющих интерес для ЛПР, а концы отрезка ОЕ — нет, так как они доминируемы точками С и Л соответственно.

В данном случае сужение множества альтернатив, само собой разумеющееся при взгляде на рис. 9.2, тем более (по сравнению с рис. 9.1) перестает быть очевидным в случае критериальных пространств более высоких размерностей п или же для более сложных множеств альтернатив X.

Обратите внимание!

Приведенные два примера показывают важность сужения множества возможных оценок У. Если в нервом примере выбор из 4 альтернатив становится значительно проще, чем первоначальный выбор из 10 вариантов, то во втором — не просто уменьшается число альтернатив, но происходит качественное преобразование первоначальной области У с конечной площадью в объединение отрезков кривой линии, имеющих нулевую площадь.

Получаемое в результате сужение множества альтернатив X называется множеством Парето — Эджворта (Френсис Эджворт1 (Francis Edgeworth, (1845—1926) — английский экономист, родившийся в Ирландии, который впервые, раньше В. Парето, ввел понятие Парето-оптимального решения для двух критериев). Именно с построения этого множества начинается анализ любой задачи теории принятия решений. Практическое применение указанного алгоритма показывает, что нередко, как и в двух приведенных примерах, сужение X и построение множества Парето — Эджворта настолько ограничивает множество оставшихся вариантов, что дальнейший выбор достаточно несложен и не составляет труда для ЛПР.

Определение

Множеством Парето — Эджворта, или множеством Парето-оптималъных решений, называется множество Р/(Х) входящих в X альтернатив х*, которые не являются доминируемыми, т.е. для которых не существует доминирующих альтернатив х, удовлетворяющих отношению строгого предпочтения: х > х*.

Из определения вытекает, что для построения множества Парето – Эджворта необходимо исключить из множества решений X все доминируемые альтернативы. Иными словами, надо отбросить все такие альтернативы х*, для которых найдется хотя бы одна доминирующая альтернатива х > х*.

Обратите внимание!

Практическая значимость множества Парето — Эджворта обусловлена тем, что любое решение х из множества альтернатив X, не входящее в РДХ), заведомо не может быть оптимальным.

Действительно, по определению решение х будет доминируемым по отношению к некоторому элементу х* множества Парето — Эджворта, т.е. ЛПР предпочтет х* вместо х.

Парето-оптимальным решениям в критериальном пространстве отвечают Парето-оптимальные векторы (оценки).

Определение

Парето-оптимальным вектором (или Парешо-оптималъной векторной оценкой) называется вектор /2(.г*), /т(х*)), соответствующий Парсто-опти-

мальному решению х*.

Приведенные примеры позволяют сделать вывод, что главный смысл рассмотрения Парето-оптимальных вариантов и их векторных оценок состоит в значительном сужении исходных множеств X и У, причем любая из оставшихся альтернатив в силу недоминируемости может быть признана оптимальной (лучшей).

Обратите внимание!

Парето-оптимальные варианты благодаря свойствам своих векторных оценок образуют существенно более узкое по сравнению с первоначальным множеством X множество Парето — Эджворта Р^Х). Тем самым окончательный выбор ЛПР наилучшего эффективного решения становится намного легче и проще.

Наряду с множеством недоминируемых альтернатив рассматривается и множество недоминируемых векторных оценок.

Определение

Множество Парето-оптимальных векторных оценок, т.е. образ множества Парето — Эджворта РХХ) в критериальном пространстве называют фронтом Парето[10] (иногда Парето-фронтом — от англ. Pareto-frontier) или множеством Парето — Эджворта в критериальном пространстве.

Из свойств алгебраической структуры, обусловленных линейной упорядоченностью группы, вытекает важное свойство Парето-оптимальных векторных оценок.

Обратите внимание!

Парето-оптимальные векторные оценки остаются Парето-оптимальными при любых линейных преобразованиях отдельных частных критериев, сохраняющих порядок.

Иначе говоря, такие преобразования шкал измерения, как параллельный перенос (сдвиг) вдоль любой оси критериального пространства или изменение масштаба (т.е. единиц измерения) с положительным коэффициентом, не меняют свойства Парето-оптимальности.

• Отношение порядка на множестве [Электронный ресурс], и К Г: http://www.algebraic.ru/сЫш.р11р?1с^1о58агу:ге1аиоп:огс1ег (дата обращения: 04.08.2015).
• Отношение порядка на множестве [Электронный ресурс], и К Г: http://www.algebraic.ru/сЫш.р11р?1с^1о58агу:ге1аиоп:огс1ег (дата обращения: 04.08.2015).
• Частично упорядоченная группа [Электронный ресурс]. 1ШЬ: http://dic.academic.ru/dic.nsf/enc_mathematics/6135/ЧACTИЧI Ю (дата обращения: 27.04.2014).
• Дискретное множество [Электронный ресурс]. ШСЬ: http://dic.academic.ru/dic.nsf/ruwiki/901372 (дата обращения: 04.08.2015).
• Частично упорядоченная группа [Электронный ресурс]. 1ШЬ: http://dic.academic.ru/dic.nsf/enc_mathematics/6135/ЧACTИЧI Ю (дата обращения: 27.04.2014).
• Дискретное множество [Электронный ресурс]. ШСЬ: http://dic.academic.ru/dic.nsf/ruwiki/901372 (дата обращения: 04.08.2015).
• Изолированная точка множества [Электронный ресурс]. ийЬ: http://school-collection.edu.ru/catalog/res/fb5e5bca-cl39-49fl-805c-cf5adfc2ca5d/view/ (дата обращения: 04.08.2015).
• ’Дискретность [Электронный ресурс]. ШИ-: http://dic.academic.ru/dic.nsf/enclp/16662(лата обращения: 04.08.2015).
• Непрерывное множество [Электронный ресурс]. 1ЖЬ: http://dic.academic.ru/dic.nst/епс_та1ЬетаЦс8/3416/ (дата обращения: 04.08.2015).
• [10] Электронное научно-техническое издание «Наука и образование». Фронт Парето [Электронный ресурс). URL: Ьир:/ДесЬпотая.Ьт5и1.ги/5еагс11.1Цт1??ок1=фронт Парето (дата обращения: 31.08.2015); Антух А. Э., Семенихин А. С., Хасанова Р. В. Приближенное построениемножества Парето в задаче многокритериальной оптимизации методом роя частиц [Электронный ресурс]. Наука и образование. 2010. № 4. URL: http://technomag.bmstu.ru/doc/141969.html (дата обращения: 04.08.2015).

В общем, мой друг ты одолел чтение этой статьи об Парето-оптимальные (эффективные) векторные оценки и варианты, их свойства. Работы в переди у тебя будет много. Смело пишикоментарии, развивайся и счастье окажется в ваших руках.
Надеюсь, что теперь ты понял что такое Парето-оптимальные (эффективные) векторные оценки и варианты, их свойства
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Теория принятия решений

Pareto efficiency or Pareto optimality is a situation where no action or allocation is available that makes one individual better off without making another worse off.^[1] The concept is named after Vilfredo Pareto (1848–1923), Italian civil engineer and economist, who used the concept in his studies of economic efficiency and income distribution. The following three concepts are closely related:

• Given an initial situation, a Pareto improvement is a new situation where some agents will gain, and no agents will lose.
• A situation is called Pareto-dominated if there exists a possible Pareto improvement.
• A situation is called Pareto-optimal or Pareto-efficient if no change could lead to improved satisfaction for some agent without some other agent losing or, equivalently, if there is no scope for further Pareto improvement.

The Pareto front (also called Pareto frontier or Pareto set) is the set of all Pareto-efficient situations.^[2]

Pareto originally used the word “optimal” for the concept, but as it describes a situation where a limited number of people will be made better off under finite resources, and it does not take equality or social well-being into account, it is in effect a definition of and better captured by “efficiency”.^[3]

In addition to the context of efficiency in allocation, the concept of Pareto efficiency also arises in the context of efficiency in production vs. x-inefficiency: a set of outputs of goods is Pareto-efficient if there is no feasible re-allocation of productive inputs such that output of one product increases while the outputs of all other goods either increase or remain the same.^[4]

Pareto efficiency is measured along the production possibility frontier (PPF), which is a graphical representation of all the possible options of output for two products that can be produced using all factors of production.

Besides economics, the notion of Pareto efficiency has been applied to the selection of alternatives in engineering and biology. Each option is first assessed, under multiple criteria, and then a subset of options is ostensibly identified with the property that no other option can categorically outperform the specified option. It is a statement of impossibility of improving one variable without harming other variables in the subject of multi-objective optimization (also termed Pareto optimization).

Overview[edit]

Formally, a state is Pareto-optimal if there is no alternative state where improvements can be made to at least one participant’s well-being without reducing any other participant’s well-being. If there is a state change that satisfies this condition, the new state is called a “Pareto improvement”. When no Pareto improvements are possible, the state is a “Pareto optimum”.

In other words, Pareto efficiency is when it is impossible to make one party better off without making another party worse off. ^[5] This state indicates that resources can no longer be allocated in a way that makes one party better off without harming other parties. In a state of Pareto Efficiency, resources are allocated in the most efficient way possible. ^[5]

Pareto efficiency is mathematically represented when there is no other strategy profile s’ such that u_i (s’) ≥ u_i (s) for every player i and u_j (s’) >  u_j (s) for some player j. In this equation s represents the strategy profile, u represents the utility or benefit, and j represents the player.^[6]

Efficiency is an important criterion for judging behavior in a game. In a notable and often analyzed game known as Prisoner’s Dilemma, depicted below as a normal form game, this concept of efficiency can be observed, in that the strategy profile (Cooperate, Cooperate) is more efficient than (Defect, Defect).^[6]

Prisoner’s Dilemma Game

	Cooperate	Defect
Cooperate	2, 2	0, 3
Defect	3, 0	1, 1

Using the definition listed above, u(C_i) ≥ u(D_i) for i ∈ {1, 2}, thus yielding this strategy as a Pareto efficient strategy. In other words, both players receive an increase in payoff by selecting Cooperate over Defect.

In zero-sum games, every outcome is Pareto-efficient.

A special case of a state is an allocation of resources. The formal presentation of the concept in an economy is the following: Consider an economy with agents and goods. Then an allocation , where for all i, is Pareto-optimal if there is no other feasible allocation where, for utility function for each agent , for all with for some .^[7] Here, in this simple economy, “feasibility” refers to an allocation where the total amount of each good that is allocated sums to no more than the total amount of the good in the economy. In a more complex economy with production, an allocation would consist both of consumption vectors and production vectors, and feasibility would require that the total amount of each consumed good is no greater than the initial endowment plus the amount produced.

Under the assumptions of the first welfare theorem, a competitive market leads to a Pareto-efficient outcome. This result was first demonstrated mathematically by economists Kenneth Arrow and Gérard Debreu.^[8] However, the result only holds under the assumptions of the theorem: markets exist for all possible goods, there are no externalities, markets are perfectly competitive, and market participants have perfect information.

In the absence of perfect information or complete markets, outcomes will generally be Pareto-inefficient, per the Greenwald–Stiglitz theorem.^[9]

The second welfare theorem is essentially the reverse of the first welfare theorem. It states that under similar, ideal assumptions, any Pareto optimum can be obtained by some competitive equilibrium, or free market system, although it may also require a lump-sum transfer of wealth.^[7]

Pareto efficiency and market failure
An ineffective distribution of resources in a free market is known as market failure. Given that there is room for improvement, market failure implies Pareto inefficiency.

For instance, excessive use of negative commodities (such as drugs and cigarettes) results in expenses to non-smokers as well as early mortality for smokers. Cigarette taxes may help individuals stop smoking while also raising money to address ailments brought on by smoking.

Pareto efficiency and equity
A Pareto improvement may be seen, but this does not always imply that the result is desirable or equitable. After a Pareto improvement, inequality could still exist.

A society may be Pareto efficient but have significant levels of inequality. The most equitable course of action would be to split the pie into three equal portions if there were three persons and a pie. The third person doesn’t lose out (even if he doesn’t partake in the pie), hence splitting it in half and giving it to two individuals would be considered Pareto efficient.

More considerations should be considered while making decisions, including social efficiency, overall wellbeing, and problems like declining marginal utility of money.

Practical implication of pareto efficiency
It is believed that Pareto efficiency arises when it is impossible to benefit one party without harming another.

When no one suffers a loss and at least one person benefits, this is known as a Pareto improvement.

On a frontier of production possibilities, Pareto efficiency will happen. It is impossible to raise the output of products without decreasing the output of services when an economy is functioning on a basic production potential frontier, such as at point A, B, or C.

According to Pareto efficiency, a decision is efficient if it benefits some individuals while harming none of them. Vilfredo Pareto, an Italian economist and sociologist renowned for his use of mathematics in economic analysis, especially in his Manual of Political Economy (1906), is credited with creating the idea.
By analyzing “ophelimity,” Pareto utilized this study to create his theory of pure economics.

Variants[edit]

Weak Pareto efficiency[edit]

Weak Pareto efficiency is a situation that cannot be strictly improved for every individual.^[10]

Formally, a strong Pareto improvement is defined as a situation in which all agents are strictly better-off (in contrast to just “Pareto improvement”, which requires that one agent is strictly better-off and the other agents are at least as good). A situation is weak Pareto-efficient if it has no strong Pareto improvements.

Any strong Pareto improvement is also a weak Pareto improvement. The opposite is not true; for example, consider a resource allocation problem with two resources, which Alice values at {10, 0}, and George values at {5, 5}. Consider the allocation giving all resources to Alice, where the utility profile is (10, 0):

• It is a weak PO, since no other allocation is strictly better to both agents (there are no strong Pareto improvements).
• But it is not a strong PO, since the allocation in which George gets the second resource is strictly better for George and weakly better for Alice (it is a weak Pareto improvement) – its utility profile is (10, 5).

A market doesn’t require local nonsatiation to get to a weak Pareto optimum.^[11]

Constrained Pareto efficiency [edit]

Constrained Pareto efficiency is a weakening of Pareto optimality, accounting for the fact that a potential planner (e.g., the government) may not be able to improve upon a decentralized market outcome, even if that outcome is inefficient. This will occur if it is limited by the same informational or institutional constraints as are individual agents.^[12]

An example is of a setting where individuals have private information (for example, a labor market where the worker’s own productivity is known to the worker but not to a potential employer, or a used-car market where the quality of a car is known to the seller but not to the buyer) which results in moral hazard or an adverse selection and a sub-optimal outcome. In such a case, a planner who wishes to improve the situation is unlikely to have access to any information that the participants in the markets do not have. Hence, the planner cannot implement allocation rules which are based on the idiosyncratic characteristics of individuals; for example, “if a person is of type A, they pay price p₁, but if of type B, they pay price p₂” (see Lindahl prices). Essentially, only anonymous rules are allowed (of the sort “Everyone pays price p“) or rules based on observable behavior; “if any person chooses x at price p_x, then they get a subsidy of ten dollars, and nothing otherwise”. If there exists no allowed rule that can successfully improve upon the market outcome, then that outcome is said to be “constrained Pareto-optimal”.

Fractional Pareto efficiency[edit]

Fractional Pareto efficiency is a strengthening of Pareto efficiency in the context of fair item allocation. An allocation of indivisible items is fractionally Pareto-efficient (fPE or fPO) if it is not Pareto-dominated even by an allocation in which some items are split between agents. This is in contrast to standard Pareto efficiency, which only considers domination by feasible (discrete) allocations.^[13][14]

As an example, consider an item allocation problem with two items, which Alice values at {3, 2} and George values at {4, 1}. Consider the allocation giving the first item to Alice and the second to George, where the utility profile is (3, 1):

• It is Pareto-efficient, since any other discrete allocation (without splitting items) makes someone worse-off.
• However, it is not fractionally Pareto-efficient, since it is Pareto-dominated by the allocation giving to Alice 1/2 of the first item and the whole second item, and the other 1/2 of the first item to George – its utility profile is (3.5, 2).

Ex-ante Pareto efficiency[edit]

When the decision process is random, such as in fair random assignment or random social choice or fractional approval voting, there is a difference between ex-post and ex-ante Pareto efficiency:

• Ex-post Pareto efficiency means that any outcome of the random process is Pareto-efficient.
• Ex-ante Pareto efficiency means that the lottery determined by the process is Pareto-efficient with respect to the expected utilities. That is: no other lottery gives a higher expected utility to one agent and at least as high expected utility to all agents.

If some lottery L is ex-ante PE, then it is also ex-post PE. Proof: suppose that one of the ex-post outcomes x of L is Pareto-dominated by some other outcome y. Then, by moving some probability mass from x to y, one attains another lottery L‘ that ex-ante Pareto-dominates L.

The opposite is not true: ex-ante PE is stronger that ex-post PE. For example, suppose there are two objects – a car and a house. Alice values the car at 2 and the house at 3; George values the car at 2 and the house at 9. Consider the following two lotteries:

1. With probability 1/2, give car to Alice and house to George; otherwise, give car to George and house to Alice. The expected utility is (2/2 + 3/2) = 2.5 for Alice and (2/2 + 9/2) = 5.5 for George. Both allocations are ex-post PE, since the one who got the car cannot be made better-off without harming the one who got the house.
2. With probability 1, give car to Alice, then with probability 1/3 give the house to Alice, otherwise give it to George. The expected utility is (2 + 3/3) = 3 for Alice and (9 × 2/3) = 6 for George. Again, both allocations are ex-post PE.

While both lotteries are ex-post PE, the lottery 1 is not ex-ante PE, since it is Pareto-dominated by lottery 2.

Another example involves dichotomous preferences.^[15] There are 5 possible outcomes (a, b, c, d, e) and 6 voters. The voters’ approval sets are (ac, ad, ae, bc, bd, be). All five outcomes are PE, so every lottery is ex-post PE. But the lottery selecting c, d, e with probability 1/3 each is not ex-ante PE, since it gives an expected utility of 1/3 to each voter, while the lottery selecting a, b with probability 1/2 each gives an expected utility of 1/2 to each voter.

Bayesian Pareto efficiency[edit]

Bayesian efficiency is an adaptation of Pareto efficiency to settings in which players have incomplete information regarding the types of other players.

Ordinal Pareto efficiency[edit]

Ordinal Pareto efficiency is an adaptation of Pareto efficiency to settings in which players report only rankings on individual items, and we do not know for sure how they rank entire bundles.

Pareto efficiency and equity[edit]

Although an outcome may be considered a Pareto improvement, this does not imply that the outcome is satisfying or equitable. It is possible that inequality persists even after a Pareto improvement. Despite the fact that it is frequently used in conjunction with the idea of Pareto optimality, the term “efficiency” refers to the process of increasing societal productivity.^[16] It is possible for a society to have Pareto efficiency while also have high levels of inequality. Consider the following scenario: there is a pie and three persons; the most equitable way would be to divide the pie into three equal portions. However, if the pie is divided in half and shared between two people, it is considered Pareto efficient – meaning that the third person does not lose out (despite the fact that he does not receive a piece of the pie). When making judgments, it is critical to consider a variety of aspects, including social efficiency, overall welfare, and issues such as diminishing marginal value.

Pareto efficiency and market failure[edit]

In order to fully understand market failure, one must first comprehend market success, which is defined as the ability of a set of idealized competitive markets to achieve an equilibrium allocation of resources that is Pareto-optimal in terms of resource allocation. According to the definition of market failure, it is a circumstance in which the conclusion of the first fundamental theorem of welfare is erroneous; that is, when the allocations made through markets are not efficient.^[17] In a free market, market failure is defined as an inefficient allocation of resources. Due to the fact that it is feasible to improve, market failure implies Pareto inefficiency. For example, excessive consumption of depreciating items (drugs/tobacco) results in external costs to non-smokers, as well as premature death for smokers who do not quit. An increase in the price of cigarettes could motivate people to quit smoking while also raising funds for the treatment of smoking-related ailments.

Approximate Pareto efficiency[edit]

Given some ε > 0, an outcome is called ε-Pareto-efficient if no other outcome gives all agents at least the same utility, and one agent a utility at least (1 + ε) higher. This captures the notion that improvements smaller than (1 + ε) are negligible and should not be considered a breach of efficiency.

Pareto-efficiency and welfare-maximization[edit]

Suppose each agent i is assigned a positive weight a_i. For every allocation x, define the welfare of x as the weighted sum of utilities of all agents in x:

Let x_a be an allocation that maximizes the welfare over all allocations:

It is easy to show that the allocation x_a is Pareto-efficient: since all weights are positive, any Pareto improvement would increase the sum, contradicting the definition of x_a.

Japanese neo-Walrasian economist Takashi Negishi proved^[18] that, under certain assumptions, the opposite is also true: for every Pareto-efficient allocation x, there exists a positive vector a such that x maximizes W_a. A shorter proof is provided by Hal Varian.^[19]

Use in engineering[edit]

The notion of Pareto efficiency has been used in engineering.^[20] Given a set of choices and a way of valuing them, the Pareto front (or Pareto set or Pareto frontier) is the set of choices that are Pareto-efficient. By restricting attention to the set of choices that are Pareto-efficient, a designer can make trade-offs within this set, rather than considering the full range of every parameter.^[21]

Use in public policy[edit]

Modern microeconomic theory has drawn heavily upon the concept of Pareto efficiency for inspiration. Pareto and his successors have tended to describe this technical definition of optimal resource allocation in the context of it being an equilibrium that can theoretically be achieved within an abstract model of market competition. It has therefore very often been treated as a corroboration of Adam Smith’s “invisible hand” notion. More specifically, it motivated the debate over “market socialism” in the 1930s.^[3]

However, because the Pareto-efficient outcome is difficult to assess in the real world when issues including asymmetric information, signalling, adverse selection, and moral hazard are introduced, most people do not take the theorems of welfare economics as accurate descriptions of the real world. Therefore, the significance of the two welfare theorems of economics is in their ability to generate a framework that has dominated neoclassical thinking about public policy. That framework is that the welfare economics theorems allow the political economy to be studied in the following two situations: “market failure” and “the problem of redistribution”.^[22]

Analysis of “market failure” can be understood by the literature surrounding externalities. When comparing the “real” economy to the complete contingent markets economy (which is considered efficient), the inefficiencies become clear. These inefficiencies, or externalities, are then able to be addressed by mechanisms, including property rights and corrective taxes.^[22]

Analysis of “the problem with redistribution” deals with the observed political question of how income or commodity taxes should be utilized. The theorem tells us that no taxation is Pareto-efficient and that taxation with redistribution is Pareto-inefficient. Because of this, most of the literature is focused on finding solutions where given there is a tax structure, how can the tax structure prescribe a situation where no person could be made better off by a change in available taxes.^[22]

Use in biology[edit]

Pareto optimisation has also been studied in biological processes.^[23] In bacteria, genes were shown to be either inexpensive to make (resource-efficient) or easier to read (translation-efficient). Natural selection acts to push highly expressed genes towards the Pareto frontier for resource use and translational efficiency.^[24] Genes near the Pareto frontier were also shown to evolve more slowly (indicating that they are providing a selective advantage).^[25]

Common misconceptions[edit]

It would be incorrect to treat Pareto efficiency as equivalent to societal optimization,^[26] as the latter is a normative concept, which is a matter of interpretation that typically would account for the consequence of degrees of inequality of distribution.^[27] An example would be the interpretation of one school district with low property tax revenue versus another with much higher revenue as a sign that more equal distribution occurs with the help of government redistribution.^[28]

Criticism[edit]

Some commentators contest that Pareto efficiency could potentially serve as an ideological tool. With it implying that capitalism is self-regulated thereof, it is likely that the embedded structural problems such as unemployment would be treated as deviating from the equilibrium or norm, and thus neglected or discounted.^[3]

Pareto efficiency does not require a totally equitable distribution of wealth, which is another aspect that draws in criticism.^[29] An economy in which a wealthy few hold the vast majority of resources can be Pareto-efficient. A simple example is the distribution of a pie among three people. The most equitable distribution would assign one third to each person. However, the assignment of, say, a half section to each of two individuals and none to the third is also Pareto-optimal despite not being equitable, because none of the recipients could be made better off without decreasing someone else’s share; and there are many other such distribution examples. An example of a Pareto-inefficient distribution of the pie would be allocation of a quarter of the pie to each of the three, with the remainder discarded.^[30]

The liberal paradox elaborated by Amartya Sen shows that when people have preferences about what other people do, the goal of Pareto efficiency can come into conflict with the goal of individual liberty.^[31]

Lastly, it is proposed that Pareto efficiency to some extent inhibited discussion of other possible criteria of efficiency. As Wharton School professor Ben Lockwood argues, one possible reason is that any other efficiency criteria established in the neoclassical domain will reduce to Pareto efficiency at the end.^[3]

See also[edit]

• Admissible decision rule, analog in decision theory
• Arrow’s impossibility theorem
• Bayesian efficiency
• Fundamental theorems of welfare economics
• Deadweight loss
• Economic efficiency
• Highest and best use
• Kaldor–Hicks efficiency
• Marginal utility
• Market failure, when a market result is not Pareto-optimal
• Maximal element, concept in order theory
• Maxima of a point set
• Multi-objective optimization
• Pareto-efficient envy-free division
• Social Choice and Individual Values for the “(weak) Pareto principle”
• TOTREP
• Welfare economics

References[edit]

Pareto, V (1906). Manual of Political Economy. Oxford University Press. https://global.oup.com/academic/product/manual-of-political-economy-9780199607952?cc=ca&lang=en&.

Further reading[edit]

• Fudenberg, Drew; Tirole, Jean (1991). Game theory. Cambridge, Massachusetts: MIT Press. pp. 18–23. ISBN 9780262061414. Book preview.
• Bendor, Jonathan; Mookherjee, Dilip (April 2008). “Communitarian versus Universalistic norms”. Quarterly Journal of Political Science. 3 (1): 33–61. doi:10.1561/100.00007028.
• Kanbur, Ravi (January–June 2005). “Pareto’s revenge” (PDF). Journal of Social and Economic Development. 7 (1): 1–11.
• Ng, Yew-Kwang (2004). Welfare economics towards a more complete analysis. Basingstoke, Hampshire New York: Palgrave Macmillan. ISBN 9780333971215.
• Rubinstein, Ariel; Osborne, Martin J. (1994), “Introduction”, in Rubinstein, Ariel; Osborne, Martin J. (eds.), A course in game theory, Cambridge, Massachusetts: MIT Press, pp. 6–7, ISBN 9780262650403 Book preview.
• Mathur, Vijay K. (Spring 1991). “How well do we know Pareto optimality?”. The Journal of Economic Education. 22 (2): 172–178. doi:10.2307/1182422. JSTOR 1182422.
• Newbery, David M.G.; Stiglitz, Joseph E. (January 1984). “Pareto inferior trade”. The Review of Economic Studies. 51 (1): 1–12. doi:10.2307/2297701. JSTOR 2297701.