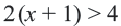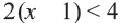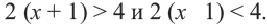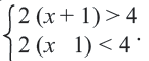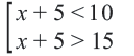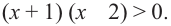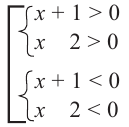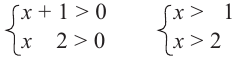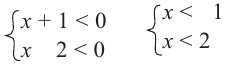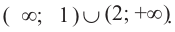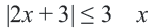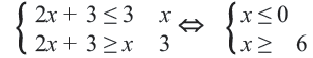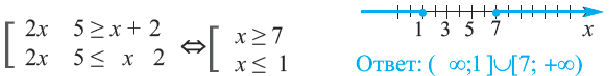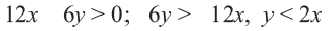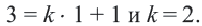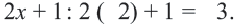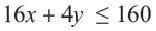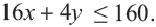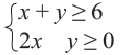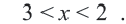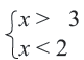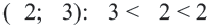Слайд 1
7. Методы решения уравнений и неравенств в целых числах Выполнила: ученица 11 «А» класса Устименко О.Д. Учитель математики: Кукса Б.И. 2014г. МОУ – СОШ № 3 г. Можайск Презентация на тему:
Слайд 2
7.1. Линейные уравнения Метод прямого перебора Использование неравенств Использование отношения делимости Метод «спуска» Использование формул 7.2. Нелинейные уравнения Метод разложения на множители Вынесение общих множителей за скобку Применение формул сокращенного умножения Использование параметра Метод решения относительно одной переменной выделение целой части Метод «спуска» метод конечного «спуска» Параметризация уравнения Функционально-графический метод 7.3. Неравенства Использование области определения Использование монотонности Использование ограниченности 7.4. Уравнения и неравенства Уравнение с одной неизвестной Показательные уравнения Неравенства Уравнения, содержащие функцию «целая часть числа» [ x ]
Слайд 3
Пример 74. В клетке сидят кролики и фазаны. Всего у них 18 ног. Узнать сколь- ко в клетке тех и других. Укажите все решения. Решение. Пусть х – количество кроликов , у – количество фазанов, тогда имеем уравнение 4 x + 2y = 18 или 2x + y = 9 Если х =1, то у=7. Если х=2, то у=5. Если х = 3, то у = 3. Если х = 4, то у = 1. При х = 5 получаем 2 ∙ 5 = 10 > 9. Ответ: (1 ;7), (2;5), (3;3), (4;1). 7.1. Линейные уравнения Метод прямого перебора
Слайд 4
Использование неравенств Пример 75. Решить в натуральных числах уравнение 5х + 8у = 39 Решение. Для уменьшения перебора вариантов рассмотрим неравенства 5х = 39 – 8у ≥ 0 8у = 39 – 5х ≥ 0 у ≤ 4 х ≤ 7 Проведем перебор по неизвестной у. Если у = 1, то х = 6,2 не является натуральным числом. Если у = 2, то х = 4,6 не является натуральным числом. Если у = 3, то х = 3. Если у = 4, то х = 1,4 не является натуральным числом. Ответ: (3; 3)
Слайд 5
Использование отношения делимости Пример 76. Имеются контейнеры двух видов: по 130 кг и 160 кг. Сколько было контейнеров первого и сколько второго вида, если вместе они весят 3 тонны? Укажите все решения Решение. Обозначим количество контейнеров первого вида через х , второго – через у . Получаем уравнение 130х + 160у = 3000 или 13х + 16у = 300. Далее имеем : 13х + 13у + 3у = 13 ∙ 23 + 1, 3у – 1 = 13 ∙ (23 – х – у). Отсюда следует, что разность 3у – 1 делится на 13. Если 3у – 1 = 0, то у не является натуральным числом. Если 3у – 1 = 13, то у не является натуральным числом. Если 3у – 1 = 26, то у = 9 и х = 12. Если 3у – 1 = 39, то у не является натуральным числом. Если 3у – 1 = 52, то у не является натуральным числом. Если 3у – 1 = 65, то у = 22 но 16 ∙ 22 = 352 > 300. Ответ: 12 контейнеров по 130 кг и 9 по 160 кг.
Слайд 6
Метод «спуска» Пример 79. Решить в целых числах уравнение 5х – 7у = 3. Решение. Выразим из уравнения то не- известное, коэффициент при котором меньше по модулю: Дробь должна быть равна целому числу. где z – целое число. Тогда 2у + 3 = 5 z . Из последнего уравнения выразим то неизвестное, коэффициент при котором меньше по модулю, и проделаем аналогичные преобразования: Дробь должна быть целым числом. Обозначим , г де t – целое число . Отсюда z = 2t – 3. Последовательно возвращаемся к неизвестным x и y . y = 3∙(2t – 3) – t = 5t – 9, x = y + z = 5t – 9 + 2t – 3 = 7t – 12. Ответ: x = 7t – 12, y = 5t – 9, где t Z . Положим ,
Слайд 7
Использование формул Теорема. Уравнение a 1 x 1 + a 2 x 2 + … + a n x n = b разрешимо в целых числах тогда и только тогда, когда d │ b , где d = НОД ( a 1, a 2 ,…, a n ). Теорема. Пусть уравнение ax + by= c разрешимо в Z и пара ( x 0 ; y 0 ) является частным решением этого уравнения. Тогда множеством всех решений в Z данного уравнения является множество пар ( x; y ) , где Следствие. Пусть а и b взаимно просты и ( x 0 y 0 ) какое-нибудь решение уравнения ax + by = c (*) Тогда формулы x = x 0 – b ∙ t , y = y 0 + a ∙ t при t є Z дают все решения уравнения (*).
Слайд 8
Пример 81. (МГУ, 1969). Остаток от деления некоторого натурального числа n на 6 равен 4, остаток от деления n на 15 равен 7. Чему равен остаток от деления n на 30? Решение. Из условия задачи следует, что существует натуральное число k такое, что n = 6k + 4. 2 k – 5l = 1. (*) Для решения этого уравнения найдем какое-нибудь частное решение в целых (не обязательно неотрицательных) числах. Подбором в качестве такого частного решения можно взять, например, k = -2 , l = -1 . Согласно следствия уравнение (*) имеет решения k = -2 +5t, l = -1 + 2t, где t є Z. Чтобы числа k и l были неотрицательными, параметр t должен принимать натуральные значения. Теперь имеем n = 6 ∙ (5t – 2) +4 = Ответ: 22. Аналогично имеем , n = 15l + 7, где l є N. Исключая из этих двух равенств n , получим уравнение 30t – 8 = 30(t – 1) + 22.
Слайд 9
Пример 83. Решить в целых числах уравнение 127 x – 52y + 1 = 0. Решение. Преобразуем отношение коэффициентов при неизвестных. Прежде всего, выделим целую часть неправильной дроби Правильную дробь заменим равной ей дробью Тогда получим Проделаем такие же преобразования с полученной в знаменателе неправильной дробью . Повторяя те же рассуждения для дроби , получим
Слайд 10
Мы получили выражение, которое называется конечной цепной или непрерывной дробью. Отбросив последнее звено этой цепной дроби – одну пятую, превратим получающуюся при этом новую цепную дробь в простую и вычтем ее из исходной дроби Приведем полученное выражение к общему знаменателю и отбросим его 127 ∙ 9 – 52 ∙ 22 + 1 = 0. 127 x -52y + 1 = 0 x = 9, y = 22 x = 9 +52t , y = 22 + 127 t , где t є Z . Ответ: x = 9 +52t , y = 22 + 127 t , где t є Z .
Слайд 11
7.2. Нелинейные уравнения Метод разложения на множители вынесение общих множителей за скобку Пример 84. Решить в целых числах уравнение 2 x 3 + xy – 7 = 0 . Решение. Приведем данное уравнение к виду x(2x 2 + y) = 7 Так как 7= 1 ∙ 7 = 7 ∙ 1 = -1 ∙ (-7) = -7 ∙ (-1), то рассмотрим четыре системы уравнений: Из каждой системы получаем решения. Ответ: (1; 5); (-1; -9); (7; -97); (-7; -99).
Слайд 12
Применение формул сокращенного умножения Пример 85. Найти все пары натуральных чисел, разность квадратов которых равна 55. Решение. Запишем условие задачи в виде уравнения n 2 – k 2 = 55 или (n – k)(n + k) = 55. Так как n + k > 0 , то n – k > 0 , причем n + k > n – k. Поскольку 55 = 1 ∙ 55 = 5 ∙ 11 то возможны два случая Решая эти уравнения, получим два ответа: n = 28, k = 27 и n = 8, k = 3. Ответ: (28; 27); (8; 3).
Слайд 13
Использование параметра Пример 88. Решить в целых числах уравнение 2 x 2 – 2yx + 9x + y = 2. Решение. Перепишем уравнение в виде 2 x 2 – x(2y – 9) + y – 2 + a = a и разложим левую часть уравнения на множители как квадратный трехчлен относительно х . Находим дискриминант D = 4y 2 – 44y + 97 – 8a. Очевидно, если , 97 – 8a = 121 , то дискриминант будет полным квадратом. При этом a = -3 и Отсюда x 1 = 0,5 и x 2 = y – 5 . Уравнение принимает вид (2x – 1)(x – y + 5) = -3 . Рассмотрите самостоятельно решение последнего уравнения. Ответ: (1; 9); (-1; 3); (2; 8); (0; 2).
Слайд 14
Метод решения относительно одной переменной выделение целой части Пример 89. (МГУ, 1997). Найти все пары целых чисел x и у, удовлетворяющие уравнению 3xy + 14x + 17y + 71 = 0. Решение. Выразим из данного уравнения у через х: При этом следует отметить, что величина 3x + 17 ≠ 0 (так как x – целое число). Выделим из дроби в правой части этого равенства правильную алгебраическую дробь (у которой степень числителя меньше степени знаменателя): Умножим обе части последнего равенства на 3:
Слайд 15
Метод «спуска» метод конечного «спуска» Пример 96. Решить в целых числах уравнение 2x 2 – 5y 2 = 7. Решение. Так как 2x 2 – четное число, а 7 – нечетное, то 5y 2 должно быть нечетным, т.е. у – нечетное. Пусть , y = 2z + 1, где z є Z , тогда данное уравнение можно переписать в виде x 2 – 10z 2 – 10z = 6. Отсюда видно, что x должно быть четным. Пусть , x = 2m , тогда последнее уравнение примет вид 2m 2 – 5z(z + 1) = 3 , что невозможно, так как число z(z + 1) – четно, а разность двух четных чисел не может быть равна нечетному числу. Таким образом, данное уравнение не имеет решений в целых числах. Ответ: нет решений.
Слайд 16
Поскольку числа 3у и 14 – целые, то 3x +17 должно быть делителем числа 25 : 3x + 17 = ±1; ±5; ±25 – всего 6 возможностей. Отсюда для x получаем три возможных значения: –4, –6, –14 (в остальных трех случаях x не является целым). Соответствующие значения у равны –3, –13, –5. Ответ: (-4; -3); (-6; -13); (-14; -5). Замечание. В данном примере суть выделения целой части состоит в избавлении переменной x из числителя (сравните с примером 77). В решении был использован прием домножения обеих частей равенства на коэффициент при x в знамена- теле. Этот прием домножения также удобно использовать при решении уравнений методом разложения на множители.
Слайд 17
Параметризация уравнения Пример 99. Решить в целых числах уравнение x 3 + y 3 + z 3 = 2 . Решение. Положим x = a + b, y = a – b. Так как x 3 + y 3 = 2a 3 + 6ab 2 , то исходное уравнение принимает вид 2a 3 + 6ab 2 + z 3 = 2. Положив a = 1, получим z 3 = -6b 2 . Считаем теперь b = 6t 2 Отсюда x = 1 + 6t 2 , y = 1 -6t 2 , z = -6t 2 . Таким образом, получено бесконечное множество решений исходного уравнения, соответствующих целочисленным значениям параметра t . Ответ: x = 1 + 6t 2 , y = 1 -6t 2 , z = -6t 2 , где t є Z
Слайд 18
Функционально-графический метод Пример 100. (МИОО 2010). Найти все пары натуральных k и n таких, что k < n и ( n ) k = ( k ) n . Решение. 1 . Преобразуем исходное равенство: k ln n = n ln k 2.
Слайд 19
откуда следует k = 1 или , k = 2, причем для каждого k может найтись не более одного значения n , удовлетворяющего уравнению в паре с этим значением k . 3. В случае k = 1 из данного уравнения получаем n = 1, ч то не соответствует условию k < n . 4. В случае k = 2 получаем уравнение , n 2 = 2 n , решение которого легко находится подбором: n = 4, причем в силу выше- сказанного это единственное решение n > e . Ответ: k = 2 , n = 4 .
Слайд 20
7.3. Неравенства Использование области определения Пример 102. (МГУ, 1973). Найти все целые числа x , удовлетворяющие неравенству Решение. Допустимые значения x определяются системой неравенств Подставляем последовательно найденные значения x в неравенство, предварительно его упростив.
Слайд 21
1. x = 1. Тогда 2. х = 2. Тогда 3. х = 3. Тогда Ответ: 2; 3.
Слайд 22
Использование монотонности Пример 103. (МГУ, 1976). Найти все целые z , удовлетворяющие неравенству Решение. Допустимые значения z определяются из системы Заметим, что левая часть неравенства увеличивается с ростом z , а правая – уменьшается. Это обстоятельство позволяет упростить перебор. В силу сделанного выше замечания, необходимости в проверке значений z = 3, 4, 5, 6 нет. Эти числа решениями не являются. Ответ: -1, 0, 1.
Слайд 23
Использование ограниченности Пример 104. (МГУ, 1996). Найти все целочисленные решения неравенства Решение. Целые решения будем искать из двух ограничений системы Первое неравенство выполняется при x = 3, 4, 5, 6. Но из этих значений исходному неравенству удовлетворяет только x = 3 . При x = 0, 1, 2 первое неравенство не выполняется. При x = -1 выполняется как первое не- равенство, так и исходное неравенство. При x = -2 первое неравенство не выполняется. При остальных значениях x = -3, -4, … первое неравенство не разрешимо, так как левая часть неравенства x(x 2 – 5) ≥ 3 будет отрицательной. Ответ: -1; 3.
Слайд 24
Метод интервалов Пример 105. (МГУ, 1972). Определить, сколько целочисленных решений имеет неравенство Решение. Методом интервалов по 2 n определяем решения (см. рис. 2): Дальше подбором находим n = ± 2, ± 3, ±4 или n = ±8, ±9,±10, ±11, ±12. Ответ: 16 решений.
Слайд 25
7.4. Уравнения и неравенства Уравнение с одной неизвестной Пример 107. Может ли квадратное уравнение ax 2 + bx + c = 0 с целыми коэффициентами иметь дискриминант, равный 23? Первое решение. Рассмотрим уравнение b 2 – 4ac = 23. Так как 23 – нечетное число, а 4 ac – четное, то b 2 и, следовательно, b – нечетное число, т.е . b = 2k – 1, k є Z . Тогда (2k – 1) 2 – 4ac = 23; 4(k 2 – k -ac) = 22. Последнее уравнение не имеет решений, так как 22 не делится на 4. Второе решение. Перепишем уравнение b 2 – 4ac = 23 в виде b 2 – 25 = 4ac – 2 и разложим обе части уравнения на множители: (b – 5)(b + 5) = 2(2ac – 1). (*) Так как в правой части уравнения – число четное, то и в левой – тоже четное, следовательно, b – 5 и b + 5 одновременно четные (докажите), т.е. b – 5 =2m, b – 5 = 2k. Левая часть уравнения (*) делится на 4 , а правая – нет, поэтому уравнение b 2 -4ac = 23 не имеет решений в целых числах. Третье решение. Перепишем уравнение b 2 -4ac = 23 в виде b 2 = 4ac + 23 или b 2 = 4(ac + 5) + 3. Получили, что квадрат натурального числа при делении на 4 дает остаток 3 , что невозможно (докажите). Ответ: не может.
Слайд 26
Показательные уравнения Теорема. Если остаток от деления a 1 на b равен r 1 , а остаток от деления a 2 на b равен r 2 , то остаток от деления a 1 +a 2 на b равен остатку от деления r 1 + r 2 на b . Опорная задача. Докажите, что оста- ток от деления на 3 числа 5 k равен 1 , если k четно, и 2 , если k нечетно.
Слайд 27
Неравенства Пример 121. (МИОО 2010). Найти все пары (x; y) целых чисел, удовлетворяющие системе неравенств : Решение. Выделяя полные квадраты, получаем: Из первого и второго неравенства системы: Подставляя x = 12 в систему, получаем: Ответ: (12; -8).
Слайд 28
Уравнения, содержащие функцию «целая часть числа» [ x ] Целой частью числа x называется наибольшее целое число, не превосходящее х . Свойства целой части числа: 1) Из равенства [y] = n следует, что a) n – целое число; б) y = n + α , где 0 ≤ α < 1; в) 0 ≤ y – n < 1. 2) Если [ u ] = [ v ] то u = m + α , v = m+ β , где 0 ≤ α < 1 и 0 ≤ β <1 , поэтому u – v = α – β и -1 < u – v < 1. 3 ) Если [ x + y ] = x то x – целое число и 0 ≤ y < 1. 4) Если n – целое число, то [ n + x ] = n + [ x ].
Система неравенств диагностической работы 12.09.2010
№ задачи в базе 561
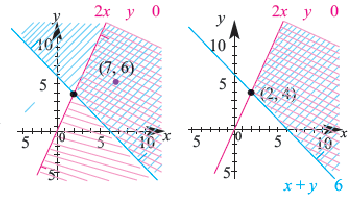
Найти все пары (x; y) целых чисел, удовлетворяющих системе неравенств
{(x^2+y^2<18x-20y-166),(32x-y^2>x^2+12y+271) :}
Ответ: (12; -8)
Ключевые слова:
Задания ЕГЭ части 2 | Алгебра | Неравенство | Система |
ФИПИ 2023 🔥 …
Примечание: Система неравенств диагностической работы 12.09.2010
10%
Рейтинг сложности задачи:
Графическое решение
Содержание:
Системы неравенств и совокупность неравенств
Исследование. Если альпинисты увеличат скорость на 1км/ч, то путь 4 км до вершины они преодолеют быстрее чем за 2 часа. Если же они уменьшат скорость на 1 км/ч, то не смогут добраться до вершины за 2 часа. С какой скоростью движутся альпинисты? Решение: Примем за
Если скорость увеличится на 1 км/ч, то длина пройденного пути будет больше 4-х км и соответствующее неравенство примет вид:
Если скорость уменьшится на 1 км/ч, то длина пройденного пути будет меньше 4-х км и соответствующее неравенство примет вид:
По условию задачи нужно найти такое значение 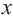
Неравенства, объединенные союзом 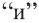
В данной задаче нужно решить систему неравенств
Если каждое неравенство системы заменить на равносильное неравенство, то получим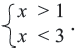
Для того, чтобы решить систему неравенств нужно найти множество решений каждого неравенства и найти пересечение этих множеств, то есть, общую часть.
Ответ: Решение системы промежуток 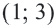
Совокупность неравенств
Задача. Наргиз и Эльшан играют в игру, построенную на числах. Каждый берег карточку с числом и прибавляет к нему 5. Если ответ будет меньше 10-ти или же больше 15-ти, то владелец карточки зарабатывает очко. Выразите с помощью неравенства ситуацию, когда Эльшан взяв одну карточку заработал очко.
Решение: Пусть число на карге будет 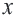
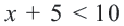
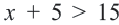
Решением данной совокупности неравенств будет множество: 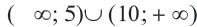
Пример.
Решите неравенство:
Решение: Для того, чтобы произведение двух множителей было положительным, нужно чтобы множители были одинакового знака. То есть, множители 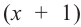

Данное неравенство сводится к решению совокупности:
Решение 1-ой системы совокупности:
Геометрическое изображение:
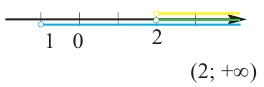
Геометрическое изображение:
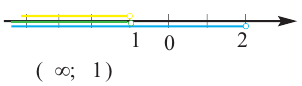
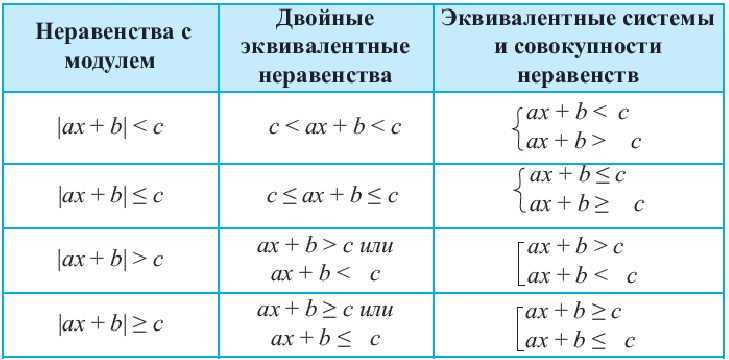
Неравенства, содержащие переменную под знаком модуля
Система неравенств, совокупность неравенств
Пример 2.
Решение:
Пример 3.
Решение:
Линейные неравенства с двумя переменными
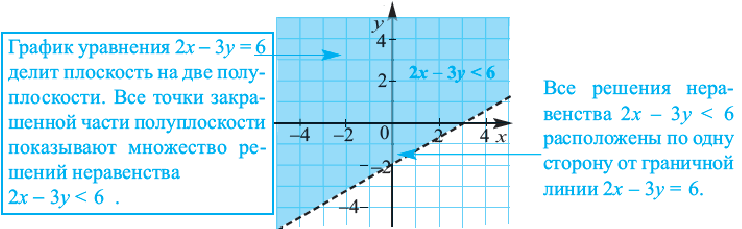
Неравенства вида 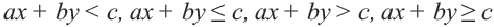
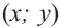
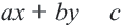
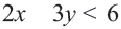
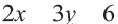
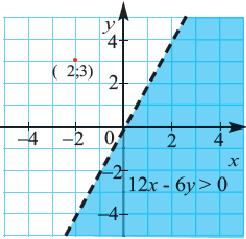
• Чтобы убедиться в правильности выбора полуплоскости, соответствующей решению неравенства, выбираются пробные точки в каждой из полуплоскостей. Закрашивается та полуплоскость, в которой расположена точка, удовлетворяющая данному неравенству.
• Если неравенство выражается знаками 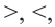
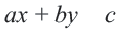
• Если неравенство выражается знаками 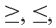
Пример 1.
1. Решим неравенство относительно переменной 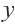
2. Нарисуем график уравнения 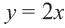
3. Проверим неравенство в точке 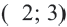
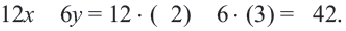
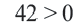
Пример 2. Напишите неравенство, соответствующее графику.
1. Определим уравнение 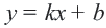
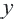
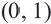
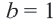
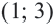
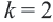
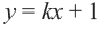
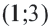
Уравнение линии границы: 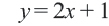
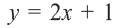
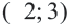
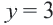
Левая часть 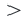
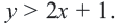
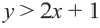
- Заказать решение задач по высшей математике
Прикладные задания.
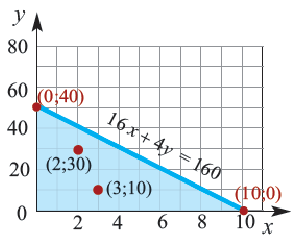
Пример 1. Билет в театр для взрослых стоит 16 манат, а детский – 4 манат. Деньги, вырученные от продажи билетов в кассе, составляют не более 160 манат. Определите различные варианты количества проданных билетов. Числовые информации и переменные, соответствующие условию задачи:
Математическая запись:
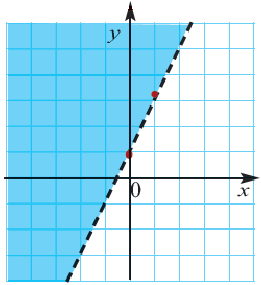
1. Чтобы решить неравенство, выразим 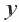
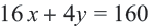
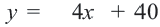
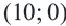
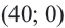
2. Закрасим фигуру, заданную графиком и осями координат.
3. Любые целые значения 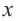
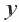
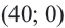
Системы линейных неравенств с двумя переменными
Решением системы линейных неравенств с двумя переменными называется множество пар чисел 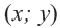
Пример 1.
1. С помощью граничной прямой 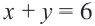
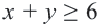
2. С помощью уравнения 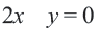
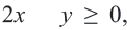
3. Множеством решений данной системы неравенств будет часть плоскости, закрашенная обоими цветами.
4. Выберем отсюда одну точку, например 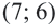
Каждая пара 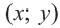
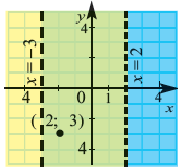
Пример 2. Изобразите графически на координатой плоскости неравенство
1. Запишем двойное неравенство 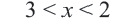
2. Изобразим неравенство 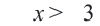

3. Изобразим неравенство 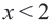
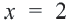
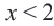
4. Часть плоскости, соответствующая неравенствам 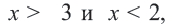
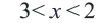
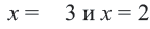
5. Проверка: проверим в точке
График системы линейных неравенств, соответствующий реальным жизненным ситуациям, в большинстве случаев строится в первой четверти координатной плоскости.
Пример 3. На одном из двух конвейеров производят кастрюли из нержавеющей стали, а на другом медные кастрюли. Если каждый из конвейеров работает на полную мощность, то ежедневно производится не более 300 кастрюль. Так как потребность в кастрюлях из нержавеющей стали больше, их ежедневно производят больше чем медных, но не меньше 150 штук. Напишите систему неравенств, показывающую ежедневное количество производимых кастрюль, и изобразите графически.
Решение: 1) Примем за 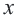
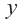
2) Решение неравенства 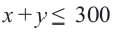
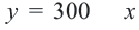
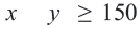
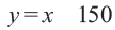
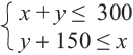
3. С помощью пробной точки 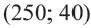
Решение системы неравенств найдено верно.
- Квадратные неравенства
- Точка, прямая и плоскость в пространстве
- Тригонометрические функции произвольного угла
- Теоремы синусов и косинусов
- Система координат в пространстве
- Иррациональные числа
- Действительные числа
- Решение уравнений высших степеней
Система неравенств записывается следующим образом:
Решить данную
систему неравенств, означает найти совокупность всех значений переменной
удовлетворяющих
каждому
неравенству системы.
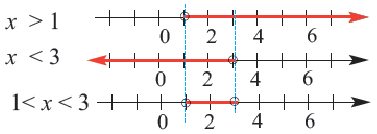
Рассмотрим конкретный пример. Пусть нам дана система неравенств:
Для её решения воспользуемся числовой прямой и изобразим интервалы значений переменной
соответствующие каждому неравенству системы:
Синим цветом обозначена совокупность всех значений переменной
,
удовлетворяющих неравенству
,
оранжевым цветом – неравенству
и зелёным цветом – неравенству
.
Чтобы найти решение системы неравенств нужно объединить интервалы значений переменной
удовлетворяющие
каждому
неравенству системы. Из рисунка (смотрим слева направо) следует, что:
Полученный результат также можно изобразить графически на числовой оси:
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha может решать и более сложные системы неравенств, чем только что рассмотренная. Обращаем Ваше внимание, что символ
≥
необходимо вводить в калькулятор как >= (в виде двух символов больше и равно), а символ
≤
– как <=.
Это хитрая задача. Возведем левую часть неравенства в квадрат и найдем экстремум :
[math]big [(x^2-6x+18)(y^2+14y+50)]’_x=2(x-3)(y^2+14y+50)=0[/math]
[math]big [(x^2-6x+18)(y^2+14y+50)]’_y=2(y+7)(x^2-6x+18)=0[/math]
квадратные уравнения в скобках – суть параболы, не имеющие пересечения с осями (корни мнимые)
Остается система
[math]x-3=0[/math]
[math]y+7=0[/math]
Откуда [math]x=3 , ;quad y=-7[/math]
Если подставить в [math](x^2-6x+18)(y^2+14y+50)[/math] , то получим [math]9[/math] или [math]3^2[/math]
То есть условию задачи подчиняется только одна точка экстремума (легко показать, что это глобальный минимум).
Следовательно, ответ [math]x=3, ; quad y=-7[/math]