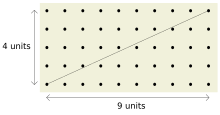
В «лесу», составленном на координатной плоскости из точек с целочисленными координатами, из начала координат «видны» только «деревья» со взаимно простыми координатами.
Взаимно простые числа — целые числа, не имеющие никаких общих делителей, кроме ±1. Равносильное определение[1]: целые числа взаимно просты, если их наибольший общий делитель (НОД) равен 1.
Например, взаимно просты числа 14 и 25, так как у них нет общих делителей; но числа 15 и 25 не взаимно просты, так как у них имеется общий делитель 5.
Для указания взаимной простоты чисел 


Это понятие было введено в книге VII «Начал» Евклида. Для определения того, являются ли два числа взаимно простыми, можно использовать алгоритм Евклида.
Понятие взаимной простоты естественным образом обобщается на любые евклидовы кольца[⇨].
Попарно взаимно простые числа[править | править код]
Если в наборе целых чисел любые два числа взаимно просты, то такие числа называются попарно взаимно простыми (или просто попарно простыми[3]). Для двух чисел понятия «взаимно простые» и «попарно простые» совпадают, для более чем двух чисел свойство попарной простоты более сильно, чем ранее определённое свойство взаимной простоты (в совокупности) — попарно простые числа будут и взаимно простыми, но обратное неверно[3]. Примеры:
- 8, 15 — не простые, но взаимно простые.
- 6, 8, 9 — взаимно простые (в совокупности) числа, но не попарно простые.
- 8, 15, 49 — попарно простые и взаимно простые (в совокупности).
Если числа 
- НОД
НОД
НОД
НОД
,
- где НОД – наибольший общий делитель.
Свойства[править | править код]
Все упомянутые в этом разделе числа подразумеваются целыми, если не оговорено иное.
- Дробь является несократимой тогда и только тогда, когда её числитель и знаменатель взаимно просты.
Таблица взаимной простоты чисел до 30[править | править код]
В каждой клетке стоит наибольший общий делитель её координат, и соответствующие взаимно-простым парам координат единицы выделены тёмным. Из описанного выше свойства следует, что средняя плотность тёмных клеток при расширении таблицы до бесконечности станет равна 
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 |
| 3 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 3 |
| 4 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 4 | 1 | 2 |
| 5 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 5 |
| 6 | 1 | 2 | 3 | 2 | 1 | 6 | 1 | 2 | 3 | 2 | 1 | 6 | 1 | 2 | 3 | 2 | 1 | 6 | 1 | 2 | 3 | 2 | 1 | 6 | 1 | 2 | 3 | 2 | 1 | 6 |
| 7 | 1 | 1 | 1 | 1 | 1 | 1 | 7 | 1 | 1 | 1 | 1 | 1 | 1 | 7 | 1 | 1 | 1 | 1 | 1 | 1 | 7 | 1 | 1 | 1 | 1 | 1 | 1 | 7 | 1 | 1 |
| 8 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 8 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 8 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 8 | 1 | 2 | 1 | 4 | 1 | 2 |
| 9 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 9 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 9 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 9 | 1 | 1 | 3 |
| 10 | 1 | 2 | 1 | 2 | 5 | 2 | 1 | 2 | 1 | 10 | 1 | 2 | 1 | 2 | 5 | 2 | 1 | 2 | 1 | 10 | 1 | 2 | 1 | 2 | 5 | 2 | 1 | 2 | 1 | 10 |
| 11 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 11 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 11 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 12 | 1 | 2 | 3 | 4 | 1 | 6 | 1 | 4 | 3 | 2 | 1 | 12 | 1 | 2 | 3 | 4 | 1 | 6 | 1 | 4 | 3 | 2 | 1 | 12 | 1 | 2 | 3 | 4 | 1 | 6 |
| 13 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 13 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 13 | 1 | 1 | 1 | 1 |
| 14 | 1 | 2 | 1 | 2 | 1 | 2 | 7 | 2 | 1 | 2 | 1 | 2 | 1 | 14 | 1 | 2 | 1 | 2 | 1 | 2 | 7 | 2 | 1 | 2 | 1 | 2 | 1 | 14 | 1 | 2 |
| 15 | 1 | 1 | 3 | 1 | 5 | 3 | 1 | 1 | 3 | 5 | 1 | 3 | 1 | 1 | 15 | 1 | 1 | 3 | 1 | 5 | 3 | 1 | 1 | 3 | 5 | 1 | 3 | 1 | 1 | 15 |
| 16 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 8 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 16 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 8 | 1 | 2 | 1 | 4 | 1 | 2 |
| 17 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 17 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 18 | 1 | 2 | 3 | 2 | 1 | 6 | 1 | 2 | 9 | 2 | 1 | 6 | 1 | 2 | 3 | 2 | 1 | 18 | 1 | 2 | 3 | 2 | 1 | 6 | 1 | 2 | 9 | 2 | 1 | 6 |
| 19 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 19 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 20 | 1 | 2 | 1 | 4 | 5 | 2 | 1 | 4 | 1 | 10 | 1 | 4 | 1 | 2 | 5 | 4 | 1 | 2 | 1 | 20 | 1 | 2 | 1 | 4 | 5 | 2 | 1 | 4 | 1 | 10 |
| 21 | 1 | 1 | 3 | 1 | 1 | 3 | 7 | 1 | 3 | 1 | 1 | 3 | 1 | 7 | 3 | 1 | 1 | 3 | 1 | 1 | 21 | 1 | 1 | 3 | 1 | 1 | 3 | 7 | 1 | 3 |
| 22 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 11 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 22 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 |
| 23 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 23 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 24 | 1 | 2 | 3 | 4 | 1 | 6 | 1 | 8 | 3 | 2 | 1 | 12 | 1 | 2 | 3 | 8 | 1 | 6 | 1 | 4 | 3 | 2 | 1 | 24 | 1 | 2 | 3 | 4 | 1 | 6 |
| 25 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 25 | 1 | 1 | 1 | 1 | 5 |
| 26 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 13 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 26 | 1 | 2 | 1 | 2 |
| 27 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 9 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 9 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 27 | 1 | 1 | 3 |
| 28 | 1 | 2 | 1 | 4 | 1 | 2 | 7 | 4 | 1 | 2 | 1 | 4 | 1 | 14 | 1 | 4 | 1 | 2 | 1 | 4 | 7 | 2 | 1 | 4 | 1 | 2 | 1 | 28 | 1 | 2 |
| 29 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 29 | 1 |
| 30 | 1 | 2 | 3 | 2 | 5 | 6 | 1 | 2 | 3 | 10 | 1 | 6 | 1 | 2 | 15 | 2 | 1 | 6 | 1 | 10 | 3 | 2 | 1 | 6 | 5 | 2 | 3 | 2 | 1 | 30 |
Вариации и обобщения[править | править код]
Понятия простого числа, наибольшего общего делителя и взаимно простых чисел естественно обобщаются на произвольные евклидовы кольца, например, на кольцо многочленов или гауссовы целые числа. Обобщением понятия простого числа является «неприводимый элемент». Данное выше определение взаимно простых чисел не годится для произвольного евклидова кольца, поскольку в кольце могут быть делители единицы; в частности, НОД определяется с точностью до умножения на делитель единицы. Поэтому определение взаимно простых чисел следует модифицировать[6].
Элементы евклидова кольца называются взаимно простыми, если множество их наибольших общих делителей содержит только делители единицы.
Равносильные формулировки[6]:
Имеет также место лемма Евклида.
Практическое применение[править | править код]
Свойство взаимной простоты не только играет важную роль в теории чисел и коммутативной алгебре, но имеет ряд важных практических приложений, в частности, число зубьев на звёздочках и число звеньев цепи в цепной передаче стремятся делать взаимно простыми, что обеспечивает равномерность износа: каждый зуб звёздочки будет поочерёдно работать со всеми звеньями цепи.
Примечания[править | править код]
- ↑ 1 2 Взаимно простые числа. // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1977. — Т. 1. — С. 690.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — М.: «Мир», 1998. — С. 139. — 703 с. — ISBN 5-03-001793-3.
- ↑ 1 2 Михелович, 1967, с. 28.
- ↑ Нестеренко Ю. В. Теория чисел. — М.: Издательский центр «Академия», 2008. — С. 40. — 272 с. — ISBN 9785769546464.
- ↑ Михелович, 1967, с. 64.
- ↑ 1 2 Ларин С. В. Алгебра и теория чисел. Группы, кольца и поля: учеб. пособие для академического бакалавриата. — 2-е изд. — М.: Юрайт, 2018. — С. 92—93. — 160 с. — (Бакалавр. Академический курс). — ISBN 978-5-534-05567-2.
Литература[править | править код]
- Взаимно простые числа // Большая советская энциклопедия : в 66 т. (65 т. и 1 доп.) / гл. ред. О. Ю. Шмидт. — М. : Советская энциклопедия, 1926—1947.
- Михелович Ш. Х. Теория чисел. — 2-е изд. — М.: Высшая школа, 1967. — 336 с.
В этом статье мы расскажем о том, что такое взаимно простые числа. В первом пункте сформулируем определения для двух, трех и более взаимно простых чисел, приведем несколько примеров и покажем, в каких случаях два числа можно считать простыми по отношению друг к другу. После этого перейдем к формулировке основных свойств и их доказательствам. В последнем пункте мы поговорим о связанном понятии – попарно простых числах.
Что такое взаимно простые числа
Взаимно простыми могут быть как два целых числа, так и их большее количество. Для начала введем определение для двух чисел, для чего нам понадобится понятие их наибольшего общего делителя. Если нужно, повторите материал, посвященный ему.
Взаимно простыми будут два таких числа a и b, наибольший общий делитель которых равен 1, т.е. НОД (a, b) =1.
Из данного определения можно сделать вывод, что единственный положительный общий делитель у двух взаимно простых чисел будет равен 1. Всего два таких числа имеют два общих делителя – единицу и минус единицу.
Какие можно привести примеры взаимно простых чисел? Например, такой парой будут 5 и 11. Они имеют только один общий положительный делитель, равный 1, что является подтверждением их взаимной простоты.
Если мы возьмем два простых числа, то по отношению друг к другу они будут взаимно простыми во всех случаях, однако такие взаимные отношения образуются также и между составными числами. Возможны случаи, когда одно число в паре взаимно простых является составным, а второе простым, или же составными являются они оба.
Это утверждение иллюстрирует следующий пример: составные числа -9 и 8 образуют взаимно простую пару. Докажем это, вычислив их наибольший общий делитель. Для этого запишем все их делители (рекомендуем перечитать статью о нахождении делителей числа). У 8 это будут числа ±1, ±2, ±4, ±8, а у 9 – ±1, ±3, ±9. Выбираем из всех делителей тот, что будет общим и наибольшим – это единица. Следовательно, если НОД (8, −9)=1, то 8 и -9 будут взаимно простыми по отношению друг к другу.
Взаимно простыми числами не являются 500 и 45, поскольку у них есть еще один общий делитель – 5 (см. статью о признаках делимости на 5). Пять больше единицы и является положительным числом. Другой подобной парой могут быть -201 и 3, поскольку их оба можно разделить на 3, на что указывает соответствующий признак делимости.
На практике довольно часто приходится определять взаимную простоту двух целых чисел. Выяснение этого можно свести к поиску наибольшего общего делителя и сравнению его с единицей. Также удобно пользоваться таблицей простых чисел, чтобы не производить лишних вычислений: если одно из заданных чисел есть в этой таблице, значит, оно делится только на единицу и само на себя. Разберем решение подобной задачи.
Условие: выясните, являются ли взаимно простыми числа 275 и 84.
Решение
Оба числа явно имеют больше одного делителя, поэтому сразу назвать их взаимно простыми мы не можем.
Вычисляем наибольший общий делитель, используя алгоритм Евклида: 275=84·3+23, 84=23·3+15, 23=15·1+8, 15=8·1+7, 8=7·1+1, 7=7·1.
Ответ: поскольку НОД (84, 275) =1, то данные числа будут взаимно простыми.
Как мы уже говорили раньше, определение таких чисел можно распространить и на случаи, когда у нас есть не два числа, а больше.
Взаимно простыми целые числа a1, a2, …, ak, k>2 будут тогда, когда они имеют наибольший общий делитель, равный 1.
Иными словами, если у нас есть набор некоторых чисел с наибольшим положительным делителем, большим 1, то все эти числа не являются по отношению друг к другу взаимно обратными.
Возьмем несколько примеров. Так, целые числа −99, 17 и −27 – взаимно простые. Любое количество простых чисел будет взаимно простым по отношению ко всем членам совокупности, как, например, в последовательности 2, 3, 11, 19, 151, 293 и 667. А вот числа 12, −9, 900 и −72 взаимно простыми не будут, потому что кроме единицы у них будет еще один положительный делитель, равный 3. То же самое относится к числам 17, 85 и 187: кроме единицы, их все можно разделить на 17.
Обычно взаимная простота чисел не является очевидной с первого взгляда, этот факт нуждается в доказательстве. Чтобы выяснить, будут ли некоторые числа взаимно простыми, нужно найти их наибольший общий делитель и сделать вывод на основании его сравнения с единицей.
Условие: определите, являются ли числа 331, 463 и 733 взаимно простыми.
Решение
Сверимся с таблицей простых чисел и определим, что все три этих числа в ней есть. Тогда их общим делителем может быть только единица.
Ответ: все эти числа будут взаимно простыми по отношению друг к другу.
Условие: приведите доказательство того, что числа −14, 105, −2 107 и −91 не являются взаимно простыми.
Решение
Начнем с выявления их наибольшего общего делителя, после чего убедимся, что он не равен 1. Поскольку у отрицательных чисел те же делители, что и у соответствующих положительных, то НОД (−14, 105, 2 107, −91) =НОД (14, 105, 2 107, 91). Согласно правилам, которые мы привели в статье о нахождении наибольшего общего делителя, в данном случае НОД будет равен семи.
Ответ: семь больше единицы, значит, взаимно простыми эти числа не являются.
Основные свойства взаимно простых чисел
Такие числа имеют некоторые практически важные свойства. Перечислим их по порядку и докажем.
Если разделить целые числа a и b на число, соответствующее их наибольшему общему делителю, мы получим взаимно простые числа. Иначе говоря, a: НОД (a, b) и b: НОД (a, b) будут взаимно простыми.
Это свойство мы уже доказывали. Доказательство можно посмотреть в статье о свойствах наибольшего общего делителя. Благодаря ему мы можем определять пары взаимно простых чисел: достаточно лишь взять два любых целых числа и выполнить деление на НОД. В итоге мы должны получить взаимно простые числа.
Необходимым и достаточным условием взаимной простоты чисел a и b является существование таких целых чисел u0 и v0, при которых равенство a·u0+b·v0=1 будет верным.
Начнем с доказательства необходимости этого условия. Допустим, у нас есть два взаимно простых числа, обозначенных a и b. Тогда по определению этого понятия их наибольший общий делитель будет равен единице. Из свойств НОД нам известно, что для целых a и b существует соотношение Безу a·u0+b·v0=НОД (a, b). Из него получим, что a·u0+b·v0=1. После этого нам надо доказать достаточность условия. Пусть равенство a·u0+b·v0=1 будет верным, в таком случае, если НОД (a, b) делит и a, и b, то он будет делить и сумму a·u0+b·v0, и единицу соответственно (это можно утверждать, исходя из свойств делимости). А такое возможно только в том случае, если НОД (a, b)=1, что доказывает взаимную простоту a и b.
В самом деле, если a и b являются взаимно простыми, то согласно предыдущему свойству, будет верным равенство a·u0+b·v0=1. Умножаем обе его части на c и получаем, что a·c·u0+b·c·v0=c. Мы можем разделить первое слагаемое a·c·u0+b·c·v0 на b, потому что это возможно для a·c, и второе слагаемое также делится на b, ведь один из множителей у нас равен b. Из этого заключаем, что всю сумму можно разделить на b, а поскольку эта сумма равна c, то c можно разделить на b.
Если два целых числа a и b являются взаимно простыми, то НОД (a·c, b)=НОД (c, b).
Докажем, что НОД (a·c, b) будет делить НОД (c, b), а после этого – что НОД (c, b) делит НОД (a·c, b), что и будет доказательством верности равенства НОД (a·c, b)=НОД (c, b).
Поскольку НОД (a·c, b) делит и a·c и b, а НОД(a·c, b) делит b, то он также будет делить и b·c. Значит, НОД (a·c, b) делит и a·c и b·c, следовательно, в силу свойств НОД он делит и НОД (a·c, b·c), который будет равен c·НОД (a, b)=c. Следовательно, НОД (a·c, b) делит и b и c, следовательно, делит и НОД (c, b).
Также можно сказать, что поскольку НОД (c, b) делит и c, и b, то он будет делить и c, и a·c. Значит, НОД (c, b) делит и a·c и b, следовательно, делит и НОД (a·c, b).
Таким образом, НОД (a·c, b) и НОД (c, b) взаимно делят друг друга, значит, они являются равными.
Если числа из последовательности a1, a2, …, ak будут взаимно простыми по отношению к числам последовательности b1, b2, …, bm (при натуральных значениях k и m), то их произведения a1·a2·…·ak и b1·b2·…·bm также являются взаимно простыми, в частности, a1=a2=…=ak=a и b1=b2=…=bm=b, то ak и bm – взаимно простые.
Согласно предыдущему свойству, мы можем записать равенства следующего вида: НОД (a1·a2·…·ak, bm) =НОД (a2·…·ak, bm) =…=НОД (ak, bm) =1. Возможность последнего перехода обеспечивается тем, что ak и bm взаимно просты по условию. Значит, НОД (a1·a2·…·ak, bm) =1.
Обозначим a1·a2·…· ak=A и получим, что НОД (b1·b2·…· bm, a1·a2·…·ak) =НОД (b1·b2·…· bm, A)= НОД (b2·…·b·bm, A)=… =НОД (bm, A) =1. Это будет справедливым в силу последнего равенства из цепочки, построенной выше. Таким образом, у нас получилось равенство НОД (b1·b2·…·bm, a1·a2·…·ak) =1, с помощью которого можно доказать взаимную простоту произведений a1·a2·…·ak и b1·b2·…·bm
Это все свойства взаимно простых чисел, о которых бы мы хотели вам рассказать.
Понятие попарно простых чисел
Зная, что из себя представляют взаимно простые числа, мы можем сформулировать определение попарно простых чисел.
Попарно простые числа – это последовательность целых чисел a1, a2, …, ak, где каждое число будет взаимно простым по отношению к остальным.
Примером последовательности попарно простых чисел может быть 14, 9, 17, и −25. Здесь все пары (14 и 9, 14 и 17, 14 и −25, 9 и 17, 9 и −25, 17 и−25) взаимно просты. Отметим, что условие взаимной простоты является обязательным для попарно простых чисел, но взаимно простые числа будут попарно простыми далеко не во всех случаях. Например, в последовательности 8, 16, 5 и 15 числа не являются таковыми, поскольку 8 и 16 не будут взаимно простыми.
Также следует остановиться на понятии совокупности некоторого количества простых чисел. Они всегда будут и взаимно, и попарно простыми. Примером может быть последовательность 71, 443, 857, 991. В случае с простыми числами понятия взаимной и попарной простоты будут совпадать.
Калькулятор взаимно простых чисел
Онлайн калькулятор определит являются ли число взаимно простыми, путем нахождения наибольшего общего делителя чисел.
Для определения взаимно простых чисел необходимо указать количество и ввести числа.
Нажмите кнопку рассчитать и калькулятор укажет как определить взаимно простые числа.
Определение взаимно простых чисел
Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен 1.
Ниже описано как определить являются ли числа 35 и 40 взаимно простыми.
- 1 Находим наибольший общий делитель чисел: НОД(35, 40)=5.
- 2 Наибольший общий делитель ≠ 1 следовательно числа не взаимно простые.
Пример Определить являются ли 77 и 20 взаимно простыми числами
 .
.
Примеры взаимно простых чисел
Рассмотрим на примере как определить взаимно простые числа.
Пример Являются ли числа 42 и 55 взаимно простыми
 .
.
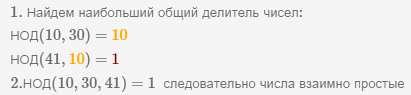
Определим что 3 числа 10, 30, 41 являются взаимно простыми.
Пример Проверить что числа 10, 30, 41 взаимно просты
 .
.
Смотрите также
Другие страницы
- Простые множители
- Разложение на множители онлайн
- Взаимно простые числа
- Проверка онлайн на взаимно простые числа
Взаимно простые числа
Разберемся, что такое взаимно простые числа. Это такие числа, которые не имеют общих делителей, кроме 1 или -1. Можно сформулировать и по другому. У взаимно простых чисел наибольший общий делитель (НОД) равен единице.

Например, числа 5 и 4 – взаимно простые, потому что число 5 имеет делители 1 и 5, а делители четверки: 1, 2 и 4. Общий делитель у них – это единица, а значит, они взаимно просты.
По второму определению: наибольший общий делитель чисел 5 и 4 равен 1, НОД(5,4) = 1, а значит они взаимно простые.
Взаимно простые числа от 1 до 100
Приведем примеры взаимно простых чисел.
2 и 99,
15 и 16,
28 и 57,
29 и 31,
12 и 1,
59 и 97 и т. д.
Чтобы образовывать взаимно простые числа, должно быть, по крайней мере, два числа.
Как проверить, являются ли взаимно простыми числа
По определению взаимно простых чисел, если числа имеют 1 или -1 в качестве единственного общего множителя, то такие числа будут взаимно простыми.
Решим примеры.
Являются ли взаимно простыми числа:
35 и 40
Решение:
Раскладываем оба числа на простые множители.
Множители первого числа: 35 = 5 х 7.
Множители второго числа: 40 = 2 х 2 х 2 х 5.
Общий множитель данных чисел равен 5. Следовательно, 35 и 40 не являются взаимно простыми.
77 и 20
Решение:
Множители первого числа: 77= 7 х 11.
Множители второго числа: 20 = 2 х 2 х 5.
НОД чисел 77 и 20 равен единице, а значит эти числа будут взаимно простыми.
231 и 280
Решение:
При разложении обоих чисел на множители получаем:
231 = 3 х 7 х 11.
280 = 2 х 2 х 2 х 5 х 7.
Наибольший общий делитель этих чисел равен 7, а значит они не взаимно простые.
Свойства взаимно простых чисел
Свойство 1: Число 1 взаимно простое с каждым числом.
Свойство 2: Все простые числа взаимно просты между собой.
Поскольку каждое простое число имеет только два делителя: 1 и само число, единственным общим делителем двух простых чисел будет 1. Например, 11 и 17 – это два простых числа. Множители 11 равны 1, 11, а делители 17 равны 1, 17. Единственный общий делитель равен 1 и, следовательно, они взаимно просты.
Свойство 3: Любые два последовательных числа всегда взаимно просты.
Рассмотрим любые два последовательных числа, например, 2 и 3, 3 и 4 или 14 и 15. У всех этих чисел общий делитель – это единица.
Свойство 4: Сумма любых двух взаимно простых чисел всегда взаимно проста с их произведением.
2 и 3 взаимно просты. Их сумма равна 5 (2+3), а произведение – 6 (2х3). Следовательно, числа 5 и 6 взаимно просты.
Решение примеров.
Являются ли взаимно простыми числа 21 и 24
21 и 24 не являются взаимно простыми числами, потому что имеют множитель равный 3. ( 21 = 3 х 7, 24 = 2 х 2 х 2 х 3).
Являются ли взаимно простыми числа 13 и 11
13 и 11 взаимно простые числа, потому что это простые числа (свойство 2).
Являются ли взаимно простыми числа 17 и 18
17 и 18 взаимно простые числа, потому что это два последовательных числа (свойство 3).
В чем разница между простыми и взаимно простыми числами?
Простое число определяется как число, которое не имеет множителя, кроме 1 и самого себя.
Но взаимно простые числа считаются парами, и два числа взаимно просты, если их общий делитель равен только 1. Их НОД равен единице.
Таким образом, взаимно простые числа – это обязательно 2 или более чисел. Составные числа также могут быть взаимно простыми.
Пример
Числа 25 и 26 – это составные числа (25 = 5 х 5, 26 = 2 х 13). Но они взаимно просты, т.к. это последовательные числа (свойство 3).
Эта статья – экскурс в мир математики и взаимно простых чисел. Но не стоит их путать с «простыми». Далее вы узнаете почему взаимно простые числа являются простыми, чем они отличаются и для чего они нужны. Будут рассмотрены все характеристики и особенности взаимно простых чисел. Все свойства и особые случаи будут рассмотрены на наглядных примерах. Шаг за шагом мы подойдем к доказательствам и рассмотрим такую вещь, как попарно простые числа.
Что такое взаимно простые числа?
Определение
Взаимно простым числом называют целое число, которое имеет с другим числом наибольший общий делитель – 1 (единицу).
Возьмем 2 простых числа и определим их, как a и b. Взаимно простыми будут те числа, которые имеют 1, как наибольший общий делитель (НОД). (a, b) = 1
У двух взаимно простых чисел будет один положительный общий делитель. И делитель будет равен 1. Только два таких числа имеют два общих делителя 1 и -1.
Пример 1:
Простым примером взаимно простых будут числа 5 и 11. Почему? Давайте посмотрим на делители этих чисел: 5 делится на 5 и на 1, а число 11 можно разделить на 11 и на 1 (без остатка). Общим положительным делителем этих двух чисел будет единица. Единица – самый большой общий делитель двух чисел – значит, что они будут взаимно простые.
Но не только простые числа могут быть взаимно простыми по отношению друг к другу. Условие взаимной простоты образуется и между составными числами.
Определение
Составное число – число, делители которого отличаются от самого числа и единицы).
Ситуаций, где в паре чисел одно является простым, а второе составным, или оба являются составными – не редкость. И мы научимся с ними работать.
Пример 2:
Возьмем для примера два числа: -9 и 8. Мы утверждаем, что они образуют взаимно простую пару. Так ли это? Давайте проверим. Для того, чтобы это доказать (или опровергнуть) нужно найти их общий делитель. Распишем делители каждого из чисел в ряд:
Для числа 8 делителями будут: ±1, ±2, ±4, ±8;
Для числа 9 делителями будут: ±1, ±3, ±9.
Выбираем из рядов делителей общий и самый большой: ±1. Из этого следует, что, если наибольший общий делитель (НОД) чисел 8 и -9 это единица, то они взаимно простые друг к другу.
А вот числа 45 и 500 не будут таковыми. Почему? Помимо единицы, они имеют еще один общий делитель 5, и он больше единицы (вспоминаем правило про наибольший общий делитель). 5 больше 1, значит о взаимной простоте чисел не может быть и речи.
Аналогичная ситуация с числами 201 и 3. Если расписать все из общие делители, то там будет число 3. А 3 больше 1, значит и в этой ситуации нет взаимной простоты между числами.
Как показывает практика, решение задач на определение взаимной простоты встречаются часто и не только в школьных учебниках. Вся их суть сводится к одному: поиск наибольшего общего делителя этих чисел и сравнение его с единицей. Расписывать все делители будет очень проблематично, в некоторых случаях. Например, число 234 567. Для упрощения задачи есть несколько вариантов:
- Использование таблицы простых чисел. Если одно из чисел в ней есть, то оно простое и делится на себя и единицу;
- Алгоритм Евклида.
Разберем решение таковой задачи на примере.
Нет времени решать самому?
Наши эксперты помогут!
Геометрический алгоритм Евклида
Данный алгоритм часто применяется для решения задач по нахождению наибольшего общего делителя двух чисел (целых). Алгоритм работает следующим образом:
Возьмем 2 целых числа и обозначим их как a и b. Представим числа в виде отрезков. Каждый из них имеет свое числовое значение.
- Из большего отрезка нужно вычесть меньший;
- Больший отрезок заменим полученной разностью величин;
- Продолжаем вычитать из большего отрезка меньший, пока они не станут равны;
- Процедуру вычитания проводим до тех пор, пока отрезки не станут равны.
Если в итоге получаем отрезки равной величины, то значит, что они соизмеримы. И последний полученный результат — это и есть показатель их наибольшей общей меры.
Если общей меры отрезков нет, то процесс будет продолжаться бесконечно.
Метод использования алгоритма Евклида. Найдем НОД двух чисел 1071 и 462. Представим и в виде буквенных обозначений. Пусть, a = 1071, b = 462.
Из 1071 вычтем 462 кратное число раз. Это можно сделать 2 раза. Количество раз, которое можно вычесть наименьшее число из большего обозначим буквой q.
1071 – 462 ⋅ 2 = 147
Из наименьшей величины (все, как в алгоритме Евклида) вычтем кратное число раз разность.
462 – 174 ⋅ 3 = 21
И снова проделываем аналогичное вычисление.
147 – 21 ⋅ 7 = 0
Последний остаток в данном примере = 21. Следовательно, НОД для чисел 1071 и 462 =21. Делаем вывод, что 21 > 1, значит данные числа не будут взаимно простыми.
Теперь можно попробовать применить данную формулу на практике.
Пример
Условие: нужно выяснить, являются ли числа 275 и 84 взаимно простыми или нет.
И то, и то число, точно имеют больше 1 делителя. Сразу сказать, что они взаимно простые нельзя. Для вычисления НОД применим алгоритм Евклида:
275 = 84 ⋅ 3 + 23 , 84 = 23 ⋅ 3 + 15 , 23 = 15 ⋅ 1 + 8 , 15 = 8 ⋅ 1 + 7 , 8 = 7 ⋅ 1 + 1 , 7 = 7 ⋅ 1
Ответ: Так как, НОД чисел 84 и 275 равен 1, то взаимная простота чисел доказана.
Если есть числовой ряд с большим количеством чисел и у всех у них наибольшим делителем является единица, то они будут проявлять свойство взаимной простоты по отношению друг к другу.
Количество чисел не имеет значение. Их может быть сколько угодно много. Главное – наибольший общий делитель – единица. Для наглядности, возьмем ряд чисел: 2, 3, 11, 19, 667. Они все делятся только сами на себя и на 1. Из это следует, что их свойство взаимной простоты доказано.
Примеры
Условие: определить наличие взаимной простоты у чисел 331, 463, 733 или опровергнуть ее.
Решение:
Используем для решения таблицу простых чисел. Проверим данные числа и таблицу. Да, в таблице можно встретить
их все. Это значит, что общим делителем чисел будет 1.
Ответ: все числа находятся в таблице простых чисел. Их наибольший делить -1. Значит все они взаимно
простые друг к другу.
Докажите, что следующие числа не являются взаимно простыми (105, — 14, — 2007, — 91).
Решение:
- Нужно найти общий наибольший делитель. Это можно сделать любым удобным способом;
- Вспоминаем, что отрицательные числа имеют те же делители, что и положительные.
- НОД для всех чисел будет = 7.
Ответ: 7 больше 1. Значит, что числа не будут являться взаимно простыми.
Свойства взаимно простых чисел и их доказательства
У таких чисел есть ряд свойств и особенностей. Давайте посмотрим на них, разберем на практике и докажем их правдивость.
Свойства
Свойство — 1
Если разделить числа a и b на их общий делитель, то полученные числа будут взаимно простыми.
a : НОД (a, b) и b: НОД (a, b) будут взаимно простыми.
Свойство — 2
Условие взаимной простоты чисел – существование целых чисел [mathrm{U}_{0}] и [mathrm{V}_{0}] при значениях которых, следующее равенство будет верно:
[a cdot u_{0}+b cdot v_{0}=1]. Эта формула называется – соотношение Безу.
Доказательство свойства 2:
Пусть данное равенство будет верно a · u0 + b · v0 = 1. Так как, НОД чисел (a, b) делит и одно и второе, то исходя из свойств делимости НОД может делить сумму чисел a · u0 + b · v0. Значит он может делить их и на 1. Такое условие будет возможно только в том случае, если НОД (a, b) будет равен 1. Из этого следует, что НОД = 1. Что и требовалось доказать.
Свойства
Свойство 3
Если число a и число b будут взаимно простыми, а их произведение обозначим, как c. В
такой ситуации, a · с будет делиться на b. Из этого следует, что и c будет делиться на
b.
Так, как числа a, b являются взаимно простыми, то исходя из Свойства 2, можно получить
следующее равенство: [a u_{0}+b v_{0}=1].
Если каждую часть уравнения перемножить на c, получим следующее:
[mathrm{acu}_{0}+mathrm{bcv}_{0}=mathrm{c}].
Слагаемое суммы [mathrm{acu}_{0}+mathrm{bc} mathrm{v}_{0}] можно разделить на число b. Так как,
число ac делится на b. Второе слагаемое тоже будет делиться на число b. Почему? Потому
что,
один из множителей будет равен числу b.
Вывод: вся сумма будет делиться на число b, так как,
[mathrm{acu}_{0}+mathrm{bcv}_{0}=mathrm{c}].
Следовательно, c будет делиться на b.
Свойство 4
Если числа a, b являются взаимно простыми, то и НОД (ac, b) будет равен НОД (c, b)
Наибольший общий делитель (ac, b) делит и ac и число b.
Следовательно, он будет делить и произведение чисел bc. Это значит, что НОД (ac, b) делит и ac
и bc. Исходя
их свойств НОД, он будет делить и НОД чисел (ac, bc), который по своим свойствам равен числу c.
Отсюда следует, что наибольший общий делитель чисел (ac, b) делит и b и c, а значит, что и
делит НОД (c, b).
Свойство 5
Возьмём числовую последовательность [a_{1}, a_{2}, ldots, a_{k}]. В ней все числа взаимно простые с каждым
из числовой последовательности [b_{1}, b_{2}, ldots, b_{m}] (Числа k и m – натуральные), то
произведения [a_{1} cdot a_{2} cdot ldots a_{k}] и [b_{1} cdot b_{2} cdot ldots b_{m}] будут взаимно простыми.
Если, [a_{1}=a_{2}=ldots=a_{k}=a] и [b_{1}=b_{2}=ldots=b_{m}=b], то [a_{k}] и [mathrm{b}_{mathrm{m}}] являются взаимно простыми числами.
Попарно простые числа
Так как, мы уже знаем, что такое взаимно простые числа, то понять, что значит взаимно простые числа попарны будет проще.
Определение
Попарно простые числа – последовательность целых чисел (a 1, a 2, … , a k a1, a2, …, ak), где каждое следующее число будет взаимно простым по отношению ко всем остальным.
Пример 1:
Возьмем числовой ряд 14, 9, 17, 25. Все пары, которые могут быть составлены из этих чисел будут взаимно простыми: 17 – 25, 9 – 25, 14 – 9, 14 – 17, 9 – 17, 14 – 25.
Главным условием для попарных чисел является условие взаимной простоты. При этом, взаимно простые числа не всегда будут попарно простыми.
Пример 2:
В числовой последовательности 8, 16, 5, 15 числа не будут попарными. Почему? Числа 16 и 8 – не являются взаимно простыми.
Возьмем совокупность и некоторое число простых чисел, особенность таковых в том, что они в любом случае будут, как попарно, так и взаимно простыми. Если рассматривать ситуацию с простыми числами, то свойства взаимной и попарной простоты совпадают.

